Study on the Mechanical Properties of Door-Shaped Rebar of a CRTS III Slab Track Under Temperature Load
Abstract
1. Introduction
2. Model Establishment and Experimental Verification
2.1. Finite Element Calculation Model of CRTS III Slab Ballastless Track
2.2. Model Parameters
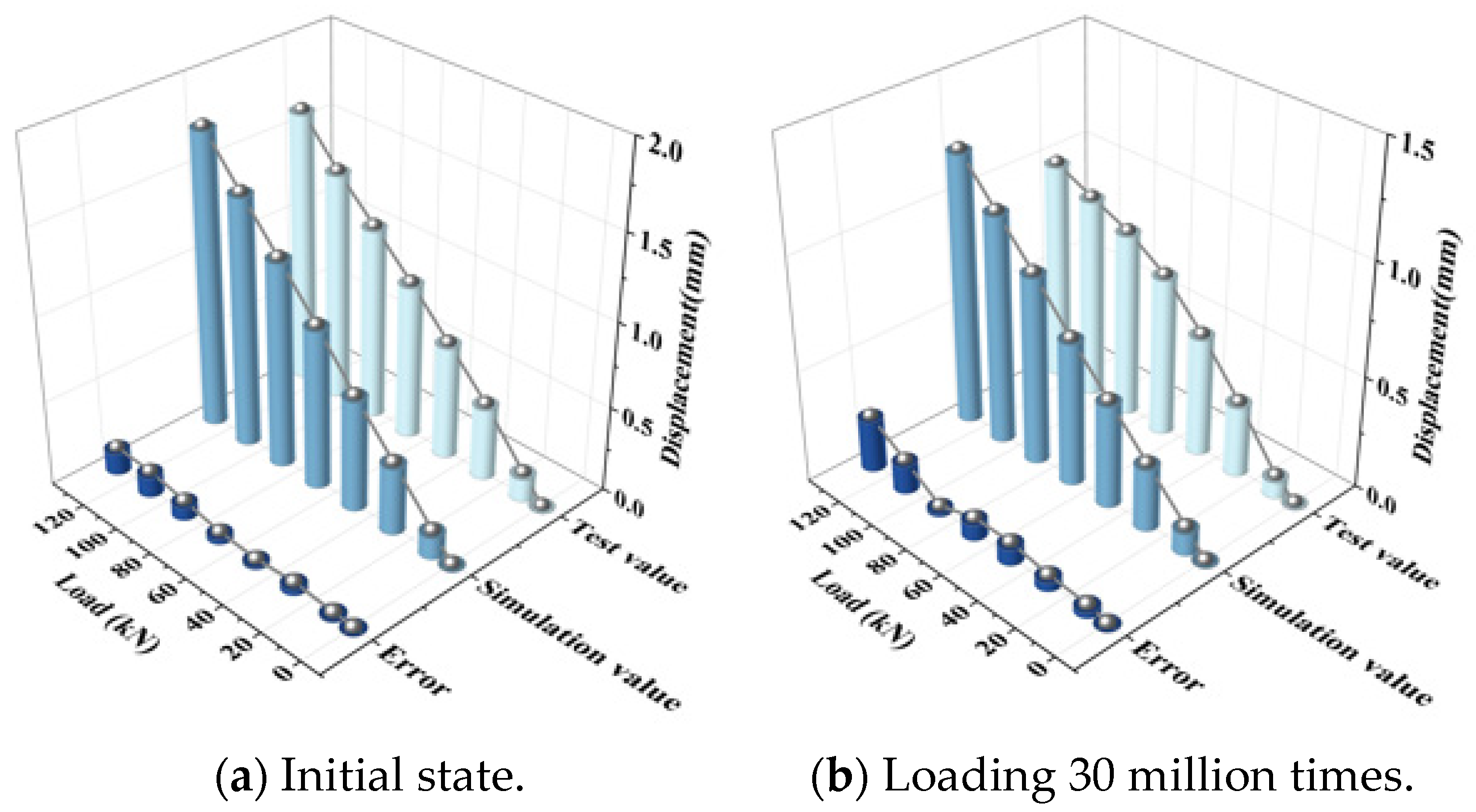
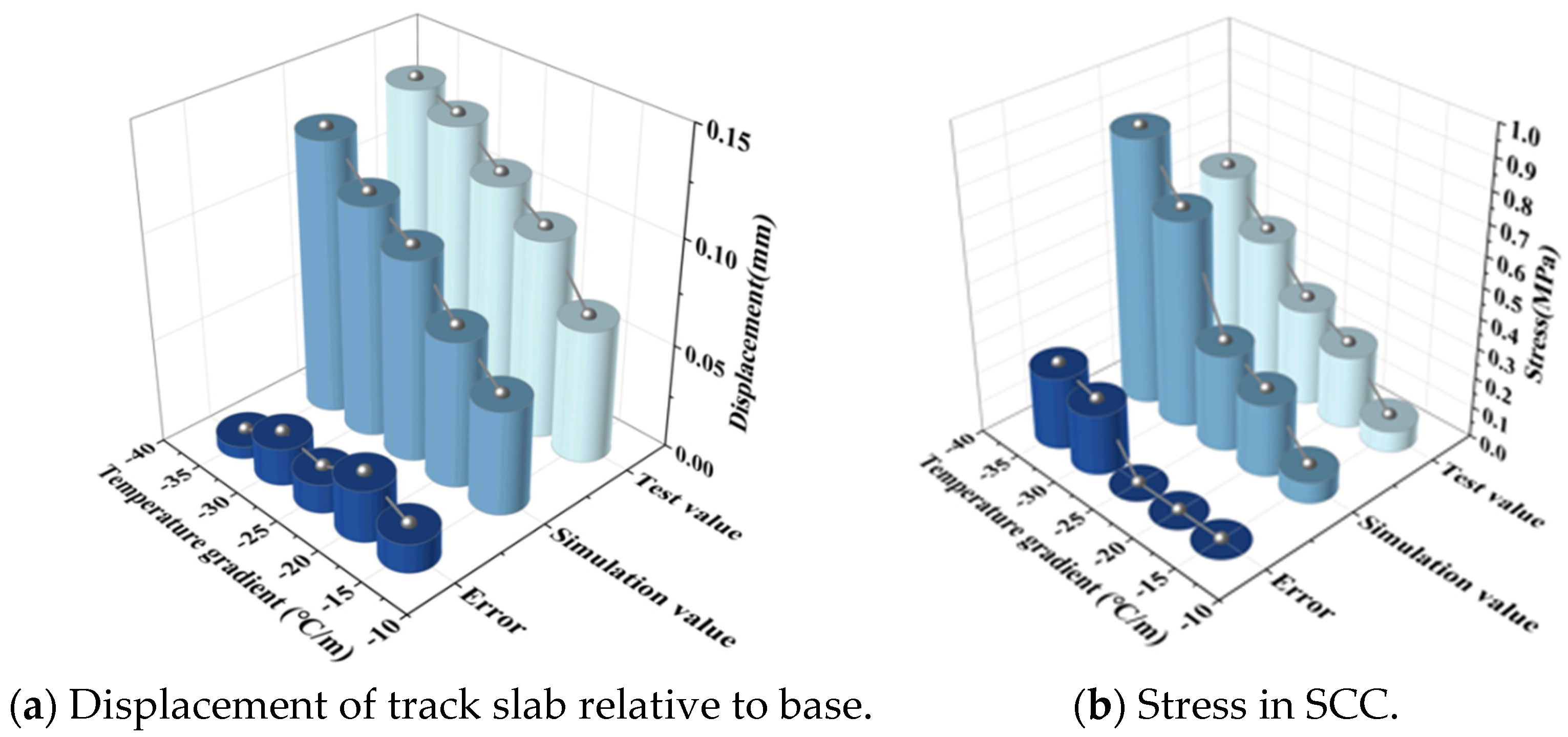
2.3. Experimental Verification of Model Calculation Reliability
2.3.1. Indoor Full-Scale Static Load Test
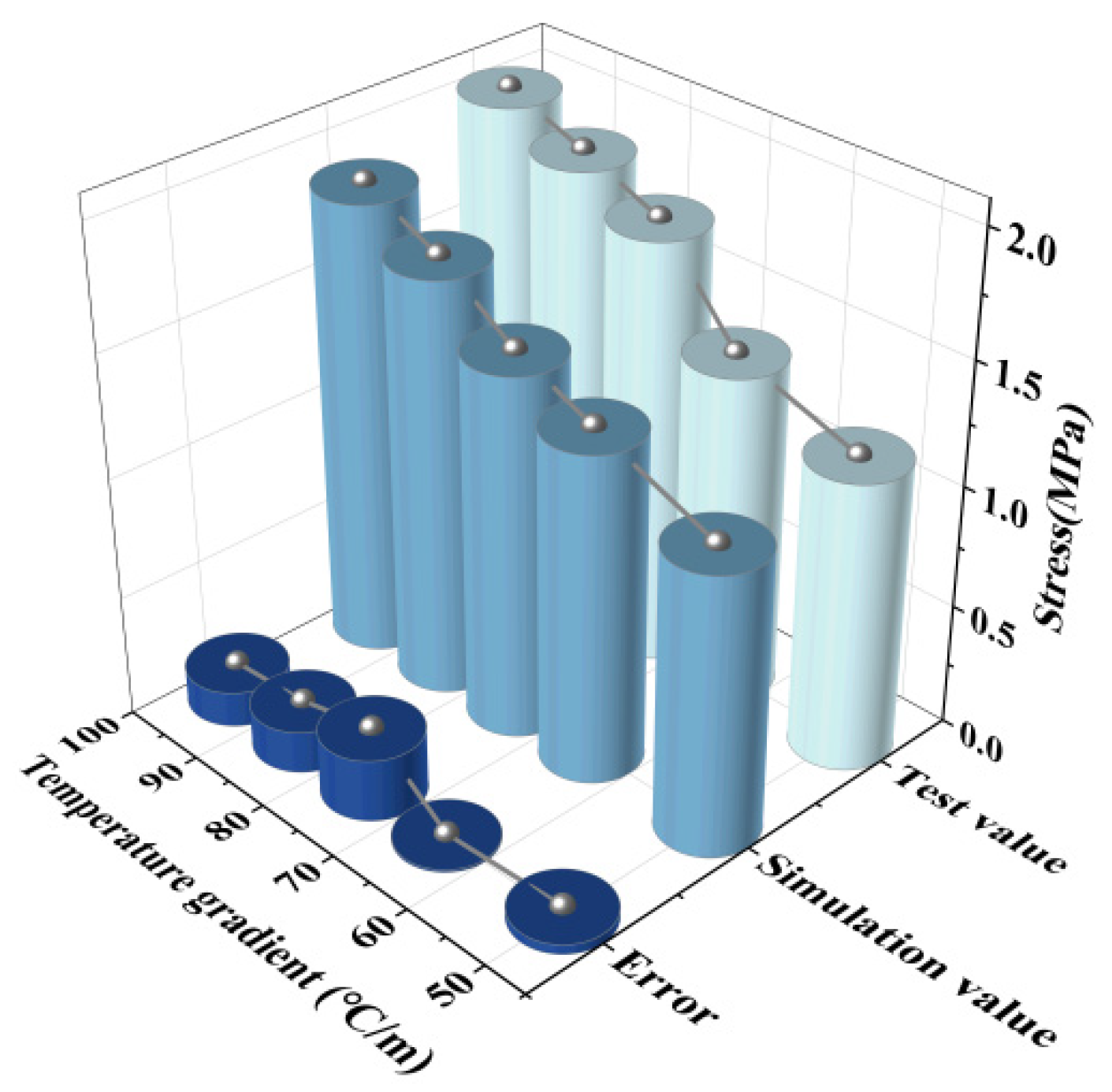
2.3.2. Comparative Verification
3. Analysis of Mechanical Characteristics of Track Structure Under Temperature Load
3.1. Load Parameters
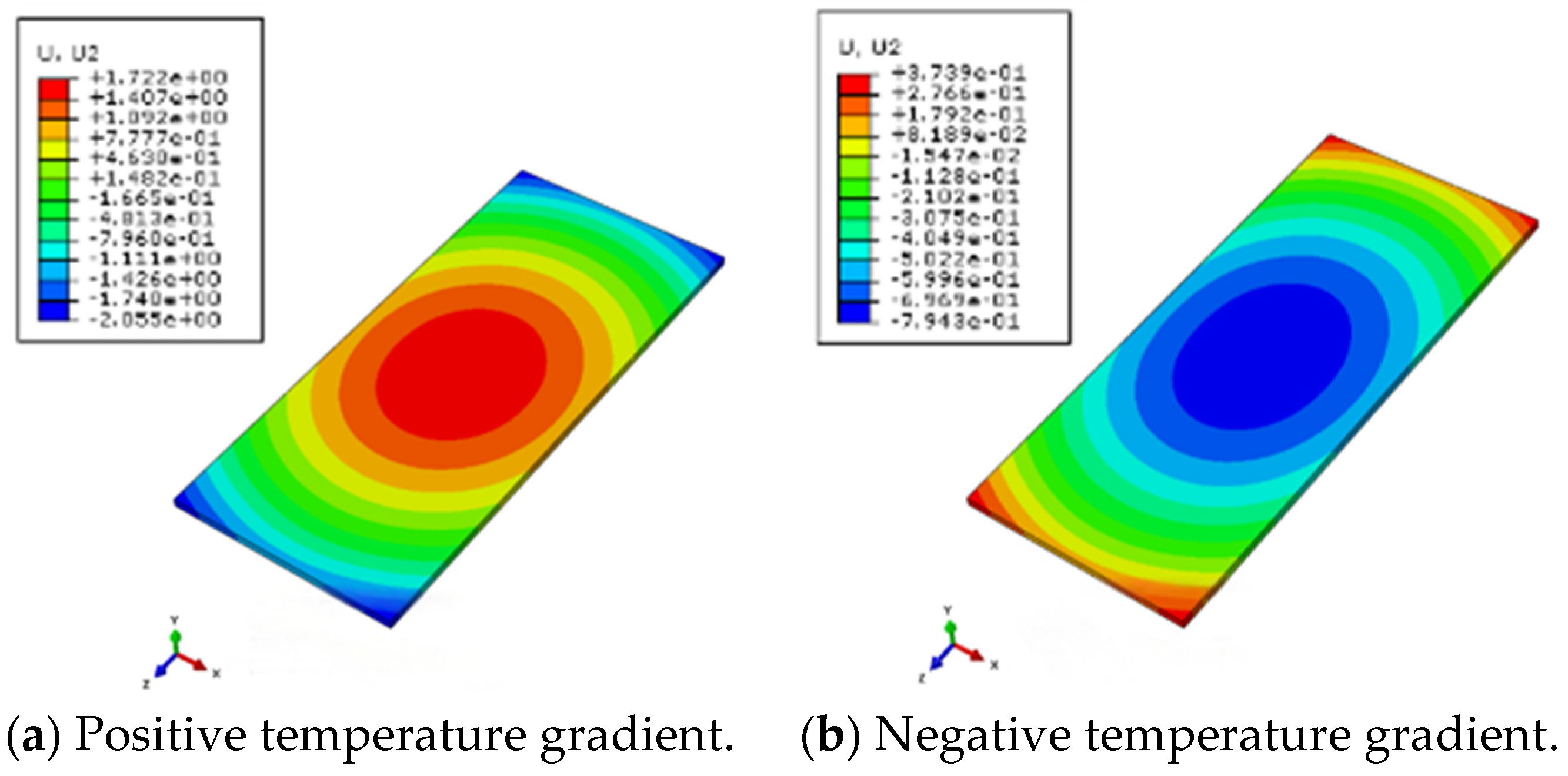
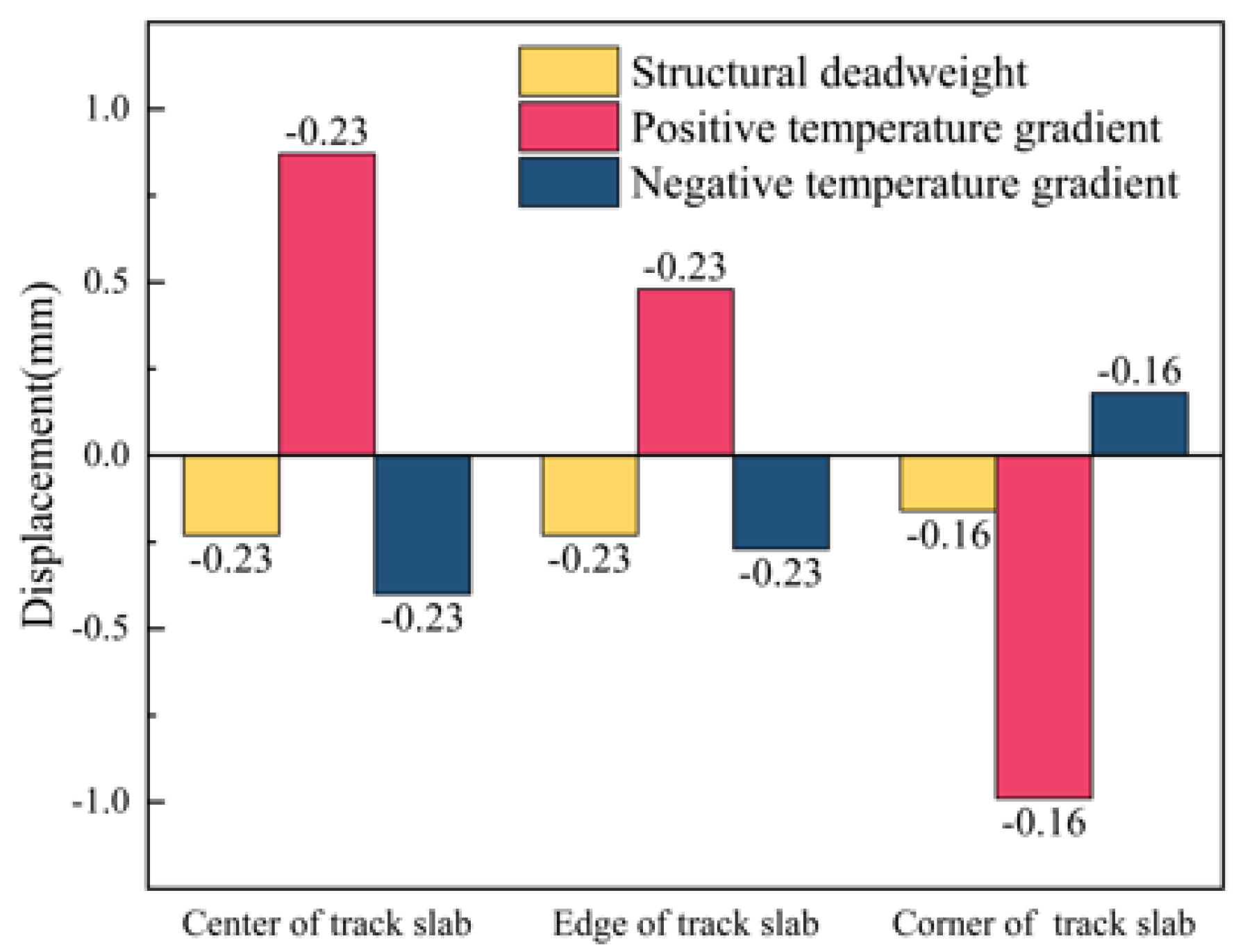
3.2. Analysis of Vertical Displacement Changes in Track Structure
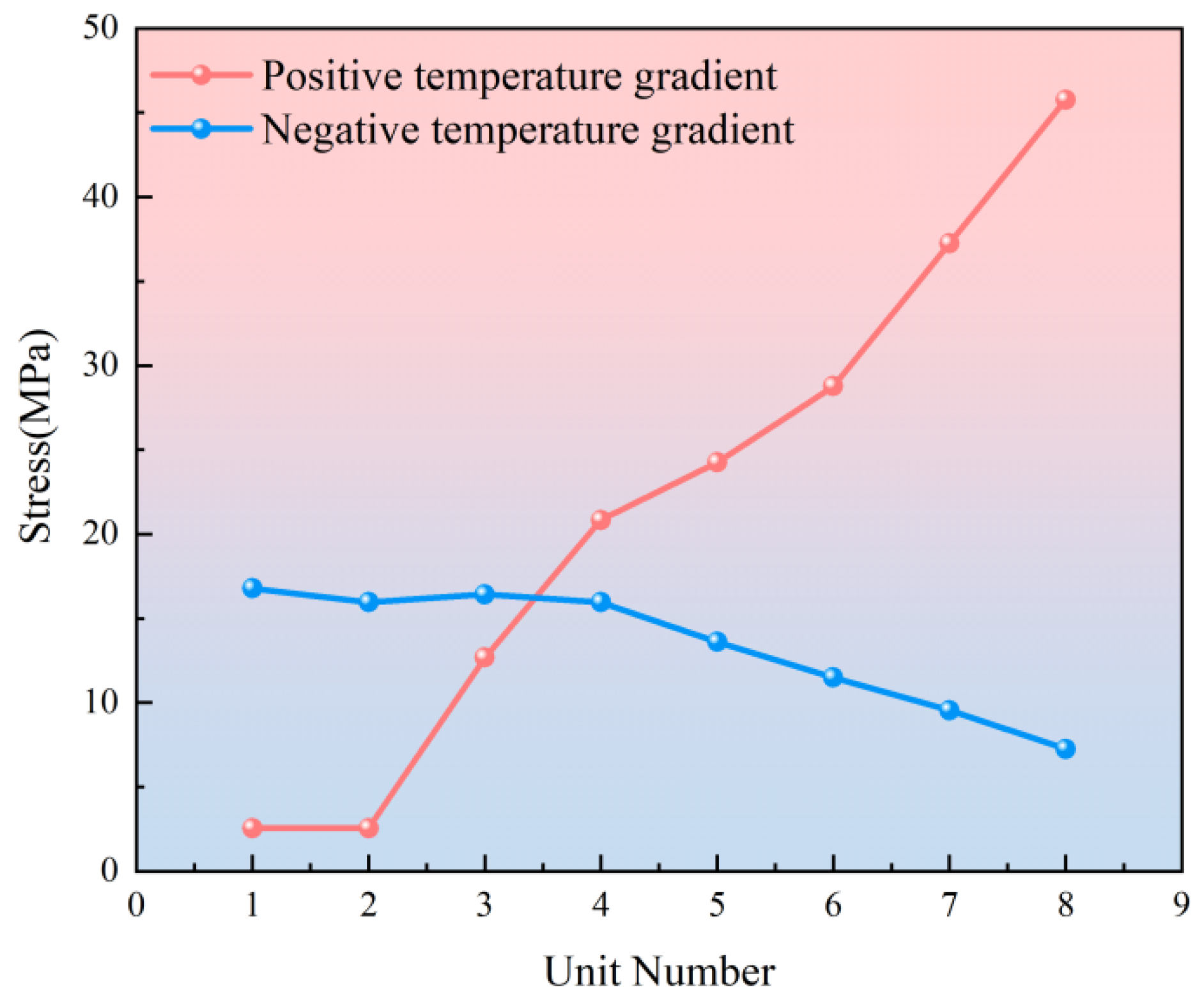
3.3. Analysis of Stress Changes of Door-Shaped Rebar
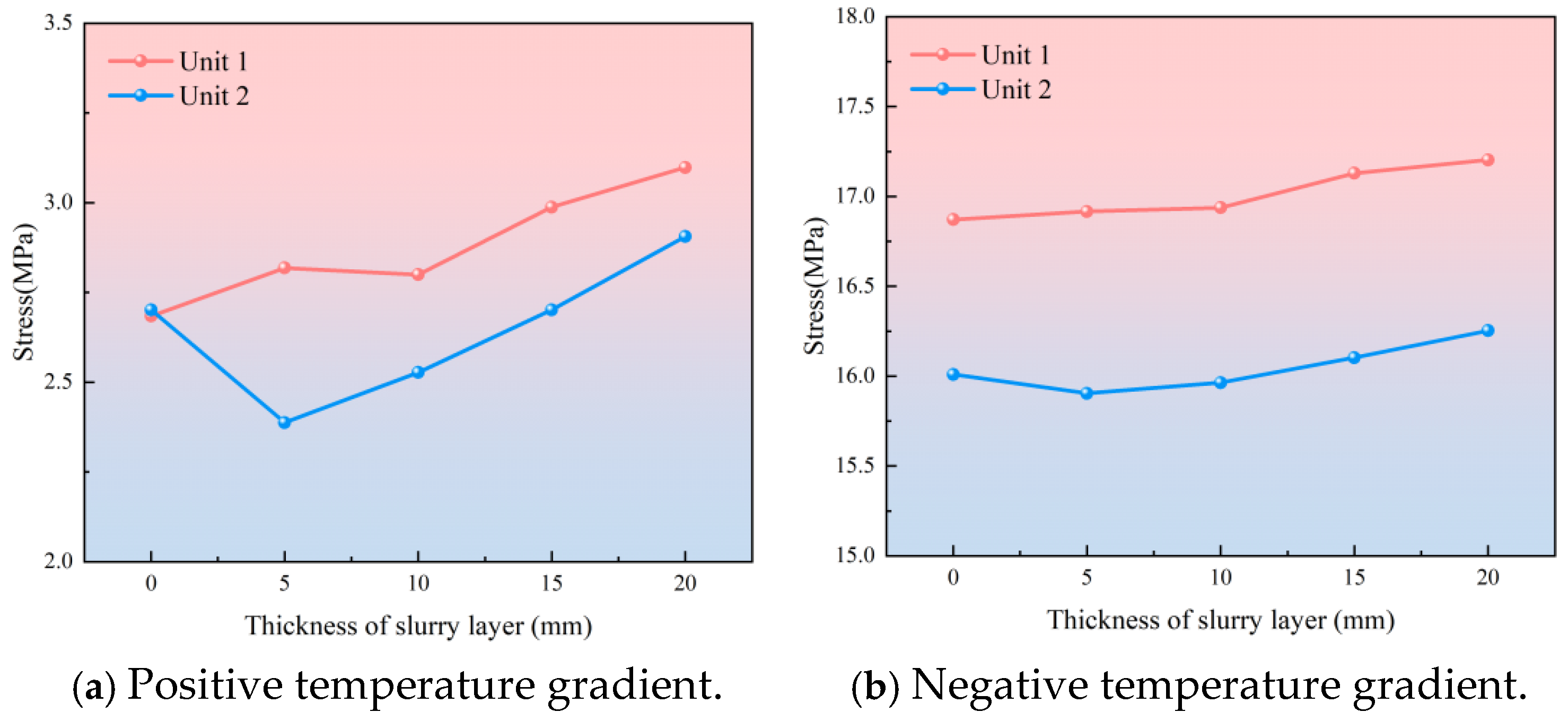
4. Stress Distribution of Door-Shaped Rebar When Defects Exist in SCC
5. Stress Distribution Law of Door-Shaped Rebar Under Interface Separation Condition
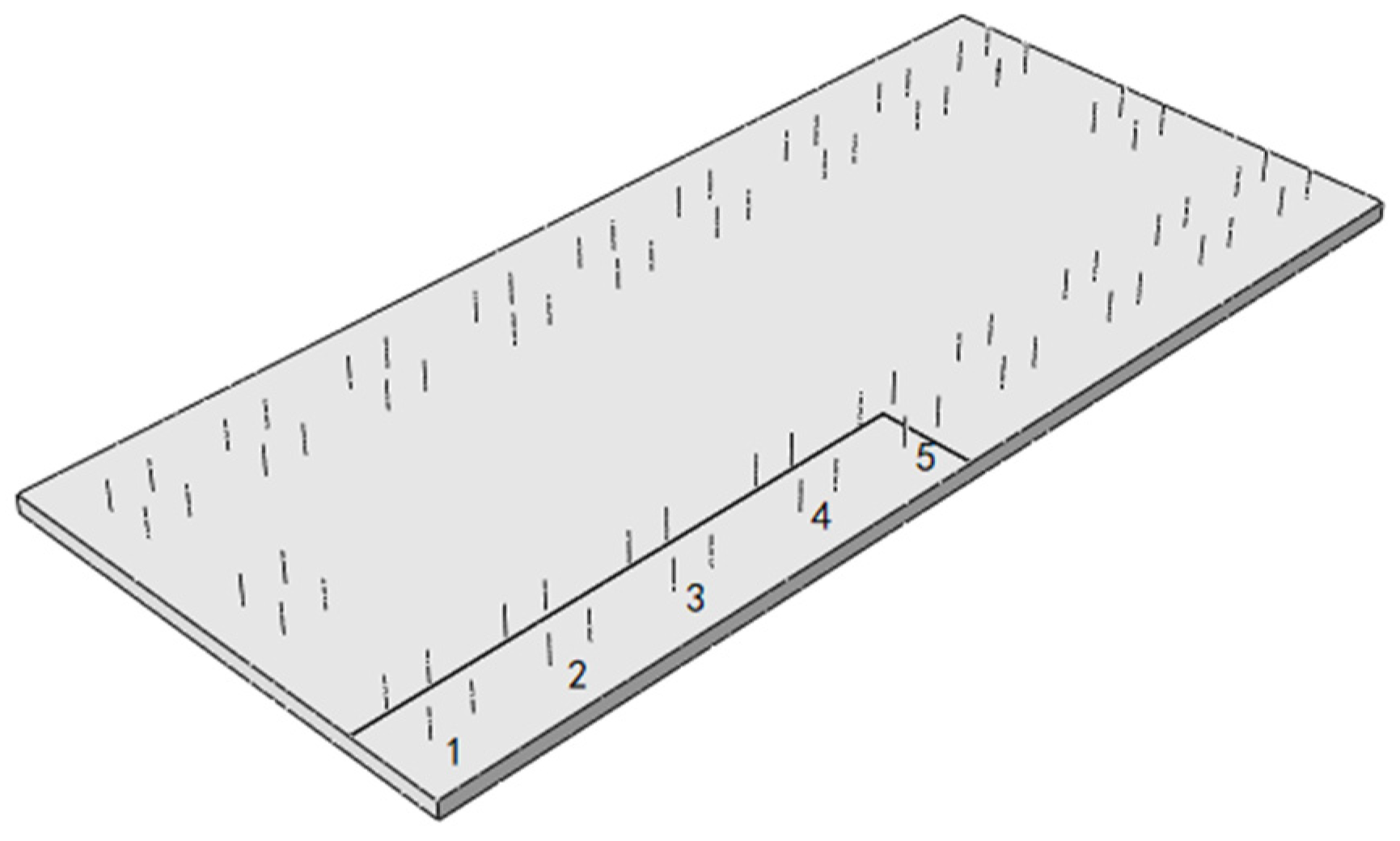
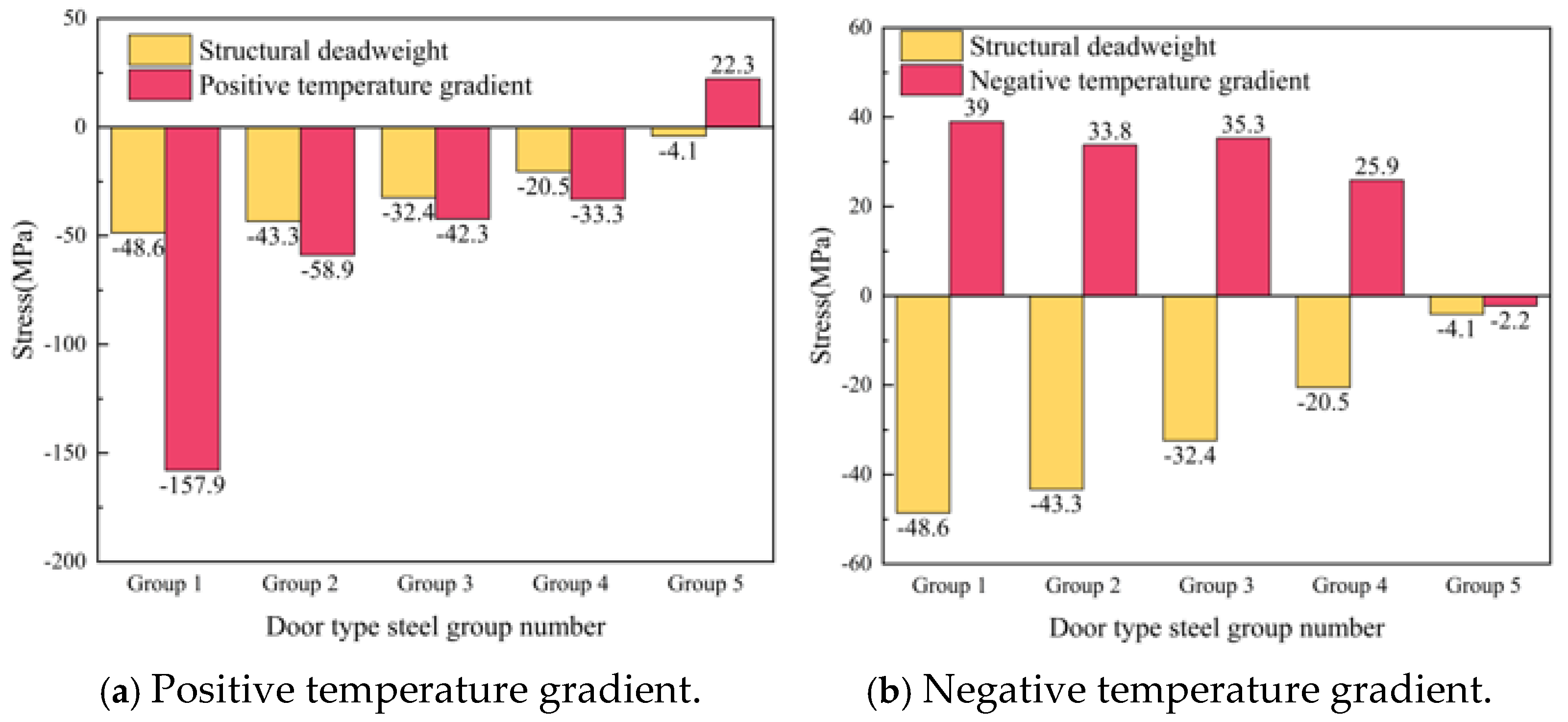
5.1. Stress Distribution of Door-Shaped Rebar Under the Track Slab Edge Gap
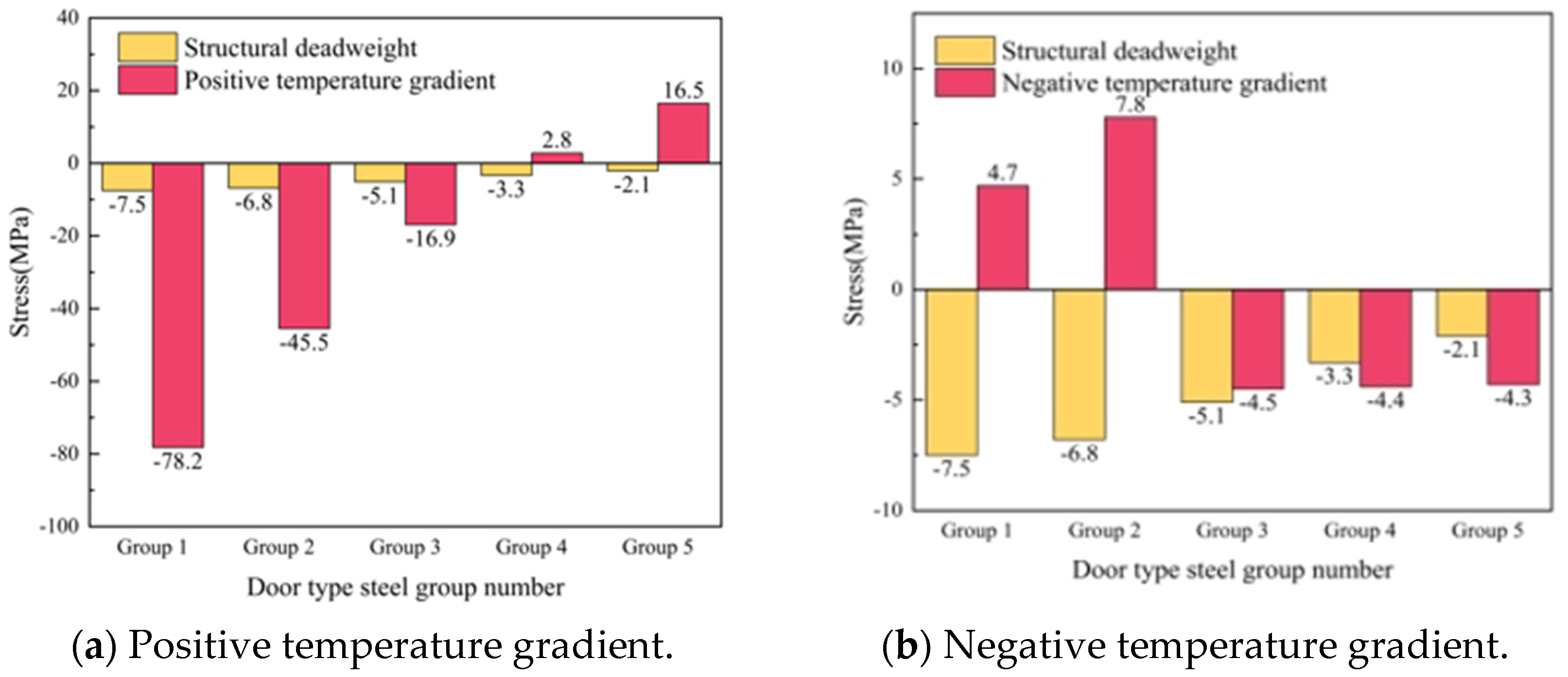
5.2. Stress Distribution of Door-Shaped Rebar Under the Gap Under the Rail
5.3. Stress Distribution of Door-Shaped Rebar Under the Track Slab Middle Gap
5.4. Stress Distribution of Door-Shaped Rebar Under Complete Interface Separation
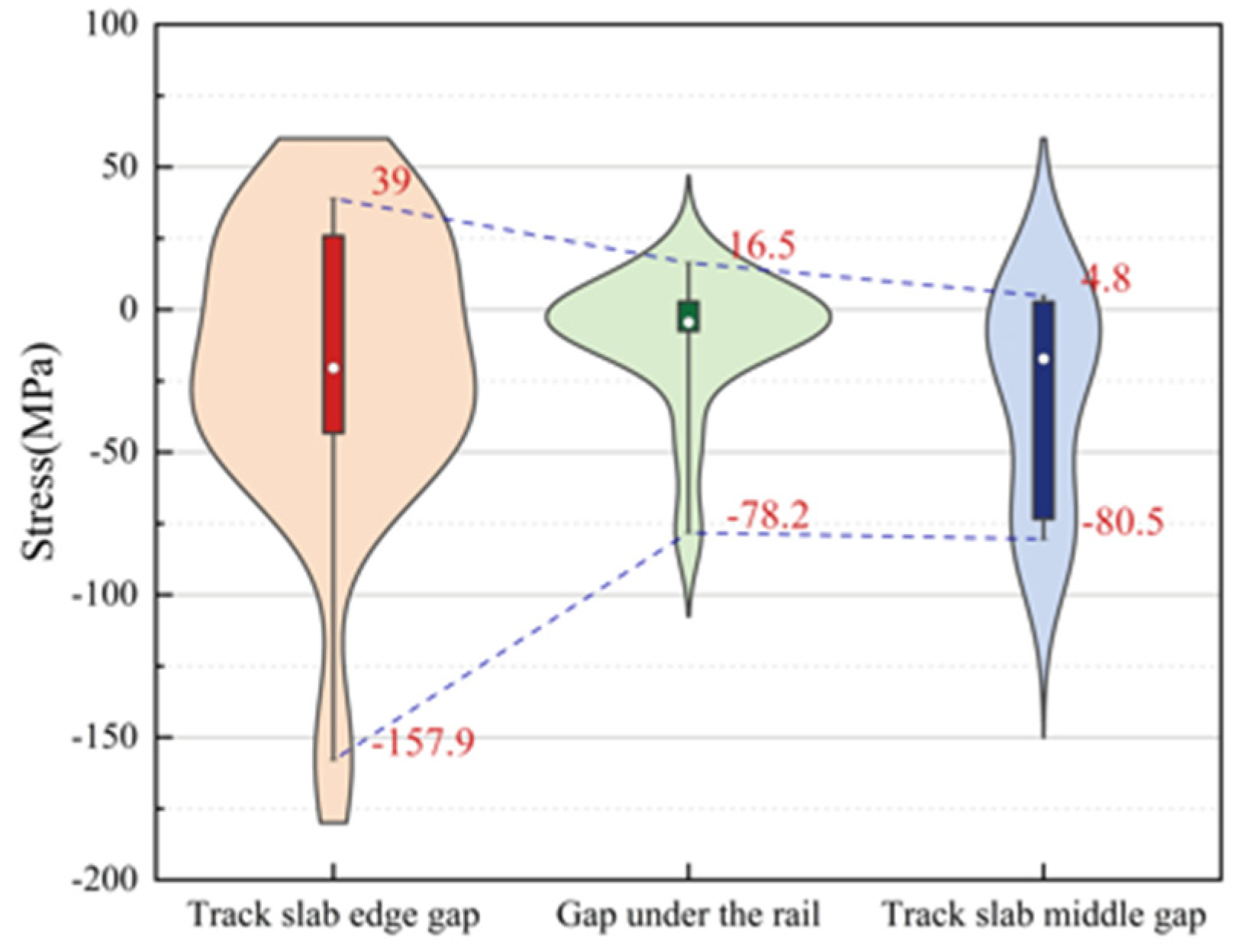
5.5. Stress Distribution Pattern of Door-Shaped Rebar Under Different Interface Gap Positions
6. Conclusions
- (1)
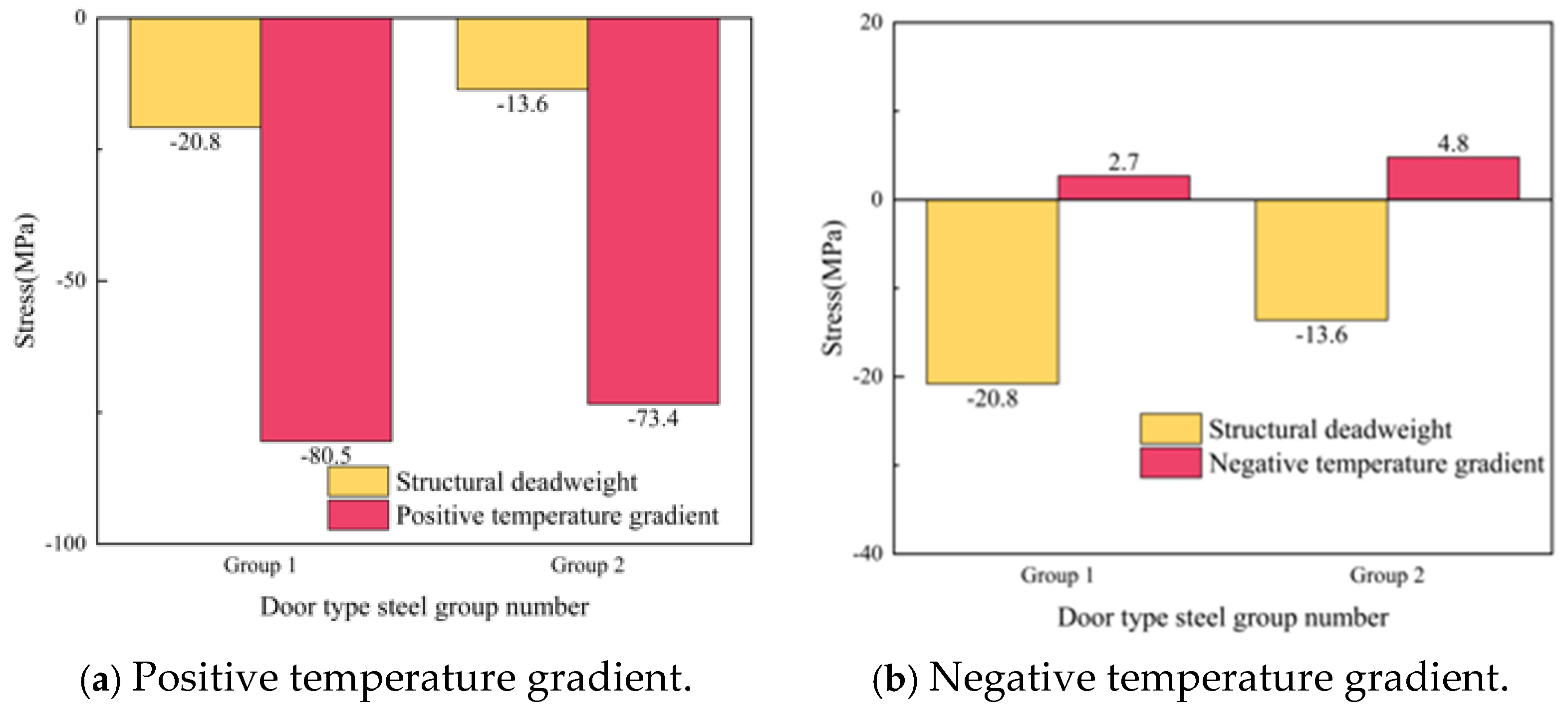
- Under the action of the temperature load, the maximum vertical displacement of the track slab occurs in the center and corner positions of the slab under a positive temperature gradient, with displacement values of 0.87 mm and −0.99 mm, respectively; under positive and negative temperature gradients, the stress of the door-shaped rebar at the interface between the track slab and the SCC layer is 12.9 MPa and 16.5 MPa, respectively.
- (2)
- When considering the conditions of the SCC slurry layer, the overall stress increase of the door-shaped rebar in the SCC layer under the action of the temperature gradient was not significant, with the increases of positive temperature gradients being 15.1% and 9.7% and those of negative temperature gradients being 2.0% and 1.6%, respectively.
- (3)
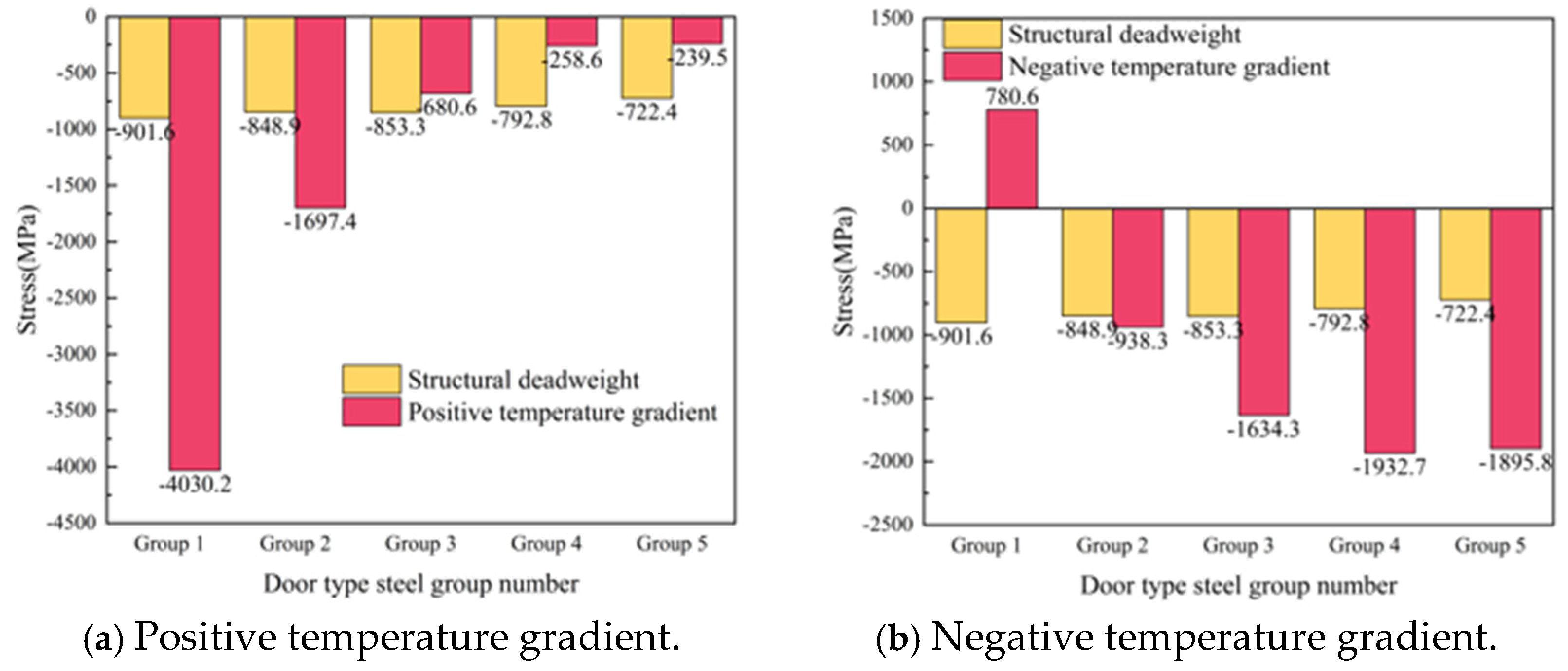
- When the interface of the SCC layer is separated, the stress of the door-shaped rebar unit located in the separation area changes significantly under the action of the deadweight of the track structure and the temperature load. Among them, the separation of the track slab edge has the greatest impact on the stress of the door-shaped rebar under the positive temperature gradient, which is 157.9 MPa. In engineering practice, monitoring and repair measures should be taken to focus on preventing and controlling this fault.
- (4)
- In future work, we will consider the coupling of more factors, because as the track structure accumulates in use time, more problems will be exposed, such as the impact of rainwater.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, H.; Li, H.; Shi, H.; Wen, J.; Wang, Z.; Huang, F.; Yang, Z.; Yi, Z. Evaluation index and improvement method for interlayer bonding property of ballastless track. Eng. Fail. Anal. 2023, 153, 107620. [Google Scholar] [CrossRef]
- Liu, M. Research on Evaluation Index of Interface Damage for CRTS III Slab Track. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2021. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Wang, J.; Shi, X.; Wang, R. Interfacial failure and arching of the CRTS II slab track reinforced by post-installed reinforcement bars due to thermal effects. Eng. Fail. Anal. 2021, 125, 105405. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, D.; Shuang, M. Investigation of temperature-induced effect on rail-road suspension bridges during operation. J. Constr. Steel Res. 2024, 215, 108542. [Google Scholar] [CrossRef]
- Wang, X.; Li, H. The withhold technology of track slab for self-compacting concrete construction of CRTS III slab ballastless track. Railw. Constr. Technol. 2015, 3, 97–101. [Google Scholar]
- Guo, G.; Hao, C.; Du, B. Static and dynamic response characteristics of a ballastless track structure of a high-speed railway bridge with interlayer debonding under temperature loads. Eng. Fail. Anal. 2023, 151, 107377. [Google Scholar] [CrossRef]
- Sadri, M.; Steenbergen, M. Effects of railway track design on the expected degradation: Parametric study on energy dissipation. J. Sound Vib. 2018, 419, 281–301. [Google Scholar] [CrossRef]
- Zeng, Z.; Luo, J.; Liu, B. Influence of interface bond damage on the dynamic characteristic of CRTS III slab track. J. Railw. Eng. Soc. 2016, 33, 34–38. [Google Scholar]
- Yang, G.; Bradford, M.A. Thermal-induced buckling and postbuckling analysis of continuous railway tracks. Int. J. Solids Struct. 2016, 97, 637–649. [Google Scholar] [CrossRef]
- Liu, H.; Song, L.; Liu, R.; Yu, Z. Temperature field and thermal effect analysis of CRTS III ballastless track structure under the outdoor natural environment. Constr. Build. Mater. 2022, 358, 129383. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, T.; Luo, Y. Insights of the vehicle-track-girder system dynamic response changes caused by the thermal deformation of CRTS III ballastless track in the natural environment. Constr. Build. Mater. 2023, 400, 132745. [Google Scholar] [CrossRef]
- Ran, L.; Li, S.; Jiwei, C.; Zhihua, X.; Zhiwu, Y. Early warping deformation of high-speed railway CRTS III track slabs. Eng. Struct. 2023, 294, 116651. [Google Scholar] [CrossRef]
- Shi, T.; Lou, P. Optimized machine learning approaches for identifying vertical temperature gradient on ballastless track in natural environments. Constr. Build. Mater. 2023, 367, 130321. [Google Scholar] [CrossRef]
- Shi, T.; Lou, P.; Zheng, W.; Sheng, X. A hybrid approach to predict vertical temperature gradient of ballastless track caused by solar radiation. Constr. Build. Mater. 2022, 352, 129063. [Google Scholar] [CrossRef]
- Piloto, P.A.; Frigeri, A.V.; Minhoto, M.; Silva, D.A. Validation of a rail temperature model with experimental measurements. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 1104–1113. [Google Scholar] [CrossRef]
- Oliveira, P.N.; Fonseca, E.M.; Campilho, R.D.; Piloto, P.A. Analytical equations applied to the study of steel profiles under fire according to different nominal temperature-time curves. Math. Comput. Appl. 2021, 26, 48. [Google Scholar] [CrossRef]
- Zhi-ping, Z.; Jun-dong, W.; Shi-wen, S.; Ping, L.; Shuaibu, A.A.; Wei-dong, W. Experimental study on evolution of mechanical properties of CRTS III ballastless slab track under fatigue load. Constr. Build. Mater. 2019, 210, 639–649. [Google Scholar] [CrossRef]
- Zeng, Z.P.; Huang, X.D.; Yan, B.; Wang, W.D.; Shuaibu, A.A.; He, X.F. Research on the fatigue performance of self-compacting concrete structure in CRTSIII slab ballastless track under the action of heavy haul train. Constr. Build. Mater. 2021, 303, 124465. [Google Scholar] [CrossRef]
- Zhiping, Z.; Yancai, X.; Weidong, W.; Zhibin, H.; Wei, W.; Boumedienne, H.S. Research on Dynamic Performance of CRTS III Type Slab Ballastless Track under Long-Term Service. Materials 2022, 15, 2033. [Google Scholar] [CrossRef]
- Yan, B.; Cheng, R.; Pan, W. Influence of interface crack on dynamic characteristics of CRTS III slab ballastless track on bridge. J. Cent. South Univ. 2022, 29, 2665–2674. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, H.; Wang, L.; Xu, L.; Chen, W.; Lou, P. Influence of vehicle number on the dynamic characteristics of high-speed train-CRTS III slab track-subgrade coupled system. Materials 2021, 14, 3662. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, L.; Zhong, Y.; Wang, J.; Huang, Y. Interlayer damage evolution of CRTS III slab track under passenger and freight train loads. Constr. Build. Mater. 2024, 436, 136944. [Google Scholar] [CrossRef]
- Zhao, L. Spatial Refinement Analysis Method of High Speed Railway Ballastless Track and Its Application Research. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2015. [Google Scholar]
- Liu, C.; Zeng, Z.P.; Yuan, J.Y.; Wu, B.; Zhu, K.T. Experimental study on vertical stiffness of WJ-8 fastener for high-speed railway. Appl. Mech. Mater. 2015, 723, 100–103. [Google Scholar] [CrossRef]
- Bertolesi, E.; Buitrago, M.; Adam, J.M.; Calderón, P.A. Fatigue assessment of steel riveted railway bridges: Full-scale tests and analytical approach. J. Constr. Steel Res. 2021, 182, 106664. [Google Scholar] [CrossRef]
- Feng, Q.; Zhu, Z.; Tong, Q.; Yu, Y.; Zheng, W. Dynamic responses and fatigue assessment of OSD in heavy-haul railway bridges. J. Constr. Steel Res. 2023, 204, 107873. [Google Scholar] [CrossRef]
- TB10621-2014; Code for Design of High Speed Railway. China Railway Press: Beijing, China, 2014.
- You, R. Study on the test methods of concrete laitance. New Build. Mater. 2017, 44, 12–14. [Google Scholar]
- Liu, W.; Wang, J.; Yang, Q. Experimental study on temperature gradient for CRTS III slab-type ballastless track on high speed railway. Railw. Eng. 2015, 3, 103–106. [Google Scholar]
- Peng, Q. CRTSIII slab ballastless track self-compacting high performance concrete filling layer of main quality defects and prevention measures. Concrete 2013, 8, 158–160. [Google Scholar]
- You, M. Study on Temperature Field Features and Effection of Slab Ballastless Track. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
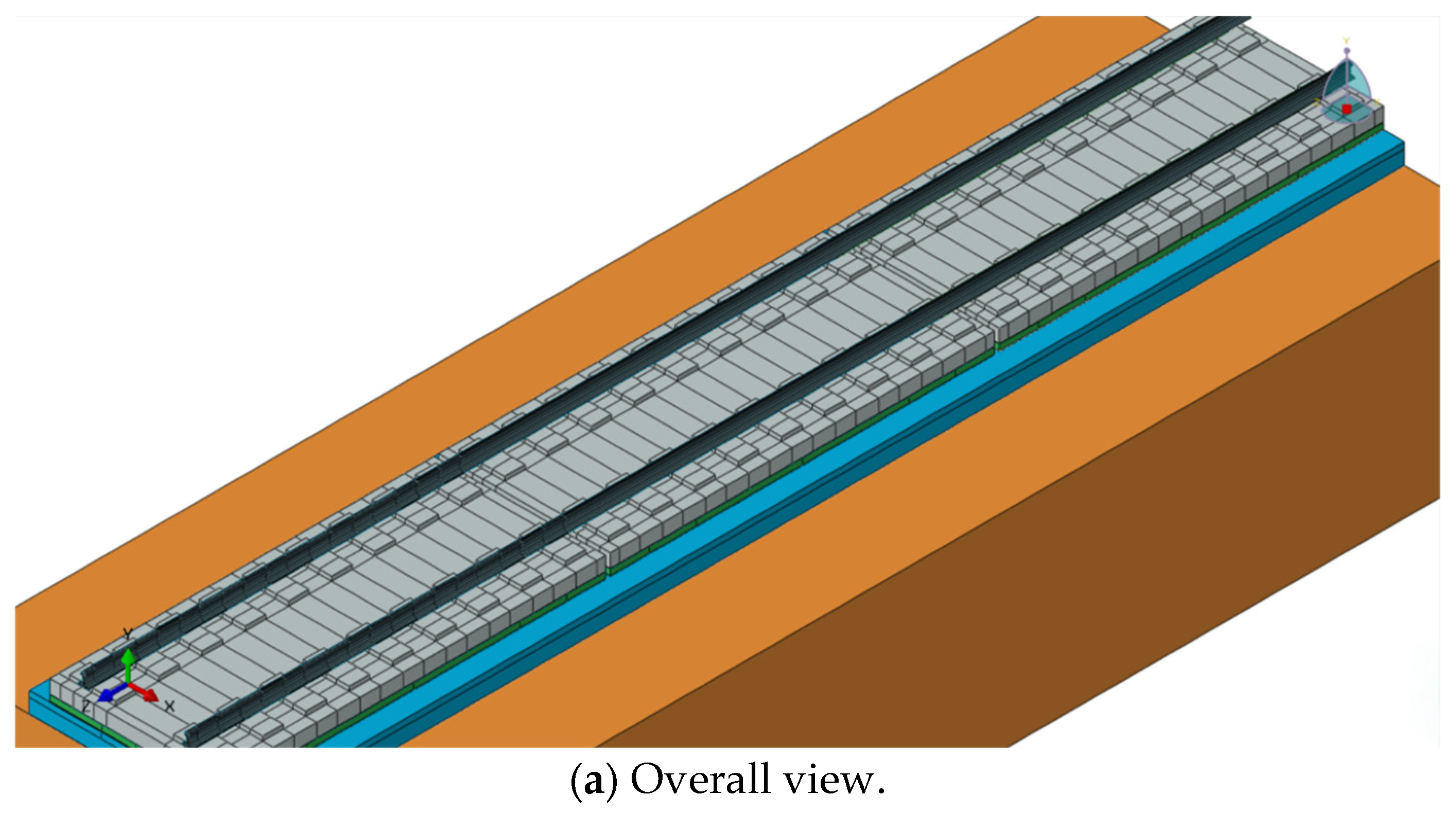
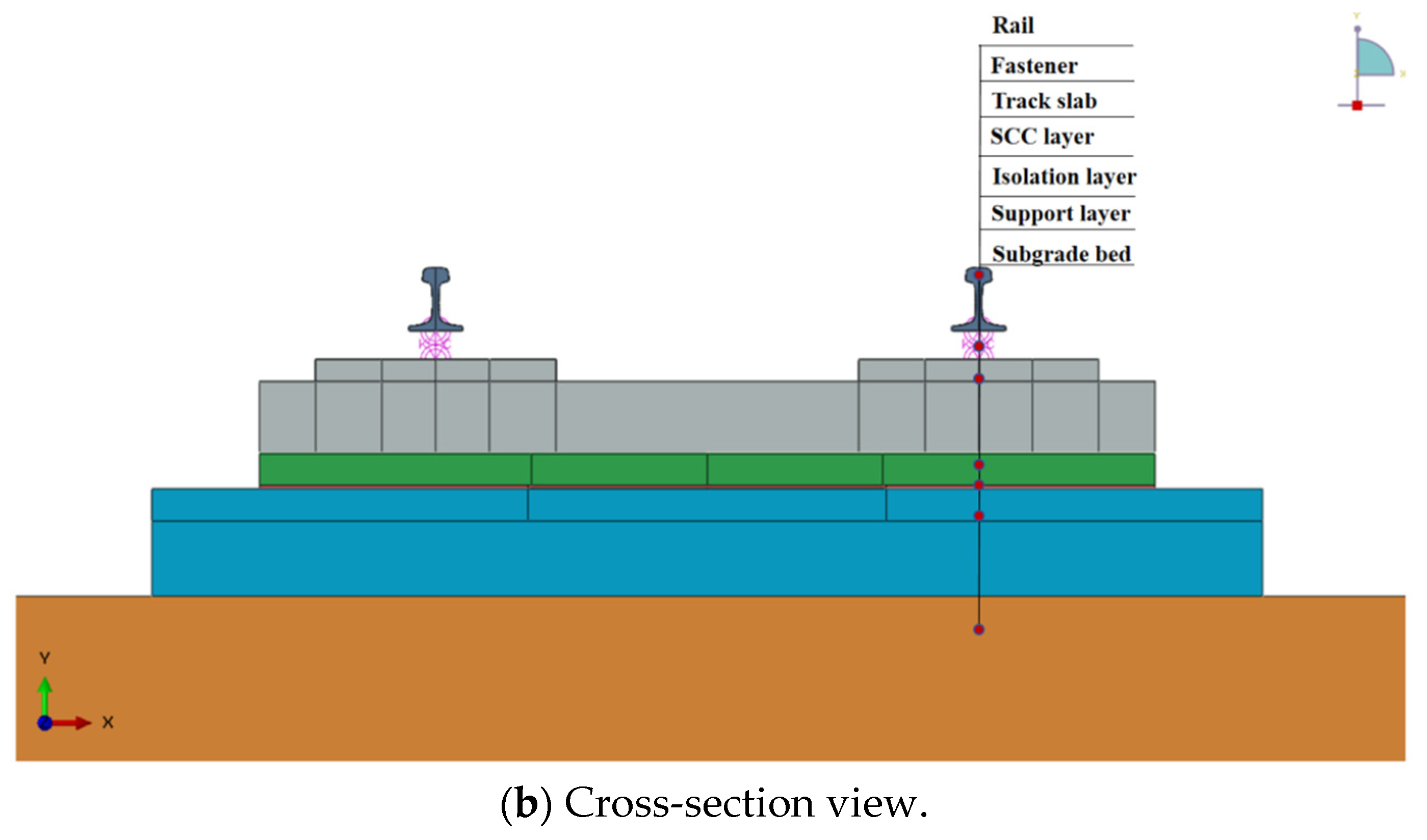
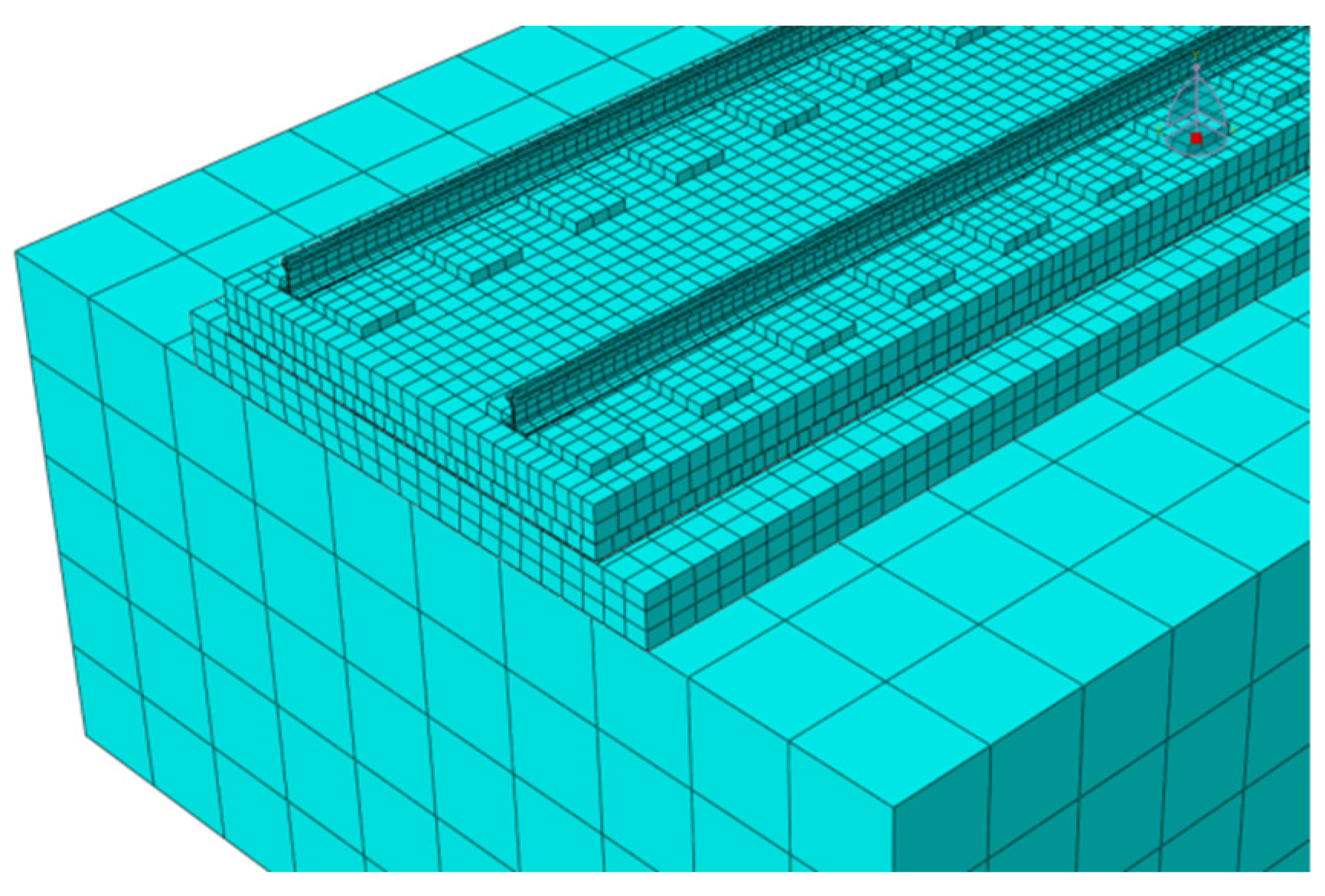

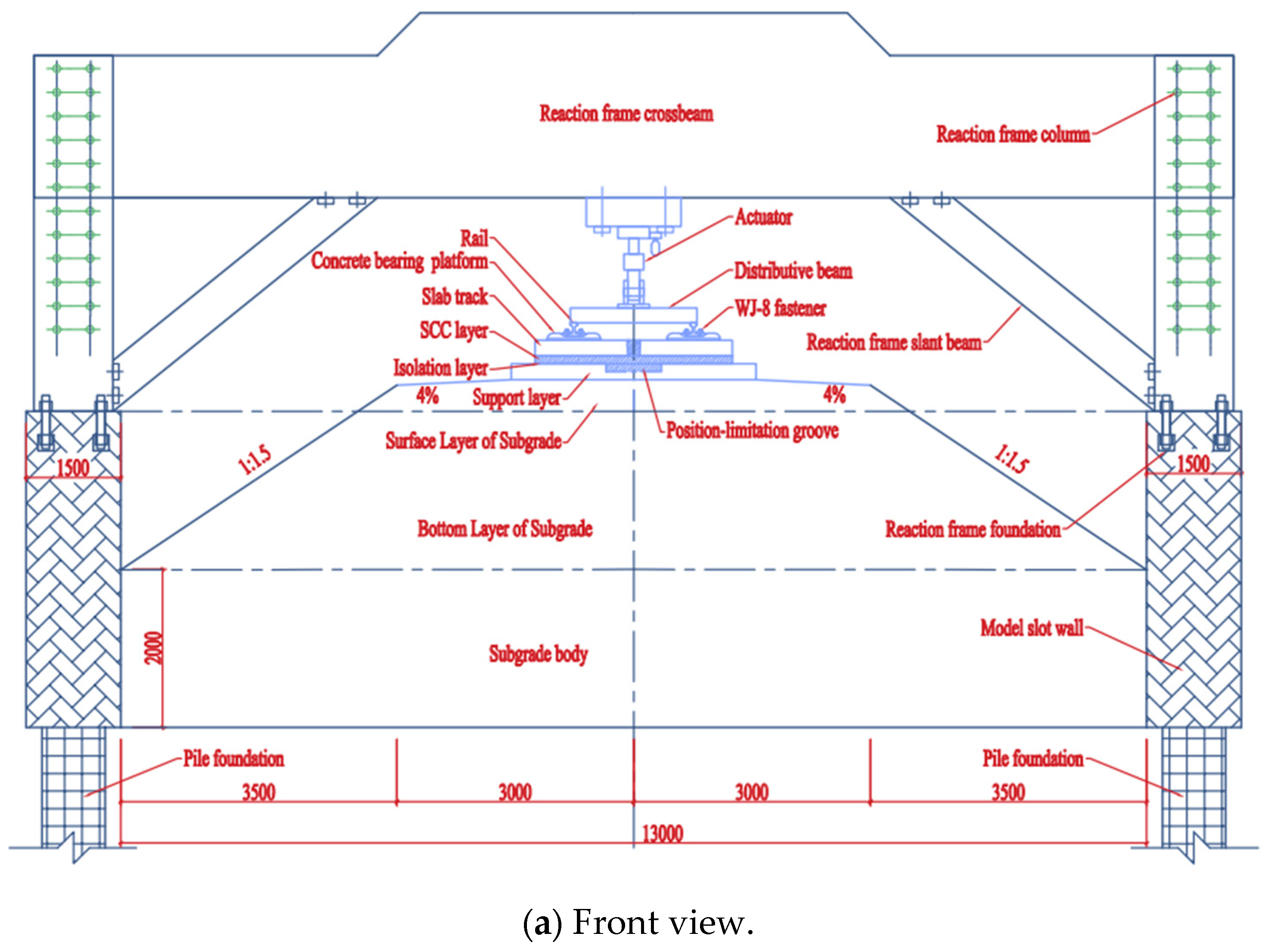
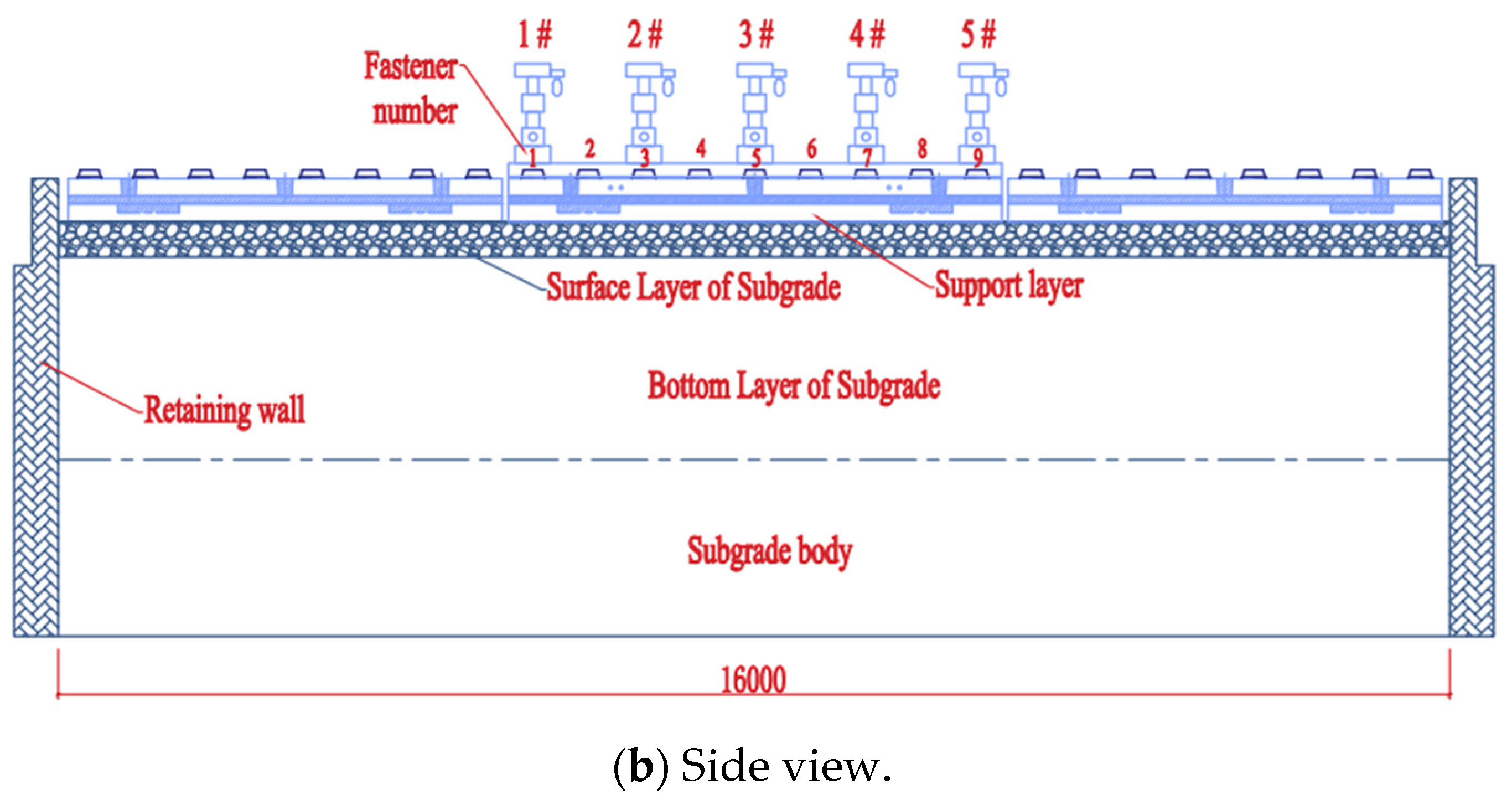
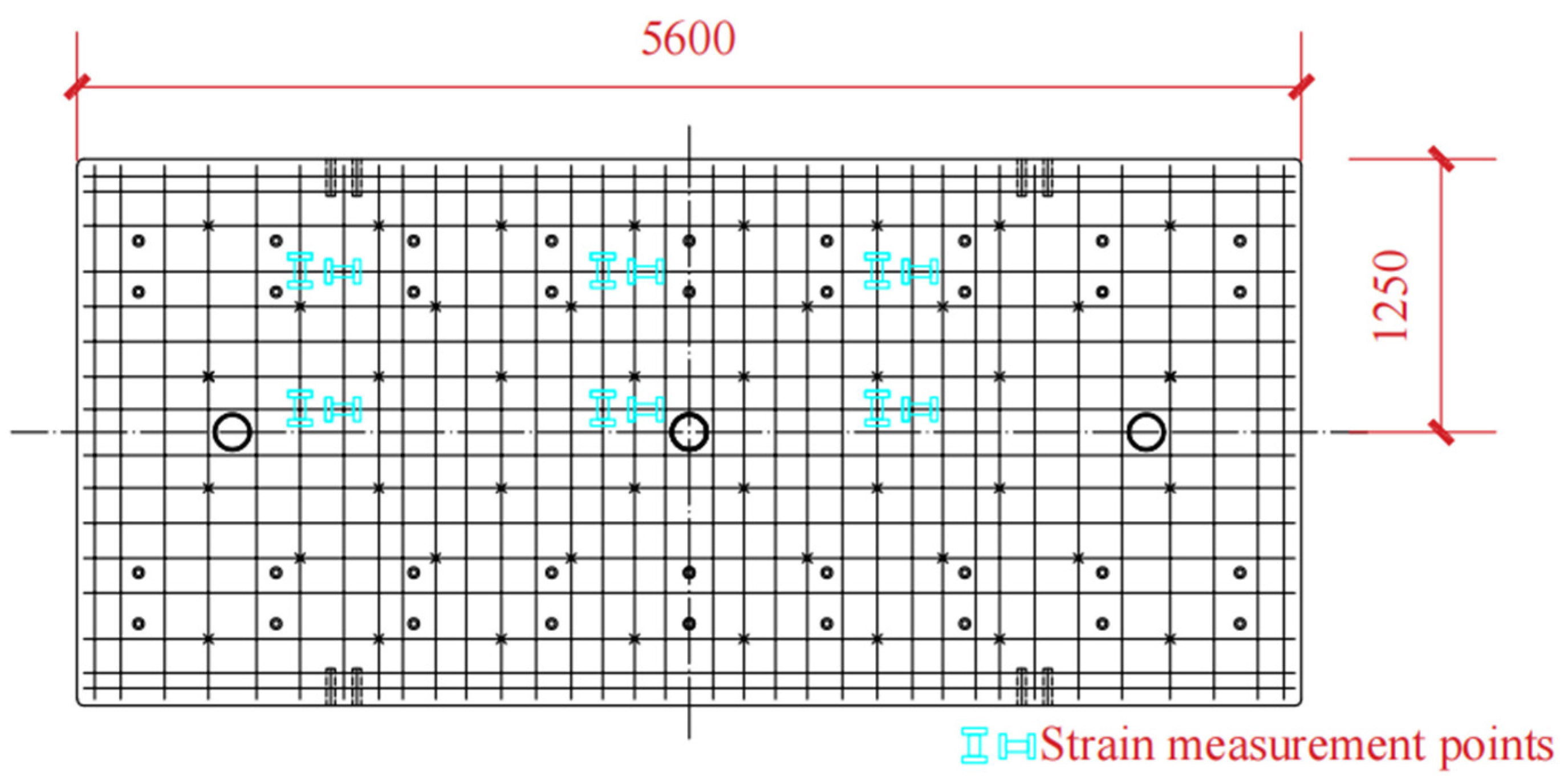





| Part | Elastic Modulus MPa | Density kg/m3 | Poisson’s Ratio | Coefficient of Thermal Expansion /°C |
|---|---|---|---|---|
| Rail | 2.06 × 105 | 7.80 × 103 | 0.3 | 1.18 × 10−5 |
| Track Slab | 3.65 × 104 | 2.50 × 103 | 0.2 | 1.0 × 10−5 |
| SCC Layer | 3.40 × 104 | 2.40 × 103 | 0.2 | 1.0 × 10−5 |
| Support Layer | 3.20 × 104 | 2.50 × 103 | 0.2 | 1.0 × 10−5 |
| Surface Layer of Subgrade | 300 | 1.95 × 103 | 0.3 | / |
| Bottom Layer of Subgrade | 250 | 1.90 × 103 | 0.25 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, M.; Zeng, Z.; Li, Q.; Li, P.; Wei, W.; Wang, W.; Shuaibu, A.A. Study on the Mechanical Properties of Door-Shaped Rebar of a CRTS III Slab Track Under Temperature Load. Materials 2025, 18, 1612. https://doi.org/10.3390/ma18071612
Han M, Zeng Z, Li Q, Li P, Wei W, Wang W, Shuaibu AA. Study on the Mechanical Properties of Door-Shaped Rebar of a CRTS III Slab Track Under Temperature Load. Materials. 2025; 18(7):1612. https://doi.org/10.3390/ma18071612
Chicago/Turabian StyleHan, Marui, Zhiping Zeng, Qiuyi Li, Peicheng Li, Wei Wei, Weidong Wang, and Abdulmumin Ahmed Shuaibu. 2025. "Study on the Mechanical Properties of Door-Shaped Rebar of a CRTS III Slab Track Under Temperature Load" Materials 18, no. 7: 1612. https://doi.org/10.3390/ma18071612
APA StyleHan, M., Zeng, Z., Li, Q., Li, P., Wei, W., Wang, W., & Shuaibu, A. A. (2025). Study on the Mechanical Properties of Door-Shaped Rebar of a CRTS III Slab Track Under Temperature Load. Materials, 18(7), 1612. https://doi.org/10.3390/ma18071612






