First-Principles Study on the Alloying Segregation and Ideal Fracture at Coherent B2-NiAl and BCC-Fe Interface
Abstract
:1. Introduction
2. Methodology
2.1. Details of DFT Calculations
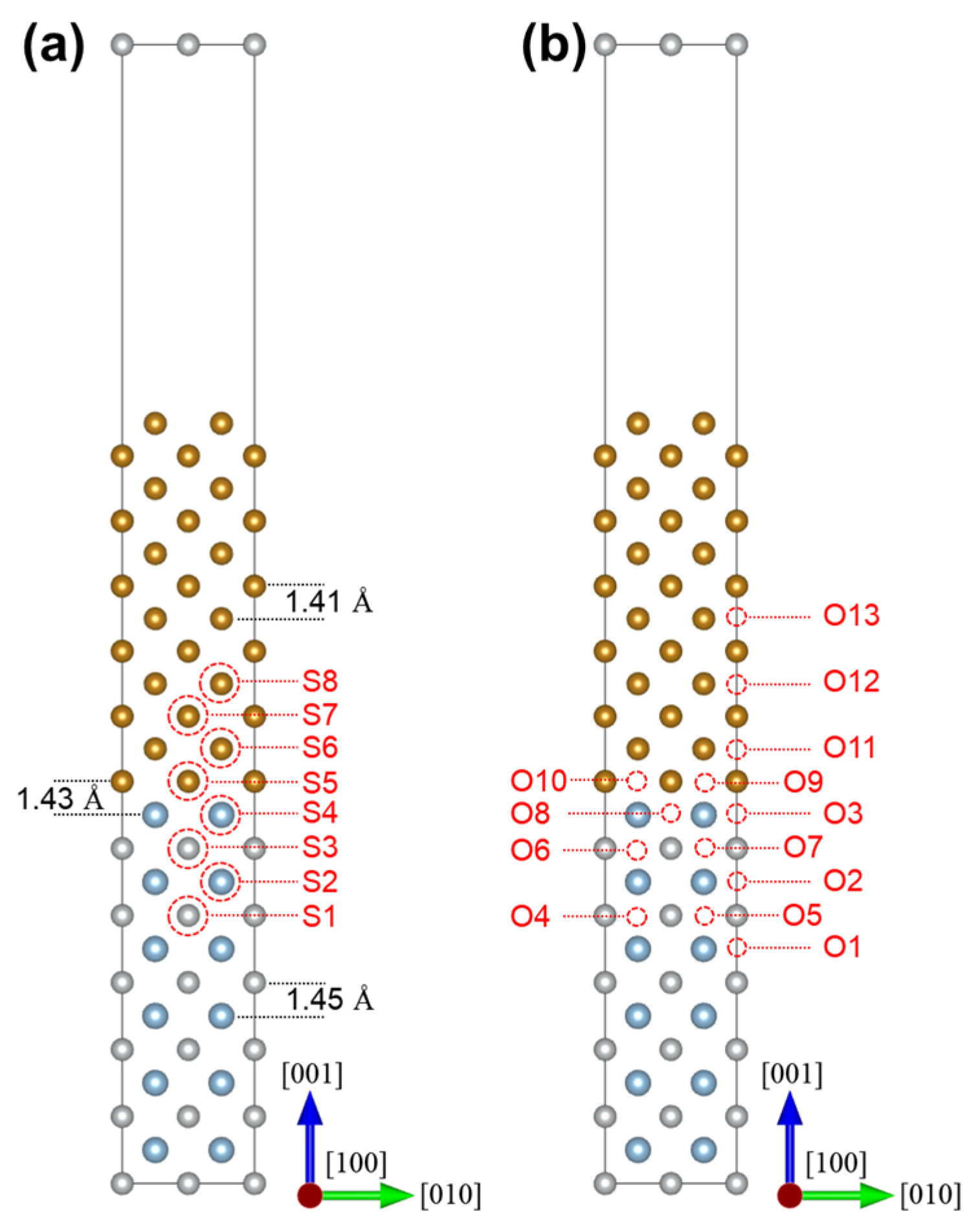
2.2. The BCC-Fe/B2-NiAl Interface Model
2.3. Ideal Fracture Energies
3. Results and Discussions
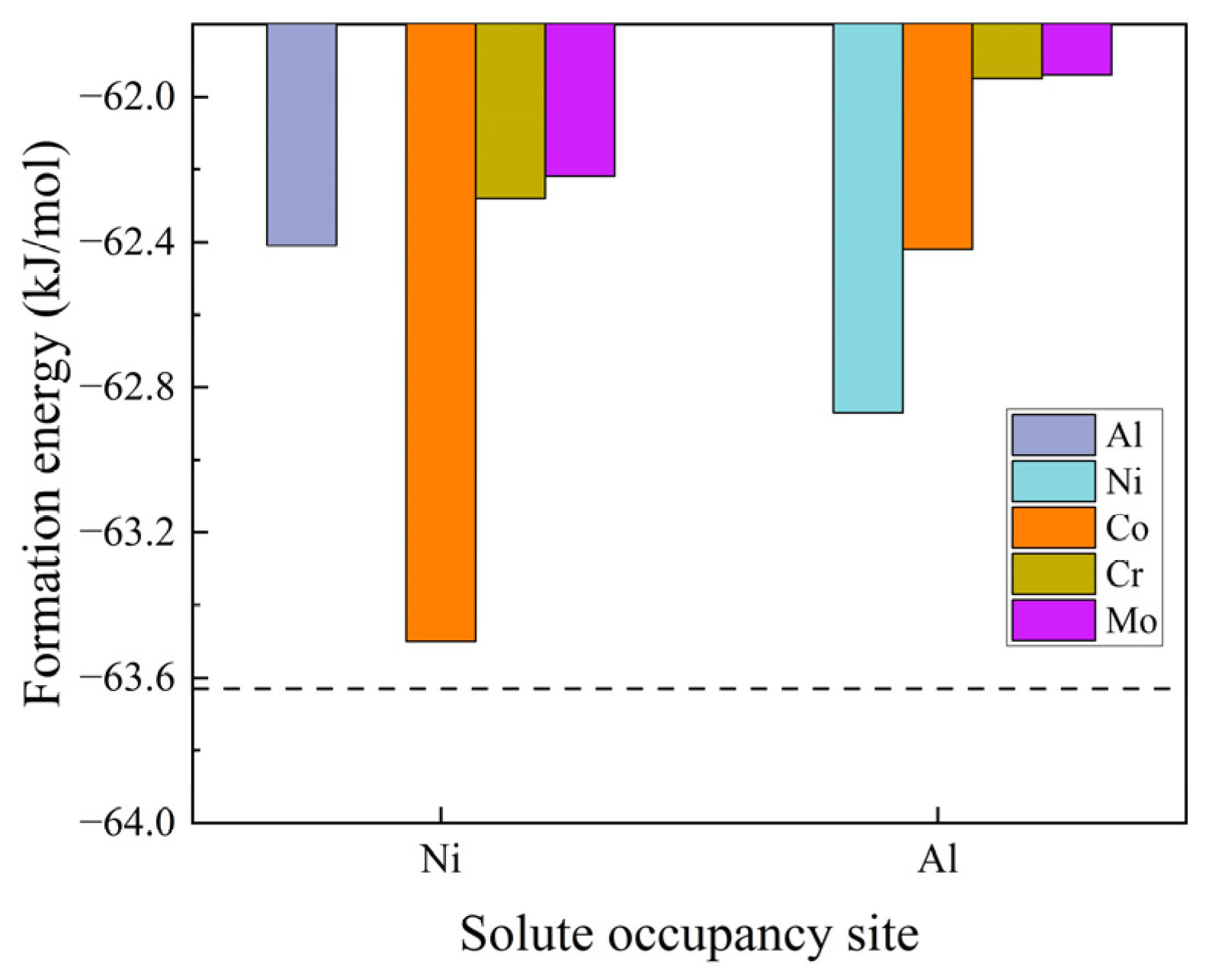
3.1. Solute Occupancy in B2-NiAl Bulk and Its Effect on Elastic Properties
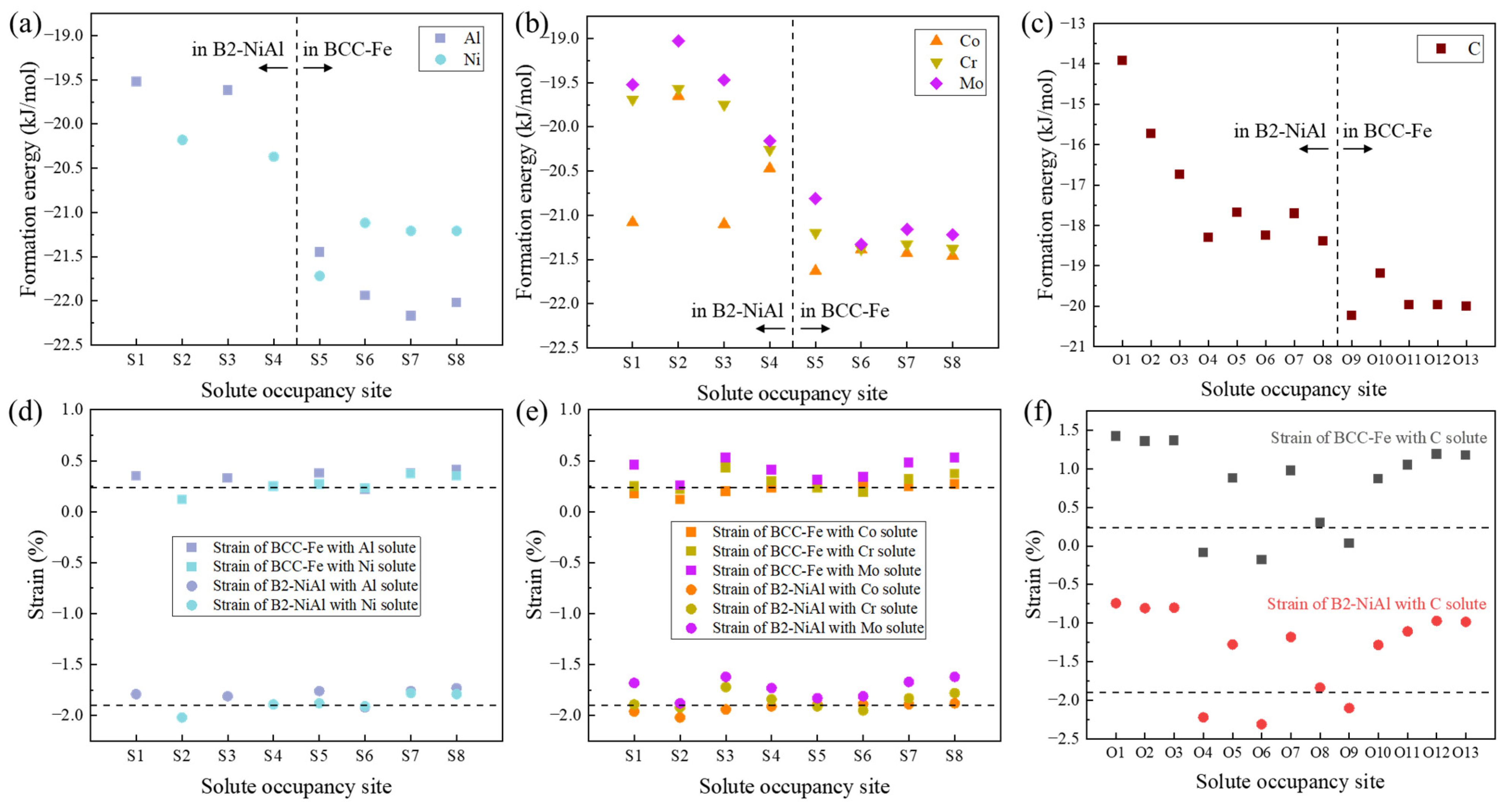
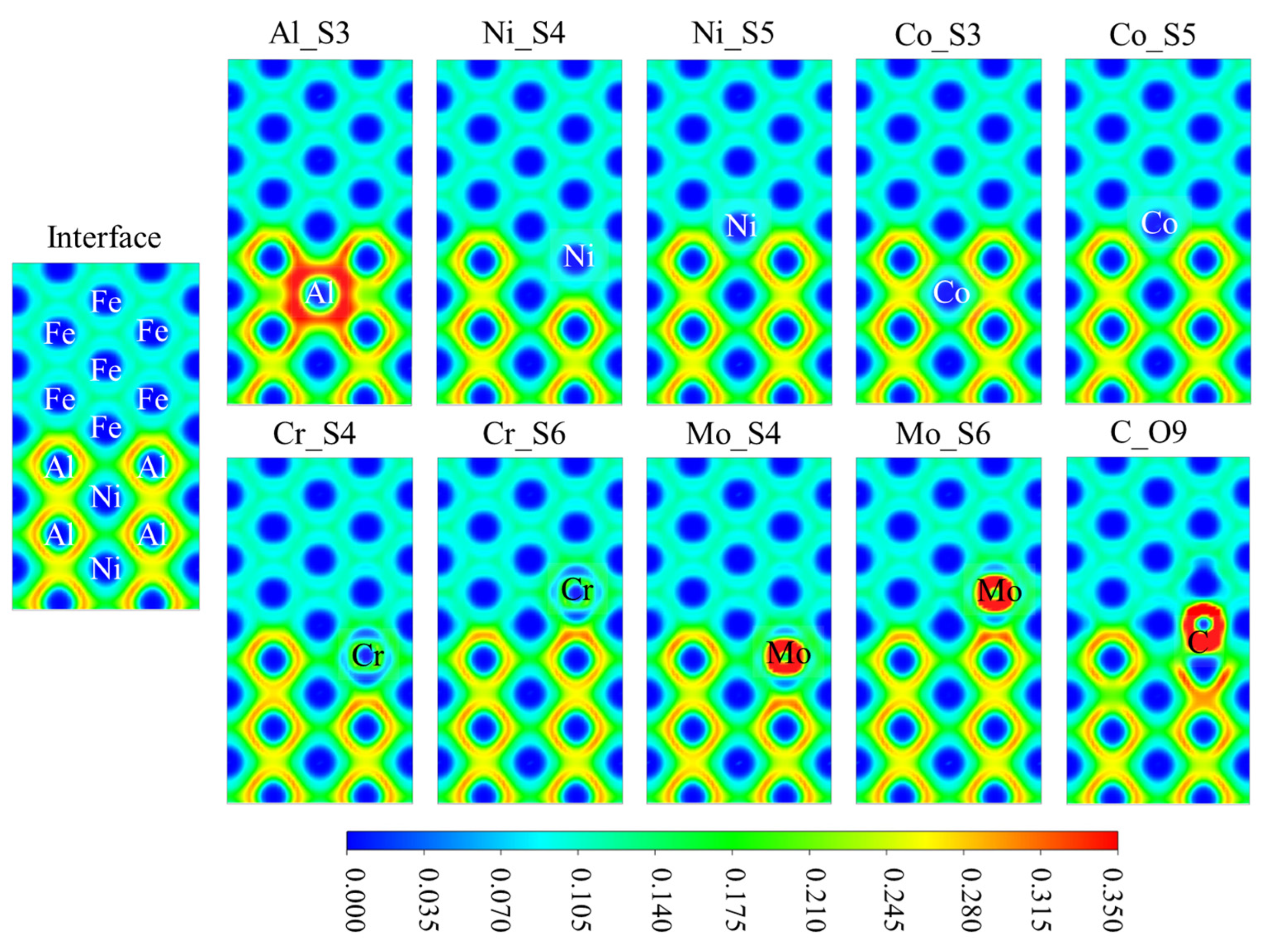
3.2. Solute Segregation at the Coherent Interface
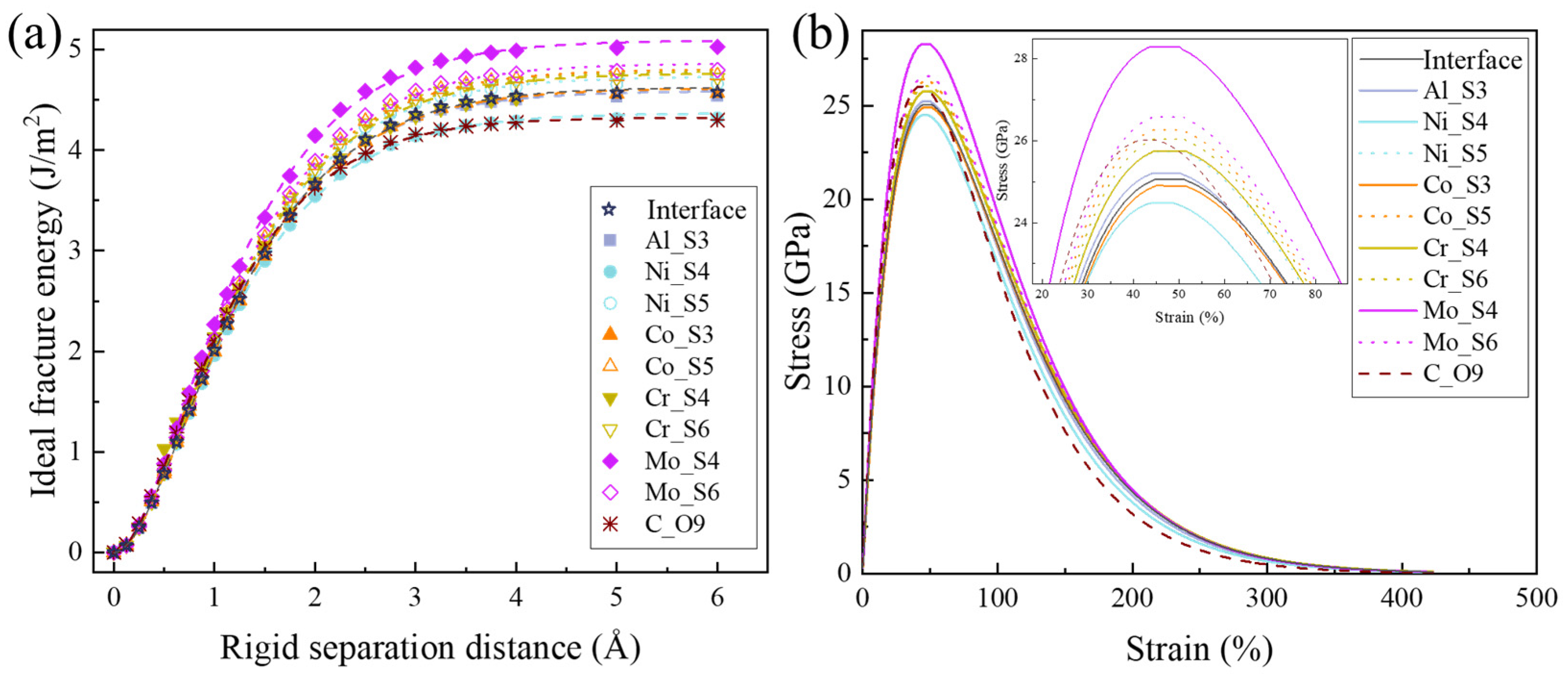
3.3. The Effect of Solute Segregation on Ideal Fracture at Interface
3.4. The Electronic Structures at the Interface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sankaran, K.K.; Mishra, R.S. Chapter 6—Ultrahigh Strength Steels. In Metallurgy and Design of Alloys with Hierarchical Microstructures; Sankaran, K.K., Mishra, R.S., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 289–343. [Google Scholar]
- Jiang, S.; Wang, H.; Wu, Y.; Liu, X.; Chen, H.; Yao, M.; Gault, B.; Ponge, D.; Raabe, D.; Hirata, A.; et al. Ultrastrong steel via minimal lattice misfit and high-density nanoprecipitation. Nature 2017, 544, 460–464. [Google Scholar] [CrossRef]
- Wang, Z.H.; Niu, B.; Wang, Q.; Dong, C.; Jie, J.C.; Wang, T.M.; Nieh, T.G. Designing ultrastrong maraging stainless steels with improved uniform plastic strain via controlled precipitation of coherent nanoparticles. J. Mater. Sci. Technol. 2021, 93, 60–70. [Google Scholar] [CrossRef]
- Sun, L.; Simm, T.H.; Martin, T.L.; McAdam, S.; Galvin, D.R.; Perkins, K.M.; Bagot, P.A.J.; Moody, M.P.; Ooi, S.W.; Hill, P.; et al. A novel ultra-high strength maraging steel with balanced ductility and creep resistance achieved by nanoscale β-NiAl and Laves phase precipitates. Acta Mater. 2018, 149, 285–301. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhou, T.; Yan, L.; Yu, H. Impact toughness and fracture propagation mechanism of NiAl precipitation-strengthened HSLA steels. Mater. Des. 2024, 241, 112927. [Google Scholar] [CrossRef]
- Zhou, B.C.; Yang, T.; Zhou, G.; Wang, H.; Luan, J.H.; Jiao, Z.B. Mechanisms for suppressing discontinuous precipitation and improving mechanical properties of NiAl-strengthened steels through nanoscale Cu partitioning. Acta Mater. 2021, 205, 116561. [Google Scholar] [CrossRef]
- Yang, X.; Di, X.; Duan, Q.; Fu, W.; Ba, L.; Li, C. Effect of precipitation evolution of NiAl and Cu nanoparticles on strengthening mechanism of low carbon ultra-high strength seamless tube steel. Mater. Sci. Eng. A 2023, 872, 144939. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Srivastava, V.C.; Chandan, A.K.; Ghosh Chowdhury, S. Enhancing the properties of Al–Ni added medium Mn steel by tailoring B2–NiAl precipitates through aging treatment. Mater. Sci. Eng. A 2022, 837, 142757. [Google Scholar] [CrossRef]
- Kapoor, M.; Isheim, D.; Vaynman, S.; Fine, M.E.; Chung, Y.W. Effects of increased alloying element content on NiAl-type precipitate formation, loading rate sensitivity, and ductility of Cu- and NiAl-precipitation-strengthened ferritic steels. Acta Mater. 2016, 104, 166–171. [Google Scholar] [CrossRef]
- Zhang, B.; Xiong, K.; Wang, M.; Liu, Z.; Shen, K.; Mao, Y.; Chen, H. Grain boundary alloying segregation to resist hydrogen embrittlement in BCC-Fe steels: Atomistic insights into solute-hydrogen interactions. Scr. Mater. 2024, 238, 115757. [Google Scholar] [CrossRef]
- Mai, H.L.; Cui, X.-Y.; Scheiber, D.; Romaner, L.; Ringer, S.P. The segregation of transition metals to iron grain boundaries and their effects on cohesion. Acta Mater. 2022, 231, 117902. [Google Scholar] [CrossRef]
- Wang, J.; Enomoto, M.; Shang, C. First-principles study on the interfacial segregation at coherent Cu precipitate/Fe matrix interface. Scr. Mater. 2020, 185, 42–46. [Google Scholar] [CrossRef]
- Geng, W.T.; Freeman, A.J.; Olson, G.B. Influence of alloying additions on grain boundary cohesion of transition metals: First-principles determination and its phenomenological extension. Phys. Rev. B 2001, 63, 165415. [Google Scholar] [CrossRef]
- Ahmed, F.A.M.; Xue, H.-T.; Tang, F.-L.; An, J.-P.; Luo, Y.-Q.; Lu, X.-F.; Ren, J.-Q. Segregation of alloying elements and their effects on the thermodynamic stability and fracture strength of γ-Ni/γ′-Ni3Al interface. J. Mater. Sci. 2020, 55, 12513–12524. [Google Scholar] [CrossRef]
- Gao, X.; Wang, H.; Ma, C.; Lv, M.; Ren, H. Segregation of alloying elements at the bcc-Fe/B2–NiAl interface and the corresponding effects on the interfacial energy. Intermetallics 2021, 131, 107096. [Google Scholar] [CrossRef]
- Calderon, H.A.; Fine, M.E.; Weertman, J.R. Coarsening and morphology of β′ particles in Fe-Ni-Al-Mo ferritic alloys. Metall. Trans. A 1988, 19, 1135–1146. [Google Scholar]
- Ping, D.H.; Ohnuma, M.; Hirakawa, Y.; Kadoya, Y.; Hono, K. Microstructural evolution in 13Cr–8Ni–2.5Mo–2Al martensitic precipitation-hardened stainless steel. Mater. Sci. Eng. A 2005, 394, 285–295. [Google Scholar]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Yu, J.; Lin, X.; Wang, J.; Chen, J.; Huang, W. First-principles study of the relaxation and energy of bcc-Fe, fcc-Fe and AISI-304 stainless steel surfaces. Appl. Surf. Sci. 2009, 255, 9032–9039. [Google Scholar] [CrossRef]
- Faraoun, H.; Aourag, H.; Esling, C.; Seichepine, J.L.; Coddet, C. Elastic properties of binary NiAl, NiCr and AlCr and ternary Ni2AlCr alloys from molecular dynamic and Abinitio simulation. Comput. Mater. Sci. 2005, 33, 184–191. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B Condens. Matter 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Manna, S.; Sankaranarayanan, S.K.R.S. Elastemp—A workflow to compute the quasi-harmonic temperature dependent elastic constants of materials. Comput. Mater. Sci. 2023, 226, 112223. [Google Scholar] [CrossRef]
- Zuo, L.; Humbert, M.; Esling, C. Elastic properties of polycrystals in the Voigt-Reuss-Hill approximation. J. Appl. Crystallogr. 1992, 25, 751–755. [Google Scholar] [CrossRef]
- Rose, J.H.; Ferrante, J.; Smith, J.R. Universal Binding Energy Curves for Metals and Bimetallic Interfaces. Phys. Rev. Lett. 1981, 47, 675–678. [Google Scholar]
- Thompson, R.P.; Clegg, W.J. Predicting whether a material is ductile or brittle. Curr. Opin. Solid State Mater. Sci. 2018, 22, 100–108. [Google Scholar] [CrossRef]
- Xing, H.; Dong, A.; Huang, J.; Zhang, J.; Sun, B. Revisiting intrinsic brittleness and deformation behavior of B2 NiAl intermetallic compound: A first-principles study. J. Mater. Sci. Technol. 2018, 34, 620–626. [Google Scholar] [CrossRef]
- Roesler, J.; Harders, H.; Baeker, M. Mechanical Behaviour of Engineering Materials: Metals, Ceramics, Polymers, and Composites; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Danoix, F.; Danoix, R.; Akre, J.; Grellier, A.; Delagnes, D. Atom probe tomography investigation of assisted precipitation of secondary hardening carbides in a medium carbon martensitic steels. J. Microsc. 2011, 244, 305–310. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Shang, S.-L.; Wang, Y.; Liu, Z.-K.; Liu, F. Martensitic transition in Fe via Bain path at finite temperatures: A comprehensive first-principles study. Acta Mater. 2018, 147, 261–276. [Google Scholar] [CrossRef]
- Park, N.Y.; Choi, J.H.; Cha, P.R.; Jung, W.S.; Chung, S.H.; Lee, S.C. First-principles study of the interfaces between Fe and transition metal carbides. J. Phys. Chem. C 2013, 117, 187–193. [Google Scholar] [CrossRef]
| Bulk | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) |
|---|---|---|---|---|---|---|---|---|
| BCC-Fe | 276.65 | 150.02 | 276.65 | 101.98 | 101.98 | 192.23 | 84.24 | 220.49 |
| B2-NiAl | 199.13 | 143.79 | 199.13 | 119.11 | 119.11 | 162.24 | 66.92 | 175.47 |
| 195.14 | 143.09 | 195.14 | 115.80 | 115.80 | 160.44 | 64.27 | 169.06 | |
| 198.51 | 145.20 | 198.51 | 120.25 | 120.25 | 162.97 | 66.41 | 174.28 | |
| 201.38 | 143.25 | 201.38 | 120.08 | 120.08 | 162.62 | 68.49 | 179.23 | |
| 183.01 | 153.44 | 183.01 | 119.94 | 119.94 | 163.29 | 54.54 | 144.79 | |
| 193.99 | 145.95 | 193.99 | 117.31 | 117.31 | 161.96 | 62.97 | 165.98 | |
| 201.34 | 142.63 | 139.76 | 206.13 | 111.61 | 161.45 | 67.25 | 176.51 |
| System | (J/m2) | (Å) | (GPa) | |
|---|---|---|---|---|
| Interface | 4.63 | 0.678 | 25.09 | 47.94 |
| Al_S3 | 4.59 | 0.669 | 25.23 | 47.24 |
| Ni_S4 | 4.37 | 0.656 | 24.50 | 46.32 |
| Ni_S5 | 4.73 | 0.675 | 25.76 | 47.72 |
| Co_S3 | 4.62 | 0.681 | 24.94 | 48.13 |
| Co_S5 | 4.81 | 0.672 | 26.30 | 47.51 |
| Cr_S4 | 4.77 | 0.680 | 25.79 | 48.01 |
| Cr_S6 | 4.79 | 0.675 | 26.07 | 47.72 |
| Mo_S4 | 5.09 | 0.661 | 28.33 | 46.72 |
| Mo_S6 | 4.86 | 0.672 | 26.61 | 47.49 |
| C_O7 | 4.33 | 0.611 | 26.02 | 43.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Wang, Y.; Zheng, J.; Zhao, C.; Li, Q.; Wei, X.; Zhang, B. First-Principles Study on the Alloying Segregation and Ideal Fracture at Coherent B2-NiAl and BCC-Fe Interface. Materials 2025, 18, 1805. https://doi.org/10.3390/ma18081805
Chen H, Wang Y, Zheng J, Zhao C, Li Q, Wei X, Zhang B. First-Principles Study on the Alloying Segregation and Ideal Fracture at Coherent B2-NiAl and BCC-Fe Interface. Materials. 2025; 18(8):1805. https://doi.org/10.3390/ma18081805
Chicago/Turabian StyleChen, Hui, Yu Wang, Jianshu Zheng, Chengzhi Zhao, Qing Li, Xin Wei, and Boning Zhang. 2025. "First-Principles Study on the Alloying Segregation and Ideal Fracture at Coherent B2-NiAl and BCC-Fe Interface" Materials 18, no. 8: 1805. https://doi.org/10.3390/ma18081805
APA StyleChen, H., Wang, Y., Zheng, J., Zhao, C., Li, Q., Wei, X., & Zhang, B. (2025). First-Principles Study on the Alloying Segregation and Ideal Fracture at Coherent B2-NiAl and BCC-Fe Interface. Materials, 18(8), 1805. https://doi.org/10.3390/ma18081805






