Assessment of Fatigue Life in Grouted Polyurethane Composites for Pavement Maintenance
Highlights
- The fatigue behavior of PACM under different stress levels and loading frequencies was evaluated.
- The effect of grading on the fatigue response of PACM was studied.
- A PACM fatigue life-prediction model was established based on the energy-dissipation theory.
Abstract
1. Introduction
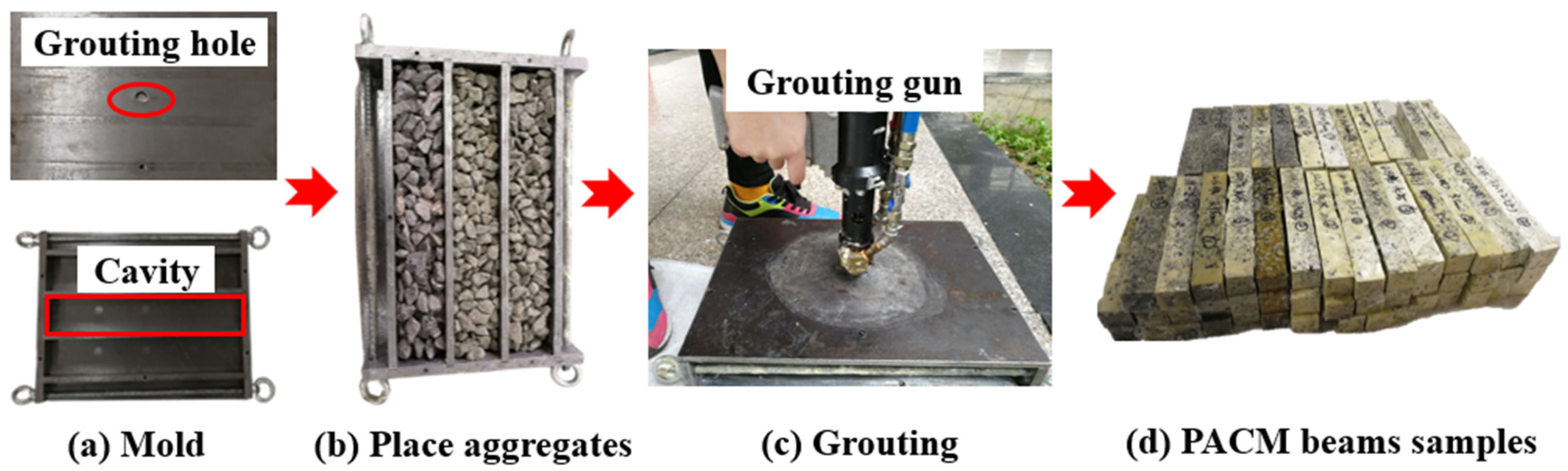
2. Materials and Sample Preparation
2.1. Raw Materials
2.1.1. Polyurethan Grouting Material
2.1.2. Aggregate
2.2. Sample Preparation
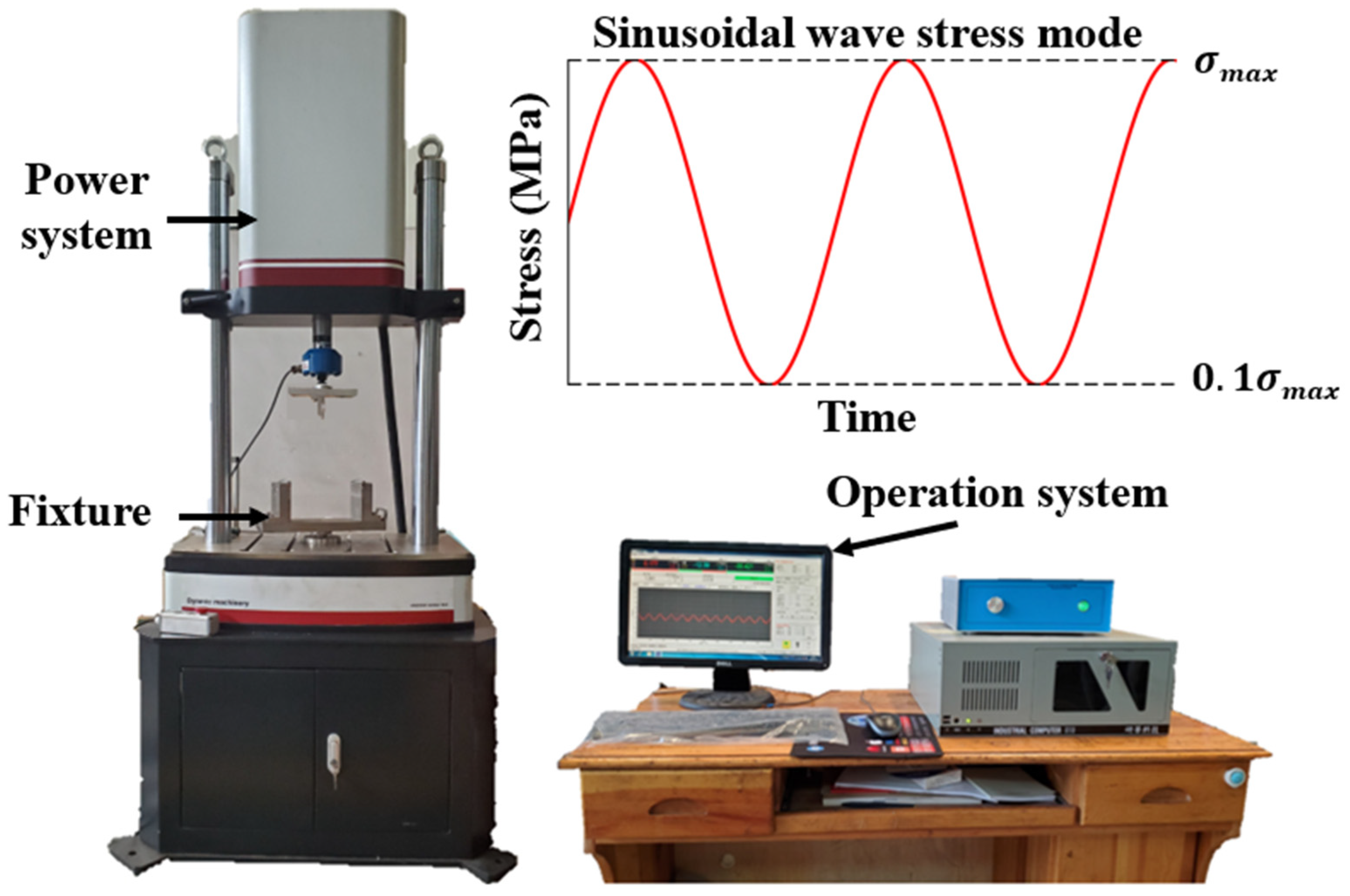
3. Three-Point Bending Fatigue Tests
4. Establishment of Fatigue Life Prediction Model
4.1. Relationship of Dissipated Energy and Loading Cycles
4.2. Relationship of Ratio of Dissipated Energy Change and Loading Cycles
4.3. Establishment of Prediction Model
5. Results and Discussion
5.1. Flexural Stiffness Modulus Analysis
5.2. Fatigue Life Analysis
5.3. Dissipated Angle Analysis
5.4. Cumulative Dissipated Energy Analysis
5.5. Prediction Model of Fatigue Life
6. Conclusions
- (1)
- The bending stiffness modulus (S) of PACM was determined by a three-point bending test as a function of stress level and loading frequency. The results showed that the S of PACM decreased with increasing stress level and increased with increasing loading frequency.
- (2)
- By comparing the fatigue properties of PACM under different grading types, it was found that regardless of the grading type, its fatigue life will shorten with the increase in stress level and increase with the growth in loading frequency. Under all conditions, PC-10 has the most extended fatigue life; that is, the smaller the aggregate size, the stronger the fatigue resistance of PACM.
- (3)
- The dissipation angle of PACM increases with the increase in stress level and decreases with the increase in loading frequency; under the same stress level and loading frequency, the dissipation angle of PACM with different gradations is ranked as PC-10 < PC-16 < PC-25.
- (4)
- The cumulative dissipated energy of PACM decreased with the increase in stress level and increased with the increase in loading frequency. Under the same stress level and loading frequency, the order of cumulative dissipated energy of PACM with different gradings was PC-10 > PC-16 > PC-25.
- (5)
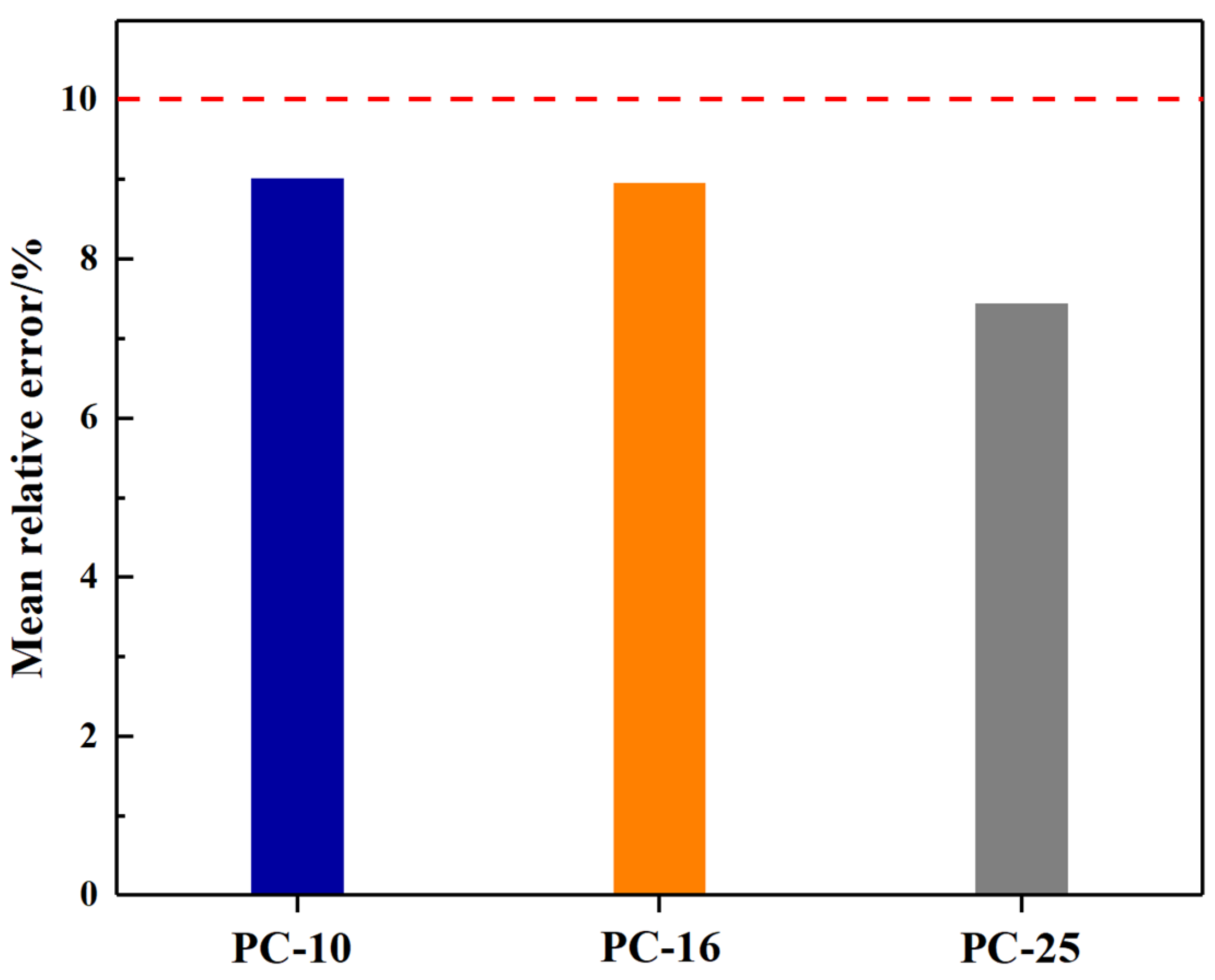
- This study correlated the platform value (PV) of the ratio of dissipated energy change (RDEC) with the fatigue life of PACM and established a fatigue life prediction model for PACM of different grading types. Compared with the measured values, the theoretical values of the prediction model were in good agreement with the experimental values, with a relative error of less than 10%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zofka, A.; Błażejowski, K.; Ostrowski, P. Fatigue performance of asphalt pavements with highly polymer-modified asphalt binders. Road Mater. Pavement Des. 2021, 22, S269–S286. [Google Scholar] [CrossRef]
- Dan, H.C.; Lu, B.; Li, M. Evaluation of asphalt pavement texture using multiview stereo reconstruction based on deep learning. Constr. Build. Mater. 2024, 412, 134837. [Google Scholar] [CrossRef]
- Hu, M.J.; Lyu, L.; Pahlavan, F.; Han, P.; Sun, D.; Fini, E.H. Toward sustainable non-emitting asphalts: Understanding diffusion-adsorption mechanisms of hazardous organic compounds. Adv. Sustain. Syst. 2025, 9, 2400868. [Google Scholar] [CrossRef]
- Yang, Q.L.; Zhu, Q.; Xu, R.; Hao, L.; Lu, G.; Wang, D. Synergism and Mechanisms of Aging Resistance in the Use of Graphene and Carbon Nanotubes in Bitumen Composites. Langmuir 2025, 41, 842–857. [Google Scholar] [CrossRef]
- Saha, D.C.; Mandal, J.N. Performance of reclaimed asphalt pavement reinforced with Bamboo geogrid and Bamboo geocell. Int. J. Pavement Eng. 2020, 21, 571–582. [Google Scholar] [CrossRef]
- Fu, C.L.; Liu, K.; Liu, Q.; Xu, P.; Dai, D.; Tong, J. Exploring directional energy conversion behavior of electromagnetic-based multifunctional asphalt pavement. Energy 2023, 268, 126573. [Google Scholar] [CrossRef]
- Hu, Y.P.; Sreeram, A.; Al-Tabbaa, A.; Airey, G.D. Physicochemical compatibility assessment of bio-additives and bitumen using solubility science-based approaches. Fuel 2025, 387, 134361. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, Y.; Wang, F.; Da, Y.; Zhang, H.; Pang, H. Investigation on the healing effects of microwave heating in eco-friendly pavement using e-waste. Mater. Struct. 2025, 58, 80. [Google Scholar] [CrossRef]
- Xiong, K.; Zhang, J.; He, Y.; Li, J.; Zhang, M.; Li, R.; Pei, J.; Li, Y.; Lyu, L. Introducing the mineral powder to strengthen polyurethane grouting materials for crack repair of asphalt pavements. Constr. Build. Mater. 2024, 453, 139023. [Google Scholar] [CrossRef]
- Vennapusa, P.K.R.; White, D.J. Field assessment of a jointed concrete pavement foundation treated with injected polyurethane expandable foam. Int. J. Pavement Eng. 2015, 16, 906–918. [Google Scholar] [CrossRef]
- Cui, C.; Guo, C.; Lu, Q.; Wang, F.; Fang, H. Fatigue performance of concrete–polyurethane composite materials under compression. J. Transp. Eng. Part B Pavements 2021, 147, 04021030. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, S.; Li, Y.; Ye, X. The expansion and mechanical property-based cavity expansion model for polyurethane grouting underneath the airport pavement. Transp. Geotech. 2023, 43, 101141. [Google Scholar] [CrossRef]
- Wang, F.M. Practice of non-water-reacting polymer grouting treatment to seepage. J. Hydroelectr. Eng. 2018, 37, 1–11. [Google Scholar] [CrossRef]
- Gao, X.; Wei, Y.; Wang, F.M.; Zhong, Y.H. Fatigue performance and microstructure evolution of polyurethane grouting materials under cyclic compression loading. Acta Mater. Compos. Sin. 2017, 34, 550–556. [Google Scholar] [CrossRef]
- Wei, Y. Microstructure and fatigue performance of polyurethane grout materials under compression. J. Mater. Civ. Eng. 2017, 29, 04017101. [Google Scholar] [CrossRef]
- Liu, K.; Tong, J.; Huang, M.; Wang, F.; Pang, H. Model and experimental studies on the effects of load characteristics and polyurethane densities on fatigue damage of rigid polyurethane grouting materials. Constr. Build. Mater. 2022, 347, 128595. [Google Scholar] [CrossRef]
- Haruna, S.I.; Ibrahim, Y.E.; Han, Z.; Farouk, A.I.B. Flexural response of concrete specimen retrofitted with pu grout material: Experimental and numerical modeling. Polymers 2023, 15, 4114. [Google Scholar] [CrossRef]
- Zhou, K.; Liang, H.; Huang, F.; Cheng, Z. Evaluation for anti-cracking performance of polyurethane grout based on overlay test. Front. Built Environ. 2024, 10, 1443587. [Google Scholar] [CrossRef]
- Opland, W.H.; Barnhart, V.T. Evaluation of the URETEK Method for Pavement Undersealing; Research and Technology Section, Materials and Technology Division, Michigan Department of Transportation: Lansing, MI, USA, 1995.
- Crawley, A.B. Evaluation of the Uretek Method for Pavement Undersealing and Faulting Correction; Interim Report; Mississippi Department of Transportation: Jackson, MS, USA, 1996.
- Zhong, Y.H.; Xu, S.; Chi, J.; Zhang, B.; Shen, G.; Yang, Z.; Chen, H.; Wang, B. Experimental study on the interface bonding characteristic of polyurethane and pavement materials. Constr. Build. Mater. 2023, 397, 132390. [Google Scholar] [CrossRef]
- Ran, M.P. Grouting mechanism of polyurethane composite materials in asphalt pavement subsidence. Materials 2023, 16, 7052. [Google Scholar] [CrossRef]
- Wu, H.; Shu, Y.; Liu, Y. Engineering performance of polyurethane bonded aggregates. Mater. Sci. 2017, 23, 166–172. [Google Scholar] [CrossRef]
- Zhou, J.L.; Zheng, M.; Wang, Q.; Yang, J.; Lin, T. Flexural fatigue behavior of polymer-modified pervious concrete with single sized aggregates. Constr. Build. Mater. 2016, 124, 897–905. [Google Scholar] [CrossRef]
- Yeon, K.S.; Choi, Y.S.; Kim, K.K.; Yeon, J.H. Flexural fatigue life analysis of unsaturated polyester-methyl methacrylate polymer concrete. Constr. Build. Mater. 2017, 140, 336–343. [Google Scholar] [CrossRef]
- Ghassemi, P.; Rajabi, H.; Toufigh, V. Fatigue performance of polymer and ordinary cement concrete under corrosive conditions: A comparative study. Eng. Fail. Anal. 2020, 111, 104493. [Google Scholar] [CrossRef]
- Xu, S.F.; Xu, M.; Zhang, Y.; Guo, Y.; Peng, G.; Xu, Y. An indoor laboratory simulation and evaluation on the aging resistance of polyether polyurethane concrete for bridge deck pavement. Front. Mater. 2020, 7, 237. [Google Scholar] [CrossRef]
- Xu, S.F.; Xu, M.; Fang, C.; Liu, H.; Ren, X.; Han, B. Laboratory investigation on traffic opening timing of polyether polyurethane concrete. J. Test. Eval. 2022, 50, 1871–1886. [Google Scholar] [CrossRef]
- Jia, Z.; Jia, D.; Sun, Q.; Wang, Y.; Ding, H. Preparation and mechanical-fatigue properties of elastic polyurethane concrete composites. Materials 2021, 14, 3839. [Google Scholar] [CrossRef]
- JTG F40-2004; Technical Specifications for Construction of Highway Asphalt Pavements. Research Institute of Highway, Ministry of Transport of China: Beijing, China, 2005.
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Research Institute of Highway, Ministry of Transport of China: Beijing, China, 2012.
- Sun, Y.; Fang, C.; Wang, J.; Ma, Z.; Ye, Y. Energy-based approach to predict fatigue life of asphalt mixture using three-point bending fatigue test. Materials 2018, 11, 1696. [Google Scholar] [CrossRef]
- Shen, S.H.; Airey, G.D.; Carpenter, S.H.; Huang, H. A dissipated energy approach to fatigue evaluation. Road Mater. Pavement Des. 2006, 7, 47–69. [Google Scholar] [CrossRef]
- Ghuzlan, K.A.; Carpenter, S.H. Energy-Derived, damage failure criterion for fatigue testing. J. Transp. Res. Rec. 2000, 1723, 141–149. [Google Scholar] [CrossRef]
- Carpenter, S.H.; Ghuzlan, K.A.; Shen, S. Fatigue endurance limit for highway and airport pavements. J. Transp. Res. Rec. 2003, 1832, 131–138. [Google Scholar] [CrossRef]
- Wu, J.; He, Y.; Yu, Z. Failure mechanism of rigid polyurethane foam under high temperature vibration condition by experimental and finite element method. J. Appl. Polym. Sci. 2020, 137, 48343. [Google Scholar] [CrossRef]
- Lou, K.K.; Wu, X.; Xiao, P.; Zhang, C. Investigation on fatigue performance of asphalt mixture reinforced by basalt fiber. Materials 2021, 14, 5596. [Google Scholar] [CrossRef] [PubMed]




| Literatures | Focus | Method | Key Findings |
|---|---|---|---|
| Gao et al. (2017) [14] | Compressive fatigue of PGM | Cyclic compression loading tests | Identified a three-stage fatigue response; failure stress threshold decreases with higher density |
| Wei et al. (2017) [15] | Fatigue behavior across densities | Experimental analysis | Confirmed three fatigue stages: elastic growth, steady development, and rapid failure |
| Liu et al. (2022) [16] | Fatigue damage evolution | Experimental and theoretical study | Fatigue life decreases with higher load and density, increases with faster loading rates |
| Haruna et al. (2023) [17] | Flexural response of retrofitted concrete | Three-point bending tests | PGMs improved deflection; top-surface retrofits showed linear deformation; bottom-surface had two stages |
| Zhou et al. (2024) [18] | Anti-cracking performance | Overlay Test | Polyurethane grout outperformed SBS asphalt in crack resistance at 25 °C |
| Xiong et al. (2024) [9] | Mineral powder in PGMs | Mechanical testing and UV aging | Excess powder reduced strength due to agglomeration; improved tensile strength by 12% post-aging |
| Opland & Barnhart (1995) [19] | Pavement stabilization using PGM | Field test before/after repair | Enhanced ride quality and load transfer at cracks and joints after PGM injection |
| Crawley et al. (1996) [20] | Joint performance post stabilization | Field evaluation | Increased load transfer efficiency; voids from initial injection mitigated by reinjection |
| Vennapusa & White (2015) [10] | Deteriorated pavement repair | Field tests | Faulting and load transfer improved after PGM grouting |
| Cui et al. (2021) [11] | Fatigue of concrete-PGM composites | Cyclic compressive loading | Identified three-stage strain response; grout thickness had most significant impact |
| Zhong et al. (2023) [21] | Bonding between PGM and pavement | Interface roughness & density tests | Denser polyurethane forms thicker film; roughness and density affect bond strength and failure modes |
| Ran et al. (2023) [22] | Grouting mechanism in asphalt subsidence | CT and GPR analysis | Polyurethane foam filled voids forming stable structures; no displacement after grouting |
| Type | Results | Specification | |
|---|---|---|---|
| Coarse aggregate | Density [g/cm3] | 2.73 | / |
| Crushing value [%] | 21.7 | ≤26 | |
| Los Angeles abrasion value | 25.2 | ≤28 | |
| Water Absorption [%] | 1.6 | ≤2.0 | |
| Content of needle and flaky particles [%] | 11.36 | ≤15 | |
| Content of soft particles | 1.2 | ≤3 | |
| Soundness | 10.5 | ≤12 | |
| Fine aggregate | Density [g/cm3] | 2.687 | / |
| Sand equivalent [%] | 67 | ≥60 | |
| Mud content [%] | 1.6 | ≤3 | |
| Limestone filler | Density [g/cm3] | 2.71 | / |
| Moisture content [%] | 0.23 | ≤1 | |
| Hydrophilic coefficient [%] | 0.67 | ≤1 |
| PC-10 | PC-16 | PC25 | |
|---|---|---|---|
| Failure load | 3.96 kN | 2.67 kN | 3.23 kN |
| Maximum deformation | 1.74 mm | 1.66 mm | 2.89 mm |
| Type | Stress Level | Dissipated Angle (°) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 Hz | SD | N | 5Hz | SD | N | 10 Hz | SD | N | ||
| PC-10 | 0.3 | 24.5 | 1.23 | 21,738 | 23.1 | 1.16 | 54,019 | 21.6 | 1.08 | 90,227 |
| 0.5 | 29.3 | 1.47 | 14,252 | 28.5 | 1.43 | 43,294 | 28.2 | 1.41 | 70,970 | |
| 0.7 | 34.7 | 1.74 | 10,001 | 31.9 | 1.60 | 36,131 | 30.4 | 1.52 | 42,835 | |
| PC-16 | 0.3 | 26.8 | 1.34 | 13,172 | 25.2 | 1.26 | 52,008 | 23.5 | 1.18 | 83,743 |
| 0.5 | 31.2 | 1.56 | 10,235 | 29.6 | 1.48 | 42,756 | 28.8 | 1.44 | 61,645 | |
| 0.7 | 37.5 | 1.88 | 4844 | 35.3 | 1.77 | 23,882 | 34.2 | 1.71 | 39,249 | |
| PC-25 | 0.3 | 35.1 | 1.76 | 8317 | 31.6 | 1.58 | 46,141 | 27.4 | 1.37 | 75,664 |
| 0.5 | 41.7 | 2.09 | 3221 | 36.2 | 1.81 | 35,919 | 33.1 | 1.66 | 52,078 | |
| 0.7 | 48.3 | 2.42 | 1445 | 43.9 | 2.20 | 20,103 | 39.5 | 1.98 | 36,404 | |
| Type | Stress Level | Cumulative Dissipated Energy (MJ/m3) | |||||
|---|---|---|---|---|---|---|---|
| 2 Hz | SD | 5 Hz | SD | 10 Hz | SD | ||
| PC-10 | 0.3 | 68.388 | 3.42 | 153.261 | 6.13 | 184.965 | 9.25 |
| 0.5 | 59.858 | 2.99 | 124.244 | 6.21 | 178.135 | 8.91 | |
| 0.7 | 43.204 | 2.16 | 118.149 | 5.91 | 112.228 | 5.61 | |
| PC-16 | 0.3 | 40.735 | 2.04 | 147.936 | 7.40 | 181.722 | 9.09 |
| 0.5 | 38.725 | 1.94 | 131.580 | 6.58 | 146.099 | 7.30 | |
| 0.7 | 20.781 | 1.04 | 84.781 | 4.24 | 118.140 | 5.91 | |
| PC-25 | 0.3 | 25.367 | 1.27 | 125.357 | 6.27 | 158.138 | 7.91 |
| 0.5 | 13.271 | 0.66 | 115.814 | 5.79 | 125.508 | 6.28 | |
| 0.7 | 6.387 | 0.32 | 70.159 | 3.51 | 113.945 | 5.70 | |
| Grading Types | A | B | R2 |
|---|---|---|---|
| PC-10 | 1.6146 | −1.095 | 0.9714 |
| PC-16 | 2.1717 | −1.072 | 0.9826 |
| PC-25 | 0.0864 | −1.515 | 0.9944 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Zhang, S.; Huang, M.; Liu, K.; Fu, C. Assessment of Fatigue Life in Grouted Polyurethane Composites for Pavement Maintenance. Materials 2025, 18, 1806. https://doi.org/10.3390/ma18081806
Wang F, Zhang S, Huang M, Liu K, Fu C. Assessment of Fatigue Life in Grouted Polyurethane Composites for Pavement Maintenance. Materials. 2025; 18(8):1806. https://doi.org/10.3390/ma18081806
Chicago/Turabian StyleWang, Fang, Shiyi Zhang, Muyang Huang, Kai Liu, and Chaoliang Fu. 2025. "Assessment of Fatigue Life in Grouted Polyurethane Composites for Pavement Maintenance" Materials 18, no. 8: 1806. https://doi.org/10.3390/ma18081806
APA StyleWang, F., Zhang, S., Huang, M., Liu, K., & Fu, C. (2025). Assessment of Fatigue Life in Grouted Polyurethane Composites for Pavement Maintenance. Materials, 18(8), 1806. https://doi.org/10.3390/ma18081806





