Rolling Contact Fatigue Behavior of Pitch Bearing Raceway in Offshore Wind Turbines
Abstract
:1. Introduction
2. Finite Element Model and Damage-Coupled Behavior
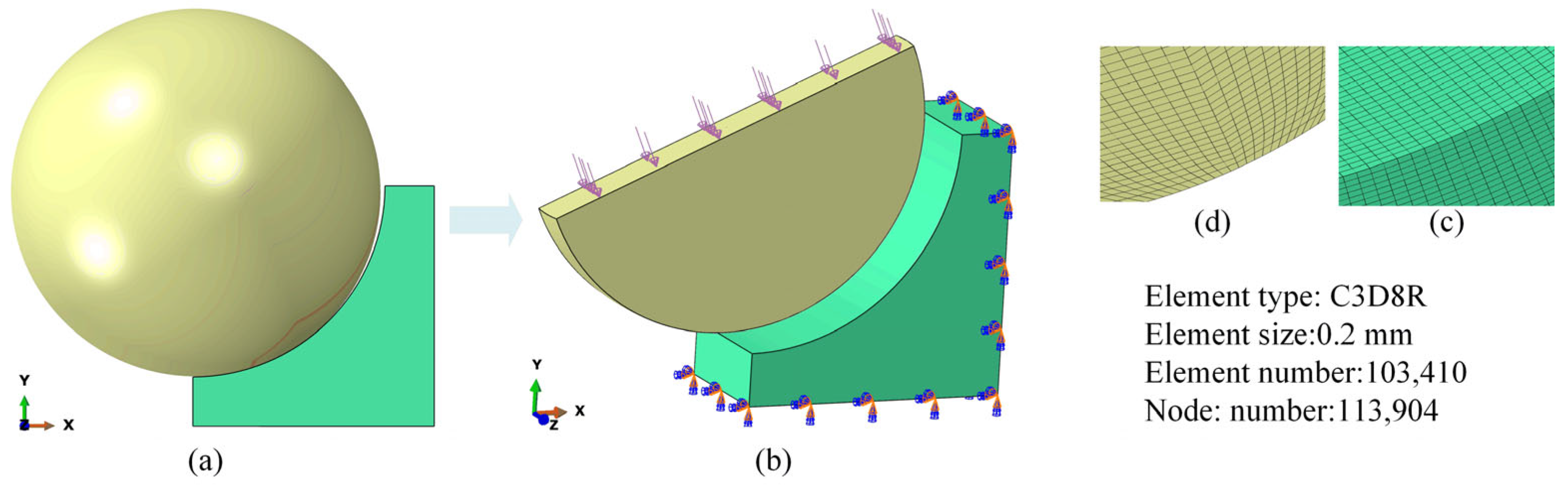
2.1. Finite Element Model
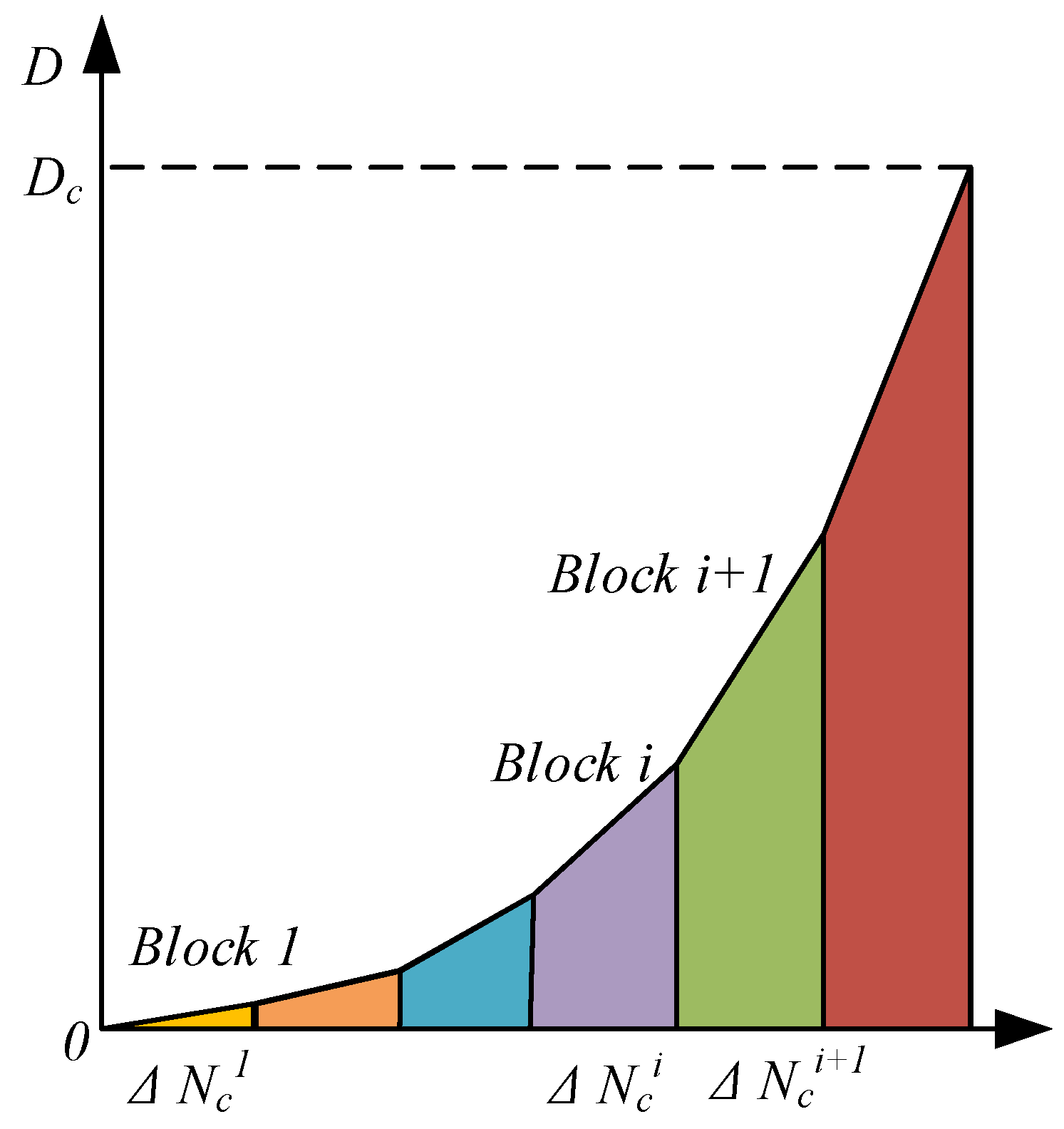
2.2. Damage-Coupled Model for Pitch Bearing
3. Results and Discussion
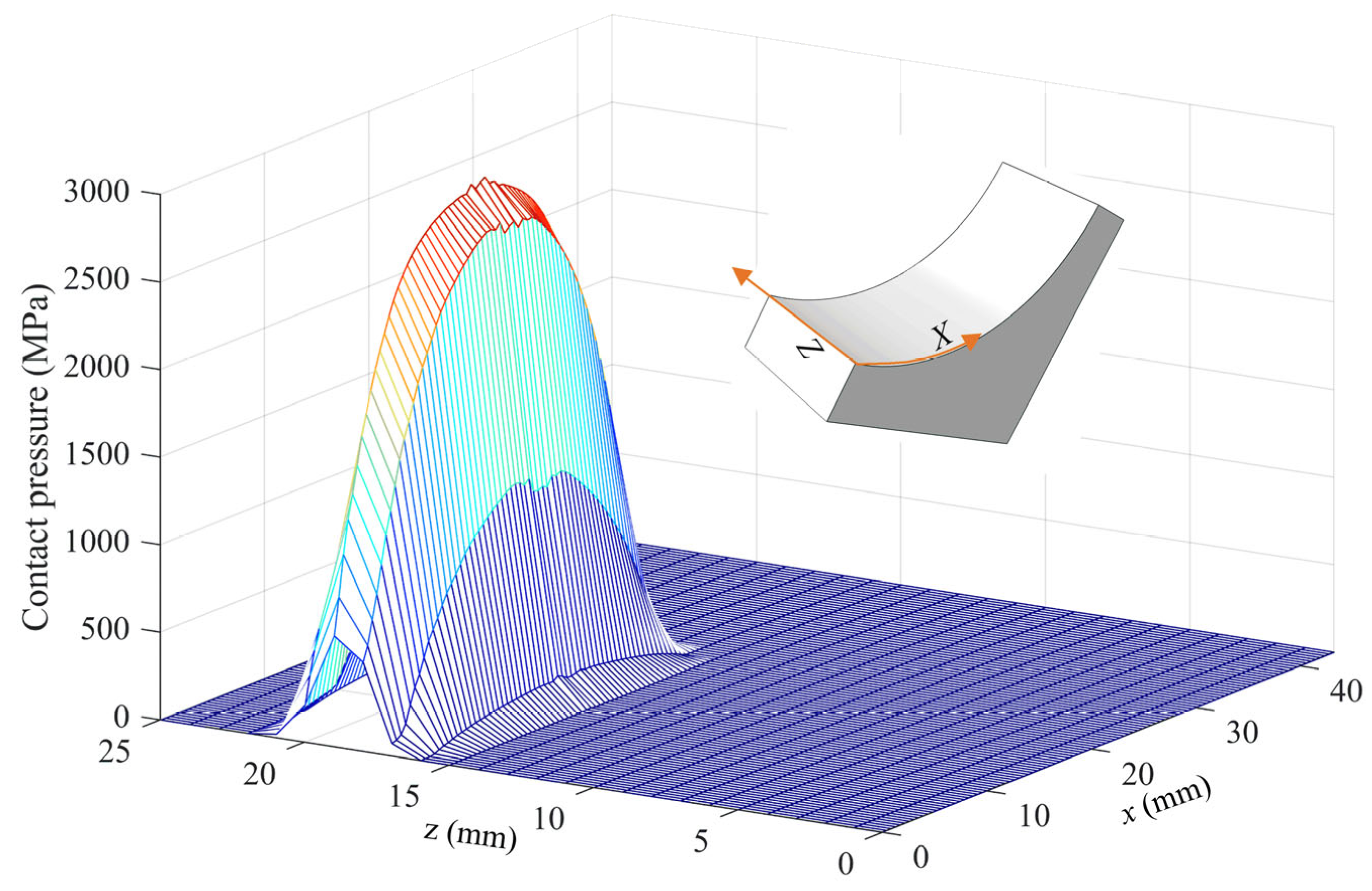
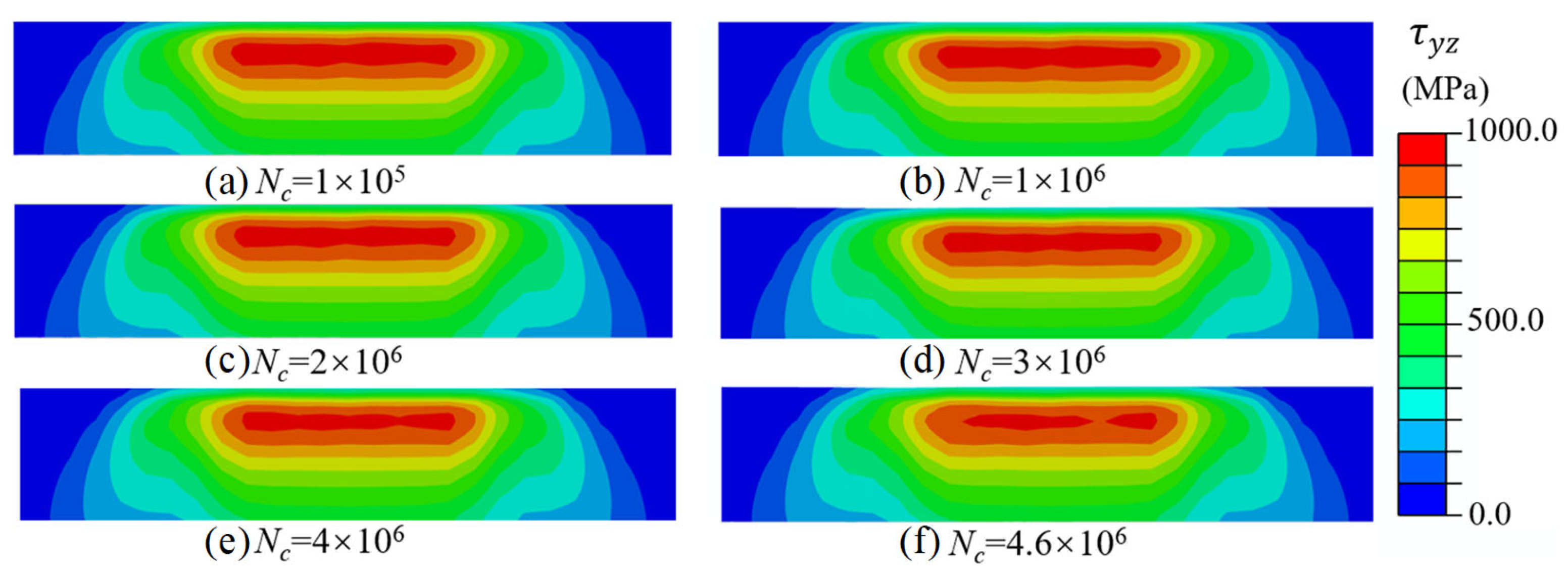
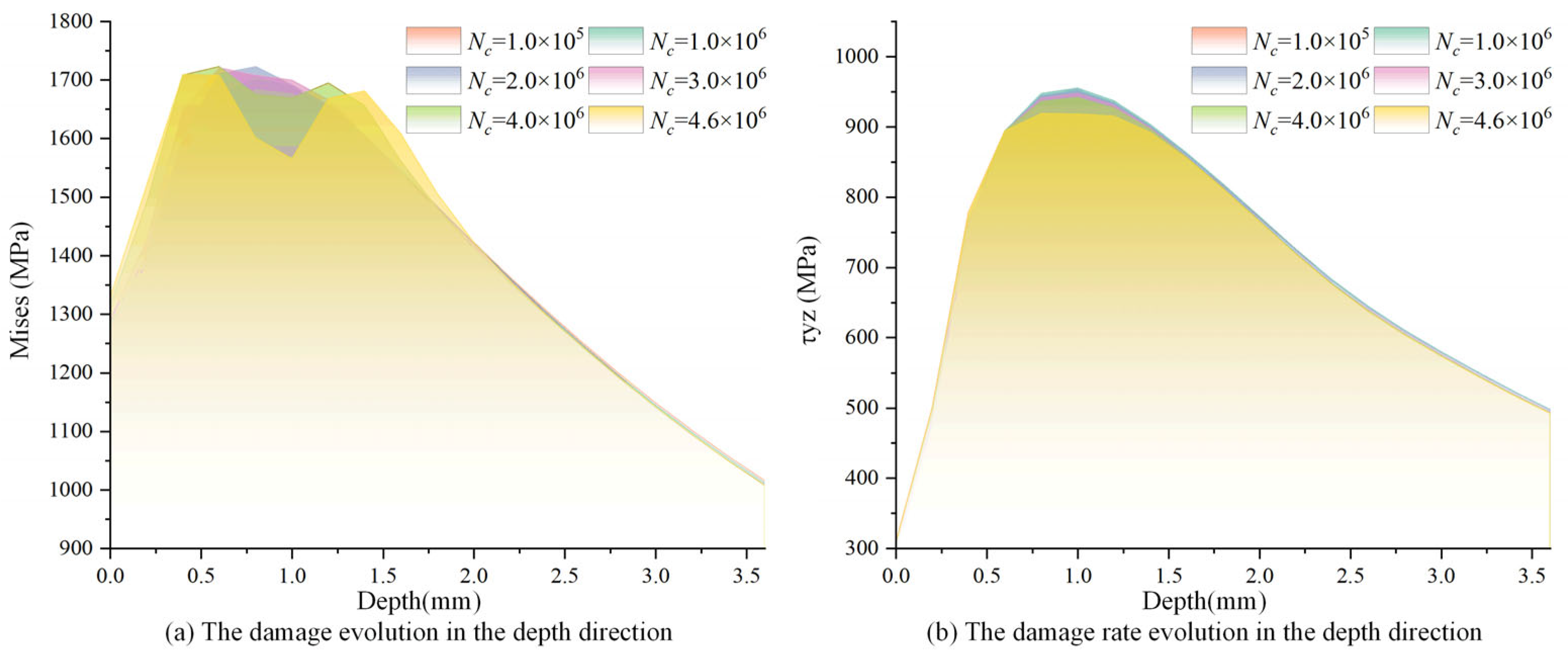
3.1. Stress Response Evolution of Pitch Bearing
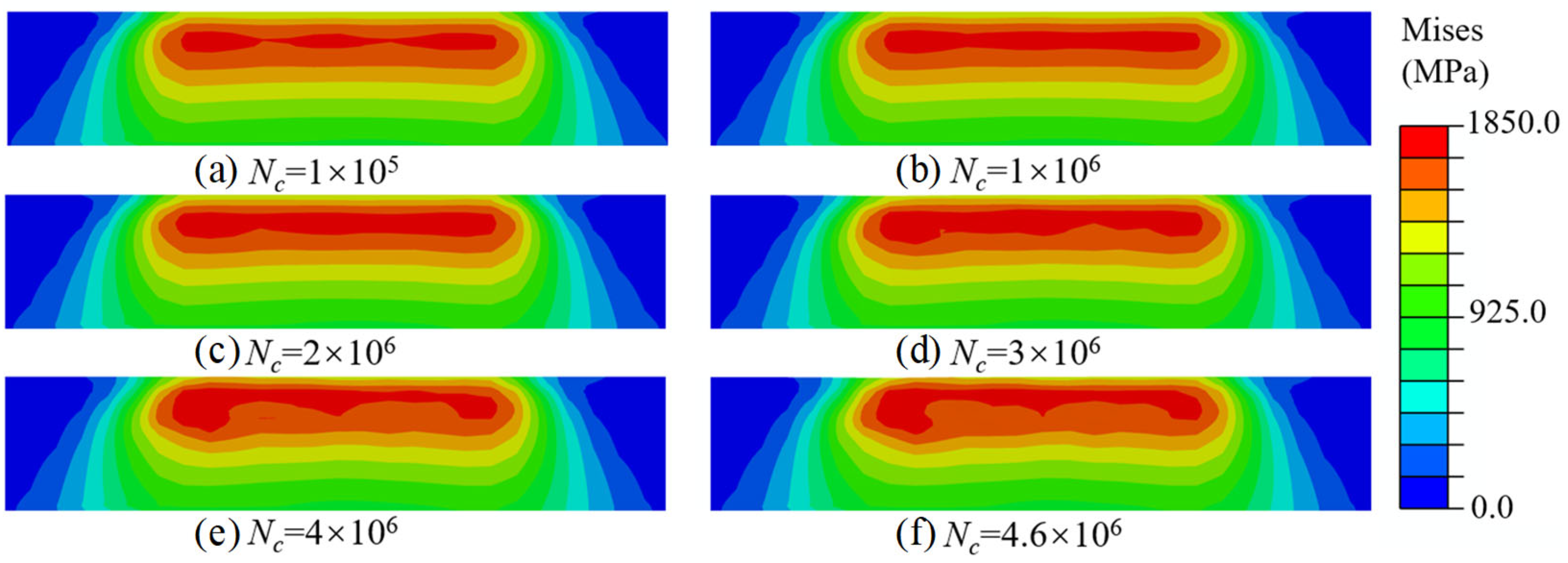
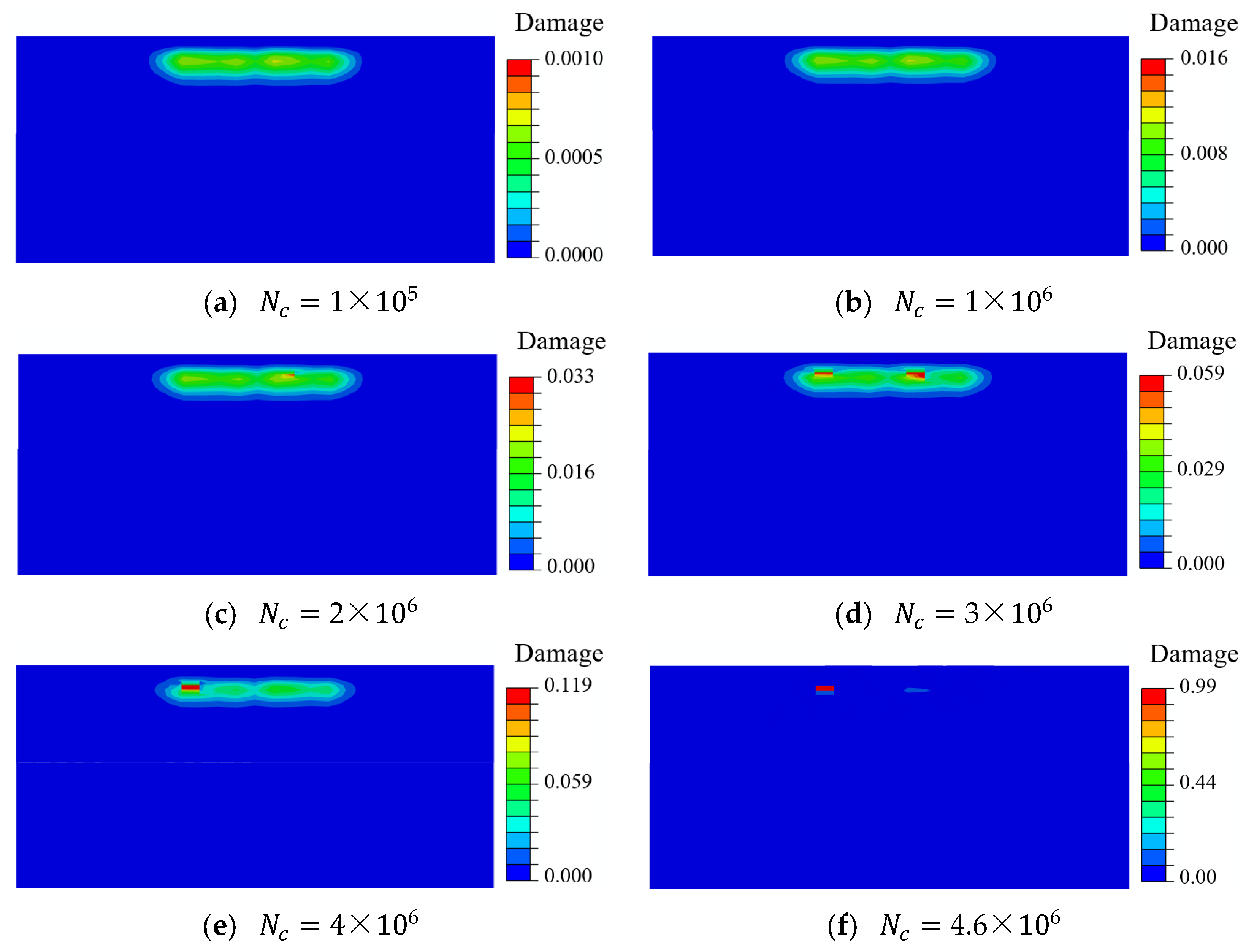
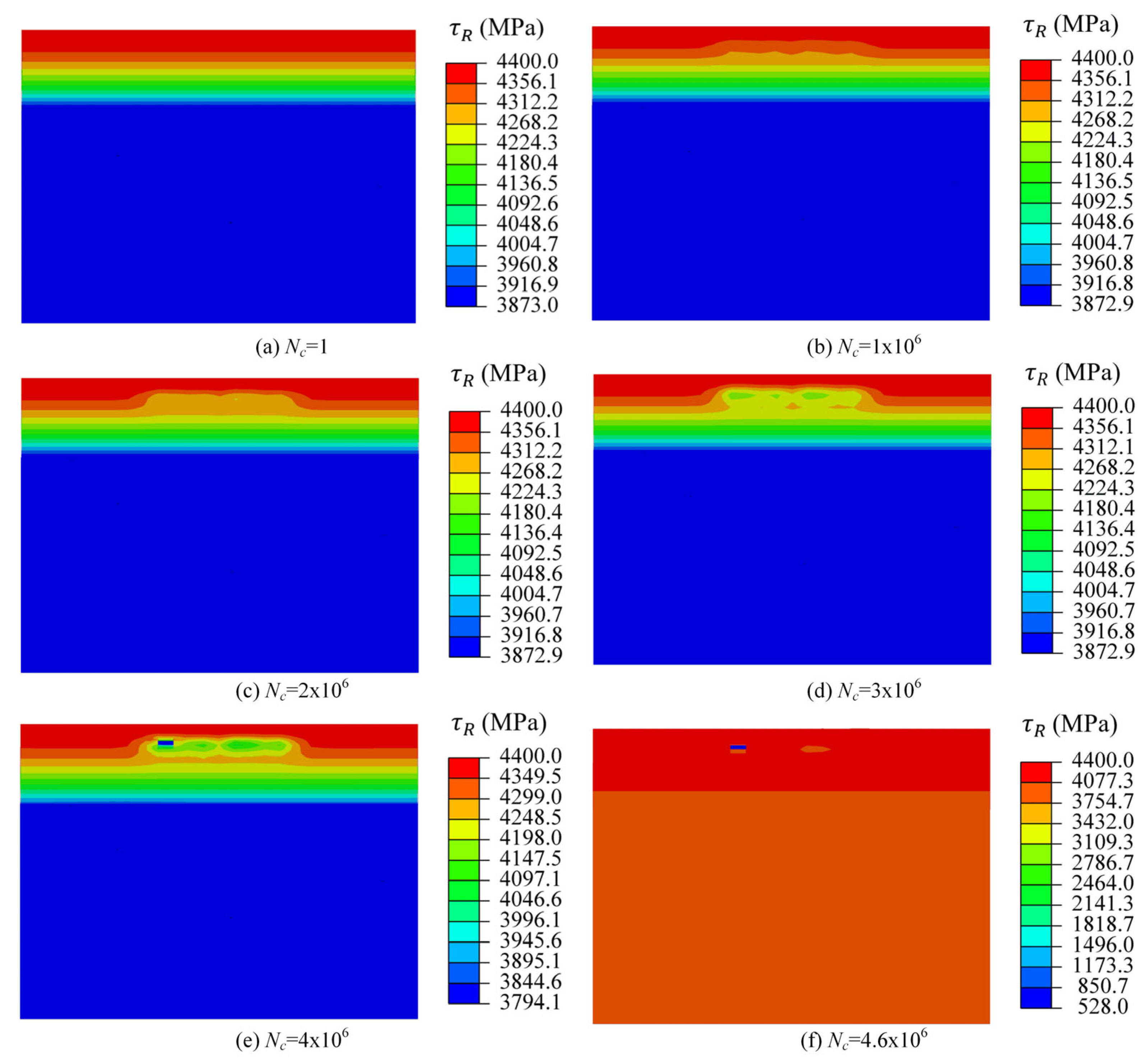
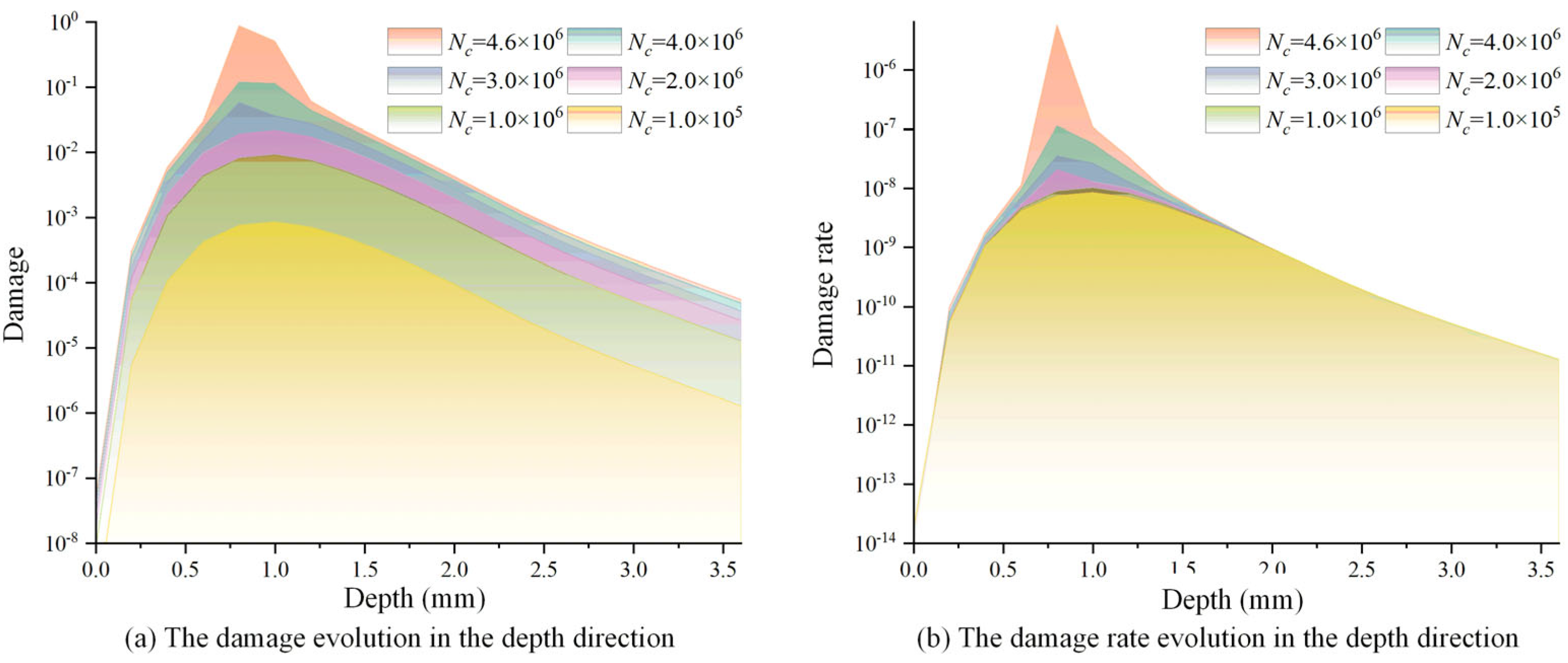
3.2. Damage and Material Properties Evolution of Pitch Bearing
4. Conclusions
- Under the rated operational condition, the pitch bearing raceway exhibited a peak contact pressure of 3307 MPa; the corresponding maximum von Mises stress was 1775 MPa within the critical subsurface layer at 0.8 mm depth.
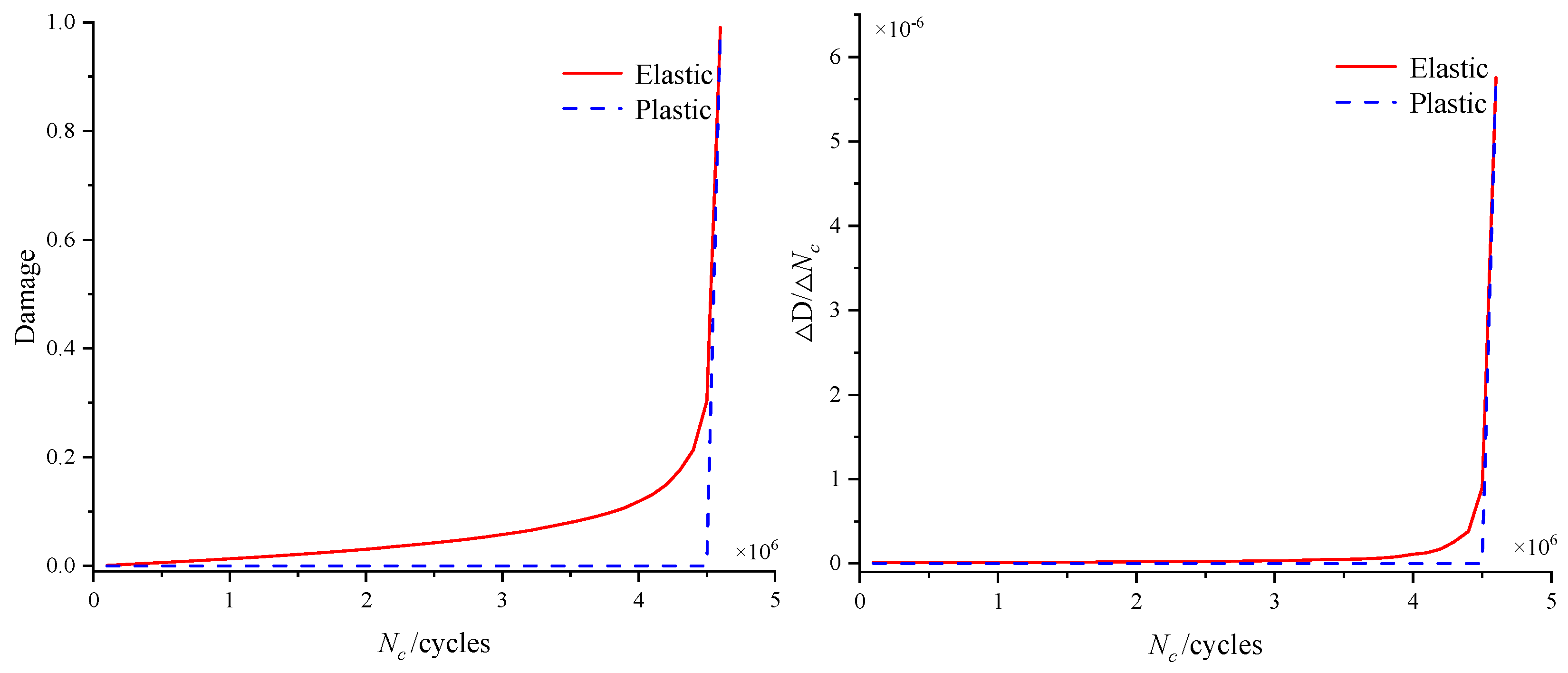
- The fatigue damage evolution demonstrated nonlinear accumulation patterns, in which the cumulative damage remained below 0.12 throughout the initial 90% of the fatigue life cycle.
- The fatigue failure of the raceway initially occurred at the position with the maximum shear stress range rather than at the position with the maximum von Mises stress.
- Elastic damage accumulation served as the predominant governing factor in determining the operational fatigue lifespan under operational cyclic loading conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schwack, F.; Bader, N.; Leckner, J.; Demaille, C.; Poll, G. A study of grease lubricants under wind turbine pitch bearing conditions. Wear 2020, 454, 203335. [Google Scholar] [CrossRef]
- Bogdan, W.; Agnieszka, C. Effect of ring misalignment on the fatigue life of the radial cylindrical roller bearing. Int. J. Mech. Sci. 2016, 111, 1–11. [Google Scholar]
- Krynke, M.; Ulewicz, R. Analysis of the influence of slewing bearing mounting on their static load capacity. Transp. Res. Procedia 2019, 40, 745–750. [Google Scholar] [CrossRef]
- Xia, Z.F.; Wu, D.; Zhang, X.C.; Wang, J.Q.; Han, E.H. Rolling contact fatigue failure mechanism of bearing steel on different surface roughness levels under heavy load. Int. J. Fatigue 2024, 179, 108042. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y. Research on the rolling contact fatigue life of the bearing considering the friction effect. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 2238–2264. [Google Scholar] [CrossRef]
- Qin, H.; Doll, G.L. Effects of water contamination on micropitting and rolling contact fatigue of bearing steels. J. Tribol. 2023, 145, 011501. [Google Scholar] [CrossRef]
- Guan, J.; Wang, L.; Zhang, Z.; Shi, X.; Ma, X. Fatigue crack nucleation and propagation at clustered metallic carbides in M50 bearing steel. Tribol. Int. 2018, 119, 165–174. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Subhash, G.; Arakere, N. Evolution of subsurface plastic zone due to rolling contact fatigue of M-50 NiL case hardened bearing steel. Int. J. Fatigue 2014, 59, 102–113. [Google Scholar] [CrossRef]
- Wang, Y.B.; Li, S.X.; Lu, S.Y.; Cao, J. New microstructure of butterfly white etching area in rolling contact fatigue of bearing steel. Tribol. Int. 2023, 188, 108811. [Google Scholar] [CrossRef]
- Abdullah, M.U.; Khan, Z.A.; Kruhoeffer, W. Evaluation of dark etching regions for standard bearing steel under accelerated rolling contact fatigue. Tribol. Int. 2020, 152, 106579. [Google Scholar] [CrossRef]
- Fu, H.W.; Wang, W.J.; Lu, Y.Y.; Zhang, J.G.; Zhang, C.; Zhang, H.; Rivera-Díaz-del-Castillo, P.E.J. The origin of microstructural alterations in M50 bearing steel undergoing rolling contact fatigue. Int. J. Fatigue 2023, 175, 12. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, A.M.; Yang, M.S. Mechanism of microstructural alterations of M50 bearing steel during rolling contact fatigue under high loads. Metals 2023, 13, 769. [Google Scholar] [CrossRef]
- Chen, J.H.; Xie, C.; Li, S.X.; Lu, S.Y. White etching area damage induced by shear localization in rolling contact fatigue of bearing steel. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 170–186. [Google Scholar] [CrossRef]
- Su, Y.S.; Li, S.X.; Yu, F.; Lu, S.Y.; Wang, Y.G. Revealing the shear band origin of white etching area in rolling contact fatigue of bearing steel. Int. J. Fatigue 2021, 142, 105929. [Google Scholar] [CrossRef]
- Morsdorf, L.; Mayweg, D.; Li, Y.; Diederichs, A.; Raabe, D.; Herbig, M. Moving cracks form white etching areas during rolling contact fatigue in bearings. Mater. Sci. Eng. A Struct. 2020, 771, 138659. [Google Scholar] [CrossRef]
- Zhu, X.T.; Pan, J.Z.; Liu, D.Y.; Zhao, X.J.; Ren, R.M. Rolling contact fatigue resistance and damage evolution of carburized bearing steel treated by surface ultrasonic rolling process (SURP). Wear 2023, 524, 204773. [Google Scholar] [CrossRef]
- Cao, Z.X.; Liu, T.Q.; Yu, F.; Cao, W.Q.; Zhang, X.D.; Weng, Y.Q. Carburization induced extra-long rolling contact fatigue life of high carbon bearing steel. Int. J. Fatigue 2020, 131, 105351. [Google Scholar] [CrossRef]
- Cai, X.; Hu, X.Q.; Lu, X.Y.; Liu, H.W.; Cao, Y.F.; Li, D.Z. Exploring the ultrahigh rolling contact fatigue life of M50 bearing steel by adjusting the cryogenic sequence. J. Mater. Sci. Technol. 2024, 169, 243–250. [Google Scholar] [CrossRef]
- Yang, L.Q.; Xue, W.H.; Gao, S.Y.; Li, L.L.; Cao, Y.F.; Liu, H.W.; Duan, D.L.; Li, D.Z.; Li, S. Rolling contact fatigue behaviour of M50 bearing steel with rare earth addition. Int. J. Fatigue 2023, 177, 107940. [Google Scholar] [CrossRef]
- Liang, X.Z.; Zhao, G.H.; Owens, J.; Gong, P.; Rainforth, W.M.; Rivera-Díaz-del-Castillo, P.E.J. Hydrogen-assisted microcrack formation in bearing steels under rolling contact fatigue. Int. J. Fatigue 2020, 134, 105485. [Google Scholar] [CrossRef]
- Qu, H.X.; Yao, L.S.; Zhan, K. Rolling contact fatigue damage analysis of G10CrNi3Mo steel bearing inner ring by x-ray measurements. Coatings 2023, 13, 13122021. [Google Scholar] [CrossRef]
- Kunzelmann, B.; Rycerz, P.; Xu, Y.L.; Arakere, N.K.; Kadiric, A. Prediction of rolling contact fatigue crack propagation in bearing steels using experimental crack growth data and linear elastic fracture mechanics. Int. J. Fatigue 2023, 168, 107449. [Google Scholar] [CrossRef]
- Shao, Z.H.; Zhu, Y.K.; Zhang, P.; Cao, Y.F.; Wang, B.; Xu, Z.K.; Liu, H.Z.; Gu, X.Z.; Liu, H.W.; Li, D.Z.; et al. Effect of primary carbides on rolling contact fatigue behaviors of M50 bearing steel. Int. J. Fatigue 2024, 179, 108054. [Google Scholar] [CrossRef]
- Wang, L.W.; Sheng, X.Y.; Yao, Z.M.; Luo, J.B. Peridynamic modeling of hydrogen-assisted white etching cracks in bearing steel under rolling contact fatigue. Int. J. Fatigue 2023, 173, 107698. [Google Scholar] [CrossRef]
- Ravi, G.; De Waele, W.; Nikolic, K.; Petrov, R.; Hertel, S. Numerical modelling of rolling contact fatigue damage initiation from non-metallic inclusions in bearing steel. Tribol. Int. 2023, 180, 108290. [Google Scholar] [CrossRef]
- Foko, F.F.; Rueth, L.; Koch, O.; Sauer, B. Study of the plastic behaviour of rough bearing surfaces using a half-space contact model and the fatigue life estimation according to the Fatemi-Socie model. Lubricants 2023, 11, 133. [Google Scholar]
- Yu, A.D.; Huang, H.Z.; Li, Y.F.; Li, H.; Zeng, Y. Fatigue life prediction of rolling bearings based on modified SWT mean stress correction. Chin. J. Mech. Eng. 2021, 34, 110. [Google Scholar] [CrossRef]
- Menck, O. The finite segment method—A numerical rolling contact fatigue life model for bearings subjected to stochastic operating conditions. J. Tribol. 2023, 145, 031201. [Google Scholar] [CrossRef]
- Vijay, A.; Sadeghi, F. A crystal plasticity and cohesive element model for rolling contact fatigue of bearing steels. Tribol. Int. 2022, 173, 107607. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, X.; Guo, R.B.; Sun, S.G. A rolling contact fatigue life prediction model for bearing steel considering its gradient structure due to cyclic hardening. Int. J. Damage Mech. 2024, 33, 293–309. [Google Scholar] [CrossRef]
- Lemaitre, J.; Desmorat, R. Engineering Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Ma, L.; Liu, J.Y.; Guo, F.; Li, X.M.; Zhang, X.H. Research on rolling contact fatigue failure of the bearing used in high-speed electric multiple units’ axle box based on a damage-coupled elastic-plastic constitutive model. Lubricants 2023, 11, 330. [Google Scholar] [CrossRef]
- Lorenz, S.J.; Sadeghi, F.; Trivedi, H.K.; Kirsch, M.S. Investigation into rolling contact fatigue performance of aerospace bearing steels. Int. J. Fatigue 2023, 172, 107646. [Google Scholar] [CrossRef]
- Lorenz, S.J.; Sadeghi, F.; Wang, C. Effect of spatial hardness distribution in rolling contact fatigue performance of bearing contacts. Tribol. Int. 2022, 171, 107550. [Google Scholar] [CrossRef]
- Lorenz, S.J.; Sadeghi, F.; Trivedi, H.K.; Kirsch, M.S.; Wang, C. Effects of grain refinement on rolling contact fatigue in bearing contacts. J. Tribol. 2021, 143, 1–32. [Google Scholar] [CrossRef]
- He, H.; Chen, Y.; Jin, X.; Liu, H.; Wang, C. Study on predicting rolling contact fatigue of pitch bearing raceway in offshore wind turbine. Int. J. Fatigue 2024, 184, 108284. [Google Scholar] [CrossRef]
- Cui, L.; Su, Y. Contact fatigue life prediction of rolling bearing considering machined surface integrity. Ind. Lubr. Tribol. 2022, 74, 73–80. [Google Scholar] [CrossRef]
- Kang, G.; Liu, Y.; Ding, J.; Gao, Q. Uniaxial ratcheting and fatigue failure of tempered 42CrMo steel: Damage evolution and damage-coupled visco-plastic constitutive model. Int. J. Plast. 2009, 25, 838–860. [Google Scholar] [CrossRef]
- He, H.; Liu, H.; Zhu, C.; Wei, P.; Sun, Z. Study of rolling contact fatigue behavior of a wind turbine gear based on damage-coupled elastic-plastic model. Int. J. Mech. Sci. 2018, 141, 512–519. [Google Scholar] [CrossRef]
- Warhadpande, A.; Sadeghi, F.; Kotzalas, M.N.; Doll, G. Effects of plasticity on subsurface initiated spalling in rolling contact fatigue. Int. J. Fatigue 2012, 36, 80–95. [Google Scholar] [CrossRef]
- Moghaddam, S.M.; Sadeghi, F.; Weinzapfel, N.; Liebel, A. A damage mechanics approach to simulate butterfly wing formation around nonmetallic inclusions. J. Tribol.-Trans. Asme 2015, 137, 011400. [Google Scholar] [CrossRef]



| C | Si | Mn | Cr | P | S | Mo |
|---|---|---|---|---|---|---|
| 0.40 | 0.30 | 0.75 | 1.05 | 0.01 | 0.004 | 0.25 |
| 12.09 | 6.05 | ||
|---|---|---|---|
| 4806.45 MPa | 28.60 MPa | ||
| 3018.25 MPa | 11.28 MPa |
| N (×105 Cycles) | Damage | Damage Rate | von Mises (MPa) | Shear Stress Range (MPa) | PEEQ |
|---|---|---|---|---|---|
| 1 | 0.0008 | 7.51 × 10−9 | 1682.8 | 918.5 | 0 |
| 10 | 0.0081 | 8.84 × 10−9 | 1702.9 | 947.4 | 0 |
| 20 | 0.0190 | 2.06 × 10−8 | 1722.3 | 944.1 | 1.07 × 10−5 |
| 30 | 0.0579 | 3.53 × 10−8 | 1708.0 | 940.7 | 2.30 × 10−4 |
| 40 | 0.1187 | 1.13 × 10−7 | 1675.0 | 936.3 | 7.28 × 10−4 |
| 46 | 0.9913 | 5.76 × 10−6 | 1601.1 | 918.5 | 1.43 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Chen, Y.; Liu, Y.; Zhu, Y.; Jin, X. Rolling Contact Fatigue Behavior of Pitch Bearing Raceway in Offshore Wind Turbines. Materials 2025, 18, 1816. https://doi.org/10.3390/ma18081816
He H, Chen Y, Liu Y, Zhu Y, Jin X. Rolling Contact Fatigue Behavior of Pitch Bearing Raceway in Offshore Wind Turbines. Materials. 2025; 18(8):1816. https://doi.org/10.3390/ma18081816
Chicago/Turabian StyleHe, Haifeng, Yiming Chen, Yang Liu, YongChao Zhu, and Xin Jin. 2025. "Rolling Contact Fatigue Behavior of Pitch Bearing Raceway in Offshore Wind Turbines" Materials 18, no. 8: 1816. https://doi.org/10.3390/ma18081816
APA StyleHe, H., Chen, Y., Liu, Y., Zhu, Y., & Jin, X. (2025). Rolling Contact Fatigue Behavior of Pitch Bearing Raceway in Offshore Wind Turbines. Materials, 18(8), 1816. https://doi.org/10.3390/ma18081816





