Cyclic Behavior of U-Shaped Flexural Plates for Their Implementation in Multidirectional Energy Dissipation Devices
Abstract
1. Introduction
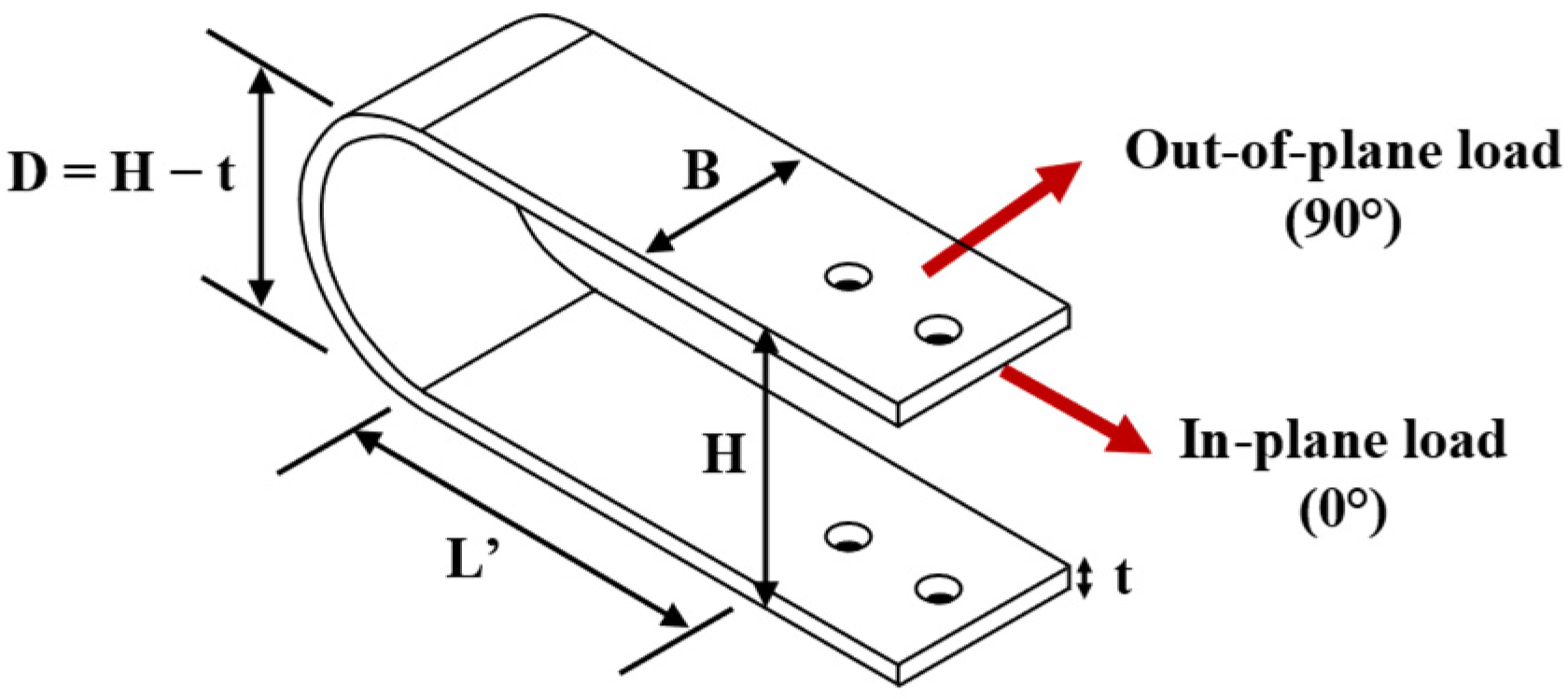
2. Experimental Program
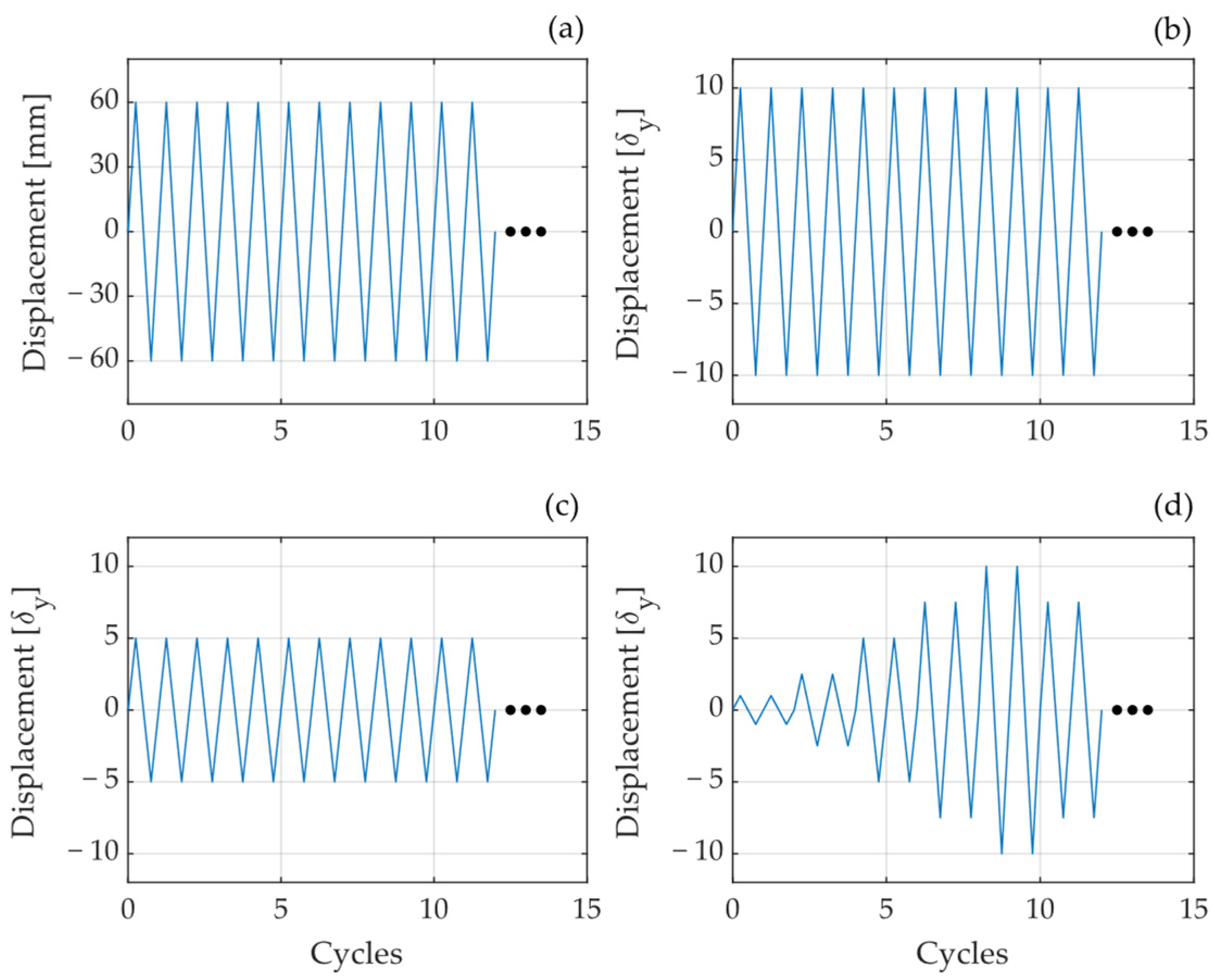
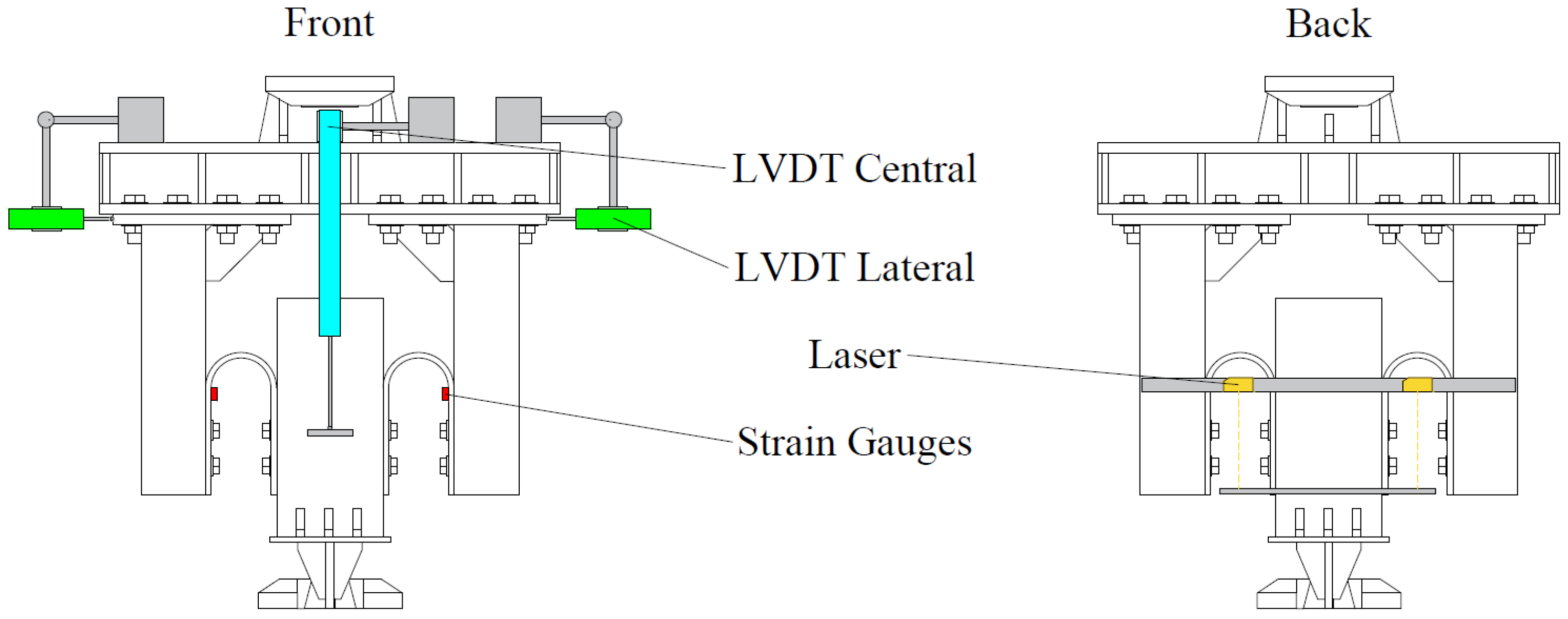
2.1. Test Procedure and Instrumentation
2.2. Test Results and Discussion
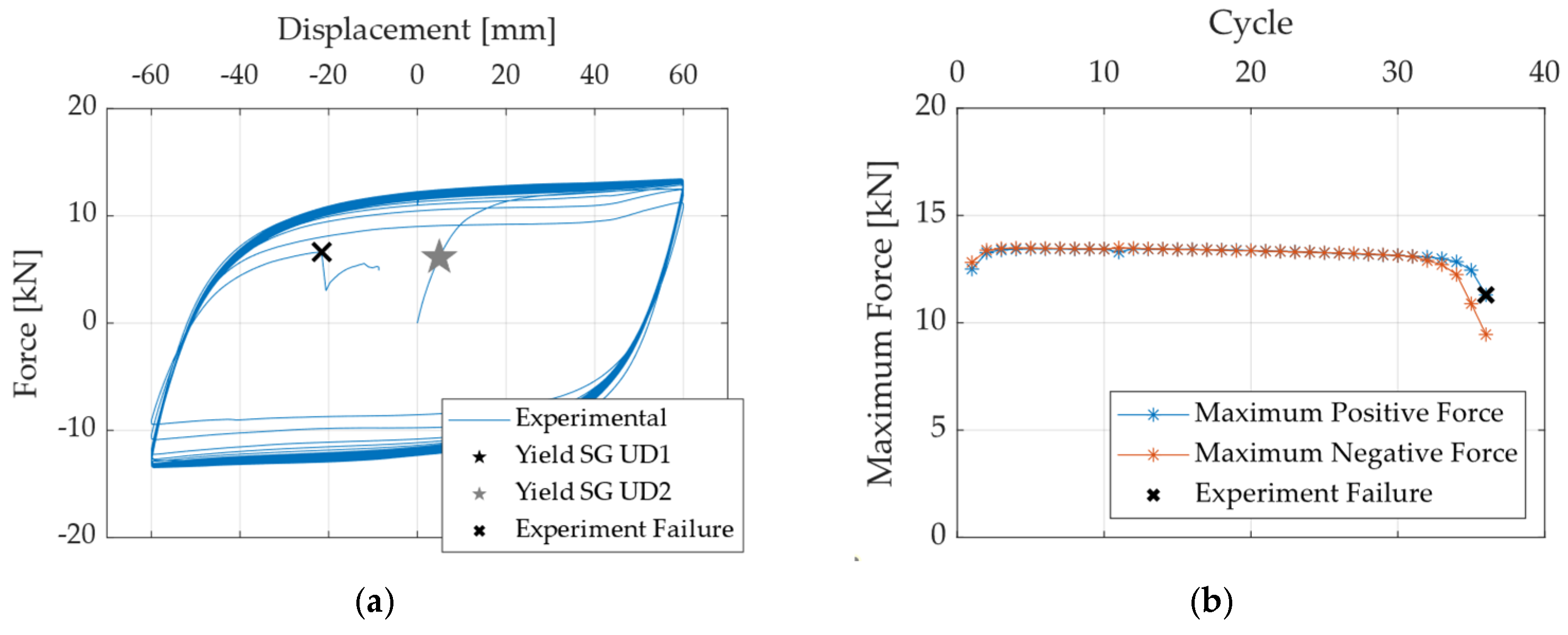
2.2.1. Deformation Mode, Damage, and Failure
2.2.2. Hysteresis Curves
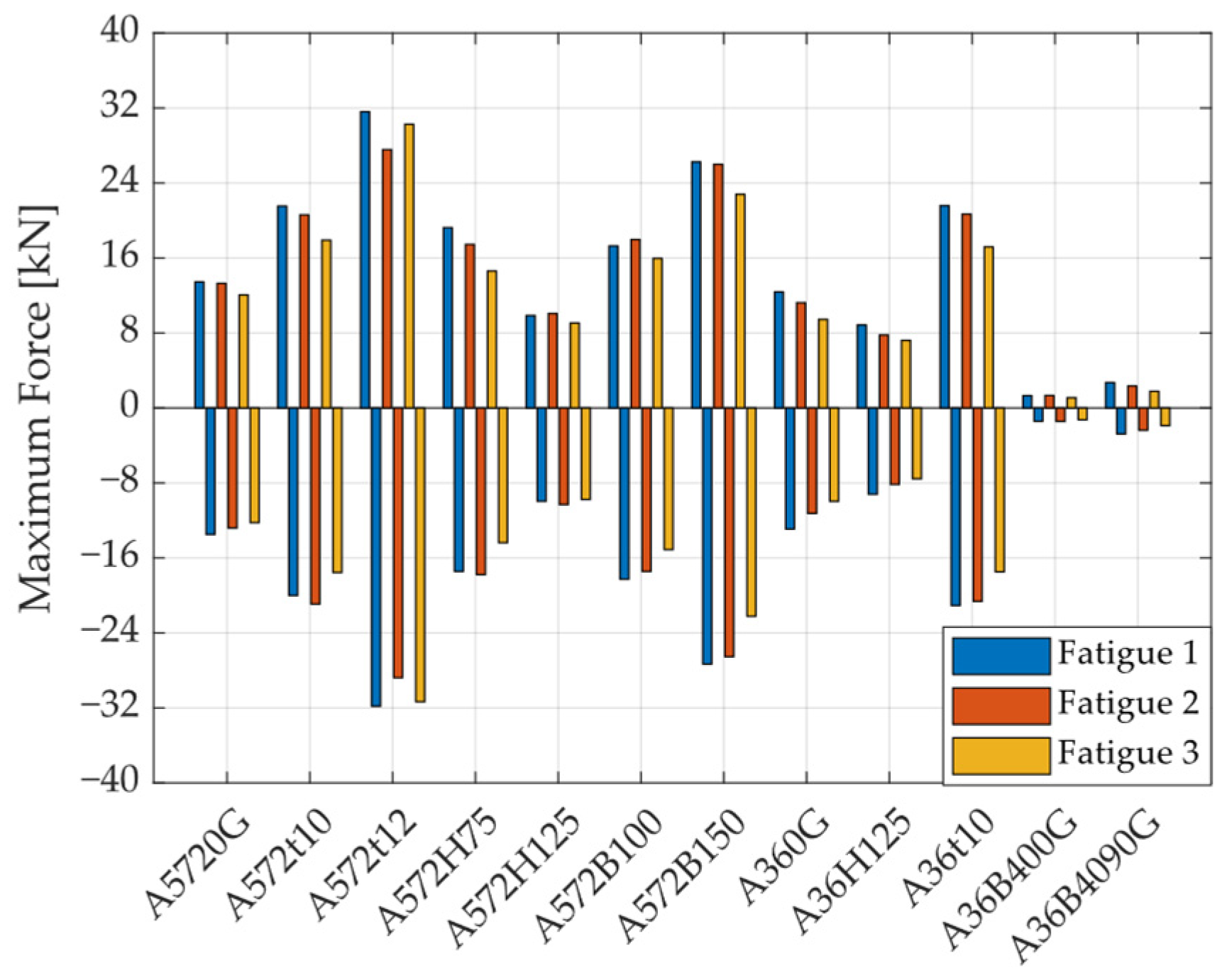
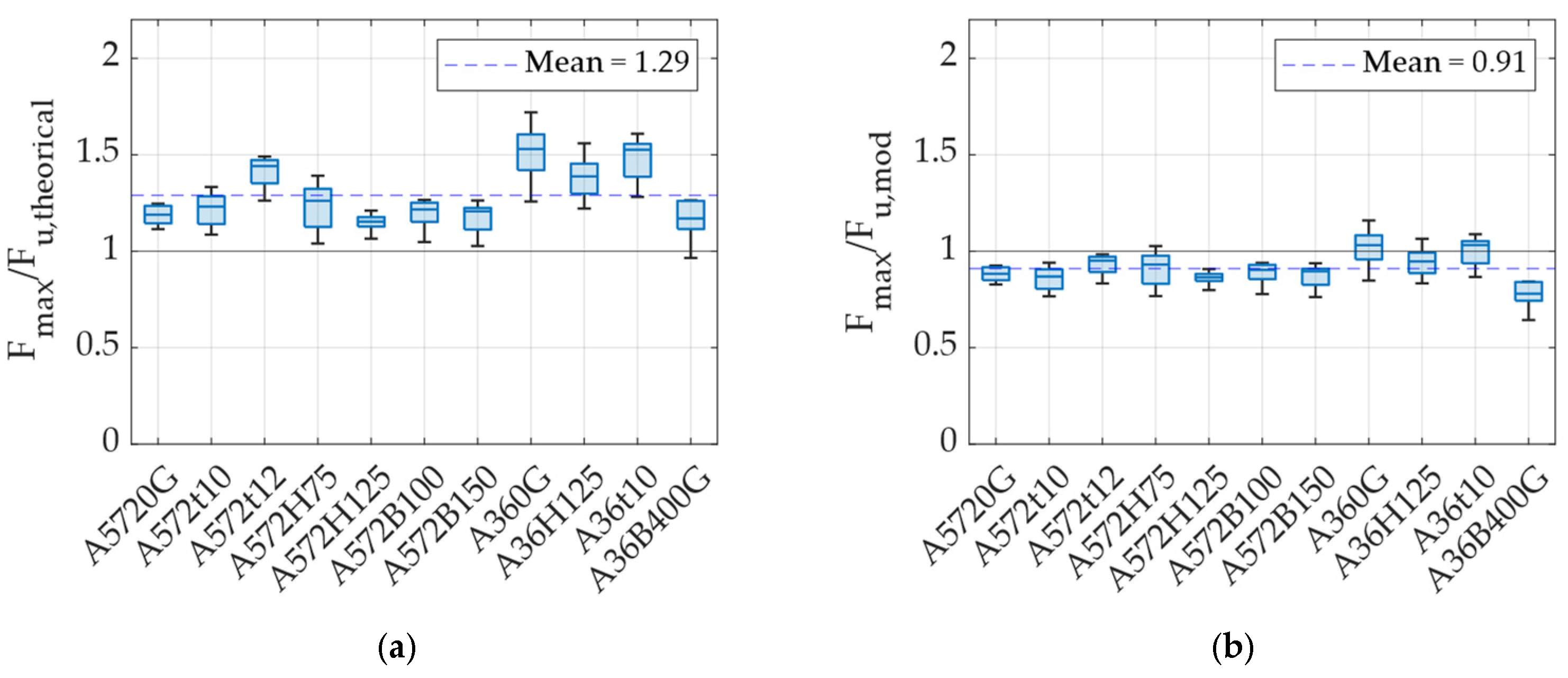
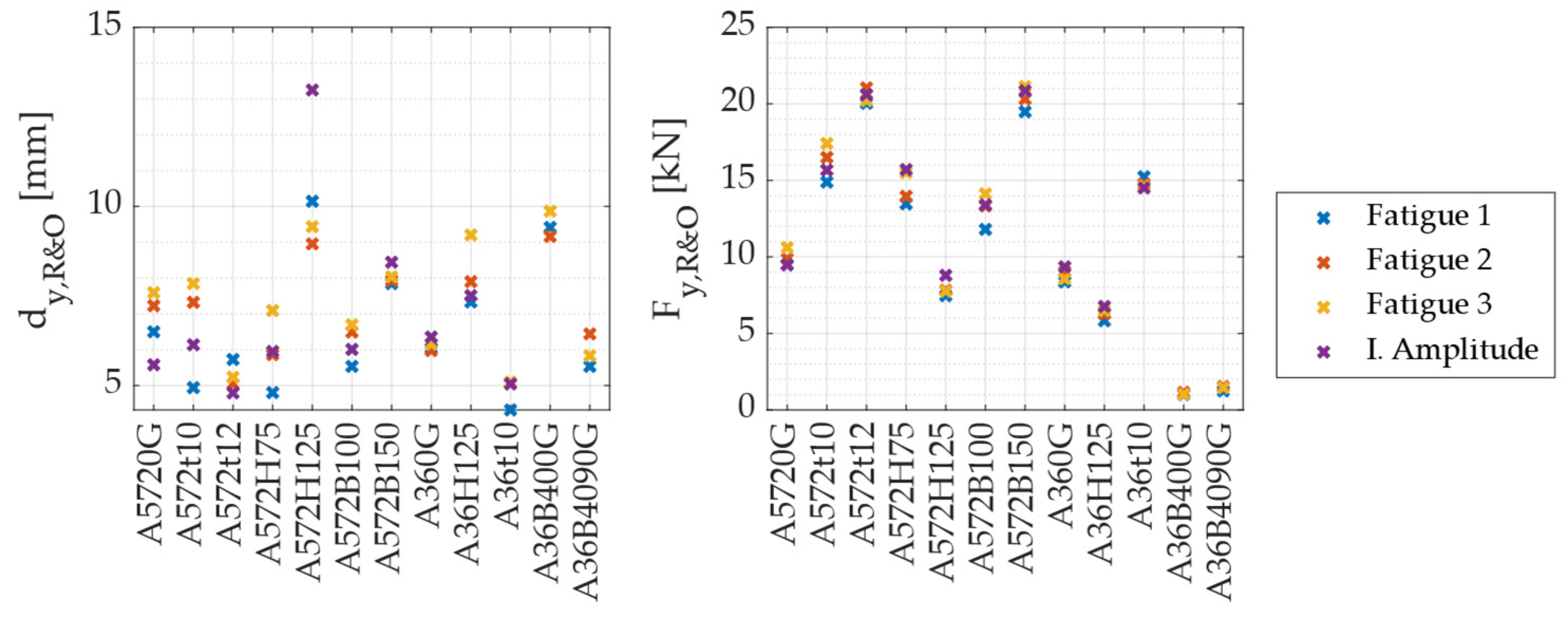
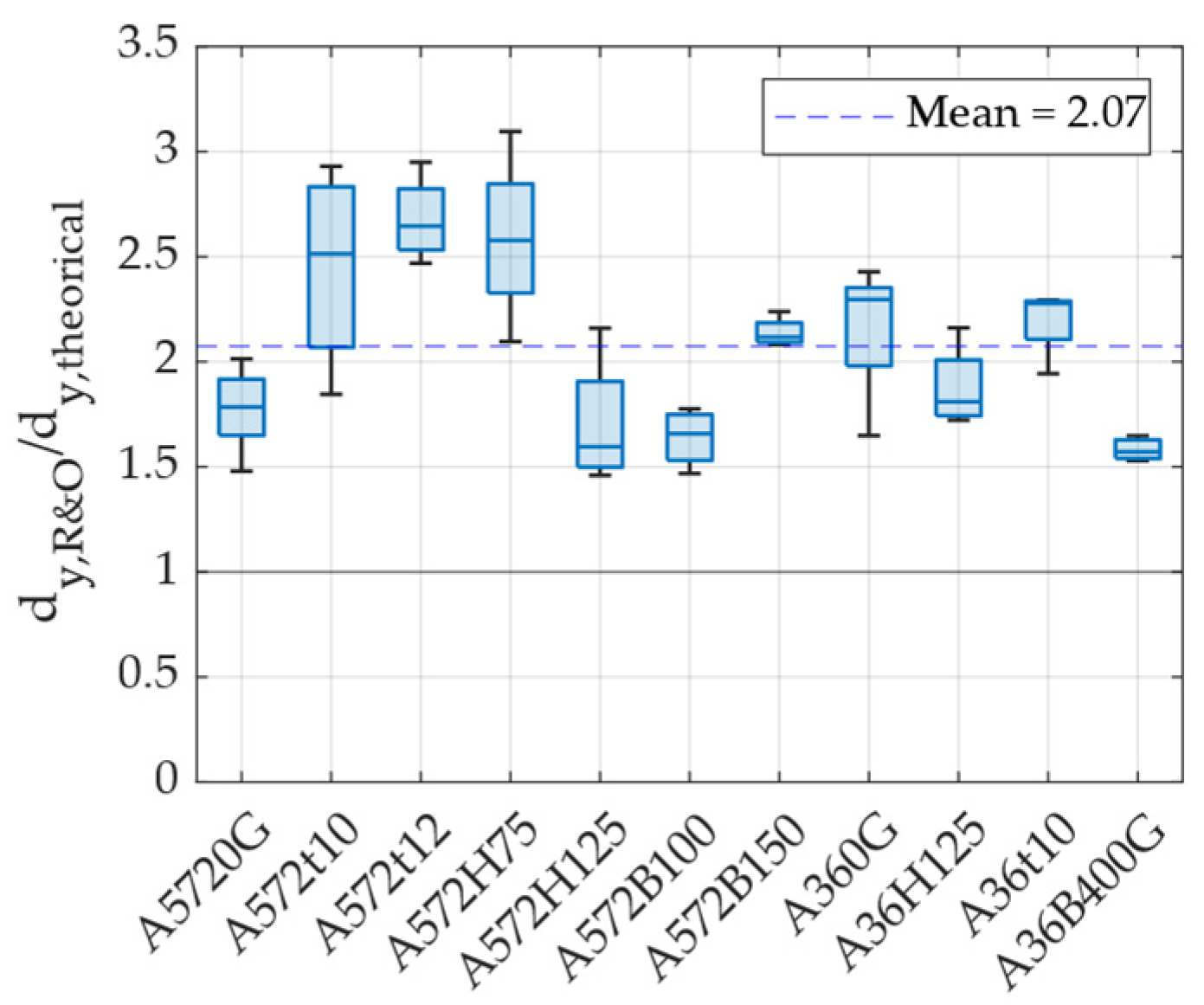
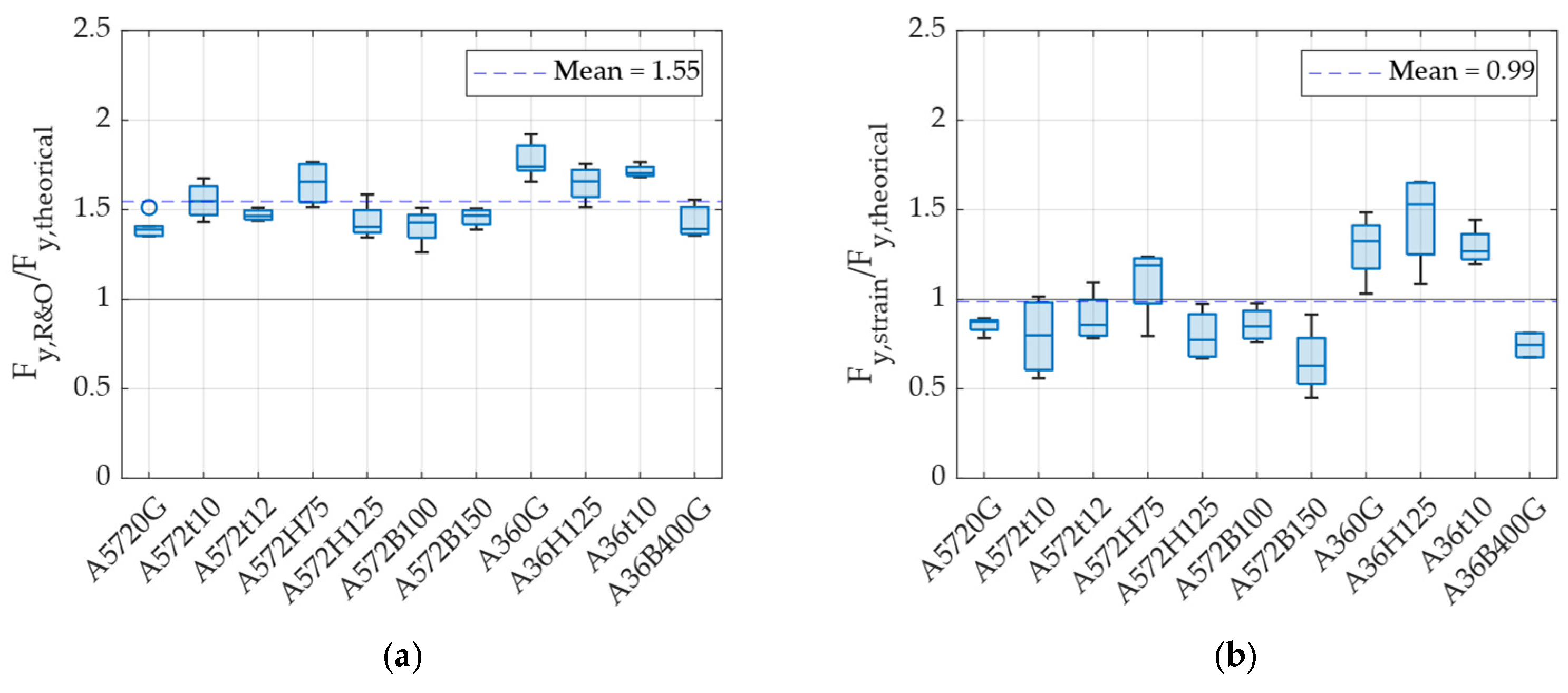
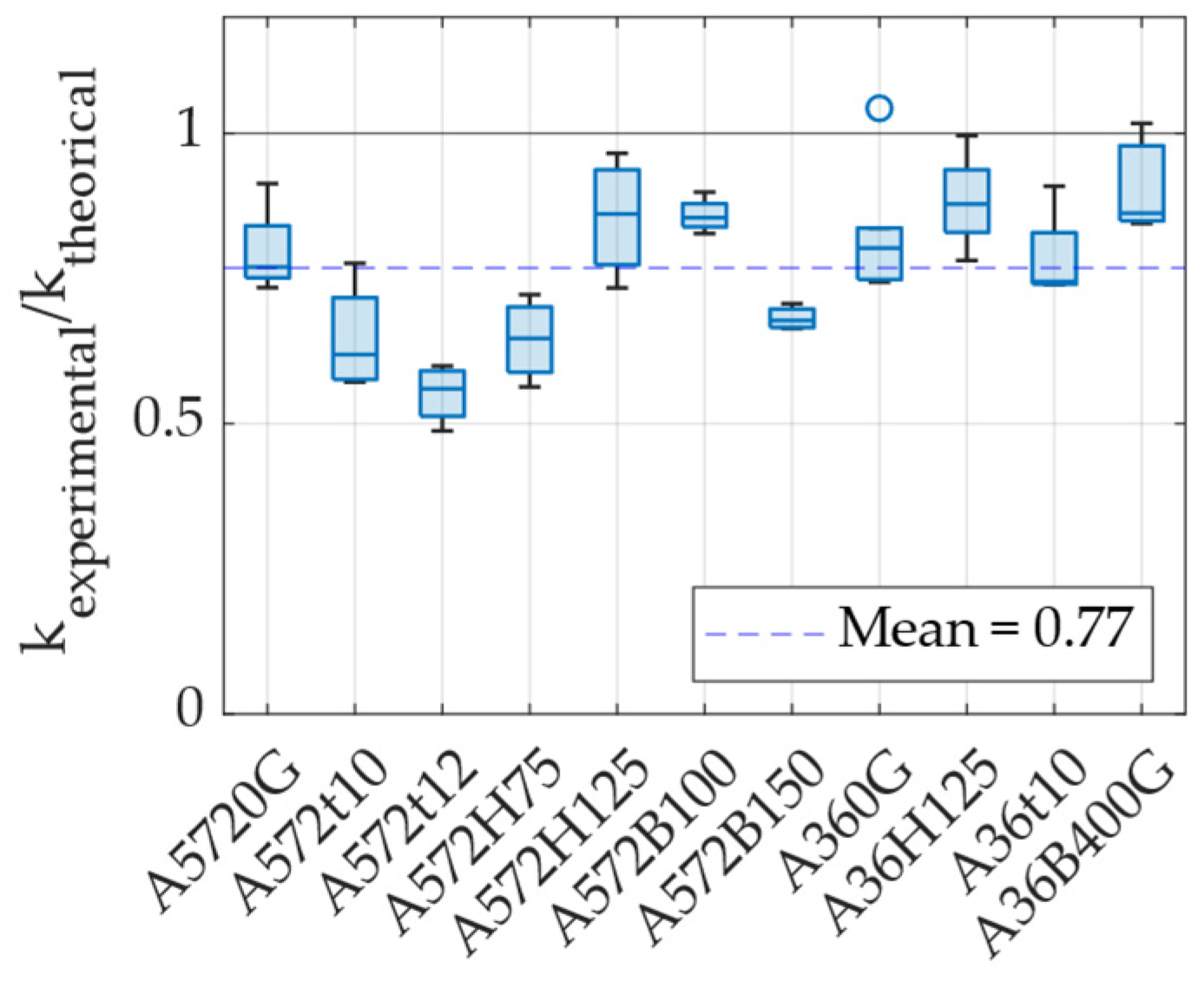
2.2.3. Yield and Ultimate Strength of UFPs
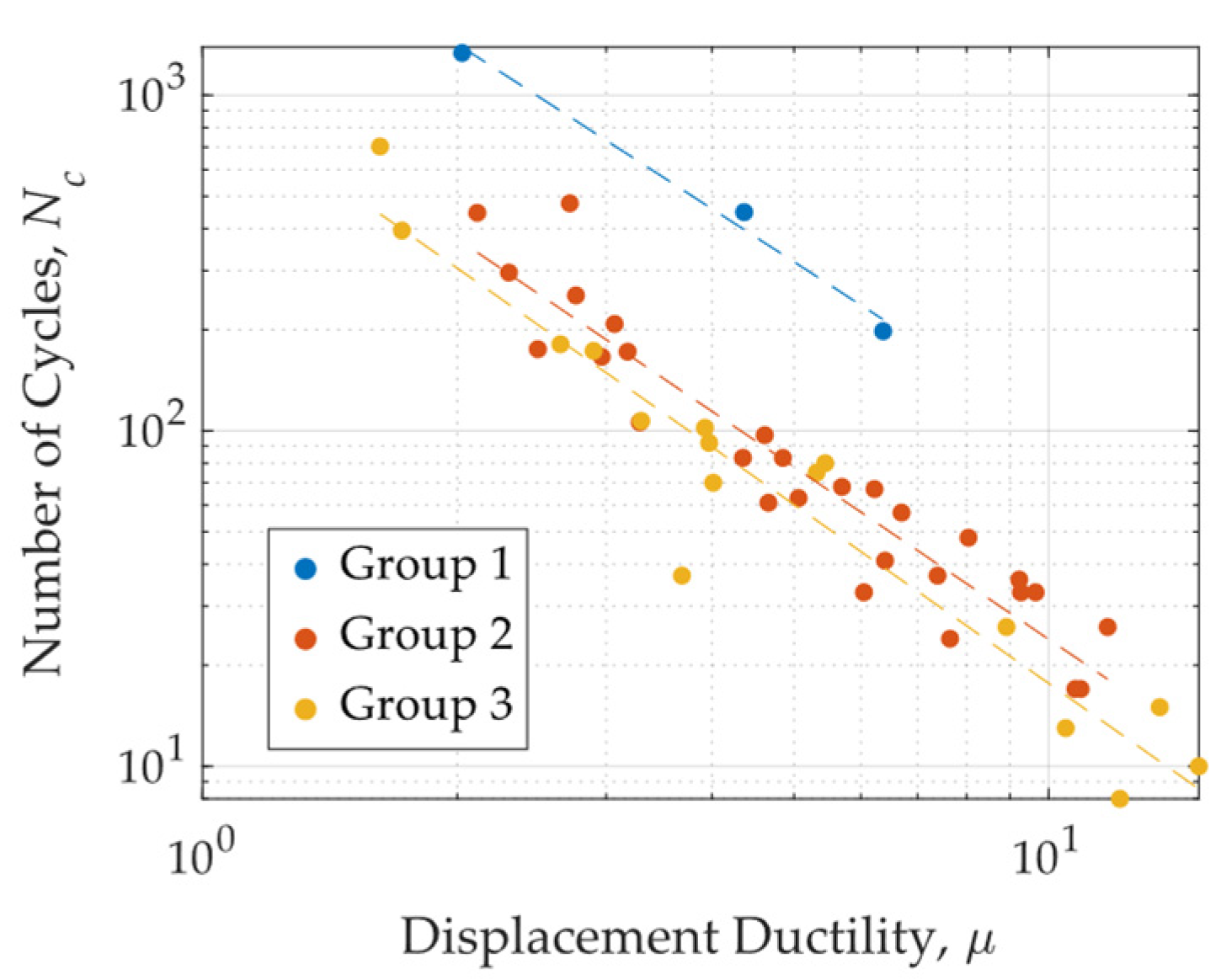
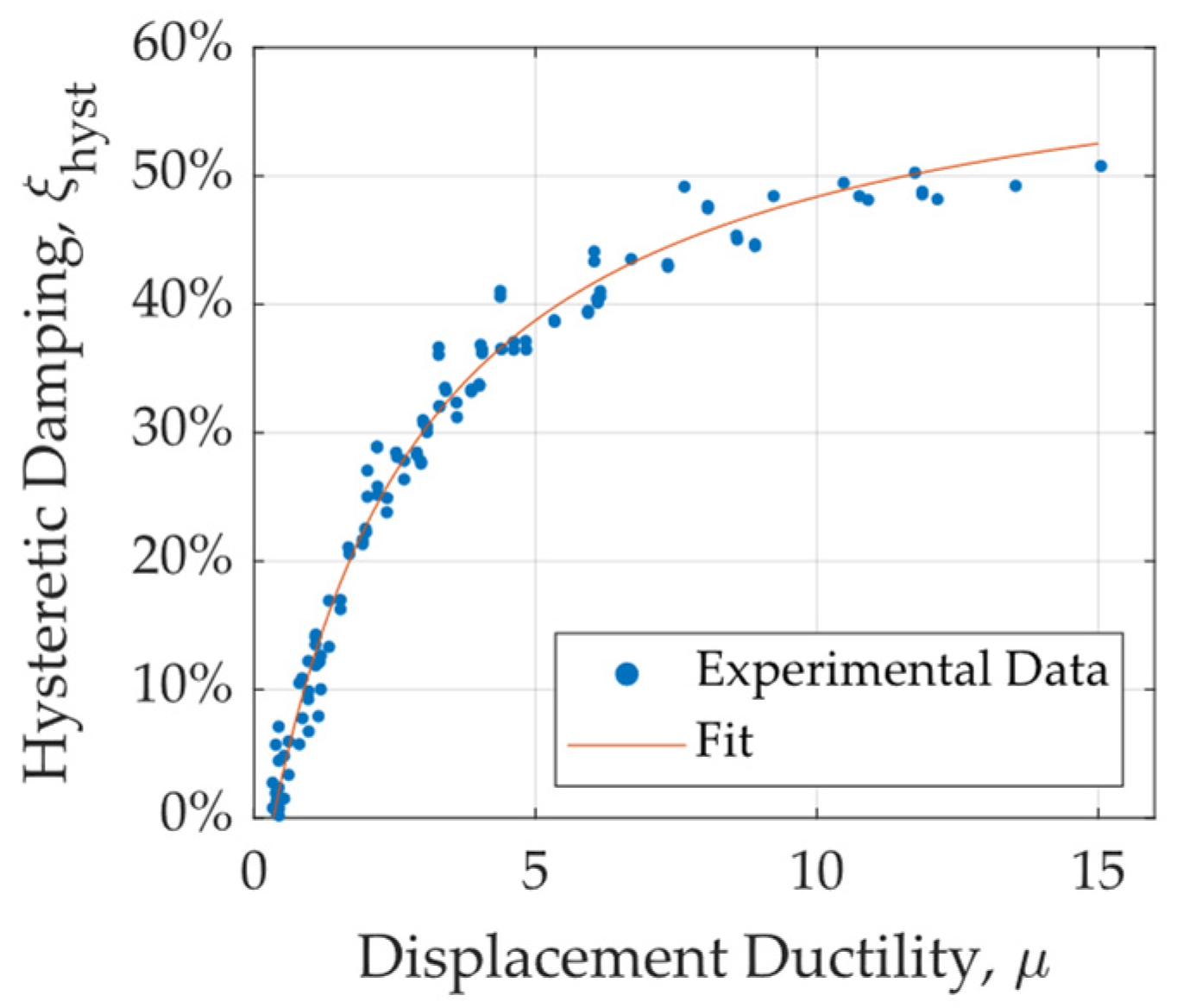
2.2.4. Displacement Ductility
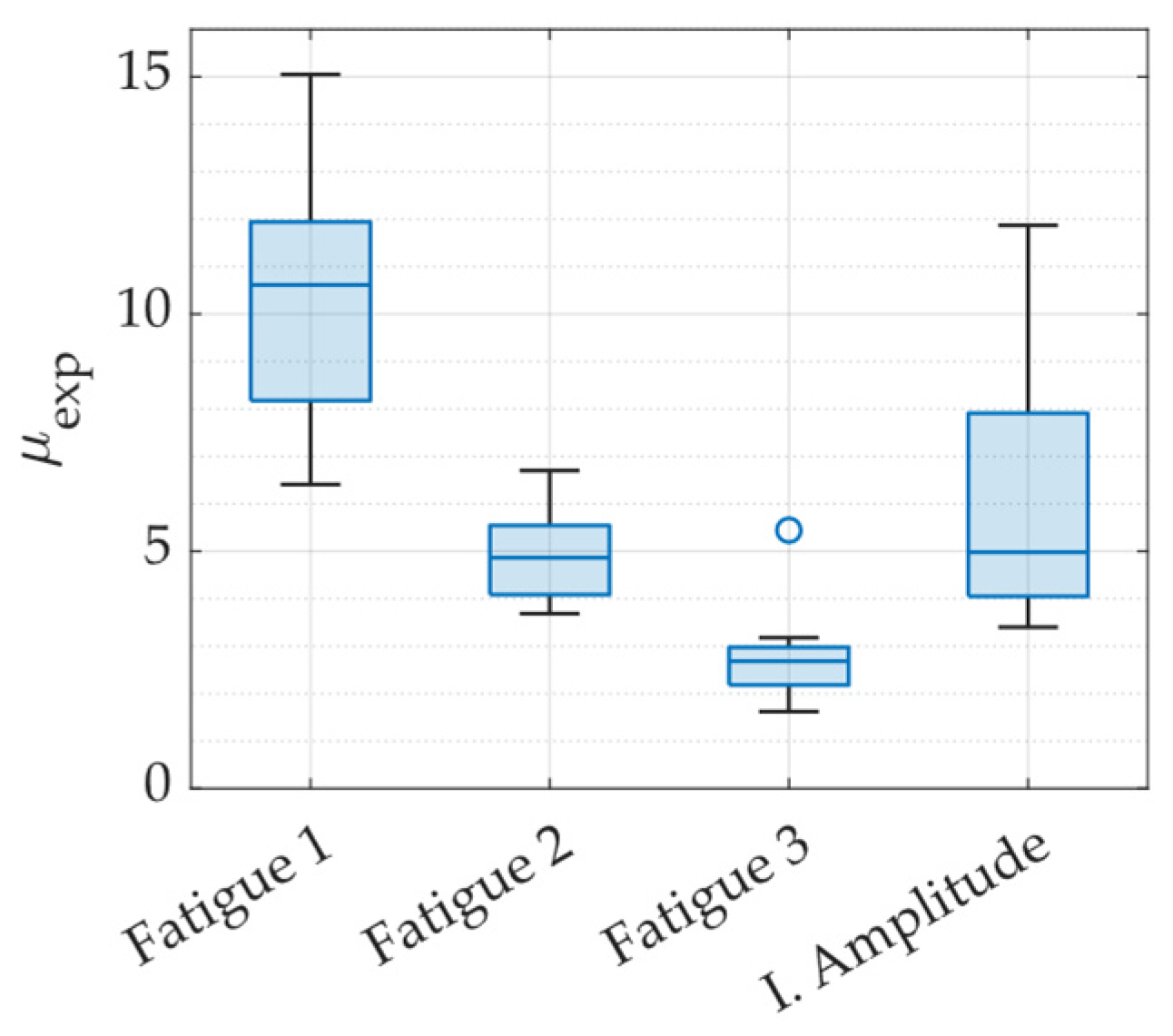
2.2.5. Low-Cycle Fatigue
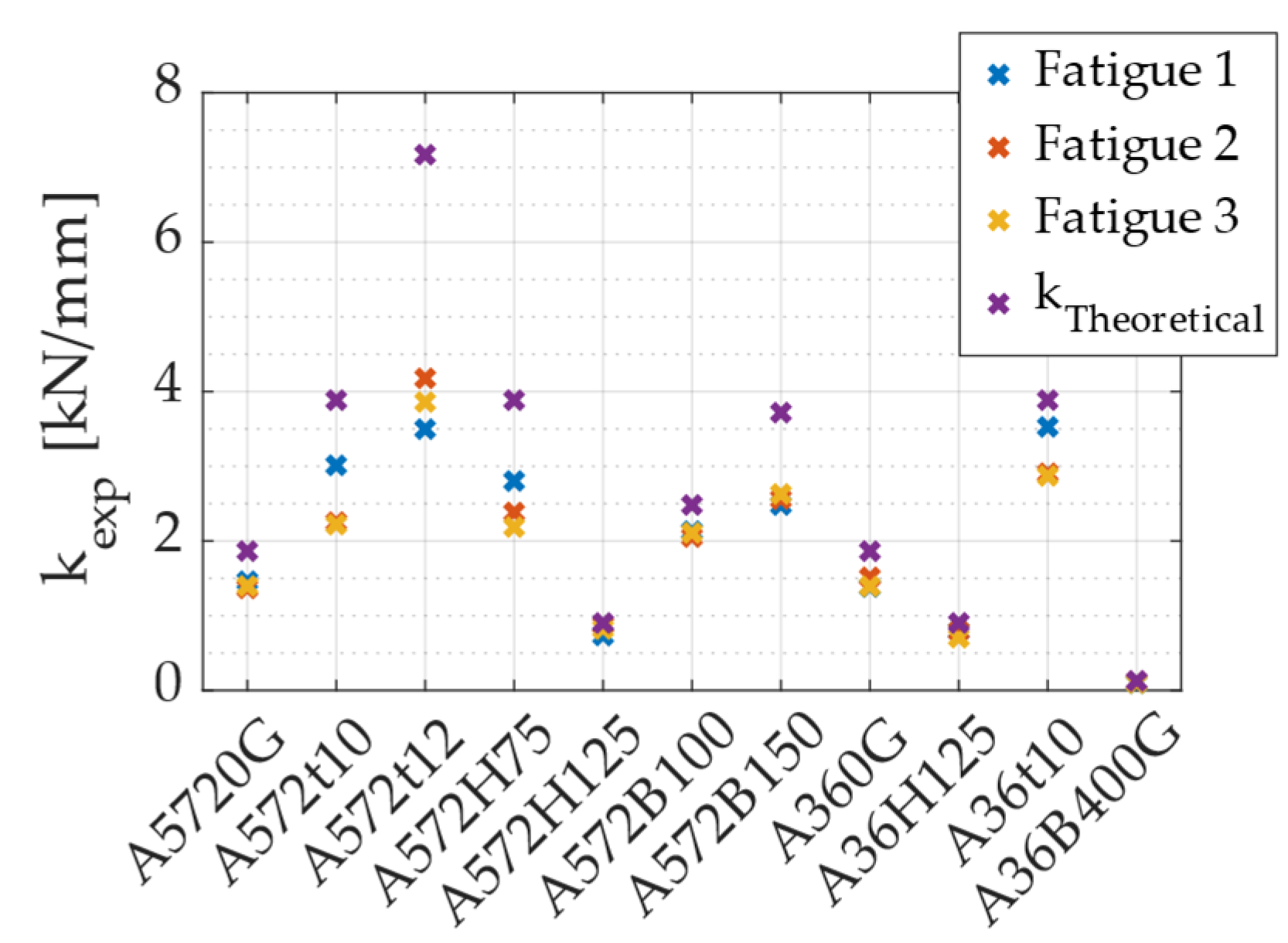
2.2.6. Stiffness and Hysteretic Damping
3. Numerical Characterization of UFPs
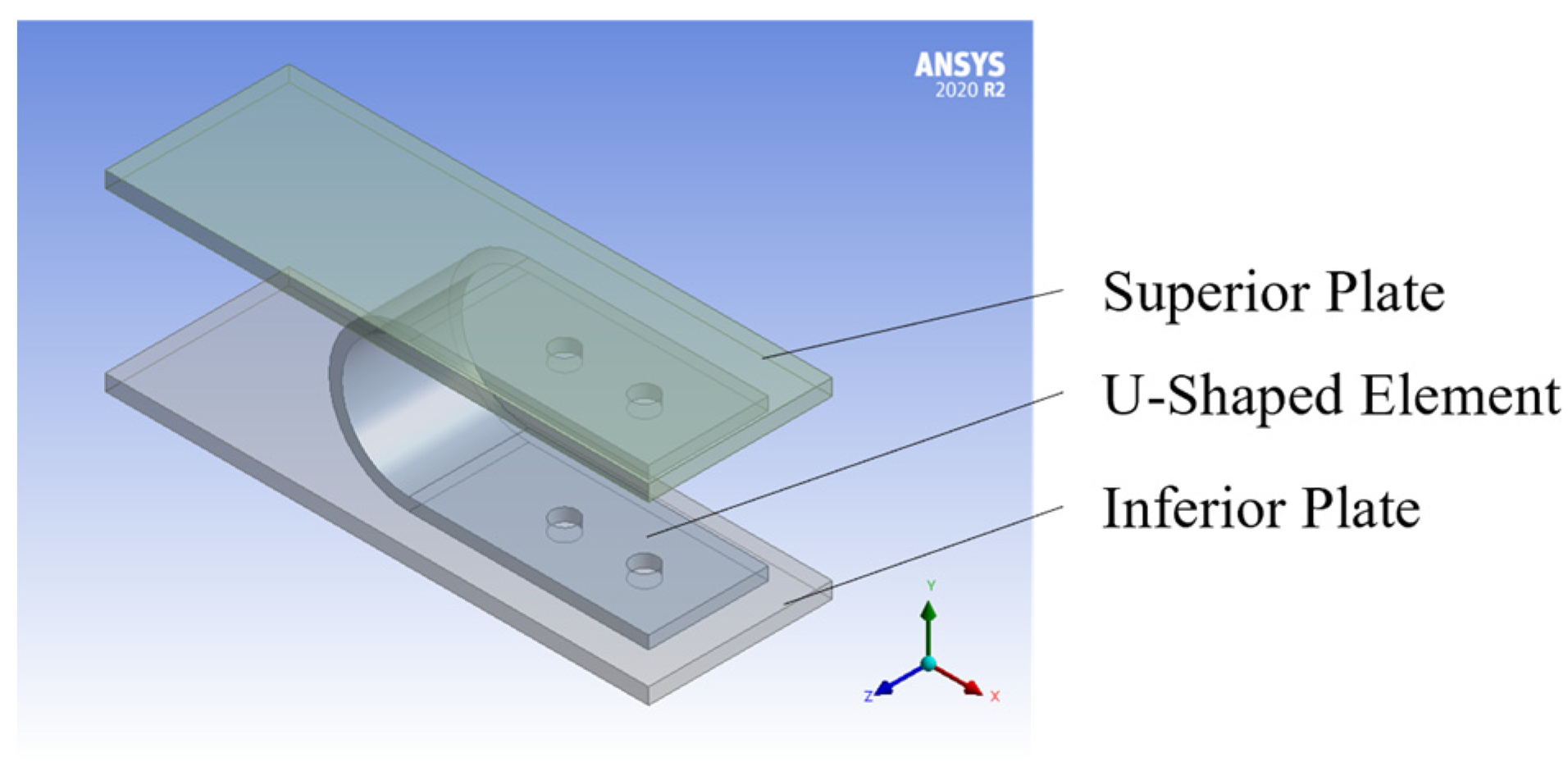
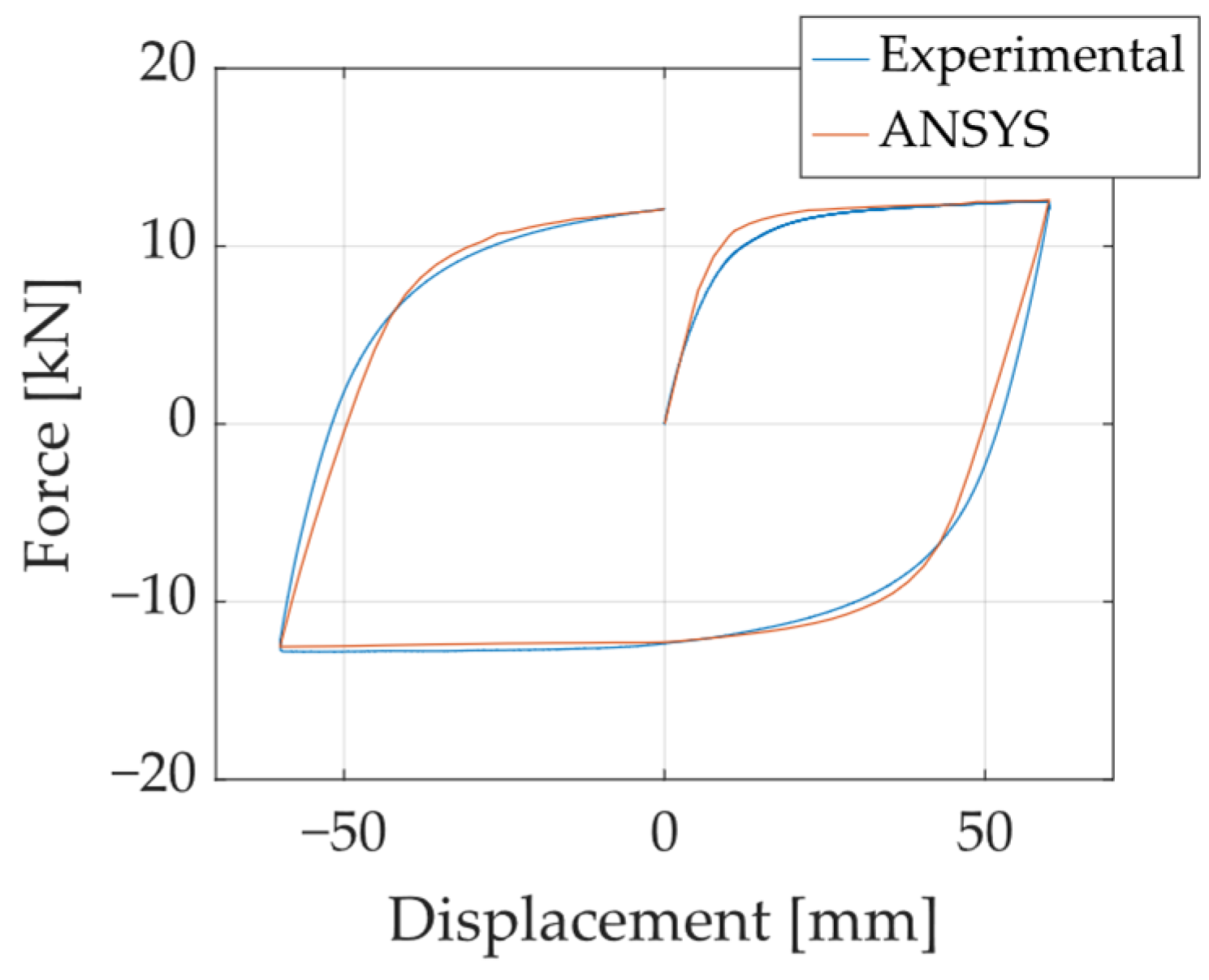
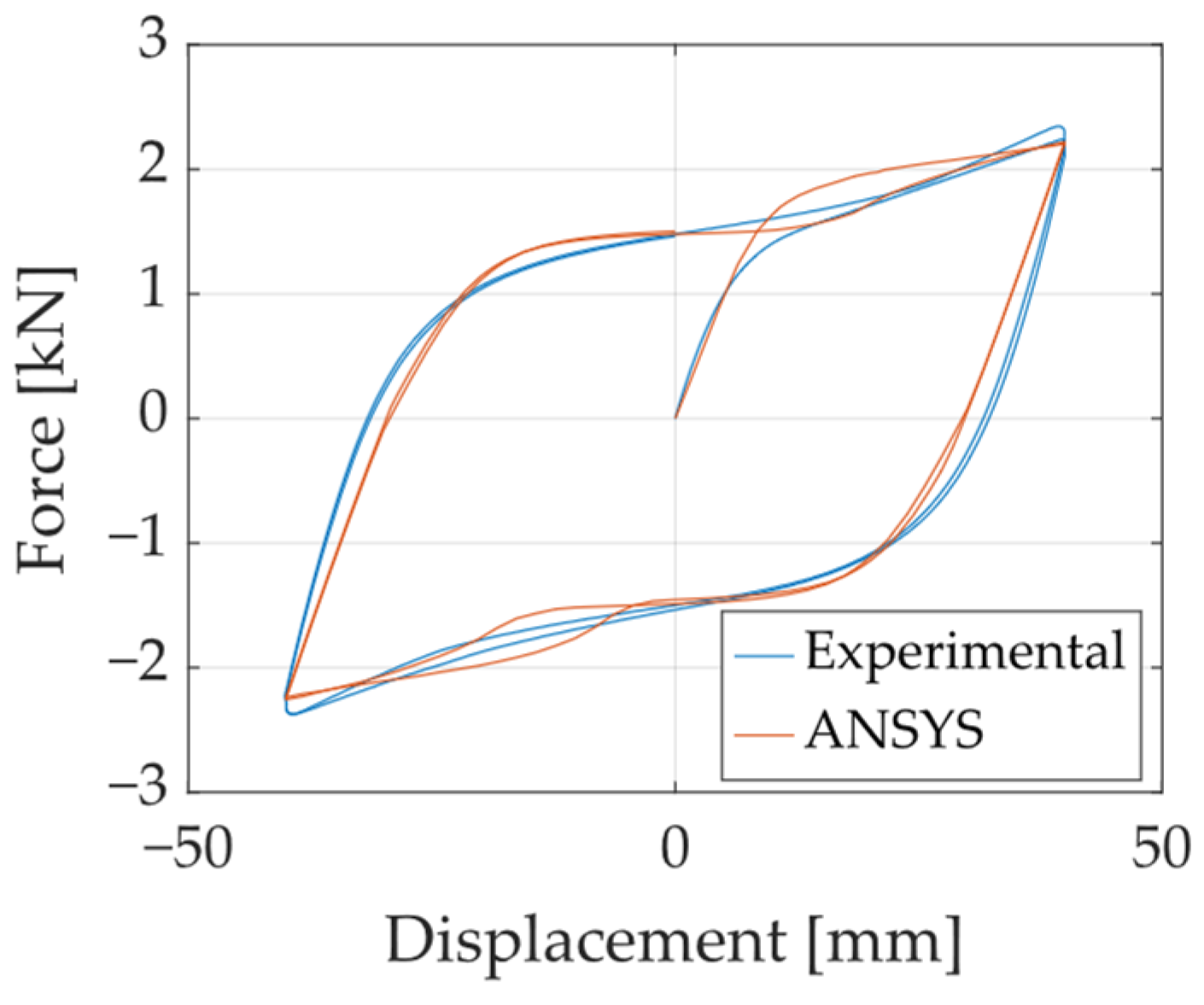
3.1. Model Description and Calibration
3.2. Influence of Loading Direction and Geometric Ratios on Stiffness and Yield Strength
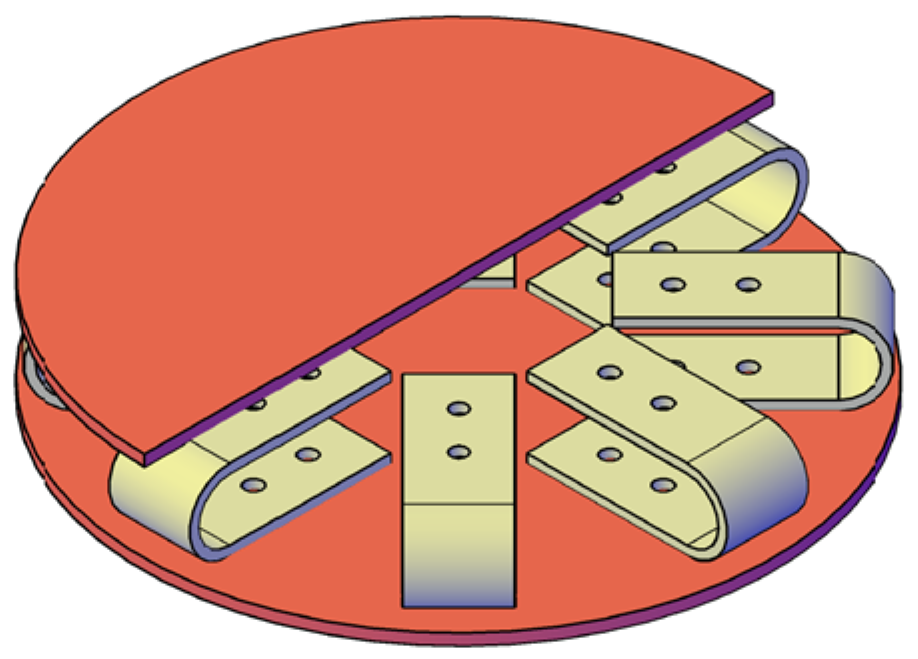
3.3. Numerical Analysis of a Multidirectional System
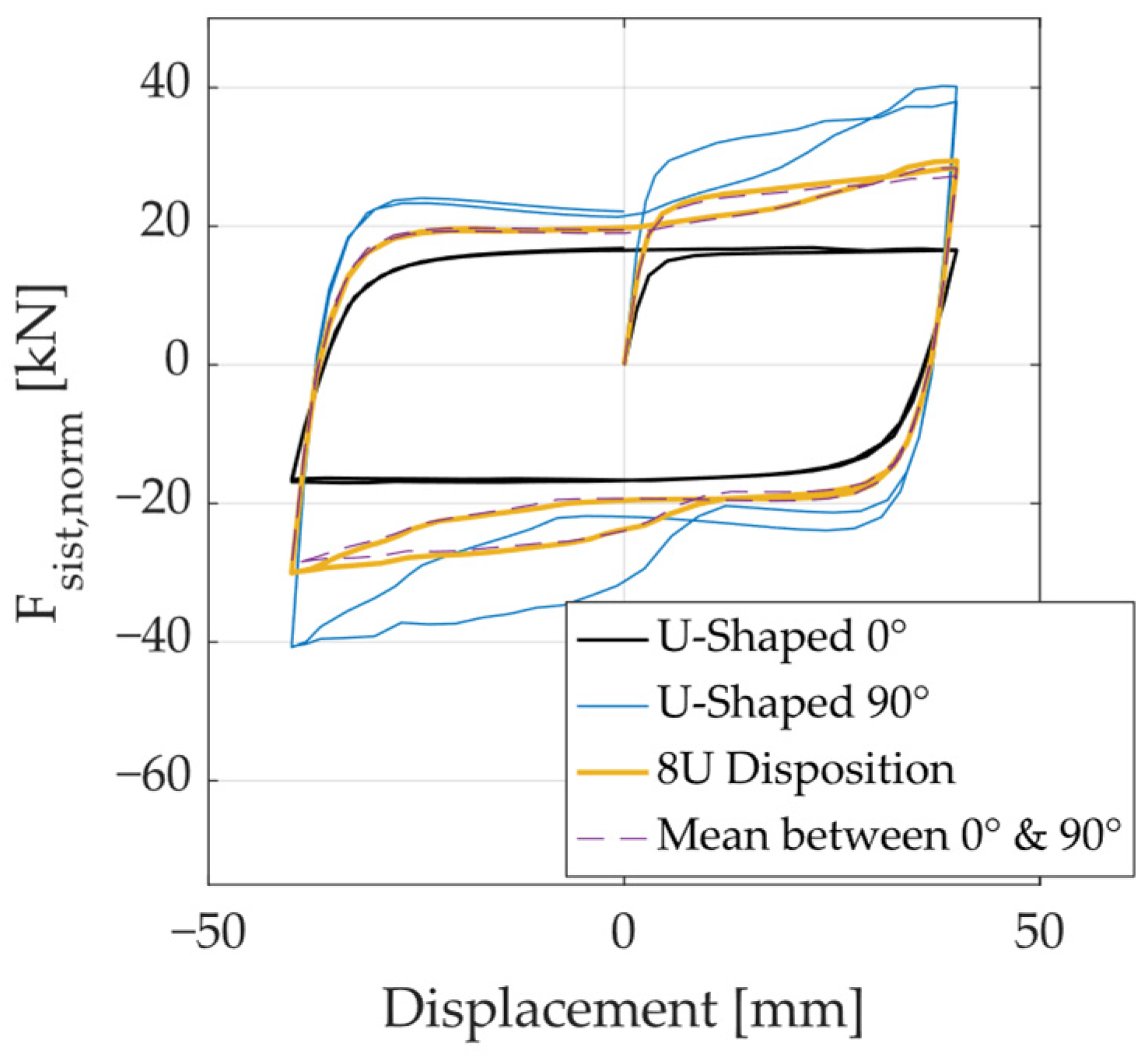
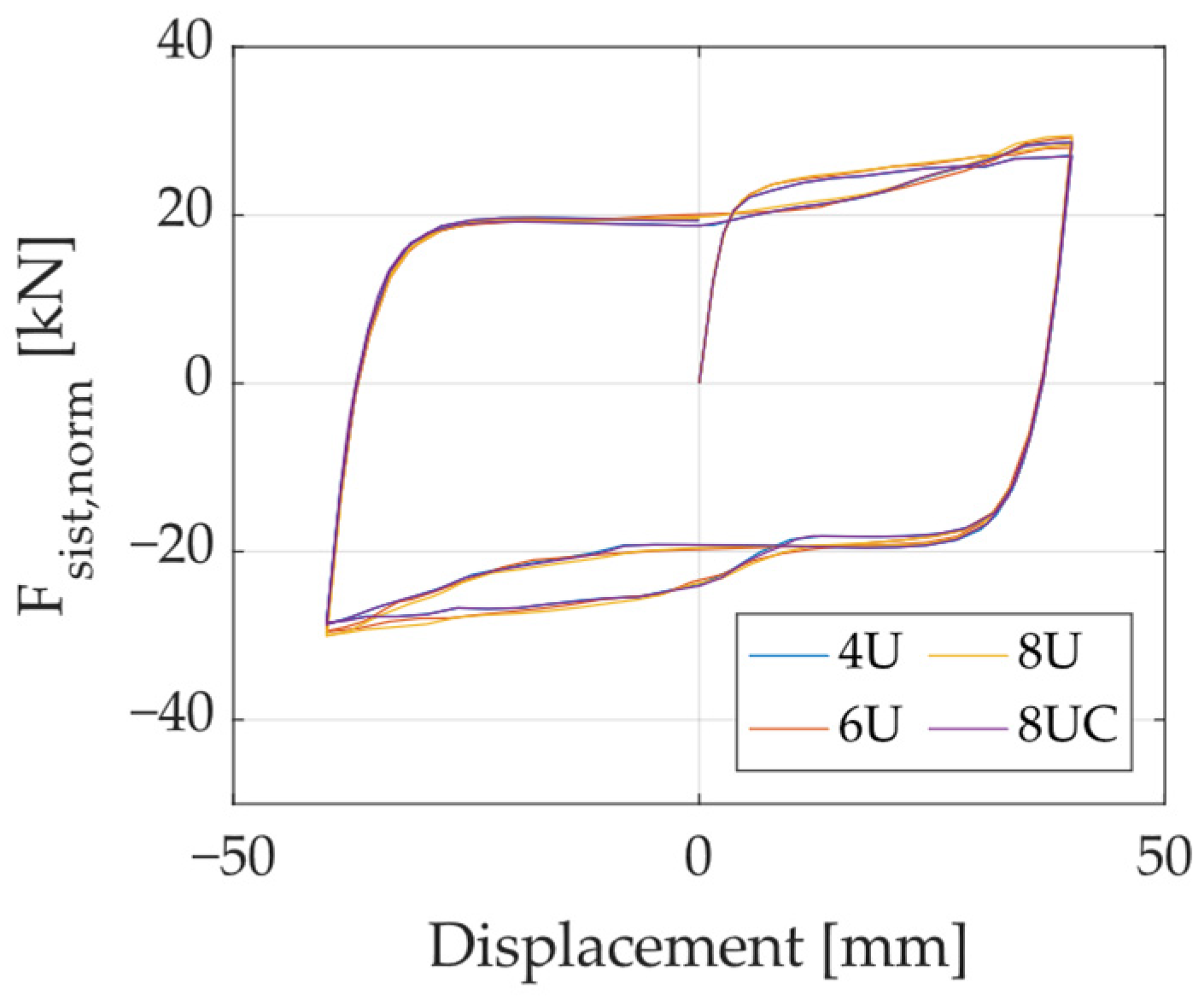
3.3.1. Results and Discussion
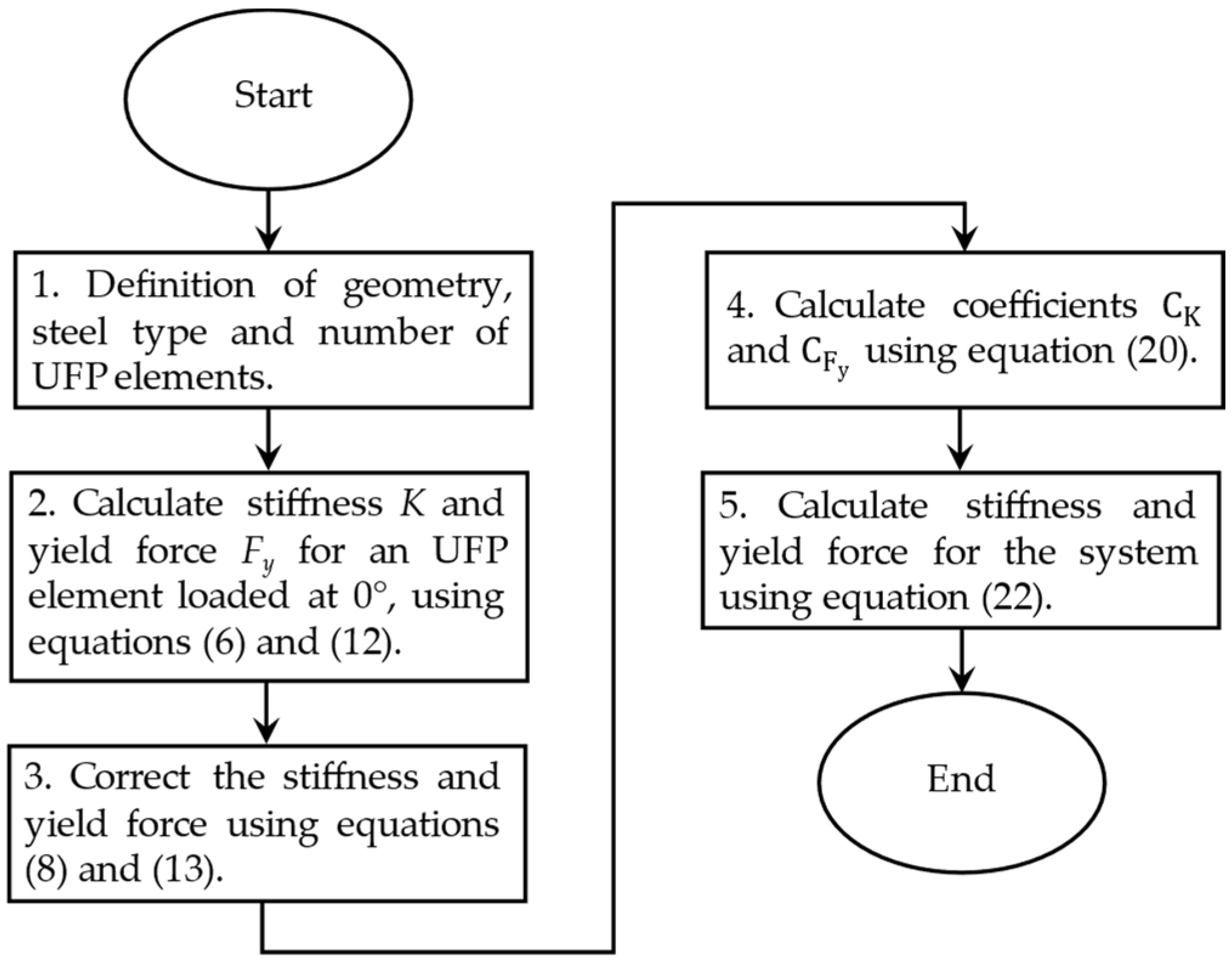
3.3.2. Proposed Procedure for Estimation of System Stiffness and Yield Force
4. Conclusions
- The yield response of UFP elements was analyzed, revealing that existing formulas estimate the first yield point rather than an effective yield point that better represents their overall nonlinear response. To improve modeling accuracy, correction factors of 2 for displacement and 1.55 for force were introduced to adjust the theoretical yield values for bilinear or simplified models.
- The fatigue life of UFPs was found to be highly dependent on displacement ductility demand and the H/t ratio. Higher ductility demand led to a faster deterioration, while increasing H/t improved fatigue performance. These findings provide design guidance for optimizing UFP elements in applications requiring enhanced performance under cyclic loading.
- FEMs developed in ANSYS were validated against experimental results, confirming their accuracy in simulating UFP hysteresis behavior. When properly calibrated with kinematic and isotropic hardening models, the numerical approach successfully reproduced the stiffness, strength, and cyclic energy dissipation characteristics observed in the laboratory. This validation supports the use of FEMs for performance prediction and design optimization of UFP-based systems.
- The study also demonstrated that the number of UFP elements in a multidirectional dissipation system affects only the total force capacity, while the normalized force–displacement response remains unchanged. This observation enabled the development of a simplified estimation method, allowing designers to predict the stiffness and yield force of a multidirectional system using only the properties of a single UFP loaded at 0°.
- The proposed formula, combined with validated correction factors, provides a practical tool for engineers seeking to implement UFP-based dissipation devices in seismic-resistant structures. The findings contribute to advancing energy dissipation technology, promoting the widespread adoption of UFP elements in bridges, base-isolated buildings, and other structures requiring enhanced seismic resilience.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kelly, J.M.; Skinner, R.I.; Heine, A.J. Mechanisms of Energy Absorption in Special Devices for use in Earthquake Resistant Structures. Bull. N. Z. Soc. Earthq. Eng. 1972, 5, 63–88. [Google Scholar] [CrossRef]
- Aiken, I.D.; Nims, D.K.; Kelly, J.M. Comparative Study of Four Passive Energy Dissipation Systems. Bull. N. Z. Soc. Earthq. Eng. 1992, 25, 175–192. [Google Scholar] [CrossRef]
- Bazaez, R.; Dusicka, P. Repair of Seismically Damaged RC Bridge Bent with Ductile Steel Bracing. Steel Compos. Struct. 2018, 26, 745–757. [Google Scholar] [CrossRef]
- Bazaez, R.; Dusicka, P. Cyclic Behavior of Reinforced Concrete Bridge Bent Retrofitted with Buckling Restrained Braces. Eng. Struct. 2016, 119, 34–48. [Google Scholar] [CrossRef]
- Bazaez, R.; Dusicka, P. Performance Assessment of Multi-Column RC Bridge Bents Seismically Retrofitted with Buckling-Restrained Braces. Bull. Earthq. Eng. 2018, 16, 2135–2160. [Google Scholar] [CrossRef]
- Aldea, S.; Bazáez, R.; Heresi, P.; Astroza, R. Effect of Bidirectional Hysteretic Dampers on the Seismic Performance of Skewed Multi-Span Highway Bridges. Buildings 2024, 14, 1778. [Google Scholar] [CrossRef]
- Sritharan, S.; Aaleti, S.; Thomas, D.J. Seismic Analysis and Design of Precast Precast Concrete Jointed Wall Systems; ISU-ERI-Ames Report ERI-07404; Iowa State University: Ames, IA, USA, 2007. [Google Scholar]
- Priestley, M.J.N.; Sritharan, S.S.; Conley, J.R.; Pampanin, S. Preliminary Results and Conclusions from the PRESSS Five-Story Precast Concrete Test Building. PCI J. 1999, 44, 42–67. [Google Scholar] [CrossRef]
- Henriques, J.; Calado, L.; Castiglioni, C.A.; Degée, H. Dissipative Connections with U-Shaped Steel Plate for Braces of Concentrically Braced Frames. Bull. Earthq. Eng. 2019, 17, 6203–6237. [Google Scholar] [CrossRef]
- Ravanbakhshian Habibabadi, M.; Izadinia, M.; Tajmir Riahi, H.; Hasan Meisami, M. Effects of Geometric Characteristics of U-Shaped Flexural Plates on Their Cyclic Performance. Structures 2023, 51, 351–371. [Google Scholar] [CrossRef]
- Cheraghi, K.; Roudsari, M.T.; Kiasat, S.; Esfandiari, J. Numerical Investigation of Cyclic Behavior of Angled U-Shaped Yielding Damper on Steel Frames. Period. Polytech. Civ. Eng. 2024, 68, 426–434. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, T.; Wang, B.; Huang, W.; Zhong, G.; Zhao, F. Experimental and Numerical Investigations of Steel U-Shaped Dampers under Vertical Loadings for Seismic Mitigation. Soil Dyn. Earthq. Eng. 2024, 179, 108571. [Google Scholar] [CrossRef]
- Mowafy, A.; Imanpour, A.; Chui, Y.H.; Daneshvar, H. Experimental Evaluation of a U-Shaped Steel Plate as a Seismic Fuse. J. Constr. Steel Res. 2024, 215, 108525. [Google Scholar] [CrossRef]
- Whittaker, A.S.; Bertero, V.V.; Thompson, C.L.; Alonso, L.J. Seismic Testing of Steel Plate Energy Dissipation Devices. Earthq. Spectra 1991, 7, 563–604. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Su, Y.; Ran, T.; Xue, Y. Development of an Energy Dissipation Restrainer for Bridges Using a Steel Shear Panel. J. Constr. Steel Res. 2014, 101, 83–95. [Google Scholar] [CrossRef]
- Baird, A.C.; Smith, T.; Palermo, A.; Pampanin, S. Experimental and Numerical Study of U-Shape Flexural Plate (UFP) Dissipators. In Proceedings of the 2014 NZSEE Conference, Auckland, New Zealand, 21–23 March 2014. [Google Scholar]
- Qu, B.; Dai, C.; Qiu, J.; Hou, H.; Qiu, C. Testing of Seismic Dampers with Replaceable U-Shaped Steel Plates. Eng. Struct. 2019, 179, 625–639. [Google Scholar] [CrossRef]
- Hu, X.; Dong, H.; Su, C.; Han, Q.; Du, X. Experimental and Numerical Studies on Hysteresis Performance of U-Shaped SMA-Steel Plates Damper. J. Constr. Steel Res. 2024, 219, 108802. [Google Scholar] [CrossRef]
- Huang, J.; Chen, Z.; Zhu, S. Low Temperature Effect on Cyclic Behavior of Shape Memory Alloy U-Shaped Dampers. Thin-Walled Struct. 2024, 201, 111962. [Google Scholar] [CrossRef]
- Zhu, H.; Bezabeh, M.A.; Iqbal, A.; Popovski, M.; Chen, Z. Seismic Design and Performance Evaluation of Post-Tensioned CLT Shear Walls with Coupling U-Shaped Flexural Plates in Canada. Earthq. Spectra 2025, 87552930251316260. [Google Scholar] [CrossRef]
- Taiyari, F.; Mazzolani, F.M.; Bagheri, S. A Proposal for Energy Dissipative Braces with U-Shaped Steel Strips. J. Constr. Steel Res. 2019, 154, 110–122. [Google Scholar] [CrossRef]
- Pampanin, S. Towards the “Ultimate Earthquake-Proof” Building: Development of an Integrated Low-Damage System. Geotech. Geol. Earthq. Eng. 2015, 39, 321–358. [Google Scholar] [CrossRef]
- Jensen, H.A.; Sepulveda, J.G. On the Reliability-Based Design of Structures Including Passive Energy Dissipation Systems. Struct. Saf. 2012, 34, 390–400. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Wang, C. Development of Crawler Steel Damper for Bridges. J. Constr. Steel Res. 2013, 85, 140–150. [Google Scholar] [CrossRef]
- Xie, X.; Chen, S.X.; Zhou, X. A Simplified Analytical Model for U-Shaped Steel Dampers Considering Horizontal Bidirectional Deformation. Bull. Earthq. Eng. 2018, 16, 6243–6268. [Google Scholar] [CrossRef]
- Jiao, Y.; Kishiki, S.; Yamada, S.; Ene, D.; Konishi, Y.; Hoashi, Y.; Terashima, M. Low Cyclic Fatigue and Hysteretic Behavior of U-Shaped Steel Dampers for Seismically Isolated Buildings under Dynamic Cyclic Loadings. Earthq. Eng. Struct. Dyn. 2015, 44, 1523–1538. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Zhang, J.; Fang, C.; Zhang, Y.; Li, Y. Emerging Steel Frames with Fe-SMA U-Shaped Dampers for Enhancing Seismic Resilience. J. Infrastruct. Preserv. Resil. 2023, 4, 6. [Google Scholar] [CrossRef]
- Costanza, G.; Mercuri, S.; Porroni, I.; Tata, M.E. Shape Memory Alloys for Self-Centering Seismic Applications: A Review on Recent Advancements. Machines 2024, 12, 628. [Google Scholar] [CrossRef]
- Ma, Q.; Rejab, M.R.M.; Siregar, J.P.; Guan, Z. A Review of the Recent Trends on Core Structures and Impact Response of Sandwich Panels. J. Compos. Mater. 2021, 55, 2513–2555. [Google Scholar] [CrossRef]
- Song, Y.; Ruan, S.; Hao, N.; Okabe, Y. A Novel Cylindrical Sandwich Plate Inspired by Beetle Elytra and Its Compressive Properties. Sci. China Technol. Sci. 2024, 67, 3465–3476. [Google Scholar] [CrossRef]
- ASTM A36/A36M-19; Standard Specification for Carbon Structural Steel. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2019.
- ASTM A572/A572M-21e1; Standard Specification for High-Strength Low-Alloy Columbium-Vanadium Structural Steel. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2021.
- American Institute of Steel Construction (AISC). Seismic Provisions for Structural Steel Buildings; ANSI/AISC 341-16; AISC: Chicago, IL, USA, 2016. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Priestley, M.J.N.; Calvi, G.M.; Kowalsky, M.J. Direct Displacement-Based Seismic Design of Structures. In Proceedings of the NZSEE Conference, Citeseer, Palmerston North, New Zealand, 30 March–1 April 2007; Volume 30, pp. 1–23. [Google Scholar]
- ANSYS, Inc. Ansys® Academic Research Mechanical, version 2020R2; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Chaboche, J.L. Constitutive Equations for Cyclic Plasticity and Cyclic Viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Voce, E. The Relationship between Stress and Strain from Homogenous Deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]





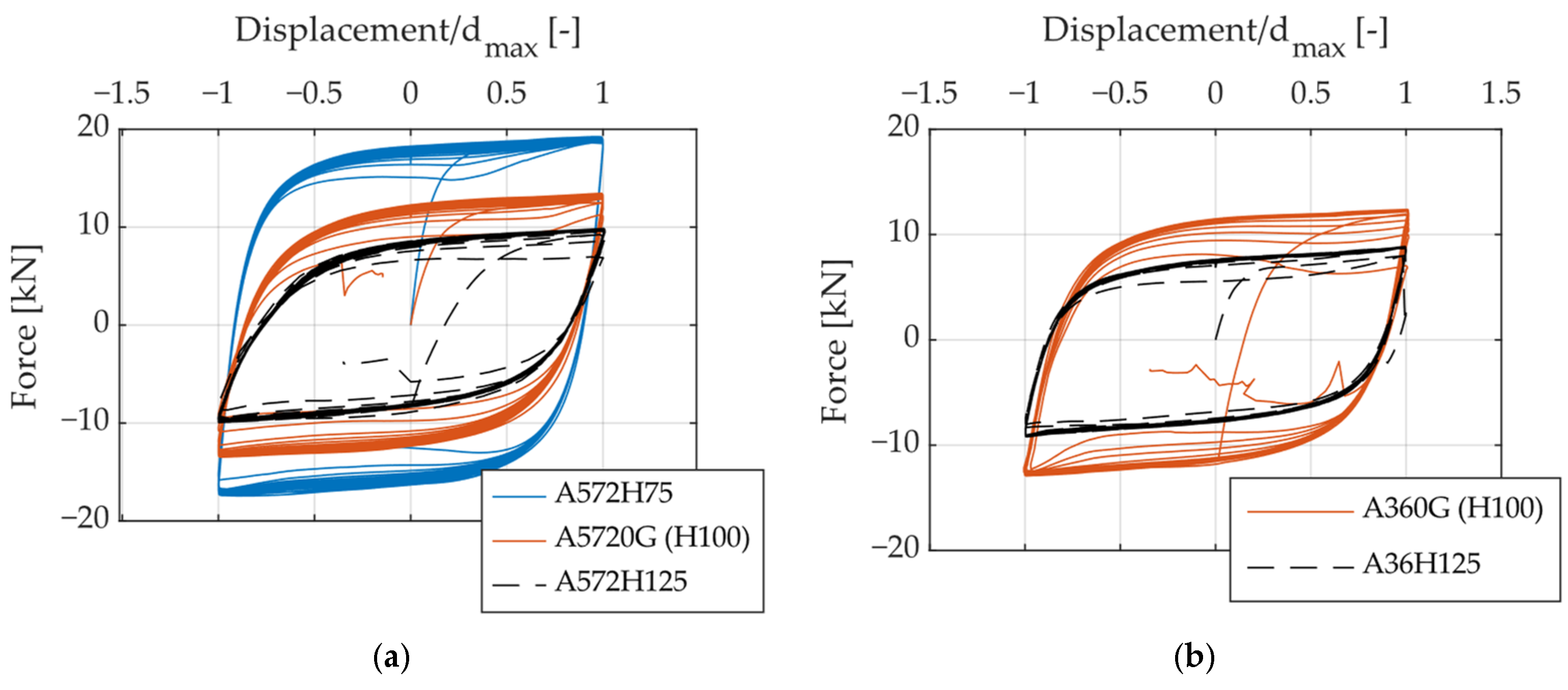
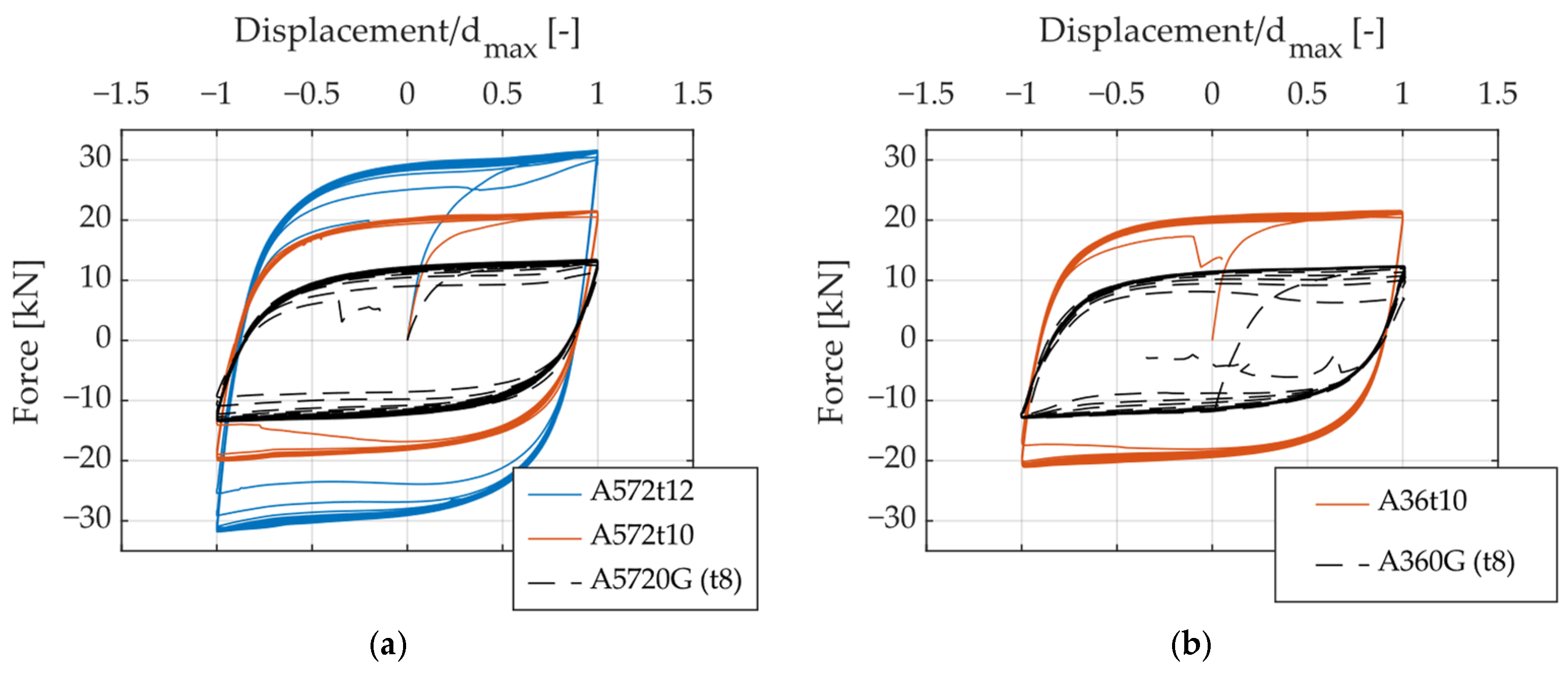
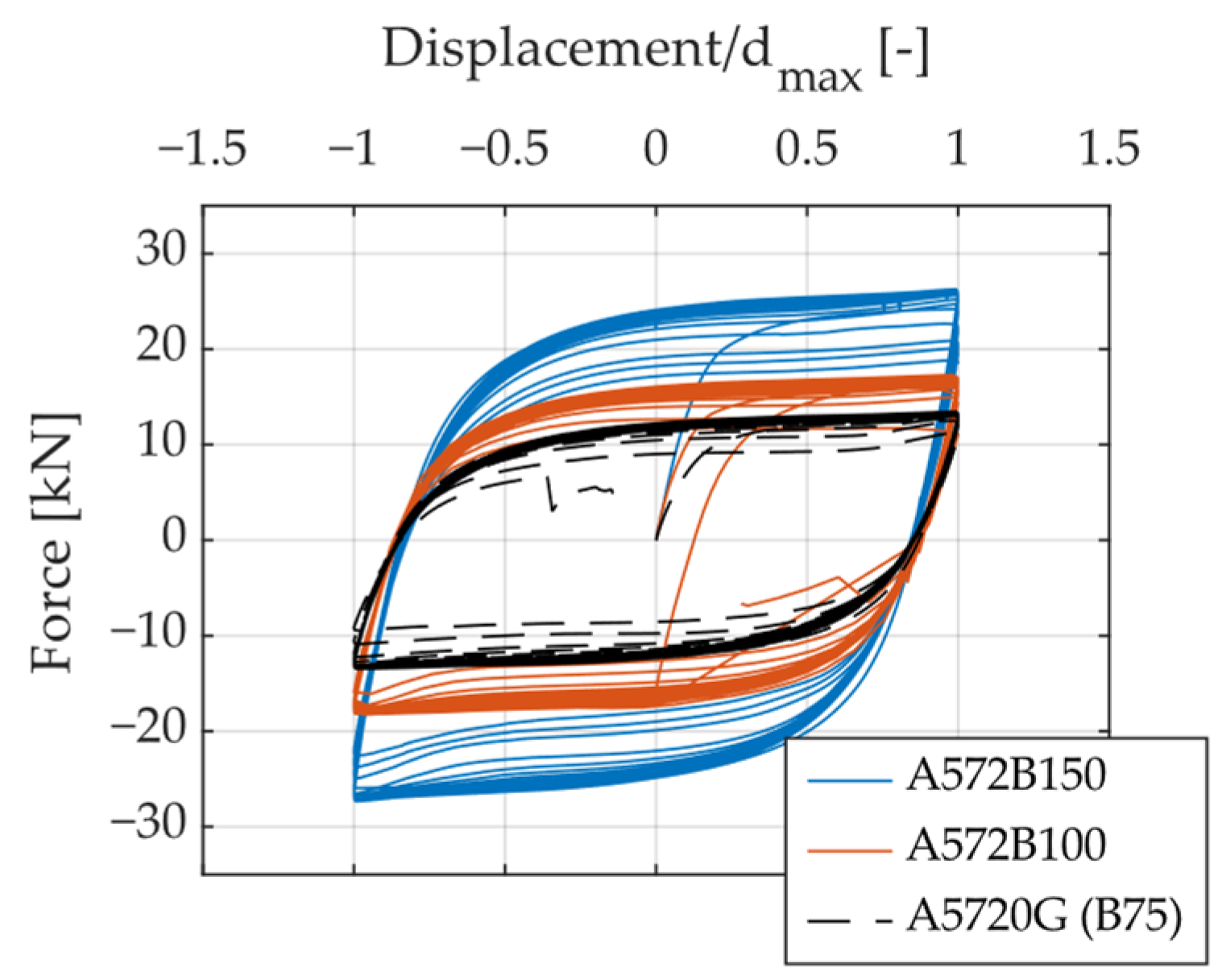
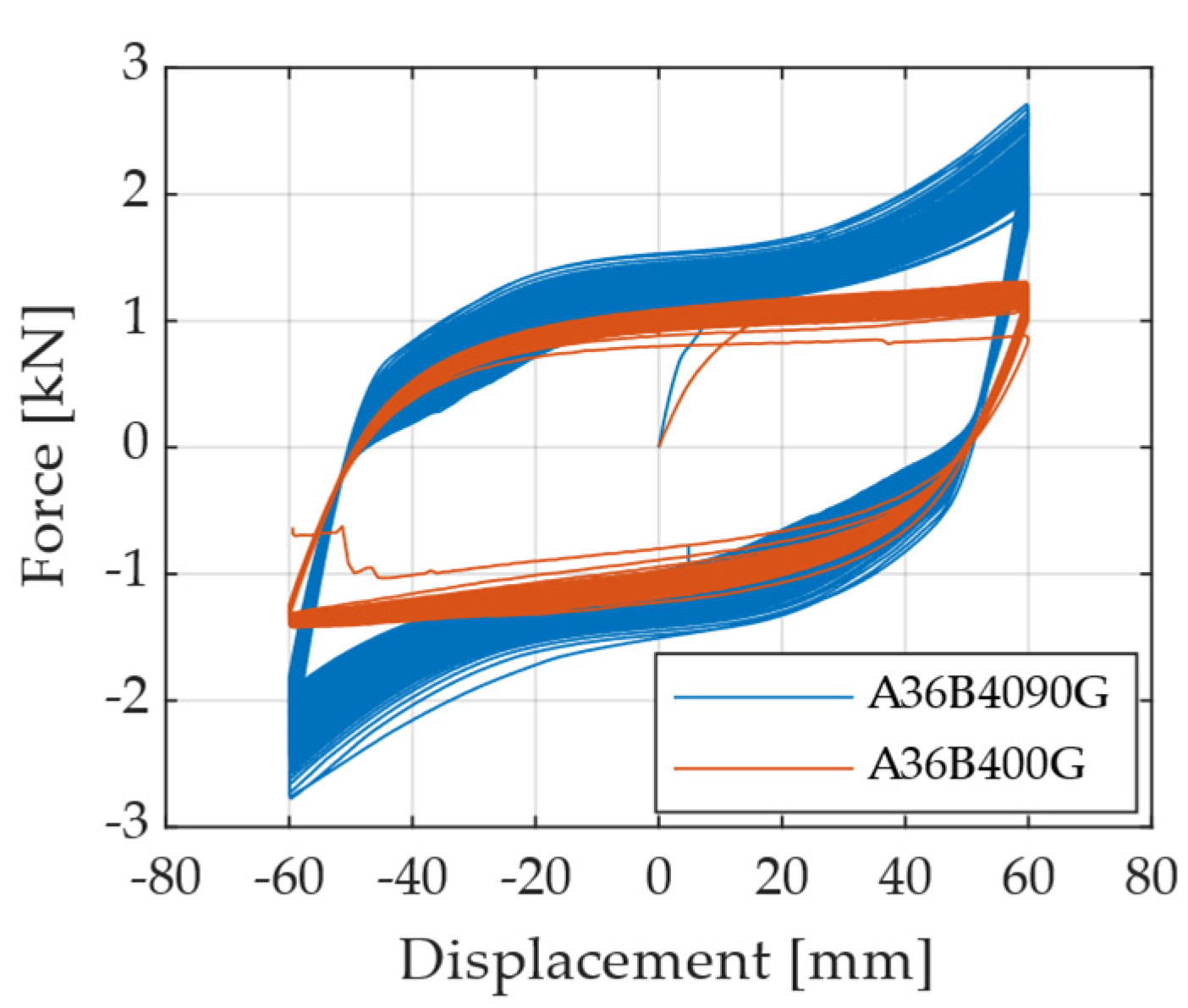



| Specimen | Structural Steel | H [mm] | B [mm] | t [mm] | Repetitions |
|---|---|---|---|---|---|
| A572-0G | A572 Gr 50 (minimum) | 100 | 75 | 8 | 4 |
| A572-t10 | 100 | 75 | 10 | 4 | |
| A572-t12 | 100 | 75 | 12 | 4 | |
| A572-H75 | 75 | 75 | 8 | 4 | |
| A572-H125 | 125 | 75 | 8 | 4 | |
| A572-B100 | 100 | 100 | 8 | 4 | |
| A572-B150 | 100 | 150 | 8 | 4 | |
| A36-0G | A36 (minimum) | 100 | 75 | 8 | 4 |
| A36-H125 | 125 | 75 | 8 | 4 | |
| A36-t10 | 100 | 75 | 10 | 4 | |
| A36-B40-0G | 120 | 40 | 5 | 3 | |
| A36-B40-90G | 120 | 40 | 5 | 3 | |
| TOTAL | 46 |
| Group | H/t Range Values |
|---|---|
| 1 | []20, +∞ [ |
| 2 | ]10, 20] |
| 3 | ]0, 10] |
| Parameter | A572 | A36 |
|---|---|---|
| [-] | 0.4 | 1 |
| [Mpa] | 60 | 160 |
| 1 | 1 | |
| [MPa] | 415 | 260 |
| [MPa] | 0 | 0 |
| [MPa] | 150 | 160 |
| Ratio | CK | CFy | |||||
|---|---|---|---|---|---|---|---|
| L’/B | B/t | ||||||
| 1 | 12.5 | −1.31 | 0.53 | −0.018 | −1.01 | 0.56 | −0.023 |
| 9.25 | −0.06 | 0.30 | −0.010 | 1.74 | 0.08 | −0.005 | |
| 6.00 | 0.36 | 0.17 | −0.005 | 2.03 | −0.06 | 0.001 | |
| 2 | 12.5 | −1.63 | 0.40 | −0.012 | −0.47 | 0.28 | −0.008 |
| 9.25 | −0.95 | 0.31 | −0.010 | −1.03 | 0.43 | −0.016 | |
| 6.00 | −0.15 | 0.16 | −0.005 | 0.40 | 0.17 | −0.006 | |
| 3 | 12.5 | −1.10 | 0.24 | −0.006 | −0.24 | 0.17 | −0.003 |
| 9.25 | −0.95 | 0.24 | −0.007 | −0.30 | 0.21 | −0.005 | |
| 6.00 | −0.40 | 0.15 | −0.004 | −0.32 | 0.23 | −0.007 | |
| Maximum Force [kN] | Difference [%] | ||
|---|---|---|---|
| Configuration | Direction A | Direction B | |
| 4U | 28.7 | 30.4 | 6.1 |
| 6U | 29.2 | 30.0 | 2.7 |
| 8U | 29.4 | 29.6 | 0.6 |
| 8UC | 28.6 | 30.3 | 5.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, J.; Barriuso, F.; Bazáez, R.; Pérez, L.; Lara-Rodríguez, G.; Astroza, R.; Heresi, P. Cyclic Behavior of U-Shaped Flexural Plates for Their Implementation in Multidirectional Energy Dissipation Devices. Materials 2025, 18, 1851. https://doi.org/10.3390/ma18081851
González J, Barriuso F, Bazáez R, Pérez L, Lara-Rodríguez G, Astroza R, Heresi P. Cyclic Behavior of U-Shaped Flexural Plates for Their Implementation in Multidirectional Energy Dissipation Devices. Materials. 2025; 18(8):1851. https://doi.org/10.3390/ma18081851
Chicago/Turabian StyleGonzález, Jorge, Fernando Barriuso, Ramiro Bazáez, Luis Pérez, Gabriel Lara-Rodríguez, Rodrigo Astroza, and Pablo Heresi. 2025. "Cyclic Behavior of U-Shaped Flexural Plates for Their Implementation in Multidirectional Energy Dissipation Devices" Materials 18, no. 8: 1851. https://doi.org/10.3390/ma18081851
APA StyleGonzález, J., Barriuso, F., Bazáez, R., Pérez, L., Lara-Rodríguez, G., Astroza, R., & Heresi, P. (2025). Cyclic Behavior of U-Shaped Flexural Plates for Their Implementation in Multidirectional Energy Dissipation Devices. Materials, 18(8), 1851. https://doi.org/10.3390/ma18081851








