Simulation and Structural Optimization of an Eccentric Rotor Extruder Feeding Section
Abstract
:1. Introduction
2. Materials and Methods
3. Research Results and Analysis
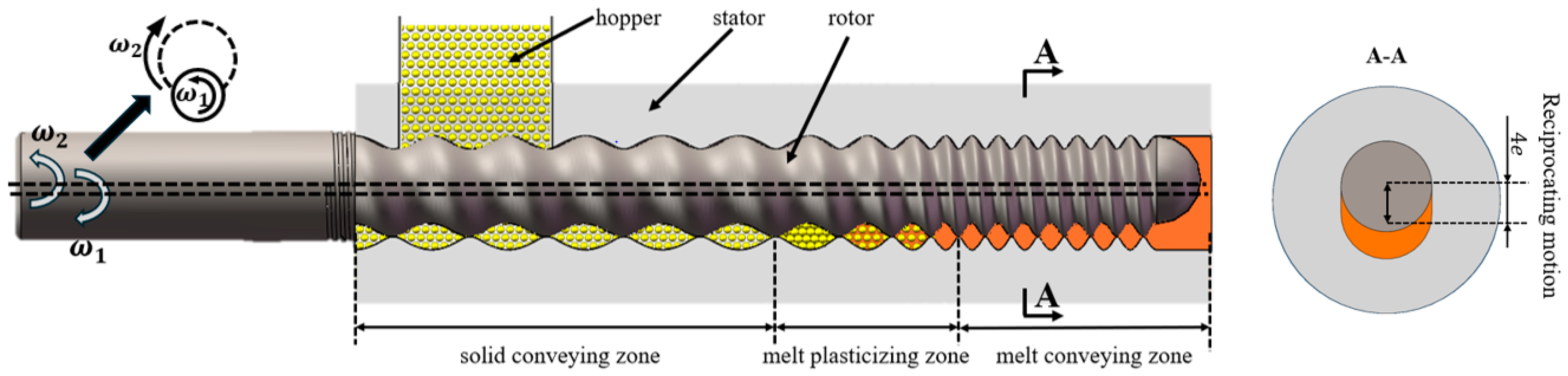
3.1. Mass Transfer Process in the Solid Conveying Section of the ERE and Problem Analysis
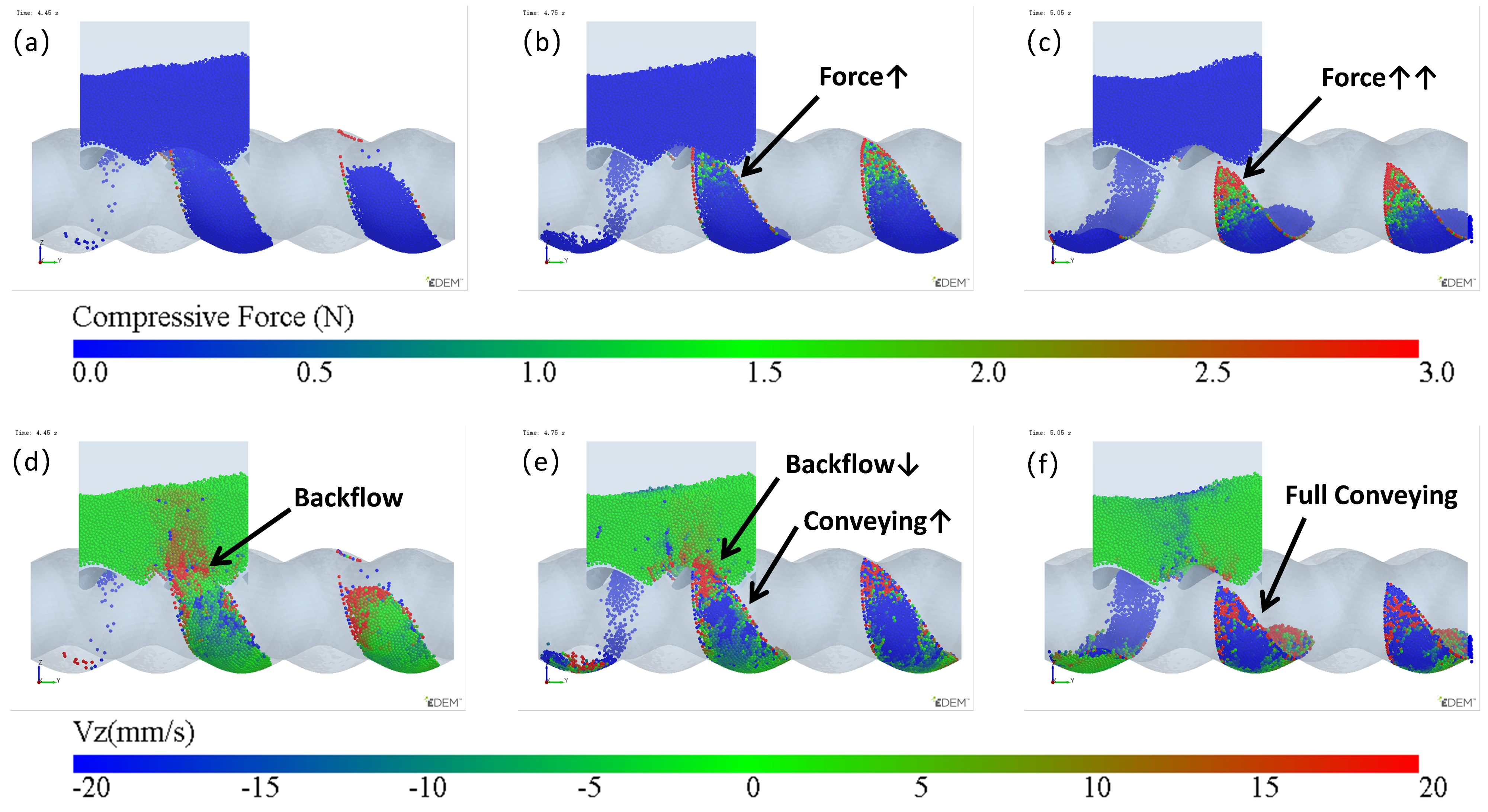
3.2. Feeding Process in the Solid Conveying Section of the ERE and Problem Analysis
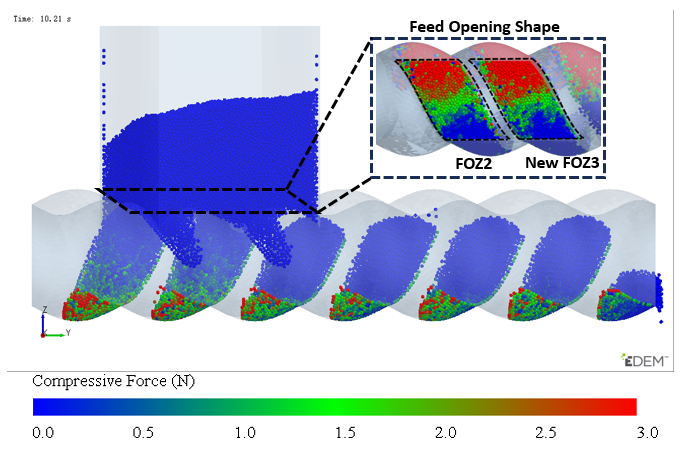
3.3. Dual-Cavity Feed Opening Adaptation Design
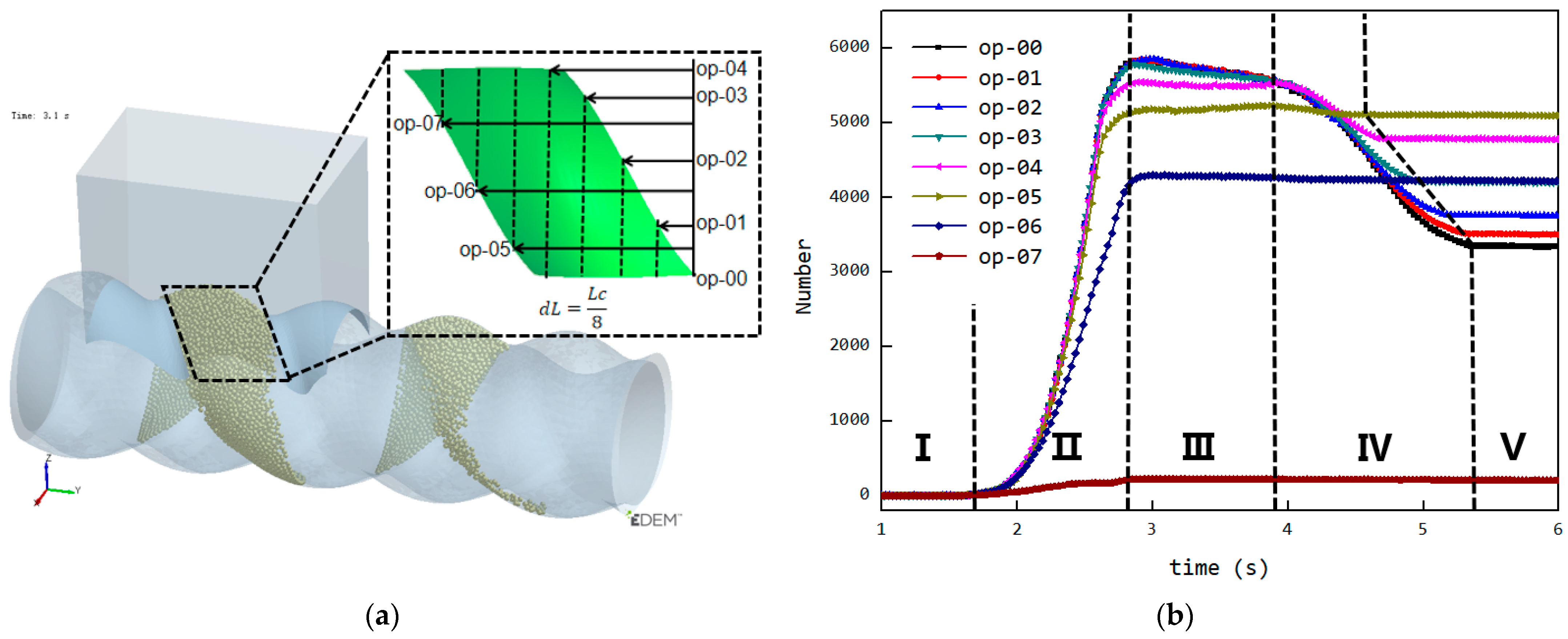
3.4. Dynamic Tracking of Cavities and Efficient Statistics of Internal Particle Quantity
3.5. Analysis of the Variation in the Number of Particles Inside the Cavity
- Stage 1—Empty Phase (pre-feeding): In this stage, the cavity has not yet been fed, and the number of particles inside the cavity remains zero;
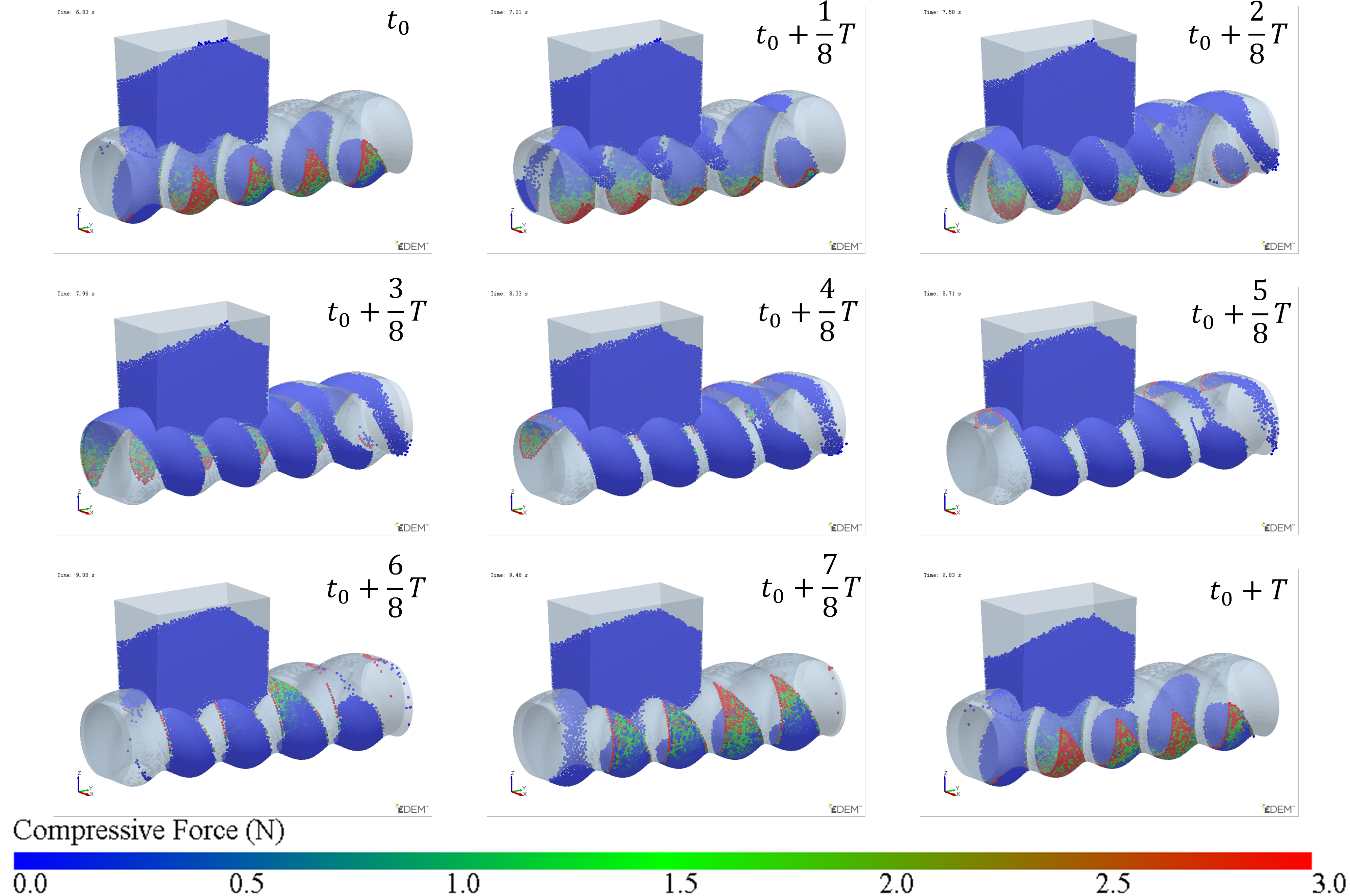
- Stage 2—Filling Phase: The cavity moves to the position where it is connected to the feed opening (as shown at t0 in Figure 6). Since the cavity has ample space at this stage, particles flow into the cavity rapidly along the cavity gap (FOZ2-Cavity2). This causes a sharp increase in the particle count, as seen in the Figure 11 curve;
- Stage 3—Exchange Balance Phase: In this stage, the cavity is filled. The curve shows a plateau, indicating that the cavity maintains its filled state (As seen in Figure 11). The particle flow observed in Figure 7 shows that particles flow back into the hopper from the upper side of the cavity (FOZ2–VCZ2), while particles from the hopper enter the cavity from the lower side (aft-side) (FOZ2–VEZ2). The inflow and outflow of particles are balanced, maintaining the filled state of the cavity;
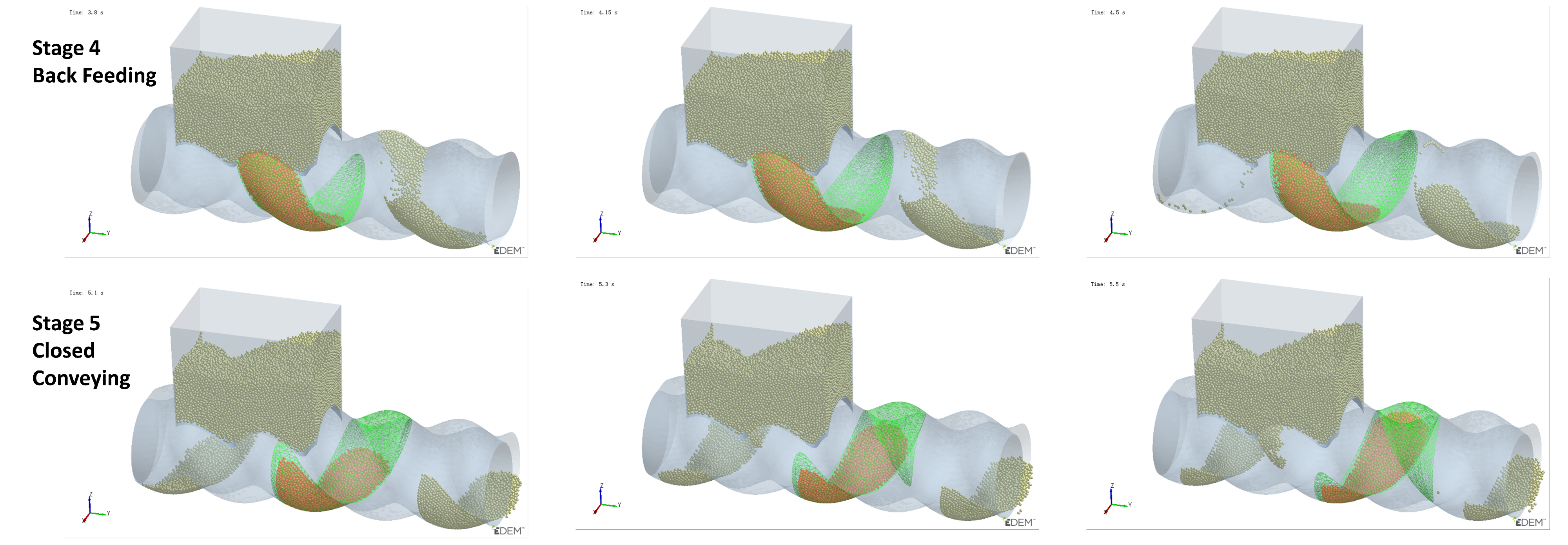
- Stage 4—Back Feeding Phase: As the cavity continues to move forward in a spiral, the volume of the VEZ expands against gravity direction. The particles, relying on their weight, cannot flow into the cavity effectively, leading to the formation of a void at the front of the cavity. The decrease in particle count at the early part of this stage is due to the number of particles flowing back from the upper side being greater than the number flowing into the cavity from the lower side, as seen at t0 + 4/8T in Figure 7. Later in this stage, after the cavity has fully passed through the feed opening, the decrease in particle count is due to the gap at the advancing face of VCZ2, which causes particles to flow back from the lower side of FOZ2 (FOZ2–VCZ2), as shown with t0 + 6/8T in Figure 7;
- Stage 5—Closed Conveying: In this final stage, the cavity becomes disconnected from the feed opening. Since the cavity is now closed, the particles inside the cavity remain in place. The number of particles retained in the cavity during this stage determines the feeding efficiency of the ERE.
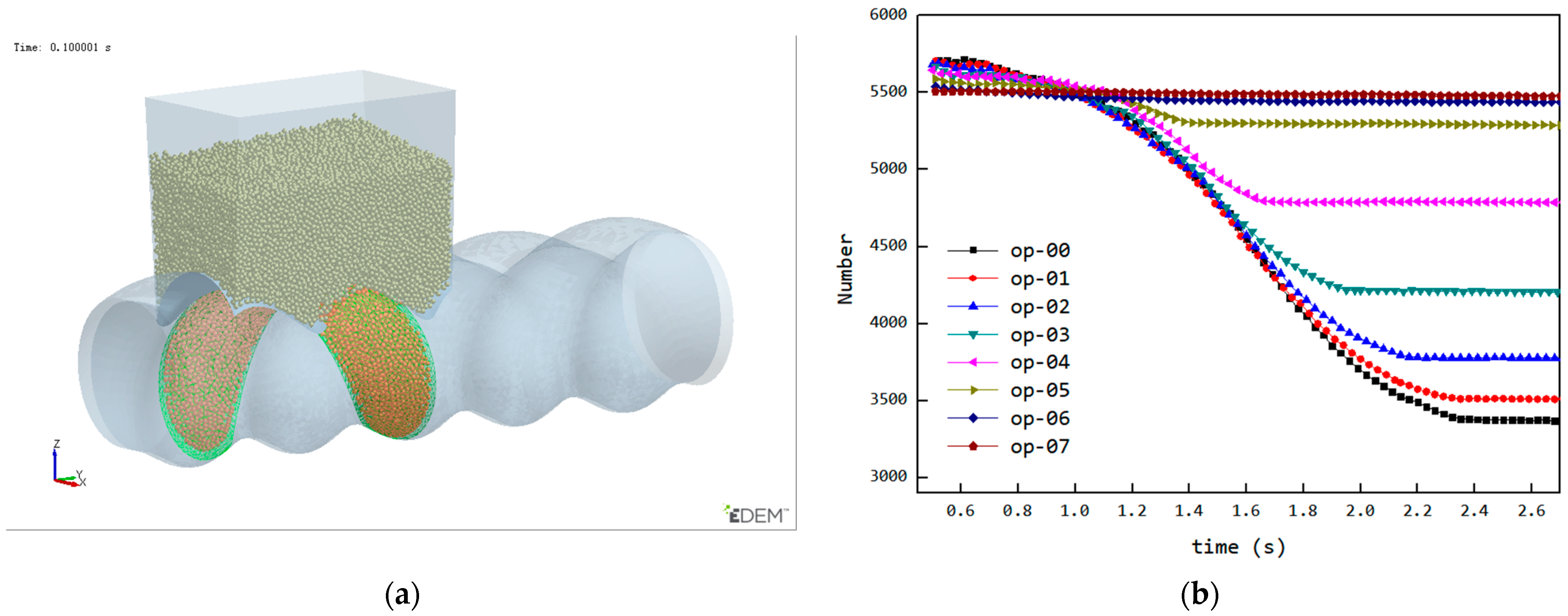
3.6. Analysis of the Back Feeding Process
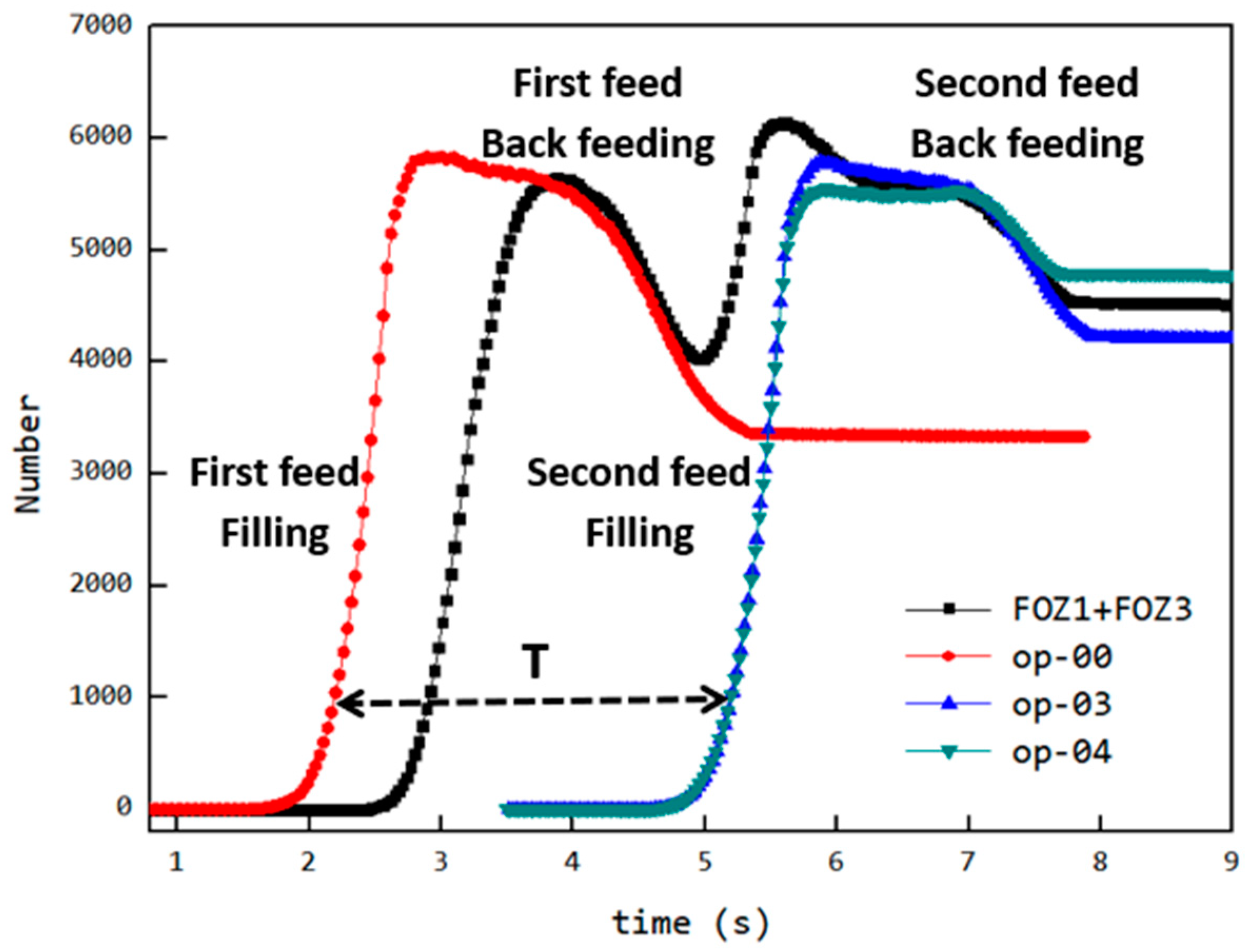
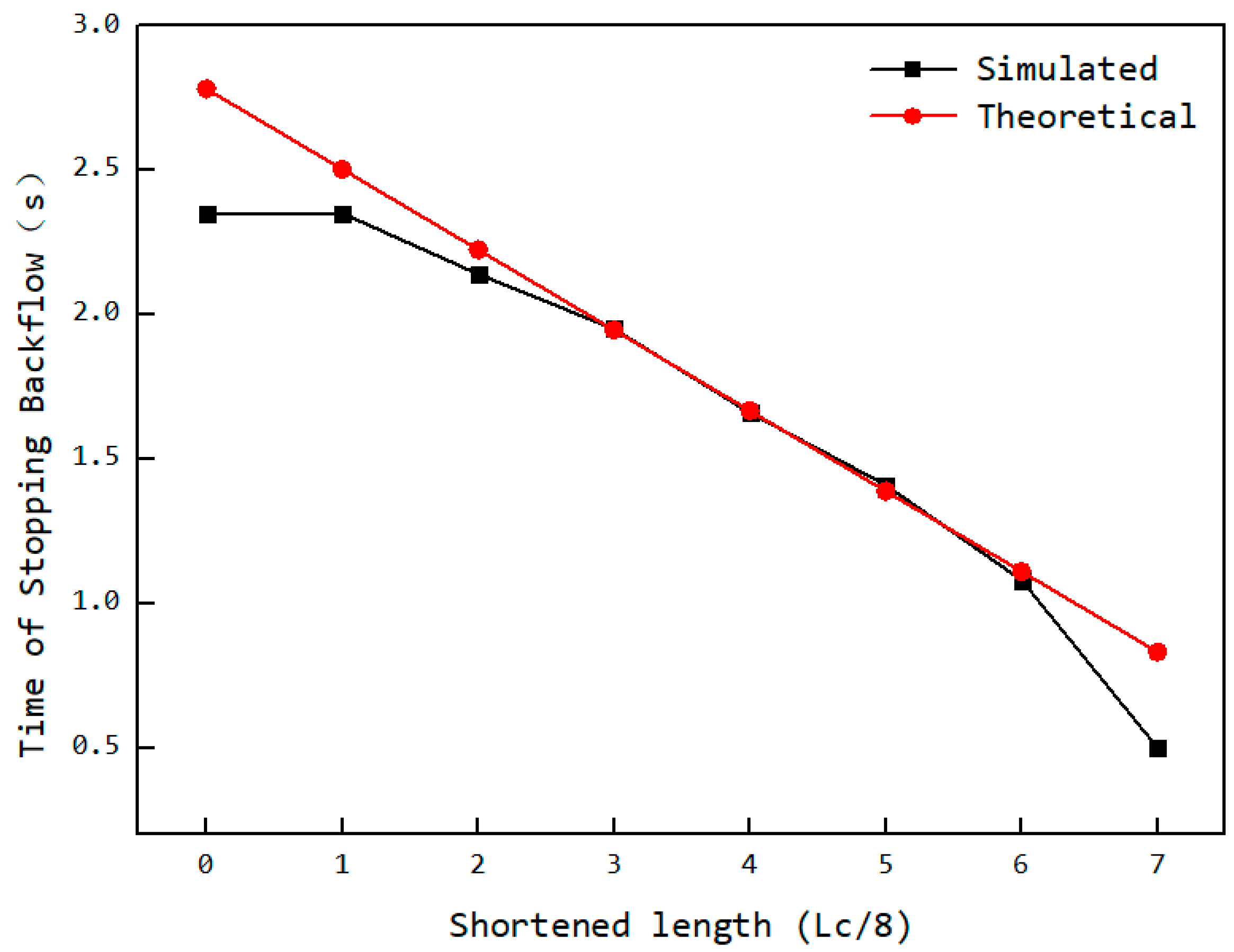
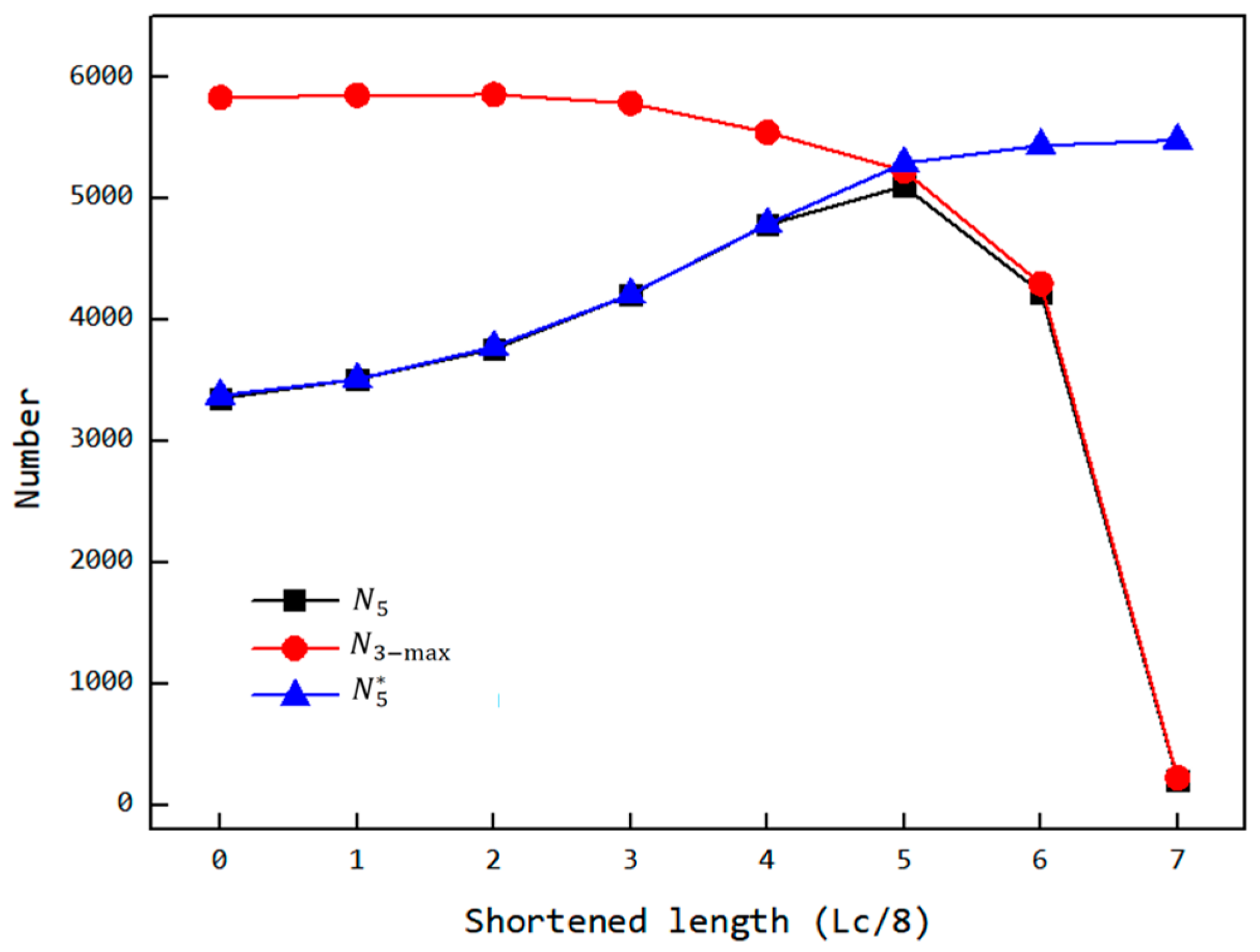
3.7. Variation of the Feeding Process with Changes in Feeding Opening Length
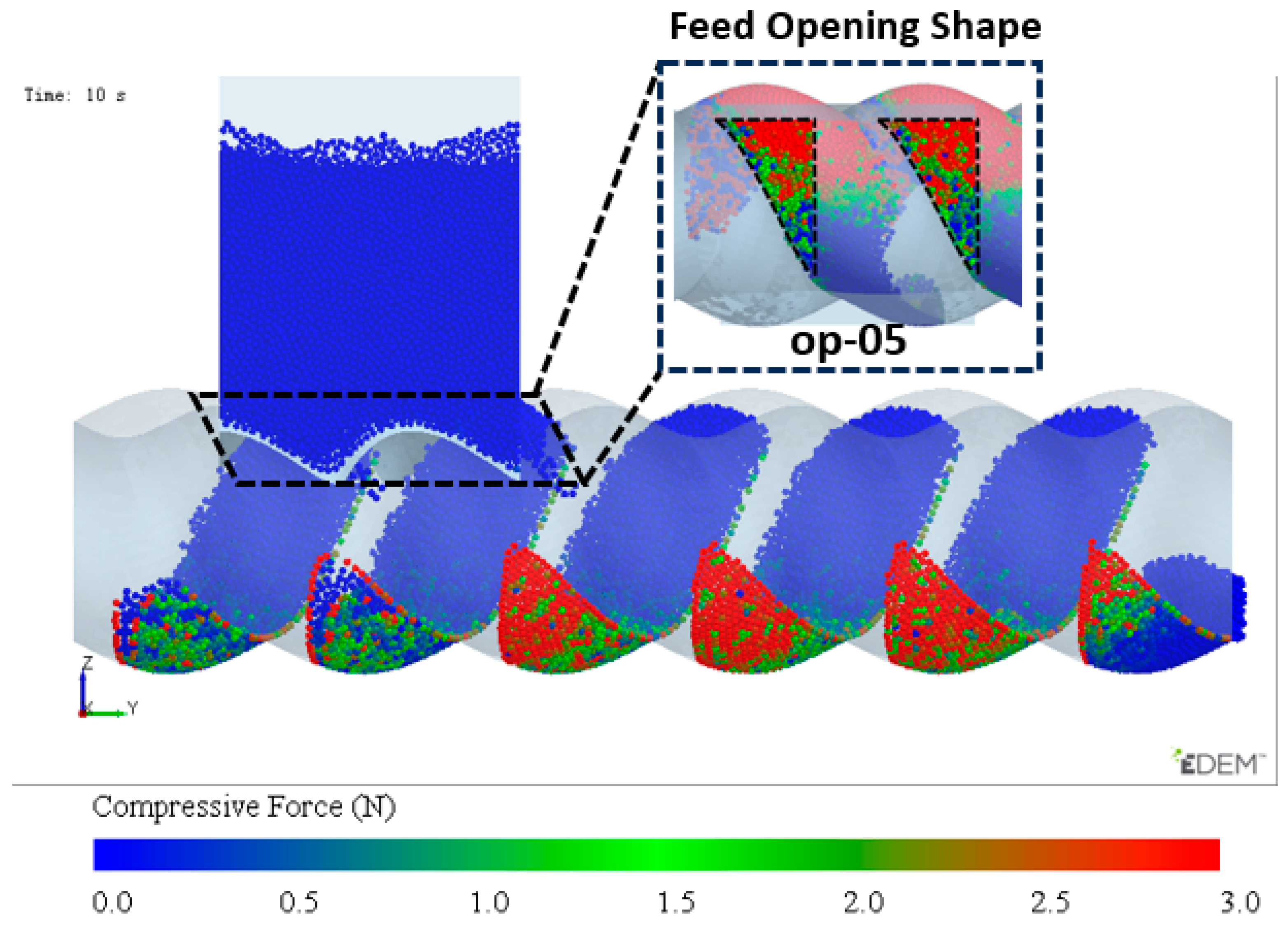
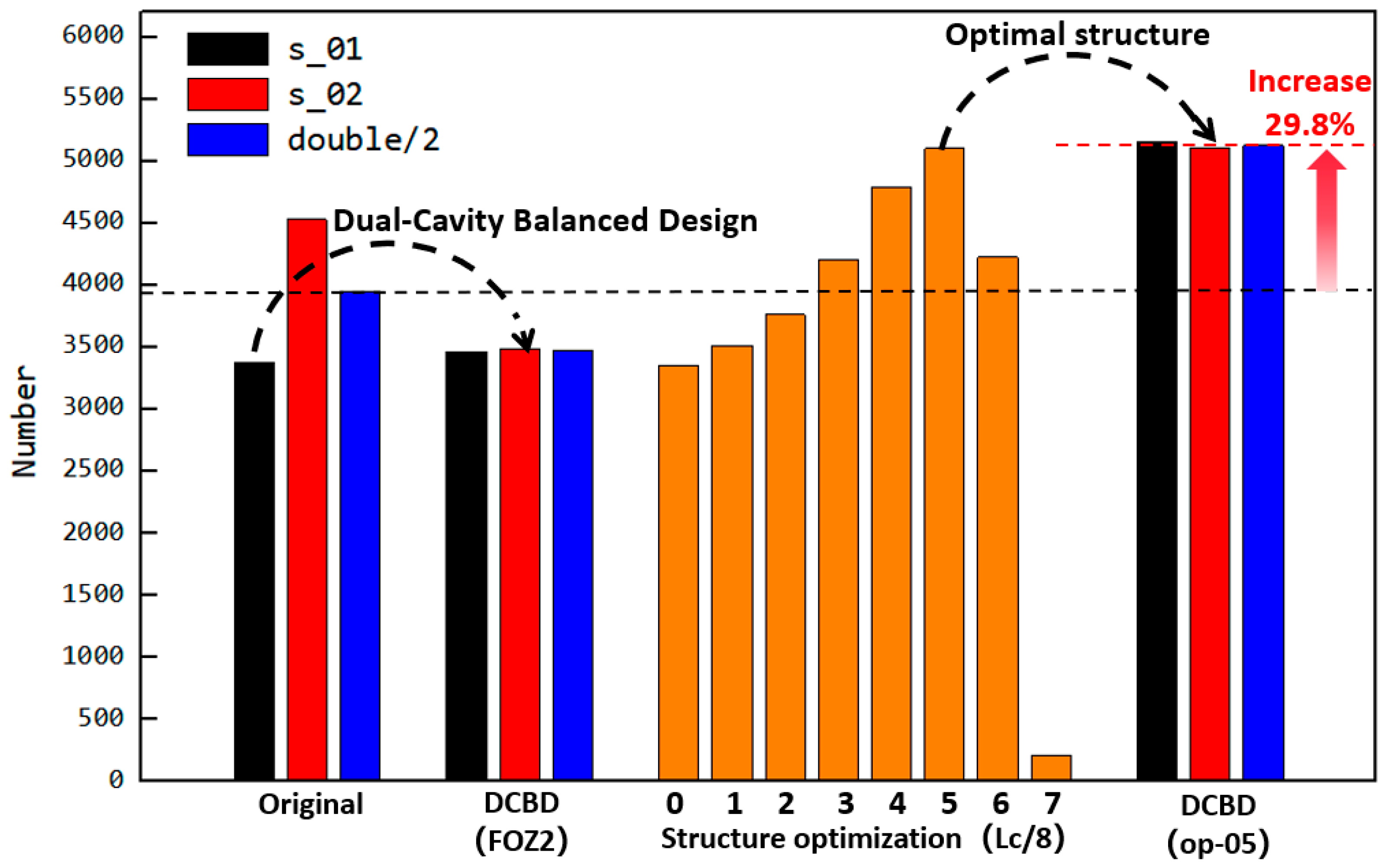
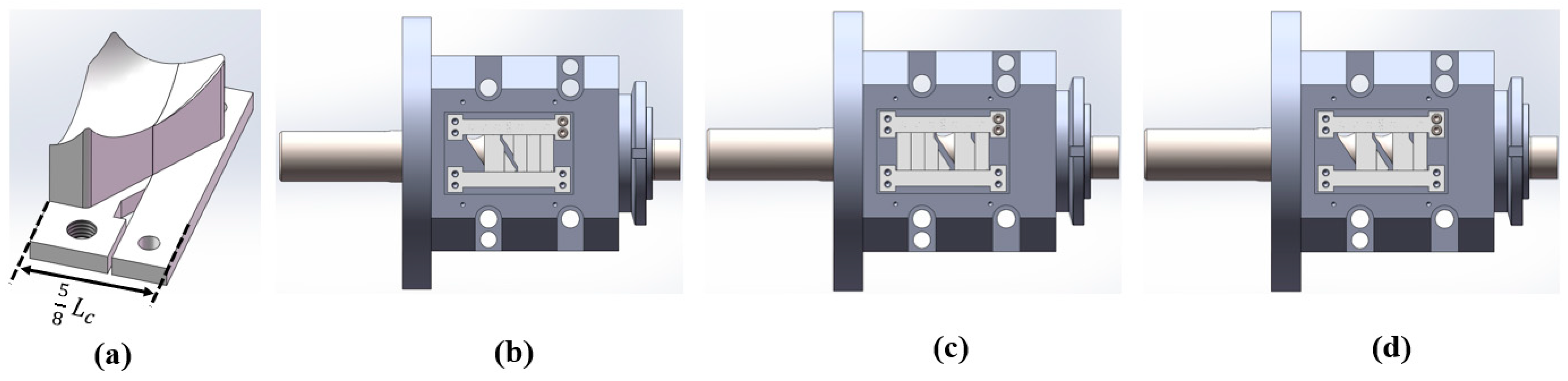
3.8. Optimization Principle and Design of the Optimized Structure
4. Experimental Validation
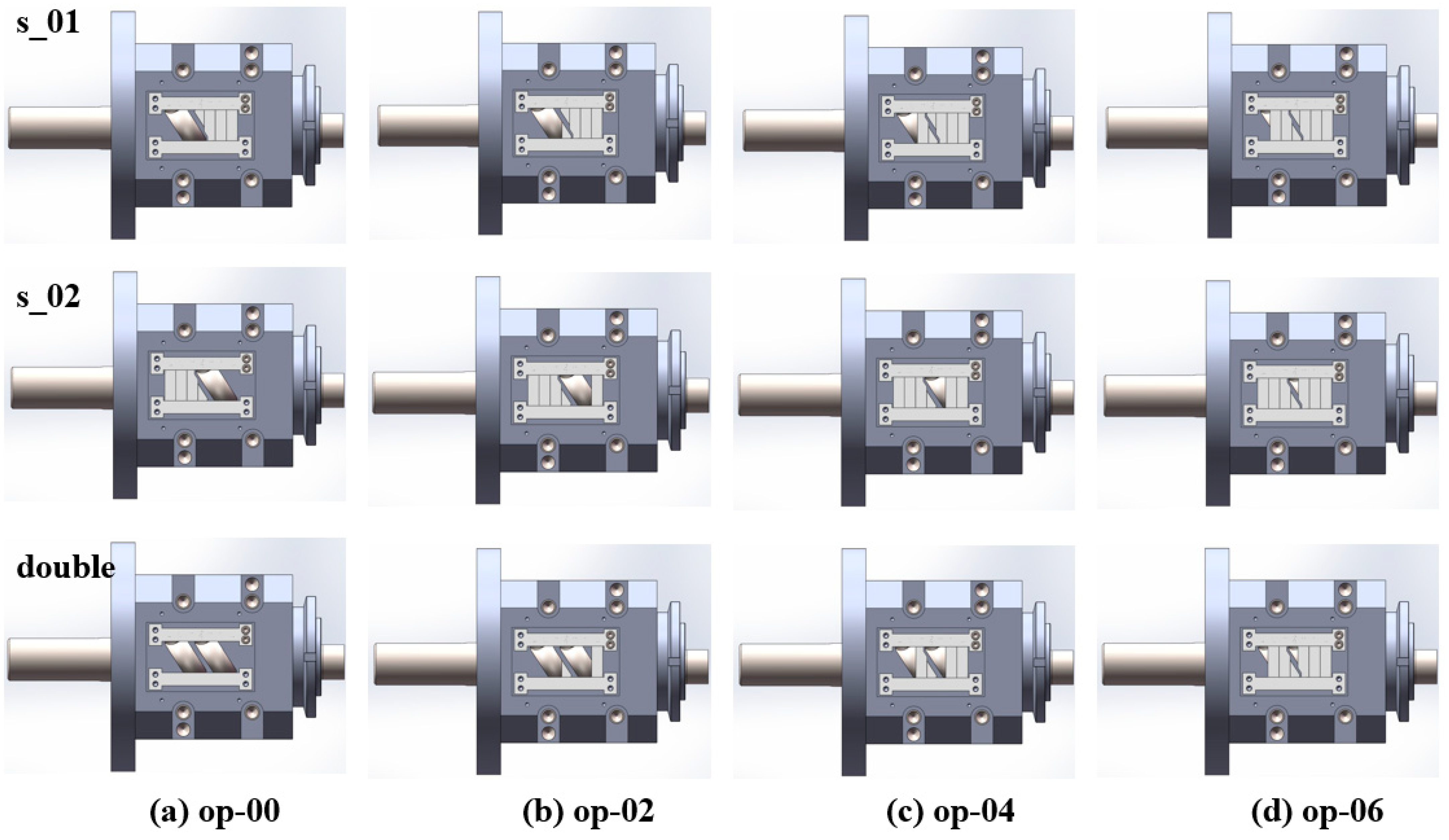
- Single feed into FOZ-A: measured the output (s-01) under different configurations (without parts, and with parts ①, ②, ③ corresponding to op-00, op-02, op-04, op-06);
- Single feed into FOZ-B: measured the output (s-02) under the same configurations;
- Simultaneous feed into FOZ-A and FOZ-B: measured the output (double/2) when both ports were fed simultaneously under different configurations.
- In addition, to validate the performance of op-05, the designed accessories and the ERE feed port configuration are illustrated in Figure 24.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ERE | Eccentric rotor extruder |
| DEM | Discrete element method |
| VCZ | Volume compression zone |
| VEZ | Volume extension zone |
| FOZ | Feed opening zone |
| DCBD | Dual-cavity balanced design |
Appendix A
References
- Yuan, Z.; Chen, X.; Yu, D. Recent advances in elongational flow dominated polymer processing technologies. Polymers 2021, 13, 1792. [Google Scholar] [CrossRef] [PubMed]
- He, G.; Lin, Z.; Yin, X.; Feng, Y. High orientation structure in UHMWPE/BN composites continuously obtained by elongational flow field leading to superior thermal conductivity. J. Appl. Polym. Sci. 2022, 139, e52640. [Google Scholar] [CrossRef]
- Wu, T.; Tong, Y.; Qiu, F.; Yuan, D.; Zhang, G.; Qu, J. Morphology, rheology property, and crystallization behavior of PLLA/OMMT nanocomposites prepared by an innovative eccentric rotor extruder. Polym. Adv. Technol. 2018, 29, 41–51. [Google Scholar] [CrossRef]
- Yu, X.; He, J.; Liu, Y.; Su, L.; Liu, F. Structure-property relationship of polycarbonate/polypropylene alloys prepared: Via eccentric rotor extruder. RSC Adv. 2019, 9, 41248–41255. [Google Scholar] [CrossRef]
- He, H.Z.; Xue, F.; Jia, P.F.; He, G.J.; Huang, Z.X.; Liu, S.M.; Xue, B. Linear low-density polyethylene/poly(ethylene terephthalate) blends compatibilization prepared by an eccentric rotor extruder: A morphology, mechanical, thermal, and rheological study. J. Appl. Polym. Sci. 2018, 135, 46489. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, X.; Qu, J.P. Microstructure evolution and mechanism of PLA/PVDF hybrid dielectrics fabricated under elongational flow. Polymer 2021, 224, 123719. [Google Scholar] [CrossRef]
- Feng, Y.; Gao, Y.; Chen, J.; Jiang, J.; Yin, X.; He, G.; Zeng, Y.; Kuang, Q.; Qu, J. Properties of compression molded ultra-high molecular weight polyethylene products pretreated by eccentric rotor extrusion. Polym. Int. 2019, 68, 862–870. [Google Scholar] [CrossRef]
- Lin, W.; Hou, A.; Feng, Y.H.; Yang, Z.T.; Qu, J.P. UHMWPE/organoclay nanocomposites fabricated by melt intercalation under continuous elongational flow: Dispersion, thermal behaviors and mechanical properties. Polym. Eng. Sci. 2019, 59, 547–554. [Google Scholar] [CrossRef]
- Qu, J.; Zhang, G.; Yin, X. Volume Pulsed Deformation Plasticating and Conveying Method and Device by Eccentric Rotor. US Patent 20170080619, 4 June 2019. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Hu, G.; Chen, J.; Jian, B.; Wan, H.; Liu, L. Modeling and simulation of transportation system of screw conveyors by the discrete element method. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, MACE2010, Wuhan, China, 26–28 June 2010; pp. 927–930. [Google Scholar]
- Pezo, L.; Jovanović, A.; Pezo, M.; Čolović, R.; Lončar, B. Modified screw conveyor-mixers—Discrete element modeling approach. Adv. Powder Technol. 2015, 26, 1391–1399. [Google Scholar] [CrossRef]
- Orefice, L.; Khinast, J.G. DEM study of granular transport in partially filled horizontal screw conveyors. Powder Technol. 2017, 305, 347–356. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Tian, R.; Wang, R.; Wang, X.; Sun, Q.; Fan, J. Numerical simulation of particle flow behavior in a screw conveyor using the discrete element method. Particuology 2019, 43, 137–148. [Google Scholar] [CrossRef]
- Yu, W.; Zou, D.; Li, D.; Wang, Q.; Peng, P. Development of Models Relating Screw Conveying Capacity of Concrete to Operating Parameters and Their Use in Conveyor Operating Strategies to Consider Batch Production. Appl. Sci. 2024, 14, 6351. [Google Scholar] [CrossRef]
- Moysey, P.A.; Thompson, M.R. Modelling the solids inflow and solids conveying of single-screw extruders using the discrete element method. Powder Technol. 2005, 153, 95–107. [Google Scholar] [CrossRef]
- Moysey, P.A.; Thompson, M.R. Investigation of solids transport in a single-screw extruder using a 3-D discrete particle simulation. Polym. Eng. Sci. 2004, 44, 2203–2215. [Google Scholar] [CrossRef]
- Fernandez, J.W.; Cleary, P.W.; McBride, W. Effect of screw design on hopper drawdown of spherical particles in a horizontal screw feeder. Chem. Eng. Sci. 2011, 66, 5585–5601. [Google Scholar] [CrossRef]
- Kretz, D.; Callau-Monje, S.; Hitschler, M.; Hien, A.; Raedle, M.; Hesser, J. Discrete element method (DEM) simulation and validation of a screw feeder system. Powder Technol. 2016, 287, 131–138. [Google Scholar] [CrossRef]
- Han, Y.; Jia, F.; Zeng, Y.; Jiang, L.; Zhang, Y.; Cao, B. DEM study of particle conveying in a feed screw section of vertical rice mill. Powder Technol. 2017, 311, 213–225. [Google Scholar] [CrossRef]
- Norouzi, H.R.; Zarghami, R.; Mostoufi, N. Insights into the granular flow in rotating drums. Chem. Eng. Res. Des. 2015, 102, 12–25. [Google Scholar] [CrossRef]
- Wu, W.N.; Liu, X.Y.; Zhang, R.; Hu, Z. DEM investigation of the power draw for material movement in rotary drums with axis offset. Chem. Eng. Res. Des. 2019, 144, 310–317. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, X.; Wu, W. Study of the critical angles of granular material in rotary drums aimed for fast DEM model calibration. Powder Technol. 2018, 340, 563–569. [Google Scholar] [CrossRef]
- Liu, X.; Hu, Z.; Wu, W.; Zhan, J.; Herz, F.; Specht, E. DEM study on the surface mixing and whole mixing of granular materials in rotary drums. Powder Technol. 2017, 315, 438–444. [Google Scholar] [CrossRef]
- Wang, X.; Yi, J.; Zhou, Z.; Yang, C. Optimal speed control for a semi-autogenous mill based on discrete element method. Processes 2020, 8, 233. [Google Scholar] [CrossRef]
- Golshan, S.; Zarghami, R.; Norouzi, H.R.; Mostoufi, N. Granular mixing in nauta blenders. Powder Technol. 2017, 305, 279–288. [Google Scholar] [CrossRef]
- Göbel, F.; Golshan, S.; Norouzi, H.R.; Zarghami, R.; Mostoufi, N. Simulation of granular mixing in a static mixer by the discrete element method. Powder Technol. 2019, 346, 171–179. [Google Scholar] [CrossRef]
- Mateo-Ortiz, D.; Méndez, R. Microdynamic analysis of particle flow in a confined space using DEM: The feed frame case. Adv. Powder Technol. 2016, 27, 1597–1606. [Google Scholar] [CrossRef]
- Ramírez-Aragón, C.; Ordieres-Meré, J.; Alba-Elías, F.; González-Marcos, A. Numerical modeling for simulation of compaction of refractory materials for secondary steelmaking. Materials 2020, 13, 224. [Google Scholar] [CrossRef]
- Bembenek, M.; Buczak, M.; Baiul, K. Modelling of the Fine-Grained Materials Briquetting Process in a Roller Press with the Discrete Element Method. Materials 2022, 15, 4901. [Google Scholar] [CrossRef] [PubMed]
- Owen, P.J.; Cleary, P.W. Prediction of screw conveyor performance using the Discrete Element Method (DEM). Powder Technol. 2009, 193, 274–288. [Google Scholar] [CrossRef]
- Li, X.; Hou, Q.; Dong, K.; Zou, R.; Yu, A. Promote cohesive solid flow in a screw feeder with new screw designs. Powder Technol. 2020, 361, 248–257. [Google Scholar] [CrossRef]
- Dun, G.; Sheng, Q.; Ji, X.; Zhang, C.; Gao, S.; Wei, Y.; Han, Y. Optimal Design and Experiment of Electronically Controlled Inclined Spiral Precision Fertilizer Discharger. Agriculture 2024, 14, 1131. [Google Scholar] [CrossRef]
- Fu, L.; Wang, K.; Hu, B.; van Xo, N. Conveying performance of drilling tool of auger miner at different strike angles based on discrete element method. Powder Technol. 2021, 378, 202–215. [Google Scholar] [CrossRef]
- Mindlin, R.D. Compliance of Elastic Bodies in Contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Jayasundara, C.T.; Yang, R.Y.; Yu, A.B.; Curry, D. Discrete particle simulation of particle flow in IsaMill Effect of grinding medium properties. Chem. Eng. J. 2008, 135, 103–112. [Google Scholar]
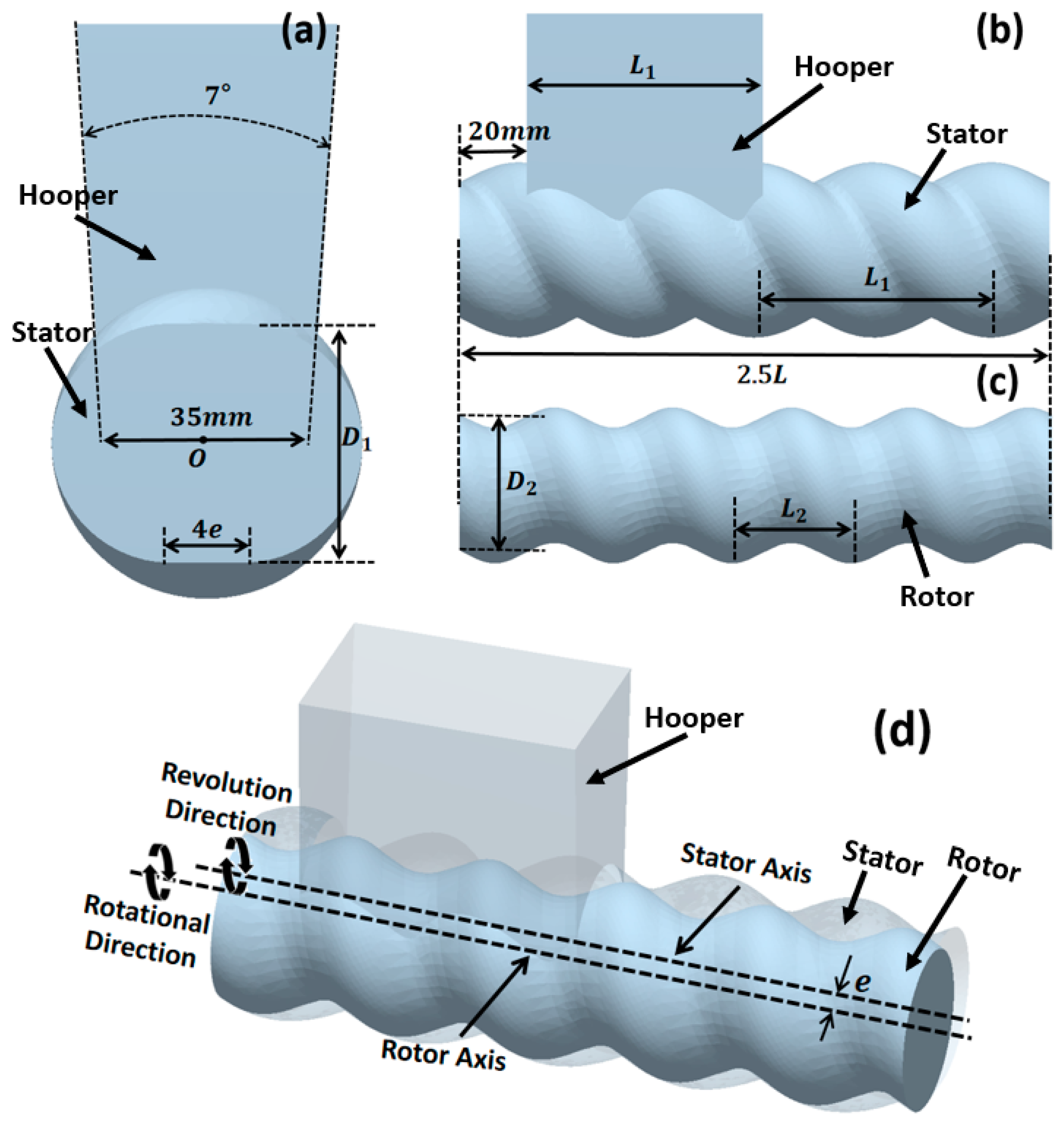











| Parameters | Value |
|---|---|
| Diameter of stator semi-circular segments D1 (mm) | 40 |
| Rotor diameter D2 (mm) | 40 |
| Rotor eccentricity e (mm) | 3 |
| Length of stator straight segments 4e (mm) | 12 |
| Pitch L1 (mm) | 70 |
| Rotor pitch L2 (mm) | 35 |
| Revolution velocity w (rpm) | 20 |
| Rotational velocity w1 (rpm) | −40 |
| Parameters | Value |
|---|---|
| Particle diameter (mm) | 0.7 |
| Particle Poisson’s ratio | 0.4 |
| Particle shear modulus (Pa) | 108 |
| Particle density (kg/m3) | 1500 |
| Geometry Poisson’s ratio | 0.29 |
| Geometry shear modulus (Pa) | 7.992 × 1010 |
| Geometry density (kg/m3) | 7861 |
| Particle-particle restitution coefficient | 0.45 |
| Particle-particle coefficient of static friction | 0.5 |
| Particle-particle coefficient of rolling friction | 0.05 |
| Particle-geometry restitution coefficient | 0.2 |
| Particle-geometry coefficient of static friction | 0.5 |
| Particle-geometry coefficient of rolling friction | 0.01 |
| Time step (s) | 2.26077 × 10−6 |
| Simulation time (s) | 6–12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Feng, Y.; Gao, S.; Yan, W.; Yin, X.; Zhang, G. Simulation and Structural Optimization of an Eccentric Rotor Extruder Feeding Section. Materials 2025, 18, 1939. https://doi.org/10.3390/ma18091939
Jiang J, Feng Y, Gao S, Yan W, Yin X, Zhang G. Simulation and Structural Optimization of an Eccentric Rotor Extruder Feeding Section. Materials. 2025; 18(9):1939. https://doi.org/10.3390/ma18091939
Chicago/Turabian StyleJiang, Jinhui, Yanhong Feng, Shuo Gao, Wenqiang Yan, Xiaochun Yin, and Guizhen Zhang. 2025. "Simulation and Structural Optimization of an Eccentric Rotor Extruder Feeding Section" Materials 18, no. 9: 1939. https://doi.org/10.3390/ma18091939
APA StyleJiang, J., Feng, Y., Gao, S., Yan, W., Yin, X., & Zhang, G. (2025). Simulation and Structural Optimization of an Eccentric Rotor Extruder Feeding Section. Materials, 18(9), 1939. https://doi.org/10.3390/ma18091939






