Development of Equivalent Material Properties of Microbump for Simulating Chip Stacking Packaging
Abstract
:1. Introduction
2. Numerical Approach of Equivalent Mechanical Properties

2.1. Equivalent Young’s Modulus of Microbump Unit


| Temperature (°C) | Young’s Modulus (GPa) | Poisson’s ratio (νx) |
|---|---|---|
| −40 | 29.6 | 0.37 |
| 0 | 29.5 | 0.37 |
| 25 | 29.5 | 0.37 |
| 70 | 29.4 | 0.37 |
| 100 | 29.3 | 0.37 |
| 125 | 29.3 | 0.37 |
| Temperature (°C) | Young’s Modulus (GPa) | Poisson’s ratio (νy) |
|---|---|---|
| −40 | 47.1 | 0.3 |
| 0 | 44.9 | 0.3 |
| 25 | 44.1 | 0.3 |
| 70 | 40.8 | 0.3 |
| 100 | 38.0 | 0.3 |
| 125 | 34.9 | 0.3 |
2.2. Equivalent Shear Modulus of Microbump Unit

| Temperature (°C) | Shear Modulus (GPa) (Gxy) | Shear Modulus (GPa) (Gyx) |
|---|---|---|
| −40 | 8.9 | 14.9 |
| 0 | 7.5 | 14.9 |
| 25 | 6.7 | 14.9 |
| 70 | 5.7 | 14.9 |
| 100 | 5.2 | 14.9 |
| 125 | 4.7 | 14.9 |
2.3. Equivalent CTE of Microbump Unit

3. Numerical Convergence of Finite Element Model with Equivalent Microbumps

| Materials | Young’s Modulus (E) | CTE (ppm/°C) | Poisson’s Ratio |
|---|---|---|---|
| Si | 169.5 GPa | 3 | 0.28 |
| Cu | E = 122 GPa Yield stress = 173 MPa Tensile strength = 1.2 GPa | 17 | 0.35 |
| Wafer-level Underfill | 5.6 GPa | 53 | 0.33 |
| Lead-free solder | Temperature dependence | 22.5 | 0.4 |
| IMC (Ni3Sn4) | 85.6 GPa | 17.6 | 0.31 |
| Ni | 186 GPa | 12.5 | 0.342 |
| Al | 72 GPa | 24 | 0.36 |



4. Sensitivity Analysis of Designed Factors in Packaging Structures with WLUF

| Designed Factor | Low Level | Middle Level | High Level |
|---|---|---|---|
| Chip thickness (A) | 50 μm | 385 μm | 720 μm |
| Substrate (B) | 50 μm | 385 μm | 720 μm |
| CTE of WLUF (C) | 10 ppm/°C | 35 ppm/°C | 60 ppm/°C |
| E-value of WULF (D) | 1 GPa | 7 GPa | 13 GPa |
4.1. Significant Influences of Designed Factors for Warpage
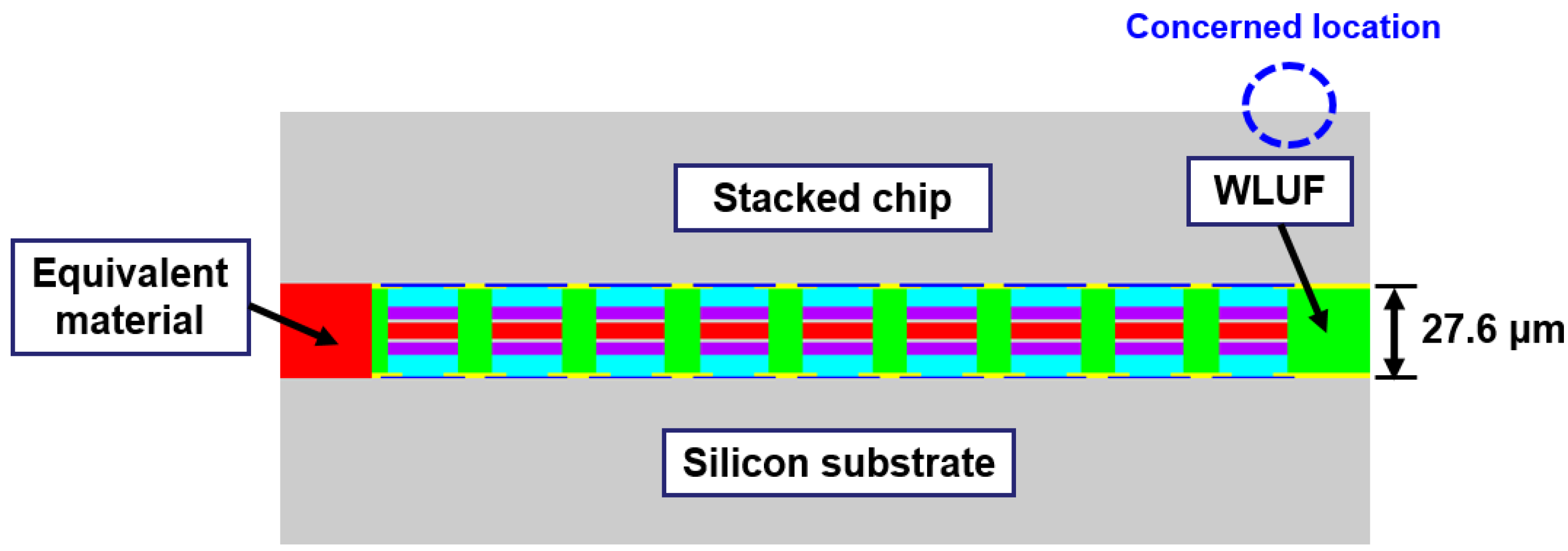




4.2. Equivalent Plastic Strain of Lead-Free Solder Induced in Microbump Interconnect




5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kuo, C.; Chen, J.J. Development of a novel stack package to fabricate high density memory modules for high-end application. Microelectron. Reliab. 2010, 50, 1116–1120. [Google Scholar] [CrossRef]
- Lim, S.P.S.; Rao, V.S.; Hnin, Y.H.; Ching, W.L.; Kripesh, V.; Lee, C.; Lau, J.; Milla, J.; Fenner, A. Process development and reliability of microbumps. IEEE Trans. Compon. Packag. Technol. 2010, 33, 747–753. [Google Scholar] [CrossRef]
- Tu, K.N. Reliability challenges in 3D IC packaging technology. Microelectron. Reliab. 2011, 51, 517–523. [Google Scholar] [CrossRef]
- Shirazi, A.; Varvani-Farahani, A.; Lu, H. An inverse analysis of warpage for trilayer thin-plate under thermal cycles. Mater. Des. 2010, 31, 4219–4228. [Google Scholar] [CrossRef]
- Shirazi, A.; Lu, H.; Varvani-Farahani, A. A hybrid inverse method for evaluating FC-PBGA material response to thermal cycles. J. Mater. Sci. Mater. Electron. 2010, 21, 737–749. [Google Scholar] [CrossRef]
- Ladani, L.J. Numerical analysis of thermo-mechanical reliability of through silicon vias (TSVs) and solder interconnects in 3-D integrated circuits. Microelectron. Eng. 2010, 87, 208–215. [Google Scholar] [CrossRef]
- Tsai, M.Y.; Chang, H.Y.; Pecht, M. Warpage analysis of flip-chip PBGA packages subject to thermal loading. IEEE Trans. Device Mater. Reliab. 2009, 9, 419–424. [Google Scholar] [CrossRef]
- Park, J.H.; Jang, K.W.; Paik, K.W.; Lee, S.B. A study of hygrothermal behavior of ACF flip chip packages with Moire interferometry. IEEE Trans. Compon. Packag. Technol. 2010, 33, 215–221. [Google Scholar] [CrossRef]
- Park, S.; Lee, H.C.; Sammakia, B.; Raghunathan, K. Predictive model for optimized design parameters in flip-chip packages and assemblies. IEEE Trans. Compon. Packag. Technol. 2007, 30, 294–301. [Google Scholar] [CrossRef]
- Lee, C.C.; Yang, T.F.; Wu, C.S.; Kao, K.S.; Fang, C.W.; Zhan, C.J.; Lau, J.H.; Chen, T.H. Impact of high density TSVs on the assembly of 3D-ICs packaging. Microelectron. Eng. 2013, 107, 101–106. [Google Scholar] [CrossRef]
- Chen, C.F.; Wu, S.T. Equivalent mechanical properties of through silicon via interposers—A unit model approach. Microelectron. Reliab. 2015, 55, 221–230. [Google Scholar] [CrossRef]
- Lee, C.C.; Yang, T.F.; Kao, K.S.; Cheng, R.C.; Zhan, C.J.; Cheng, T.H. Development of Cu/Ni/SnAg microbump bonding process for thin chip-on-chip packages via wafer-level underfill film. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 1412–1419. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-C.; Tzeng, T.-L.; Huang, P.-C. Development of Equivalent Material Properties of Microbump for Simulating Chip Stacking Packaging. Materials 2015, 8, 5121-5137. https://doi.org/10.3390/ma8085121
Lee C-C, Tzeng T-L, Huang P-C. Development of Equivalent Material Properties of Microbump for Simulating Chip Stacking Packaging. Materials. 2015; 8(8):5121-5137. https://doi.org/10.3390/ma8085121
Chicago/Turabian StyleLee, Chang-Chun, Tzai-Liang Tzeng, and Pei-Chen Huang. 2015. "Development of Equivalent Material Properties of Microbump for Simulating Chip Stacking Packaging" Materials 8, no. 8: 5121-5137. https://doi.org/10.3390/ma8085121
APA StyleLee, C.-C., Tzeng, T.-L., & Huang, P.-C. (2015). Development of Equivalent Material Properties of Microbump for Simulating Chip Stacking Packaging. Materials, 8(8), 5121-5137. https://doi.org/10.3390/ma8085121





