Study on Stress Development in the Phase Transition Layer of Thermal Barrier Coatings
Abstract
:1. Introduction
2. Theoretical Models
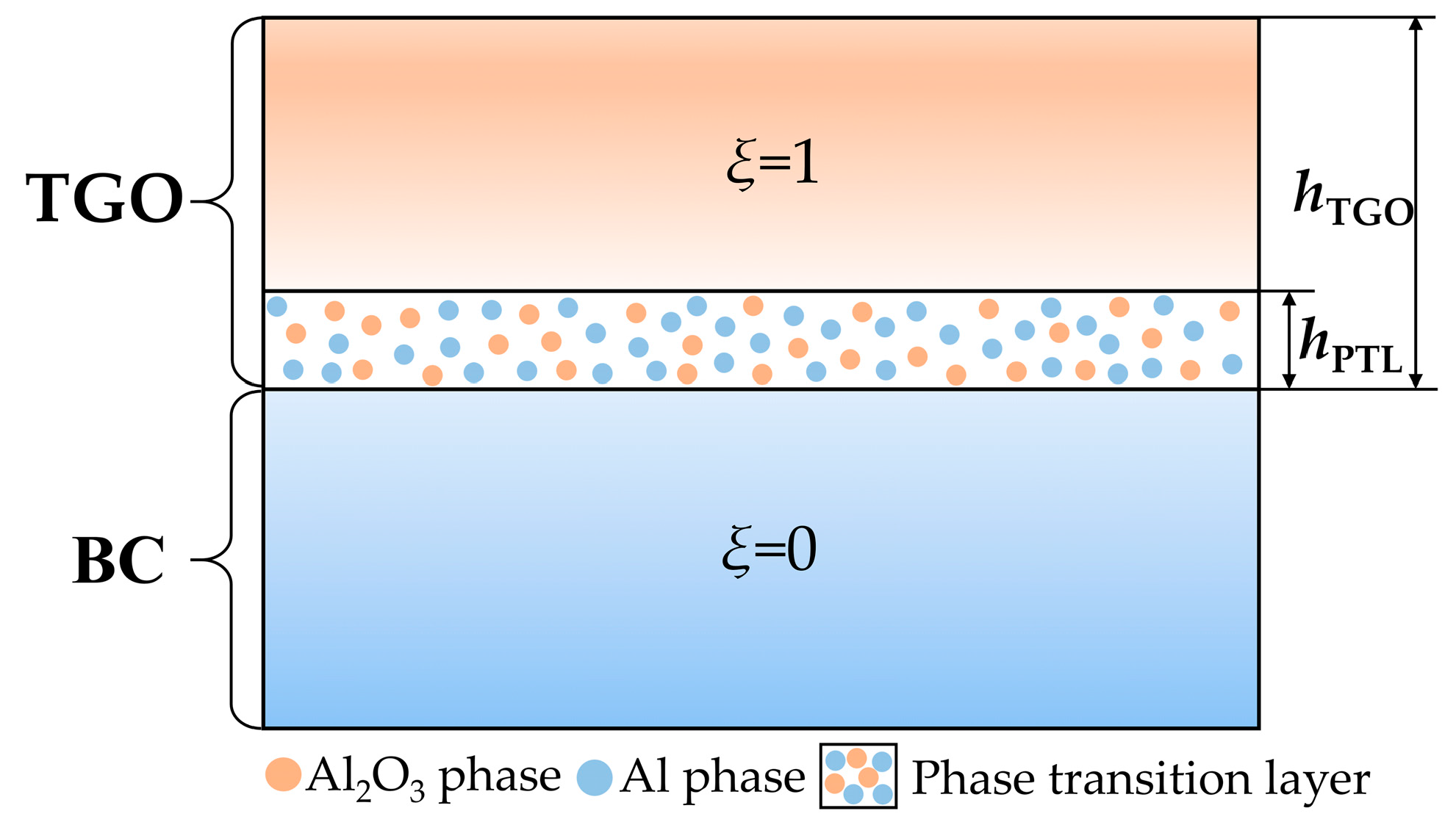
2.1. Diffusion-Oxidation Reaction Model for the TGO Layer
2.2. The Constitutive Equation for the Phase Transition Layer
2.2.1. Constitutive Equation based on Reuss Model
2.2.2. Constitutive Equation based on the Voigt Model
3. Numerical Examples
3.1. Finite Element Model
3.2. Physical and Mechanical Properties
4. Results and Discussion
4.1. Growth of the Phase Transition Layer
4.2. Stress State in the Phase Transition Layer
5. Conclusions
- A large oxygen diffusion coefficient increases the oxidation rate of metal material in the phase transition layer, and leads to a smaller part of the PTL taking part in the TGO thickness.
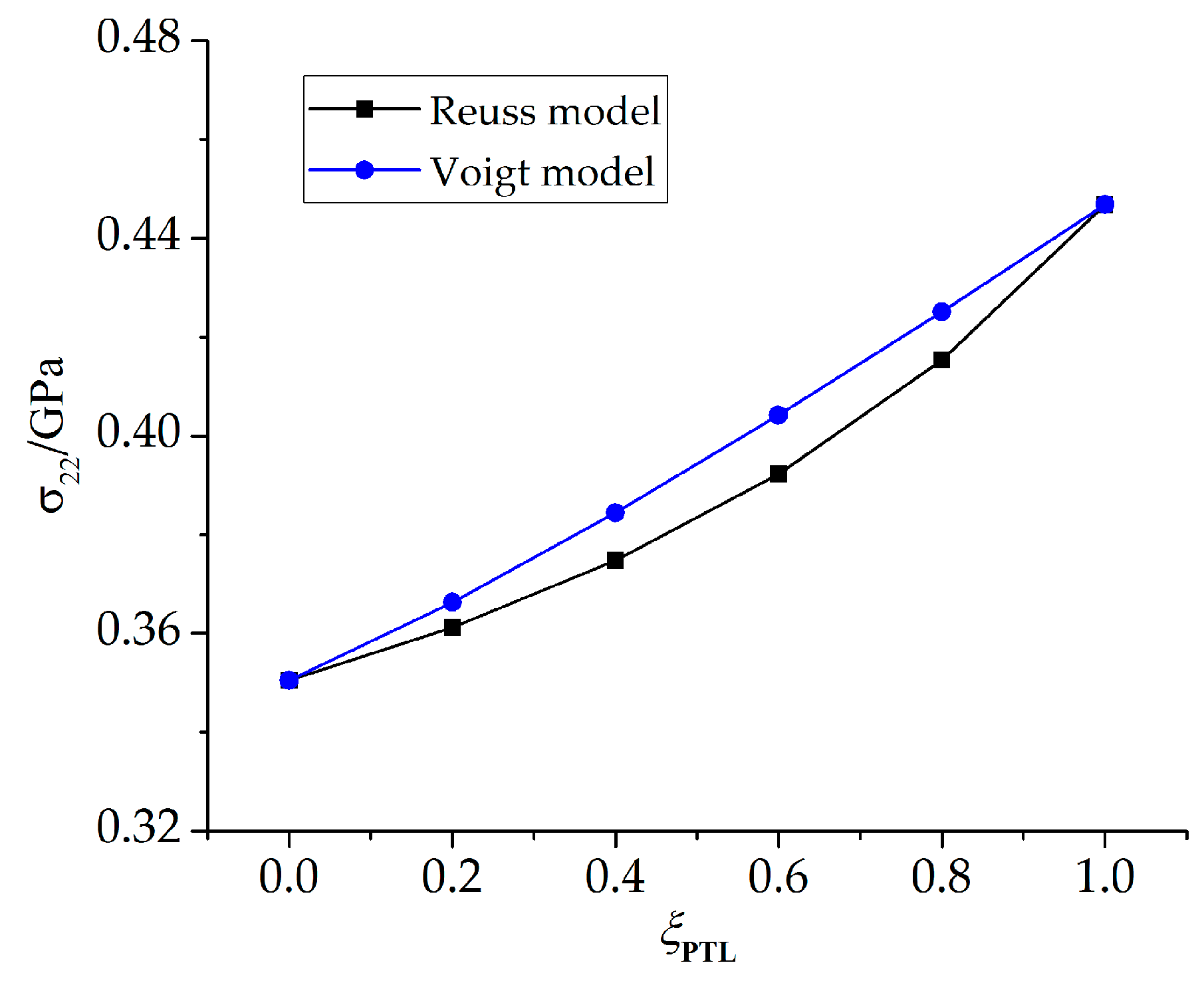
- The stresses in the PTL based on the Reuss model are slightly smaller than those of the Voigt model. With the Al2O3 dimensionless molar fraction in the PTL ξPTL increasing, the stresses based on the Voigt model increase linearly, while the stresses based on the Reuss model increase non-linearly. Meanwhile, with the thickness ratio of phase transition layer in the TGO increasing, the stress difference caused by different constitutive models becomes more evident.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Beele, W.; Marijnissen, G.; van Lieshout, A. The Evolution of Thermal Barrier Coatings-Status and Upcoming Solutions for Today’s Key Issues. Surf. Coat. Technol. 1999, 120, 61–67. [Google Scholar] [CrossRef]
- Vaßen, R.; Jarligo, M.O.; Steinke, T.; Mack, D.E.; Stöver, D. Overview on Advanced Thermal Barrier Coatings. Surf. Coat. Technol. 2010, 205, 938–942. [Google Scholar] [CrossRef]
- Clarke, D.R.; Oechsner, M.; Padture, N.P. Thermal Barrier Coatings for More Efficient Gas-Turbine Engines. MRS Bull. 2012, 37, 891–898. [Google Scholar] [CrossRef]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal Barrier Coatings for Gas-Turbine Engine Applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Clarke, D.R.; Phillpot, S.R. Thermal Barrier Coating Materials. Mater. Today 2005, 8, 22–29. [Google Scholar] [CrossRef]
- Feuerstein, A.; Knapp, J.; Taylor, T.; Ashary, A.; Bolcavage, A.; Hitchman, N. Technical and Economical Aspects of Current Thermal Barrier Coating Systems for Gas Turbine Engines by Thermal Spray and EBPVD: A Review. J. Therm. Spray Technol. 2007, 17, 199–213. [Google Scholar] [CrossRef]
- Pollock, T.M.; Lipkin, D.M.; Hemker, K.J. Multifunctional Coating Interlayers for Thermal-Barrier Systems. MRS Bull. 2012, 37, 923–931. [Google Scholar] [CrossRef]
- Miller, R.A. Current Status of Thermal Barrier Coatings—An Overview. Surf. Coat. Technol. 1987, 30, 1–11. [Google Scholar] [CrossRef]
- Hille, T.S.; Turteltaub, S.; Suiker, A.S.J. Oxide Grown and Damage Evolution in Thermal Barrier Coatings. Eng. Fract. Mech. 2011, 78, 2139–2052. [Google Scholar] [CrossRef]
- Busso, E.P. Oxidation-Induced Stresses in Ceramic-Metal Interfaces. J. Phys. IV France 1999, 9, 287–296. [Google Scholar] [CrossRef]
- Busso, E.P.; Lin, J.; Sakurai, S. A Mechanistic Study of Oxidation-Induced Degradation in a Plasma-Sprayed Thermal Barrier Coating System: Part I: Model Formulation. Acta Mater. 2001, 49, 1515–1528. [Google Scholar] [CrossRef]
- Doghri, I.; Ouaar, A. Homogenization of Two-Phase Elasto-plastic Composite Materials and Structures: Study of Tangent Operators, Cyclic Plasticity and Numerical Algorithms. Int. J. Solids Struct. 2002, 40, 1681–1712. [Google Scholar] [CrossRef]
- Lin, C.; Li, Y.M. Stress Evolution Considering the Combined Creep-Plastic Behavior in Thermal Barrier Coatings. Mater. Des. 2016, 89, 245–254. [Google Scholar]
- Ammar, K.; Appolaire, B.; Cailletaud, G.; Forest, S. Combining Phase Field Approach and Homogenization Methods for Modeling Phase Transformation in Elastoplastic Media. Eur. J. Comput. Mech. 2009, 18, 485–523. [Google Scholar]
- Evans, H.E. Stress Effects in High-Temperature Oxidation of Metals. Int. Mater. Rev. 1995, 40, 1–40. [Google Scholar] [CrossRef]
- Cheng, J.; Jordan, E.H.; Barber, B.; Gell, M. Thermal/Residual Stress in an Electron Beam Physical Vapor Deposited Thermal Barrier Coating Systems. Acta Mater. 1998, 46, 5839–5850. [Google Scholar] [CrossRef]
- Rӧsler, J.; Bäker, M.; Volgmann, M. Stress State and Failure Mechanisms of Thermal Barrier Coatings: Role of Creep in Thermal Grown Oxide. Acta Mater. 2001, 49, 3659–3670. [Google Scholar] [CrossRef]
- Quested, P.N.; Brooks, R.F.; Chapman, L.; Morrell, R.; Youssef, Y.; Mills, K.C. Measurement and Estimation of Thermophysical Properties of Nickel Based Superalloys. Mater. Sci. Technol. 2009, 25, 154–162. [Google Scholar] [CrossRef]
- Martena, M.; Botto, D.; Fino, P.; Sabbadini, S.; Gola, M.M.; Badini, C. Modeling of TBC System Failure: Stress Distribution as a Function of TGO Thickness and Thermal Expansion Mismatch. Eng. Fail. Anal. 2006, 13, 409–426. [Google Scholar] [CrossRef]
- Bäker, M.; Rösler, J.; Heinze, G. A Parametric Study of the Stress State of Thermal Barrier Coatings Part II: Cooling Stresses. Acta Mater. 2005, 53, 469–476. [Google Scholar] [CrossRef]
- Bäker, M.; Rösler, J.; Affeldt, E. The Influence of Axial Loading on the Interface Stresses of Thermal Barrier Coatings. Comput. Mater. Sci. 2009, 47, 466–470. [Google Scholar] [CrossRef]













| T/°C | 20 | 200 | 400 | 600 | 800 | 1000 | 1100 | |
|---|---|---|---|---|---|---|---|---|
| TC | E/GPa [16] | 48 | 47 | 44 | 40 | 34 | 26 | 22 |
| ν [16] | 0.1 | 0.1 | 0.1 | 0.11 | 0.11 | 0.12 | 0.12 | |
| α (10−6/°C) [16] | 9.7 | 9.8 | 9.9 | 9.9 | 10 | 10.1 | 10.1 | |
| BC | E/GPa [16] | 200 | 190 | 175 | 160 | 145 | 120 | 110 |
| ν [16] | 0.3 | 0.3 | 0.31 | 0.31 | 0.32 | 0.33 | 0.33 | |
| α (10−6/°C) [16] | 12.3 | 13.2 | 14.2 | 15.2 | 16.3 | 17.2 | 17.7 | |
| TGO | E/GPa [16] | 400 | 390 | 380 | 370 | 355 | 325 | 320 |
| ν [16] | 0.23 | 0.23 | 0.24 | 0.24 | 0.25 | 0.25 | 0.25 | |
| α (10−6/°C) [16] | 8 | 8.2 | 8.4 | 8.7 | 9 | 9.3 | 9.5 | |
| Substrate | α (10−6/°C) [16] | 14.8 | 15.2 | 15.6 | 16.2 | 16.9 | 17.2 | 17.6 |
| Parameter | Value | |
|---|---|---|
| oxygen diffusion in TC | DTC/(m2/s) | ∞ |
| oxygen diffusion in BC/TGO [17] | DBC = DTGO/(m2/s) | 3.5 × 10−14 |
| Reference value for the diffusion-oxidation model | A [18]/(mol/m3) | 0.24 × 106 |
| γ [19]/(m3/(mol·s)) | 1.25 × 10−4 |
| Parameter | Value | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D (3.5 × 10−14 m2/s) | 0.1 | 0.2 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 1.3 | 1.7 | 2 | 3 | 4 | 5 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Y.; Lin, C.; Wang, X.; Li, Y. Study on Stress Development in the Phase Transition Layer of Thermal Barrier Coatings. Materials 2016, 9, 773. https://doi.org/10.3390/ma9090773
Chai Y, Lin C, Wang X, Li Y. Study on Stress Development in the Phase Transition Layer of Thermal Barrier Coatings. Materials. 2016; 9(9):773. https://doi.org/10.3390/ma9090773
Chicago/Turabian StyleChai, Yijun, Chen Lin, Xian Wang, and Yueming Li. 2016. "Study on Stress Development in the Phase Transition Layer of Thermal Barrier Coatings" Materials 9, no. 9: 773. https://doi.org/10.3390/ma9090773
APA StyleChai, Y., Lin, C., Wang, X., & Li, Y. (2016). Study on Stress Development in the Phase Transition Layer of Thermal Barrier Coatings. Materials, 9(9), 773. https://doi.org/10.3390/ma9090773





