Small-Scale Hybrid Methanol–Methane Production Based on Biogas: Stochastic Sensitivity Analysis of the Economic Sustainability
Abstract
:1. Introduction
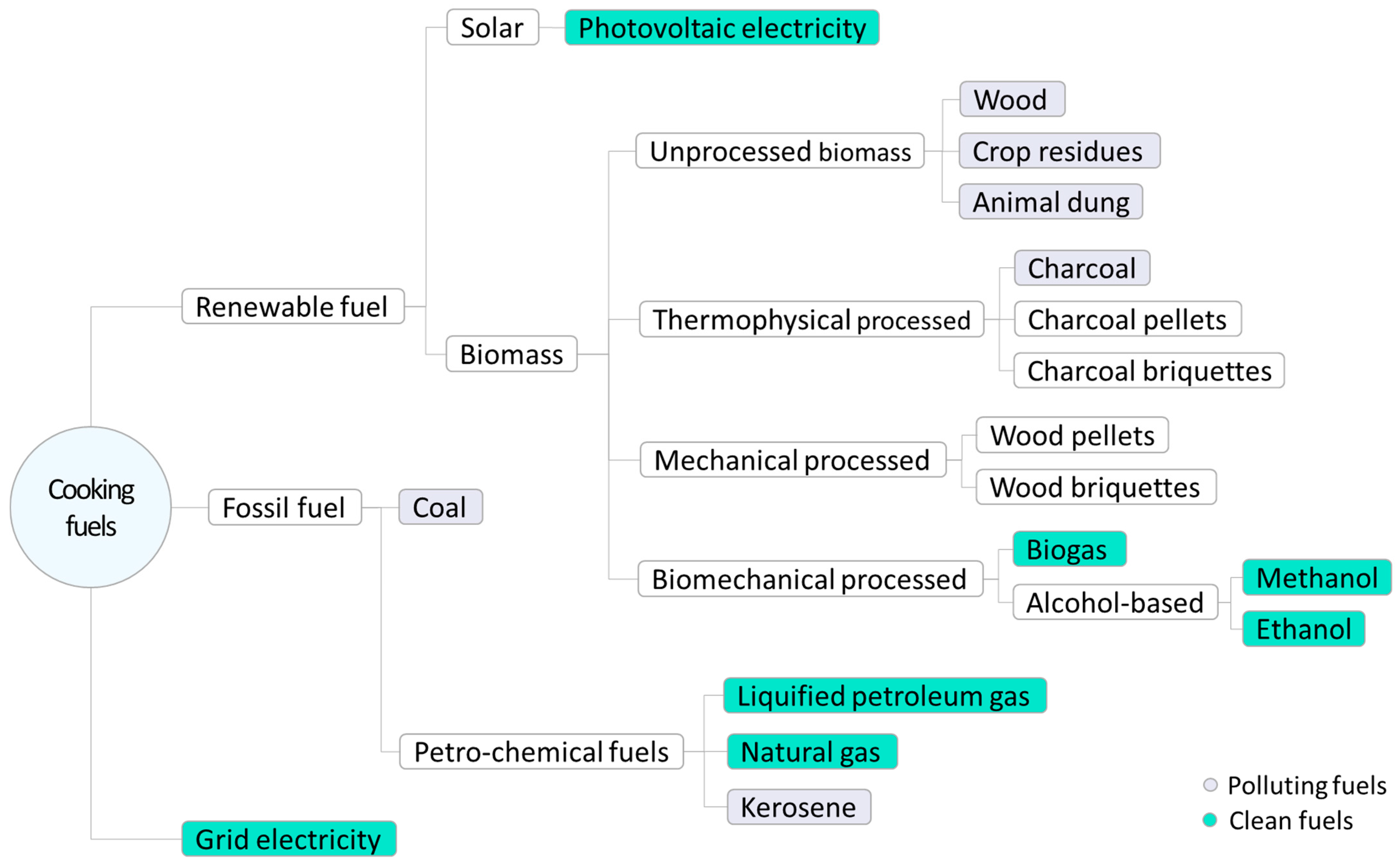
2. Background on Clean Cooking Fuels
3. Methods
3.1. ANOVA Analysis
3.2. Response Surface Methodology
Experimental Design for Fitting Response Surfaces
4. Plant Layout Description
4.1. Anaerobic Digestion
4.2. Biogas Cleaning and Upgrading
4.3. Methanol Synthesis Unit
4.4. PEM Water Electrolyzer
4.5. Photovoltaic Power Plant
5. Economic Calculation
5.1. Feedstock Price
5.2. Electricity Price
5.3. Products Selling Price
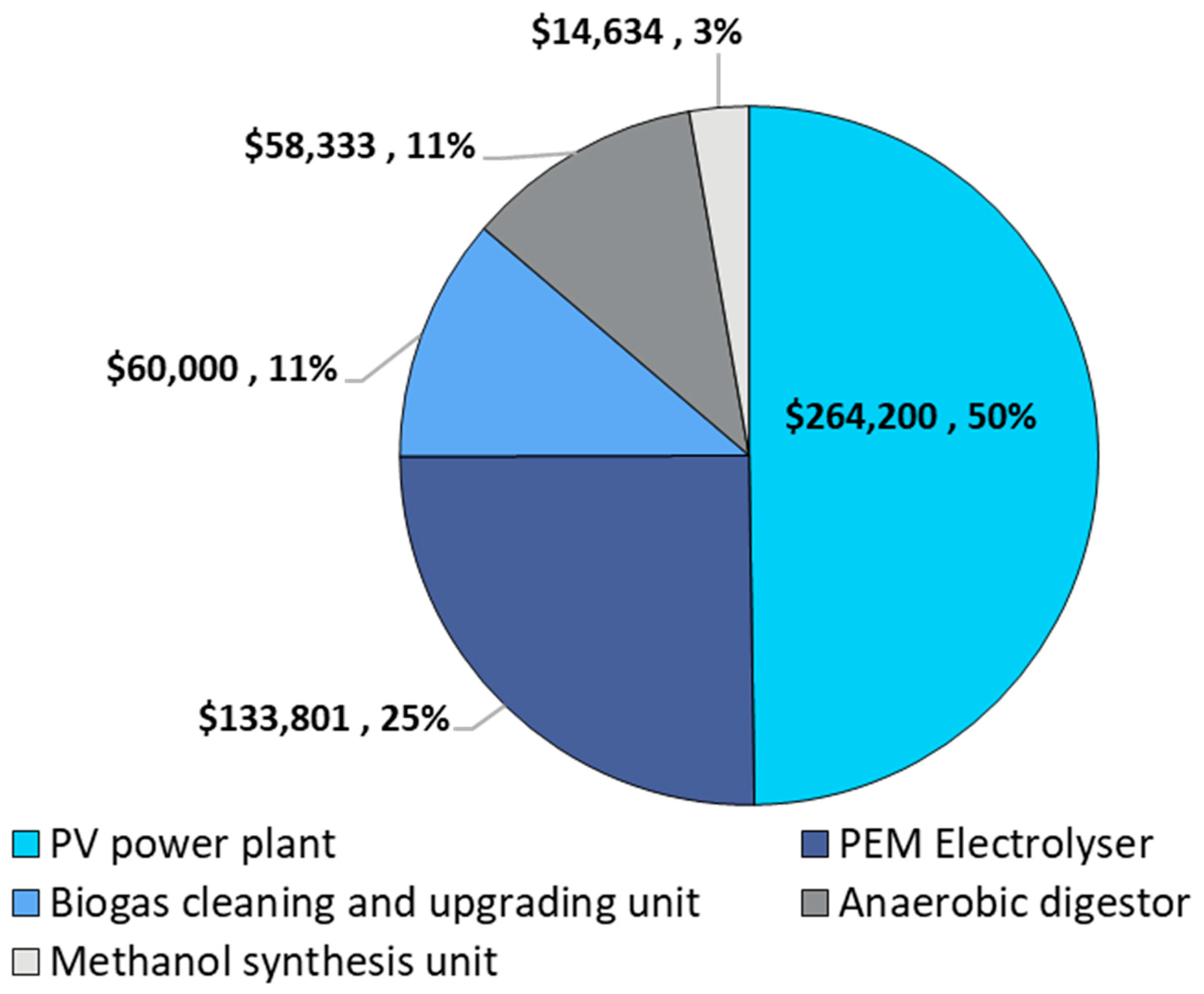
5.4. Purchased Equipment Cost Estimation
5.5. Economic Analysis
6. Results and Discussion
6.1. Base Case Results
6.2. Sensitivity Analysis Results
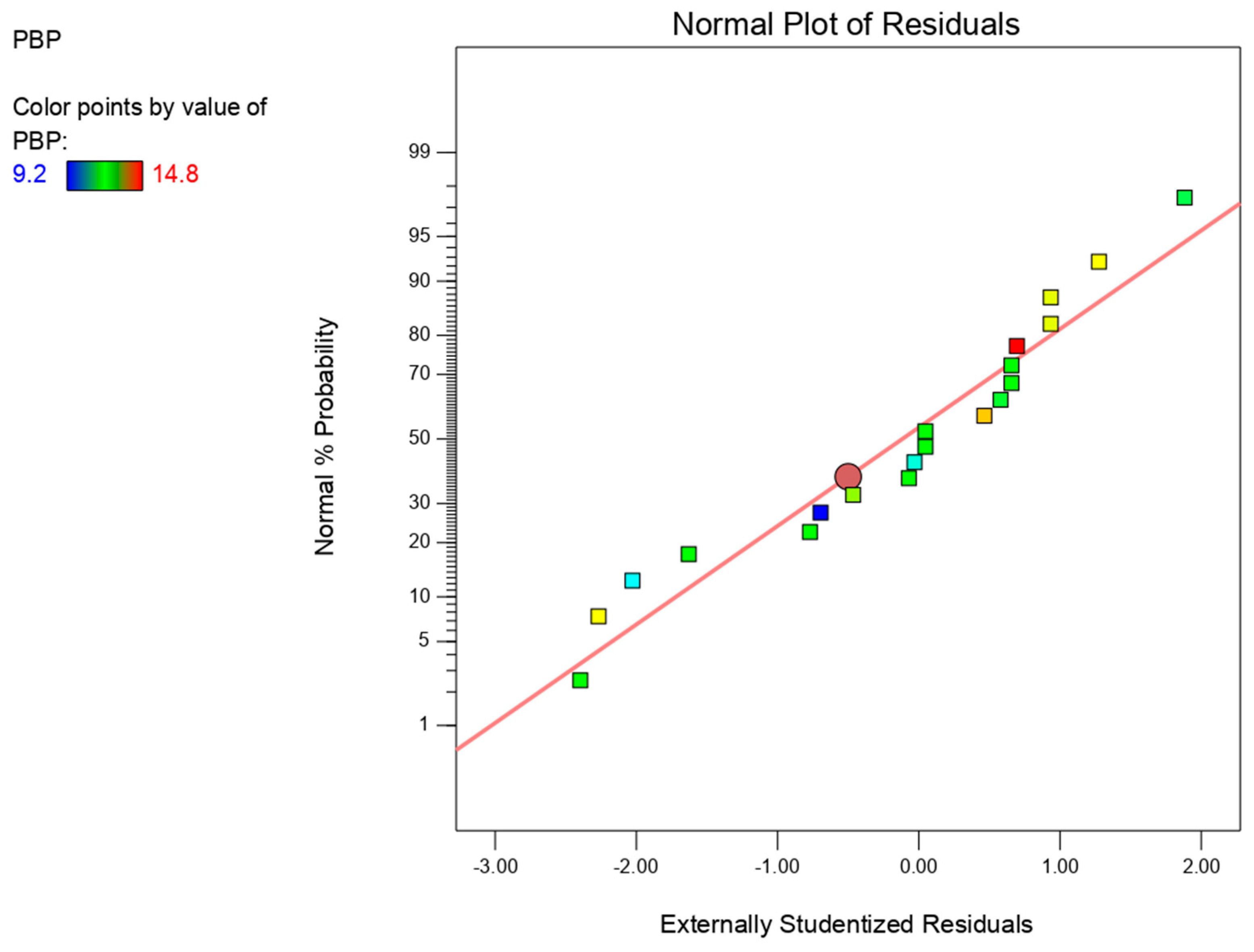
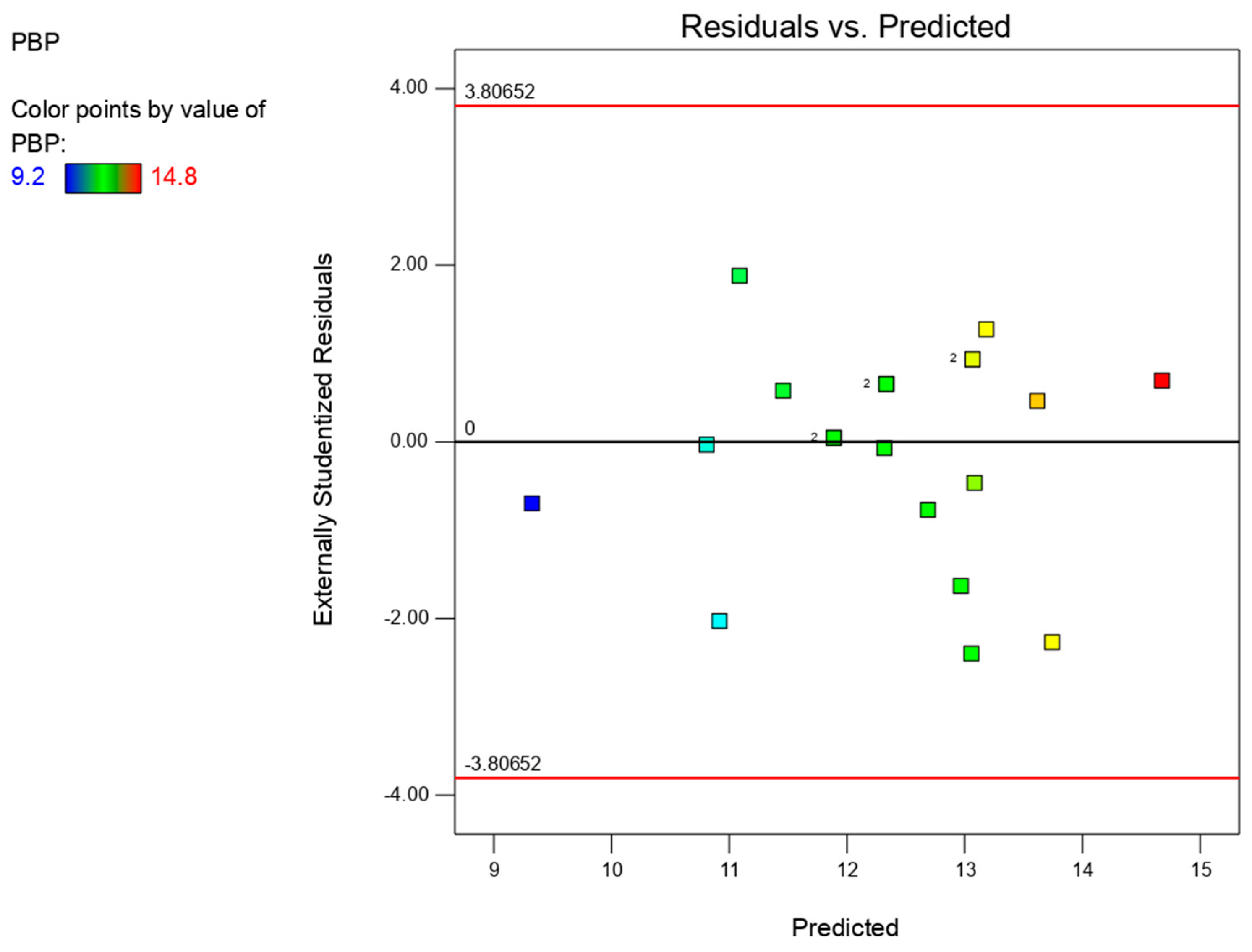
6.2.1. Statistical Evaluation of the Model
6.2.2. Response Surface Analysis
6.2.3. Optimum Condition
7. Study Limitations
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. WHO Guidelines for Indoor Air Quality: Household Fuel Combustion. 2014. Available online: https://www.who.int/publications/i/item/9789241548885 (accessed on 14 March 2022).
- Energy Sector Management Assistance Program. What Drives the Transition to Modern Energy Cooking Services? A Systematic Review of the Evidence; World Bank: Washington, DC, USA, 2021; Available online: https://openknowledge.worldbank.org/handle/10986/35199 (accessed on 22 March 2022).
- Quinn, A.K.; Bruce, N.; Puzzolo, E.; Dickinson, K.; Sturke, R.; Jack, D.W.; Mehta, S.; Shankar, A.; Sherr, K.; Rosenthal, J.P. An analysis of efforts to scale up clean household energy for cooking around the world. Energy Sustain. Dev. 2018, 46, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Putti, V.R.; Michael, T.; Mehta, S.; Kammila, S. The State of the Global Clean and Improved Cooking Sector; World Bank: Washington, DC, USA, 2015; Available online: https://openknowledge.worldbank.org/bitstream/handle/10986/21878/96499.pdf?sequence=1&isAllowed=y (accessed on 5 April 2022).
- Lwiza, F.; Mugisha, J.; Walekhwa, P.N.; Smith, J.; Balana, B. Dis-adoption of Household Biogas technologies in Central Uganda. Energy Sustain. Dev. 2017, 37, 124–132. [Google Scholar] [CrossRef] [Green Version]
- Lutaaya, F. Quality and Usage of Biogas Digesters in Uganda. Master’s Thesis, Royal Institute of Technology, Stockholm, Sweden, 2013. Available online: https://www.diva-portal.org/smash/get/diva2:661963/FULLTEXT01.pdf (accessed on 7 July 2022).
- Clemens, H.; Bailis, R.; Nyambane, A.; Ndung’u, V. Africa Biogas Partnership Program: A review of clean cooking implementation through market development in East Africa. Energy Sustain. Dev. 2018, 46, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Figueroa, A.; Boshell, F.; van Velzen, L.; Anisie, A. Biogas for Domestic Cooking: Technology Brief; IRENA: Abu Dhabi, United Arab Emirates, 2017; Available online: https://www.irena.org/publications/2017/Dec/Biogas-for-domestic-cooking-Technology-brief (accessed on 19 August 2022).
- Puzzolo, E.; Pope, D.; Stanistreet, D.; Rehfuess, E.A.; Bruce, N.G. Clean fuels for resource-poor settings: A systematic review of barriers and enablers to adoption and sustained use. Environ. Res. 2016, 146, 218–234. [Google Scholar] [CrossRef] [PubMed]
- Vijay, V.K.; Kapoor, R.; Trivedi, A.; Vijay, V. Biogas as Clean Fuel for Cooking and Transportation Needs in India. In Advances in Bioprocess Technology; Ravindra, P., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 257–275. [Google Scholar] [CrossRef]
- Ozier, A.; Charron, D.; Chung, S.; Sarma, V.; Dutta, A.; Jagoe, K.; Obueh, J.; Stokes, H.; Munangagwa, C.L.; Johnson, M.; et al. Building a consumer market for ethanol-methanol cooking fuel in Lagos, Nigeria. Energy Sustain. Dev. 2018, 46, 65–70. [Google Scholar] [CrossRef] [PubMed]
- Moioli, E.; Wötzel, A.; Schildhauer, T. Feasibility assessment of small-scale methanol production via power-to-X. J. Clean Prod. 2022, 359, 132071. [Google Scholar] [CrossRef]
- Topriska, E.; Kolokotroni, M.; Dehouche, Z.; Wilson, E. Solar hydrogen system for cooking applications: Experimental and numerical study. Renew. Energy 2015, 83, 717–728. [Google Scholar] [CrossRef] [Green Version]
- Topriska, E.; Kolokotroni, M.; Dehouche, Z.; Novieto, D.T.; Wilson, E.A. The potential to generate solar hydrogen for cooking applications: Case studies of Ghana, Jamaica and Indonesia. Renew. Energy 2016, 95, 495–509. [Google Scholar] [CrossRef]
- Onwe, C.A.; Rodley, D.; Reynolds, S. Modelling and simulation tool for off-grid PV-hydrogen energy system. Int. J. Sustain. Energy 2020, 39, 1–20. [Google Scholar] [CrossRef]
- Rivera, X.C.S.; Topriska, E.; Kolokotroni, M.; Azapagic, A. Environmental sustainability of renewable hydrogen in comparison with conventional cooking fuels. J. Clean Prod. 2018, 196, 863–879. [Google Scholar] [CrossRef]
- Owusu, P.A.; Banadda, N. Livestock waste-to-bioenergy generation potential in Uganda. Environ. Res. Eng. Manag. 2017, 73, 45–53. [Google Scholar] [CrossRef] [Green Version]
- Okello, C.; Pindozzi, S.; Faugno, S.; Boccia, L. Bioenergy potential of agricultural and forest residues in Uganda. Biomass Bioenergy 2013, 56, 515–525. [Google Scholar] [CrossRef]
- World Health Organization. WHO Air Quality Guidelines Global Update 2005: Particulate Matter, Ozone, Nitrogen Dioxide and Sulfur Dioxide; World Health Organization: Copenhagen, Denmark, 2006; Available online: https://www.euro.who.int/__data/assets/pdf_file/0005/78638/E90038.pdf (accessed on 18 March 2022).
- World Health Organization. WHO Guidelines for Indoor Air Quality: Selected Pollutants; World Health Organization: Bonn, Germany, 2010; Available online: https://www.euro.who.int/__data/assets/pdf_file/0009/128169/e94535.pdf (accessed on 18 March 2022).
- Rehfuess, E.; Pope, D.; Bruce, N.; Dherani, M.; Jagoe, K.; Naeher, L.; Noonan, C. WHO Indoor Air Quality Guidelines: Household Fuel Combustion—Review 6: Impacts of interventions on PM and CO; WHO: Geneva, Switzerland, 2014. [Google Scholar]
- Pope, D.; Bruce, N.; Dherani, M.; Jagoe, K.; Rehfuess, E. Real-life effectiveness of ‘improved’ stoves and clean fuels in reducing PM2.5 and CO: Systematic review and meta-analysis. Environ. Int. 2017, 101, 7–18. [Google Scholar] [CrossRef] [PubMed]
- Pope, D.; Johnson, M.; Fleeman, N.; Jagoe, K.; Duarte, R.; Maden, M.; Ludolph, R.; Bruce, N.; Shupler, M.; Adair-Rohani, H.; et al. Are cleaner cooking solutions clean enough? A systematic review and meta-analysis of particulate and carbon monoxide concentrations and exposures. Environ. Res. Lett. 2021, 16, 83002. [Google Scholar] [CrossRef]
- Bates, M.N.; Bruce, N.; Lam, N.L.; Smith, K.R.; Gauthier, A. WHO Indoor Air Quality Guidelines: Household Fuel Combustion—Review 9: Summary of systematic review of household kerosene use. J. Toxicol. Environ. Health B Crit. Rev. 2021, 15, 396–432. [Google Scholar]
- Lam, N.L.; Smith, K.R.; Gauthier, A.; Bates, M.N. Kerosene: A review of household uses and their hazards in low-and middle-income countries. J. Toxicol. Environ. Health Part B Crit. Rev. 2012, 15, 396–432. [Google Scholar] [CrossRef] [Green Version]
- Hoefsloot, H.C.J.; Vis, D.J.; Westerhuis, J.A.; Smilde, A.K.; Jansen, J.J. Multiset Data Analysis: ANOVA Simultaneous Component Analysis and Related Methods. Compr. Chemom. 2009, 2, 453–472. [Google Scholar] [CrossRef]
- Sarabia, L.A.; Ortiz, M.C. Response Surface Methodology. Compr. Chemom. 2009, 1, 345–390. [Google Scholar]
- Jankovic, A.; Chaudhary, G.; Goia, F. Designing the design of experiments (DOE)—An investigation on the influence of different factorial designs on the characterization of complex systems. Energy Build 2021, 250, 111298. [Google Scholar] [CrossRef]
- Box, G.E.P.; Wilson, K.B. On the Experimental Attainment of Optimum Conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–45. Available online: https://www.jstor.org/stable/2983966 (accessed on 14 September 2022). [CrossRef]
- Cochran, W.G.; Cox, G.M. Experimental Designs, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1957. [Google Scholar]
- Box, G.E.P.; Hunter, J.S. Multi-Factor Experimental Designs for Exploring Response Surfaces. Ann. Math. Stat. 1957, 28, 195–241. Available online: https://www.jstor.org/stable/2237033 (accessed on 25 August 2022). [CrossRef]
- Hurtubia, B.; Sauma, E. Economic and environmental analysis of hydrogen production when complementing renewable energy generation with grid electricity. Appl. Energy 2021, 304, 117739. [Google Scholar] [CrossRef]
- Holst, M.; Aschbrenner, S.; Smolinka, T.; Voglstätter, C.; Grimm, G. Cost Forecast for Low Temperature Electrolysis—Technology Driven Bottom-up Prognosis for PEM and Alkaline Water Electrolysis Systems; Fraunhofer Institute for Solar Energy Systems ISE: Freiburg, Germany, 2021; Available online: https://www.ise.fraunhofer.de/content/dam/ise/de/documents/publications/studies/cost-forecast-for-low-temperature-electrolysis.pdf (accessed on 7 September 2022).
- Kannah, R.Y.; Kavitha, S.; Preethi; Karthikeyan, O.P.; Kumar, G.; Dai-Viet, N.V.; Banu, J.R. Techno-economic assessment of various hydrogen production methods—A review. Bioresour. Technol. 2020, 319, 124175. [Google Scholar] [CrossRef] [PubMed]
- Black, M.J.; Roy, A.; Twinomunuji, E.; Kemausuor, F.; Oduro, R.; Leach, M.; Sadhukhan, J.; Murphy, R. Bottled biogas—An opportunity for clean cooking in Ghana and Uganda. Energies 2021, 14, 14. [Google Scholar] [CrossRef]
- Nock, W.J.; Walker, M.; Kapoor, R.; Heaven, S. Modeling the water scrubbing process and energy requirements for CO2 capture to upgrade biogas to biomethane. Ind. Eng. Chem. Res. 2014, 53, 12783–12792. [Google Scholar] [CrossRef] [Green Version]
- Bekkering, J.; Broekhuis, A.A.; van Gemert, W.J.T. Optimisation of a green gas supply chain—A review. Bioresour. Technol. 2010, 101, 450–456. [Google Scholar] [CrossRef]
- Sun, Q.; Li, H.; Yan, J.; Liu, L.; Yu, Z.; Yu, X. Selection of appropriate biogas upgrading technology-a review of biogas cleaning, upgrading and utilization. Renew. Sustain. Energy Rev. 2015, 51, 521–532. [Google Scholar] [CrossRef]
- Twinomunuji, E.; Kemausuor, F.; Black, M.; Roy, A.; Leach, M.; Sadhukhan, R.O.J.; Murphy, R. The Potential for Bottled Biogas for Clean Cooking in Africa; Modern Energy Cooking Services. 2020. Available online: https://www.mecs.org.uk/wp-content/uploads/2020/12/Potential-for-bottled-biogas-for-clean-cooking-in-Africa_Feb-2020-working-paper.pdf (accessed on 20 July 2022).
- Ushikoshi, K.; Mori, K.; Watanabe, T.; Takeuchi, M. A 50 kg/day class test plant for methanol synthesis from CO2 and H2. Adv. Chem. Convers. Mittigating Carbon Dioxide 1998, 114, 357–362. [Google Scholar]
- Schemme, S.; Breuer, J.L.; Koller, M.; Meschede, S.; Walman, F.; Samsun, R.C.; Peters, R.; Stolten, D. H2-based synthetic fuels: A techno-economic comparison of alcohol, ether and hydrocarbon production. Int. J. Hydrog. Energy 2020, 45, 5395–5414. [Google Scholar] [CrossRef]
- Korpås, M.; Greiner, C.J. Opportunities for hydrogen production in connection with wind power in weak grids. Renew Energy 2008, 33, 1199–1208. [Google Scholar] [CrossRef]
- Aarakit, S.M.; Ssennono, V.F.; Adaramola, M.S. Estimating Market Potential for Solar Photovoltaic Systems in Uganda. Front. Energy Res. 2021, 9, 602468. [Google Scholar] [CrossRef]
- Oloya, I.T.; Gutu, T.J.L.; Adaramola, M.S. Techno-economic assessment of 10 MW centralised grid-tied solar photovoltaic system in Uganda. Case Stud. Therm. Eng. 2020, 25, 100928. [Google Scholar] [CrossRef]
- Electricity Regulatory Authority. Electricity Tariff Schedules in Uganda. Electricity Regulatory Authority. 2022. Available online: https://www.era.go.ug/index.php/tariffs/tariff-schedules (accessed on 7 June 2022).
- Garland, C.; Jagoe, K.; Wasirwa, E.; Nguyen, R.; Roth, C.; Patel, A.; Shah, N.; Derby, E.; Mitchell, J.; Pennise, D.; et al. Impacts of household energy programs on fuel consumption in Benin, Uganda, and India. Energy Sustain. Dev. 2015, 27, 168–173. [Google Scholar] [CrossRef]
- Price, R. ‘Clean’ Cooking Energy in Uganda—Technologies, Impacts, and Key Barriers and Enablers to Market Acceleration; K4D Helpdesk Report; Institute of Development Studies: Brighton, UK, 2017; p. 2. [Google Scholar]
- Bruce, N.G.; Aunan, K.; Rehfuess, E.A. Liquefied Petroleum Gas as a Clean Cooking Fuel for Developing Countries: Implications for Climate, Forests, and Affordability. 2017. Available online: https://www.kfw-entwicklungsbank.de/PDF/Download-Center/Materialien/2017_Nr.7_CleanCooking_Lang.pdf (accessed on 20 April 2022).
- Amigun, B.; von Blottnitz, H. Capital cost prediction for biogas installations in Africa: Lang factor approach. Environ. Prog. Sustain. Energy 2009, 28, 134–142. [Google Scholar] [CrossRef]
- Guthrie, K.M. Data and Techniques for Preliminary Capital Cost Estimating; McGraw-Hill: New York, NY, USA, 1969; pp. 114–142. [Google Scholar]
- Ulrich, G.D. A Guide to Chemical Engineering Process Design and Economics; John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
- International Energy Agency. Capital Costs of Utility-Scale Solar PV in Selected Emerging Economies. 2020. Available online: https://www.iea.org/data-and-statistics/charts/capital-costs-of-utility-scale-solar-pv-in-selected-emerging-economies (accessed on 23 September 2022).



| Parameters | Specifications |
|---|---|
| Raw biogas flow rate | 25 Nm3/h |
| Raw biogas specification | 50–65% CH4; 50–35% CO2; 500 ppm H2S |
| Inlet biogas pressure | 7–20 mbar |
| Outlet methane gas pressure | 3–5 bar |
| Outlet methane gas pressure after compression | 250 bar |
| Outlet methane specification | 2% CO2; 97–98% CH4; 5 mg/m3 H2S |
| Upgrading and compression energy consumption | 0.5 kWh/Nm3 of raw biogas |
| Water consumption with regeneration | 2 L of water/ Nm3 of raw biogas |
| Sub-System | Parameter |
|---|---|
| Anaerobic digestion | Raw biogas output flow rate: 25 Nm3/h Chemical composition of biogas [6]: 54% CH4 and 46% CO2 |
| Biogas cleaning and upgrading | CH4 losses [37]: 2% CO2 losses [38]: 20% Electricity consumption [39]: 0.5 kWh/Nm3 raw biogas |
| Methanol synthesis unit | Stoichiometric H2: CO2 ratio: 3:1 Working Pressure: 50 bar Temperature: 250 °C Conversion efficiency: 96% Electrical energy demand: 0.154 kWh/kg of methanol [41] |
| PEM water electrolyzer | Specific power consumption: 56.7 kWh/kg [13] |
| Photovoltaic power plant | Performance ratio: 75.84%, [44] Daily solar radiation [44]: Minimum: 5.22 kWh/m2/day Average: 5.85 kWh/m2/day Maximum: 6.28 kWh/m2/day |
| Sub-System | Method/Reference |
|---|---|
| Anaerobic digester | Retrieved from Black et al. (2021) [35] |
| Biogas upgrading and compression | Retrieved from Black et al. (2021) [35] |
| Methanol synthesis unit | Bare module cost as a function of the equipment type (), material (), volume, and pressure () [50,51]: The material considered is stainless steel and the cost is actualized to current price through the Chemical Engineering Plant Cost Index (CEPCI) |
| PEM water electrolyzer | Based on the estimates of Holst et al. (2021) |
| Photovoltaic power plant | Based on the estimates of the International Energy Agency International Energy Agency [52] |
| Parameter | Value | Unit |
|---|---|---|
| PV plant production | 323.9 | MWh/year |
| Electrical energy purchased from the grid | 892.7 | MWh/year |
| Electrical energy consumption | 1216.5 | MWh/year |
| Methanol production | 33.3 | ton/year |
| Biomethane production | 70.1 | ton/year |
| Oxygen production | 155.8 | ton/year |
| Annual Revenue | |
|---|---|
| Methane income | USD 172,821 |
| Methanol income | USD 38,861 |
| Oxygen income | USD 20,254 |
| Sub-total | USD 231,936 |
| Annual costs | |
| Variable costs | USD 102,656 |
| Sub-total | USD 102,656 |
| Annual cash inflow | |
| Total | USD 129,279 |
| Factor | Name | Unit | Values of Coded Levels | ||
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| A | PV plant size | kW | 200 | 450 | 700 |
| B | Percentage reduction in PEM capital cost | % | 0 | 20 | 40 |
| C | Electricity price | USD/kWh | 0.115 | 0.132 | 0.149 |
| Run | Block | Factors | Response | ||
|---|---|---|---|---|---|
| PV Plant Size (kW) | Percentage Reduction in PEM Capital Cost (%) | Electricity Price (USD/kWh) | Payback Period (Years) | ||
| 1 | 1 | 700 | 0 | 0.149 | 14.8 |
| 2 | 1 | 450 | 20 | 0.132 | 13.3 |
| 3 | 1 | 700 | 40 | 0.115 | 13.7 |
| 4 | 1 | 200 | 0 | 0.115 | 10.6 |
| 5 | 1 | 200 | 40 | 0.149 | 12.7 |
| 6 | 1 | 450 | 20 | 0.132 | 13.3 |
| 7 | 2 | 450 | 20 | 0.132 | 12.5 |
| 8 | 2 | 200 | 0 | 0.149 | 13.4 |
| 9 | 2 | 700 | 40 | 0.149 | 13.0 |
| 10 | 2 | 450 | 20 | 0.132 | 12.5 |
| 11 | 2 | 700 | 0 | 0.115 | 13.4 |
| 12 | 2 | 200 | 40 | 0.115 | 9.2 |
| 13 | 3 | 450 | 20 | 0.132 | 11.9 |
| 14 | 3 | 450 | 40 | 0.132 | 11.6 |
| 15 | 3 | 450 | 20 | 0.115 | 11.5 |
| 16 | 3 | 700 | 20 | 0.132 | 12.6 |
| 17 | 3 | 450 | 0 | 0.132 | 12.3 |
| 18 | 3 | 200 | 20 | 0.132 | 10.8 |
| 19 | 3 | 450 | 20 | 0.132 | 11.9 |
| 20 | 3 | 450 | 20 | 0.149 | 12.5 |
| Source | Std. Dev. | R² | Adjusted R² | Predicted R² | PRESS | Sequential p-Value |
|---|---|---|---|---|---|---|
| Linear | 0.5905 | 0.8031 | 0.7609 | 0.3485 | 16.15 | <0.0001 |
| 2FI | 0.2472 | 0.9729 | 0.9581 | 0.7303 | 6.69 | <0.0001 |
| Quadratic | 0.2057 | 0.9863 | 0.971 | 0.7549 | 6.08 | 0.1218 |
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | Contribution |
|---|---|---|---|---|---|---|
| Block | 4.78 | 2 | 2.39 | |||
| Model | 24.12 | 6 | 4.02 | 65.77 | <0.0001 | |
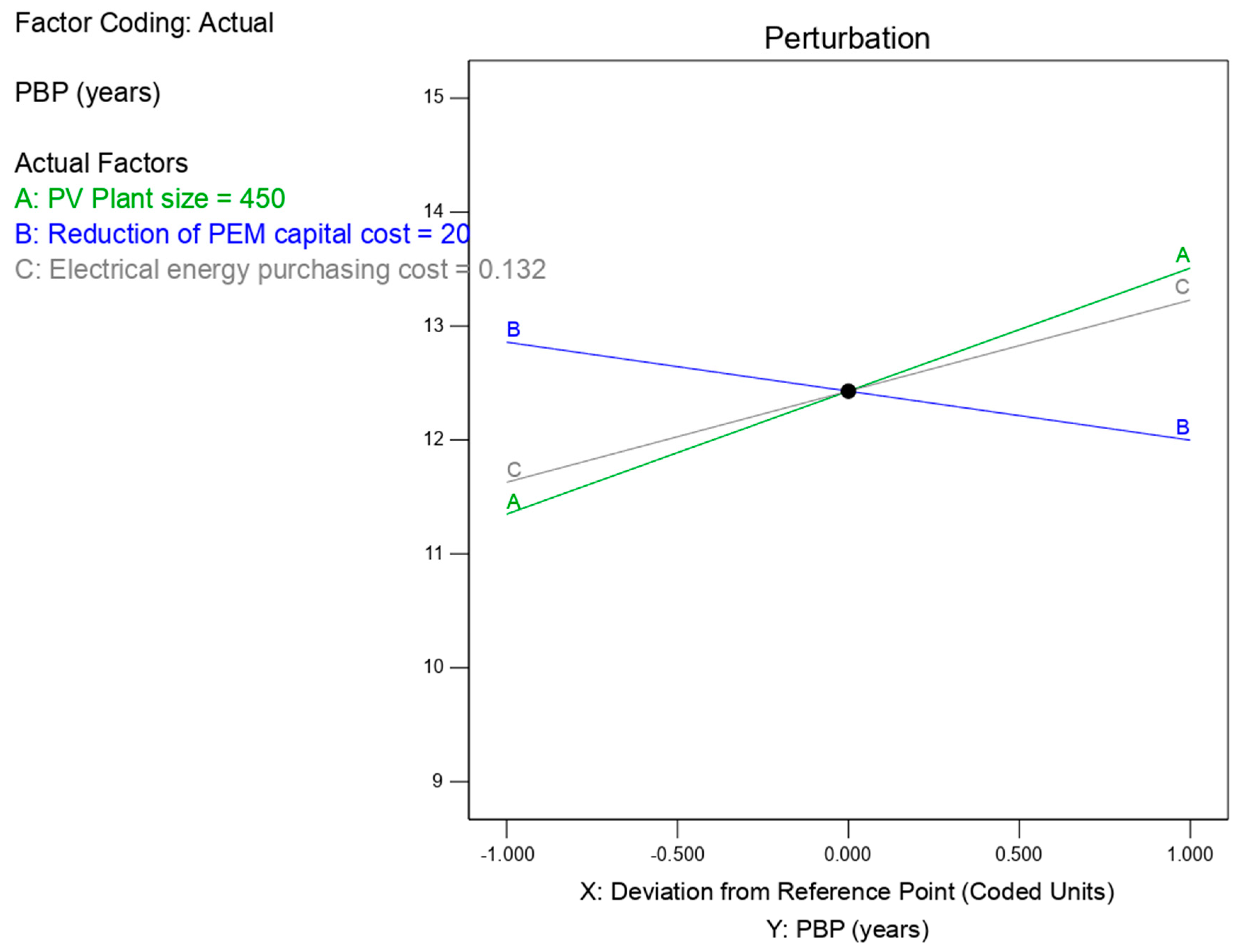
| A-PV plant size | 11.66 | 1 | 11.66 | 190.81 | <0.0001 | 48.34% |
| B-Reduction in PEM capital cost | 1.85 | 1 | 1.85 | 30.25 | 0.0002 | 7.67% |
| C-Electrical energy purchasing cost | 6.4 | 1 | 6.4 | 104.7 | <0.0001 | 26.53% |
| AB | 0.045 | 1 | 0.045 | 0.7362 | 0.4092 | 0.19% |
| AC | 3.92 | 1 | 3.92 | 64.13 | <0.0001 | 16.25% |
| BC | 0.245 | 1 | 0.245 | 4.01 | 0.0706 | 1.02% |
| Residual | 0.6724 | 11 | 0.0611 | |||
| Cor Total | 29.58 | 19 |
| Statistical Parameter | Value |
|---|---|
| R2 | 0.9612 |
| Adjusted R2 | 0.9492 |
| Predicted R2 | 0.8606 |
| Adeq Precision | 33.2568 |
| Std. Dev. | 0.2721 |
| Mean | 12.38 |
| C.V.% | 2.2 |
| Source | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | Contribution |
|---|---|---|---|---|---|---|
| Block | 4.78 | 2 | 2.39 | |||
| Model | 23.83 | 4 | 5.96 | 80.48 | <0.0001 | |
| A-PV plant size | 11.66 | 1 | 11.66 | 157.55 | <0.0001 | 48.93% |
| B-Reduction in PEM capital cost | 1.85 | 1 | 1.85 | 24.98 | 0.0002 | 7.76% |
| C-Electrical energy purchasing cost | 6.4 | 1 | 6.4 | 86.45 | <0.0001 | 26.86% |
| AC | 3.92 | 1 | 3.92 | 52.95 | <0.0001 | 16.45% |
| Residual | 0.9624 | 13 | 0.074 | |||
| Cor Total | 29.58 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuloeta Bonilla, R.; Bhandari, R. Small-Scale Hybrid Methanol–Methane Production Based on Biogas: Stochastic Sensitivity Analysis of the Economic Sustainability. Energies 2022, 15, 9329. https://doi.org/10.3390/en15249329
Zuloeta Bonilla R, Bhandari R. Small-Scale Hybrid Methanol–Methane Production Based on Biogas: Stochastic Sensitivity Analysis of the Economic Sustainability. Energies. 2022; 15(24):9329. https://doi.org/10.3390/en15249329
Chicago/Turabian StyleZuloeta Bonilla, Rosa, and Ramchandra Bhandari. 2022. "Small-Scale Hybrid Methanol–Methane Production Based on Biogas: Stochastic Sensitivity Analysis of the Economic Sustainability" Energies 15, no. 24: 9329. https://doi.org/10.3390/en15249329
APA StyleZuloeta Bonilla, R., & Bhandari, R. (2022). Small-Scale Hybrid Methanol–Methane Production Based on Biogas: Stochastic Sensitivity Analysis of the Economic Sustainability. Energies, 15(24), 9329. https://doi.org/10.3390/en15249329








