Drum Water Level Control Based on Improved ADRC
Abstract
:1. Introduction
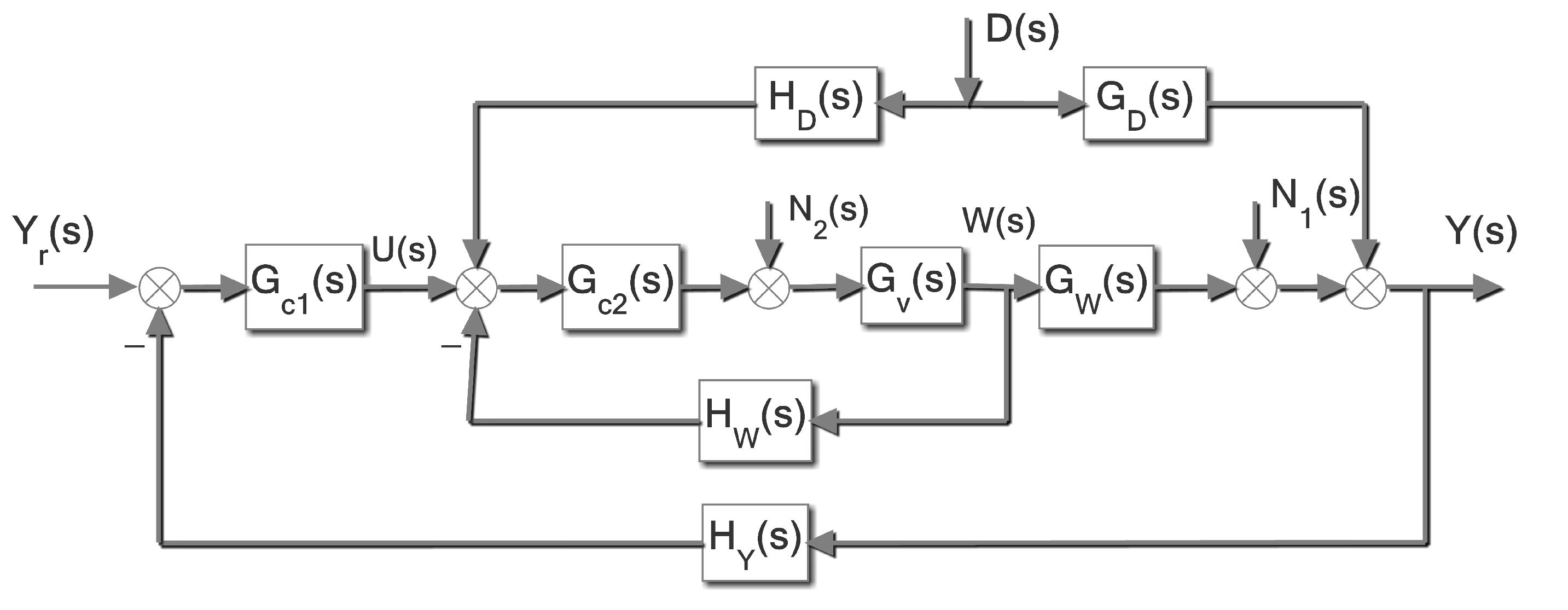
2. ILADRC of Drum Water Level
2.1. Traditional LADRC
2.2. ILADRC
2.3. Parameter Setting
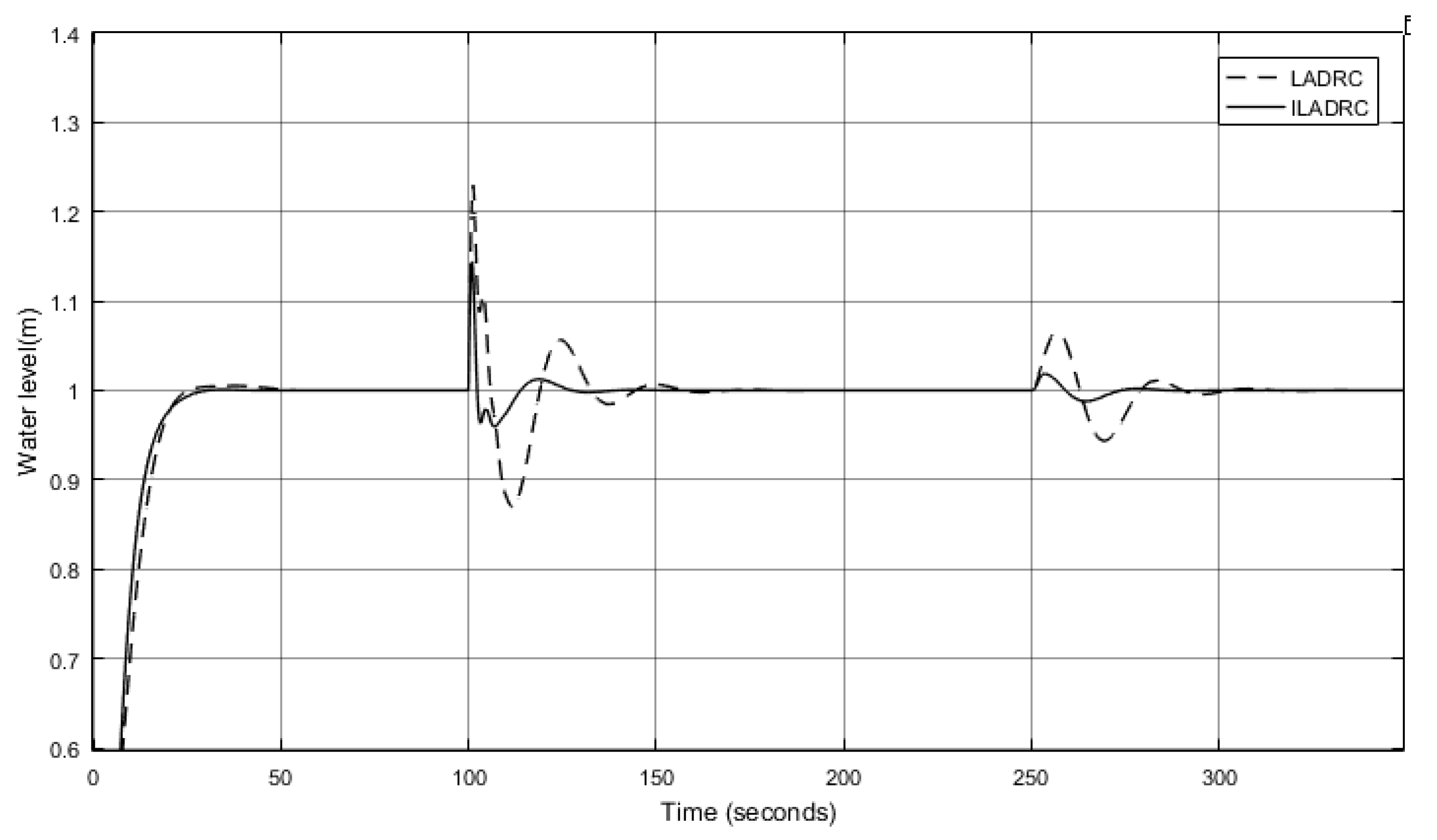
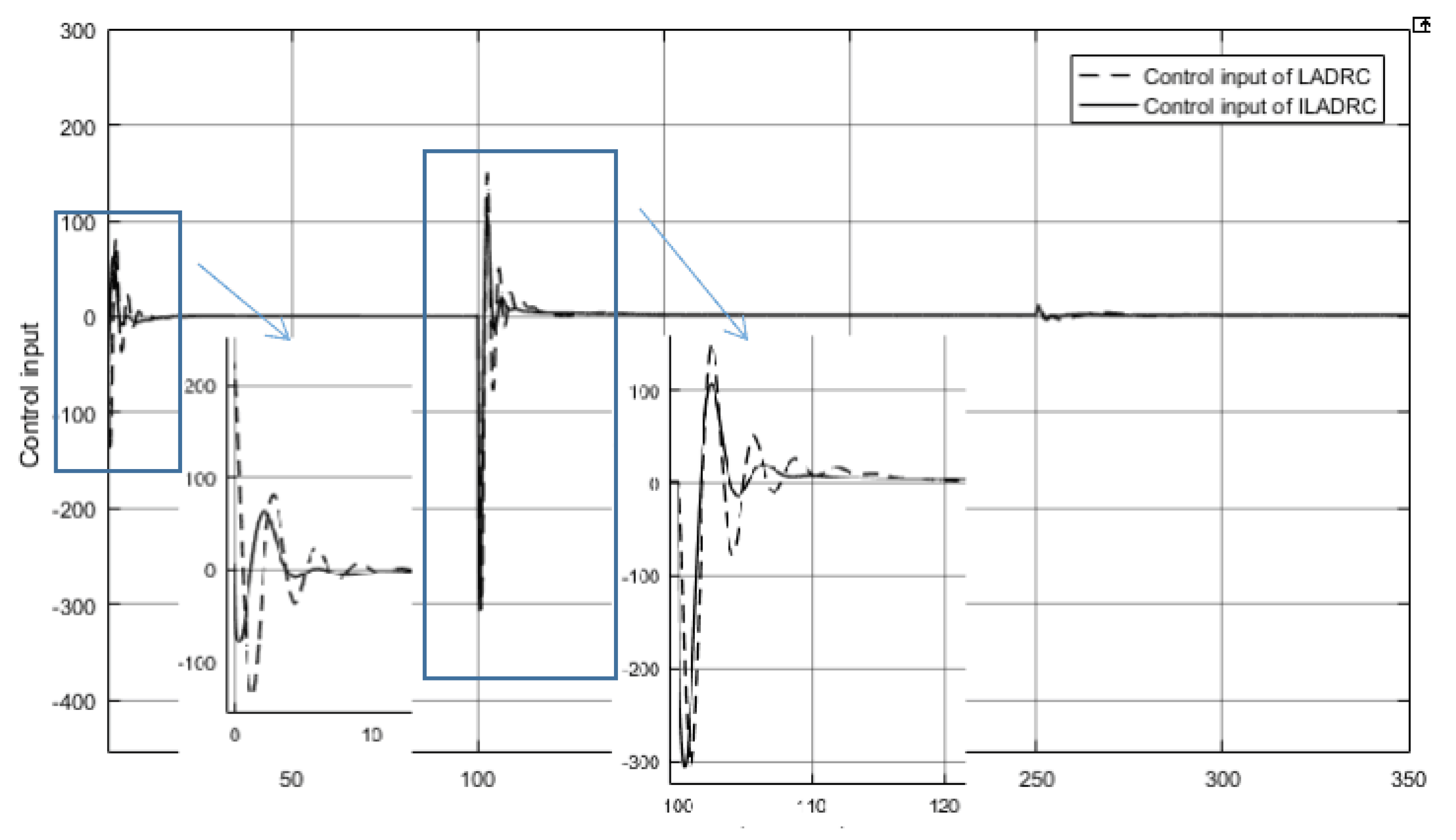
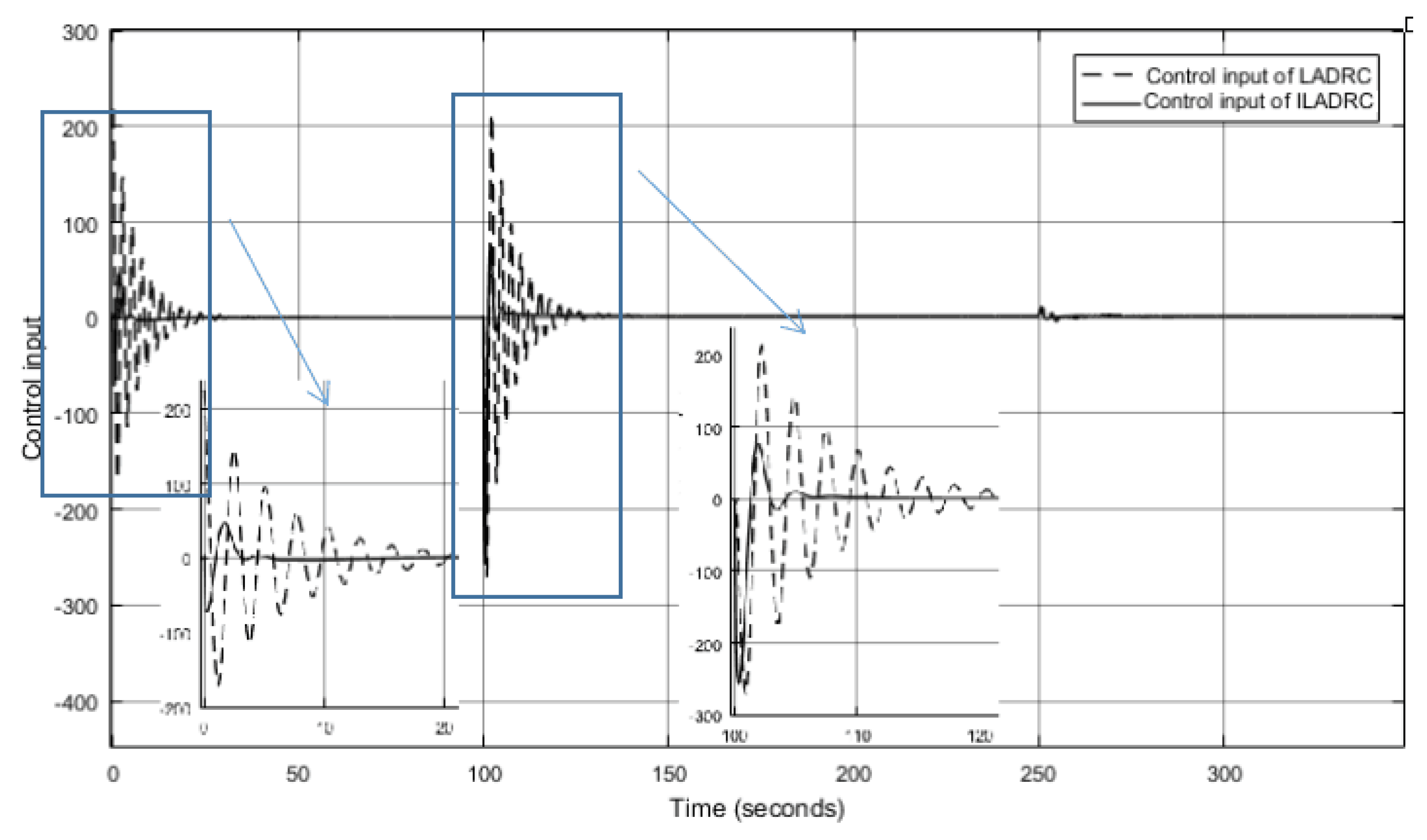
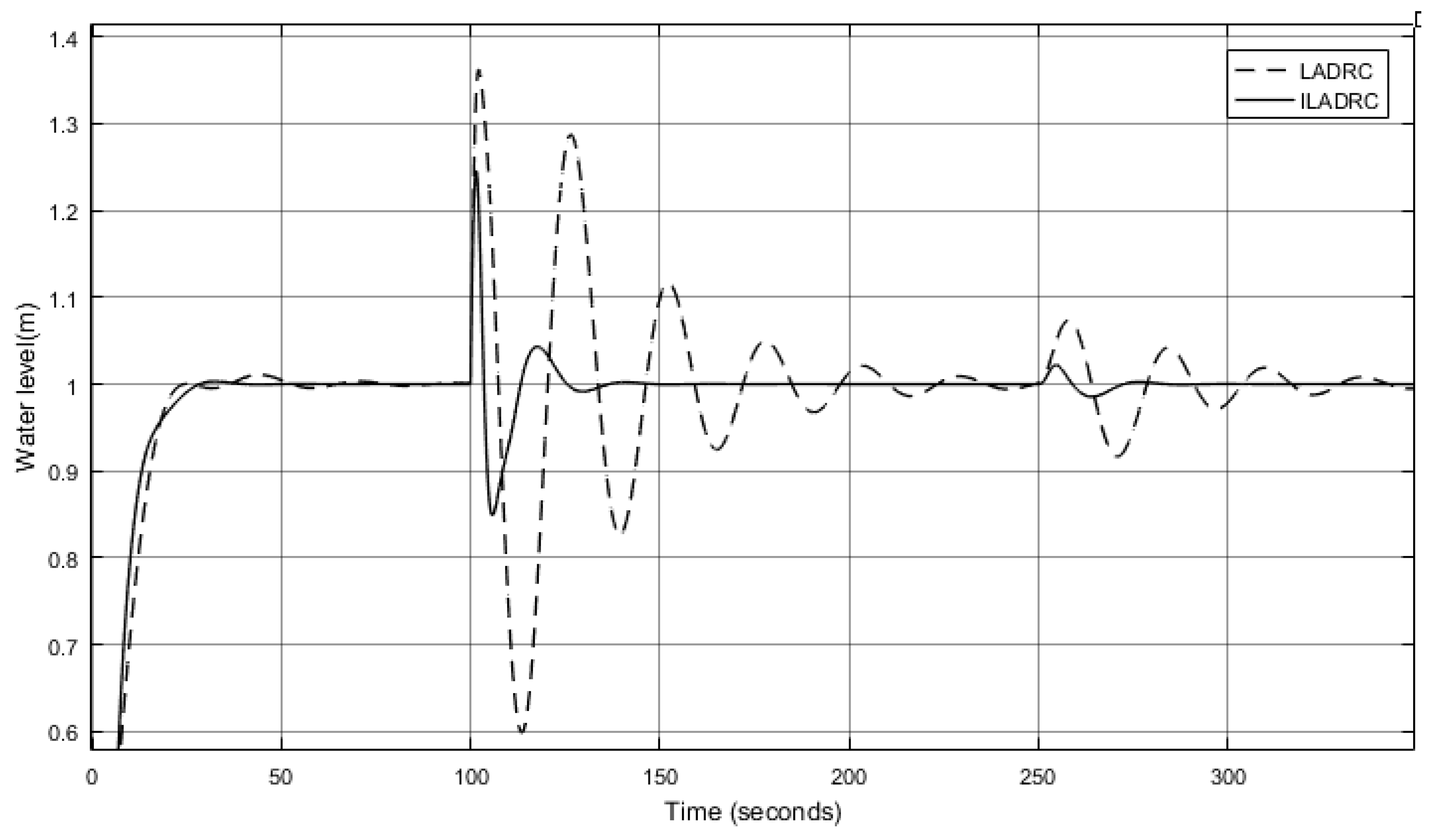
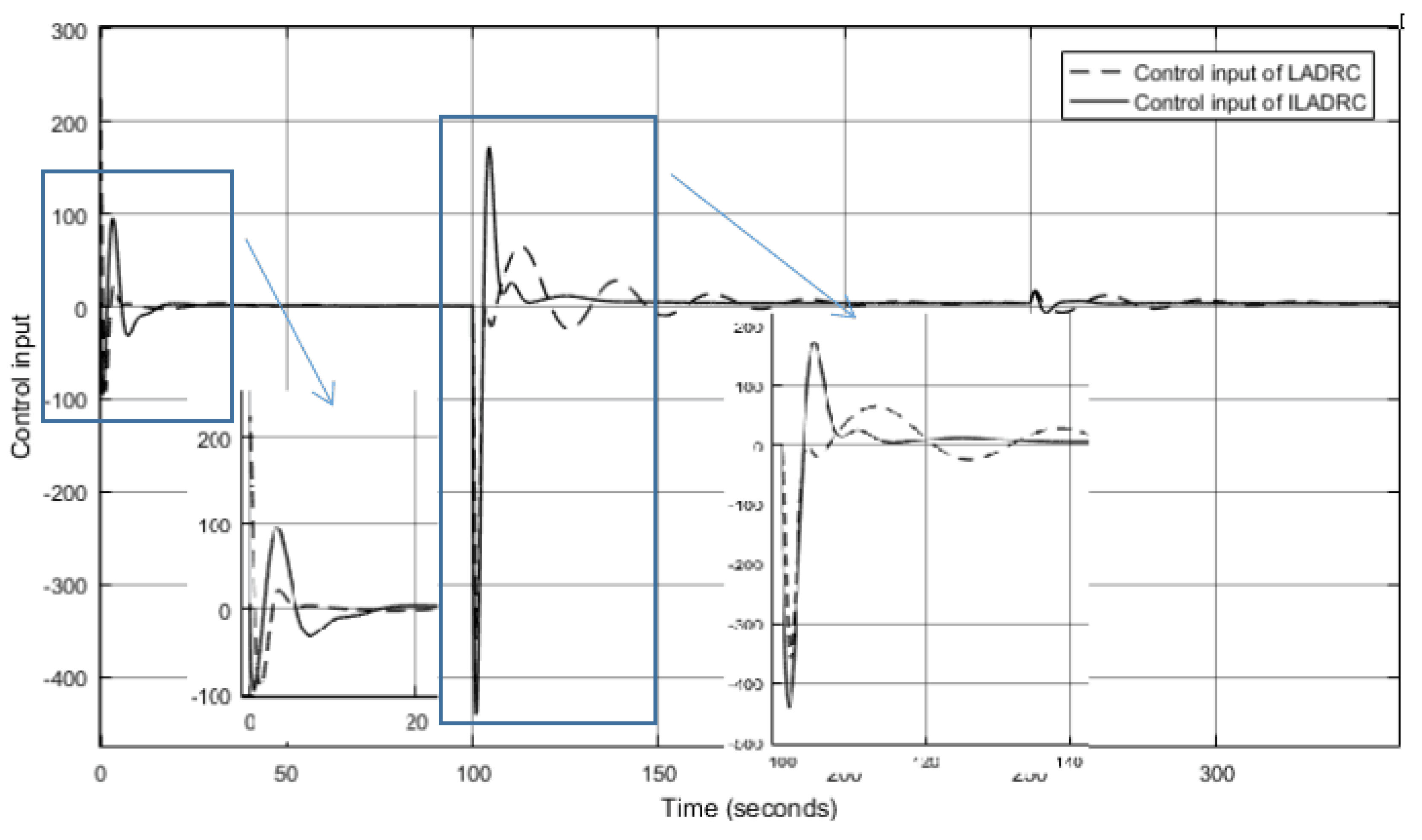
3. Simulation and Performance Analysis of Drum Water Level ILADRC
3.1. Performance Analysis under External Disturbance
3.2. Robustness Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Feng, L.Q. Research on Boiler Drum Water Level Control Based on Neural Network. Master’s Thesis, North China University of Science and Technology, Tangshan, China, 2018. [Google Scholar]
- Zhao, W. Design of Improved ADRC for Drum Water Level Regulation of Ship Boiler. Navig. China 2018, 41, 35–37. [Google Scholar]
- Jin, J.R.; Huang, H.S.; Sun, J.M.; Pang, Y. Study on Fuzzy Self-Adaptive PID Control System of Biomass Boiler Drum Water. J. Sustain. Bioenergy Syst. 2013, 3, 93–98. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Meng, Q. Research on optimal control system of boiler drum water level based on LQR. In Proceedings of the 2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE), Changchun, China, 16–18 December 2011; pp. 1092–1094. [Google Scholar]
- Huang, Q.; Song, S.; Lin, X.; Peng, K. Research on water level optimal control of boiler drum based on dual heuristic dynamic programming. In International Symposium on Neural Networks; Springer: Berlin/Heidelberg, Germany, 2011; pp. 455–463. [Google Scholar]
- Zhao, R.; Wang, X.; Teng, F. The PID control system of steam boiler drum water level based on genetic algorithms. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014; pp. 1983–1986. [Google Scholar]
- Wang, J.H.; Meng, Q.J. Water Level Control of Boiler Drum Based on PFC-PID. J. Univ. Jinan 2012, 26, 171–174. [Google Scholar]
- Swarnakar, A.; Marquez, H.J.; Chen, T. A new scheme on robust observer-based control design for interconnected systems with application to an industrial utility boiler. IEEE Trans. Control Syst. Technol. 2008, 16, 539–547. [Google Scholar] [CrossRef]
- Senanayaka, J.S.L.; Karimi, H.R.; Robbersmyr, K.G. Sensorless small wind turbine with a sliding-mode observer for water heating applications. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 863–868. [Google Scholar]
- Mystkowski, A. Lyapunov Sliding-Mode Observers With Application for Active Magnetic Bearing Operated With Zero-Bias Flux J. Dyn. Syst. Meas. Control 2019, 141, 041006. [Google Scholar] [CrossRef]
- Han, J.Q. ADRC and Its Applications. Control Decis. Mak. 1998, 13, 19–23. [Google Scholar]
- Han, J.Q. ADRC Ttechnique—A Control Technique that Estimates and Compensates for Uncertainties; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Han, J.Q. An Extended State Observer for a Class of Uncertain Objects. Control Decis. 1995, 10, 85–88. [Google Scholar]
- Cheng, Q.M.; Zheng, Y.; Du, X.F.; Guo, R.Q. Three-element Drum Water-level Cascade Control System Featuring ADRC based on High Order Controller Design. J. Eng. Therm. Energy Power 2008, 23, 69. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 6, pp. 4989–4996. [Google Scholar]
- Gao, Z. Active disturbance rejection control: A paradigm shift in feedback control system design. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 7. [Google Scholar]
- Su, J.B. Robotic Un-calibrated Visual Serving based on ADRC. Control Decis. 2015, 30, 1–8. [Google Scholar]
- Su, J.B.; Qiu, W.B.; Ma, H.Y.; Woo, P.Y. Calibration-free Robotic Eye-hand Coordination based on an Auto Disturbance-rejection Controller. IEEE Trans. Robot. 2004, 20, 899–907. [Google Scholar]
- Xiang, G.F.; Huang, Y.; Yu, J.R.; Zhu, M.D.; Su, J.B. Intelligence evolution for service robot: An ADRC perspective. Control Theory Technol. 2018, 16, 324–335. [Google Scholar] [CrossRef]
- Medjebouri, A.; Mehennaoui, L. Active Disturbance Rejection Control of a SCARA Robot Arm. Int. J. Serv. Sci. Technol. 2015, 8, 435–446. [Google Scholar] [CrossRef]
- Liu, X.L.; Xiong, L.P. Mechanical arm active disturbance rejection control based on artificial bee colony algorithm. In Applied Mechanics and Materials; Trans Tech Publications: Zürich, Switzerland, 2014; pp. 1511–1514. [Google Scholar]
- Wang, L.; Su, J.B. Attitude Tracking of Aircraft based on Disturbance Rejection Control. Control Theory Appl. 2013, 30, 1609–1616. [Google Scholar]
- Wang, L. Observer-Based Disturbance Rejection Control Methodology and Performance Evaluation. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2015. [Google Scholar]
- Tan, W.; Zhou, H.; Fu, C. Linear active disturbance rejection control for load frequency control of power systems. Control Theory Appl. 2013, 30, 1607–1615. [Google Scholar]
- Gao, Z.Q.; Li, S.; Zhou, X.S.; Ma, Y.J.; Shi, X.Q. Design of MPPT controller for photovoltaic generation system based on LADRC. Power Syst. Prot. Control 2018, 46, 52–59. [Google Scholar]
- Jiang, J.G.; Liu, Y.Q.; Guo, M.L. Linear Auto Disturbance Rejection Control System for Water Level in Drum. Therm. Power Gener. 2016, 45, 110–114. [Google Scholar]
- Fu, Y.M.; Wang, Y.H.; Guo, F. Design of Linear Active Disturbance Rejection Controller for Drum Water Level of Heat Recovery Boiler. Therm. Power Eng. 2018, 33, 83–89. [Google Scholar]
- Li, Z.J. Thermal Automatic Control System; China Electric Power Press: Beijing, China, 2001. [Google Scholar]
- Zhou, T.M. Improved Active Disturbance Rejection Control and Its Application to Thermal System in Power Plant. Master’s Thesis, North China Electric Power University, Beijing, China, 2017. [Google Scholar]
- Liu, X.; Li, D.H.; Jiang, X.Z.; Hu, X.J. Simulation study of auto disturbance rejection controller for high-order systems. J. Tsinghua Univ. 2001, 6, 95–99. [Google Scholar]



| LADRC | ILADRC | |
|---|---|---|
| main-controller | ||
| sub-controller | ||
| Time | Index | LADRC | ILADRC |
|---|---|---|---|
| s | 21 | 21 | |
| 0.52 | 0.09 | ||
| s | /s | 30 | 11 |
| 23 | 14 | ||
| s | /s | 26 | 0 |
| 6.5 | 1.8 |
| Time | Index | ||||
|---|---|---|---|---|---|
| LADRC | ILADRC | LADRC | ILADRC | ||
| t = 0 s | t/s | 21 | 20 | 20 | 20 |
| 0.65 | 0.05 | 1.1 | 0.32 | ||
| t = 100 s | /s | 28 | 8 | 105 | 22 |
| 18.6 | 10.7 | 36.2 | 24.5 | ||
| t = 250 s | /s | 26 | 0 | 50 | 0 |
| 6.5 | 1.7 | 7.4 | 2.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, C.; Zhu, Y.; Su, J. Drum Water Level Control Based on Improved ADRC. Algorithms 2019, 12, 132. https://doi.org/10.3390/a12070132
Pu C, Zhu Y, Su J. Drum Water Level Control Based on Improved ADRC. Algorithms. 2019; 12(7):132. https://doi.org/10.3390/a12070132
Chicago/Turabian StylePu, Cuiping, Yicheng Zhu, and Jianbo Su. 2019. "Drum Water Level Control Based on Improved ADRC" Algorithms 12, no. 7: 132. https://doi.org/10.3390/a12070132
APA StylePu, C., Zhu, Y., & Su, J. (2019). Drum Water Level Control Based on Improved ADRC. Algorithms, 12(7), 132. https://doi.org/10.3390/a12070132





