Abstract
The dimensional synthesis of multi-linkage robots has great significance for improving flexibility and efficiency. With the increase of the degree of freedom and restrictions on special occasions, the solution of dimensional synthesis becomes complicated and time-consuming. Theory of workspace density function, maneuverability, and energy expenditure had been studied. With high flexibility and low energy consumption as the design goal, the method for dimensional and joint angle synthesis of multi-linkage robots was proposed based on a niched Pareto genetic algorithm. The Pareto solution set has been obtained. The method was verified by two application examples, which is occlusion of the solar salt evaporation pool and the secondary scattering of solid 2,2′-azobis(2,4-dimethylvaleronitrile). Through the application of NPGA (niched Pareto genetic algorithm) compared with KPCA (kernel principal component analysis), it can save 12.37% time in occlusion of one evaporating pool and reduce energy consumption by 3.85%; it can save 9.96% time in scattering of remain materials per barrel and reduce energy consumption by 1.77%. The study reduces the labor intensity of manual workers in the salt making industry, ensures the safe production of dangerous chemicals, and provides new ideas and methods for the dimensional synthesis of multi-linkage robots.
1. Introduction
A multi-linkage robot is a linkage mechanism composed of multiple movable joints connecting rigid rods in series [1,2]. It has the advantages of large range of working space, high flexibility, simple mechanical structure, good obstacle avoidance performance, and better avoidance of singularity of mechanism. They are widely used in medical surgery, underwater detection, construction, and many other engineering fields.
The fact shows that dimensional synthesis for multi-linkage robots has been paid much attention by scholars. Gosselin proposed a global condition index (GCI) that combines the working space and the Jacobian condition number to design the structure size of multi-linkage robots [3]. Based on the optimization goal of the subjective minimum robot criterion, Amir optimized the robot size with the Lagrange multiplier method [4]. José-Alfredo et al. used the means of a multi-objective optimization to carry out dimensional synthesis of a spherical parallel manipulator, the method of multi-objective evolutionary algorithm based on decomposition (MOEA/D) was proposed, objective functions were the dexterity, the variability of the dexterity, the maximum required torque, and the stiffness. The optimization of robots’ workspace was performed using non-dominated sorting genetic algorithm- II (NSGA-II), multi-objective particle swarm optimization algorithm (OMOPSO), MOEA/D separately, the results showed better performance of MOEA/D algorithm [5]. Ramon et al. obtained the best linkage by means of hybridizing a local search (LS) approach and an evolutionary algorithm (EA). Hybrid optimization strategy was selected by cluster and elite analyses, for the design of planar linkages, the best options were highlighted [6]. In [7], attitude maneuverability was used to optimize the links. The maneuverability as objective function designed robot parameters in [8]. In [9], the workspace distance, stiffness performance, and velocity fluctuation were taken as the standards, the link lengths were designed and optimized for service robots. In [10], link length optimization of 3R linkage robot was done based on the range that the end-effector reached. In [11], the method, which took the distribution area of workspace density function maximum value as the standard, was proposed for dimension design. In the literature [3,4,5,6,7,8,9,10,11], one or more algorithms and theories are used to design the size of multi-linkage robots with a single target or several targets as the optimized objective function. The reliability and superiority of the method are verified by means of software and simulation. However, whether the new method can achieve better results in the practical application has not been further studied, and its application value remains to be verified.
In [12], a ‘magic hand’ robot was developed on the basis of study regarding dimension synthesis, manipulators can complete the surgery basic operation and can replace an attending doctor. In [13], the structure size was solved by least squares in the view of energy consumption analysis, effectiveness was verified by means of KUKA robot. In [14], the size of collaborative space volume was quantified by the number of space cloud points, mechanical dimensional of the robot arm was were optimized aimed as maximum of collaborative space volume. In [15], the leg structure parameters of quadruped robot were analyzed based on the dynamic dimensional synthesis. In [16], the robot dimensional parameters, which combined with the signal-to-noise ratio (SNR) theory and Taguchi technology, were determined by taking the maximum SNR as the optimization object. In [17], the design of parameters was divided into three levels, it was verified that shortened the design cycle and difficulty and improved the design efficiency for industrial robots. In [18], bionics theory was cited to design the parameters of the crawling robot, which had high reliability, low cost, and good flexibility. In [19], in order to improve the load-capacity of the mechanical arm, the method employing workbench goal-driven methodology optimized analysis was adopted, reducing the arms weight and increasing the load of the manipulator. In [20], structural parameters of the bionic rescue robot were optimized based on genetic algorithm. In the literature [12,13,14,15,16,17,18,19,20], for the dimensional synthesis of multi-linkage robots in different application situations, the effectiveness of the methods is verified respectively, and good performance of multi-linkage robots is obtained. However, the universality of these methods in other situations needs to be further verified.
For complex scenes or high flexibility requirements, the methods proposed in these studies have problems such as tedious solution expression, large amount of calculation, and poor rationality of multi group solution verification. Although the design method in the reference [17] is concise, which improves the design efficiency and shortens the design time. However, the energy consumption factor in the motion of multi-linkage robots was not included as the objective function in these studies, and the research on the joint angle of the robot was also not involved. Therefore, it is necessary to design multi-linkage robots with high flexibility and low energy consumption in order to improve computing efficiency and accuracy.
Kinematical theory, workspace density function [21], genetic algorithm [22,23,24,25], and multi-objective algorithm theory had been fully researched before. In this paper, we set the density function, maneuverability [26,27,28], and energy expenditure as objective functions. Multi-link robots have high flexibility and low energy consumption, which can meet the application requirements under special circumstances. In order to guide the design of multi-link robots, we proposed a design method of multi-linkage robots’ dimensions and joint angles based on the niched Pareto genetic algorithm, shorted as NPGA. Apply proposed method to actual scenes, which are retracting and releasing shielding cloth of salt evaporating pool and separation of the remaining solid 2,2′-azobis(2,4-dimethylvaleronitrile) (shorted ADVN) from the barrel. The multiple dimensions and joint angles of the 2R and 3R link robots were obtained, which verified the reliability of the method. The method provides new ideas and methods for the dimensional synthesis of multi-linkages robots.
The rest of the paper is organized as follows. In Section 2, three objective functions are researched by calculating appropriate cases, then the relevant calculation formula are derived. In Section 3, the parameters and design process of NPGA are determined. In Section 4, the mathematical model of operation is established. In Section 5, two application examples of parameter synthesis are given to verify the proposed method. Finally, we present our conclusions in Section 6.
2. Objective Functions of NPGA
NPGA adopts Pareto winning relation to select tournament. We choose objective functions combining the application of the n–R linkage robot based on the fitness sharing mechanism.
2.1. Workspace Density Function
The mechanical mechanism workspace is divided into equal-sized units uniformly. The ratio of point number in each unit to point number in entire workspace end-effector can reached divided by unit volume is workspace density [29]. The greater workspace density, the better flexibility of the mechanism. The Monte Carlo method conducts statistics and tests with random numbers and takes the mean value and probability as the numerical solutions to unsolved problems, also known as Monte Carlo simulation. We study the workspace density, use the Monte Carlo method and then describe the shape, characteristics, and properties of flexible workspace more intuitively with the help of computer technology in the view of probability statistics. In the paper, calculation and simulation are implemented using the method combined with density function.
2.1.1. Calculation of Monte Carlo method
The principle of the Monte Carlo method for workspace solution is
where is workspace, is the generalized joint variable, is forward kinematics expression, and is the joint space sets.
The Monte Carlo method generates a large number joint space points randomly, map them to flexible workspace, obtain corresponding end-position data, and then computes the boundary of the flexible workspace statistically. The specific flow of the algorithm is as follows:
- Divide the samples of each joint angle, construct the sample space according to the definition of flexible workspace;
- Calculate the positions end-effector reached on the basis of forward kinematics expression ;
- Construct the flexible workspace using outputted the end-effector position. The larger the sample size, the geometric contour will be clearer and the flexible workspace will be more accurate.
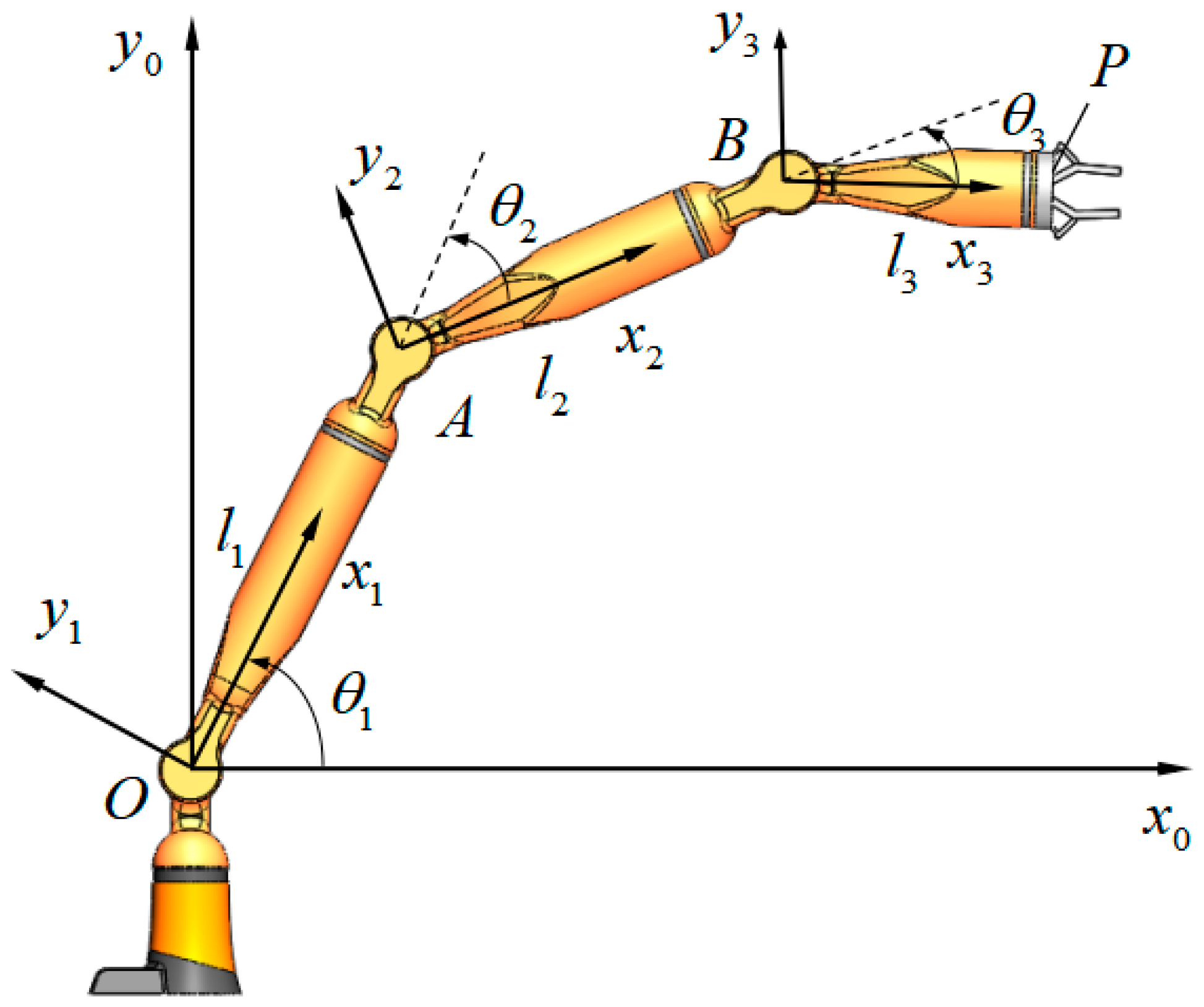
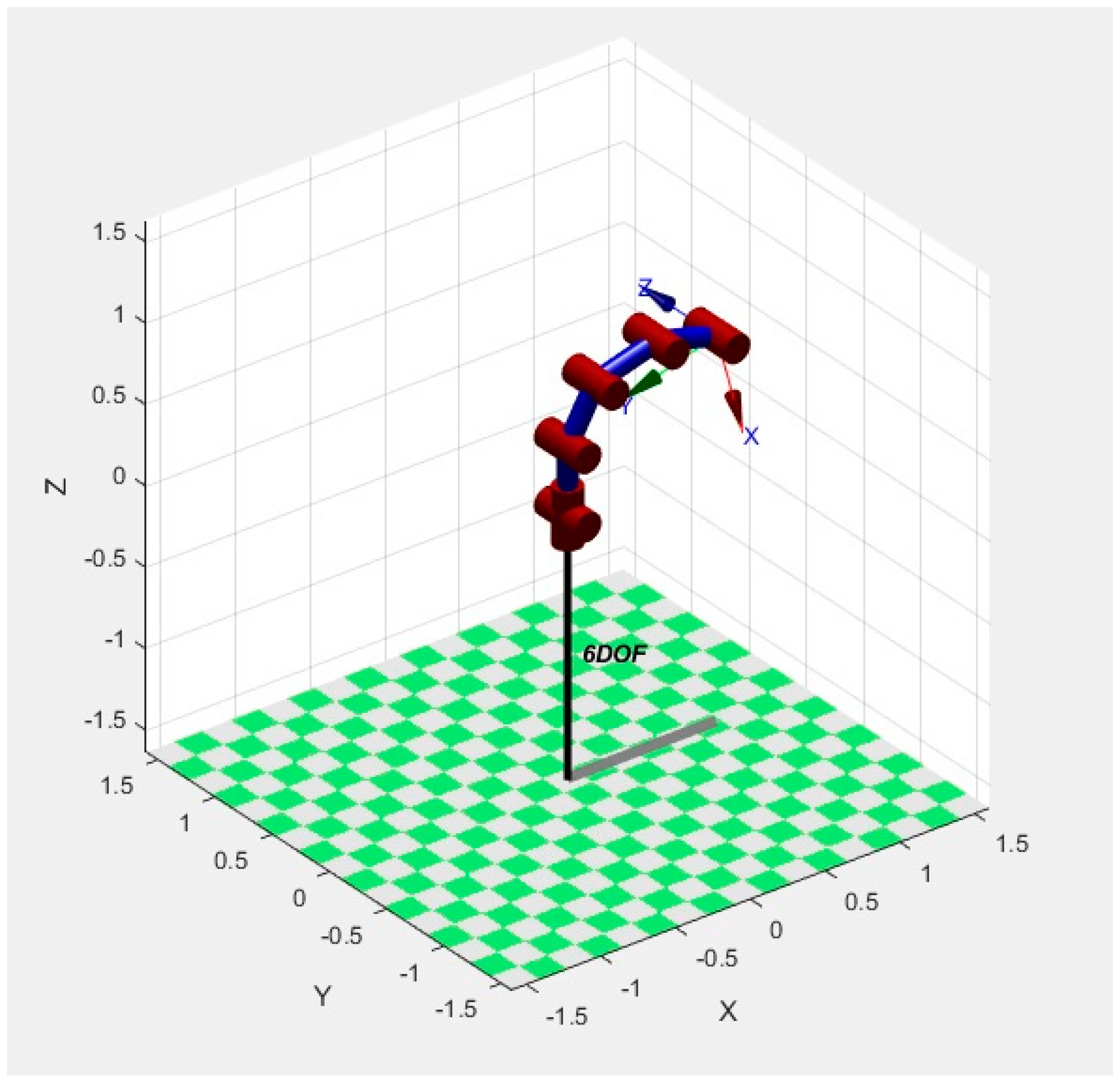
The forward kinematics equation was established based on Denavit–Hartenberg method (D–H method), according to the geometric relationship between the robot end-effector position, bar lengths, and joint angles in Figure 1.
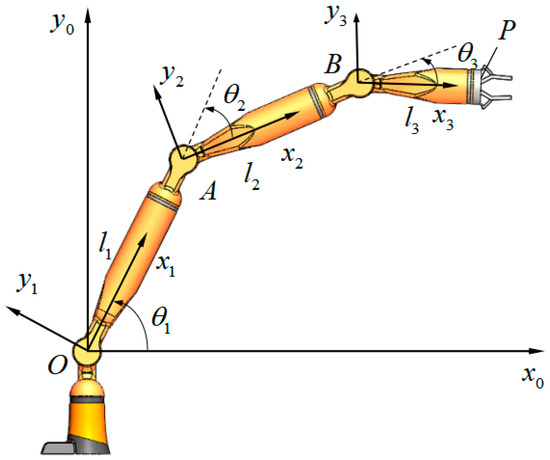
Figure 1.
Forward kinematics model of 3R linkage robot.
Let the coordinate axis , , be perpendicular to paper outward, in that way the homogeneous rotation transformation matrix from to is shown in Equation (2).
The homogeneous rotation transformation matrix from to is shown in Equation (3).
The homogeneous rotation transformation matrix from to is shown in Equation (4).
Then we can get the homogeneous rotation transformation matrix from to , as shown in Equation (5).
Therefore, the position vector of the end-effector can be expressed by Equation (6).
The forward kinematics equation of 3R linkage robot is shown in Equation (7) and the forward kinematics equation of the n–R linkage robot is shown in Equation (8) in cartesian coordinate system.
In the above equations, , , and represent the length of the , , and bars respectively; , , and represent the angles of the , , and bars respectively.
The forward kinematics equation in rectangular coordinate system and in polar coordinate system can be expressed in Equations (9) and (10) respectively.
2.1.2. Construction of Density Functions
Monte Carlo method calculates the workspace of series manipulator. According to the characteristics that the workspace density function conforms to the random density function, the mathematical model is built to describe the workspace density.
Assume that is the density function of the manipulator bars, which . The workspace density function of linkage manipulator can be expressed as:
Among them, represents the convolution operation on ; represents the convolution operation on .
The random variables can be continuously evaluated in the workspace which is a continuous space. Therefore, all the continuous random variables can be expressed by the probability density function, which is shorted PDF. The multivariate normal distribution (Gaussian distribution) density function is defined as Equation (13) considering that x is a multidimensional variable.
Strictly generalization of Equation (13) obtain Equation (14), where μ is mean value, ∑ is order symmetric positive definite matrix.
The solution of , are as follows in Equations (15) and (16) respectively.
Since the sum of discrete probability distributions is 1, integration of probability density function is 1 always, as shown in Equation (17).
The continuous probability density function is not limited to 1, so in the study of workspace, all continuous random variables are measurable, and all continuous distributions have density. For a NR manipulator, if each link angle has states, the samples number is in the linkage manipulator workspace, the variance of this sample space can be written as Equation (18).
When is sufficiently large, the variance of the actual workspace density function can be rewritten as Equation (19)
where , is order identity matrix, is variance. Therefore, according to convolution iteration and extreme value theorem, the workspace density function constructed by Gaussian probability-density function is expressed in Equation (20), is expected value.
2.1.3. Numerical Example
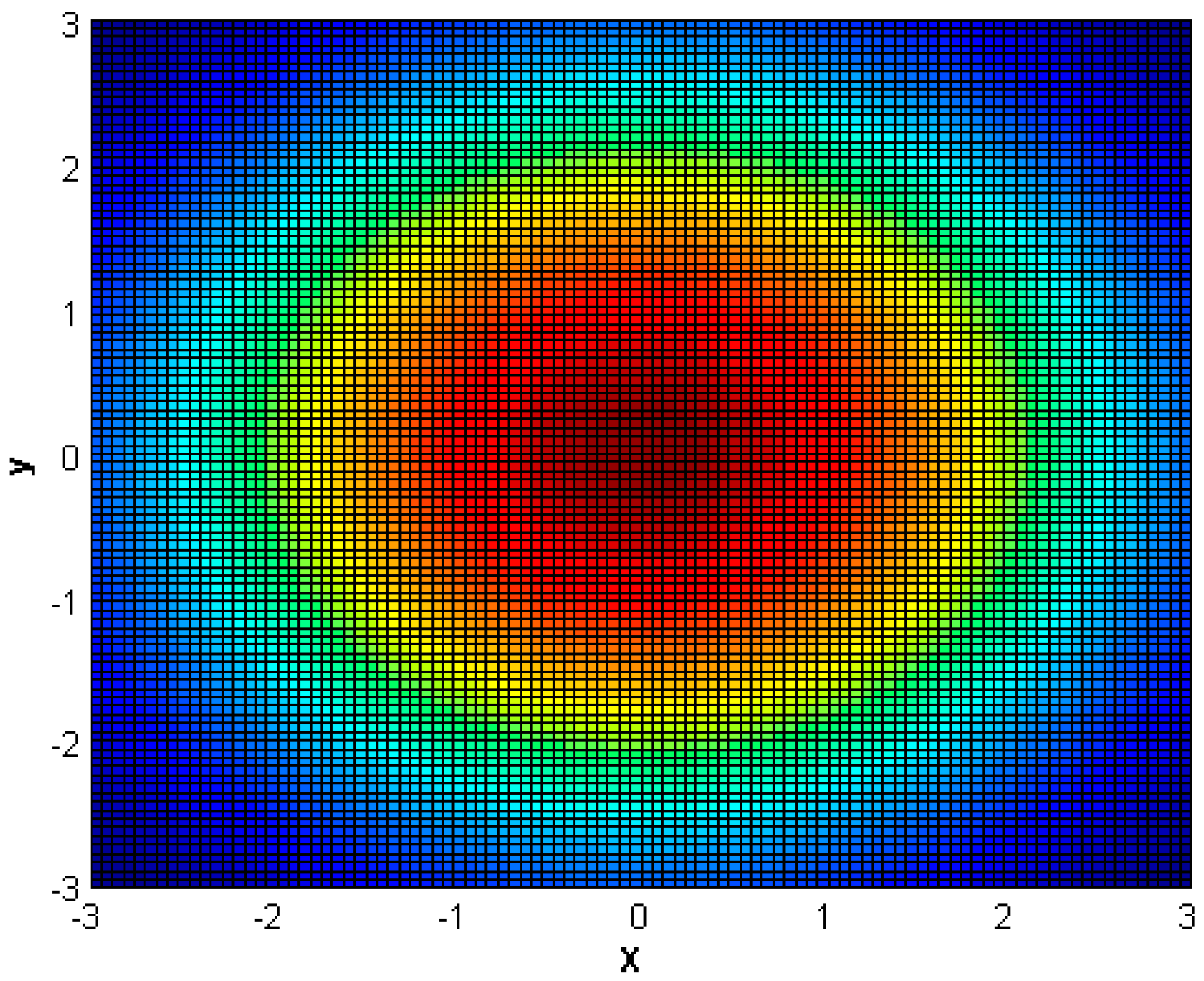
1. Set bar length , , , , , are not restricted, we take 8000 sample points according to Equations (8) and (20) and draw a workspace density figure, as shown in Figure 2.
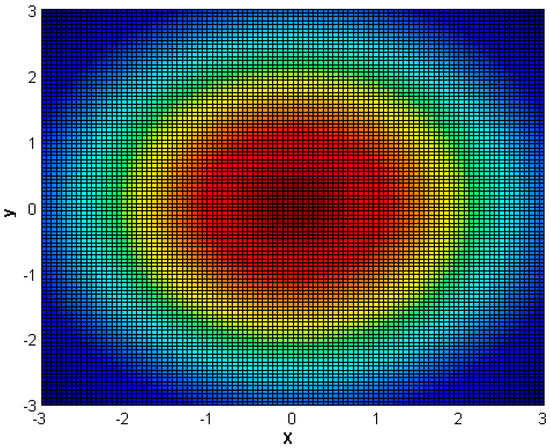
Figure 2.
X–Y workspace density of 3R linkage robot.
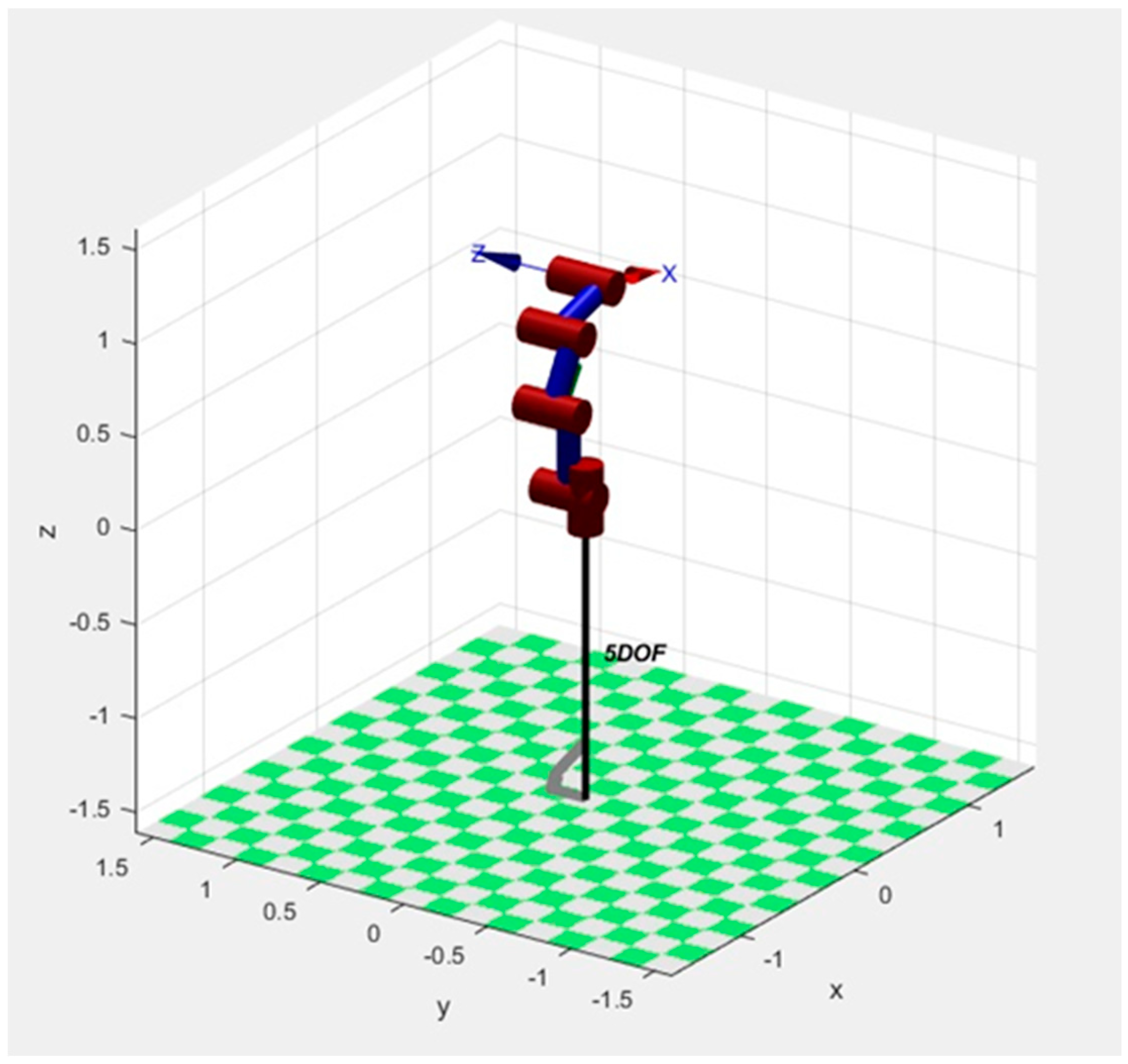
2. Figure 3 shows the 5R linkage robot model, in which , , , offset is 0.1, 0.2, 0.3 respectively in the same direction with the base axis as the reference.
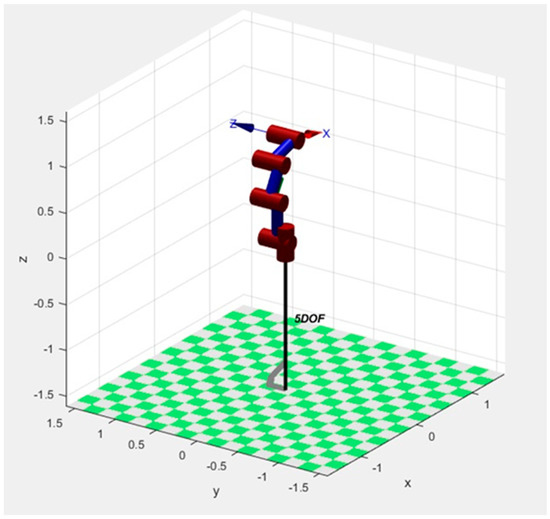
Figure 3.
Model of 5R linkage robot.
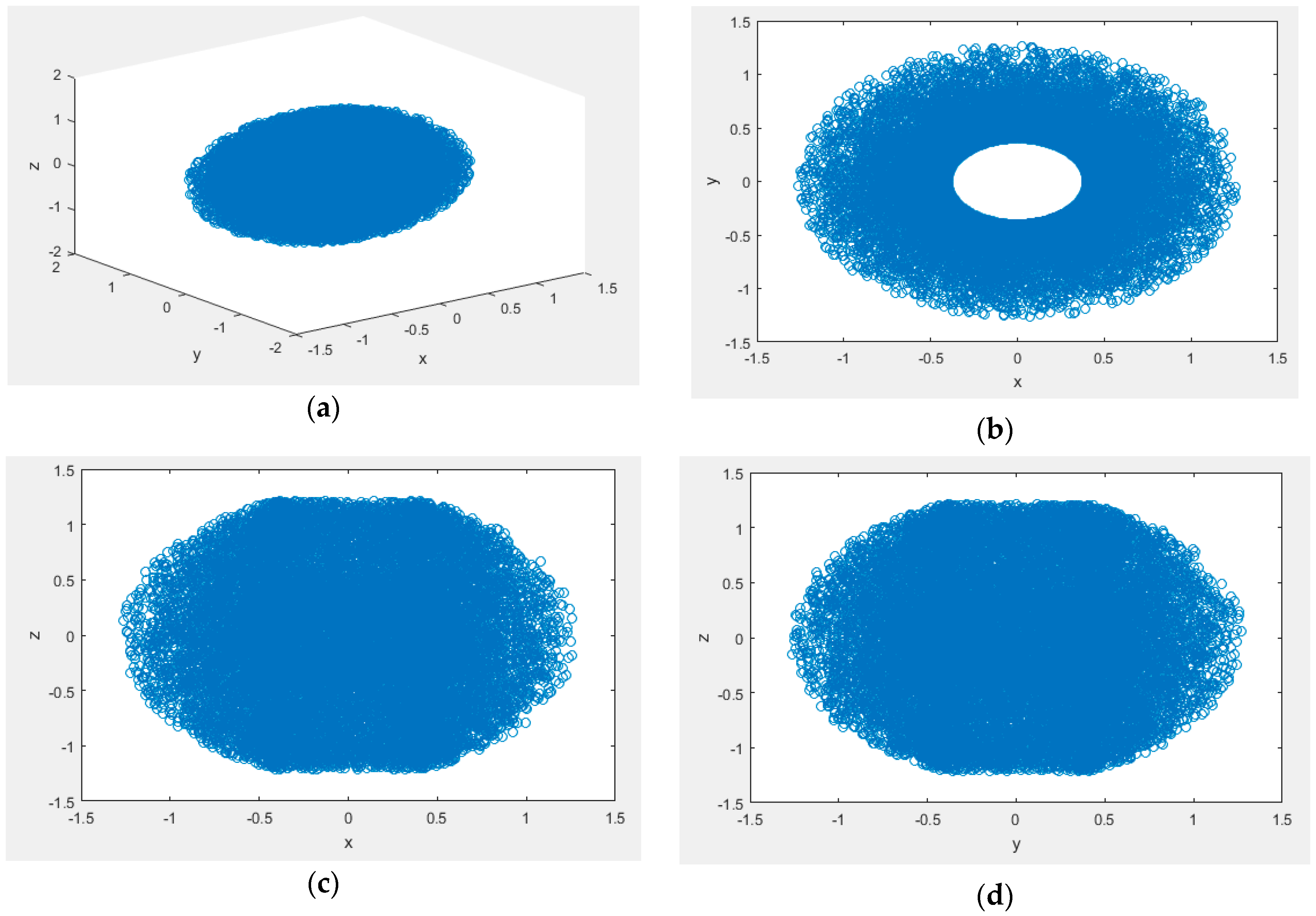
All angles have no limit, 20,000 sample points are taken to calculate the workspace nephogram based on Monte Carlo method, the results are shown in Figure 4.
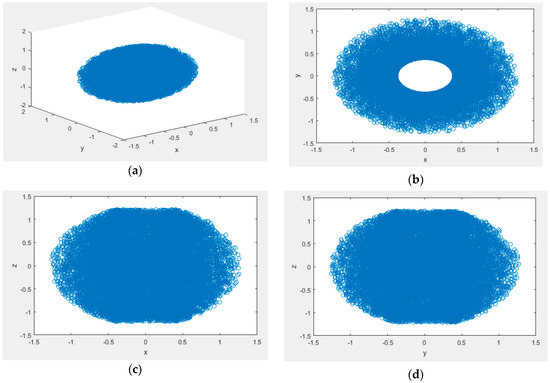
Figure 4.
(a) Three-dimensional workspace nephogram of 5R linkage robot based on Monte Carlo method; (b) View in the x–y coordinate system; (c) View in the x–z coordinate system; (d) View in the y–z coordinate system.
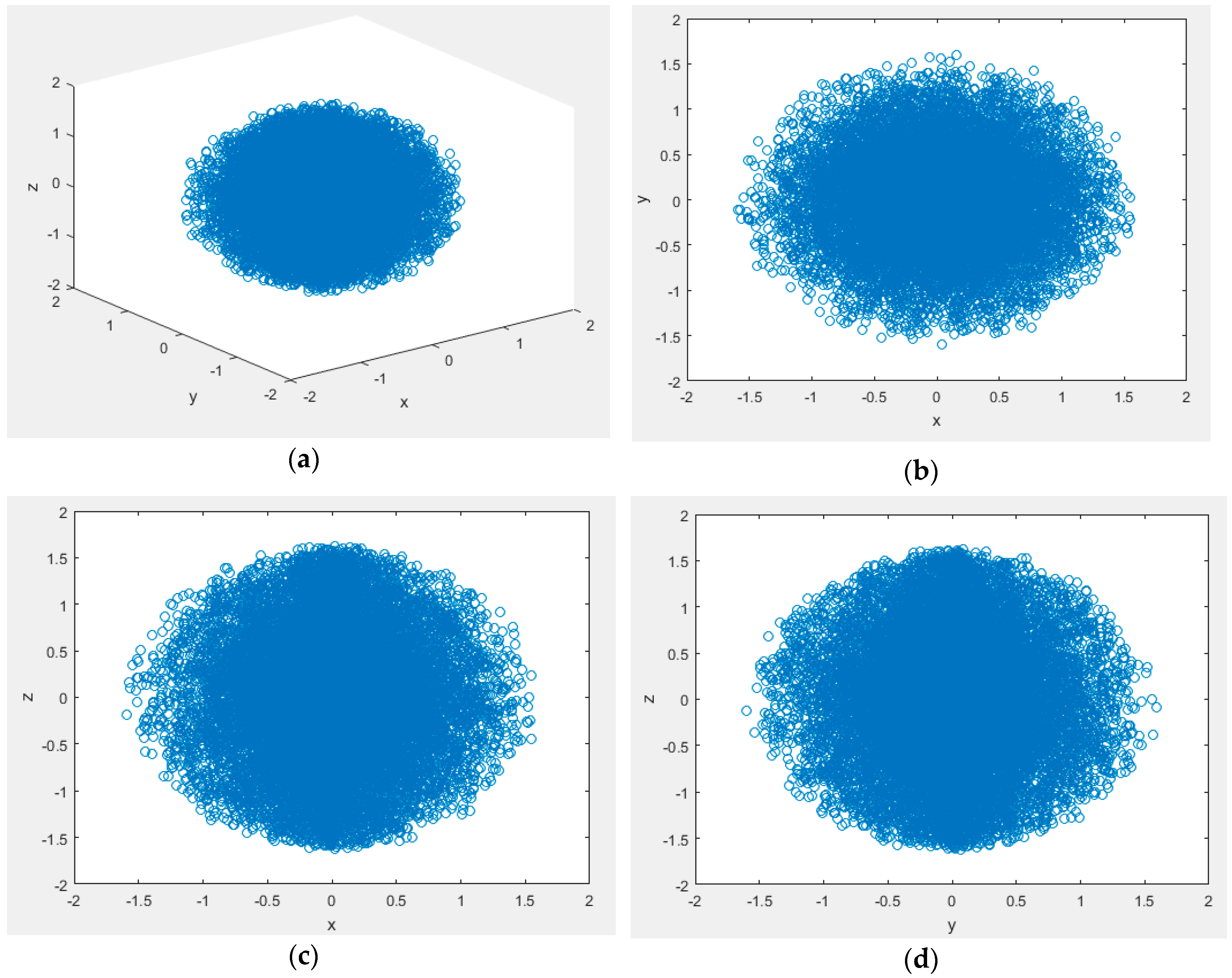
3. 6R linkage robot model is established in Figure 5 , , , , there is no offset.
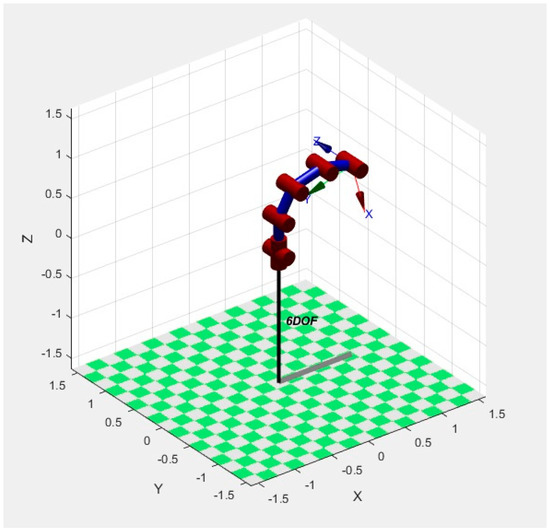
Figure 5.
Model of 6R linkage robot.
All angles have no limit, we also take 20,000 sample points, the workspace nephogram based on Monte Carlo method are shown in Figure 6. The four views comprehensively describe the workspace density by the Monte Carlo method.
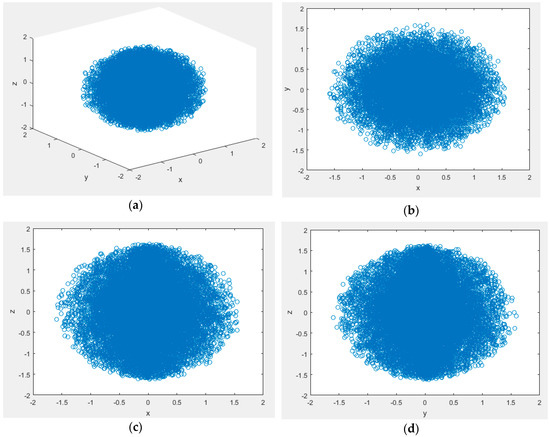
Figure 6.
(a) Three-dimensional view of the 6R linkage robot workspace simulated by Monte Carlo method; (b) View in the x–y coordinate plane; (c) View in the x–z coordinate plane; (d) View in the y–z coordinate plane.
2.2. Maneuverability
When determining the parameters of the linkage robot, flexibility is an important considered factor. Yoshikawa [30] defined the maneuverability and gave the solution method. The flexibility variation of the linkage robot is demonstrated accurately by quantitative value. The maneuverability can be solved by Equation (21).
Among them, describes the workspace flexibility of the linkage robot, is Jacobian matrix. Therefore, the Jacobian matrix plays an important role in maneuverability solution. Combined with Equation (6), the relationship that between the end-effector position , and the angles , , in Figure 1 is shown in Equation (22).
Take the partial derivative of that, Equation (23) is gained.
We define the Jacobian matrix, as shown in Equation (24), each term can be gotten from Equation (25).
As a result, the Jacobian matrix of the n–R linkage robot can be written as Equation (26).
The maneuverability of the n–R linkage robot can be written as Equation (27).
2.3. Energy Expenditure
In Figure 1, define the quality of , , is ,, respectively. Without considering linkage robot’s friction, energy expenditure includes kinetic energy and potential energy. In this study, energy expenditure is analyzed taking 3R linkage robot as an example to obtain the energy expenditure of n–R linkage robot. The kinetic energy of is shown in Equation (28). The kinetic energy of is shown in Equation (29). The kinetic energy of is shown in Equation (30).
The total potential energy of , , , is represented in Equation (31). So far, the energy expenditure of the 3R linkage robot can be expressed in Equation (32).
The following is energy expenditure calculation of the n–R linkage robot. The centroid position of the rod is provided in Equation (33).
The centroid velocity can be expressed with Equation (34).
The kinetic energy of can be derived as Equation (35).
The potential energy of can also be written as Equation (36).
Therefore, the energy expenditure of e R linkage robot can be summarized as Equation (37), where is total potential energy can be shown with Equation (38).
3. Niche Pareto Genetic Algorithms
Based on Darwinian evolution theory, evolution is in the process of natural selection and adaptive. For intractable nonlinear complex problems in traditional algorithms, it has important application value that design and construct new evolutionary algorithm to solve the multi-objective optimization problem. We gain one solution in Pareto sets usually in traditional algorithms. However, more—or even all—Pareto sets can be solved using the genetic algorithm.
The pennant selection system of NPGA is different from comparisons among individuals distinctly. NPGA also selects other individuals for comparison. Let individuals evolve in certain living environment for forming multiple niches, then individuals will always evolve in each niche until they reach a peak in the niche. Therefore, the global optimal solutions are obtained [31].
3.1. NPGA Sharing Function
In order to ensure data diversity, according to individual similarity, population is divided into different sub-populations in parameter space and gene space. The sharing function between populations can express in Equation (39)
where is the distance between population and , is a shared parameter controlled allowable sharing degree, generally.
3.2. NPGA Fitness
The fitness between populations is adjusted with sharing function of populations’ similarity degree. In that way, the sub-population is divided by new fitness in iterative evolution, so the niche evolution environment [32] is produced. The population fitness can be expressed as Equation (40)
where is the adjacent population number of the population, is fitness after sharing, is fitness before sharing, and is population size.
3.3. Design of NPGA
3.3.1. Choice of Coding Method
Each gene value is represented by floating point numbers in the algorithm, the encoding length is the number of variables. The method of floating-coding can deal with complex variable constraint conditions. It is convenient for genetic searching. Therefore, the floating-coding method is selected for the established mathematical model the variables of which are length of a structural member and joint angle. The mathematical model’s aims are the density function, maneuverability, and energy expenditure. At the same time, it is also easy to mix NPGA with classical computing methods. In the floating-point encoding,
- The symbol bit is represented by S: 0 is positive, 1 is negative;
- N represents the binary bits of an int;
- The exponent bit is denoted by E;
- Mantissa is represented by M;
3.3.2. Choice of Operators
The purpose of choosing appropriate operators is to ensure the computational efficiency and improve the convergence of the algorithm. The survival of the fittest is carried out with elitist strategy, the worst individual is always replaced by the best, and it can limit the reproduction of certain individuals into the next generation. In this paper, the niche technique and Pareto optimal individual are applied to solve problems such as calculating the optimal solution of individual sub-objective function. The number of niches () is the number of individuals in the niche segment of the genotype space (). If two non-inferior individuals , are selected based on the niche, let and are respectively the niche number of individuals , in the niche . Then, the corresponding individual is selected from (the individual is selected with the smallest number of niche).
3.3.3. Choice of Crossover Operator
Crossover operation is the main method to generate new individuals, which determines the global search ability of the algorithm. It should not damage the good character of individual coding string too much, but also effectively generate good new individuals. Adopting the method of uniform block crossover operator, the operation between individual and create two new individuals, as shown in Equation (41), where is a constant, and such a crossover operation is called uniform arithmetic crossover.
3.3.4. Choice of Mutation Operator
The mutation operation determines the local searching ability of genetic algorithm. Its purpose is to change the local searching ability of genetic algorithm and maintain the diversity of population. Because of the choice of floating-point encoding, a Gaussian mutation operator is used in this study. We define the value range of aberrance point that is , then mean value and variance with normal distribution can be expressed as Equations (42) and (43) separately.
Then new genic value may be determined in Equation (44), in which is the sum of Uniformly distributed random Numbers in [0,1].
3.3.5. Operation Flow Chart
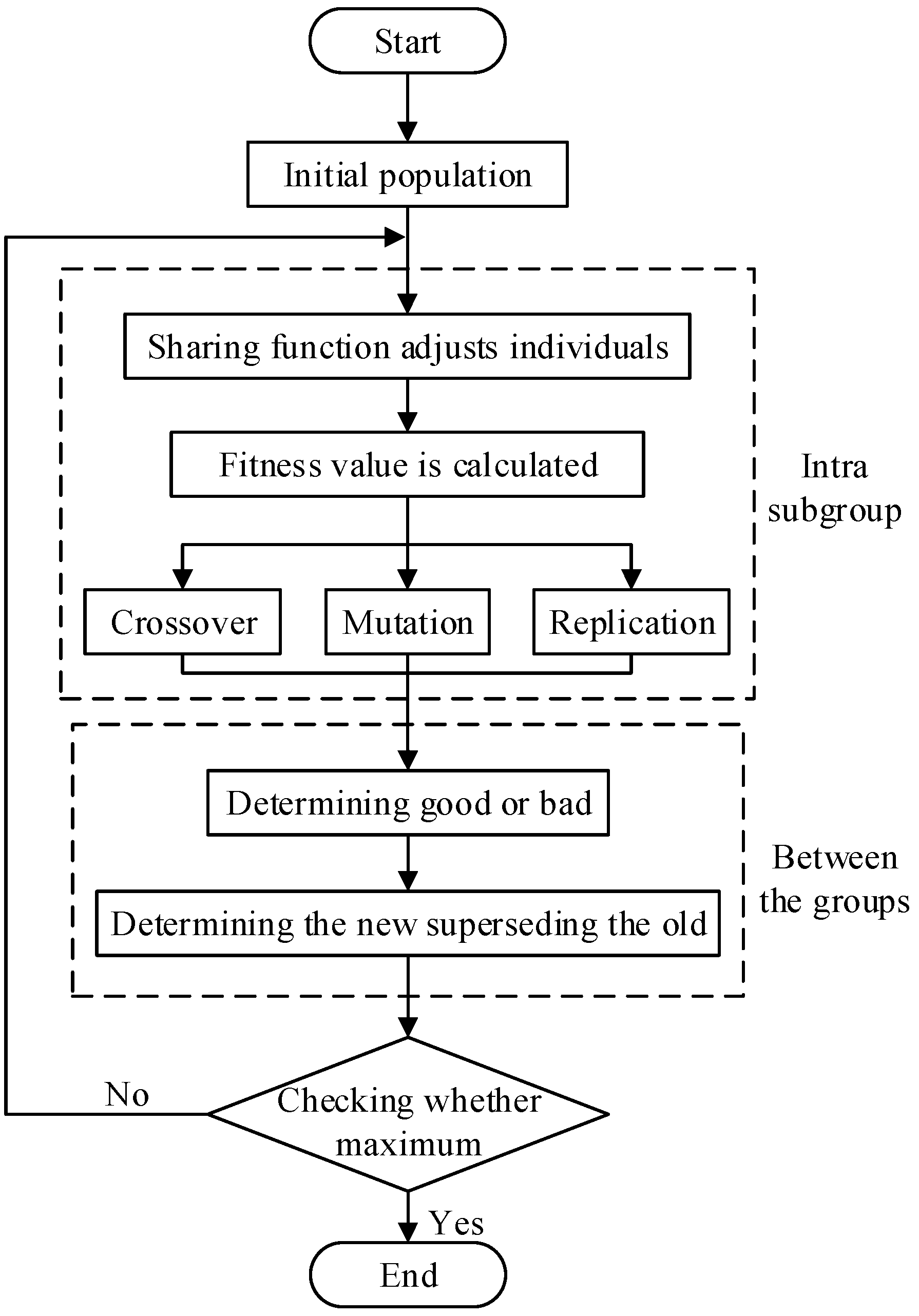
The operation flow chart of NPGA is shown in Figure 7. The procedure is as follows:
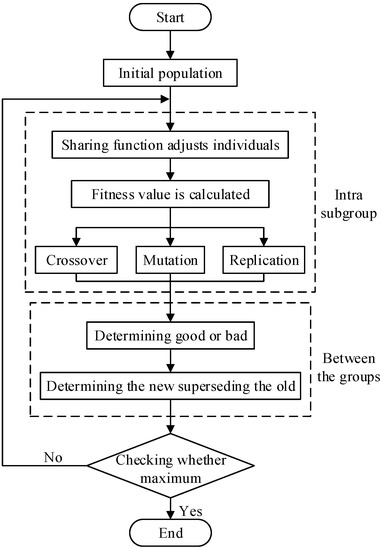
Figure 7.
Operation flow chart of NPGA.
- Initialization of algorithm, produce new initial population and set up genetic parameters;
- Calculate the sharing degree;
- Calculate individuals’ fitness of population according to the individual sharing;
- Process of selecting, crossing, and mutating;
- Comparing of fitness size between offspring and last generation individuals;
- Offspring replace last generation individuals, forming a new population;
- The algorithm stops until the termination condition is activated, otherwise go back to Step 2.
4. Mathematical Model of Dimensional Synthesis
There are many performance indexes of a multi-linkage robot, especially on specific occasions and in specific engineering applications. Workspace density function, maneuverability, and energy expenditure are ordinary. Determining the parameters of the linkage robot to make it have higher flexibility and lower energy consumption has important application significance. In this study, we define the parameter variable is Equation (45).
The objective functions are shown in (46), maximum workspace density function (gained by Equation (20)), maximum maneuverability (gained by Equation (27)) and minimum energy expenditure (Equation (38)).
For avoiding normalized operation, transform the energy expenditure into the as the objective function. Constraint angles in Equation (47), if the workspace boundary is not determined.
5. Engineering Example of the Method Application and Analysis
The method of dimensional synthesis can be verified better in actual engineering. In this paper, the method is applied in salt industry and chemical industry. In addition, kernel principal component analysis (KPCA) was used to calculate the two-link and three-link robots in the study and application examples [33], and the results were compared with those obtained by NPGA in this paper.
5.1. Method Application in Salt Industry
Solar salt is the process of making salt from seawater, including moisture absorption, halogen generation, crystallization, and other processes. The salt-making process of seawater is generally stored in the evaporation pond for 7–15 days. According to the influence from weather, brine concentration, and other external factors, occlusion of the solar salt evaporation pool is necessary, it has great significance for improving the solar salt efficiency. Without manual retracting and retracting, the shielding cloth (as shown in Figure 8) will get off the track and become entangled, affecting the evaporation of the salt field. At present, the occlusion cloth is put in with the help of human, as shown in Figure 8 Due to the large number of evaporation pools, so it is very labor-intensive, time-consuming, and also less efficient.

Figure 8.
Human assistance.
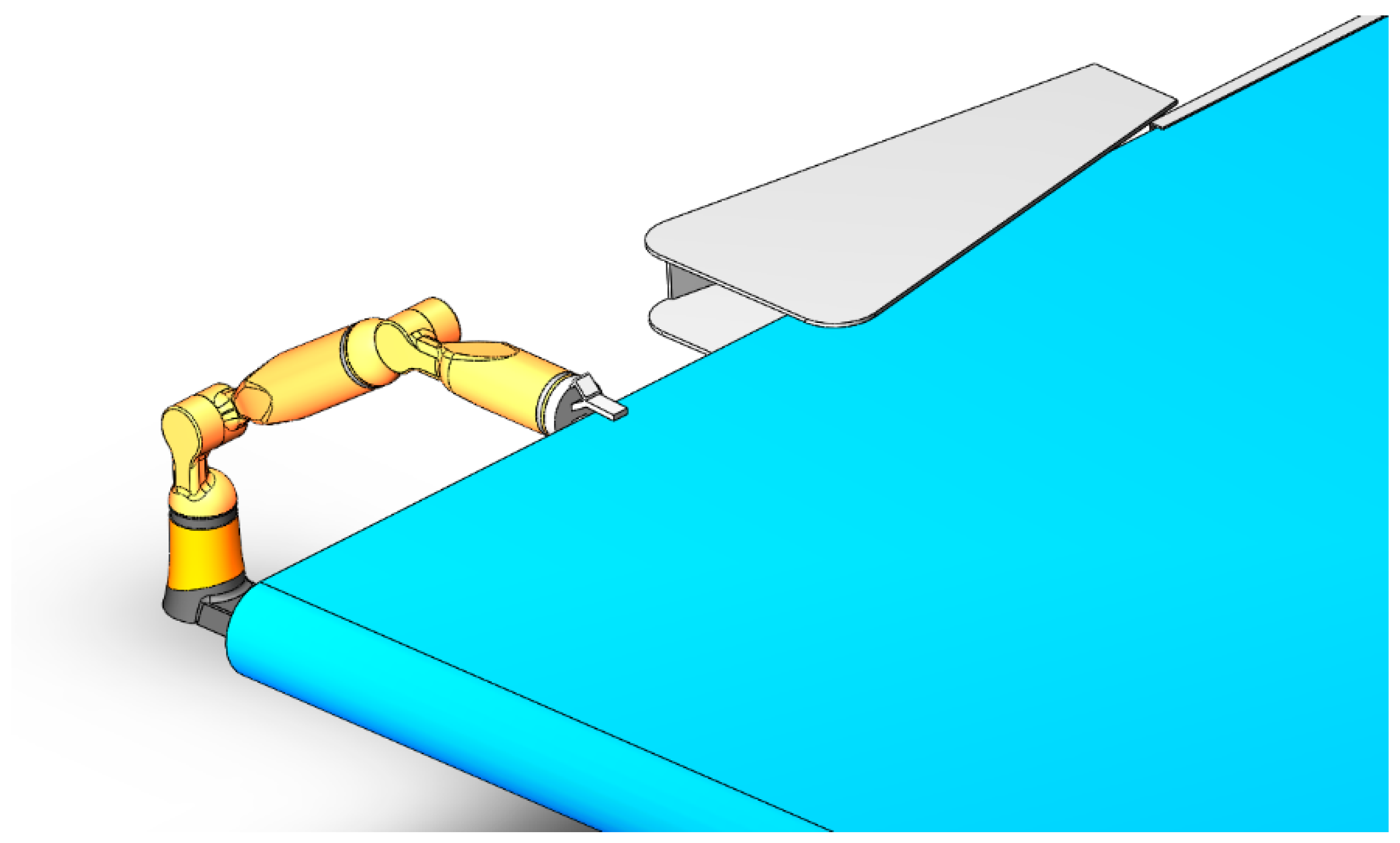
As shown in Figure 9, a 2R linkage robot is designed instead of manually retracting or releasing of the shielding cloth. The two-lever robot actuator can clamp the blocking cloth to ensure the smooth rolling and releasing of the blocking cloth in the salt field, so as to save labor and improve the rolling and releasing efficiency of the blocking cloth in multiple evaporation pools in the salt field.
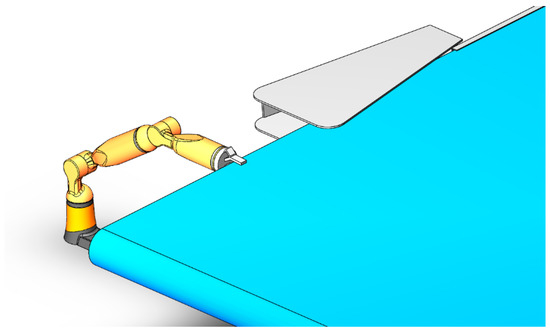
Figure 9.
Robot assistance.
The dimensional synthesis data of two-link robot obtained by the KPCA is shown in Table 1.

Table 1.
Partial data table of two-link dimensional synthesis (NPGA).
In Table 1, dimensional parameters, we take , , , after radian convert to angles.
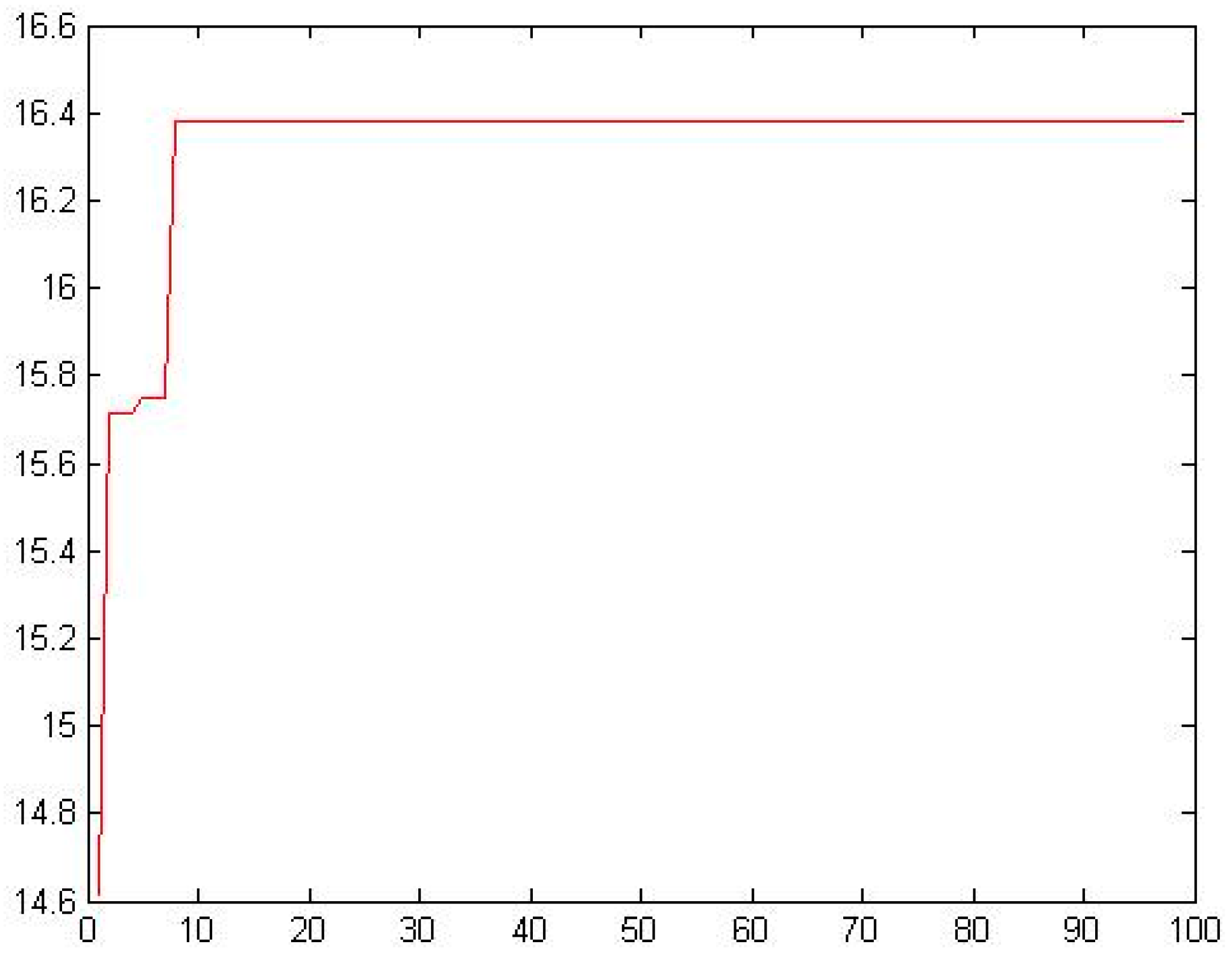
The design solution is based on NPGA method. For the calculation model constructed in this paper, the population size is set as 100 and the chromosome length is set as 32 bits in binary order to obtain the global optimal solution quickly based on experience. The choice of crossover operator affects whether it can converge to the optimal solution region, so the crossover operator is 0.08. If the mutation operator is selected larger, on the one hand, increasing the diversity of samples can also cause instability. On the other hand, if the selection is small, it can be difficult to find the global optimal solution. Thus, mutation operator is set to select 0.65, termination of algebra for 100 generations, and the result is shown in Figure 10. According to the data, the convergence is good, the global Pareto solution is set, some data are shown in Table 2.
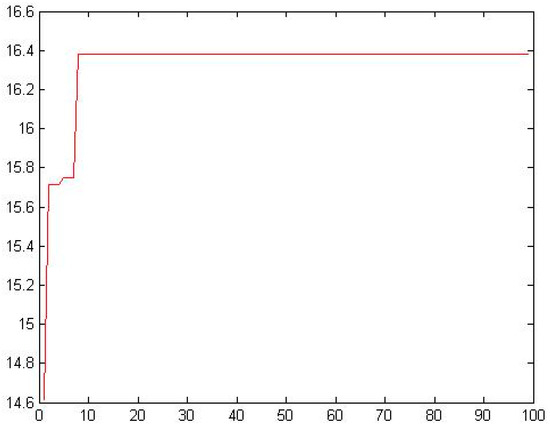
Figure 10.
Output results of NPGA in salt industry.

Table 2.
Some dimensional synthesis data of 2R linkage robot.
In Table 2, for dimensional parameters, we take , , , after radian convert to angles.
It can be seen from the data comparison in Table 3 that the multi-linkage robot is used to assist the rolling and releasing of the shielding cloth. From the rolling and releasing process of 3–6 times per day, it takes time for each evaporation pool under the KPCA method. While for the NPGA method, it takes time . Only one evaporation pool saves the rolling and releasing time, which improves the rolling and releasing efficiency of the evaporation pool shielding cloth in the salt making process. The energy consumption of multi-linkage robot was estimated from the change of joint angle, and the NPGA method reduced the energy consumption by about compared with the KPCA method.

Table 3.
Application data of the two methods in the salt field.
5.2. Method Application in Chemical Industry
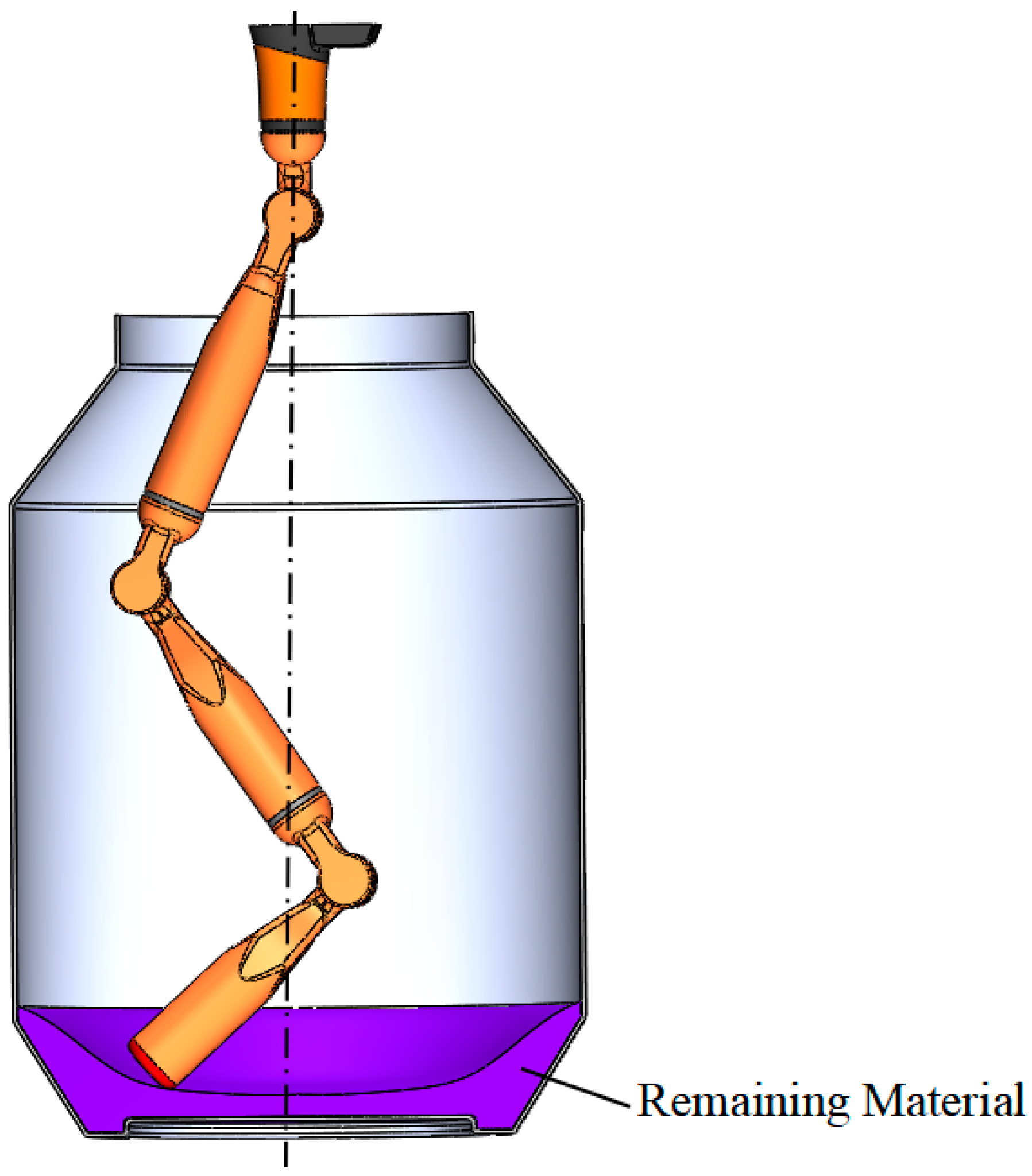
2,2′-azobis(2,4-dimethylvaleronitrile)(shorted ADVN) (molecular formula: C14H24N4) is widely used in industrial production for polyvinyl chloride(PVC), polyacrylonitrile (PAN), polymethyl methacrylate(PMMA), anticorrosive paint, etc. Due to its strong toxicity, flammability, and explosive risk, the workers should have little or no contact with it as much as possible. In this, the use of linkage robots is very important to ensure human health. In the process of barreled solid ADVN scattering, there is some surplus in the barrel. In order not to damage the material barrel, we designed the 3R linkage robot for the secondary scattering of remaining materials, as shown in Figure 11.
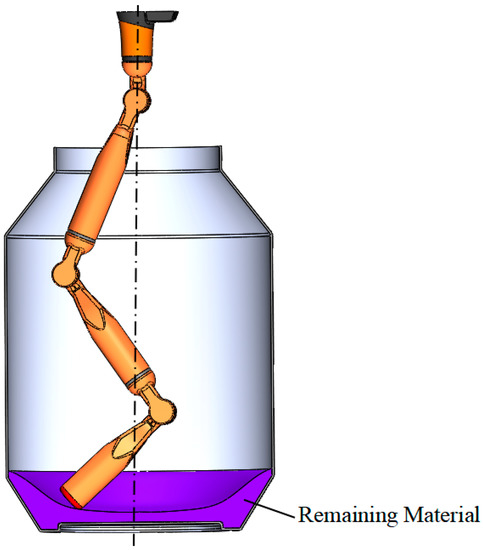
Figure 11.
Scattering of remaining ADVN.
In this application, the height of the barrel is , the maximum diameter is , and bunghole diameter is . The dimensional synthesis data of three-link robot obtained by the KPCA is shown in Table 4.

Table 4.
Partial data table of three-link dimensional synthesis (NPGA).
In Table 4, dimensional parameters, we take , , , , , after radian convert to angles.
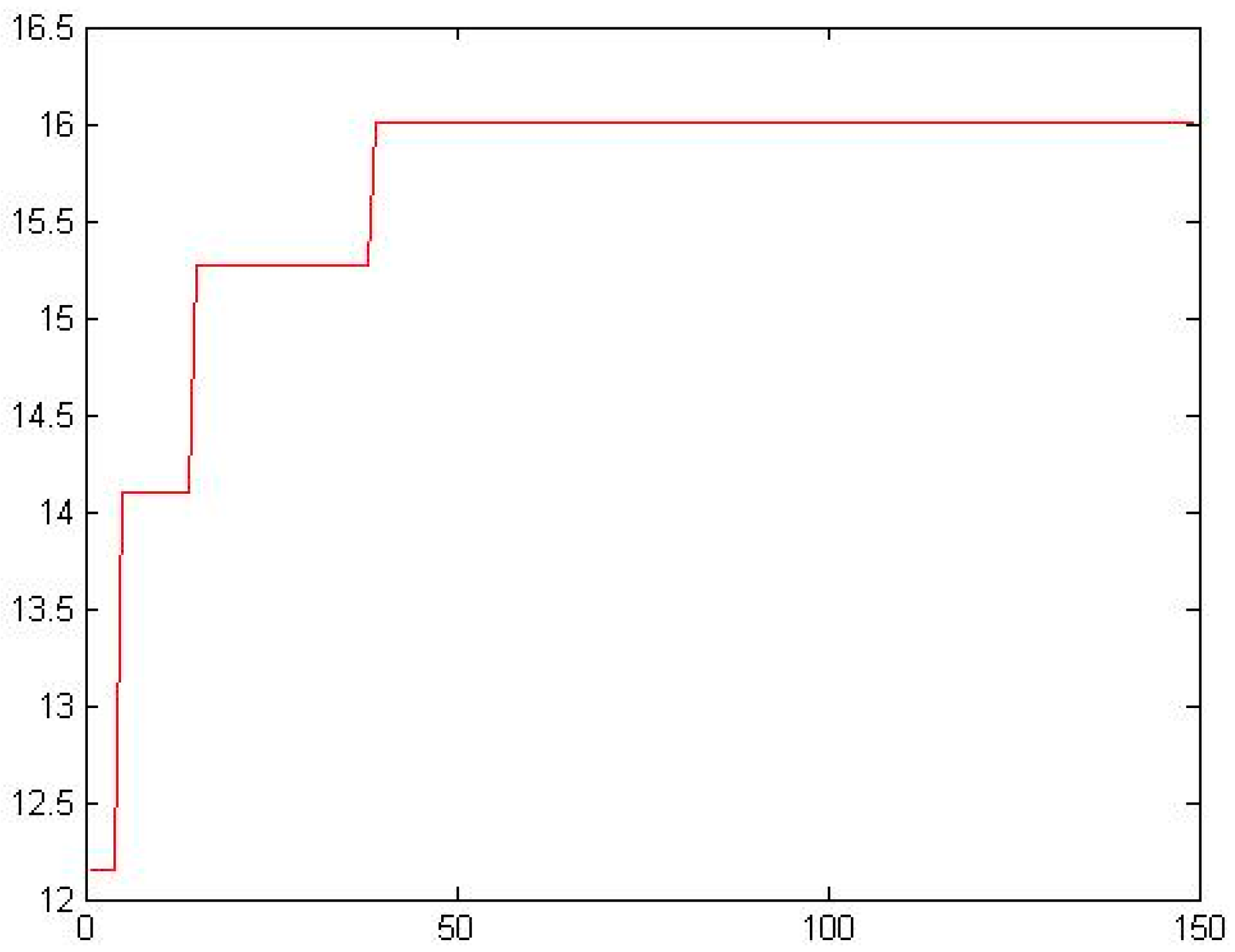
Design solution is carried out based on the NPGA method. According to the mathematical model constructed and the application example of two-link robot in salt field, population size is , chromosome length in binary is , crossover operator is , mutation operator is , termination generation is . The output results are indicated in Figure 12. It is observed that data convergence is good. We gained the global Pareto sets, some data are listed in Table 5.
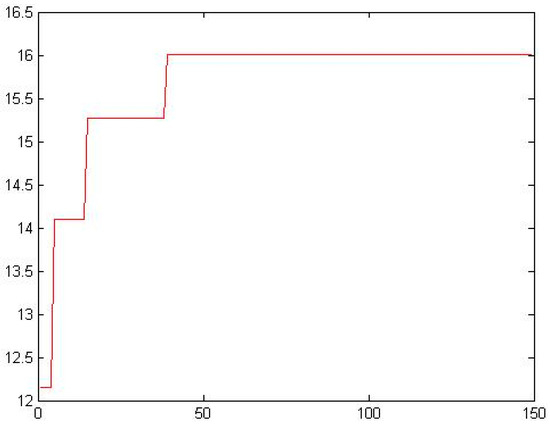
Figure 12.
Output results of NPGA in chemical industry.

Table 5.
Some parameter synthesis data of 3R linkage robot.
In Table 5, synthesizing various parameters, we take , , , , , after radian convert to angles.
From the data comparison in Table 6, the average processing time of a single barrel of ADVN in solid state is time spent under the KPCA method, while that under the NPGA method is time saved by single barrel processing. It improves the processing efficiency of powder making and reduces the manual time spent. From the change of joint angle, the NPGA method can reduce the energy consumption about compared with the KPCA method.

Table 6.
Application data of the two methods in chemical industry.
Figure 13 shows the remaining ADVN in the barrel. Figure 14 shows the scattered ADVN that it has been completely separated from the barrel. This meet the requirement with the next step into the grinder.

Figure 13.
Remaining ADVN.

Figure 14.
Scattered ADVN.
6. Conclusions
A component’s size is an important issue in mechanical design. Reasonable selection of construction size is of great significance for reducing energy consumption and improving the performance of multi-linkage robots. Based on theory and experiment, this paper studies the calculation method of dimensional synthesis of multi-linkage robots and draws the following conclusions:
- Based on the study of workspace, maneuverability, and energy expenditure, the NPGA method for dimensional synthesis of multi-linkage robot was proposed and applied. Then, the NPGA was applied;
- The superiority of NPGA method was verified by comparing with the KPCA method in two applications. The study provided new ideas and methods for the salt field’s unmanned mechanized production and design of hazardous chemical processing equipment;
- For the method of dimensional synthesis of multi-linkage robots, it is possible to obtain a locally convergent solution set under a special environment and specific constraint conditions, but the Pareto solution set with global convergence cannot be obtained. It is possible to obtain a locally convergent solution set, and the algorithm needs to be further improved.
Author Contributions
Conceptualization, H.W. and X.L.; Methodology, H.W. and X.L.; Software, X.L.; Validation, H.W. and X.L.; Formal analysis, H.W. and X.L.; Investigation, H.W. and X.L.; Resources, X.Y.; Writing—original draft preparation, H.W. and X.L.; Writing—review and editing, H.W. and X.L.; Supervision, X.Y.; Funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China by grant no. 51905320.
Acknowledgments
The authors would like to thank the two anonymous reviewers for their valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lv, B.H. Research on Key Technology of Multi Degrees of Freedom Dexterous Hand for Space Robot. Beijing. Master’s Thesis, The First Academy of China Aerospace Science and Technology Corporation, Beijing, China, 2019. [Google Scholar]
- Huang, A.; Yao, D.; Yang, W.; Zhang, G.; Li, Y. Kinematics and Dexterity Analysis of Mobile Manipulator. Mod. Manuf. Technol. Equip. 2019, 7, 28–31. [Google Scholar]
- Gosselin, C.; Angeles, J. A Global Performance Index for the Kinematic Optimization of Robotic Manipulators. ASME J. Mech. Des. 1991, 113, 220–226. [Google Scholar] [CrossRef]
- Dastjerdi, A.H.; Sheikhi, M.M.; Masouleh, M.T. A Complete Analytical Solution for the Dimensional Synthesis of 3-DOF Delta Parallel Robot for a Prescribed Workspace. Mech. Mach. Theory 2020, 153, 103991. [Google Scholar] [CrossRef]
- Leal-Naranjo, J.A.; Soria-Alcaraz, J.A.; Torres-San Miguel, C.R.; Paredes-Rojas, J.C.; Espinal, A.; Rostro-González, H. Comparison of Metaheuristic Optimization Algorithms for Dimensional Synthesis of a Spherical Parallel Manipulator. Mech. Mach. Theory 2019, 140, 586–600. [Google Scholar] [CrossRef]
- Sancibrian, R.; Sedano, A.; Esther, G.S.; Jesus, M.B. Hybridizing differential evolution and local search optimization for dimensional synthesis of linkages. Mech. Mach. Theory 2019, 140, 389–412. [Google Scholar] [CrossRef]
- Jia, S.; Jia, Y.; Xu, S. Dimensional Optimization Method for Manipulator Based on Orientation Manipulability. J. Beijing Univ. Aeronaut. Astronaut. 2015, 41, 1693–1700. [Google Scholar]
- Zhao, K.; Fu, Y.; Niu, G.; Pan, B. Mechanical Design and Dimensional Optimization of Minimally Invasive Celiac Surgical Robot. Huazhong. Univ. Sci. Tech. (Nat. Sci. Ed.) 2013, 41, 324–328. [Google Scholar]
- Ma, G.Q. Structure Design and Optimization Research of Mechanical Arm of Mobile Service Robot. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2014. [Google Scholar]
- Surbhi, G.; Sankho, T.S.; Amod, K. Design Optimization of Minimally Invasive Surgical Robot. Appl. Soft Comput. 2015, 32, 241–249. [Google Scholar]
- Dong, H.; Wu, W.T.; Sun, H. Dimension Optimization of Manipulator Based on Workspace Density Function. Mach. Build. Autom. 2019, 36, 143–146. [Google Scholar]
- Wang, S.; Wang, X.; Zhang, J. A New Robot to Assist Minimally Invasive Abdominal Surgery. Robot. Tech. Appl. 2011, 4, 6–11. [Google Scholar]
- Wu, Y.; Tang, X.; Song, W.; Jiang, P.; Zhou, J.; Chen, Y. Power Equivalent Model of Industrial Robot and Parameter Identification. J. Chongqing Univ. 1–13. Available online: https://kns.cnki.net/kcms/detail/50.1044.N.20200610.1138.002.html (accessed on 10 June 2020). (In Chinese).
- Jing, X.; Xue, Y.; Chen, Y. Analysis and Parameters Optimization of 6R Dual-Arm Service Robot Collaborative Space. Mech. Sci. Technol. Aerosp. Eng. 1–6. Available online: https://kns.cnki.net/kcms/detail/61.1114.TH.20200707.1003.003.html (accessed on 7 July 2020). (In Chinese).
- Zhang, L.; Tang, K.; Zhao, Y.; Wang, X.; Yu, D.; Lu, X.; Wang, X. Optimization of Leg Structure Parameter of Quadruped Laser Weeding Robot. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2020, 36, 7–15. [Google Scholar] [CrossRef]
- Wang, L.; Wang, C.; Du, W.; Xie, G.Z.; Song, K.K.; Wang, X.J.; Zhao, F. Parameter Optimization of a Four-Legged Robot to Improve Motion Trajectory Accuracy Using Signal-to-Noise Ratio Theory. Robot. Comput.-Integr. Manuf. 2018, 51, 85–96. [Google Scholar] [CrossRef]
- Feng, H.; Miao, Q.; Fan, S.; Wang, H.L.; Wang, W. Modular and Parametric Design for Mechanical Structure of Industrial Robots. Mach. Tool. Hydraul. 2019, 47, 60–63. [Google Scholar]
- Chen, J.X. Mechanism Design and Parameter Calculation of a New Crawling Robot. Mod. Manuf. Technol. Equip. 2019, 271, 76–77. [Google Scholar]
- Gao, W.; Liu, M.; Zhang, J.; Zhang, H. Structure Analysis and Optimization of Manipulator’s Structure of the Robotic Explorer in Nuclear Environment. Mach. Des. Manuf. 2020, 5, 245–252. [Google Scholar]
- Xiao, X.; Fang, Y. Design and Optimization of Hydraulic-Driven Coal Mine Rescue Wheeled Robot. Mach. Des. Manuf. 2020, 3, 265–268. [Google Scholar]
- Dong, H. Kinematics of Rdundant Manipulator and Dead-Reckoning and Path Planning Research of Mobile Platform. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Ye, C.; Mao, Z.; Liu, M. A Novel Multi-Objective Five-Elements Cycle Optimization Algorithm. Algorithm 2019, 12, 244. [Google Scholar] [CrossRef]
- Xiao, Y.; Hua, Z. Misalignment Fault Prediction of Wind Turbines Based on Combined Forecasting Model. Algorithm 2020, 13, 56. [Google Scholar] [CrossRef]
- Alekseeva, N.; Tanev, I.; Shimohara, K. PD Steering Controller Utilizing the Predicted Position on Track for Autonomous Vehicles Driven on Slippery Roads. Algorithm 2020, 13, 48. [Google Scholar] [CrossRef]
- Sai, Q.; Bi, J.; Chai, J. Optimal Model for Carsharing Station Location Based on Multi-Factor Constraints. Algorithm 2020, 13, 43. [Google Scholar] [CrossRef]
- Xie, B.; Jing, Z. Advances in Robotic Kinematic Dexterity and Indices. Mech. Sci. Technol. Aerosp. Eng. 2011, 30, 1386–1393. [Google Scholar]
- Xie, B.; Jing, Z. Directional Manipulability Constrained by the Condition Number. J. Mech. Eng. 2010, 46, 8–15. [Google Scholar] [CrossRef]
- Zhang, P.; Yao, Z.Q.; Du, Z.C. Global Performance Index System for Kinematic Optimization of Robotic Mechanism. ASME J. Mech. Des. 2014, 136, 1–11. [Google Scholar] [CrossRef]
- Dong, H.; Du, Z. Obstacle Avoidance Path Planning of Planar Redundant Manipulators using Workspace Density. Int. J. Adv. Robot. Syst. 2014, 12, 1–10. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of robotic mechanism. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Jose, S.; Vijayalakshmi, C. Design and Analysis of Multi-Objective Optimization Problem Using Evolutionary Algorithms. Procedia Comput. Sci. 2020, 172, 896–899. [Google Scholar] [CrossRef]
- Martín, D.; Alcalá-Fdez, J.; Rosete, A.; Herrera, F. NICGAR: A Niching Genetic Algorithm to Mine a Diverse Set of Interesting Quantitative Association Rules. Inf. Sci. 2016, 355, 208–228. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, J.; Li, L. Application of Simultaneous Mechanism Analysis and Synthesisin Serial Robots. J. Beijing Univ. Technol. 2014, 3, 321–327. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).