1. Introduction
Image segmentation is a fundamental problem in image processing and computer vision. Its goal is to divide the given image into regions that represent different objects in the scene, which can be identified taking into account different features. The research on image segmentation has made several advances in the last decades and various approaches have been developed to satisfy the requirements coming from different applications. In this work, we focus on variational models for image segmentation, which have been widely investigated, proving to be very effective on different images—see, e.g., [
1,
2,
3,
4]. Other recent approaches to image segmentation include learning-based methods, which often exploit deep-learning techniques [
5,
6,
7,
8]. However, in this case, a large amount of data must be available to train learning networks, thus making those approaches impractical in some applications.
Roughly speaking, when a variational approach is used, the segmentation may be obtained by minimizing a cost functional that linearly combines regularization and data fidelity terms:
where
provides a representation of the segmentation and
is a parameter that controls the weight of the fidelity term
G versus the regularization term
F. A widely-used segmentation model is the two-phase partitioning model that was introduced by Chan, Esedoḡlu, and Nikolova [
3], which we refer to as the CEN model:
Here,
denotes the image to be segmented, which is assumed to take its values in
. The CEN model allows us to obtain one of the two domains defining the segmentation,
and
, by setting
where
u is the solution of problem (
2). Note that (
2) is the result of a suitable relaxation of the Chan–Vese model [
2] leading to a convex formulation of that problem for any given
.
In this work, we start from a discrete version of the CEN model. Let
be a discretization of
consisting of an
grid of pixels and let
where
and
are the forward finite-difference operators in the
x- and
y-directions, with unit spacing, and the values
with indices outside
are defined by replication. We consider the following discrete version of (
2) with anisotropic discrete total variation (TV):
After the minimization problem (
3) is solved, the segmentation is obtained by taking
for some
. Problem (
3) is usually solved by alternating the minimization with respect to
u and the minimization with respect to
and
. In the sequel, we denote
the objective function in (
3), and
and
its discrete regularization and fidelity terms, respectively.
The selection of a parameter
able to balance
and
and to produce a meaningful solution is a critical issue. Too large values of
may produce oversegmentation, while too small values of
may produce undersegmentation [
9]. Furthermore, a constant value of
may not be suitable for the whole image, i.e., different regions of the image may need different values. In recent years, spatially adaptive techniques have been proposed, focusing on local information, such as gradient, curvature, texture, and noise estimation cues—see, e.g., [
10]. Space-variant regularization has been also widely investigated in the context of image restoration, using TV and its generalizations—see, e.g., [
11,
12,
13,
14,
15].
In this work, we propose some techniques for setting the parameter
in an adaptive way based on spatial information, in order to prevent excessive regularization of smooth regions while preserving spatial features in nonsmooth areas. Our techniques are based on the so-called cartoon-texture decomposition of the given image, on the mean and median filters, and on a thresholding technique. The resulting locally adaptive segmentation model can be solved either by smoothing the discrete TV term—see, e.g., [
16,
17]—and applying optimization solvers for differentiable problems, such as spectral gradient methods [
18,
19,
20,
21], or by using directly optimization solvers for nondifferentiable problems, such as Bregman, proximal and ADMM methods [
22,
23,
24,
25,
26,
27,
28]. In this work, we use an alternating minimization procedure exploiting the split Bregman (SB) method proposed in [
24]. The results of numerical experiments on images with different characteristics show the effectiveness of our approach and the advantages coming from using local regularization.
The rest of this paper is organized, as follows. In
Section 2 we propose our spatially adaptive techniques. In
Section 3, we describe the solution of the segmentation model using those techniques by the aforementioned SB-based alternating minimization method. In
Section 4 we discuss the results obtained with our approaches on several test images, also performing a comparison with the CEN model and a segmentation model developed for images with texture. The results show the effectiveness of our approach and the advantages coming from the use of local regularization. Some conclusions are provided in
Section 5.
2. Defining Local Regularization by Exploiting Spatial Information
The regularization parameter
plays an important role in the segmentation process, because it controls the tradeoff between data fidelity and regularization. In general, the smaller the parameter in (
3) the smoother the image content, i.e., image details are flattened or blurred. Conversely, the larger the parameter the more the enhancement of image details and, hence, noise may be retained or amplified. Therefore,
should be selected according to local spatial information. A small value of
should be used in the smooth regions of the image to suppress noise, while a large value of
should be considered to preserve spatial features in the nonsmooth regions. In other words, a matrix
should be associated with the image, where
weighs pixel
, as follows:
Furthermore, in order to avoid oversegmentation or undersegmentation, it is convenient to fix a minimum and a maximum value for the entries of , so as to drive the level of regularization in a reasonable range, depending on the image to be segmented.
We define
as a function of the image
to be segmented:
where
. We propose three choices of
f, detailed in the next subsections.
We note that problem (
5) still has a unique solution for any fixed
, as a consequence of the next proposition.
Proposition 1. For any fixed , problem (5) is a convex problem. Proof. Because the CEN model is convex for any fixed , the thesis immediately follows from the fact that the parameters are constant with respect to u. □
2.1. Regularization Based on the Cartoon-Texture Decomposition
We define
by using the Cartoon-Texture Decomposition (CTD) of the image discussed in [
29]. CTD splits any image
u into the sum of two images,
w and
v, such that
w represents the cartoon or geometric (piecewise-smooth) component of
u, while
v represents the oscillatory or textured component, i.e.,
v contains essentially textures, oscillating patterns, fine details, and noise. The algorithm for computing CTD acts as described next. For each image pixel, we decide whether it belongs to the cartoon or the textural part by computing a local indicator associated with an image window around the pixel. The main feature of a textured region is its high TV, which decreases very fast under low-pass filtering. This leads to the following definition of local total variation (LTV) at a pixel
:
where
is a low-pass filter,
is a scale parameter,
, and ∗ denotes the convolution product. The relative reduction rate of LTV,
gives the local oscillatory behavior of the image. A value of
close to 0 means that there is little relative reduction of LTV by the low-pass filter, thus the pixel
belongs to the cartoon. Conversely,
close to 1 indicates that the relative reduction is large and, hence, the pixel belongs to a textured region.
We use (
8) for defining the weights
. The basic idea is that a large regularization parameter is needed if the pixel
belongs to the cartoon, while the parameter must be reduced in texture regions. Therefore, we set the function
f in (
6) as
and
is defined by using the given image
. Following [
30], we set
equal to the Gaussian filter.
2.2. Regularization Based on the Mean and Median Filters
We define a technique that is based on spatial filters that are commonly used to enhance low-frequency details or to preserve edges [
31,
32]. More precisely, we combine the mean and median filters; the former aims at identifying smooth regions, where the regularization parameter can take small values, the latter aims at identifying edges, where the parameter must remain large. Mean filtering is a simple and easy-to-implement method for smoothing images, i.e., for reducing the intensity variation between a pixel and its neighbors. It also removes high-frequencies components due to the noise and the edges in the image, so the mean filter is a low-pass filter. The median filter preserves edges and useful details in the image.
Based on these considerations, we define a weight function, as follows:
where
is the window size of the mean filter
,
is the window size of the median filter
, and
t is a threshold value acting as a cutoff between the two filters. Note that
and the pixels in homogeneous regions have
close to 1. The function
f in (
6) is set as
where MM stands for “Mean and Median”.
2.3. Regularization Based on Thresholding
This approach implicitly exploits the definition of
in (
4) in order to set
. The idea is to use large values of
when
is close to 1 and small values when
is close to 0. Therefore, the parameters
are not defined in terms of the given image
only. If the function
u identifying the segmentation were known a priori, we could define
as follows:
where
and
.
Because the function
u must be computed by minimizing (
3) and this is done by using an iterative procedure, we decided to update
at each iteration, while using the current value of
. On the other hand, in this case evaluating
f is computationally cheaper than in the previous approaches, which apply two-dimensional convolution operators; thus, the cost of the iterative update of
is practically negligible.
3. Solution by Split Bregman Iterations
As mentioned in
Section 1, we use an alternating minimization method to solve problem (
5). Given
, by imposing the first-order optimality conditions with respect to
and
, we get
For the solution of (
5) with respect to
u, we use the split Bregman (SB) method [
24]. Let
where
Following [
33], we reformulate the minimization problem, as follows:
Given
and
, the SB method applied to (
15) reads:
where
.
Closed-form solutions of the minimization problems with respect to
and
can be computed using the soft-thresholding operator:
where, for any
and any scalar
,
Finally, an approximate solution to the minimization problem with respect to
u can be obtained by applying Gauss–Seidel (GS) iterations to the following system, as explained in [
33]:
where
is the classical finite-difference discretization of the Laplacian. If the solution to (
17) lies outside
, then it is projected onto that set. We denote
the corresponding projection operator.
The overall solution method is outlined in Algorithm 1. Note that, when the approach in
Section 2.3 is used, the values
must be updated at each iteration
k, using (
12) with
.
| Algorithm 1 Split Bregman (SB)-based method for spatially adaptive segmentation |
| Input: (with f defined in (9) or (11) or (12)) |
| Output: |
| Set |
| Compute |
| for do |
![Algorithms 13 00226 i001]() | Compute and by (13) |
| Compute by applying GS iterations to system (17) |
|
|
|
| Update and according to (16) |
| end |
| Set |
4. Results and Comparisons
in (
7) is defined as a rotationally symmetric Gaussian filter with size 3 and standard deviation
. The mean and median filters use windows of size 3 and 7, respectively, and the parameter
t in (
10) is set as
. The parameter
is used to identify the domain
according to (
4).
In the original and modified codes, the SB iterations are stopped, as follows:
where
is a given tolerance and
denote the maximum number of outer iterations. The stopping criterion for the GS iterations is
where
and
and
are the tolerance and the maximum number of iterations for the GS method, respectively. In our experiments we set
,
,
and
.
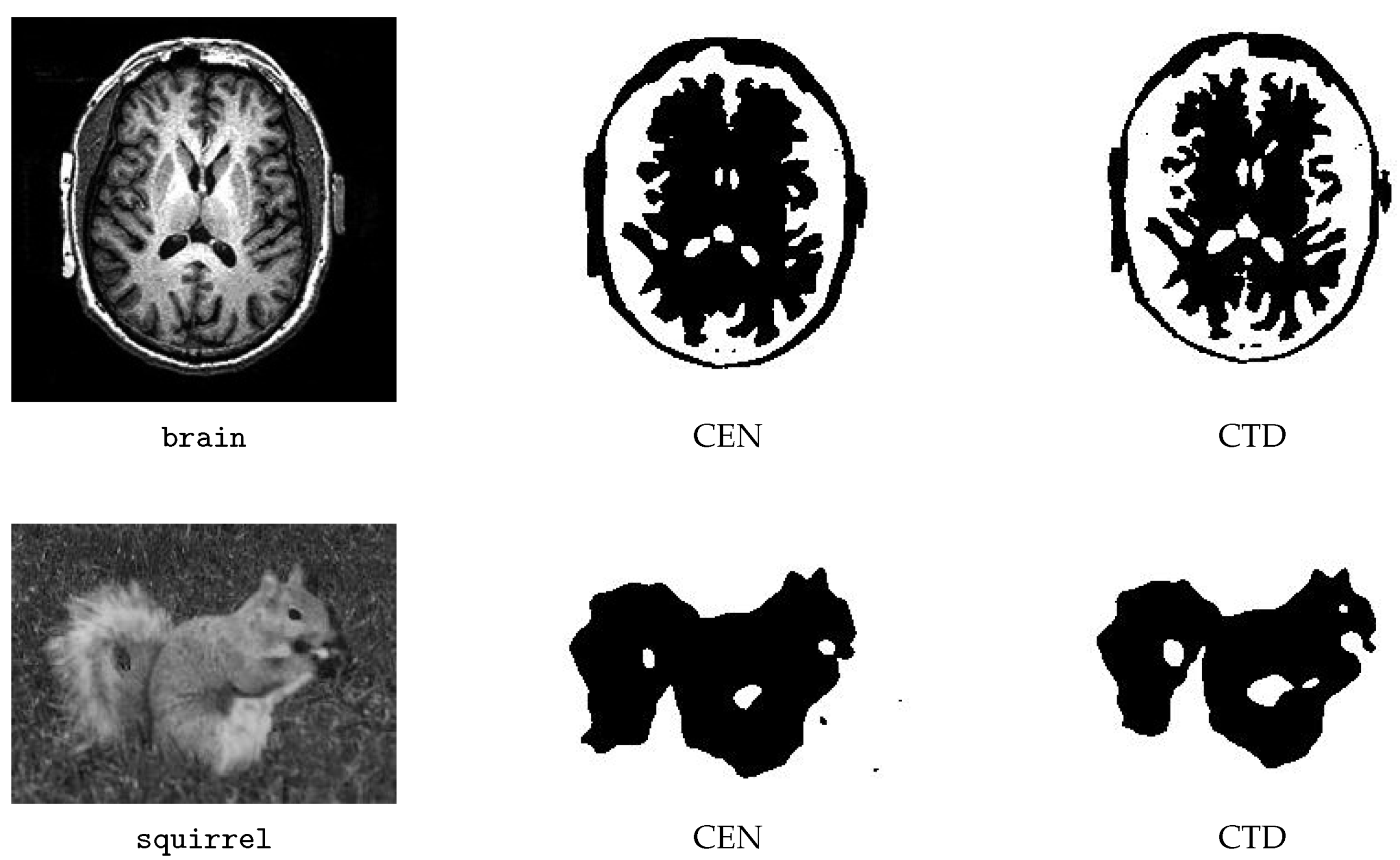
The adaptive models are compared with the original CEN model on different images widely used in image processing tests, as listed in
Table 1 and shown in
Figure 1,
Figure 2,
Figure 3 and
Figure 4. In particular, the images
bacteria,
bacteria2,
brain,
cameraman,
squirrel, and
tiger are included in Bresson’s code distribution,
flowerbed has been downloaded from the Berkeley segmentation dataset [
34] available from
https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/resources.html (image
#86016), and
ninetyeight is available from
https://tineye.com/query/2817cf0d186fbfe263a188952829a3b5e699d839. We note that
tiger is included in Bresson’s code as a test problem for a segmentation model specifically developed for images with texture [
35], which is also implemented in the code. This model uses the well-known Kullback–Leibler divergence function regularized with a TV term. The model is solved with the SB method. We perform the segmentation of
tiger with the CEN model, the textural segmentation model, and our approaches, in order to investigate whether our locally adaptive model can be also suitable for textural images. The
cameraman image is perturbed with additive Gaussian noise, with zero mean and two values of standard deviation,
, with the aim of evaluating the behavior of our adaptive approaches on noisy images. The noisy images are called
cameraman15 and
cameraman25.
For the images provided with Bresson’s code, the values of
and
associated with the original CEN model are set as in that code. For the remaining images, the values of
and
are set by trial and error, following the empirical rule reported in Bresson’s code. The values of
and
used in the spatially adaptive approaches are chosen, so that the corresponding
in the original CEN model is in
, with few exceptions. The associated values of
are set as in the non-adaptive case. The values of
,
,
and
used for each image are specified in
Table 2,
Table 3 and
Table 4. The values of
in the adaptive models are initialized, as specified in (
9), (
11), and (
12). As described in
Section 2.3, in the strategy based on thresholding those values change at each iteration
k of Algorithm 1. It is worth noting that our adaptive approaches also simplify the choice of the regularization parameter, which may be a time-consuming task.
The initial approximation
is set equal to the given image
, which takes its values in
, as specified in
Section 1. This is used to compute the starting values of
and
, and
for all
. In the original non-adaptive code, the value of
is scaled using the difference between the maximum and the minimum value of
; the same scaling is applied to
and
in the implementations of the adaptive approaches.
We run the tests on an Intel Core i7 processor with clock frequency of 2.6 GHz, 8 GB of RAM, and a 64-bit Linux system.
For each of the six images
bacteria,
bacteria2,
brain,
flowerbed,
ninetyeight, and
squirrel, we show the results that were obtained with the spatially adaptive strategy yielding the best segmentation for that image. The corresponding (unscaled) values of
,
,
, the value of
, as well as the number of outer iterations and the mean number of GS iterations per outer iteration are reported in
Table 2. Note that, for
squirrel, we use two values of
, one equal to the value of
in the CEN model and the other greater than that, obtained by trial and error. Both values of
produce the same segmentation, but the larger value of
reduces the number of outer and GS iterations. The segmentations corresponding to the data in
Table 2 are shown in
Figure 1,
Figure 2 and
Figure 3. For
squirrel, we display the CTD segmentation computed by using the larger value of
.
We see that, on selected problems, CTD reduces the number of outer and GS iterations with respect to the CEN model; on the other hand, the setup of the regularization parameters is computationally more expensive. In terms of iterations, there is no clear winner between CEN and MM and between CEN and THR. The models based on the spatially adaptive techniques are slightly more expensive than the CEN model in this case too. A significant result is that the segmentations obtained with the adaptive techniques appear better than those obtained with the non-adaptive model, i.e., the spatially adaptive models can better outline boundaries between objects and foreground. This is clearly visible by looking at the segmentations of brain, bacteria2 (see the upper right corner), ninetyeight, bacteria (see the shape of the bacteria). It is also worth noting that the adaptive model based on THR removes textural details that do not belong to the flowerbed in the homonymous image.
The latter observation is confirmed by the experiments performed on
tiger.
Table 3 reports the corresponding model and algorithmic details, while the segmentations are shown in
Figure 4 along with (visual) information on quantities used to define
(see (
8) and (
10)). We see that the CTD and MM strategies produce satisfactory results, although they have been obtained by generalizing a non-textural model.
Finally, we show the results obtained on
cameraman and its noisy versions by using CEN, CTD, MM, and THR. The methods perform comparable numbers of inner and GS iterations (see
Table 4), but the spatially adaptive model THR yields some improvement over the CEN model in the segmentation of the images that are affected by Gaussian noise (
Figure 5).