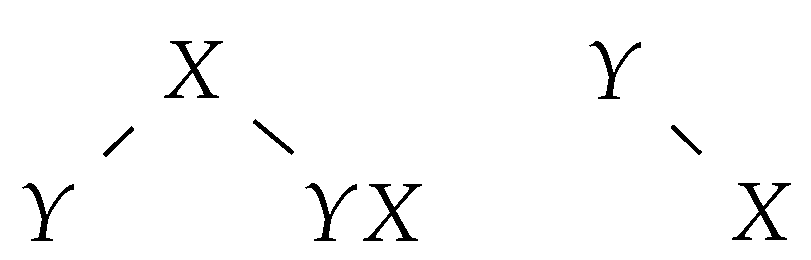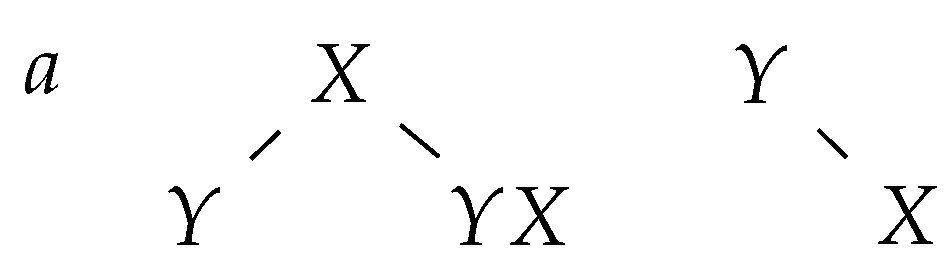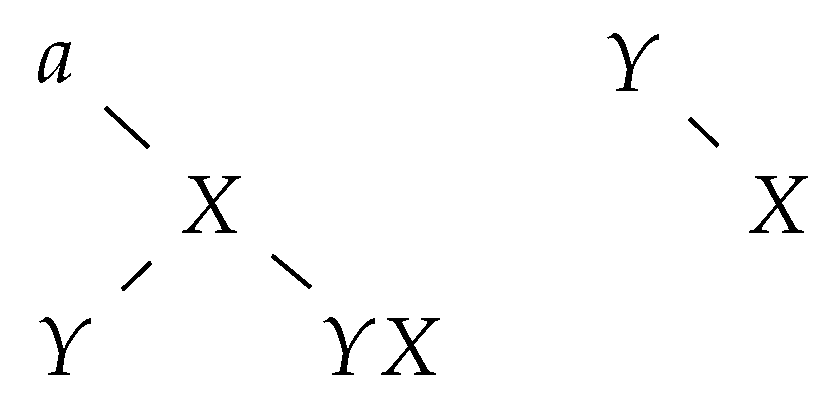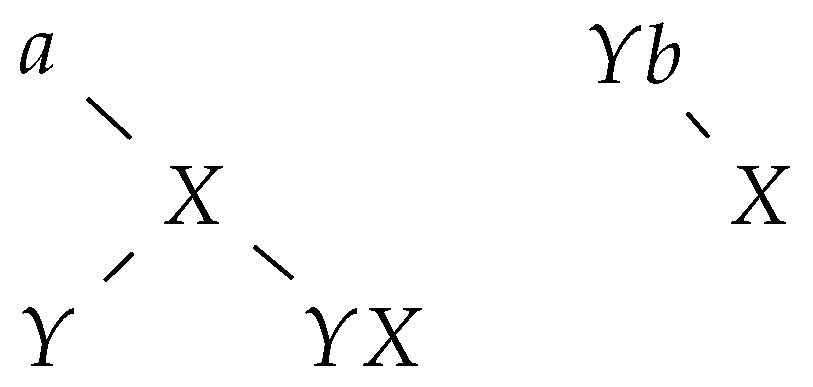Abstract
Insertion-deletion systems have been introduced as a formalism to model operations that find their counterparts in ideas of bio-computing, more specifically, when using DNA or RNA strings and biological mechanisms that work on these strings. So-called matrix control has been introduced to insertion-deletion systems in order to enable writing short program fragments. We discuss substitutions as a further type of operation, added to matrix insertion-deletion systems. For such systems, we additionally discuss the effect of appearance checking. This way, we obtain new characterizations of the family of context-sensitive and the family of recursively enumerable languages. Not much context is needed for systems with appearance checking to reach computational completeness. This also suggests that bio-computers may run rather traditionally written programs, as our simulations also show how Turing machines, like any other computational device, can be simulated by certain matrix insertion-deletion-substitution systems.
1. Introduction
Insertion-deletion systems, or ins-del systems for short, are well-established as computational devices and as a research topic within Formal Languages throughout the past nearly 30 years, starting off with the PhD thesis of Lila Kari [1]. Corresponding to the mismatched annealing of DNA sequences, both the insertion and deletion operations have a strong biological background, which led to their study in the molecular computing framework (cf. [2]). Insertion rules add a substring to a string, given a specified left and right context, while deletion rules remove a substring from a string, again taking a specified left and right context into consideration. The replacement of single letters (possibly within some context) by other letters by an operation, called substitution, is discussed in [3,4], again from a bio-computing background.Interestingly, all of the theoretical studies on grammatical mechanisms involving insertions and deletions (except [5]) omitted, including the substitution operation in their studies. In [6,7,8], we started out a project to formally and systematically study insertion-deletion systems with substitutions as an additional operation, leading to ins-del-sub systems (for short).
It can be argued that the potentially most error-prone part of a bio-computing implementation of ins-del-sub systems are context checks concerning the site where the operation (be it an insertion, a deletion or a substitution operation) may be applied. Therefore, it is interesting to study how much context dependency is necessary for achieving computational completeness, given the ability to add a substring of length n and to delete a substring of length p.
Conversely, assuming that one can prove that ins-del-sub systems with limited context checks exist that can simulate arbitrary Turing machines (or phrase structure grammars, or any arbitrary computational mechanism that can be used to define terms like computability), then this means that there is some hope that some day one could build computers that are no longer silicon-based, but that compute with RNA, DNA, or protein structures. It should be noted that all of our computational completeness proofs are constructive, which means that algorithms exist that will finally turn any program written in some high-level programming language of your choice into an ins-del-sub system that executes this program based on insertion, deletion, or substitution operations.
As the following definitions will show, the ’derivation relation’, although formally defined as a sequential series of insertion, deletion, or substitution operations, can be easily seen to allow an inherent parallelism, as all operations that are ‘far enough’ from each other can be executed in parallel. Because the potentially high degree of parallelism in bio-computing is argued as one of the main attractive features of this form of computation, this gives another reason as to why one should strive for operations that are as context-independent as possible, as context dependencies could be seen as semaphore-like synchronization points. Namely, on the level of bio-computing, checking certain strings means building up some structures (mostly proteins) that read and check ‘matching structures’ by forming chemical links between molecules. This means that ‘checking from one side’ prevents and, hence, rules out ’checking from the other side’ in parallel.
Ins-del systems can be extended with some form of control to further reduce their context dependency. Matrix insertion-deletion systems, or matrix ins-del systems for short, were introduced in [9,10]. These systems group insertion and deletion rules in sequences, called matrices; either the whole sequence of operations is applied consecutively, or no rule is applied at all, thus resembling traditional matrix grammars, originally introduced with a linguistic motivation [11]. From the perspective of bio-computing, the matrices correspond to small program fragments without jumps that are easier to implement than longer and more involved ones. Allowing such program fragments should also make a better fit for finally implementing compilers that produce executable ’bio-code’ from traditional high-level programming languages, as the sequential execution of commands is one of the cornerstones of basically any of the programming languages of today. There is certainly a certain trade-off between the potentially high degree of parallelism and these new sequential program fragments. This is one of the motivations to limit (on top of context lengths) the length of these program fragments (i.e., technical speaking the length of the matrices).
Additionally, we discuss appearance checking in the context of matrix ins-del-sub systems. In the case of matrix grammars, it is known that allowing certain rules of a matrix to be skipped if not applicable increases the computational power [12]. In this paper, we investigate the effect of appearance checking on matrix ins-del-sub systems. We show that the context dependency of ins-del systems can be greatly reduced if matrices, appearance checking, and substitution rules are allowed. For instance, it is shown that a matrix ins-del-sub system that only allows context-free single letter insertions and two-letter deletions in addition to context-free substitution is sufficient for generating any recursively enumerable language. In addition, we show that a ‘normal form’ for matrix ins-del-sub systems exists, in which only matrices of size at most 2 occur. On the downside, it can be argued that appearance checks is a particularly expensive feature when it comes to implementing it in bio-computing devices, as many sites of potential rule applications have to be checked before being able to execute the next command in the matrix. However, one clearly sees a trade-off in our results between the necessity to have larger contexts and the necessity to have appearance checks. Because it is not clear which of these mechanisms is really harder to implement when it comes to build real bio-computers, it appears to be reasonable to study the general possibilities of these mechanisms, hence paving the way to future generations of new computing devices.
2. Definitions
We assume the reader to be familiar with the standard notations in formal language theory. By we denote the empty string. Let w be an arbitrary string. We denote by the reversal or mirror image of w. By and , we denote the reversal of a language L and a language family , respectively. We denote, by RE, CS, CF, and REG, the families of recursively enumerable, context-sensitive, context-free, and regular languages, respectively. We are interested in computational completeness results, i.e., in describing RE with matrix ins-del-sub systems with little resources as formally explained next.
2.1. Matrix Grammars
A matrix grammar is a tuple where N, T and S are the finite set of nonterminals, the finite set of terminals and the start symbol, respectively. is a finite set of sequences of the form , with rewriting rules with and . Such a sequence m is called a matrix [12]. The relation ⇒ induced by G is defined, as follows. For words , holds if a matrix and with and exist, such that holds for all . The language that is generated by G is . We denote, by , the language family that is generated by matrix grammars with context-free rewriting rules [12]. A matrix grammar with appearance checking is a tuple , where N, T, , and S are defined as in usual matrix grammars. F is a set of rewriting rules occurring in matrices of . All of the rules in F may be skipped in a transition of , if not applicable. Thus, the absence of symbols can be checked.
2.2. Insertion-Deletion Systems
An insertion-deletion system (ins-del system for short) is a five-tuple , consisting of two alphabets V and T with , a finite language A over V, a set of insertion rules I and a set of deletion rules D. Both sets of rules are formally defined as sets of triples of the form with and . We call elements occurring in T terminal symbols, while referring to elements of as nonterminals. Elements of A are called axioms.
Let and , with , , be strings. The application of an insertion rule (also written ) to corresponds to inserting the string between u and v, which results in the string . The application of a deletion rule (also written ) to results in the removal of a substring a from the context , which results in the string . The relation is defined, as follows: Let . Afterwards, we write iff y is the result of applying an insertion or deletion rule to x. We write / if y is obtained via an insertion/ a deletion rule. We denote, by and , the transitive and the reflexive and transitive closure, respectively. The language that is generated by is defined by . Consider or . We refer to u as the left context and v as the right context of /. A sentential form of is a string over V. The size of describes its complexity and it is defined by a vector , where , , , , and .
By , we denote the family of all insertion-deletion systems of size [13,14]. Depending on the context, we also denote the family of languages that can be generated by insertion-deletion systems of size by .
We first study a concrete example now to clarify the definitions and also to return to some of the general discussions of the introduction.
Example 1.
Consider the following ins-del system where , , , and . Clearly this system is of size and the generated language is .
As mentioned in the introduction, ins-del systems offer a high degree of parallelism. The system ID, for instance, exhibits this trait when considering the rules and . It is easy to see that the order in which these rules are applied is insignificant and, thus, these rules do not affect each other. Hence, and are "far enough” from each other to be applied in parallel without affecting the computation. However, note that the deletion rule cannot be applied in parallel with any insertion rule as the order does matter in this case. More precisely, the deletion cannot be applied before applying an insertion, as it removes necessary context information.
Finally, observe that the amount of parallelism that is observable in generating the language can be further significantly increased by adding the insertion rules and .
2.3. Combining Ideas: Matrix Insertion-Deletion Systems
The idea of regulating ins-del systems with matrix control goes back to [10,15]. A matrix ins-del system [10] is a construct where V, T and A are defined as in usual ins-del systems. , , is a finite set of sequences, called matrices, of the form , where . , with , , is either an insertion or a deletion rule. A sentential form of is a string . Consider a matrix . A transition is performed if there exist strings such that with and . Let . The language that is generated by is defined as
We say that has matrices of size k if . If is an ins-del system of size with matrices of size k, we also say that is of size . We denote by either the family of languages that are generated by ins-del systems of size or the family of ins-del systems of size , depending on the context. Denote, by , the family of matrix ins-del-sub systems with matrices of arbitrary size and insertion rules and deletion rules, of size and , respectively. The following matrix ins-del systems are known to describe RE:
- and [16]
- , and [17]
- , and [10].
The incompleteness results for matrix ins-del sub systems include , for instance. More precisely, the following theorem holds.
Theorem 1.
, testified by .
This result follows from [18], as stated as in [10]. For reasons of completeness, we give a formal proof of this result in the following.
Proof.
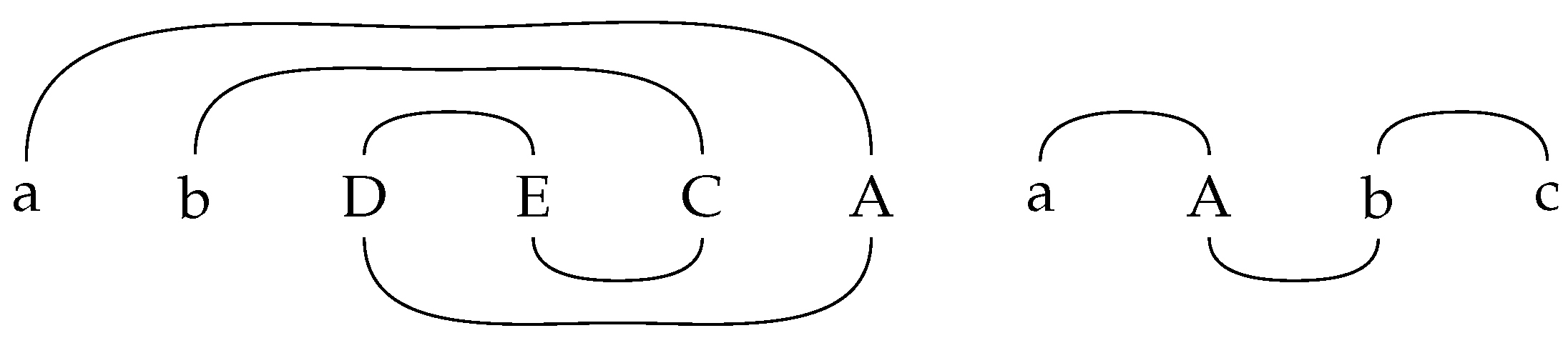
Before we begin with our proof, we introduce ’markings’ [14,19] in the following paragraph. We explain the details of the marking approach with the following example. Consider the derivation
of an ins-del system of size . Then we introduce ‘markings’, as follows: Two symbols that have been introduced together are joined with an overline, while two symbols that are deleted together are joined with an underline. The overlines and underlines mark the insertion pairs and the deletion pairs, respectively. The marking to a word , which is derived in the manner presented above, is shown in Figure 1.

Figure 1.
Marking corresponding to a derivation of [14,19].
Interpreting all of the symbols as labelled nodes and all lines as edges, it is easy to see that any word w that is generated by an arbitrary ins-del system of size corresponds to a graph, which consists of disjoint paths and/or cycles. If a symbol A is deleted by a deletion rule , then we replace the corresponding node in the graph with . The node is interpreted as . Additionally, the application of an insertion rule corresponds to adding a path, which consists of a single edge with nodes and A, to the graph at the corresponding position. We assume that all letters of the axiom have been introduced by such insertion rules. There is clearly no interaction between two symbols of two different paths/cycles or between a symbol of a cycle and a symbol of a path. We remark that all of the symbols/nodes, which have a degree of two, are deleted and hence only symbols with a degree of one contribute to the final word w. Note that all of the symbols of degree one only have an ‘overline’ edge, while nodes of degree two have both types of edges. Therefore, it is clear that at most two symbols of a path can contribute to w. We refer to [14,19] for more details on the ’marking’ approach. Clearly, the marking approach can be applied to matrix-ins-del systems of size , as well.
We now show that the language cannot be generated by any matrix ins-del systems of size by contradiction. Assume that there is a matrix insertion-deletion system , which generates the language . Subsequently, clearly the word , where and n is the length of the longest axiom, can also be generated. Consider the graph that corresponds to . It is clear that this graph consist of more than paths. Then there is at least one path which does not involve any symbols of the axiom and contributes at least one letter a (and no b) to . Because this path does not involve any letters of the axiom, all symbols of this path have been introduced with context-free insertion rules. We denote this path as P. Consider the derivation of . Because there is no interaction between two symbols of different paths and /or cycles, it is clear that there is a derivation that applies all of the matrices used in the derivation of in the same order, but in which all insertions and deletions corresponding to the path P occur right of the final b. This, in turn, means that also generates a word in . □
2.4. Adding Substitutions
With substitution rules, we now introduce the central notion of this paper. We define substitution rules to be of the form ; ; . Let ; be a string over V. Afterwards, applying the substitution rule allows us to substitute a single letter a with another letter b in the context of u and v, which results in the string .
Formally, we define an insertion-deletion-substitution system, or ins-del-sub system for short, to be specified by a six-tuple , where , and D are defined as in the case of usual ins-del systems and S is a set of substitution rules.
Let and be the strings over V. The substitution rules define a relation , as follows: if there is a substitution rule .
In the context of ins-del-sub systems, we write to denote any of the relations , or . We define and as usual, denoting the reflexive-transitive and transitive closure of , respectively.
The language that is generated by an ins-del-sub system is defined as
As with usual ins-del system, we measure the complexity of an ins-del-sub system via its size, which is, an eight-tuple , where , and are defined as in the case of usual ins-del systems and r and limit the maximal length of the left and right context of a substitution rule, respectively, i.e., , . denotes the family of all ins-del-sub systems of size Note that as only one letter is replaced by any substitution rule, there is no subscript at SUB. Depending on the context, we also refer to the family of languages generated by ins-del-sub systems of size by
As with ins-del systems, ins-del-sub systems can be regulated with matrix control introducing matrix ins-del-sub systems. A matrix ins-del-sub system is a construct , where V, T and A are defined as in usual ins-del systems. , , is a finite set of sequences, called matrices, of the form , where . , with , , is either an insertion, a deletion or a substitution rule.
We define the relation between the strings w and over V , as well as the generated language of , analogously to the case without substitution rules. We say that matrix ins-del-sub systems, which have insertion rules, deletion rules, substitution rules, and matrices of size ,, , and k, respectively, is of size . By , denote the family of matrix ins-del-sub systems of size , as well as the family of languages generated by such systems, depending on the context. Consider a language family . Concerning the reversal operator (that reads words from right to left), the following lemma holds.
Lemma 1.
Let be a family of languages that is closed under reversal. Then:
- 1.
- iff .
- 2.
- iff .
- 3.
- iff .
Proof.
These claims follow analogously to [17]. □
By definition, it is also clear that the following lemma holds.
Lemma 2.
.
2.5. Appearance Checking: An Additional Feature
It is known that matrix grammars with context-free production are not computationally complete, but they can reach computational completeness if used with appearance checking. Transferring this idea to matrix ins-del-sub systems, we introduce matrix ins-del-sub systems with appearance checking and show that, similar to the matrix grammar case, formerly computationally incomplete matrix ins-del-sub systems can reach computational completeness if they are used in conjunction with appearance checking. We begin by defining matrix ins-del-sub systems and appearance checking. A matrix ins-del-sub systems and appearance checking is a tuple , where V, T, A, and are defined as in usual matrix ins-del-sub systems. F is a subset of all rules occurring in .
Let and z be an arbitrary rule occurring in . We define the relation , as follows: if one of the following conditions hold: (a) the rule z is applicable to , such that or (b) the rule z is not applicable to , and . Basically, this means that, if some rule in F is not applicable, we can skip that rule. Let and . Then iff . The language that is generated by is defined as
We define the size of analogously to matrix ins-del-sub systems without appearance checking. We denote the language family that is generated by matrix ins-del-sub systems with appearance checking of size by the term .
Again, we like to clarify these definitions by presenting a concrete example of a matrix ins-del-sub system that makes use of appearance checking.
Example 2.
Consider the matrix ins-del-sub systems with appearance checking of size with , , , and . The language that is generated by is . This can be shown, as follows.
Let , and , such that .
Assume that during the application of m the nonterminal X is inserted to the right of b. Subsequently, clearly the deletion rule is applicable after the insertion and we delete X along with b. However, now the substitution rule cannot be applied anymore and, as , this means that the matrix as a whole cannot be applied.
Assume that, during the application of m, the nonterminal X is inserted somewhere left of b. Clearly, is not applicable and, as , we skip this rule and proceed with the application of . Applying m in this way effectively inserts the letter a somewhere left of b and, therefore, .
Using the argument above inductively yields our claim. We remark that, for any word w derived from the axiom b, holds, as any X introduced during the application of m is resolved at the end of m.
The example above clarifies that appearance checking can result in an increase in computational power, as is known (Theorem 1).
3. Computational (In-)Completeness Results
In this section, we present the main results of our research.
3.1. A Normal Form Theorem
We begin by introducing a (binary) normal form for matrix ins-del-sub systems that are similar to the two-normal form (also known as binary normal form) for matrix grammars ([12] Def. 1.2.1). Recall our discussion in the introductory section concerning possible applications of matrix ins-del-sub systems: there, we argued that short matrices offer advantages, as they help allow for parallel execution in this type of computational devices. However, when looking at the proof of the next theorem, one sees that it enforces some sequentialization by introducing a shared resource in the form of specific nonterminals. Therefore, in essence, the question of parallelizability within computational devices, like (matrix) ins-del-sub systems, remains an interesting topic of future research.
A matrix ins-del-sub systems is said to be in normal form if all the matrices are either of the form or , where r is some insertion, deletion, or substitution rule and . Clearly, all matrix ins-del-sub systems in normal form are included in . We show that, for every matrix ins-del-sub system, there is a matrix ins-del-sub system in normal form that generates the same language.
Theorem 2.
For every , , there is a system , such that .
Proof.
Let and all matrices of be labelled in a one-to-one manner, i.e., a bijection from to a set of labels exists. Subsequently, we define , where and . Without a loss of generality we assume . For every matrix of , where , with , is some insertion, deletion, or substitution rule and i is the label of m, we add the following matrices
to . For every label of some matrix of and every matrix of , we add a matrix to . By definition, the second component of every matrix of is either a context-free deletion rule of the form or a context-free substitution rule of the form , where i and are the labels of some matrices of and . Furthermore, the first rule of any matrix of does not involve any nonterminals in .
Consider a sentential form with . It can be shown that all the sentential forms of are either of this form or of the form . The basic idea is that the nonterminal serves as an indicator where the matrix is to be applied next. For instance, the occurrence of in signifies that the next rule to be applied is either if the length of the matrix of labelled by i is greater than j or / , otherwise. We note that, in every derivation of , a matrix of the form is applied at most once. Furthermore, we remark that, if a sentential form occurs during a derivation of , then the derivation cannot proceed as the second rule of any matrix cannot be applied. We now prove the correctness of the construction, i.e., , by showing both inclusion directions separately.
‘⊇’: Consider the following derivation , where r is some insertion, deletion, or substitution rule and . because r does not involve any nonterminals in , clearly holds. We now extend this result. Consider a matrix labelled by i. Subsequently, clearly
or
implies .
‘⊆’: Conversely, it can be shown that implies
and
We remark that, in the simulation of the application a matrix of , we can assume that the leftmost symbol of any sentential form of a derivation of is of a nonterminal (unless a matrix of the form is applied). □
Similarly, for every matrix ins-del-sub system , one can construct in normal form, such that .
Theorem 3.
Let . Afterwards, it is possible to construct a system in normal form, such that .
Proof.
Let and all matrices of be labelled in a one-to-one manner, i.e., a bijection to a set of labels exists. We define the set of symbols as
where k denotes the maximal length of a matrix in . We now describe how to construct an equivalent matrix ins-del-sub system of the same size, such that is in normal form.
For every , every label of a matrix of and every matrix of , where , with , is some insertion or substitution rule and i is the label of m, we add the following matrices
to . Intuitively, any letters of any sentential form of may be substituted or used as a context of some rule. Hence, to simulate , any letter of the form may have to be substituted or used as a context. Therefore, if one of the matrices added to is of the form , we add the matrix to , as well. Additionally, we add to if . Furthermore, if one of the matrices added to is of the form with , then we add the matrix . Additionally, if a matrix of the form occurs in , then is also added to .
The cases
are treated analogously. The set of axioms is defined as
Additionally, if , for every matrix of , which has the form
with , we add to , where i is the label of m. This simulates the case that is the axiom of a derivation of and the matrix m is applied.
The basic overall idea is the same as in Theorem 2. Here, nonterminals control the derivations. Hence, we can hence forego a formal inductive proof. □
3.2. One-Sided Context Dependence
Our previous computational completeness results either required two-sided contexts for insertion or two-sided contexts for deletions. As argued in the introduction, there are good motivations to try to reduce the context dependence. Hence, we are now looking at one-sided contexts for deletions and insertions. We are going to prove two main results in this subsection: first, we show that uni-directional (for instance, left) single-symbol context in insertions and deletions of single symbols suffice in achievinf computational completeness, which this is in contrast with the second result that tells that we cannot completely forego using context information: we do need one-sided context dependency for both deletions and for insertions.
3.2.1. Computational Completeness
As a consequence of the previously introduced normal form for matrix ins-del-sub systems, we obtain the following result:
Corollary 1.
The following statements hold.
- 1.
- .
- 2.
- .
- 3.
- .
- 4.
- .
- 5.
- .
- 6.
- .
This follows easily with Theorem 2, as computational completeness has been shown for and for , see [16]. Furthermore, computational completeness for , , , and has been shown in [10]. Clearly, context-free substitution rules improve the existing completeness results by reducing the complexity of matrices.
3.2.2. Computational Incompleteness
Though ins-del systems with matrix control and substitution rules are powerful devices, they are not always sufficient for achieving computational completeness.
Lemma 3.
Let be a a matrix ins-del-sub systems of size . Subsequently, .
Proof.
Let be in normal form and constructed according to the construction in Theorem 2. Subsequently, we construct the following matrix grammar with . For every , we add a matrix to .
For every matrix of the form X of , we add a matrix of the form Y to .
| form X | form Y |
For every matrix of the form of and every , we add matrices of the form to .
| form | form |
| , | |
| , |
Furthermore, we add matrices of the form to if .
By induction, it can be shown that if and only if
Whenever a matrix is applicable to , some matrix of the form is applicable to and vice versa.
We remark that, if a sentential form occurs during either a derivation of or G, the derivation cannot proceed, as no matrix is applicable any more. (see Theorem 2). Hence, the case that the axiom of a derivation of is is covered by an application of .
Therefore, it is easy to see that holds.
Moreover, . □
Although systems of size do not reach computational completeness, they do characterize matrix grammars.
Lemma 4.
Let G be a matrix grammar, such that . Subsequently, there exists a matrix ins-del system with substitution rules of size , such that .
Proof.
Let be a matrix grammar with context-free production rules. Afterwards, we construct as follows: We define and .
Consider a context-free production rule of the form . Clearly, this rule is equivalent to a deletion rule . Analogously, a production rule is essentially the same as a substitution rule .
Consider a production rule of the form , , , and the following sequence of substitution and deletion rules
Clearly, applying this sequence to a word is the same as applying the production rule .
Hence, we add the matrices that were obtained by the Algorithm 1 to . □
Lemmas 3 and 4 yield the following result.
| Algorithm 1 Generate(M) |
| Require: set of matrices with context-free production rules |
| for alldo |
| 1. replace every occurrence of a rule of the form in m with |
| 2. replace every occurrence of a rule of the form in m with |
| 3. replace every occurrence of a rule of the form in m with the sequence
|
| 4. add the resulting matrix to |
| end for |
Theorem 4.
if and only if there is a matrix ins-del-sub systems of size , such that .
Because matrix grammars with context-free production are not computationally complete [20], matrix ins-del-sub systems of size are not computationally complete either. It is known [12] that is closed under reversal. With Lemma 1, we can conclude:
Corollary 2.
.
We will now show that is not computationally complete, either. Consequently, we arrive at the conclusion that is not computationally complete either.
Consider the following construction for the proof. For each derivation of a matrix ins-del-sub system of size , we construct a group of trees that represents the structure of the derivation.
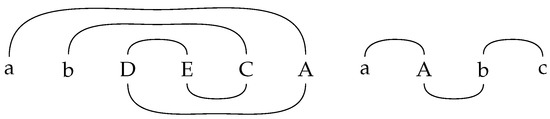
Each tree node is labelled by a string over V, such that reading the rightmost symbols of all root labels of the corresponding group of trees from left to right yields w (we refer to Figure 2).
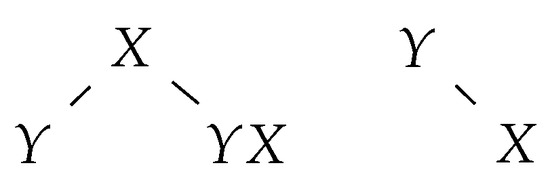
Figure 2.
The tree group corresponding to a sentential form .
If an insertion rule adds the letter a at some position of the sentential form, we add a new tree with a single node labelled a at the corresponding position in the group of trees (see Figure 3).
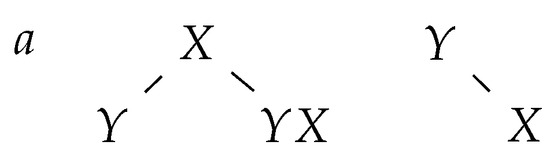
Figure 3.
The tree group following the application of .
Applying a deletion rule has the following effect on the group of trees: the node corresponding to X becomes the rightmost child of the node corresponding to a (see Figure 4).
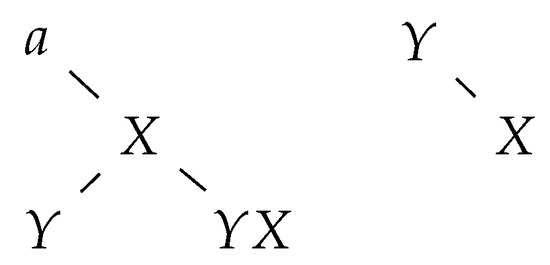
Figure 4.
The tree group following the application of .
Let be the string of the node corresponding to a letter Y. If a substitution rule is applied, then we concatenate b right of (see Figure 5).
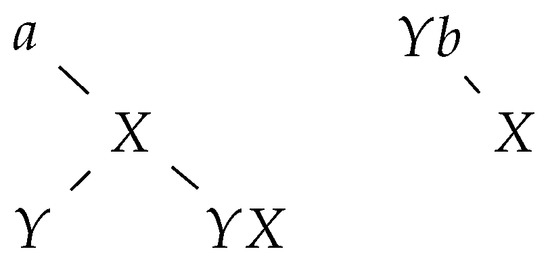
Figure 5.
The tree group following the application of .
Let the axiom of the derivation be . Subsequently, the group of trees consists initially of n trees with single nodes, each being labelled by a symbol of the axiom, such that reading the labels of the respective roots from left to right yields . Each root node corresponds to a letter of the current sentential form.
By construction, it is clear that only (the rightmost letter of) root labels contribute letters to the final word, i.e., each tree contributes, at most, one letter to the final word. Furthermore, it is clear that there is no interaction between letters of two different trees, i.e., a letter belonging to certain tree is not a context for some operation on a letter of another tree.
Before explaining the weaknesses of matrix ins-del-sub systems with their size limited to , we illustrate their power by presenting a concrete example.
Example 3.
Consider a matrix ins-del-sub system of size , which has the axiom . Let
be matrices of . Clearly holds and the corresponding group of trees is
Note that all of the letters corresponding to the eventual a-tree originate from context-free insertions. Furthermore, because there is no interaction between letters of two different trees, inserting all letters of the eventual a-tree (in the order specified by the a-tree) left or right of all letters belonging to eventual b-trees does not affect the b-trees. Thus, and also hold.
Theorem 5.
Proof.
We show that there is no matrix ins-del-sub system of size generating the regular language . Assume to the contrary that generates . Subsequently, generates the word , , as well, where is the length of the longest axiom of . Consider the group of trees corresponding to a derivation of starting from the axiom . Because , there exists a tree t with the following properties: (1) the tree contributes a letter a to and (2) all nodes of the tree originate from the application of some insertion rule. Consider the derivation from to . Subsequently, also generates . The string is generated by applying the same matrices used in the derivation from to in the same order. All of the insertion rules corresponding to nodes of the tree t that are specified above are applied right of all letters belonging to (eventual) b-trees. Because there is no interaction between letters of two different trees, none of the letters that correspond to nodes of t are used as context to delete symbols not affiliated with nodes of t. Thus, inserting these letters right of all letters belonging to (eventual) b-trees changes nothing for the other trees. Note that the tree t specifies the position of the inserted letters in relation to each other as well as how the rest of the rules concerning symbols of t are applied. □
Interestingly, while neither nor are computationally complete, by Theorem 4 at least the context-free languages are included in . does not even include all regular languages. Consequently, we can also state:
Corollary 3.
We remark that Corollary 2 and Theorem 5 show that the result of Corollary 1 is optimal, i.e., the context dependency cannot be reduced any further without losing computational power.
3.3. Context-Free Substitutions Do Not Always Help
We now show that extending context-free matrix ins-del systems with context-free substitution rules does not result in an increase in computational power.
Theorem 6.
with .
Proof.
Because holds by definition, we only prove the converse.
Let be of size . Subsequently, there exists a system of size where X is a new symbol not in V, which simulates . It is sufficient to prove that context-free substitution rules can be simulated by . Let be a context-free substitution rule. Consider the sequence . Applying this sequence to , , is equivalent to applying the substitution rule , i.e., . Note that the string has to be directly inserted right of a letter a, as, otherwise, cannot be applied.
Therefore, the set is constructed, as follows: let , then we replace all of the occurrences of substitution rules in m with the sequence , . The resulting matrix is added to . This procedure is applied to all . □
By Theorem 1, we deduce that the matrix ins-del systems of size are not computationally complete.
Corollary 4.
.
3.4. One-Sided Substitutions
We now consider matrix ins-del systems with one-sided substitution rules. In particular, the families of systems that are discussed in detail now are and .
Theorem 7.
.
Proof.
Let . Subsequently, is defined as follows: Let . Without a loss of generality, we assume .
The following procedure is applied to all matrices of . Consider an arbitrary matrix m of . We replace every occurrence of an insertion rule of the form with an insertion rule and a substitution rule . Additionally, any deletion rule of the form is replaced with a substitution rule and a deletion rule . The matrix that is obtained by these replacements is added to .
Clearly, . The basic idea of this proof is that the nonterminal X is immediately resolved after being introduced. It is easy to see that applying the substitution rule immediately after the insertion rule is essentially the same as applying a rule of the form . Likewise, applying the deletion rule immediately after the substitution rule is basically the same as applying the deletion rule .
Therefore, clearly . □
It has been shown in [10] that holds. Therefore, . We can improve this result by using the result that is presented in Theorem 2. Together with Lemma 1, the next corollary follows.
Corollary 5.
.
We now show that omitting deletion rules in the systems mentioned above yields a characterization of context-sensitive languages, which is quite rare with ins-del systems.
Lemma 5.
Proof.
Let be constructed according to Theorem 3. The basic idea is the same as in Lemma 3. We define the matrix grammar with , as in Lemma 3 with the following addition: For every matrix of the form in we add a matrix of the form to M (we remark that the second component of every matrix of is a context-free substitution rule).
Clearly, G is a matrix grammar with context-sensitive production rules. In ([12] [Theorem 1.2.1]), it is shown that holds. Therefore, our claim holds. □
We now prove the converse.
Lemma 6.
Proof.
Let be a context-sensitive grammar in Penttonen normal form [21]. Subsequently, we construct the following matrix ins-del-sub systems to simulate G:
with and . Without a loss of generality, we assume .
The simulation of a production rule of the form is carried out by the following matrix
A production rule of the form is simulated by the matrix
while a production rule of the form is simulated by a matrix . We make the following observation: all nonterminals , , which are introduced by a matrix m, are resolved at the end of m.
In the following paragraph, we prove the equality by induction. We begin by proving that, if there are matrices with , such that
then holds. The base case, i.e., , is clear. We now consider the inductive step. Let
Let the matrix that is used in the derivation step be a matrix of the form
Subsequently, and follow. Consider an application of . Clearly due to our observation. Therefore, the substitution rule of must be applied to a letter B whose left context is A. Otherwise, the substitution rule of (and itself) cannot be applied. Hence, it is easy to see that and hold. Because of our induction hypothesis holds. Because of our construction, the existence of a matrix of the form implies the existence of a production rule . Clearly,
holds. The case
is handled analogously (clearly, the insertion rule must insert left of , otherwise cannot be applied), while the case is obvious.
The converse follows analogously. □
More specifically, with Lemmas 1, 5 and 6, we can state the following result.
Theorem 8.
.
3.5. Adding Appearance Checking
We have previously shown that there are even regular languages not included in . We now show that expanding these systems with appearance checking yields computational completeness. More precisely, we show that the expanded systems can simulate type-0 grammars in Penttonen normal form, which means that all of the production rules are of the form
where are nonterminal symbols and a is a terminal symbol.
Theorem 9.
.
Proof.
Because the inclusion is clear, we now proceed to prove the converse by simulating a type-0 grammar in Penttonen normal form. The matrix ins-del-sub systems with appearance checking simulating G is defined as , with and . The nonterminal $ is an auxiliary symbol that marks the beginning of a sentential form, and it is eventually deleted by the matrix . We now describe how the rules of G are simulated.
For every rule of G of the form , we add a matrix to , and, for every rule , we add the matrix to . We remark that the following matrices that are introduced to require the sentential form to have $ as the leftmost symbol. Hence, these rules cannot be applied if $ is absent. For every rule of the form , to , we add a matrix
with . Add to F. These deletion rules are used to check whether the left context of the B, which is substituted by X, has been A. The basic idea is as follows: consider the application of the matrix above to , where w is a string over . It is clear that the letter B, which is substituted by X, must have some symbol as its left context, i.e., this B cannot be the leftmost symbol. Furthermore, if the matrix above has been successfully applied, neither of the deletion rules in F has been applicable, as, otherwise, the substitution rule could not have been applied. Therefore, the application of these deletion rules has been skipped during the processing of the matrix above. Because the letter B (which is eventually substituted by X) must have some left context, but neither of the deletion rules from F has been applicable, this means that the left context of this B could not have been a letter from . Hence, the left context of this B has been A. Therefore, it is easy to see that the matrix above correctly simulates .
For every production rule of the form , we add a matrix
with to . The deletion rules and are added to F.
Consider a string w over . Let the matrix above be applied to the string . Using the same argumentation as before, in F ensure that the left context of the inserted is not an element of . Additionally, if the matrix above has been successfully applied, then the deletion rule could not have been applicable, as, otherwise, the substitution rule could not have been be applied. Thus, has not been inserted left of . This in turn means that must have been inserted left of and, therefore, it is clear that the above matrix simulates .
We remark that applying any of the matrices, which simulate a production rule of G, to a sentential form of , whose leftmost symbol is $, results in a string whose leftmost symbol remains $. By induction, we can show that iff . □
Additionally, we can show that is also computationally complete.
Theorem 10.
.
Proof.
The idea is the same as in Theorem 9. Replacing all the deletion rules of the form in the matrices of the system constructed in Theorem 9 with deletion rules of the form yields our claim. □
This result shows that appearance checking is indeed powerful, as we have previously seen that does not even include all regular languages. Furthermore, we can conclude the following from this result.
Theorem 11.
.
Proof.
All of the substitution rules occurring in matrices of the construction in Theorem 9 can be replaced, as specified in the proof of Theorem 6. □
Additionally, the following can be derived from [22], based on ideas on P systems. This is interesting, as P systems (also known as membrane systems, introduced in [23]) are another formalization of a bio-computing device, when considering a cell (abstractly viewed as a membrane structure) as a computing mechanism.
An insertion-deletion P system is a construct where
- O is a finite alphabet,
- is the terminal alphabet,
- is the tree structure of the system which has n nodes,
- , , is a finite language associated to the membrane i, and
- , , is a set of insertion and deletion rules with target indicators of the node i. The rules are of the form: , where is an insertion rule or a deletion rule, and .
A configuration of is an n-tuple of finite languages over O. The transition between two configurations consists of applying rules in parallel to all possible strings, non-deterministically with respect to the target indications associated with the rules. A sequence of transitions between configurations of a given insertion-deletion P system starting from the initial configuration is called a computation with respect to . The result of ’s computations is collected in the language that consists of all strings over T that are sent out of the root node during its computations.
An insertion-deletion P system has the priority of deletion rules over insertion rules if a rule , where is an insertion rule, is only allowed to be applied if no rule , where is a deletion rule, is applicable.
Theorem 12.
.
Proof.
Consider an insertion-deletion P system with the priority of deletion rules over insertion rules. It is known that such systems with insertion rules of size and deletion rules of size are computationally complete, see [22]. We now show that such an insertion-deletion P system with a priority of deletion rules over insertion rules can be simulated by an matrix ins-del system with the appearance checking of size .
Let be such a system. An equivalent matrix ins-del system with appearance checking , where X is a trap symbol, is constructed, as follows. We define . For every deletion rule , we add a matrix to , where if , if and if and is the parent node of i. Furthermore, if the node i has no parent node and if the deletion rule is in , then we add the matrix to .
Let denote the set of all deletion rules, which satisfy if . For every insertion rule , we add the matrix
to , where if , if and if and is the parent node of i. In the case the node i has no parent node, we add
to . All insertion rules, which introduce the trap symbol X are added to F.
The basic idea is as follows. By definition of , an insertion rule can only be applied if no deletion rule is applicable. In other words, can only be applied if the current sentential form does not have any occurrence of . This is simulated via the insertion rules in our matrices. Clearly, if any of these rules is applicable, then a trap symbol is introduced.
Becayse the language generated by consists of all words over T sent outside of the system during the computation, it can be shown that . □
4. Conclusions
Our results complement the results that were obtained in the long versions of [6,7]. In particular, in these papers we have shown that extending ordinary ins-del systems with substitution rules yields, in most cases, an increase in computational power. In some cases, this increase can be quite significant. To give an overview, the main characterization results for RE and for CS of [6] and [7] have been, as follows.
| Previous Result | Extended with Substitution | ||
| Size | Family | Size | Family |
The incompleteness results of systems without substitution rules can be found in [19] ([Th. 3.5] and [Th. 4.2]) and [24] [Th. 7], respectively.
We remark that deletion rules are essential for computational completeness results, as we have shown that, even with the addition of substitution rules, systems that do not have deletion rules lack computational power beyond CS. Furthermore, we have shown that , i.e., ins-del-sub systems require some context information; otherwise, substitution rules do not offer any benefits in regards to the size complexity of those systems.
We have shown that matrix ins-del systems do not need much context to reach computational completeness if substitution rules and appearance checking are used. For instance, we have shown that, in this setting, no context other than single symbol context for deletion rules is necessary for computational completeness. In the case of no context other than single symbol context for insertion rules, we have shown that appearance checking is a necessary and sufficient feature for ensuring computational completeness. Notice that the term "appearance checking” might, indeed, be a bit misleading, as it usually applies to checking the non-applicability of certain rules. Because we (always) test for the absence of single symbols, it might be better to formalize or interpret our results in the context of (forbidden) random context [25,26,27,28,29], or, more generally speaking, to semi-conditional (matrix) grammars. So-called generalized forbidding matrix grammars (GFM) have been presented at ICMC 2020 (the corresponding paper will appear in the Springer LNCS volume 12687 of CMC21) and cover the idea of associating tests for the absence of symbols (or even words) as a filter prior to applying a matrix. The mentioned paper uses (more traditional) context-free rules within the matrices. In a sense, the results of our paper could also be seen as initializing the study of generalized forbidding matrix ins-del-sub systems. Subsequently, also studies on random context with respect to ins-del systems are also interesting for comparison, see [30,31]. Another interpretation could be in terms of ordered variants of matrix ins-del-sub systems, a topic so far explored only in connection with context-free grammars [32], because ordered grammars and forbidden context grammars mostly coincide, also see [12,33,34]. To provide an overview, our completeness results are collected in the following table.
| Normal Matrix | Extended with Substitution | |||
| ins-del Systems | and Appearance Checking | |||
| Size | Family | Size | Family | ac? |
| - | ||||
| - | ||||
| √ | ||||
| √ | ||||
| √ | ||||
| √ | ||||
The incompleteness reults for normal matrix ins-del systems follow from [10] and Theorem 1, Theorems 8, Theorem 5, and Corollary 2.
Although matrix ins-del systems extended with substitution rules are powerful devices, this extension is not always sufficient for reaching computational completeness. More precisely, our incompleteness results have been thus as follows.
| Incompleteness Results | |
| Size | Family |
Coming back to the original motivation of our study, that of exploring the limits of computability with bio-computing devices, it is not that clear whether appearance checks (which always mean that the whole, say, RNA string has to be checked for possible sites where a rule might apply) can be efficiently implemented in real bio-computing mechanisms. Yet, they may serve as a yardstick, showing what is possible and also indicating in which way one might want to modify the formalisms in order to achieve computational completeness with smaller context dependencies for the different types of rules. Conversely, we suppose that, if bio-computing devices based on processing RNA or other large molecules leaves the experimental laboratories one day, turning into an industrial-strength technology, then computational completeness results, as presented in this paper on matrix ins-del-sub systems, as well as in previous papers for ins-del-sub systems, may serve as a basis of implementing compilers and so forth to master these future machines.
Author Contributions
Conceptualization, H.F.; writing—original draft preparation, M.V.; writing—review and editing, H.F., M.V.; supervision, H.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DNA | Deoxyribonucleic acid |
| RNA | Ribonucleic acid |
| RE | Recursively enumerable (languages) |
| CS | Context-sensitive (languages) |
| CF | Context-free (languages) |
| REG | Regular (languages) |
| ac | Appearance checking |
| INS/ins | Insertion |
| DEL/del | Deletion |
| SUB/sub | Substitution |
| MAT/M | Matrix |
| P system | Păun (membrane) system |
References
- Kari, L. On Insertions and Deletions in Formal Languages. Ph.D. Thesis, University of Turku, Turku, Finland, 1991. [Google Scholar]
- Kari, L.; Păun, G.; Thierrin, G.; Yu, S. At the crossroads of DNA computing and formal languages: Characterizing recursively enumerable languages using insertion-deletion systems. In DNA Based Computers III; the Center for Discrete Mathematics and Theoretical Computer Science: Piscataway, NJ, USA; the Association for Computer Machinery (ACM): NewYork, NY, USA, 1999; Volume 48, pp. 329–338. [Google Scholar]
- Beaver, D. Computing with DNA. J. Comput. Biol. 1995, 2, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kari, L. DNA computing: Arrival of biological mathematics. Math. Intell. 1997, 19, 9–22. [Google Scholar]
- Freund, R.; Rogozhin, Y.; Verlan, S. Generating and accepting P systems with minimal left and right insertion and deletion. Nat. Comput. 2014, 13, 257–268. [Google Scholar] [CrossRef]
- Vu, M.; Fernau, H. Insertion-Deletion Systems With Substitutions I. Computability in Europe, CiE; Anselmo, M., Vedova, G.D., Manea, F., Pauly, A., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2020; Volume 12098, pp. 366–378. [Google Scholar]
- Vu, M.; Fernau, H. Insertion-Deletion Systems With Substitutions II. In Proceedings of the Descriptional Complexity of Formal Systems—22nd International Conference, DCFS, Vienna, Austria, 24–26 August 2020; Jiraskova, G., Pighizzini, G., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2020; Volume 12442, pp. 231–243. [Google Scholar]
- Vu, M. On Insertion-Deletion Systems with Substitution Rules. Master’s Thesis, Informatikwissenschaften, Universität Trier, Trier, Germany, 2019. [Google Scholar]
- Kuppusamy, L.; Mahendran, A.; Krishna, S.N. On Representing Natural Languages and Bio-molecular Structures using Matrix Insertion-deletion Systems and its Computational Completeness. In Proceedings of the 1st International Workshop on AI Methods for Interdisciplinary Research in Language and Biology (ICAART 2011), Rome, Italy, 28–30 January 2011; pp. 47–56. [Google Scholar]
- Petre, I.; Verlan, S. Matrix insertion-deletion systems. Theor. Comput. Sci. 2012, 456, 80–88. [Google Scholar] [CrossRef]
- Ábrahám, S. Some questions of phrase-structure grammars, I. Comput. Linguist. 1965, 4, 61–70. [Google Scholar]
- Dassow, J.; Păun, G. Regulated Rewriting in Formal Language Theory; EATCS Monographs in Theoretical Computer Science; Springer-Verlag: Berlin/Heidelberg, Germany, 1989; Volume 18. [Google Scholar]
- Alhazov, A.; Krassovitskiy, A.; Rogozhin, Y.; Verlan, S. Small size insertion and deletion systems. In Applications of Language Methods; Martin-Vide, C., Ed.; Imperial College Press: River Edge, NJ, USA, 2010; pp. 459–515. [Google Scholar]
- Verlan, S. Recent Developments on Insertion-Deletion Systems. Comput. Sci. J. Mold. 2010, 18, 210–245. [Google Scholar]
- Kuppusamy, L.; Mahendran, A.; Krishna, S.N. Matrix Insertion-Deletion Systems for Bio-Molecular Structures. In Proceedings of the Distributed Computing and Internet Technology—7th International Conference, ICDCIT, Bhubaneshwar, India, 9–12 February 2011; Natarajan, R., Ojo, A.K., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2011; Volume 6536, pp. 301–312. [Google Scholar]
- Fernau, H.; Kuppusamy, L.; Raman, I. Investigations on the power of matrix insertion-deletion systems with small sizes. Nat. Comput. 2018, 17, 249–269. [Google Scholar] [CrossRef]
- Fernau, H.; Kuppusamy, L.; Raman, I. On Matrix Ins-Del Systems of Small Sum-Norm. In SOFSEM: Theory and Practice of Computer Science; Catania, B., Královič, R., Nawrocki, J., Pighizzini, G., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2019; Volume 11376, pp. 192–205. [Google Scholar]
- Krassovitskiy, A.; Rogozhin, Y.; Verlan, S. Computational power of insertion-deletion (P) systems with rules of size two. Nat. Comput. 2011, 10, 835–852. [Google Scholar] [CrossRef]
- Verlan, S. On Minimal Context-Free Insertion-Deletion Systems. J. Autom. Lang. Comb. 2007, 12, 317–328. [Google Scholar]
- Hauschildt, D.; Jantzen, M. Petri net algorithms in the theory of matrix grammars. Acta Inform. 1994, 31, 719–728. [Google Scholar] [CrossRef]
- Penttonen, M. One-sided and two-sided context in formal grammars. Inf. Control (Now Inf. Comput.) 1974, 25, 371–392. [Google Scholar] [CrossRef]
- Alhazov, A.; Krassovitskiy, A.; Rogozhin, Y.; Verlan, S. P systems with minimal insertion and deletion. Theor. Comput. Sci. 2011, 412, 136–144. [Google Scholar] [CrossRef]
- Păun, G. Computing with Membranes. J. Comput. Syst. Sci. 2000, 61, 108–143. [Google Scholar] [CrossRef]
- Matveevici, A.; Rogozhin, Y.; Verlan, S. Insertion-Deletion Systems with One-Sided Contexts. In Proceedings of the Machines Computations, and Universality, 5th International Conference, MCU, Orléans, France, 10–13 September 2007; Durand-Lose, J.O., Margenstern, M., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2007; Volume 4664, pp. 205–217. [Google Scholar]
- Fernau, H.; Kuppusamy, L.; Raman, I. Descriptional Complexity of Matrix Simple Semi-conditional Grammars. In Proceedings of the Descriptional Complexity of Formal Systems—21st IFIP WG 1.02 International Conference, DCFS; Košice, Slovakia, 17–19 July 2019, Hospodár, M., Jirásková, G., Konstantinidis, S., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2019; Volume 11612, pp. 111–123. [Google Scholar]
- Fernau, H.; Kuppusamy, L.; Oladele, R.O.; Raman, I. Improved descriptional complexity results on generalized forbidding grammars. Discret. Appl. Math. 2021. [Google Scholar] [CrossRef]
- Meduna, A. Generalized forbidding grammars. Int. J. Comput. Math. 1990, 36, 31–39. [Google Scholar] [CrossRef]
- Păun, G. A variant of random context grammars: Semi-conditional grammars. Theor. Comput. Sci. 1985, 41, 1–17. [Google Scholar] [CrossRef]
- Van der Walt, P.J. Random context languages. In Processing IFIP Congress; North-Holland Publishing Company: Amsterdam, The Netherlands, 1972; pp. 66–68. [Google Scholar]
- Fernau, H.; Kuppusamy, L.; Raman, I. Computational Completeness of Simple Semi-conditional Insertion-Deletion Systems. In Unconventional Computation and Natural Computation, UCNC; Stepney, S., Verlan, S., Eds.; Springer International Publishing AG, Part of Springer Nature: Cham, Switzerland, 2018; Volume 10867, pp. 86–100. [Google Scholar]
- Ivanov, S.; Verlan, S. Random Context and Semi-conditional Insertion-deletion Systems. Fundam. Inform. 2015, 138, 127–144. [Google Scholar] [CrossRef]
- Dassow, J.; Păun, G. On ordered variants of some regulated grammars. J. Inf. Process. Cybern. EIK 1985, 21, 491–504. [Google Scholar]
- Fernau, H. Closure properties of ordered languages. EATCS Bull. 1996, 58, 159–162. [Google Scholar]
- Freund, R. A General Framework for Sequential Grammars with Control Mechanisms. In Proceedings of the Descriptional Complexity of Formal Systems—21st International Conference DCFS, Košice, Slovakia, 17–19 July 2019; Hospodár, M., Jirásková, G., Konstantinidis, S., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2019; Volume 11612, pp. 1–34. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).