Optimization of Fiber-Reinforced Polymer Bars for Reinforced Concrete Column Using Nonlinear Finite Element Algorithms

Abstract

The ductility and strength of reinforced concrete (RC) columns could be noticeably improved by replacing steel bars with polymeric bars. Despite the previous research on RC columns, most of those studies focused only on the lateral load capacity of this structural member and were mainly costly experimental studies. However, this paper is concentrated on the previously occurred damages to the reinforced columns in the previous earthquakes. Subsequently, finite element analysis has been performed to examine 24 models including the various shapes of RC columns. In employing the plastic behavior of steel, carbon fiber-reinforced polymer (CFRP), and glass fiber reinforced polymer (GFRP) bars, the bilinear hardening has been considered. To capture both compressive and tensile behavior of the concrete, the concrete damage plasticity model has been implemented. Furthermore, the optimization technique is used for CFRP models to compare with other models. In this paper, the parameters of energy, seismic factor, stiffness, and ductility have been computed using the method proposed by the authors. This suggested method is considered to compare the results from each parameter. Finite element results of steel bars are compared with carbon and glass models. The results show the stiffness of models is improved by CFRP bars, while the energy absorption and ductility factor are enhanced with steel bars. Moreover, GFRP bars can enhance the seismic factor. The reduction of column stiffness to almost half would occur in some rectangular cross-section columns.

1. Introduction

Reinforced concrete (RC) structures are a common construction in many areas. The A majority of our infrastructure, including bridges, elevated water tanks, and those buildings that must be functional even after an earthquake, are built using reinforced concrete. Therefore, their performance is a crucial issue. For instance, the necessity of drinking water and quenching water during a fire event shows the importance of the water tanks. Moreover, bridges and culverts must be stable during an earthquake to have the vital needs delivered to their intended place on time. Past events such as fires [1,2,3], earthquakes [4,5,6], and defects such as corrosion [7,8,9] of steel in reinforced concrete member, durability issues including shrinkage cracking [10,11], thermal cracking [3,12], chemical attack [11,13,14], alkali-silica reaction [15,16,17], alkali-carbonate reaction as well as carbonation, delayed ettringite formation, freeze-thaw [17] and scaling [18,19] were observed in many reinforced concrete structures and infrastructures previously studied by the researchers. The results of these studies have shown the vulnerability of these types of buildings. Reinforced concrete structures are susceptible to environmental deterioration such as the loss of the member’s mechanical properties due to corrosion and the durability of the RC structure [20,21,22,23,24]. Moreover, the performance of the RC member decreases progressively over time, which leads to the failure of the whole building. However, Fiber Reinforced Polymer (FRP) bars might be an alternative reinforcement where the corrosion of the steel bars becomes a serious issue in both new and existing construction since FRP can resist corrosion, particularly in a corrosive environment such as offshore construction [25]. Furthermore, comparing FRP bars to steel bars, the former has the higher tensile capacity and lower weight as well as low elasticity modulus [26,27]. Currently, Carbon Fiber Reinforced Polymer (CFRP) and Glass Fiber Reinforced Polymer (GFRP) bars have been used in the construction sites to replace the steel bars.

FRP has been commonly used in RC beams. The majority of the researchers focused merely on the flexural behavior of these members using FRP sheets. Xiao and Ma performed research in which four circular columns were tested. The results of three columns retrofitted with 4 to 5 layers of GFRP sheets showed that the confined specimens have higher load carrying capacity [26]. Wang and Hsu conducted a theoretical study and suggested a closed-form design equation to evaluate the axial load strength of the RC columns confined with FRP. The values from the prediction of the equations calibrate the experimental results [28]. Colomb et al. tested eight short columns subjected to axial load to study the shear failure of RC columns. Seven samples were partially or fully- wrapped by CFRP or GFRP. For those continuous wrapped columns, the increase in both resistance and ductility, have been reported [29]. Saadatmanesh et al. [30] performed a study to investigate the behavior of reinforced concrete columns confined with carbon and glass fiber reinforced polymer sheets. Their results showed that both the compressive strength and its corresponding strain at failure experience a significant increase when the CFRP or GFRP is wrapped. They concluded that the concrete compressive strengths and strains at failure increased significantly when the column is confined with GFRP and CFRP straps [30]. In a review paper presented by Ma et al. [31], it was shown that among all jacketing techniques, FRP confinement is an effective method when it comes to integrity. There were also some studies carried out by Sen and Mullins [25], Mullins et al. [32], Sen et al. [33], and Mullins et al. [34]. The developed techniques are studied to repair the underwater RC structures that are subjected to corrosion. In these techniques both CFRP and GFRP sheets have been considered to retrofit the piles. These studies recommended strategies to optimize the cost of repairs. Furthermore, the compressive strength of the reinforced concrete, ductility, and energy dissipation can significantly be improved by wrapping with CFRP sheets [35].

There are only a few studies that have concentrated on the flexural behavior of RC beams where the GFRP bars are embedded in the beam, such as the study conducted by Tu et al. [36]. They investigated the buckling failure of the GFRP-reinforced concrete square columns. Their results indicated that the failure of this type of beam is controlled by the spacing between stirrups. In their research, GFRP longitudinal reinforcement and confined GFRP stirrups were considered as the only reinforcement bars. However, due to difficulties in having the GFRP bent by the factories, it might not be feasible or economic to be considered at the industrial scale. FRP bars have been used as a substitute rebars for RC structures since FRP reinforcement bars have noncorrosive and nonconductive properties in comparison to steel reinforcement [37]. Having constructed and immersed in the seawater, steel rebars in RC columns need to be protected against corrosion. In addition, it has been proved that longitudinal FRP bars increase the axial compression performance [38,39,40,41,42] as well as improve the chemical and physical corrosion [43] because the polymeric materials used in FRP composite have the ability to resist corrosion [44,45]. Moreover, using FRP rebars materials in RC structures enhances the durability of the concrete and its resistance to the corrosive environment which makes the structure to perform better over a long period of time and reduces maintenance costs in comparison to the steel rebars [46].

Based on the aforementioned discussion, there are many studies that focused on the importance of FRP materials to improve the structural performance. Although many of these prove that FRP sheets and bars pave the way for enhancing structural integrity, none of them evaluated the simultaneous factors of cross-section, reinforcing pattern and its material properties on structural capacities. Moreover, there is no related study to show the optimization aspects of the stated variables. Therefore, this research represents the effect of FRP bar materials on structural performances for various types of cross-sections and height. It also presents a new model development approach to compute the seismic behavior of structural components.

The theoretical study of the current research focuses on the effect of stress-strain behavior of different cross-sections of reinforced concrete columns in which the FRP bars are embedded as a reinforcing material in order to improve the axial compression with the novel method presenting in this paper. To conduct finite element analysis for this research, the experimental data are employed from Silvia Rocca’s experimental setup [47]. The experimental setups featured eight different groups, of which seven are the subject of this research (In fact, seven of eight specimens, having different configurations and specifications with steel rebars). The specimens were modeled to validate with experimental results. In this regard, the three-dimensional finite element models’ results were compared with the experimental results. The optimization technique is also used to compare the effect of bar diameter on the seismic performance of RC columns. Finally, the new models with different characteristics have been considered to study the behavior of different types of bars in the reinforced concrete column. A method will be presented to calculate the seismic parameters based on the FE results as previously published by the authors [48].

2. Materials and Methods

2.1. Finite Element Modeling and Experimental Verification

The experimental calibrations included several comparisons with the selected previous experimental results obtained by Silvia Rocca [48]. The research herein investigated large-size reinforced concrete (RC) columns subjected to axial loading. It follows the experimental program conducted by the University of California at San Diego and the Building Fire Research Laboratory at the National Institute of Standards and Technology. The cross-sections of the columns were circular, rectangular, and square. According to the experimental program, the specimens were divided into eight different groups with various variables. Figure 1 illustrates the geometry information of the experimental tests. Different dimension ratios had been considered to compare the results where h/b indicates the largest cross-section side (h) to the other side (b) [48].

Table 1. Geometrical Properties of the experimental specimens.

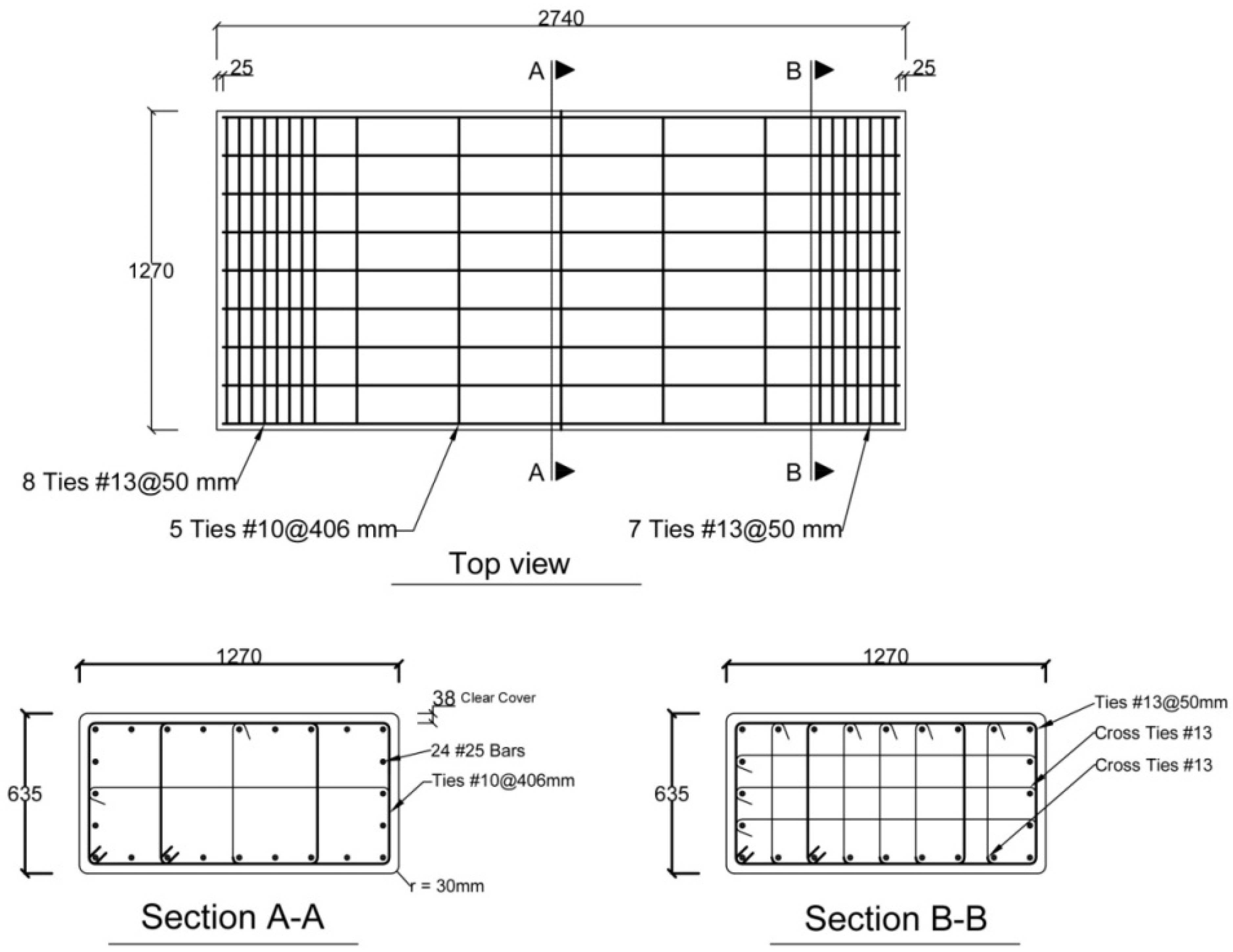
Group	$\mathit{D}\mathit{o}\mathit{r}$ $\mathit{b}\times \mathit{h}$ $\left(\mathit{m}\mathit{m}\right)$	$\mathit{h}/\mathit{b}$	$\mathit{H} \left(\mathit{m}\mathit{m}\right)$	${\mathit{f}}_{\mathit{c}}^{\prime }\left(\mathbf{MPa}\right)$	Number of Longitudinal Bars	Number of Stirrups at Ordinary Zones	Number of Stirrups at Specific Zones
A1	$508$	N/A *	1.1	31.7	6	2	9
B1	$315\times 635$	2.0	1.4	30.2	6	3	9
C1	$457\times 457$	1.0	1.0	32.1	8	3	8
D1	$648\times 648$	1.0	1.4	30.7	12	4	13
E1	$324\times 324$	1.0	0.7	32.3	4	3	7
F1	$324\times 324$	1.0	1.4	31.5	4	5	12
G1	$914\times 914$	1.0	2.0	31.6	26	3	17
H1	$635\times 1270$	2.0	2.7	30.3	24	5	15

* N/A: Sample A is circular with no ratio.

shows the geometrical properties of each group [48]. It should be noted that the longitudinal bars’ diameter is 25.4 mm. The values of 9.5 mm and 12.7 mm are for the ordinary stirrups and specific zones, respectively. The material properties of the steel were selected according to ASTM A370 based on grade 60 with the yield and ultimate stresses of 450 MPa and 600 MPa [49]. To perform the simulation, the validation plays an indispensable role to ensure the accuracy of modeling. In this regard, the experimental data are employed to validate with the finite element results. Therefore, three-dimensional finite element (FE) models were built using Abaqus to simulate the behavior of the reinforced concrete columns. In this case, the RC columns (groups A to H) were modeled to validate the experimental results. In this 3D FE model, the concrete was modeled as a homogeneous-deformable solid using the C3D8R element type (3D 8-node linear isoperimetric elements with reduced integration). Both longitudinal and transversal steel bars were modeled as truss elements using the T3D2 element type (a two-node, 3-dimensional truss element). The concrete damage plasticity (CDP) model has been considered to simulate the properties of the concrete. Stress and strain properties can be defined by the CDP model including linear and nonlinear parts in which the plastic parameter must be used in CDP. In addition, stress-strain parameters should be computed in both compressive and tensile sides which both have their own damage parameters. The bottom line is to have enough data to calculate CDP parameters. This requires information that can be obtained through the experimental results. In other words, the compressive strength of concrete and failure strain should be known as the initial values of CDP. After computing those compressive and tensile stress-strain relationships and their corresponding damage parameters, the nonlinear parts should be separated from the linear side. According to ACI 318 [50], 40 percent of the compressive strength can be considered as a boundary of plastic and elastic parts. In fact, these values have been computed for each group, and thus Equation (1) is used to calculate the modulus of elasticity of concrete ACI 318 [50].

$$E=4700 \sqrt{f_c^{\prime }}$$

(1)

E is modulus of elasticity and $f_c^{\prime }$ is the concrete compressive strength. It should be noted that the dilation angle of concrete is defined as 38-degrees. The steel material is considered as an isotropic hardening with a modulus of 200 GPa. Yield and ultimate stresses are considered according to the ASTM A370 as nominal values of 450 MPa and 600 MPa, respectively. Moreover, the connection of reinforcing bars and concrete is made by embedded region constraints. The nonlinear static analysis step is considered to simulate the models.

The boundary condition of the bottom surface of the column is pinned (Ux = Uy = Uz = 0) and the top surface is loaded using displacement controls in which the loading rate is constant for all validations.

The nonlinear static general analysis technique is employed to simulate the models. The loading stop rate is dependent on the yield stress of the bars and the failure of concrete. However, the Smooth-Step loading amplitude is applied to the load cell. The loading amplitude has 0.05 magnitude of failure load per second.

To determine the appropriate mesh size for the analysis of the RC column, three sizes of finite element mesh were selected, and mesh sensitivity analysis was performed. Several attempts were made to reach the finite element results that coincide with the experimental results. However, independence to the mesh size will be considered by this technique. The discretization of concrete is shown in Figure 2.

As stated previously, the experimental results of specimens are compared to finite element results. The strain-stress diagrams and the maximum corresponding values are shown in Figure 3 and

Table 2. Difference Between the Finite Element and Laboratory Results.

	Laboratory Results		Finite Element Results		Difference (FEM vs. Laboratory)
Specimen	Compressive Strength (MPa)	Maximum Axial Strain (mm/mm)	Compressive Strength (MPa)	Maximum Axial Strain (mm/mm)	Compressive Strength (%)	Maximum Axial Strain (%)
A1	26	2.94 × 10−3.	29	3.00 × 10−3	11.9	2.5
B1	23.94	1.60 × 10−3	25.1	1.50 × 10−3	4.9	−6.6
C1	26.6	3.25 × 10−3	27.3	3.30 × 10−3	2.5	1.6
D1	24.5	3.16 × 10−3	24.7	3.12 × 10−3	0.6	−2.0
E1	20.4	2.20 × 10−3	20.55	2.13 × 10−3	0.4	5.3
F1	26.2	7.70 × 10−3	24.7	7.40 × 10−3	−7	−4
G1	28.5	6.99 × 10−3	30	7.11 × 10−3	5.2	2.5
H1	-	-	22.35	7.20 × 10−3	-	-

. The results corresponding to specimen H are not reported in this table because of the inconvenience with the data acquisition system in the last step of the loading. Therefore, there is no record of the maximum axial strain [48]. In Figure 3 and Table 2, the difference of finite element compared with experimental results shows that the maximum stress and strain for specimen A (Figure 3a) is 11.5 and 2.5 percent, respectively. In Figure 3b, it is clear that the strain-stress diagram for both stress and strain parts is closely intertwined by having 4.9 and −6.6 percent. It should be noted that the minus factor indicates the finite element’s maximum value is less than the experimental one. In Figure 3c,d, although the trend of the plastic part is not well matched, the difference of maximum stress is 2.5 and 0.6 for specimens C and D, respectively. Based on Figure 3e–g, and Table 2, it can be seen that the validation of these specimens is reasonable by having 5.3, −4, and 2.5% as the strain difference, and 5.4, −7, and 2.5% for the difference of maximum stress. Moreover, the small difference of FEM and experimental results could reasonably be a result of the nature of experimental setups. In fact, the laboratory tests can have reading errors of strain gauges, load cell and/or the failure of the concrete element that could cause higher/lower results. Therefore, having approximately 10% or less difference between the FEM and experimental results is indicative of a good agreement.

It should be noted that the slop pattern of experimental and finite element ones for all specimens are almost match except Figure 3d,g. The reason of different slop pattern is due to dilatancy criteria of concrete. This means that the granular movements of fine and coarse aggregate of the laboratory admixture have a compact or loose condition. In compact condition, the stress causes an aggregate motion inside of the concrete core (volume). Due to the interlock phenomenon for aggregates, the fine and/or coarse aggregates are unable to freely move to neighbor aggregates. In this case, when the amount of pressure increases, more stress occurs on the concrete core. Therefore, the elastic portion of the concrete shows a high slope, indicating higher modulus of elasticity. On the other side, having a loose granular motion in the concrete core induces a lower slope and less modulus of elasticity. It needs to be declared that the dilatancy of concrete, which is also called dilation angle, was not reported in the experimental tests. The dilation angle of the normal concrete is between 30–40 degrees. However, higher reinforced concrete compressive strength requires higher dilation angle value. Therefore, the dilation angle of concrete for all models is considered to be 38-degrees based on the concrete compressive strength range. Since the majority of the compressive strength of concrete is higher than the normal concrete compressive strength, 38-degrees are applied for all the models to avoid the effect of the dilation angle.

2.2. Numerical Development of the Models

After the validation of the experimental results, all specimens were modeled and analyzed based on the data illustrated in Table 1. In this study, the models were developed by two variables as an RC column embedded with steel bars and an RC column embedded with FRP bars.

The first model was validated by the results of the concrete column that was reinforced by steel bars, while in the other models, Fiber Reinforced Polymer (FRP) bars were considered instead of using steel bars. In the modeling process, the FRP longitudinal bars are the Carbon and Glass type. In addition, CFRP bars were analyzed to optimize the samples. Therefore, the #12 longitudinal bars’ diameter was utilized. The smaller diameters were analyzed to compare the load capacity of CFRP bars with GFRP and steel bars.

The mechanical properties of CFRP and GFRP are shown in

Table 3. Mechanical Properties of FRP Bars.

Name	Ultimate Stress (MPa)	Failure Strain	Modulus of Elasticity [1]
CFRP	3690	0.031	580
GFRP	1600	0.17	51

[51]. It should be noted that the FRP bars do not show yield stress and thus the yield and ultimate stress are defined almost the same due to consideration of the brittle attributes of FRP bars. These characteristics are defined by the assignment of the plastic property using bilinear hardening.

In the modeling process, all model criteria were the same except for the reinforcement materials. Different models were simulated based on validation characteristics. The geometry and concrete properties of specimens are shown in Table 1. The symbols and properties of RC columns are shown in

Table 4. Model’s Name.

Group of Specimens	Steel (S)	CFRP Bars (C)	GFRP Bars (G)	Number of Longitudinal Bars #25	Optimized CFRP with #12 Bars
A	AS	AC	AG	6	AO
B	BS	BC	BG	6	BO
C	CS	CC	CG	8	CO
D	DS	DC	DG	12	DO
E	ES	EC	EG	4	EO
F	FS	FC	FG	4	FO
G	GS	GC	GG	26	GO
H	HS	HC	HG	24	HO

. In this table, it can be seen that the optimized models are developed with the same number of bars but different bar diameters. In this regard, the goal is to use CFRP bars to substitute with steel bars in order to obtain the same approximate load capacity and stiffness. To approach this, the bar’s diameter is reduced to #12 which is almost half of the original bar’s diameter. After performing the optimization techniques, load capacity, energy, seismic factor “R”, stiffness and ductility factors of all models are compared. It should be stated that the optimized specimens are modeled as aforementioned in the materials and methods section (based upon the validation) and only the bar’s diameters are modified.

3. Seismic Parameters Model Development

Different criteria such as stiffness, energy absorption, ductility, and seismic factors are discussed herein [51,52]. All parameters were computed numerically using the load-displacement curve of each group, and the results are compared. The simplified procedures of converting a full graph into a bilinear graph are shown in Figure 4. This figure shows the procedures that calculate the parameters needed for the finite element analysis [53].

As can be seen in this figure, the first step is to add the load-displacement diagram. This diagram is added based on finite element results. The second step is to find out the first plastic hinge. The plastic hinge usually occurs after the crack tip and at the time of crack propagation. It is worth mentioning that the plastic hinge is automatically calculated with the developed script. In step three, the developed script is defined to calculate the yield and failure load and corresponding displacement. In the next step, the time and “k” factor are defined. In step five, the data of step three are employed to calculate the ductility factor. Step six is scripted to choose a different method of computing factor of “R”. In the final steps (seven and eight), the accuracy of all previous steps is determined, based on two main conditions (see step eight). In fact, these eight steps are subjected to recursion to achieve the required accuracy.

In Figure 5, the approach of the parametrical study is shown. In general, the concept of finding these parameters is carried out by converting the load-displacement diagram into a bilinear diagram. In fact, two linear parts of the bilinear diagram contributed to the calculations of the parameters based on a boundary between the linear and nonlinear parts. In Figure 6, the parametrical approach of the bilinear diagram of group FS (group F with steel bars) is presented. In order to create a two-linear graph, the first plastic hinge and its corresponding displacement were considered. It should be mentioned that the failure criteria are the maximum load and displacement. After finding the yield force and its corresponding displacement by employing linear analysis of Equation (2), the boundary of linear and nonlinear parameters is generated. Further, finding a linear analysis parameter requires the lateral force which can be computed by C and W in which C = ABI/R and W is the weight of the RC element [51,52] (A: Design base acceleration (in relation to gravity acceleration g), B: Response coefficient of the building obtained from the design response spectrum, I: Importance factor and R is the Behavior coefficient of the building).

$$V=C·W$$

(2)

On the other hand, there are some conditions that are needed to confirm and control the obtained values. One of the most important conditions is controlled by the area under the graph. It indicates that linear and nonlinear area of the bilinear graph that has been computed. It should be noted that the area under the curve of linear and nonlinear parts must be almost the same. A small difference in the computed area may still be considered as high accuracy of the computation. Another condition is to control the yield force (0.6V_y) and detect the corresponding displacement in order to confirm the boundary of the elastic and non-elastic zone (the parts of the bilinear graph) [53].

Also, the parameters such as ductility, stiffness, energy absorption, and seismic factor were computed to meet the conditions. Generally, ductility plays an essential role in the seismic design of structural elements (It also can be acknowledged as the capability of large deformation of structures after being yield). In general, the ductility can be computed using Equation (3) by dividing the ultimate lateral displacement ${\mathsf{\Delta }}_u$ by the yield lateral displacement ${\mathsf{\Delta }}_y$ meaning that displacement at corresponding of yield force [54].

$$\mu =\frac{{\mathsf{\Delta }}_u}{{\mathsf{\Delta }}_y}$$

(3)

Furthermore, the stiffness can be computed in a similar way to the mentioned methodology. Considering the concept of Figure 5, the yield force and its corresponding displacement can be computed. Thus, the stiffness can be determined by Equation (4) which requires finding first the slope of the load-displacement diagram [52].

$$E=\frac{V_y}{{\mathsf{\Delta }}_y}$$

(4)

The energy absorption can be calculated using the same approach as present in Figure 5. In fact, the area under the force-displacement curve is the energy absorption parameter which consists of two parts that were calculated separately. Simpson’s rule was performed to obtain the area of every single step. Then, by summation of all computed values, the energy absorption of the specimen is calculated. Finally, the seismic parameter is another factor to be considered. The seismic factor R can be computed using Equation (5) [55,56,57,58,59,60,61].

$$R=R_u·R_s$$

(5)

where $R_u$ is a reduction factor (due to ductility defined in Equation (6)). In this case, $V_{el}$ is the ultimate force of the structural element if the member stays in elastic performance [55].

$$R_u=\frac{V_{el}}{V_y}$$

(6)

where $V_y$ is also noted as yield force based on the safety performance of the structure. Moreover, the over strength factor $R_s$ can be computed by Equation (7). V_s is the yield force based on the first plastic hinge [55].

$$R_s=\frac{V_y}{V_s}$$

(7)

4. Results (Finite-Element Analysis)

In this section, we illustrate the results of the load-displacement and strain-stress curves. The RC columns reinforced with steel bars are considered as a control group to compare with carbon and glass reinforcement. The load-displacement graphs are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. As seen in these figures, the load capacity of the RC columns reinforced with FRP bars is higher than that reinforced with steel bars. Figure 7 shows the load capacity of group A (In this figure, it can be seen that AC, which is the carbon bar (according to Table 3), has a greater bearing load).

As can be seen in this figure, the CFRP model has a higher load capacity compared with the control and GFRP models. Also, the OCFRP, which indicates the optimized model, shows that reducing the bar’s diameter from 25 mm to 12 mm has almost the same load capacity of the control and GFRP models. Moreover, Figure 8 and Figure 9 show groups B and C, indicating the rectangular and square cross-section, respectively. As shown in Figure 8, BG has more displacement than BC, BS, and BO. However, due to the greater ductility of steel bars, the maximum displacement value of glass bar specimens is less than it is for steel ones.

In this figure, comparing the stress-strain behavior also shows that the CFRP model is more brittle and has higher modulus of elasticity than two others. This phenomenon is due the nature of composite materials. In fact, CFRP material has higher modulus of elasticity and much lower failure strain than GFRP materials.

Figure 9 demonstrates that FRP bars have higher load and displacement capacity performance. Looking at stress-strain diagrams of this figure indicates that the steel model (control specimen) has a better ductility factor. However, the maximum stress capacity of the control sample (about 26 MPa) is much less than the CFRP model (about 33 MPa). On the other side, the GFRP model has almost 5% more stress capacity than the control sample.

In addition, by comparing Figure 10 and Figure 11, which display groups D and E, one can notice that increasing the cross-section dimension can enhance both load capacity and displacement. In fact, by comparing CS to DS, the maximum load capacity is 8576 kN in contrast to 17,505, which confirms the effect of the cross-section. Also, by comparing the results of CC and DC, it can be noted that the maximum load capacity of the mentioned specimens is 14,407 kN and 24,778 kN, respectively. One of the most important issues can be seen in Figure 11 and Figure 12 regarding the group of E and F. As has been shown in Table 1, the cross-section of group E and F are the same at 324 × 324 (mm), but the height of group F is twice that of group E (1.4 m compared to 0.7 m). The results are performed according to the stop rate of the loading conditions. This loading rate for models with steel bars was stopped when the bars were at yield, and the concrete is at compression failure. To address this matter for the models in which FRP bars were embedded, simultaneous failure of the bars and concrete is considered, since FRP bars are subjected to brittle behavior in contrast to ductile steel bars.

In Figure 13, the load displacement and stress-strain diagrams of group G are shown. In this figure, the CFRP model has about 40 kN load capacity, while the value for control, GFRP and OCFRP is about 30 kN, 24 kN and 28 kN, respectively. Moreover, the maximum displacement of the CFRP model shows about 47% reduction compared with that of the control model. In terms of failure strain, control samples have the maximum strain (about 0.007) compared with CFRP (0.004) and GFRP (0.0055).

Furthermore, in Figure 14, the maximum load of models shows that the CFRP specimen has about 30% more load capacity than the control model, while it has about 50% less displacement versus the control sample. Looking at the stress-strain behavior of this figure also demonstrates that the CFRP model has very brittle behavior. In fact, the CFRP diagram (stress-strain) shows a sharp upward slope, and once it surged up to the pick, it immediately failed. This issue happens due to failure of the CFRP bars. Because CFRP bars do not have yield stress and strain, once the bearing capacity of these bars reach the maximum value, the bars failed. Therefore, the concrete core started to have a very sharp and fast crack propagation and failure. On the other hand, looking at the control sample of H shows that the steel bars help the concrete at the post-failure stage, and it enhances the strain failure of the concrete. In general, in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, the CFRP models have better performance in load capacity while the control specimens (reinforced with steel bars) have better displacement capacity. Also, using the optimization method shows that reducing the CFRP bar’s size (from 25 mm to 12 mm) has almost the same load capacity of the control specimen, but less displacement.

5. Discussion

Based on the parametrical investigation, the energy absorption values are shown in Figure 15. It is clear that group H holds the highest energy absorption due to its dimensions. However, the CFRP bar has better behavior in enhancing energy absorption compared to GFRP. However, the models with steel bars have better energy absorption due to yield and failure points of steel material. To investigate the effect of the cross-section, group D (648 × 648 mm) and F (324 × 324 mm), and the height of 1.4 m are compared. The energy absorption of DC was about 184% higher than FC. The values were 159 and 56, respectively. Also, DG has 364% more energy absorption value than FG. On the other hand, it is necessary to compare the energy absorption of each group to evaluate the effect of each specimen. In Figure 15, the circular section (Group A: 508 mm) indicates that the AS specimen has more energy absorption than AC and AG, which shows the energy absorption of (153.77 $\mathrm{G}\times {10}^6$) 63 and 75 percent more than AC and AG, respectively.

The specimen AO, which is the optimized sample of AC, has the least value of energy. By comparing group B and D, which have the same height (1.4) and different cross-sections, shows that the square cross-section has a better absorption capability. In other words, comparison between specimens reinforced with steel bars BS ($315\times 635$ mm) and DS ($648\times 648$ mm) represents energy absorption of 113.2 $\mathrm{G}\times {10}^6$ and 302.7 $\mathrm{G}\times {10}^6$, respectively. Moreover, the values for energy absorption of BC, BO, DC and DO are 63 $\mathrm{G}\times {10}^6$, 46.12 $\mathrm{G}\times {10}^6$, 161 $\mathrm{G}\times {10}^6$, and 118.86 $\mathrm{G}\times {10}^6$, respectively.

Figure 16 shows the seismic factor of specimens. By comparing the seismic factor in Figure 16 between group B ($315\times 635$ mm) and F ($324\times 324$, both of which have the same height (1.4 m), it can be seen that the seismic value of BS is 90%higher than that for FS. Furthermore, comparing BG and FG, the seismic value increases with the increase in the cross-section (4.9 and 2.9, respectively). Furthermore, comparison between group E and F, which have the same cross-section $324\times 324$ mm and different heights (E = 0.7 and F = 1.4 m) demonstrates that the higher the height, the lower the seismic factor is. The results from groups E and F show that the seismic factor of FS is 12% higher than ES, while this difference for FG and EG is 33%. In order to compare the effect of cross-section, group D ($648\times 648$ mm) and F ($324\times 324$ mm) is chosen. These groups have the same height (1.4 m). The results show that the difference of the seismic factor is too closed, meaning that the cross-section does not have a big influence on the seismic factor (However, the smaller cross-section has better performance in seismic factor). As a case in point, FS is 6.6% more than DS, and this difference for optimized model FO and DO is subjected to have 0.39 and 0.38 which is less than 2.7%.

In Figure 17, the stiffness of all models is shown. By comparing groups of steel, carbon and glass bars, it can be declared that carbon bars have better performance in enhancing the stiffness. This may be due to the mechanical properties of carbon fiber reinforced polymer bars. On the other side, the stiffness of steel bars is much higher than that for the glass groups. This is because of the much higher modulus of elasticity of steel (200 GPa) in comparison to 51 GPa for glass bars. In order to evaluate the detailed comparison of stiffness based on cross-section parameters, groups D and F are selected. As \mentioned above, these group have the same height, but the cross-section of D is twice that of F (The comparison of FS and DS shows that DS has more stiffness than FS (about 153%); also this difference for the carbon and glass model is 120% and 215%, respectively). On the other hand, comparing group E (0.7 m) and F (1.4 m) and having the same cross-section shows that the stiffness of ES is about 40% higher than FS. Also, the difference of stiffness is 22% (EC vs. FC), 67% (EG vs. FG) and 97% (EO vs. FO). Comparing the two largest groups also shows that the square cross-section has higher stiffness than the rectangular ones. To approve this issue, GC and HC are compared, and GC is shown to be about 41% of HC.

In contrast to stiffness, the ductility parameter, shown in Figure 18, of the steel group is more than that for both glass and carbon. In fact, the steel bars have better performance in increasing the ductility factor than CFRP and GFRP bars. The comparison of group B and D displays that the rectangular shape has better performance in improving the ductility factor (For instance, BC and DC have 5.5 and 3.7). The height factor is also an issue for the parametrical studies. The results have shown that an increase in the height can enhance the ductility factor. This is evident in specimens EC and FC with values of 4.2 and 4.9, respectively. The heights of group E and F were 0.7 and 1.4 m, respectively. The bottom line is that the circular cross-section has the highest ductility among all groups. Comparing the ductility of AS with the second highest steel specimens (ES and FS) shows that this difference is about 30% for AS compared to the two others. Moreover, this difference for carbon, glass and the optimized model is 22.5%, 7.6%, and 7.1%, respectively.

6. Conclusions

Nonlinear FE analysis is used herein to study the behavior of reinforced concrete columns reinforced with various types of bars including steel, carbon, and glass as polymeric bars. The new simplified method is presented here to calculate the seismic parameters based on the FE results. The agreement of numerical modeling with the experimental behavior of steel reinforced columns is also satisfactory. The contributions of CFRP and GFRP bars in the improvement of different seismic parameters were investigated, and it was found that the CFRP bars can improve the stiffness of the RC column. On the other hand, steel bars can improve the behavior of the RC columns when it comes to energy absorption and ductility. Moreover, GFRP bars can enhance the seismic factor. The reduction of column stiffness to almost half would occur in some rectangular cross-section columns. The geometry of the cross-section as well as the type of bars affects the variation and stress on FRP bars. The optimized method for the CFRP model shows that by decreasing the bar’s diameter, the load capacity and seismic behavior of optimized models are closely intertwined with GFRP and steel models.