Using Graph Embedding Techniques in Process-Oriented Case-Based Reasoning
Abstract
:1. Introduction
- a comprehensive encoding scheme that enables the integration of semantic graphs with their semantic annotations and structure to be used in GNNs;
- two specialized, adapted GNN architectures for learning similarities between semantic graphs, based on GNNs from the literature [23];
- an evaluation of the GNNs in different retrieval scenarios with regard to performance and quality.
2. Foundations and Related Work
2.1. Semantic Graph Representation
2.2. Similarity Assessment of Semantic Graphs
2.3. Similarity-Based Retrieval of Semantic Graphs
2.4. Related Work
3. Neural Networks for Graph Embedding
3.1. General Neural Network Structure
3.2. Embedder
3.3. Propagation Layer
3.4. Aggregator and Graph Similarity
4. Neural-Network-Based Semantic Graph Similarity Measure
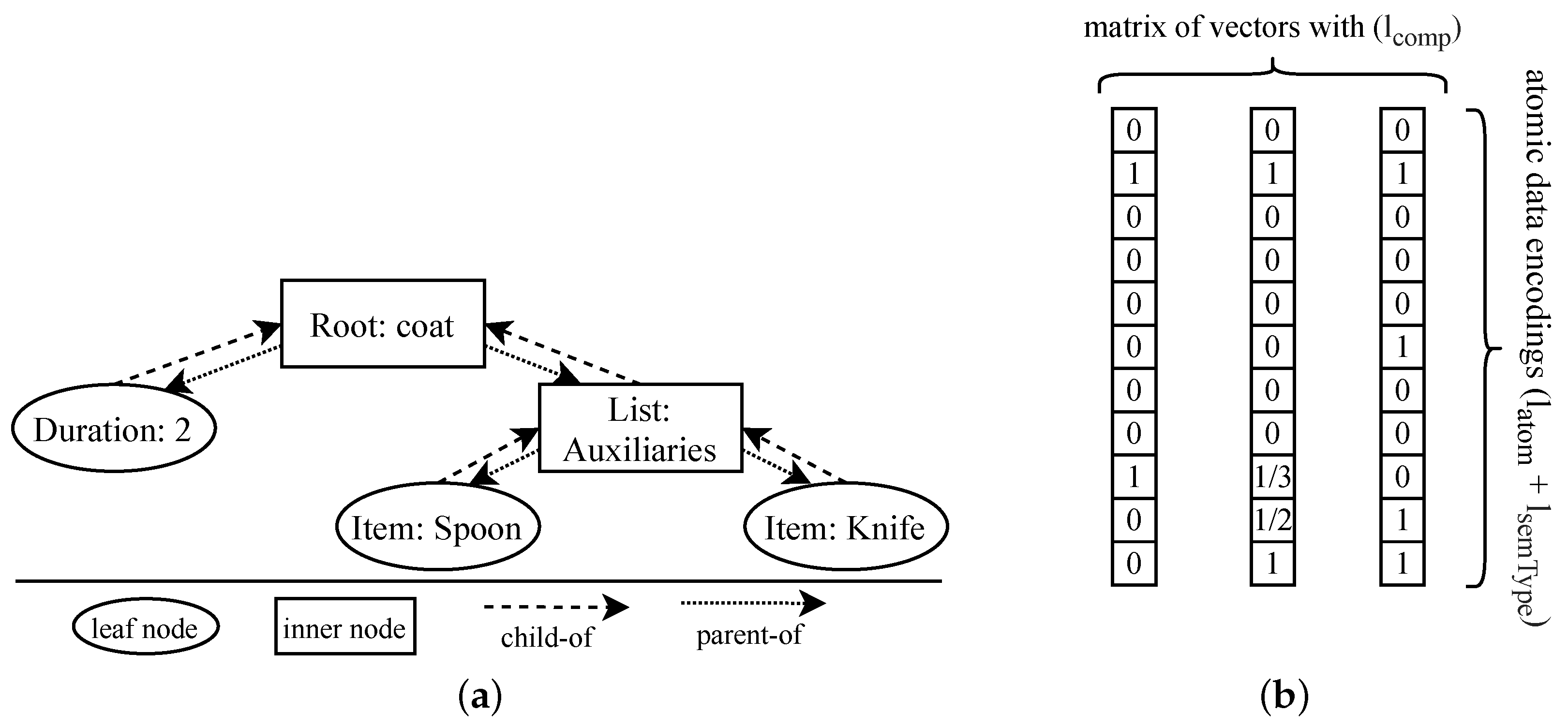
4.1. Encoding Semantic Graphs
4.1.1. Encoding Node and Edge Types
4.1.2. Encoding Semantic Descriptions
4.2. Adapted Neural Network Structure
4.2.1. Adapted Embedder
4.2.2. Constrained Propagation in the Semantic Graph Matching Network
4.2.3. Trainable Graph Similarity of Semantic Graph Matching Network
4.2.4. Training and Optimization
5. Application of Semantic Graph Embedding Model and Semantic Graph Matching Network in Similarity-Based Retrieval
5.1. Offline Training
5.2. Retrieval
6. Experimental Evaluation
| sGEM | sGEM used with sequence encoding; |
| sGEMtree | sGEM used with tree encoding; |
| sGMN | sGMN used with sequence encoding; |
| sGMNtree | sGMN used with tree encoding; |
| sGMNconst | sGMN used with matching constraints; |
| sGMNtree,const | sGMN used with tree encoding and matching constraints. |
6.1. Experimental Setup
6.2. Experimental Results
6.3. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aamodt, A.; Plaza, E. Case-Based Reasoning: Foundational Issues, Methodological Variations, and System Approaches. AI Commun. 1994, 7, 39–59. [Google Scholar] [CrossRef]
- Richter, M.M.; Weber, R.O. Case-Based Reasoning: A Textbook; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Müller, G. Workflow Modeling Assistance by Case-Based Reasoning; Springer: Wiesbaden, Germany, 2018. [Google Scholar] [CrossRef]
- Malburg, L.; Seiger, R.; Bergmann, R.; Weber, B. Using Physical Factory Simulation Models for Business Process Management Research. In Business Process Management Workshops; Del Río Ortega, A., Leopold, H., Santoro, F.M., Eds.; Springer eBook Collection; Springer International Publishing and Imprint Springer: Cham, Switzerland, 2020; Volume 397, pp. 95–107. [Google Scholar] [CrossRef]
- Zeyen, C.; Malburg, L.; Bergmann, R. Adaptation of Scientific Workflows by Means of Process-Oriented Case-Based Reasoning. In Case-Based Reasoning Research and Development; Bach, K., Marling, C., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11680, pp. 388–403. [Google Scholar] [CrossRef]
- Minor, M.; Montani, S.; Recio-García, J.A. Process-Oriented Case-Based Reasoning. Inf. Syst. 2014, 40, 103–105. [Google Scholar] [CrossRef]
- Bergmann, R.; Gil, Y. Similarity Assessment and Efficient Retrieval of Semantic Workflows. Inf. Syst. 2014, 40, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Bergmann, R.; Müller, G. Similarity-Based Retrieval and Automatic Adaptation of Semantic Workflows. In Synergies between Knowledge Engineering and Software Engineering; Nalepa, G.J., Baumeister, J., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2018; Volume 626, pp. 31–54. [Google Scholar] [CrossRef]
- Grumbach, L.; Bergmann, R. Using Constraint Satisfaction Problem Solving to Enable Workflow Flexibility by Deviation (Best Technical Paper). In Artificial intelligence XXXIV; Bramer, M.A., Petridis, M., Eds.; Lecture Notes in Computer Science Lecture Notes in Artificial Intelligence; Springer: Cham, Switzerland, 2017; Volume 10630, pp. 3–17. [Google Scholar] [CrossRef]
- Bunke, H. Recent Developments in Graph Matching. In Proceedings of the 15th International Conference on Pattern Recognition, ICPR’00, Barcelona, Spain, 3–8 September 2000; IEEE Computer Society: Washington, DC, USA, 2000; pp. 2117–2124. [Google Scholar] [CrossRef]
- Ontañón, S. An overview of distance and similarity functions for structured data. Artif. Intell. Rev. 2020, 53, 5309–5351. [Google Scholar] [CrossRef] [Green Version]
- Bergmann, R.; Stromer, A. MAC/FAC Retrieval of Semantic Workflows. In Proceedings of the Twenty-Sixth International Florida Artificial Intelligence Research Society Conference, FLAIRS 2013, St. Pete Beach, FL, USA, 22–24 May 2013; Boonthum-Denecke, C., Youngblood, G.M., Eds.; AAAI Press: Palo Alto, CA, USA, 2013. [Google Scholar]
- Hanney, K.; Keane, M.T. The adaptation knowledge bottleneck: How to ease it by learning from cases. In Case-Based Reasoning Research and Development; Leake, D.B., Plaza, E., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1266, pp. 359–370. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, NSW, Australia, 6–11 August 2017; Volume 70, pp. 1263–1272. [Google Scholar]
- Goyal, P.; Ferrara, E. Graph Embedding Techniques, Applications, and Performance: A Survey. Knowl.-Based Syst. 2018, 151, 78–94. [Google Scholar] [CrossRef] [Green Version]
- Cai, H.; Zheng, V.W.; Chang, K.C.C. A Comprehensive Survey of Graph Embedding: Problems, Techniques and Applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef] [Green Version]
- Klein, P.; Malburg, L.; Bergmann, R. Learning Workflow Embeddings to Improve the Performance of Similarity-Based Retrieval for Process-Oriented Case-Based Reasoning. In Case-Based Reasoning Research and Development; Bach, K., Marling, C., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11680, pp. 188–203. [Google Scholar] [CrossRef]
- Müller, G.; Bergmann, R. A Cluster-Based Approach to Improve Similarity-Based Retrieval for Process-Oriented Case-Based Reasoning. In Proceedings of the ECAI 2014—21st European Conference on Artificial Intelligence—Including Prestigious Applications of Intelligent Systems (PAIS 2014), Prague, Czech Republic, 18–22 August 2014; Schaub, T., Friedrich, G., O’Sullivan, B., Eds.; Frontiers in Artificial Intelligence and Applications. IOS Press: Amsterdam, The Netherlands, 2014; Volume 263, pp. 639–644. [Google Scholar] [CrossRef]
- Hoffmann, M.; Malburg, L.; Klein, P.; Bergmann, R. Using Siamese Graph Neural Networks for Similarity-Based Retrieval in Process-Oriented Case-Based Reasoning. In Case-Based Reasoning Research and Development; Watson, I., Weber, R., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12311, pp. 229–244. [Google Scholar] [CrossRef]
- Hoffmann, M.; Bergmann, R. Informed Machine Learning for Improved Similarity Assessment in Process-Oriented Case-Based Reasoning. arXiv 2021, arXiv:2106.15931. [Google Scholar]
- Li, Y.; Gu, C.; Dullien, T.; Vinyals, O.; Kohli, P. Graph Matching Networks for Learning the Similarity of Graph Structured Objects. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 3835–3845. [Google Scholar]
- Bergmann, R.; Grumbach, L.; Malburg, L.; Zeyen, C. ProCAKE: A Process-Oriented Case-Based Reasoning Framework. In Proceedings of the Twenty-seventh International Conference on Case-Based Reasoning (ICCBR 2019), Otzenhausen, Germany, 8–12 September 2019; Volume 2567, pp. 156–161. Available online: CEUR-WS.org (accessed on 13 December 2021).
- Lenz, M.; Ollinger, S.; Sahitaj, P.; Bergmann, R. Semantic Textual Similarity Measures for Case-Based Retrieval of Argument Graphs. In Case-Based Reasoning Research and Development; Bach, K., Marling, C., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11680, pp. 219–234. [Google Scholar] [CrossRef]
- Leake, D.; Crandall, D. On Bringing Case-Based Reasoning Methodology to Deep Learning. In Case-Based Reasoning Research and Development; Watson, I., Weber, R., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12311, pp. 343–348. [Google Scholar] [CrossRef]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.F.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Richter, M.M. Foundations of Similarity and Utility. In Proceedings of the Twentieth International Florida Artificial Intelligence Research Society Conference, Key West, FL, USA, 7–9 May 2007; Wilson, D., Sutcliffe, G., Eds.; AAAI Press: Palo Alto, CA, USA, 2007; pp. 30–37. [Google Scholar]
- Bergmann, R. Experience Management: Foundations, Development Methodology, and Internet-Based Applications; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2432. [Google Scholar] [CrossRef]
- Zeyen, C.; Bergmann, R. A*-Based Similarity Assessment of Semantic Graphs. In Case-Based Reasoning Research and Development; Watson, I., Weber, R., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12311, pp. 17–32. [Google Scholar] [CrossRef]
- Forbus, K.D.; Gentner, D.; Law, K. MAC/FAC: A Model of Similarity-based Retrieval. Cogn. Sci. 1995, 19, 141–205. [Google Scholar] [CrossRef]
- Kendall-Morwick, J.; Leake, D. A Study of Two-Phase Retrieval for Process-Oriented Case-Based Reasoning. In Successful Case-based Reasoning Applications-2; Springer: Berlin/Heidelberg, Germany, 2014; pp. 7–27. [Google Scholar]
- Mathisen, B.M.; Bach, K.; Aamodt, A. Using extended siamese networks to provide decision support in aquaculture operations. Appl. Intell. 2021, 51, 8107–8118. [Google Scholar] [CrossRef]
- Amin, K.; Lancaster, G.; Kapetanakis, S.; Althoff, K.D.; Dengel, A.; Petridis, M. Advanced Similarity Measures Using Word Embeddings and Siamese Networks in CBR. In Intelligent Systems and Applications; Bi, Y., Bhatia, R., Kapoor, S., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; Volume 1038, pp. 449–462. [Google Scholar] [CrossRef]
- Corchado, J.M.; Lees, B. Adaptation of Cases for Case Based Forecasting with Neural Network Support. In Soft Computing in Case Based Reasoning; Pal, S.K., Ed.; Springer: London, UK, 2001; pp. 293–319. [Google Scholar] [CrossRef] [Green Version]
- Dieterle, S.; Bergmann, R. A Hybrid CBR-ANN Approach to the Appraisal of Internet Domain Names. In Case-Based Reasoning Research and Development; Lamontagne, L., Plaza, E., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8765, pp. 95–109. [Google Scholar] [CrossRef]
- Mathisen, B.M.; Aamodt, A.; Bach, K.; Langseth, H. Learning similarity measures from data. Prog. Artif. Intell. 2020, 9, 129–143. [Google Scholar] [CrossRef] [Green Version]
- Leake, D.; Ye, X.; Crandall, D. Supporting Case-Based Reasoning with Neural Networks: An Illustration for Case Adaptation. In Proceedings of the AAAI 2021 Spring Symposium on Combining Machine Learning and Knowledge Engineering, Stanford University, Palo Alto, CA, USA, 22–24 March 2021; Martin, A., Hinkelmann, K., Fill, H.G., Gerber, A., Lenat, D., Stolle, R., van Harmelen, F., Eds.; CEUR-WS.org: Palo Alto, CA, USA, 2021. [Google Scholar]
- Liao, C.K.; Liu, A.; Chao, Y.S. A Machine Learning Approach to Case Adaptation. In Proceedings of the 2018 IEEE First International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), Laguna Hills, CA, USA, 26–28 September 2018; pp. 106–109. [Google Scholar] [CrossRef]
- Leake, D.; Ye, X. Harmonizing Case Retrieval and Adaptation with Alternating Optimization. In Case-Based Reasoning Research and Development; Sánchez-Ruiz, A.A., Floyd, M.W., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2021; Volume 12877, pp. 125–139. [Google Scholar] [CrossRef]
- Gabel, T.; Godehardt, E. Top-Down Induction of Similarity Measures Using Similarity Clouds. In Case-Based Reasoning Research and Development; Hüllermeier, E., Ed.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9343, pp. 149–164. [Google Scholar] [CrossRef]
- Keane, M.T.; Kenny, E.M. How Case-Based Reasoning Explains Neural Networks: A Theoretical Analysis of XAI Using Post-Hoc Explanation-by-Example from a Survey of ANN-CBR Twin-Systems. In Case-Based Reasoning Research and Development; Bach, K., Marling, C., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2019; Volume 11680, pp. 155–171. [Google Scholar] [CrossRef]
- Bromley, J.; Bentz, J.W.; Bottou, L.; Guyon, I.; LeCun, Y.; Moore, C.; Säckinger, E.; Shah, R. Signature Verification Using A “Siamese” Time Delay Neural Network. Int. J. Pattern Recognit. Artif. Intell. 1993, 7, 669–688. [Google Scholar] [CrossRef] [Green Version]
- Baldi, P.; Chauvin, Y. Neural Networks for Fingerprint Recognition. Neural Comput. 1993, 5, 402–418. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; Alessandro Moschitti, Q.C.R.I., Bo Pang, G., Walter Daelemans, U.o.A., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2014; pp. 1724–1734. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., von Luxburg, U., Bengio, S., Wallach, H.M., Fergus, R., Vishwanathan, S.V.N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 5998–6008. [Google Scholar]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R.S. Gated Graph Sequence Neural Networks. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. In Proceedings of the 1st International Conference on Learning Representations, ICLR 2013, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- von Rueden, L.; Mayer, S.; Beckh, K.; Georgiev, B.; Giesselbach, S.; Heese, R.; Kirsch, B.; Walczak, M.; Pfrommer, J.; Pick, A.; et al. Informed Machine Learning—A Taxonomy and Survey of Integrating Prior Knowledge into Learning Systems. IEEE Trans. Knowl. Data Eng. 2021, 18, 19–20. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, OSDI’16, Savannah, GA, USA, 2–4 November 2016; USENIX Association: Berkeley, CA, USA, 2016; pp. 265–283. [Google Scholar]
- Stram, R.; Reuss, P.; Althoff, K.D. Dynamic Case Bases and the Asymmetrical Weighted One-Mode Projection. In Case-Based Reasoning Research and Development; Cox, M.T., Funk, P., Begum, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11156, pp. 385–398. [Google Scholar] [CrossRef]
- Cheng, W.; Rademaker, M.; de Baets, B.; Hüllermeier, E. Predicting Partial Orders: Ranking with Abstention. In Cellular automata; Bandini, S., Manzoni, S., Umeo, H., Vizzari, G., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2010; Volume 6321, pp. 215–230. [Google Scholar] [CrossRef] [Green Version]
- Mougouie, B.; Bergmann, R. Similarity Assessment for Generalized Cases by Optimization Methods. In Advances in Case-Based Reasoning; Craw, S., Preece, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2416, pp. 249–263. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.Y. Learning to Rank for Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]




| sGEM | sGEMtree | sGMN | sGMNtree | sGMNconst | sGMNtree,const | FBM | EBM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fs | k | Quality | Time | Quality | Time | Quality | Time | Quality | Time | Quality | Time | Quality | Time | Quality | Time | Quality | Time | |
| CB-I | 5 | 5 | 0.508 | 16 | 0.511 | 14 | 0.489 | 1051 | 0.490 | 2067 | 0.489 | 1074 | 0.489 | 2169 | 0.557 | 510 | 0.499 | 17 |
| 50 | 5 | 0.613 | 100 | 0.600 | 95 | 0.522 | 1137 | 0.523 | 2156 | 0.511 | 1165 | 0.505 | 2263 | 0.836 | 611 | 0.562 | 100 | |
| 10 | 10 | 0.520 | 24 | 0.536 | 22 | 0.502 | 1061 | 0.503 | 2077 | 0.500 | 1085 | 0.505 | 2180 | 0.585 | 522 | 0.516 | 25 | |
| 80 | 10 | 0.623 | 155 | 0.609 | 151 | 0.581 | 1195 | 0.576 | 2225 | 0.548 | 1224 | 0.575 | 2330 | 0.862 | 671 | 0.613 | 158 | |
| 25 | 25 | 0.545 | 50 | 0.567 | 48 | 0.534 | 1088 | 0.536 | 2106 | 0.518 | 1113 | 0.534 | 2208 | 0.652 | 554 | 0.549 | 53 | |
| 100 | 25 | 0.606 | 192 | 0.593 | 187 | 0.646 | 1240 | 0.678 | 2268 | 0.607 | 1266 | 0.676 | 2373 | 0.833 | 714 | 0.642 | 195 | |
| CB-II | 5 | 5 | 0.392 | 66 | 0.394 | 84 | 0.381 | 2811 | 0.449 | 3539 | 0.399 | 2729 | 0.463 | 3666 | 0.646 | 457 | 0.329 | 57 |
| 50 | 5 | 0.557 | 866 | 0.563 | 895 | 0.629 | 3150 | 0.757 | 3833 | 0.671 | 3016 | 0.767 | 3928 | 0.922 | 619 | 0.385 | 295 | |
| 10 | 10 | 0.432 | 113 | 0.448 | 123 | 0.467 | 2825 | 0.516 | 3572 | 0.457 | 2785 | 0.508 | 3690 | 0.667 | 477 | 0.362 | 84 | |
| 80 | 10 | 0.625 | 1146 | 0.637 | 1158 | 0.745 | 3406 | 0.837 | 4064 | 0.749 | 3372 | 0.853 | 4197 | 0.939 | 744 | 0.444 | 430 | |
| 25 | 25 | 0.506 | 281 | 0.511 | 628 | 0.550 | 3004 | 0.623 | 3683 | 0.547 | 2856 | 0.628 | 3793 | 0.694 | 533 | 0.416 | 198 | |
| 100 | 25 | 0.683 | 1371 | 0.697 | 1303 | 0.799 | 3597 | 0.872 | 4234 | 0.797 | 3537 | 0.881 | 4320 | 0.907 | 866 | 0.500 | 518 | |
| Domain | CB-I | CB-II | ||||
|---|---|---|---|---|---|---|
| Retriever | MAE | Correctness | Time | MAE | Correctness | Time |
| sGEM | 0.158 | 0.017 | 1.3 | 0.337 | 0.331 | 1.1 |
| sGEMtree | 0.219 | 0.053 | 0.9 | 0.323 | 0.310 | 0.9 |
| sGMN | 0.033 | 0.287 | 1025.5 | 0.034 | 0.583 | 2697.8 |
| sGMNtree | 0.039 | 0.322 | 2115.1 | 0.026 | 0.724 | 3508.1 |
| sGMNconst | 0.029 | 0.330 | 1051.9 | 0.033 | 0.583 | 2643.7 |
| sGMNtree,const | 0.037 | 0.327 | 2118.3 | 0.024 | 0.732 | 3403.8 |
| FBM | 0.193 | 0.598 | 482.7 | 0.199 | 0.584 | 335.4 |
| EBM | 0.380 | 0.224 | 1.2 | 0.397 | 0.006 | 1.1 |
| A*M | 0.062 | 0.669 | 1265.5 | 0.041 | 0.824 | 3801.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffmann, M.; Bergmann, R. Using Graph Embedding Techniques in Process-Oriented Case-Based Reasoning. Algorithms 2022, 15, 27. https://doi.org/10.3390/a15020027
Hoffmann M, Bergmann R. Using Graph Embedding Techniques in Process-Oriented Case-Based Reasoning. Algorithms. 2022; 15(2):27. https://doi.org/10.3390/a15020027
Chicago/Turabian StyleHoffmann, Maximilian, and Ralph Bergmann. 2022. "Using Graph Embedding Techniques in Process-Oriented Case-Based Reasoning" Algorithms 15, no. 2: 27. https://doi.org/10.3390/a15020027
APA StyleHoffmann, M., & Bergmann, R. (2022). Using Graph Embedding Techniques in Process-Oriented Case-Based Reasoning. Algorithms, 15(2), 27. https://doi.org/10.3390/a15020027







