Optimal Integration of Dispersed Generation in Medium-Voltage Distribution Networks for Voltage Stability Enhancement

Abstract

This study addresses the problem of the maximization of the voltage stability index ($\lambda$-coefficient) in medium-voltage distribution networks considering the optimal placement and sizing of dispersed generators. The problem is formulated through a mixed-integer nonlinear programming model (MINLP), which is solved using General Algebraic Modeling System (GAMS) software. A numerical example with a 7-bus radial distribution network is employed to introduce the usage of GAMS software to solve the proposed MINLP model. A new validation methodology to verify the numerical results provided for the $\lambda$-coefficient is proposed by using recursive power flow evaluations in MATLAB and DigSILENT software. The recursive evaluations allow the determination of the $\lambda$-coefficient through the implementation of the successive approximation power flow method and the Newton–Raphson approach, respectively. It is effected by fixing the sizes and locations of the dispersed sources using the optimal solution obtained with GAMS software. Numerical simulations in the IEEE 33- and 69-bus systems with different generation penetration levels and the possibility of installing one to three dispersed generators demonstrate that the GAMS and the recursive approaches determine the same loadability index. Moreover, the numerical results indicate that, depending on the number of dispersed generators allocated, it is possible to improve the $\lambda$-coefficient between $20.96\%$ and $37.43\%$ for the IEEE 33-bus system, and between $18.41\%$ and $41.98\%$ for the IEEE 69-bus system.

1. Introduction

Electrical distribution networks provide electrical energy to all end-users at medium- and low-voltage levels [1]. These grids interface the power system in the distribution substation with residential, industrial, and commercial consumers by following a radial connection among nodes [2]. Utilities prefer the radial connection owing to lower investment costs in conductors and protective devices. However, these structures deteriorate the performance in terms of different service reliability indexes [3,4]. Additionally, distribution networks have high energy losses when compared with the transmission counterparts. In some cases, energy losses can be between 6% and 18%, depending on the utility maintenance practices, whereas, in transmission networks, the energy losses are between 1.5% and 2% [2]. These power losses are primarily caused by the radial structure of the network. The extant literature presents several methodologies to address the energy losses based on the optimal location of shunt devices and grid topology variations. These methods include optimal location of dispersed generators [5,6], optimal location of capacitor banks [7,8], optimal location of distribution static compensators [9,10], optimal integration of battery energy storage systems [11,12], and grid reconfiguration [13,14], among other strategies. The distinctive characteristic of these approaches is the usage of advanced optimization techniques to improve the grid performance, most of which are from the family of metaheuristic optimization techniques because of their ease of implementation with a master-slave structure using simple power flow formulations [15].

Reducing total grid power losses is, thus, an important and current research aspect in optimization studies for electrical distribution grids [16]. Correspondingly, the voltage stability performance of the network is an additional aspect that has attracted considerable attention owing to its implications in the quality and operation reliability indexes [17]. The voltage stability performance measures the ability of the distribution grid to support load increments without causing a blackout [18,19]. Several studies have addressed the improvement of grid stability using a simplified line-to-load indicator, primarily using dispersed generators [20]. However, the central drawback of these approaches is that the adopted stability index does not measure the global state of the distribution grid and its ability to support simultaneous load increments [21].

In the specialized literature, the voltage stability issues in distribution grids are usually addressed using numerical indexes that concern the voltage profile and the total power consumption. Ghaffarianfar and Hajizadeh, in Reference [22], analyzed the voltage stability problem in AC distribution networks considering the large-scale integration of photovoltaic generation. The authors developed a stability index that depends on the line data, active and reactive power demands, and the voltage values, which are obtained using a classical load flow method. The main contribution of the authors relates to their identification of the possible positive and negative effects associated with the installation of renewable energy resources, which allowed the authors to provide some guidelines regarding the optimal location of these devices in electrical distribution grids. The authors of Reference [21] presented the voltage stability analysis in AC distribution grids using a second-order cone programming model. Numerical simulation shows that the conic formulation allows for the maximum simultaneous increment in all the loads of the network by ensuring the global optimum finding. Numerical results in the IEEE 33- and IEEE 69-node test feeders demonstrated the effectiveness of the conic model when compared with the exact nonlinear model and classical recursive approaches based on power flow solutions. Reference [17] proposed a stability indicator that allowed identifying nodes on the verge of voltage collapse. This indicator is calculated for each node using a modification of the load flow method for voltage stability analysis, which incorporates the load variations and composite load models. Numerical results demonstrated the effectiveness of the proposed index when compared with others in the existing literature. Aly and Abdel-Akher, in Reference [23], proposed an extension of the classical Newton–Raphson power flow method through the continuation approach. Numerical results in the IEEE 33-bus system demonstrate the effectiveness of the proposed method to obtain the voltage collapse point. Their results were corroborated with the PSAT tool for MATLAB software (2021a, Natick, MA, USA). In the case of the optimal placement of dispersed generators for distribution networks, most of the approaches, in their objective formulations, consider the improvement of the voltage stability index of the network [24]. Some of these approaches include population-based incremental learning [25], genetic algorithms [26,27], particle swarm optimization [28], and heuristic-based methods based on sensitive formulas [29,30]. In general, these approaches are based on the calculation of a voltage stability index based on the branch-to-load equivalent of each branch of the network. Further, as mentioned previously, these approaches do not consider in their formulations the simultaneous increment of the loads in all the nodes, which is indeed a complication. The present study aims to contribute to the current literature by addressing the aforementioned complication.

In this study, we propose a mixed-integer nonlinear programming (MINLP) model for voltage stability improvement in medium-voltage distribution networks that includes the possibility of optimal siting and sizing of dispersed generators considering a global stability index named the $\lambda$-coefficient [21]. The solution of this MINLP model was achieved using the General Algebraic Modeling System (GAMS) and the large-scale solver BONMIN [31,32]. In addition, we propose two recursive validations using the successive approximation power flow method in the MATLAB programming environment [33] and the Newton–Raphson power flow method in DigSILENT software [34], which allow the final value of the $\lambda$-coefficient to be verified via an iterative procedure by fixing the sizes and locations of the dispersed generators based on the solution provided by GAMS software. The main contributions of this study include: (i) the validation of the optimal value of the $\lambda$-coefficient using two recursive power flow methods programmed in MATLAB and DigSILENT programming environments based on the successive approximation power flow method and the Newton–Raphson approach, respectively; and (ii) the evaluation of multiple simulation scenarios with different numbers of available dispersed generators with limitations of 40% and 60% in the total injection of active power by the distributed sources. These simulation cases demonstrate that the areas with the worse voltage profiles are the best places for locating the dispersed generators.

It is worth mentioning that this research is primarily focused on the optimal placement and sizing of dispersed generators in medium-voltage networks in order to improve voltage stability. We are not proposing a novel approach to determine the voltage stability factor, i.e., the $\lambda$-coefficient, since multiple such approaches are available in the existing literature, such as the continuation method [23], line-to-load approach [20], and convex optimization [21]. However, the recursive validations in MATLAB and DigSILENT environments can be considered a new possibility to determine the maximum loadability index in distribution networks using recursive power flow solutions, particularly since they coincide perfectly with the GAMS results. Further, it is important to emphasize that, in relation to the dispersed generators, the proposed approach is independent of the type of generation technology implemented; however, to ensure that the $\lambda$-coefficient is effectively maximized, it is mandatory that they generate the designed nominal power during the peak hour. This can be achieved by combining renewable generation technology with energy storage systems or by using dispatchable generation sources.

The remainder of this paper is organized as follows: Section 2 presents the general MINLP formulation for the studied problem. Section 3 illustrates the main aspects of the solution methodology based on GAMS software and the recursive validations using power flow solutions in MATLAB and DigSILENT programming environments. Section 4 outlines the primary characteristics of the IEEE 33- and IEEE 69-bus systems. Section 5 presents the main numerical results with their corresponding analysis and discussion. Lastly, Section 6 lists the main concluding remarks derived from this research and some suggestions for potential future research.

2. Mathematical Formulation

The problem of the maximization of the voltage stability margin by considering the optimal placement and sizing of dispersed generators in AC distribution grids can be formulated through an MINLP model [21]. The integer part of this formulation corresponds to the decision of whether or not to locate the dispersed sources, while the continuous part of the model is associated with the electrical variables, such as voltages, power, and current flows. The complete mathematical formulation of the studied problem is presented below.

2.1. Objective Function

The objective function corresponds to the maximization of the loadability index, i.e., the maximum simultaneous increment of the constant power consumptions, which is labeled in this research as the $\lambda$-coefficient. It can be formulated as follows:

$$\begin{array}{c}\hfill \max z_l=\lambda ,\end{array}$$

(1)

where $z_l$ is the objective function value associated with maximum apparent power consumption of the network before entering the voltage collapse point.

It is to be noted that, in power system analysis, the $\lambda$-coefficient is typically used to construct the nose curve that defines the maximum possible increment of a particular load before reaching the voltage collapse point for a branch-to-load equivalent [35]; nonetheless, in this research, we extrapolate this concept to a general AC distribution network considering dispersed generation. This corresponds with the primary objective of this research, which is to maximize the global stability margin coefficient through the optimal placement and sizing of distributed generation sources.

2.2. Set of Constraints

There are several constraints associated with the optimal integration of dispersed generators in distribution grids to increase the loadability capacities of the network before reaching the point of voltage collapse. These constraints include active and reactive power flow equations, generator capabilities, and possible locations of generators. The complete list of constraints is provided below.

$$\begin{array}{c}\hfill P_i^{cg}+P_i^{dg}-\left(1+\lambda \right)P_i^d=V_i\sum _{i\in \mathcal{N}}{Y}_{ij}{V}_j\cos \left({\theta }_i-{\theta }_j-{\delta }_{ij}\right),\forall i\in \mathcal{N},\end{array}$$

(2)

$$\begin{array}{c}\hfill Q_i^{cg}-\left(1+\lambda \right)Q_i^d=V_i\sum _{i\in \mathcal{N}}{Y}_{ij}{V}_j\sin \left({\theta }_i-{\theta }_j-{\delta }_{ij}\right),\forall i\in \mathcal{N},\end{array}$$

(3)

$$\begin{array}{c}\hfill V_{\min }\le V_i\le V_{\max },\forall i\in \mathcal{N},\end{array}$$

(4)

$$\begin{array}{c}\hfill 0\le P_i^{dg}\le x_i{P}_{\max }^{dg},\forall i\in \mathcal{N},\end{array}$$

(5)

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{N}}{x}_i\le N_{\max }^{dg},\end{array}$$

(6)

$$\begin{array}{c}\hfill \sum _{i\in \mathcal{N}}{P}_i^{dg}\le \beta \sum _{i\in \mathcal{N}}{P}_i^d,\end{array}$$

(7)

$$\begin{array}{c}\hfill x_i\in \left\{0,1\right\},\forall i\in \mathcal{N},\end{array}$$

(8)

$$\begin{array}{c}\hfill \lambda \ge 0,\end{array}$$

(9)

where $P_i^{cg}$ and $Q_i^{cg}$ denote the active and reactive power injections at the conventional generator, i.e., the slack source; $p_i^{dg}$ is the active power injection in the dispersed generators; $P_i^d$ and $Q_i^d$ correspond to the active and reactive power demands at each node; $V_i$ and $V_j$ are the voltage magnitudes at nodes i and j, which have angles ${\theta }_i$ and ${\theta }_j$, respectively; $Y_{ij}$ is the magnitude of the admittance connecting nodes i and j, with an angle ${\delta }_{ij}$; $V_{\min }$ and $V_{\max }$ represent the minimum and maximum voltage regulation bounds allowed in all nodes of the network; $x_i$ is a binary variable related to the presence or absence of a dispersed generator at node i; $P_{\max }^{dg}$ indicates the maximum size allowed for a distributed generator; $N_{\max }^{dg}$ indicates the maximum number of dispersed generators available for allocation in the network; and $\beta$ is the maximum penetration level of dispersed generation in the distribution grid. Note that $\mathcal{N}$ is the set that contains all the demand nodes of the network.

2.3. Model Interpretation

The optimization model defined in (1) to (9) can be interpreted as follows: Equation (1) corresponds to the objective function regarding the simultaneous maximization of the active power consumption in all the nodes in the network; Equations (2) and (3) outline the application of Tellegen’s theorem to all the nodes in the network (i.e., the apparent power definition to each node) [36], which generates the classical active and reactive power balance constraints; inequality constraint (4) defines the voltage regulation limits in all the nodes of the grid (this constraint is generally defined by regulatory policies and utility operative practices); inequality constraint (5) limits the maximum size of the dispersed generator that can be connected at node i; inequality constraint (6) defines the maximum number of dispersed generators that can be installed along the distribution network; inequality constraint (7) defines the maximum percentage of dispersed generation penetration in the entire distribution network; restriction (8) indicates the binary nature of the decision variable $x_i$; and inequality constraint (9) represents the positiveness definition of the loadability coefficient.

Remark 1.

The core complication of the optimization model (1)–(9) corresponds to the non-convexity of the solution space due to the presence of products among decision variables and trigonometric functions in the active and reactive power balance constraints, in addition to the binary nature of the decision variable $x_i$. As a result, it is necessary to use advanced optimization techniques in conjunction with its solution, as presented in the following section.

3. Solution Methodology

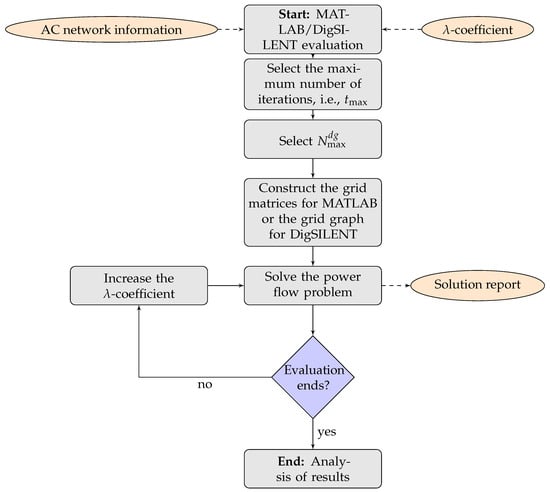
Here, we adopt an optimization methodology composed of three steps to present the optimal solution of the optimization problem defined in (1) to (9). The three steps are as follows: (i) solving the optimization model with the aid of GAMS software; (ii) validating the solution using a recursive solution of the power flow problem by increasing the load consumption using loop cycles; and (iii) validating the results in DigSILENT software by implementing a program in DigSILENT Programming Language (DPL). Some of the most critical aspects in the implementation of the solution methodology are described below.

3.1. GAMS Implementation

GAMS software is a popular optimization tool used in academics and industry to solve large-scale optimization problems in science and engineering [37]. Some of the well-known applications of GAMS software include renewable energy and battery energy storage integration in power and distribution networks [5,7,38], optimization of pump and valve schedules in complex large-scale water distribution systems [39], multi-objective optimization of the stack of a thermoacoustic engine [40], and application in DC distribution networks [41,42].

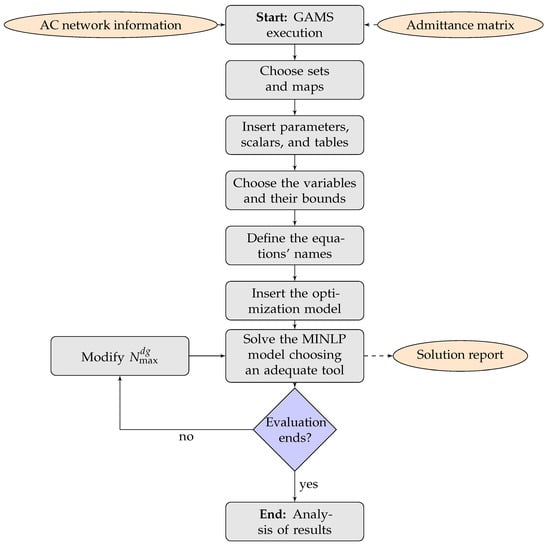
Figure 1 illustrates the general implementation of an optimization model in GAMS software. It should be noted that, since the software uses advanced optimization techniques, such as branch & bound and interior point methods, to decouple and solve the complete optimization model, the primary requirement in the GAMS implementation corresponds to ensuring a feasible optimization model [32,43].

Remark 2.

The solution of the optimization model (1)–(9) was reached using the BONMIN solver by varying the number of dispersed generators from 1 to 3 in order to identify the effect on the loadability factor of the network.

References [32,43] provide several numerical examples and tips for GAMS beginners and serve as useful guides when consulting particular aspects of GAMS software.

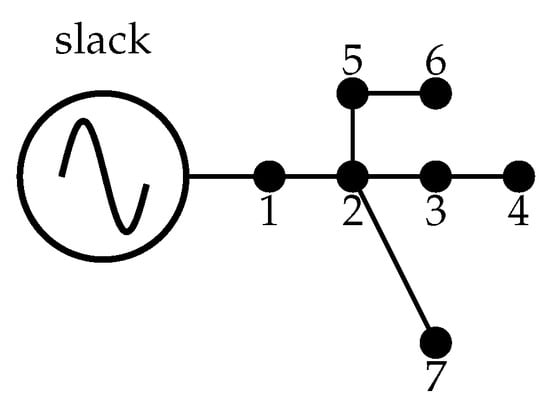
The general methodology for solving MINLP models in GAMS software, as depicted in Figure 1, is illustrated here using a numerical example with a grid of 7 nodes taken from Reference [31]. The electrical configuration of this grid is depicted in Figure 2, and information concerning the branches and loads is presented in

Table 1. Branch and nodal parameters for the 7-bus system.

Node i	Node j	${\mathit{R}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{X}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)
1	2	0.5025	0.3025	1000	600
2	3	0.4020	0.2510	900	500
3	4	0.3660	0.1864	2500	1200
2	5	0.3840	0.1965	1200	950
5	6	0.8190	0.7050	1050	780
2	7	0.2872	0.4088	2000	1150

. This grid is operated with 23 kV at the substation bus and has a radial configuration. Note that the GAMS implementation uses 1 MVA and 23 kV as power and voltage bases, respectively.

The optimization model (1)–(9), when implemented for the 7-bus test feeder, assumes that each generator can produce a maximum power of 2 MW, thus implying the possibility of installing two dispersed sources. The GAMS implementation is illustrated in Listing 1. Note that, in this implementation, the minimum and maximum voltages are set at $0.40$, and $1.20$; in addition, the $\beta$-coefficient is set as 0.30 for this numerical illustration.

Listing 1. GAMS implementation of the voltage stability model (1)–(9).

Listing 1. GAMS implementation of the voltage stability model (1)–(9).

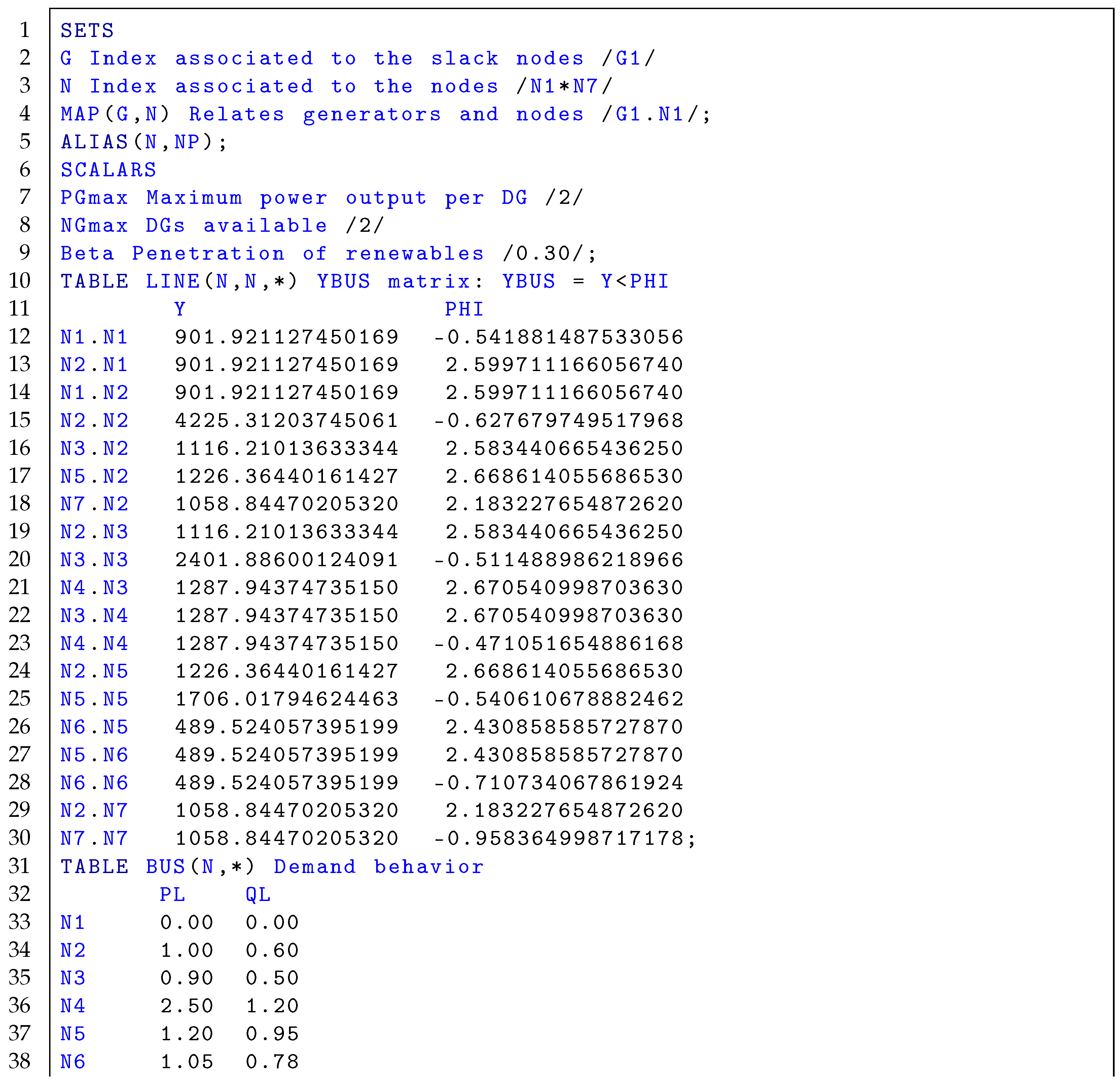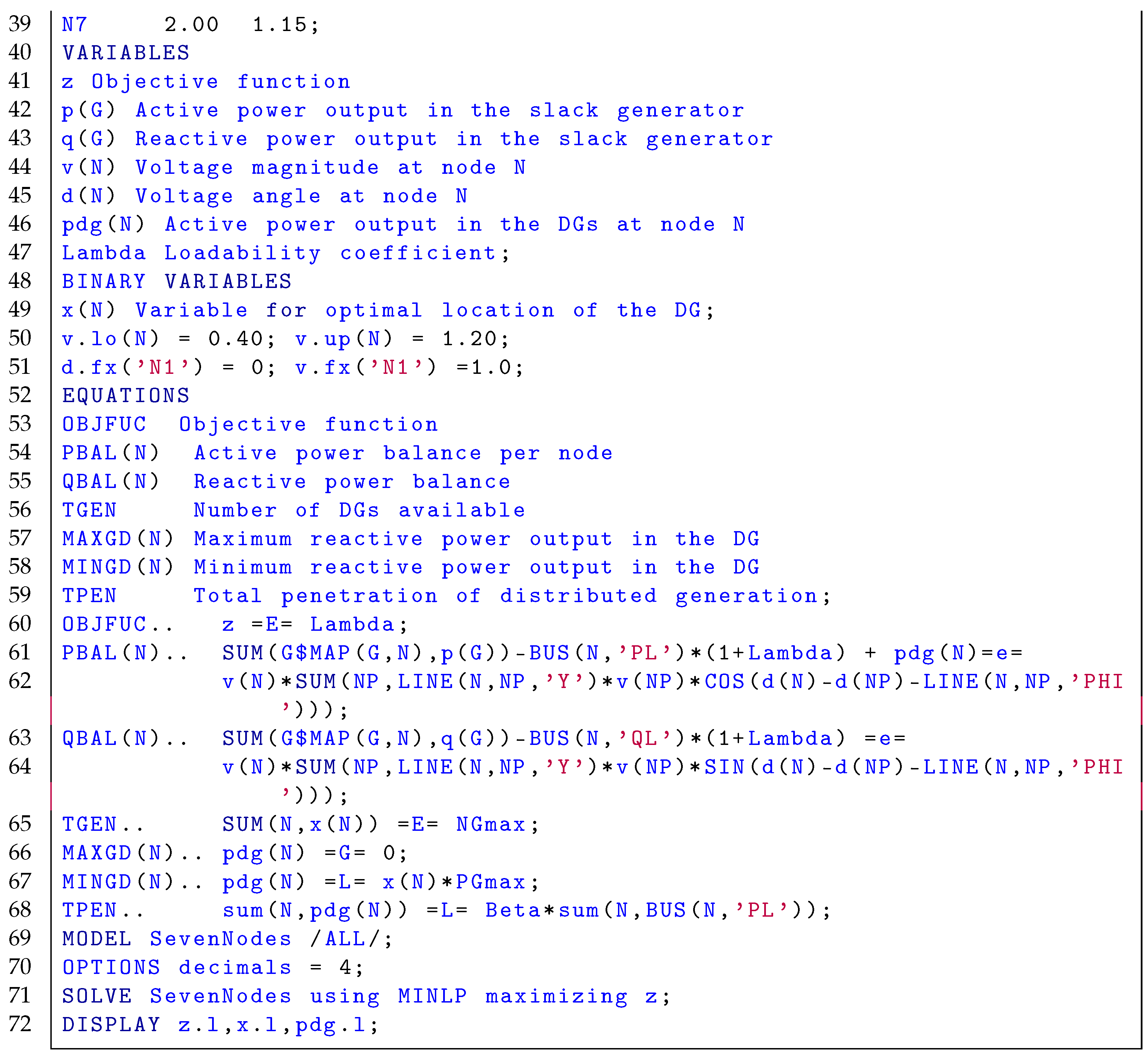The following observations can be isolated from the GAMS implementation illustrated in Listing 1:

✓

GAMS software is a mathematical interpreter where the set of equations that described the studied problem is implemented using a very similar syntax.

✓

It has multiple MINLP solvers, and it selects the most adequate solver depending on the internal complexity of the studied model. We have selected the BONMIN solver as it combines both the Branch & Cut method and the interior point method in its approach to solving MINLP problems.

✓

The complete implementation of the model using the nodal admittance matrix implies that this matrix must be calculated and introduced to the model manually. For the 7-bus system, this matrix was calculated using the successive approximation power flow method and introduced in the GAMS model between lines 10 and 30 in Listing 1.

Once the GAMS code in Listing 1 is executed, it was found that the dispersed generators for this system are located at nodes 4 and 6 with capacities of 2000 kW and 595 kW, respectively. In addition, the $\lambda$-coefficient takes a value of $15.8965$. Reference [32] provides comprehensive details about the implementation of GAMS to solve electrical engineering problems. It is also important to highlight that, once GAMS software has resolved the optimization problem with the BONMIN solver, i.e., once the location and sizes of the generators have been identified, the value of the $\lambda$-coefficient is verified with the recursive validation using MATLAB/DigSILENT. This recursive validation is described in the following subsection.

3.2. Recursive Solution and DigSILENT Validation

To validate the solution provided by GAMS software, the validation stage of the proposed solution methodology was implemented using the power flow method (successive approximation power flow method [33]) in the MATLAB programming environment, which was evaluated recursively until the convergence failed. An identical approach was adopted in DigSILENT software using the Newton–Raphson power flow method. The general flow diagram for the numerical validation in MATLAB and DigSILENT is depicted in Figure 3.

The primary advantage of the proposed validation methodology using power flow approaches implemented in MATLAB and DigSILENT software corresponds to the possibility of storing the voltage profile for each simulation scenario to construct the nose curve for the most critical nodes.

The power flow formula in the case of the recursive implementation of the successive approximation method is presented below:

$$\begin{array}{c}\hfill {\mathbb{V}}_d^{t+1}={\mathbb{Y}}_{dd}^{-1}\left[{\mathbf{diag}}^{-1}\left({\mathbb{V}}_d^{t,\star }\right)\left({\mathbb{S}}_{dg}^{t,\star }-{\mathbb{S}}_d^{t,\star }\right)-{\mathbb{Y}}_{ds}{\mathbb{V}}_s\right],\end{array}$$

(10)

where ${\mathbb{V}}_d^t$ denotes the vector containing all the complex voltages in demand nodes, ${\mathbb{Y}}_{dd}$ corresponds to a sub-matrix that relates demand nodes among them, ${\mathbb{S}}_{dg}^{t,\star }$ indicates the vector containing all the complex power generation in dispersed generators, ${\mathbb{S}}_d^{t,\star }$ represents the vector that contains all the complex power demands, ${\mathbb{Y}}_{ds}$ corresponds to a rectangular sub-matrix that relates the demand and the slack nodes, and ${\mathbb{V}}_s$ corresponds to the vector that contains all the voltages in the slack node. Note that t is the iterative counter, implying that, for $t=0$, the initial voltage vector is assigned as ${\mathbb{V}}_d^0=\mathbf{1}\angle 0^{\circ }$ [44].

Note that the successive approximation power flow Formula (10) is evaluated until the convergence error is reached or the maximum number of iterations is fulfilled. The convergence criterion takes the following form:

$$\begin{array}{c}\hfill \max \left\{\left|{\mathbb{V}}_d^{t+1}||-\left|{\mathbb{V}}_d^t\right|\right|\right\}\le \epsilon ,\end{array}$$

(11)

where $\epsilon$ corresponds to the maximum convergence error, which was assigned, as recommended in Reference [44], as $1\times {10}^{-10}$.

Remark 3.

The most significant advantage of the successive approximation power flow method defined in (11) is that its convergence is ensured through the application of the Banach fixed-point theorem [33]. However, when the system approaches the voltage collapse point, the number of iterations increases, which can be used as a stopping criterion to finalize the search of the λ-coefficient, as explained in Figure 3.

4. Test Feeders

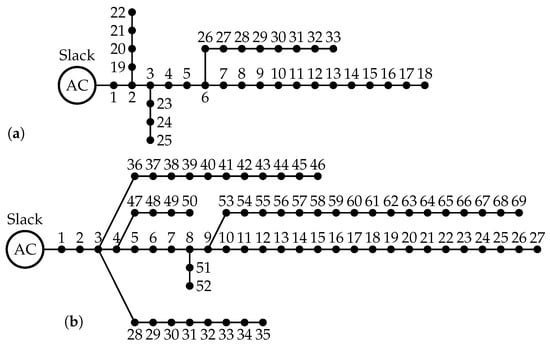
Two test feeders were employed to validate the proposed solution methodology for enhancing the voltage stability margin in AC distribution networks by considering the optimal placement and sizing of dispersed generators. The test feeders correspond to the IEEE 33-bus system and the IEEE 69-bus system, both with a radial structure and operated at the substation bus with 12.66 kV of nominal voltage output. The electrical configuration of both the test feeders is depicted in Figure 4.

Parametric information related to the active and reactive power consumption and the line resistance and reactance parameters for both the test feeders are reported in

Table 2. IEEE 33-bus system parameters.

Node i	Node j	${\mathit{R}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{X}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)	Node i	Node j	${\mathit{R}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{X}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)
1	2	0.0922	0.0477	100	60	17	18	0.7320	0.5740	90	40
2	3	0.4930	0.2511	90	40	2	19	0.1640	0.1565	90	40
3	4	0.3660	0.1864	120	80	19	20	1.5042	1.3554	90	40
4	5	0.3811	0.1941	60	30	20	21	0.4095	0.4784	90	40
5	6	0.8190	0.7070	60	20	21	22	0.7089	0.9373	90	40
6	7	0.1872	0.6188	200	100	3	23	0.4512	0.3083	90	50
7	8	1.7114	1.2351	200	100	23	24	0.8980	0.7091	420	200
8	9	1.0300	0.7400	60	20	24	25	0.8960	0.7011	420	200
9	10	1.0400	0.7400	60	20	6	26	0.2030	0.1034	60	25
10	11	0.1966	0.0650	45	30	26	27	0.2842	0.1447	60	25
11	12	0.3744	0.1238	60	35	27	28	1.0590	0.9337	60	20
12	13	1.4680	1.1550	60	35	28	29	0.8042	0.7006	120	70
13	14	0.5416	0.7129	120	80	29	30	0.5075	0.2585	200	600
14	15	0.5910	0.5260	60	10	30	31	0.9744	0.9630	150	70
15	16	0.7463	0.5450	60	20	31	32	0.3105	0.3619	210	100
16	17	1.2860	1.7210	60	20	32	33	0.3410	0.5302	60	40

and

Table 3. IEEE 69-bus system parameters.

Node i	Node j	${\mathit{R}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{X}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)	Node i	Node j	${\mathit{R}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{X}}_{\mathit{ij}}$ ($\mathsf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)
1	2	0.0005	0.0012	0.00	0.00	3	36	0.0044	0.0108	26.00	18.55
2	3	0.0005	0.0012	0.00	0.00	36	37	0.0640	0.1565	26.00	18.55
3	4	0.0015	0.0036	0.00	0.00	37	38	0.1053	0.1230	0.00	0.00
4	5	0.0251	0.0294	0.00	0.00	38	39	0.0304	0.0355	24.00	17.00
5	6	0.3660	0.1864	2.60	2.20	39	40	0.0018	0.0021	24.00	17.00
6	7	0.3810	0.1941	40.40	30.00	40	41	0.7283	0.8509	1.20	1.00
7	8	0.0922	0.0470	75.00	54.00	41	42	0.3100	0.3623	0.00	0.00
8	9	0.0493	0.0251	30.00	22.00	42	43	0.0410	0.0478	6.00	4.30
9	10	0.8190	0.2707	28.00	19.00	43	44	0.0092	0.0116	0.00	0.00
10	11	0.1872	0.0619	145.00	104.00	44	45	0.1089	0.1373	39.22	26.30
11	12	0.7114	0.2351	145.00	104.00	45	46	0.0009	0.0012	29.22	26.30
12	13	1.0300	0.3400	8.00	5.00	4	47	0.0034	0.0084	0.00	0.00
13	14	1.0440	0.3450	8.00	5.50	47	48	0.0851	0.2083	79.00	56.40
14	15	1.0580	0.3496	0.00	0.00	48	49	0.2898	0.7091	384.70	274.50
15	16	0.1966	0.0650	45.50	30.00	49	50	0.0822	0.2011	384.70	274.50
16	17	0.3744	0.1238	60.00	35.00	8	51	0.0928	0.0473	40.50	28.30
17	18	0.0047	0.0016	60.00	35.00	51	52	0.3319	0.1114	3.60	2.70
18	19	0.3276	0.1083	0.00	0.00	9	53	0.1740	0.0886	4.35	3.50
19	20	0.2106	0.0690	1.00	0.60	53	54	0.2030	0.1034	26.40	19.00
20	21	0.3416	0.1129	114.00	81.00	54	55	0.2842	0.1447	24.00	17.20
21	22	0.0140	0.0046	5.00	3.50	55	56	0.2813	0.1433	0.00	0.00
22	23	0.1591	0.0526	0.00	0.00	56	57	1.5900	0.5337	0.00	0.00
23	24	0.3463	0.1145	28.00	20.00	57	58	0.7837	0.2630	0.00	0.00
24	25	0.7488	0.2475	0.00	0.00	58	59	0.3042	0.1006	100.00	72.00
25	26	0.3089	0.1021	14.00	10.00	59	60	0.3861	0.1172	0.00	0.00
26	27	0.1732	0.0572	14.00	10.00	60	61	0.5075	0.2585	1244.00	888.00
3	28	0.0044	0.0108	26.00	18.60	61	62	0.0974	0.0496	32.00	23.00
28	29	0.0640	0.1565	26.00	18.60	62	63	0.1450	0.0738	0.00	0.00
29	30	0.3978	0.1315	0.00	0.00	63	64	0.7105	0.3619	227.00	162.00
30	31	0.0702	0.0232	0.00	0.00	64	65	1.0410	0.5302	59.00	42.00
31	32	0.3510	0.1160	0.00	0.00	11	66	0.2012	0.0611	18.00	13.00
32	33	0.8390	0.2816	14.00	10.00	66	67	0.0470	0.0140	18.00	13.00
33	34	1.7080	0.5646	19.50	14.00	12	68	0.7394	0.2444	28.00	20.00
34	35	1.4740	0.4873	6.00	4.00	68	69	0.0047	0.0016	28.00	20.00

. This information was obtained from Reference [15].

In the case of dispersed generators for the IEEE 33-bus system, it is assumed that each dispersed generator can generate a maximum rating of 1200 kW, and for the IEEE 69-bus system, the threshold is extended to 2500 kW. Moreover, the numerical evaluation used 12.66 kV and 100 kVA as the voltage and power bases, respectively.

5. Computational Validation

The simulation cases outlined below were considered to validate the proposed methodology, i.e., to find the maximum loadability factor $\lambda$:

✓

Case 1 (C1): Corresponds to the benchmark case of the network, i.e., without including dispersed generators.

✓

Case 2 (C2): Considers the possibility of installing one to three dispersed generators with a total grid penetration of 40%, i.e., $\beta =0.40$.

✓

Case 3 (C3): Considers the possibility of installing one to three dispersed generators with a total grid penetration of 60%, i.e., $\beta =0.60$.

5.1. Results in the IEEE 33-Bus System

The voltage regulation bounds were relaxed to $V_{\max }=1.20$ pu and $V_{\min }=0.30$ pu to ensure that GAMS software solves the optimization model (1)–(9), since the primary objective is to determine the maximum value of the $\lambda$-coefficient before reaching the voltage collapse point, implying that the typical regulation bounds of $\pm 10\%$ do not correspond under this extreme condition.

Table 4. Numerical performance of the $\lambda$-coefficient in the IEEE 33-bus system for all the simulation cases.

Case	${\mathit{N}}_{\mathit{ava}}^{\mathit{dg}}$	Location (node)	PG1 (pu)	PG2 (pu)	PG3 (pu)	GAMS ($\mathit{\lambda }$)	MATLAB DigSILENT ($\mathit{\lambda }$)
1	0	0	—	—	—	2.4079	2.4079
	1	18	1.2000	—	—	2.9128	2.9128
2	2	(18,32)	0.9316	0.5544	—	3.0590	3.0590
	3	(17,18,32)	0.5735	0.3663	0.5462	3.0635	3.0635
	1	18	1.2000	-	—	2.9128	2.9128
3	2	(17,32)	1.2000	1.029	—	3.3068	3.3068
	3	(17,18,32)	0.8324	0.3885	1.0080	3.3091	3.3091

lists the numerical results in the IEEE 33-bus system for all the simulation cases studied.

From the numerical results in Table 4, the following can be summarized: (i) the active power injection allowed the loadability factor to increase by approximately $27.22\%$ and $37.43\%$ for the simulation cases C2 and C3, respectively, with the maximum number of dispersed generators installed, i.e., $N_{ava}^{dg}=3$; (ii) the optimization methodology identified an identical set of nodes for one to three dispersed generators independent of the percentage of generation penetration allowed, i.e., nodes 17, 18, and 32; however, depending on the $\beta$-coefficient, the final value of the loadability coefficient showed important variations, which was an expected behavior; as the percentage of generation increases, the capacity of the grid to support a load also increases; and (iii) the $\lambda$-coefficient identified by the BONMIN solver in GAMS was exactly the same as that provided by the recursive approach in the MATLAB/DigSILENT environments. However, the maximum variation step in the $\lambda$ increments was set as $1\times {10}^{-6}$ to ensure this equivalence; this implies that $2.9128$ million power flow solutions are required in C2 with one dispersed generator, and $3.3091$ million power flow solutions are required in C3 with three dispersed generators.

Further, the following observations were noted concerning the processing times. For the IEEE 33-bus system, the solution of the benchmark case in GAMS software with the BONMIN solver took about $0.387$ ms; in addition, the processing time was about $3.0632$ s in the case of one dispersed generator, about $6.770$ s for two generators, and about 3.423 s for three generators. Note that these processing times confirm the effectiveness and robustness of GAMS software in solving MINLP models, as demonstrated in Reference [32].

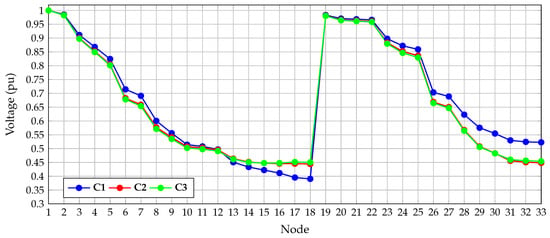
Figure 5 presents the voltage profiles in the benchmark case and the C2 and C3 cases with three dispersed generators installed. These profiles were obtained from DigSILENT software to illustrate the effect of the optimal placement and sizing of dispersed generators in the IEEE 33-bus system.

The voltage profiles shown in Figure 5 indicate that the minimum voltage profile in C1 was caused at node 18 with a magnitude of 0.3905 pu, which directly relates to the numerical results in Table 4. Accordingly, in all the simulation cases, node 18 was selected as the optimal location for the dispersed generators, particularly since the unique increase in the voltage profile at this node reduces the total power consumption through the injection of active power locally.

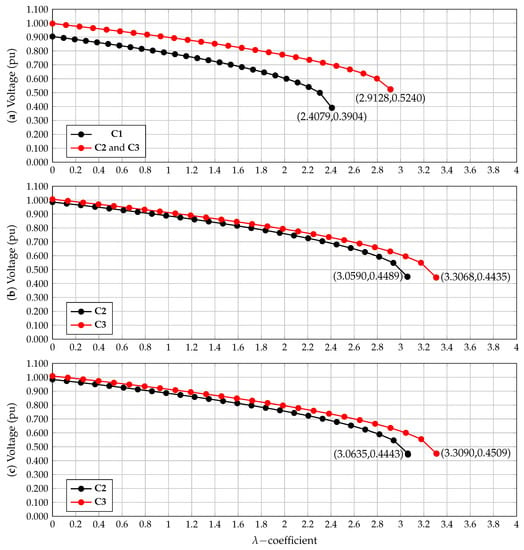
Figure 6 depicts the voltage performance at the worst node, i.e., bus 18, for all the simulation cases and for different numbers of dispersed generators.

From the results in Figure 6, we can note that (i) the worst voltage profile occurs in C1, when the grid does not have the penetration of dispersed generation, with a magnitude of 0.3904 pu when the loadability index assumes a value of 2.4079 (Figure 6a); however, when one dispersed generator was installed in C2 and C3, the voltage profile increased to 0.5240 pu with the $\lambda$-coefficient increasing to 2.9128, which is an improvement of approximately $20.96\%$ with respect to the benchmark case; (ii) when two dispersed generators were installed for C2 and C3, it was observed that the $\lambda$-coefficient values became 3.0590 and 3.30968, respectively, which correspond to improvements of approximately $5.02\%$ and $13.53\%$ with respect to the same scenarios with one dispersed generator; however, the voltage collapse point does not present high variations; it was approximately 0.4489 pu and 0.4435 pu in C2 and C3, respectively; and (iii) when three dispersed generators were installed, the increments of the $\lambda$-coefficient were approximately $0.15$% and $0.07\%$, respectively. It can be concluded from these values that the limitation imposed by the $\beta$-coefficient saturates the total improvement of the loadability index when the possibility of installing dispersed generators increases. However, the numerical results in the IEEE 33-bus system exhibited the effectiveness of using dispersed generation to enhance the grid voltage stability index.

5.2. Results in the IEEE 69-Bus System

For the computational evaluation of the test feeder, the voltage regulation constraints were relaxed to $V_{\max }=1.20$ pu and $V_{\min }=0.45$ pu during the GAMS implementation of the model (1)–(9). It is worth recalling that these relaxations were only used to determine the maximum $\lambda$-coefficient. During normal operative conditions, these bounds must be restored to $\pm 10\%$ to ensure the fulfillment of regulatory policies.

Table 5. Numerical performance of the $\lambda$-coefficient in the IEEE 69-bus system for all the simulation cases.

Case	${\mathit{N}}_{\mathit{ava}}^{\mathit{dg}}$	Location (node)	PG1 (pu)	PG2 (pu)	PG3 (pu)	GAMS ($\mathit{\lambda }$)	MATLAB DigSILENT ($\mathit{\lambda }$)
1	0	0	—	—	—	2.2118	2.2118
	1	58	1.5562	—	—	2.6191	2.6191
2	2	(64,65)	1.3289	0.2273	—	2.8408	2.8408
	3	(61,64,65)	0.4276	0.9011	0.2274	2.8432	2.8431
	1	59	2.3343	—	—	2.8825	2.8825
3	2	(61,64)	1.1140	1.2202	—	3.1394	3.1394
	3	(61,64,65)	1.1172	0.9719	0.2451	3.1403	3.1403

reports the numerical performance for all the simulation cases in the IEEE 69-bus system using the BONMIN solver in the GAMS environment and the verification in MATLAB and DigSILENT software.

The numerical results listed in Table 5 yield the following observations: (i) For C2 and C3 with three units of generation, increments of approximately $28.55\%$ and $41.98\%$, respectively, were observed in the $\lambda$-coefficient. Moreover, the verification processes in MATLAB and DigSILENT indicated that, for all the simulation cases, the $\lambda$-coefficient was the same as that provided by GAMS software, which confirms the efficacy of the recursive evaluation processes. In C2 with two distributed generators, an estimation error lower than $4\times {10}^{-3}\%$ was noted, which is attributable to convergence errors of the power flow methods used in the recursive validations owing to the near singularity behavior of the Jacobian matrix when approaching the voltage collapse point. (ii) In the case of one dispersed generator, when the $\beta$-coefficient was varied from 40% to 60%, it was observed that the location of the generator changed from node 58 to 59. However, in both the cases, the $\lambda$-coefficient was higher than 2.84, which improved the loadability coefficient by approximately $28.43\%$ and $30.32\%$, respectively. (iii) When two and three dispersed generators were installed, they always appeared at nodes 64 and 65; however, node 65 had minimum generation with values of $0.2274$ pu and $0.2451$ pu, respectively. This behavior can be explained as follows: since the active power injection in upstream nodes reduces the power requirement at this node, voltage profiles increase owing to the power injections at nodes 61 and 64, respectively.

It was observed that the total processing times required for GAMS software with the BONMIN solver in the IEEE 69-bus system was $648$ ms for the base cases, $23.353$ s for one dispersed source, $11.867$ s in the case of two generators, and about $9.585$ s for three generators. These processing times confirm the effectiveness and robustness of the GAMS in solving complex MINLP models [32].

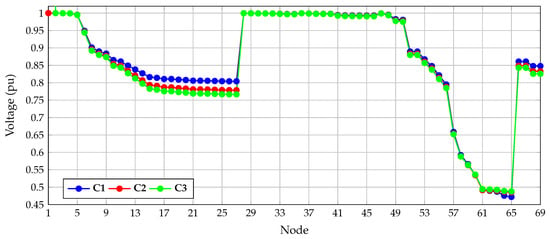
Figure 7 presents the voltage profiles in the benchmark case and C2 and C3 with three dispersed generators installed. These profiles were obtained from DigSILENT software to illustrate the effect of the optimal placement and sizing of dispersed generators in the IEEE 69-bus system.

Figure 7 presents the weakest node in the IEEE 69-bus system, which is node 65; it has a voltage magnitude of $0.4720$ pu in C1. Moreover, the figure confirms that all the best nodes for the optimal placement and sizing of dispersed generators to improve the voltage stability index are in the region between nodes 58 and 65, as presented in Table 5.

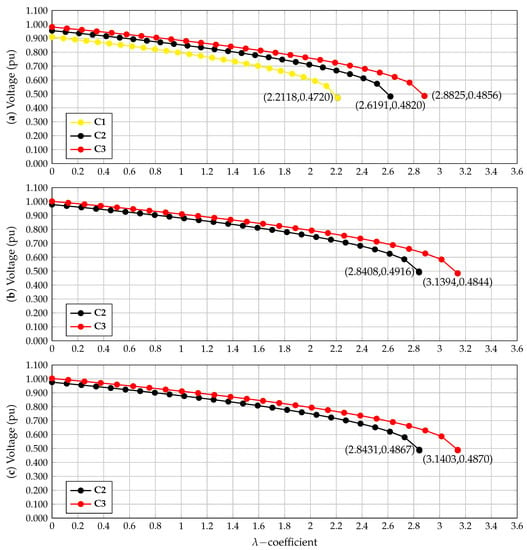
Figure 8 depicts the voltage performance at the worst node, i.e., bus 65, for all the simulation cases with different numbers of dispersed generators.

The numerical results in Figure 8 indicate the following: (i) the installation of one dispersed generator increased the loadability factor in the range of $18.41\%$ and $30.32\%$, while the point of voltage collapse improved from $0.4720$ pu to $0.4820$ pu and $0.4856$ pu, respectively; (ii) in general, the possibility of installing three dispersed generators allows better voltage profile performances in the 65-node bus system, independent of the value of the $\beta$-coefficient, since distributed power injections allow better load flow redistribution, which is directly linked to the final voltage values; and (iii) for $\lambda$ values between 0 and 0.60, it can be assured that, independent of the number of generators installed in the network, the voltage profile at the worst node, i.e., node 65, will be higher than 0.90 pu. This confirms the efficacy of installing dispersed generators to improve the voltage stability index of the network and simultaneously fulfill regulatory policies regarding voltage profiles under normal operating conditions.

6. Conclusions and Future Research

An exact MINLP formulation was proposed to solve the problem of determining the maximum loadability in medium-voltage networks by considering the optimal placement and sizing of dispersed generators. The solution of the MINLP model was reached using the BONMIN solver in the GAMS environment. A small 7-bus system was used as a numerical example to illustrate the usage of GAMS from a tutorial perspective. The value of the $\lambda$-coefficient provided by GAMS in both the test feeders was verified through evaluations implemented in MATLAB using the successive approximation power flow and also in DigSILENT software using the Newton–Raphson power flow method. Numerical results demonstrated that the $\lambda$-coefficient can be improved between $20.96\%$ and $37.43\%$ for the IEEE 33-bus system when one to three dispersed generators are installed and between $18.41\%$ and $41.98\%$ for the IEEE 69-bus system in identical simulation conditions.

The numerical results indicated that, in both the test feeders, the regions where the dispersed generators corresponded to the nodes were associated with the worst voltage profiles, i.e., node 18 for the IEEE 33-bus system and node 65 for the IEEE 69-bus system. In addition, the number of dispersed generators available for installation in conjunction with the values of the $\beta$-coefficient directly influence the total improvement of the loadability coefficient; for two or three dispersed sources, the differences in the indicator were lower than 2%, implying that the limitation imposed by the $\beta$-coefficient produces a saturation effect in the $\lambda$-coefficient.

Future studies can consider the following research directions: (i) the reformulation of the exact MINLP model through a mixed-integer conic model to ensure the determination of the global optimum owing to the convexity properties assignable to the conic solution spaces; (ii) the formulation of an optimization model with reactive power compensators (STATCOMs or capacitor banks) to enhance the voltage stability margin in medium-voltage distribution networks; and (iii) economical aspects regarding batteries and renewable generation can be included in the proposed model for stability studies in distribution networks.