Particle Swarm Optimization-Based Unconstrained Polygonal Fitting of 2D Shapes

Abstract

In this paper, we present a general version of polygonal fitting problem called Unconstrained Polygonal Fitting (UPF). Our goal is to represent a given 2D shape S with an N-vertex polygonal curve P with a known number of vertices, so that the Intersection over Union (IoU) metric between S and P is maximized without any assumption or prior knowledge of the object structure and the location of the N-vertices of P that can be placed anywhere in the 2D space. The search space of the UPF problem is a superset of the classical polygonal approximation (PA) problem, where the vertices are constrained to belong in the boundary of the given 2D shape. Therefore, the resulting solutions of the UPF may better approximate the given curve than the solutions of the PA problem. For a given number of vertices N, a Particle Swarm Optimization (PSO) method is used to maximize the IoU metric, which yields almost optimal solutions. Furthermore, the proposed method has also been implemented under the equal area principle so that the total area covered by P is equal to the area of the original 2D shape to measure how this constraint affects IoU metric. The quantitative results obtained on more than 2800 2D shapes included in two standard datasets quantify the performance of the proposed methods and illustrate that their solutions outperform baselines from the literature.

1. Introduction

Polygonal shape fitting is a key problem in computer vision and computer graphics with several applications, including object recognition, computational cartography, signal summarization, and compression [1,2,3]. When curves are modeled, straight-line segments are usually preferred due to their simplicity. The polygonal fitting process saves memory space, reduces rendering time on graphics applications, and gives a more compact representation of the original shape.

According to the classical polygonal approximation problem of a 2D shape, the goal is to compute an N-vertex polygonal curve P that approximates the boundary B of the original shape S according to a predefined error criterion. In the classical polygonal approximation, the vertices of P are an ordered sub-sequence of the boundary points B [1]. The classical polygonal shape fitting provides poor results, especially when the number of vertices is low and the shape complexity is high. In this work, we study a general version of polygonal fitting, called the Unconstrained Polygonal Fitting (UPF) problem, to provide better solutions with the same number of vertices. According to UPF, the N-vertices of P can be placed anywhere in the 2D space. Therefore, the search space of UPF problem is a superset of the classical polygonal approximation (PA) problem, where the vertices are constrained to belong in the boundary of the given 2D shape. This means that the resulting solutions of UPF may better approximate the given curve than the PA problem solutions. This theoretically interesting computer vision problem has a compact and easy-to-grasp description, but a very high algorithmic complexity due to the large search space. Even if just a triangle ($N=3$) is used, there does not exist any trivial method to compute the optimal solution of UPF problem.

Different error criteria have been proposed for shape fitting/polygonal approximation problems. In this research, the Intersection over Union (IoU) metric between S and P is maximized given a fixed number of polygonal vertices N, without any assumption or prior knowledge of the object structure. IoU metric can be easily replaced by any other segmentation metric, for example accuracy and dice coefficient ($DICE$), without any change in the proposed methodology. Another problem instance that we experimentally study is to define the problem under the Equal Area constraint, which states that the area covered by the polygonal curve P should be equal to the area of the given shape S.

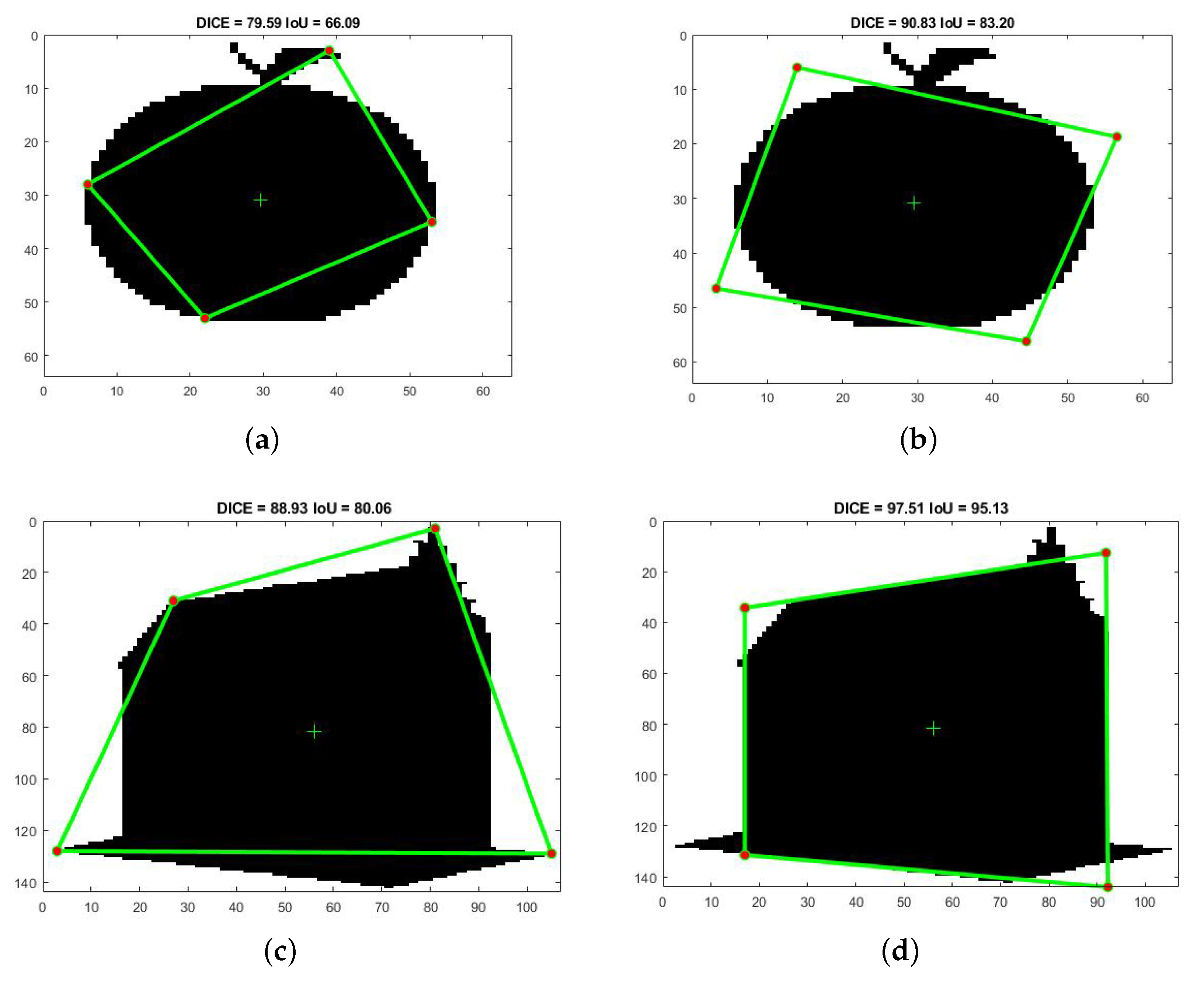
Figure 1 shows two example outputs of the classical polygonal approximation using the Douglas–Peucker algorithm [4] (left) and the unconstrained polygonal fitting using the proposed method (right) for $N=4$ vertices. In both cases, it holds that the solution of the UPF problem provides higher IoU, DICE values compared with the results of Douglas–Peucker algorithm. In the first example with an apple, the Douglas–Peucker algorithm yields $DICE=79.6\%$, $IoU=66.1\%$ (Figure 1a), while the proposed method yields $DICE=90.8\%$, $IoU=83.2\%$ (Figure 1b). In the second example with a building, the Douglas–Peucker algorithm yields $DICE=88.9\%$, $IoU=80.1\%$ (Figure 1c), while the proposed method yields $DICE=97.5\%$, $IoU=95.1\%$ (Figure 1d). There exist several examples where there exist significant differences in performance between the optimal solutions of the two problems, especially for lower values of N, where the optimal solutions of UPF space may be far from the shape boundary.

In summary, the main contributions of our work are the following: To the best of our knowledge, this is the first work to define and solve the UPF problem. The proposed method solves the UPF problem via Particle Swarm Optimization (PSO) [5] that quickly explore the search space. The proposed framework suggests solutions that outperform baselines in quantitative terms, even if are not necessarily optimal due to the PSO. Especially in a low-dimensional search space, which is true for low number of vertices, the proposed method clearly outperforms baselines of classical PA, since even the optimal solutions of the classical PA problem usually fail to obtain high performance results due to the limited search space (shape boundary) of PA problem.

2. Related Work

The problem of shape fitting/polygonal approximation has been studied extensively during the last five decades [1,3,4,6]. The methods that have been developed solve the problem by approximating the original shape S by a polygonal curve P under the constraint that the P vertex sequence is an ordered sub-sequence of the vertices along shape boundary. The polygonal approximation problem can be formulated in two ways [1,6]:

• The problem of better fitting, where the approximation error is minimized or the fitting accuracy is maximized given the number of vertices N.
• The problem of minimum number of vertices, where the approximation error or the fitting accuracy is bounded and the goal is to find the minimum number of vertices that satisfy the given bound.

The polygonal approximations algorithms can be classified as (1) optimal or non-optimal and (2) supervised or unsupervised algorithms [6]. The non-optimal algorithms do not guarantee any kind of optimum as optimal algorithms, but can find reasonable polygonal approximations faster than the optimal ones. The supervised algorithms take into account parameters to generate polygonal approximations, while the unsupervised algorithms generate the polygonal approximations without parameters. The Douglas–Peucker algorithm [4] is one of the first successful algorithms developed for polygonal approximation and cartographic generalization [7]. The algorithm is also widely used in robotics to perform simplification [8]. The purpose of the algorithm is, given a curve composed of line segments, to find a similar polygonal curve with fewer points so that the simplified curve consists of a subset of the points that defined the original curve. Yin [9] presents a polygonal approximation approach based on the discrete particle swarm optimization (PSO) algorithm. Each particle represented as a binary vector corresponds to a candidate solution to the polygonal approximation problem. A swarm of particles is initiated and flies through the solution space for targeting the optimal solution. In [10], the authors proposes a non-optimal and unsupervised algorithm for generation of polygonal approximations based on the convex hull of the 2D closed curves or contours. The significance levels of the contour points are computed using a symmetric version of the well-known Douglas–Peucker algorithm and, finally, a thresholding process is applied to obtain the vertices or dominant points of the polygonal approximation.

In the case of 2D shape fitting, a 2D binary image is given with foreground points representing the shape to be modeled. This image can be the result of any object detection or image segmentation method (e.g., [11,12,13]). Several models can be used to solve the 2D shape fitting problem. In the literature, there exists several approaches that fit a set of ellipses to the given 2D shape based on (a) the Hough Transform, (b) Genetic and Optimization Algorithms, and (c) edge-following [13,14]. In [13], a framework has been proposed to represent a given 2D shape with an automatically determined number of ellipses based on expectation maximization criterion, so that the total area covered by the ellipses is equal to the area of the original shape. In [3], an algorithm is proposed to extract and vectorize objects in images with low-complexity polygons based on local merging and splitting of cells. Departing from a polygonal partition that oversegments an image into convex cells, the algorithm refines the geometry of the partition while labeling its cells by a semantic class. The authors applied their method to a variety of scenes, from organic shapes to human-made objects through floor maps and line-drawing sketches.

Concerning the metrics that have been used to measure the performance on shape fitting problem, they can be classified into:

• Boundary-based metrics that compare the distance between the boundary of given shape and the approximated curve. Some of the most well-known metrics are the root mean square error ($RMSE$) between the two curves and the maximum error between the boundary S and their corresponding subcurves of P. These metrics have the advantage that can also be applied on given curves (non closed contours), but are sensitive to boundary noise [1,6].
• Region-based metrics that compare the region of the approximated shape and the given shape. Region-based metrics are more tolerant to noise, since they do not restrict themselves to the boundaries of shapes but rather take into account all shape points [13]. Common metrics of this category are the Intersection over Union (IoU) and the Dice coefficient (DICE), which is defined by twice the area of the shapes’ intersection divided by the sum of the areas of each shape. Both of them have also been used to measure the performance of image segmentation methods [15].

3. Unconstrained Polygonal Fitting

3.1. Problem Formulation

We assume a binary image I that represents a 2D shape S. A pixel p of I belongs either to the foreground S ($I\left(p\right)=1$) or to the background ($I\left(p\right)=0$). The area A of the 2D shape is given by

$$A\left(S\right)=\sum _{p\in S}I\left(p\right).$$

(1)

We also assume a closed polygonal curve P with N vertices $P_i$, $i\in \{1,...,N\}$, which belong in the 2D space (not necessary on the boundary of S). The binary image $I_P$ is also defined so that $I_P\left(p\right)=1$ at points p that are inside any of the polygonal curve P and $I_P\left(p\right)=0$, otherwise. Then, the Intersection over Union $IoU\left(P\right)$ metric between the 2D shape S and P is calculated as follows:

$$IoU\left(P\right)=\frac{{\sum }_{p\in S}{I}_P\left(p\right)}{{\sum }_{p\in I}max(I\left(p\right),I_P\left(p\right))}.$$

(2)

Essentially, $IoU\left(P\right)$ is the percentage of the 2D shape points that are under polygonal curve P divided by the number of 2D points that belong to shape S either polygonal curve P. The optimal solution of Unconstrained Polygonal Fitting problem is the closed polygonal curve P that maximizes the $IoU\left(P\right)$.

$$P^{*}=argma{x}_{P}IoU\left(P\right)$$

(3)

3.2. Equal Area Principle

The equal area principle (constraint) has been used in [13] restricting the area of P to be equal with the area of the given shape. This is a reasonable constraint, in the sense that we except in many cases that the optimal solutions of the UPF problem have almost the same area with the given shape S. So, by adding this extra constraint, we reduce the search space of the problem without mainly affecting the performance of the method. Additionally, some applications may also include this requirement. Let $A\left(P\right)$ denote the areas of polygonal curve P, $A\left(P\right)={\sum }_{p\in I}{I}_P\left(p\right)$. According to the Equal Area constraint, it holds that the area of polygonal curve P is equal with the area of shape S meaning that $A\left(P\right)=A\left(S\right)$. Therefore, the optimal solution of Unconstrained Polygonal Fitting problem under equal area principle is the closed polygonal curve P that maximizes the $IoU\left(P\right)$ under equal area principle.

$$P^{*}=argma{x}_{P}IoU\left(P\right),A\left(P\right)=A\left(S\right)$$

(4)

Hereafter, we describe a simple procedure that applies the equal area principle on a polygonal curve P, yielding a new polygonal curve $\overline{P}$ so that $A\left(\overline{P}\right)=A\left(S\right)$. Let C be the centroid of S (the centroid of P can be also used; the centroid of S is more preferable for stability reasons in an iterative process) and ${\overline{P}}_i$ be the i vertex of polygonal curve $\overline{P}$, $i\in \{1,...,N\}$.

$$C=\frac{1}{A\left(S\right)}\sum _{p\in S}p$$

(5)

$${\overline{P}}_i=C+\sqrt{\frac{A\left(S\right)}{A\left(P\right)}}·(P_i-C)$$

(6)

3.3. UPF-PSO and UPF-PSO-EA Algorithms

In this work, we cast the search for a single polygonal curve as a stochastic optimization problem that is solved based on Particle Swarm Optimization (PSO) [5,16,17]. PSO is a derivative-free optimization method that handles multi-modal, discontinuous objective functions with several local minima. Optimization is performed through the evolution of particles (candidate solutions) of a population (swarm). Particles lie in the parameter space of the objective function to be optimized, and evolve through a limited number of generations (iterations) according to a policy which emulates “social interaction”. The main parameters of PSO are the number of particles and generations, the product of which determines its computational budget (i.e., the number of objective function evaluations). PSO achieves near-optimal solutions, and has been successfully applied in several challenging optimization problems in computer vision and pattern recognition such as classification, clustering, prediction, image segmentation, video co-segmentation, object tracking [16,18,19,20].

The proposed Unconstrained Polygonal Fitting based on Particle Swarm Optimization Algorithm (UPF-PSO) optimizes the IoU metric (see Equation (3)) for different polygonal curves that are directly represented by PSO particles. The input to UPF-PSO is the binary image I, representing the given shape S and the number of vertices N of the polygonal closed curve that will be fitted to S. The UPF-PSO method quickly explores the search space starting from random solutions. Iteratively, PSO searches for a polygonal curve that maximizes the IoU metric.

We represent each particle by a $2·N$ vector with the 2D coordinates of the N points of the polygonal curve. In order to simplify the search space, we assume that the vertices are in clockwise order; otherwise, in the evolution process, we correct the order of vertices of each particle according to this hypothesis. The fitness (objective function) of the particle is directly given by the IoU metric of the particle (see Equation (2)). The UPF-PSO Algorithm is analytically described hereafter.

Initially, we create a population of M (e.g., $M=20$) particles that are located in random positions around the centroid of the shape S under the Equal Area Principle (see Section 3.2) to be in valid positions of the search space. In the evolution process, PSO finds the current optimal solution in order to update the best global solution. Additionally, the best local solution of each particle is also updated, where the IoU of the particle reaches a better solution. The method terminates when the number of iterations of the evolution process exceeds the given number of generations. In this work, we use the upper limit of 100 generations.

The proposed Unconstrained Polygonal Fitting based on Particle Swarm Optimization Algorithm under equal area principle (UPF-PSO-EA) is the UPF-PSO algorithm with the extra modification of applying the transform of Equation (6) at each iteration of PSO. This means that in each step of the method, the area of P is equal with the area of the given shape. Therefore, the solutions of UPF-PSO-EA can be completely different from the original UPF-PSO.

4. Experimental Evaluation

The evaluation of the proposed approach was based on two standard datasets from the literature. More specifically, we employ:

• MPEG-7 [21], which consists of 1400 binary shapes organized in 70 categories with 20 shapes per category. This dataset has been extensively used in shape tasks [13,22].
• A subset of LEMS [23]; that is, 1462 shapes that come from the following categories of the original database: Buildings, Containers, Fish, Fruit and vegetables, Misc Animal, People, Robots, Toddlers, and Turtles [13].

Figure 2 shows twelve sample images form the MPEG-7 dataset and LEMS dataset. The code implementing the proposed method together with the datasets are publicly available at https://sites.google.com/site/costaspanagiotakis/research/unconstrained-polygonal-fitting (accessed on 4 January 2024). The proposed methods have been implemented using MATLAB. All experiments were executed on an Intel I7 CPU processor at 2.3 GHz with 40 GB RAM. The average processing time for the execution of UPF-PSO given a single shape of our dataset is 0.809 s without any speed optimization and parallelization. It should be noticed that the processing time of the PSO based methods can be reduced up to $95\%$ via the parallelization of the $M=20$ particles. The average processing time of DP and SM methods is 0.013 and 0.213, respectively. The using of the equal area principle essentially does not affect the above processing times.

We compared the proposed Unconstrained Polygonal Fitting based on Particle Swarm Optimization Algorithm (UPF-PSO) and UPF-PSO under equal area principle (UPF-PSO-EA) methods with the Douglas–Peucker algorithm (DP) [4] and Douglas–Peucker algorithm under equal area principle (DP-EA) [4]. In each execution, the PSO based methods may yields slightly different results due to Particle Swarm Optimization, so we have executed 10 times each PSO based method (UPF-PSO, UPF-PSO-EA), getting the average IoU. Additionally, inspired by the Decremental Ellipse Fitting Algorithm method proposed in [13], which decreases the number of ellipses starting with a large number to approximate a given 2D shape with a number of ellipses, we have implemented a sequential baseline method of classical Polygonal Approximation that maximizes IoU. This method uses an initial polygonal curve that is given by the execution of the Douglas–Peucker algorithm (DP) with high number of vertices (e.g., $50>>N$). In each step, it sequentially removes the vertex of the polygonal curve so that the IoU of the resulting polygonal curve is maximized. The method terminates when the number of vertices are reduced to N. This baseline method is called Sequential Maximization of IoU (SM). After the execution of SM, the equal area principle can be applied yielding the SM-EA method.

In our experiments, we have evaluated the methods for different values of N. Since our framework makes sense to be applied for low values of N, where the difference in performance between the solutions of UPF and PA usually is significant, we have fitted polygonal curves with $3\le N\le 10$ (eight cases). According to the formulation of the UPF problem, we have compared the performance of UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, and SM-EA on the IoU metric.

For a given dataset, we also compute $Pr(m/IoU)$, where m is a method in {UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA}. $Pr(m/IoU)$ is quantified as the percentage of shapes of the datasets where the method m outperforms the others under the IoU, defined as follows:

$$Pr(m/IoU)=\frac{{\sum }_{I\in D}H(Io{U}_m\left(I\right)-ma{x}_{n\ne m}Io{U}_n\left(I\right))}{\left|D\right|}$$

(7)

where H is the unit step function, $\left|D\right|$ denotes the number of shapes of dataset D and $Io{U}_m\left(P\right)$ is the $IoU$ metric of method m given the binary image I. This also means that the value $100\%-{\sum }_{m}Pr(m/IoU)$ gives the percentage of images, for which there is no clear winner method.

Table 1. The average IoU, DICE, Pr(m/IOU), UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods computed on all images of MPEG7 dataset. For each metric, the best results are highlighted in bold.

Methods	IoU	DICE	Pr (m/IOU)
UPF-PSO	0.776	0.866	0.477
UPF-PSO-EA	0.770	0.861	0.322
DP	0.645	0.764	0.005
DP-EA	0.661	0.771	0.031
SM	0.732	0.833	0.084
SM-EA	0.731	0.831	0.080

and

Table 2. The average IoU, DICE, Pr(m/IOU), of the methods UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA methods computed on all images of LEMS dataset. For each metric, the best results are highlighted in bold.

Methods	IoU	DICE	Pr (m/IOU)
UPF-PSO	0.801	0.885	0.404
UPF-PSO-EA	0.803	0.886	0.382
DP	0.679	0.793	0.008
DP-EA	0.685	0.794	0.024
SM	0.751	0.848	0.093
SM-EA	0.751	0.847	0.089

present the average IoU, DICE and Pr(m/IOU) metrics computed on all images from the MPEG7 and LEMS datasets, respectively. It holds that UPF-PSO and UPF-PSO-EA clearly outperform the other methods in any dataset. UPF-PSO slightly outperforms UPF-PSO-EA. UPF-PSO or UPF-PSO-EA outperform all the other methods in about $80\%$ of shapes under MPEG-7 and LEMS datasets. SM or SM-EA outperform all the other methods in about $17\%$ of shapes under MPEG-7 dataset and LEMS dataset. DP or DP-EA outperform all the rest methods in about $3\%$ of shapes under MPEG-7 and LEMS datasets.

Figure 3 depicts the average IoU of UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM and SM-EA computed for different values of $N\in \{3,...,10\}$ in the two datasets used. UPF-PSO and UPF-PSO-EA clearly outperform the rest methods under any dataset and $N\le 8$. As expected, the lower the N, the better outer-performance of the proposed methods compared to the classical PA methods. For high values of N ($N>8$), the problem search space increases, so it is more difficult for the PSO to find near-optimal solutions. At the same time, when N obtains high values, the solutions of classical PA significantly better approximate the given shape, reducing the gap from the UPF methods. Theoretically, it holds that as N tends to infinity, the optimal solution of both problems (classical PA and UPF) converges to the initial shape having IoU equal to one ($li{m}_{N\to \infty }IoU=1$). When equal area principle is applied it holds that the EA-results slightly underperforms the corresponding solutions. The equal area principle provides better results for the special case of $N=3$, where the fitting polygon is less complex. The results under DICE metric depicted in Figure 4 agree with the results of Figure 3.

Figure 5 illustrates the Pr(m/IoU), $m\in${UPF-PSO, UPF-PSO-EA, DP, DP-EA, SM, SM-EA} over the 1400 images of MPEG-7 dataset (Figure 5a) the 1462 of LEMS dataset (Figure 5b). The results agree with the results of Figure 3. If we sum the cases where UPF-PSO or UPF-PSO-EA outperforms all the rest methods, it holds that for $N\le 8$ is more than $70\%$ and $68\%$ under MPEG-7 dataset and LEMS dataset. As it was expected, when $N=3$, UPF-PSO or UPF-PSO-EA clearly outperform the rest method on more than $98\%$ of shapes and any dataset.

Finally, Figure 6, Figure 7 and Figure 8 depict several output examples of the proposed methods and baselines to further study their behavior. The DICE-IoU metrics and the used method-N are depicted in the title and caption of each result, respectively. These figures depict results for $N=3,6,9$ vertices on a turtle, bat, and horse shapes from MPEG 7 and LEMS datasets. The results of $N=3$, $N=6$ and $N=9$, corresponds to low, middle, and high values of N according to the proposed framework. In most of the cases, the proposed methods outperform the baselines. As was expected, the difference in performance between the proposed methods and baselines is higher for low value of N ($N=3$), due to the limited classical polygonal approximation problem/search space that is restricted on the shape boundary. PSO-based methods yield high performance results, when it is more possible to find near-optimal solutions, which is true under low values of N and less complex given shapes. On other cases (high values of N and complex shapes), the PSO-based methods may fail to provide high performance solutions due to the complicated and high-dimensional search space. For example, in the case of $N=9$ and horse shape (see Figure 8) that is the most complex shape, the results of UPF-PSO and UPF-PSO-EA underperform the SM method. However, it should be noticed that under this complex shape, when $N=3$ or $N=6$ it seems that the proposed methods outperform all baselines. Concerning the other two simpler shapes, it holds that UPF-PSO or UPF-PSO-EA outperform any other method even when $N=9$, showing that the proposed methods are capable of providing high performance results even for high values of N.

5. Conclusions

In this work, a novel PSO based polygonal fitting algorithm (UPF-PSO) has been proposed to solve a general version of the polygonal fitting problem called Unconstrained Polygonal Fitting (UPF), that is defined and solved for the first time in this work. According to the UPF-PSO algorithm, the location of the N-vertices of P that can be placed anywhere in the 2D space, generally providing better solutions compared to those of the classical polygonal approximation problem, where the vertices are restricted to belong in the boundary of the given 2D shape.

In our experimental results, we have also compared the proposed UPF-PSO with several baselines in two standard datasets of 2D shapes of more than 2800 images, showing the high performance of the proposed framework. As was expected, when the number of vertices is low, the difference in performance between UPF-PSO and the rest baseline methods increases as the solutions of classical polygonal approximation problem generally fails to provide well fitting results due to the limited search space of PA problem. On the other side, when N obtains high values, the solutions of classical PA significantly better approximate the given shape, reducing the gap from the UPF methods. The equal area principle, which is also studied in this work, usually provides better results for low values of N (especially for $N=3$), where the fitting polygon is less complex. If we could obtain the optimal solutions of UPF problem given a 2D shape, the optimal solution of UPF would outperform or be equivalent with optimal solutions of the PA. However, in some cases, the results of UPF-PSO, which correspond to sub-optimal solutions of UPF due to the PSO optimization, are obviously not the optimal ones, especially for high values of N where the search space is more complex for the PSO.

The goal of this work is to provide high performance solutions for low values of N, where even the optimal solutions of PA are not sufficient to well approximate the given shape. Our experimental results show that for low values of N, the results of UPF-PSO are almost always better than the corresponding results of PA methods. As N increases, and it tends to infinity, the optimal solution PA converges to the initial shape having IoU equal to one, therefore even if we could obtain the optimal solutions of UPF, then the performance difference between UPF and PA methods will tend to zero, showing that the cases for high values of N are less promising to provide improvements, compared to the cases with low values of N.

In ongoing and future work, our aim is to study more unconstrained fitting problems and to provide better solutions by combining solutions of PA problem, e.g., in initialization step of particles and better exploring the search space of UPF. Additionally, we plan to consider extensions of UPF-PSO towards handling more complex shapes than polygons. Finally, we plan to extend the proposed framework on 3D shape and to explore real applications in which the proposed system may be useful.