The Parallel Machine Scheduling Problem with Different Speeds and Release Times in the Ore Hauling Operation

Abstract

Ore hauling operations are crucial within the mining industry as they supply essential minerals to production plants. Conducted with sophisticated and high-cost operational equipment, these operations demand meticulous planning to ensure that production targets are met while optimizing equipment utilization. In this study, we present an algorithm to determine the minimum amount of hauling equipment required to meet the ore transport target. To achieve this, a mathematical model has been developed, considering it as a parallel machine scheduling problem with different speeds and release times, focusing on minimizing both the completion time and the costs associated with equipment use. Additionally, another algorithm was developed to allow the tactical evaluation of these two variables. These procedures and the model contribute significantly to decision-makers by providing a systematic approach to resource allocation, ensuring that loading and hauling equipment are utilized to their fullest potentials while adhering to budgetary constraints and operational schedules. This approach optimizes resource usage and improves operational efficiency, facilitating continuous improvement in mining operations.

1. Introduction

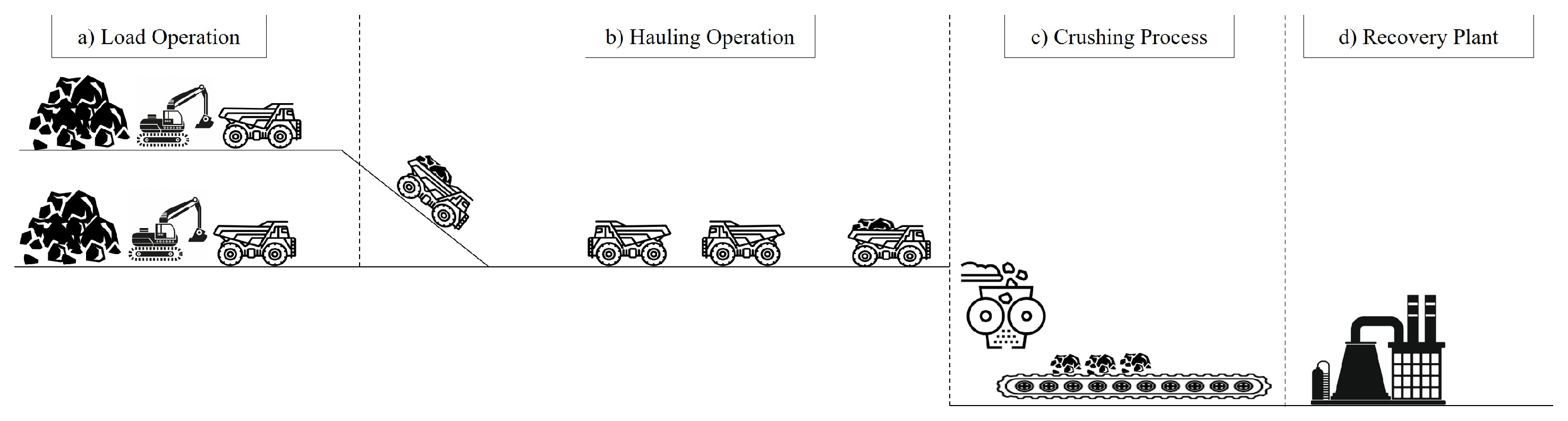
One of the most essential activities in mining operations is ore hauling; this process involves moving fragmented rock from the blasting site using loading and hauling equipment [1]. The ore rocks are then transported to the crushing process to reduce their size before being sent to the recovery plant, where valuable metals such as copper, gold, molybdenum, and aluminum, among others, are extracted [2,3,4]. Figure 1 illustrates the schematic of the described process. Poor planning of ore hauling operations can decrease productivity levels, affect the achievement of production targets within the established timelines, and consequently impact operational costs. Several factors must be considered to effectively plan ore hauling operations, such as the amount of available loading and hauling equipment and their scheduled maintenance [5]. It is also essential to account for the established production targets, working hours, and topographic levels. Other important aspects include the ore grade, the number of available loading ramps for loading operations, and the environmental impact [6].

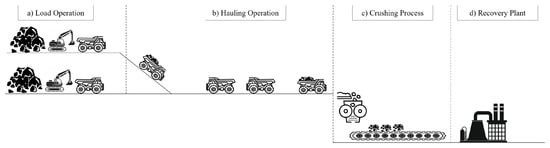
Figure 1. Schematic of the ore hauling operation.

Mining companies have a defined amount of loading and hauling equipment allocated based on the production targets set for a specific period. It is crucial to determine the necessary amount of this equipment to efficiently transport ore rocks to control associated costs, which can be substantial depending on the time required to meet these targets [7]. Knowing the minimum amount of equipment needed optimizes operations and facilitates tactical analysis. This analysis enables better decision-making in the face of contingencies, ensuring the achievement of production targets at the lowest possible cost.

As shown in Figure 1, the ore hauling process involves assigning hauling equipment to loading equipment. These do not necessarily operate at the same loading speed because some equipment have different loading capacities. The loading is performed simultaneously, and is described as a system of parallel machines with different speeds. Since the number of hauling equipment is finite, they are used as many times as necessary to meet the production target. However, they are unavailable while transporting the ore to the crushing process, having a “release time” before they are available again to be reloaded. Thus, this scenario can be adapted to a problem of parallel machines with different speeds and release times.

The novelty of this work lies in incorporating different speeds and release times into the mathematical model for parallel machine scheduling in mineral hauling operations (PMSPOHO). These features allow for a more realistic and accurate representation of operational conditions in the mining environment. The speed of the loading equipment plays a crucial role in this model. Variations in loading speeds can significantly impact the efficiency of the ore hauling operation. By considering different loading speeds, the model can more precisely allocate resources to match the dynamic nature of mining operations. This ensures that faster-loading equipment is utilized to its maximum potential while slower equipment is assigned tasks that better suit its capabilities, optimizing the overall workflow.

Incorporating the speed of the loading equipment into the scheduling algorithm maximizes equipment use and minimizes idle time for the hauling equipment. This enhances operational efficiency by reducing delays and ensuring a continuous flow of materials. The developed mathematical model addresses these critical variables, optimizing the allocation of hauling equipment, maximizing their use, and reducing idle time. This approach ensures greater operational efficiency by aligning equipment capabilities with the demands of the mining process. The strategic allocation of resources, guided by the speed and availability of each loading machine, contributes to a more streamlined and cost-effective operation, highlighting the importance of these variables in achieving optimal performance.

The mathematical model contributes significantly to several vital aspects. It facilitates more efficient planning and scheduling of hauling operations, allowing for dynamic adjustments based on changing conditions. Additionally, it enables a comparative analysis between costs and completion times, optimizing economic and productivity decisions. By reducing downtime and improving resource utilization, the model effectively addresses the logistical and financial challenges in mining operations and adapts to various operational scenarios, increasing its applicability and relevance in the sector. The remainder of this paper is structured as follows: Section 2 presents the related work. Section 3 details the methodology. Computational experiments and results analysis are discussed in Section 4. Finally, conclusions drawn from the study are presented in Section 5.

2. Related Works

Table 1 presents an overview of related works addressing the problem. It details the characteristics considered in our area of interest, such as release times ($r_i$) and different speeds ($Q_m$). The objective functions used are also analyzed, such as completion time ($C_{max}$) and costs (k), among others. Additionally, the solution methods employed are examined and categorized as exact or approximate, along with the number of machines utilized and the approaches adopted in each instance. This comparison allows for a visualization of the various methodologies and techniques implemented in the literature, highlighting their differences and similarities concerning the current analysis.

The characteristic $r_i$ has yet to be sufficiently explored, particularly in mining research where the availability of hauling equipment is crucial, as shown by [8,9]. In contrast, studying $Q_m$ has garnered more academic attention, though the focus largely remains on identical machines. Regarding the objective function, studies have generally centered on minimizing variables such as k and $C_{max}$ in isolation. Meza [2] exemplifies a more complex integration, which incorporates a time and cost analysis of loading and hauling equipment through a simulation model. Hong and Lin [10] focused on minimizing maximum lateness ($L_{max}$), while Koryagin and Voronov [11] and Oliskevych et al. [12] considered meeting P as essential for maintaining operational continuity in production plants.

In comparison, our work significantly expands the level of analysis by including both $Q_m$ and $r_i$, allowing us to model the production environments more realistically, especially in ore hauling operations. This is particularly relevant in configurations where the number of machines exceeds five, a scenario in which many studies prefer approximate methods due to their computational efficiency. Additionally, our approach includes an iterative study that enables tactical-level analysis to define the optimal utilization of equipment, complemented by robust analytical support for decision-making to maximize operational effectiveness. Our approach also incorporates a complexity analysis that has yet to be explored [10,13,14]. Thus, our work addresses a significant gap in the literature and provides critical insights that facilitate strategic decisions and enhance operational effectiveness in the mining industry.

Table 1. Related works on the parallel machine scheduling problem.

	Characteristics		Objective Function			Methods		Num. Machines
Reference	${\mathit{Q}}_{\mathit{m}}$	${\mathit{r}}_{\mathit{i}}$	${\mathit{C}}_{\mathit{max}}$	$\mathit{k}$	Other	Exact	Approximate	m ≤ 5	m ≥ 6	Complexity Analysis	Approaches
[2]	x		x	x			x		x		FIFO simulation model
[15]			x			x		x			Branch-and-price algorithm with single server
[16]			x			x	x	x	x		MIP formulation and hybrid heuristic algorithm with single server
[17]			x			x	x	x			MIP formulation and Tabu-Search with single server
[18]			x			x		x			MIP formulation with non-identical job sizes
[19]	x			x		x		x			MIP formulation
[20]	x			x		x		x			MILP formulation
[21]	x			x		x	x	x	x		MILP formulation and Insertion Heuristic under time-of-use tariffs
[22]	x			x		x		x			MILP formulation under time-of-use tariffs
[8]		x	x			x	x	x	x		MILP formulation and GA algorithm
[11]	x				P		x	x			Heuristic algorithm
[23]			x			x		x			MIP formulation with setup time and single server
[10]			x		$L_{max}$		x	x		x	Dynamic constructive algorithms
[24]			x			x	x				Constraint programming model under unavailability constraints and modify LPT
[13]			x			x	x	x		x	MIP formulation and Tabu-Search
[25]				x		x			x		MIP formulation
[14]			x			x		x	x	x	MIP formulation with independent jobs
[26]	x		x			x		x			MIP formulation with function constrain
[12]	x				P	x		x			MIP formulation
[27]				x			x	x			Monte Carlo simulation model
[9]		x	x				x	x			VNS and ACO algorithms
[28]	x		x			x	x		x		MIP and TSP algorithm
[29]			x			x		x			Constraint programming model
[30]				x		x	x	x			MIP formulation and MOBSO algorithm
[31]	x			x		x	x	x			MILP formulation with time-of-use and SPT, MDPC, MDEC
[32]	x		x			x	x		x		MIP formulation and GA–GWO hybrid algorithm
Our paper	x	x	x	x		x		x	x	x	Iterative MIP formulation

Table 1. Related works on the parallel machine scheduling problem.

	Characteristics		Objective Function			Methods		Num. Machines
Reference	${\mathit{Q}}_{\mathit{m}}$	${\mathit{r}}_{\mathit{i}}$	${\mathit{C}}_{\mathit{max}}$	$\mathit{k}$	Other	Exact	Approximate	m ≤ 5	m ≥ 6	Complexity Analysis	Approaches
[2]	x		x	x			x		x		FIFO simulation model
[15]			x			x		x			Branch-and-price algorithm with single server
[16]			x			x	x	x	x		MIP formulation and hybrid heuristic algorithm with single server
[17]			x			x	x	x			MIP formulation and Tabu-Search with single server
[18]			x			x		x			MIP formulation with non-identical job sizes
[19]	x			x		x		x			MIP formulation
[20]	x			x		x		x			MILP formulation
[21]	x			x		x	x	x	x		MILP formulation and Insertion Heuristic under time-of-use tariffs
[22]	x			x		x		x			MILP formulation under time-of-use tariffs
[8]		x	x			x	x	x	x		MILP formulation and GA algorithm
[11]	x				P		x	x			Heuristic algorithm
[23]			x			x		x			MIP formulation with setup time and single server
[10]			x		$L_{max}$		x	x		x	Dynamic constructive algorithms
[24]			x			x	x				Constraint programming model under unavailability constraints and modify LPT
[13]			x			x	x	x		x	MIP formulation and Tabu-Search
[25]				x		x			x		MIP formulation
[14]			x			x		x	x	x	MIP formulation with independent jobs
[26]	x		x			x		x			MIP formulation with function constrain
[12]	x				P	x		x			MIP formulation
[27]				x			x	x			Monte Carlo simulation model
[9]		x	x				x	x			VNS and ACO algorithms
[28]	x		x			x	x		x		MIP and TSP algorithm
[29]			x			x		x			Constraint programming model
[30]				x		x	x	x			MIP formulation and MOBSO algorithm
[31]	x			x		x	x	x			MILP formulation with time-of-use and SPT, MDPC, MDEC
[32]	x		x			x	x		x		MIP formulation and GA–GWO hybrid algorithm
Our paper	x	x	x	x		x		x	x	x	Iterative MIP formulation

Considering related studies on the optimization of the ore hauling operation, it was found that Meza [2] developed a model for the application of simulation concepts of a surface mining operation loading and hauling system, considering the type of loading and hauling equipment, arrival time, waiting time, positioning time, loading time, going time, setting time, unloading time, and return time, in addition to the number of trips as a production target, and considering a FIFO system for loading and unloading. On the other hand, Vasquez et al. [3] performed an integer programming model to minimize the total working time of a low-profile loader fleet in an underground mine, in addition to developing a polynomial time optimal algorithm integrated into the decision-making process, obtaining results quite close to the optimal total time. Eivazy and Askari-Nasab [33] developed a multi-destination mixed integer linear programming (MILP) model to minimize operations costs in surface mining; in the model, they considered stockpiles and mixing piles in addition to horizontal direction loading systems and ramp decision-making. Anjomshoa et al. [34] developed a simulation and mixed integer programming model (MIP) to optimize overtaking bays, sizing, and scheduling hauling equipment fleet in underground mining.

Moreover, Gligoric [35] developed an investigation on the overtaking bays for hauling equipment in underground mining, in which they sought to optimize the necessary amount of bays and the optimal location to minimize waiting times. Gonen et al. [36] conducted a study for underground mining where they evaluated annual production capacities with different hauling systems, considering unit hauling costs and mine depth. Eivazy and Askari-Nasab [37] presented a methodology based on production scheduling hierarchies for surface mining for the medium term, developing an MILP to minimize operating costs; the scheduling included stockpiles, processing plants, and dumps, as well as a selection of routes and ramps. Tom-Socarras [38] generated a tool for cost management based on a decision tree for material transportation in surface mining. Uribe [39] developed a study that analyzed the functionality and performance of semi-automatic operation in loading and hauling equipment used in underground mining. Więcek [40] proposed a suitable method for controlling the loading and transporting of ore in a mine with a piles and chambers system. Wiest [41] developed a scheduling model for surface mining, focusing on cost reduction.

Solomon [42] modeled ore loading and hauling systems in surface mining, developing a model that considered the excavation face, routes, equipment, and ore destinations. Gaspar and Jhasmin [43] analyzed utilization and availability indicators for ore hauling cost optimization. Li et al. [44], in their research for underground mining, developed a bee swarm algorithm to maximize the total revenue during a planning period; in addition, they created a genetic algorithm for the planning for hauling equipment dispatching to minimize the waiting time of this equipment. Elijah [45] developed a mathematical model for calculating the arrival and service rate of different amounts of hauling equipment involved in material transportation. Huisa [46] improved the use of loading and hauling equipment to reduce the cost of these operations.

Choi et al. [47] developed an intelligent non-supervisory system to predict the performance of the hauling equipment system in surface mining using a combination of different optimization models. Li et al. [48] focused on a mathematical model for rescheduling operations considering the requirements of production spaces, operating environment, and production equipment wear, while seeking to obtain the maximum planning completion rate and the lowest ore grade fluctuation. Abolghasemian et al. [49] presented a multi-objective optimization in the surface mine system, seeking the maximum amount of extraction and minimizing the transportation time, considering the storage capacity, transportation equipment, and budget. Shamsi et al. [50] performed an IP with operational restrictions to schedule the transportation system in surface mining, considering the best net present value as an objective. Parichehreh et al. [51] addressed the energy-efficient unrelated parallel machine scheduling problem, incorporating job deterioration and the learning effects of operators, providing valuable insights into multi-objective optimization for complex production environments.

Our study introduces a novel and significant approach to optimizing ore loading and hauling operations by modeling a tactical problem using a scheduling model typically employed for operational decisions. This model accounts for parallel machines with different speeds, adding greater realism. Specifically, the nature of the problem is reflected in the dynamic availability of loading equipment, represented through dynamic release times, where jobs are not known in advance but are revealed as they are executed. This approach allows for deeper and more detailed analyses that are better suited to the complexities of mining production environments. Implementing this model can be integrated into tactical and operational strategies to make them more efficient and effective, supporting decision-making in mining companies by significantly improving operational efficiency, reducing costs, and increasing productivity. Furthermore, this study will contribute to both theoretical development and practical application in mining engineering, enhancing essential operations in the sector.

3. Methodology

This section outlines the methodology employed in this study. It is structured as follows: Section 3.1 defines the problem and sets the context for the research. Section 3.2 details the modeling assumptions and presents the mathematical formulation of the problem, including the objective functions and constraints. Section 3.3 describes the algorithms used for determining and evaluating the optimal amount of ore hauling equipment. This includes the procedure for determining the minimum amount of hauling equipment and the evaluation of the cost–time trade-offs. The following subsections systematically address the research objectives and provide a comprehensive understanding of the applied methods.

3.1. Problem Definition

Due to the critical importance of ore hauling for production, this research aims to determine the minimum amount of hauling equipment necessary to minimize both the costs associated with equipment usage and the completion time of the production target within a defined time horizon. Ore hauling operations are pivotal for continuously supplying essential minerals to production plants. However, technical decisions regarding the required equipment are often made based on experience and under time pressure. While these decisions may be quick, they might only sometimes be optimal, potentially leading to increased costs or delays that impact plant production.

This research addresses the inefficiency and potential sub-optimality of traditional decision-making processes in determining the minimum amount of hauling equipment needed to realize the production target. This can result in either overestimating or underestimating hauling equipment, leading to unnecessary expenses or bottlenecks during ore transport. By developing a mathematical model that considers the parallel machine scheduling problem with different speeds and release times, we aim to provide a systematic and data-driven approach to optimizing equipment allocation.

A detailed analysis of how costs relate to completion time could reveal valuable scenarios, enabling more informed and appropriate decisions in the event of any contingency in the transportation operation. This model will allow decision-makers to balance the trade-offs between equipment costs and operational efficiency, ensuring that the right amount of equipment is deployed to meet production targets without incurring unnecessary expenses.

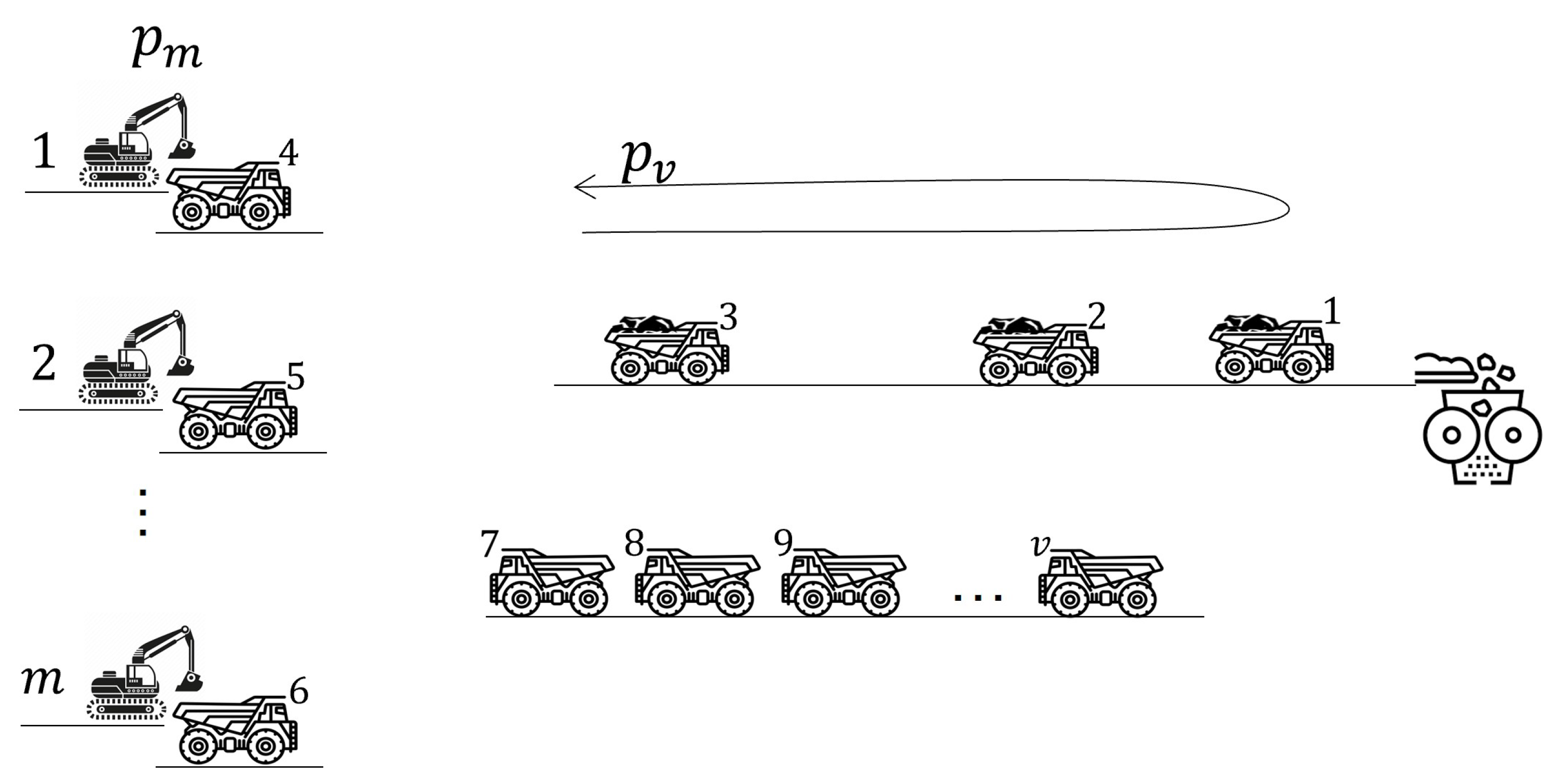
The problem can be conceptualized as a parallel machine scheduling problem with different speeds and release times. While the primary focus is a tactical decision to determine the minimum amount of hauling equipment and analyze costs related to completion time, an adaptation to this scheduling problem under an integer programming model is executed. According to the notation established by Graham [52], an operations scheduling problem is defined by three fields ($\alpha \left|\beta \right|\gamma$): $\alpha$ represents the system configuration, $\beta$ the constraints and characteristics of the system, and $\gamma$ the objective function. Using this framework and following the nomenclature described by Pinedo and Hadavi [53], the system configuration corresponds to parallel machines with different speeds ($Q_m$), where these machines are the loading equipment with varying processing times. A significant system characteristic includes the release times ($r_i$) incorporated within the hauling time. The objective function aims to minimize both costs and completion time. Figure 2 illustrates the schedule of the ore hauling operation conceptualized as the problem previously mentioned.

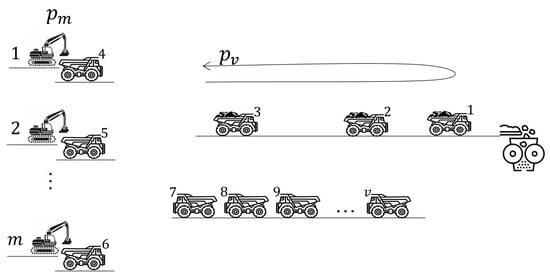
Figure 2. Schedule considering ore hauling operation.

3.2. Modeling

Model assumptions. The assumptions of the model are as follows, based on the work presented by Meza [2]:

• Only one ore unloading point was considered.
• The refueling time is negligible.
• The loading and hauling equipment is available at all times.
• The ore unloading waiting time is insignificant.

Notation. Table 2 provides the notation for the model proposed, showing the type and definition, respectively.

Table 2. Notation for the model proposed.

Var	Type	Definition
$\mathcal{M}$	Set	Set of loading equipment $\mathcal{M}=\{1,2,\dots ,m\}$.
$\mathcal{V}$	Set	Set of hauling equipment $\mathcal{V}=\{1,2,\dots ,v\}$.
$\mathcal{T}$	Set	Set of units of time: $\mathcal{T}=\{1,2,\dots ,h\}$.
$p_j^l$	Parameter	Loading time for loading equipment j.
$p_i^h$	Parameter	Hauling time for hauling equipment i.
P	Parameter	The production target is the total amount of trips to be made.
h	Parameter	Time horizon to complete the production target.
$k_j^l$	Parameter	Cost associated with use loading equipment.
$k_i^h$	Parameter	Cost associated with use hauling equipment.
$x_{ijt}$	Variable	Principal decision variable, takes the value of 1 if the hauling equipment i is using the loading equipment j at time t, 0 otherwise.
$y_{jt}$	Variable	The auxiliary decision variable takes the value of 1 if loading equipment j is using at time t, 0, otherwise.
$z_{it}$	Variable	The auxiliary decision variable takes the value of 1 if hauling equipment i is using at time t, 0, otherwise.
$C_{max}$	Variable	Completion time of the production target
k	Variable	Costs associated with equipment usage

Objective function. The first objective function (Equation (1)) seeks to minimize k associated to use equipment. The second objective function (Equation (2)) seeks to minimize $C_{max}$ of all trips.

$$mink$$

(1)

$$min{C}_{max}$$

(2)

Constraints. With respect to constraints, the set of constraints in Equation (3) ensures the assignment of only one hauling vehicle i to one loading vehicle j at time t. The set of constraints in Equation (4) ensures only one loading equipment j per hauling equipment i at time t.

$$\sum _{i\in V}{x}_{ijt}\le 1\forall j\in \mathcal{M},t\in \mathcal{T}$$

(3)

$$\sum _{j\in M}{x}_{ijt}\le 1\forall i\in \mathcal{V},t\in \mathcal{T}$$

(4)

The set of constraints in Equations (5) and (6) ensures that the loading and hauling equipment are used for the required duration when assigned.

$$\sum _{\tau =t+1}^{t+p_j^l}{y}_{j\tau }\ge (p_j^l-1)·x_{ijt}\forall i\in \mathcal{V},j\in \mathcal{M},t\in \mathcal{T}\setminus (t\le h-p_j^l)$$

(5)

$$\sum _{\tau =t+1}^{t+p_j^l+p_i^j}{z}_{i\tau }\ge (p_i^h+p_j^l-1)·x_{ijt}\forall i\in \mathcal{V},j\in \mathcal{M},t\in \mathcal{T}\setminus (t\le h-p_i^h-p_j^l)$$

(6)

The set of constraints in Equations (7) and (8) ensures that loading and hauling equipment are not double-booked and are used only when available.

$$x_{ijt}\le 1-y_{jt}\forall i\in \mathcal{V},j\in \mathcal{M},t\in \mathcal{T}$$

(7)

$$x_{ijt}\le 1-z_{it}\forall i\in \mathcal{V},j\in \mathcal{M},t\in \mathcal{T}$$

(8)

The set of constraints in Equation (9) ensures $C_{max}$.

$$C_{max}\ge t·x_{ijt}+p_i^h+p_j^l\forall i\in \mathcal{V},j\in \mathcal{M},t\in \mathcal{T}$$

(9)

The set of constraints in Equation (10) ensures that P is met.

$$\sum _i^V\sum _j^M\sum _t^T{x}_{ijt}\ge P\forall i\in \mathcal{V},j\in \mathcal{M},t\in \mathcal{T}$$

(10)

Equation (11) calculates k.

$$k=\sum _i^V\sum _t^T{k}_i^h·z_{it}+\sum _j^M\sum _t^T{k}_j^l·y_{jt}\forall i\in \mathcal{V},j\in \mathcal{M},t\in \mathcal{T}$$

(11)

The set of constraints in Equations (12) and (13) ensures the nature of the variables.

$$x_{ijt},y_{jt},z_{it}\in \{0,1\}\forall i\in \mathcal{V},j\in \mathcal{M},t\in \mathcal{T}$$

(12)

$$C_{max},k\ge 0$$

(13)

The proposed model can be used in tactical and operational decision-making processes, as it accurately specifies both decisions. However, the complexity of this mixed-integer linear programming model in terms of the amount of integer variables is i·j·t + j·t + i·j, and it has two more continuous variables. If we analyze the number of constraints, we find a total of 7·i·j·t + j·t + i·j. The fact that the model relies on binary vectors (to indicate truck start times and activity periods) inherently increases complexity but also opens the possibility for (i) the inclusion of valid inequalities to discard solutions that do not fit the structure of the problem or (ii) decomposition techniques, such as using combinatorial Benders’ cuts, or adopting a rolling horizon framework [54], to leverage divide and conquer strategies; these are both part of ongoing research. One could consider reducing the periods, but this would prevent using these models in control schemes such as those provided by a digital twin, a technique widespread in mining operations management [55].

3.3. Algorithms for Determining and Evaluating the Optimal Amount of Ore Hauling Equipment

To incorporate the dual objectives of the model of minimizing both the completion time and cost, an iterative approach was utilized in which models are created using only one objective function. As shown in Algorithms 1 and 2, the iterative process allows for the exploration of the trade-off between completion time and costs, providing a set of solutions that balance both objectives.

Considering the tactical-level analysis, the following procedure was proposed to determine the optimal amount of hauling equipment, as detailed in Algorithm 1. The algorithm starts by defining the input data, which include $\mathcal{M}$, $\mathcal{V}$, $\mathcal{T}$, $p_i^h$, $p_j^l$, h, and P. Then, defining the output data, which include the minimum number of hauling equipment ($v_{opt}$), and the hauling equipment’ assignment to loading equipment ($Schedule$) including $C_{max}$.

Then, assign v to the magnitude of $\mathcal{V}$, the total number of hauling equipment available (line 1). The variable $Continue$ is set to true to initiate the loop (line 2). As long as it remains true, a model is created (considering Equations (2)–(13) of PMSPOHO model, input data and v), and a $Result$ that minimizes the $C_{max}$ is obtained (lines 3–5). A feasibility evaluation is conducted, where if the $Result$ is feasible, v is reduced by one unit (attempting to solve the problem with fewer hauling equipment) (lines 6–8). If it is not feasible, $v_{opt}$ is increased by one unit, and the loop terminates (lines 9–13). This algorithm returns $v_{opt}$ and $Schedule$ (line 14).

Algorithm 1 Optimal hauling equipment determinator.

Input: $\mathcal{M}$, $\mathcal{V}$, $\mathcal{T}$, $p_i^h$, $p_j^l$, h, P; Output: $v_{opt}$: minimum hauling equipment, $Schedule$: hauling equipment’ assignment to loading equipment including the $C_{max}$. 1: $v\leftarrow \left|\mathcal{V}\right|$ 2: $Continue\leftarrow \mathbf{true}$ 3: while $Continue$ do 4:     $model\leftarrow \mathrm{Createmodel}$($Equations \left(2\right)$–$\left(13\right),\mathrm{Input},v$) 5:     $Result\leftarrow \mathrm{Solve}(\mathit{model},\mathrm{Minimize})$ 6:     if IsFeasible($Result$) then 7:         $v\leftarrow v-1$ 8:         $Result$, $Schedule$ 9:     else 10:         $v_{opt}\leftarrow v+1$ 11:         $Continue\leftarrow \mathbf{false}$ 12:     end if 13: end while 14: return $v_{opt}$, $Schedule$

The following procedure was proposed for an analysis of the relationship between k and $C_{max}$, detailed in Algorithm 2. This pseudocode allows for observing the behavior of k as $C_{max}$ is incremented. The algorithm starts by defining the input data, which includes the same factors as in Algorithm 1: $k_i^h$, $k_j^l$, and v. Then, defining the output data includes a list of costs and a list of termination times ($C_{max}$). Define v (line 1). The $mode{l}_{lb}$ is created (considering Equations (2)–(13) of PMSPOHO model and input data) (line 2), and a $Resul{t}_{lb}$ from the minimization of $C_{ma{x}_{lb}}$ is obtained (line 3), extracting this result (line 4). A $mode{l}_{ub}$ is created (considering Equations (1), (3)–(13) of PMSPOHO model and input data) (line 5), and a $Resul{t}_{ub}$ from the minimization of k is obtained (line 6), extracting $C_{ma{x}_{ub}}$ for this result (line 7).

A progressive evaluation is carried out that iterates $C_{ma{x}_{ref}}$ by 1 from $C_{ma{x}_{lb}}$ to $C_{ma{x}_{ub}}$ (line 8). For each value, a $mode{l}_{ref}$ is created (considering Equations (1), (3)–(8), and (10)–(13) of PMSPOHO model and input data) (line 9). $Resul{t}_{ref}$ is obtained by minimizing k for each iteration (line 10); k is extracted and added to a list ($Cost$) for each corresponding $C_{ma{x}_{ref}}$ (lines 11–12). This algorithm returns the list of pairs ($C_{ma{x}_{ref}}$,k) (lines 14), providing a detailed evaluation of how k varies about changes in $C_{ma{x}_{ref}}$. In the algorithm, $C_{ma{x}_{ref}}$ serves as an intermediate reference value to iteratively evaluate the trade-off between minimizing $C_{max}$ and k. This iterative evaluation provides insights into the cost–time trade-offs in the model.

Algorithm 2 Progressive cost–time evaluator

Input: $\mathcal{M}$, $\mathcal{V}$, $\mathcal{T}$, $p_i^h$, $p_j^l$, $k_i^h$, $k_j^l$, h, P, and v; Output: ListPair($C_{max},k$): List of cost respect to $C_{max}$. 1: Define v 2: $mode{l}_{lb}\leftarrow \mathrm{Createmodel}$($Equations \left(2\right)$–$\left(13\right),\mathrm{Input}$) 3: $Resul{t}_{lb}\leftarrow \mathrm{Solve}(mode{l}_{lb},\mathrm{Minimize})$ 4: $C_{ma{x}_{lb}}\leftarrow \mathrm{ExtractCmax}\left(Resul{t}_{lb}\right)$ 5: $mode{l}_{ub}\leftarrow \mathrm{Createmodel}(Equations (1),\left(3\right)$–$\left(13\right),\mathrm{Input})$ 6: $Resul{t}_{ub}\leftarrow \mathrm{Solve}(mode{l}_{ub},\mathrm{Minimize})$ 7: $C_{ma{x}_{ub}}\leftarrow \mathrm{ExtractCmax}\left(Resul{t}_{ub}\right)$ 8: for $C_{ma{x}_{ref}}$ in $C_{ma{x}_{lb}}$ to $C_{ma{x}_{ub}}$ do 9:       $mode{l}_{ref}\leftarrow \mathrm{Createmodel}(Equations \left(1\right),\left(3\right)$–$\left(8\right),\left(10\right)$–$\left(13\right),\mathrm{Input})$ 10:     $Resul{t}_{ref}\leftarrow \mathrm{Solve}(mode{l}_{ref},\mathrm{Minimize})$ 11:     $Cost\leftarrow \mathrm{ExtractCost}\left(Resul{t}_{ref}\right)$ 12:     ListPair($C_{max},k$) $\leftarrow \mathrm{AddToList}(C_{ma{x}_{ref}},\mathrm{Cost})$ 13: end for 14: return $C_{max},k$

4. Computational Experiments and Results Analysis

This section presents the computational experiments to evaluate the performance of the proposed PMSPOHO model and algorithms. All experiments were conducted on a computer with a Windows 11 operating system, 12th Gen Intel(R) Core(TM) i5-12450H, 2.50 GHz processor, and 8 GB RAM. The Python 3.11 programming language was used for the development. The Gurobi 10.0.1 commercial optimizer and CBC free optimizer were used with a search time limit of 3600 s and a GAP of 0.01.

Based on actual data provided in the studies by Meza [2], Vásquez [3], and Anchiraico and Rojas [4], which include the numbers of loading and hauling equipment, loading times, hauling times, time horizons, and production targets, 34 experimental instances were generated. These instances are designed to simulate real-world scenarios, enabling a robust evaluation of our proposed methodologies under various conditions. This approach ensures that our experimental setup is based on realistic operational parameters, enhancing the applicability and relevance of our findings. It is important to note that a direct comparison with the authors’ studies above was not conducted, as their research methodologies differ significantly from our proposed approach.

4.1. Tuning the Values for the Optimizer Parameters

Gurobi Optimizer version 10.0.1 features an extensive range of parameters designed to fine-tune the optimizer performance. Given the vast array of options among possible configurations, identifying the optimal combination of parameters that enhance the overall model performance poses a significant challenge. The TuningAPI from Gurobi offers a valuable tool for exploring various parameter settings that can improve model performance in specific cases [56].

Considering the procedure indicated by Cuellar-Usaquén et al. [57], a sample of seven instances was created to identify the appropriate parameter settings for our model using TuningAPI. This sample includes those instances where the computation time obtained by the PMSPOHO model using the default parameters (PMSPOHO-D) exceeds the meantime of its respective class by two standard deviations.

Table 3 shows the results of Gurobi parameter tuning across seven different problem instances. Each table row represents an instance, with columns indicating the specific Gurobi parameters adjusted for that instance. The parameters include Symmetry, DegenMove, Heuristics, GomoryPasses, PreDepRow, MIPFocus, Method, CutPasses, and BranchDir.

Table 3. Parameters configurations found for the mathematical model.

Summary				Value Parameters
Inst	$\mathit{v}$	$\mathit{m}$	$\mathit{P}$	Symmetry	DegenMoves	Heuristics	GomoryPasses	PreDepRow	MIPFocus	Method	CutPasses	BranchDir	Tc-D	Tc-T	Variation
1	3	2	20	2									0.8	0.79	1.25%
2	6	2	20		2								1.22	1.15	5.74%
3	8	4	81			0	1	1					69.59	55.03	20.92%
4	12	4	81						2				46.54	44.4	4.60%
5	15	4	81							0			32.53	31.64	2.74%
6	8	4	90				1					1	139.22	120.68	13.32%
7	20	4	100								1		81.62	79.9	2.11%

The third instance stands out significantly because it shows the highest variation (20.92%) between the default computational time (Tc-D) and the tuned computational time (Tc-T), indicating a significant improvement in performance with the adjusted parameters. In this instance, the parameters Heuristics, GomoryPasses, and PreDepRow were adjusted, resulting in a substantial reduction in computation time from 69.59 to 55.03 time units. This adjustment reduced the overall calculation time and optimized the use of computational resources, making the process more efficient and effective. The considerable difference between Tc-D and Tc-T underscores the importance of customization and fine-tuning model parameters to achieve maximum efficiency in solving complex mathematical problems.

In this instance, the adjusted parameter Heuristics emerges as a key player in accelerating the solving process. By increasing the use of heuristic methods, which are solving strategies that employ simple and fast rules to generate satisfactory solutions quickly, the model explored and evaluated potential solutions more efficiently. This approach significantly reduced the time required to reach a feasible solution, demonstrating its practicality and effectiveness. Applying heuristics is a valuable tool, particularly in scenarios where speed is critical and some precision can be sacrificed for improved resolution speed.

GomoryPasses, another adjusted parameter, controls the amount of Gomory cut passes. These passes are optimization techniques that strengthen the model linear relaxation, leading to faster convergence. Adjusting the amount of these passes can significantly impact the solution efficiency, balancing the need to improve the solution with the additional time required for each cut. PreDepRow, which handles the preprocessing of dependent rows, also fundamentally improved efficiency by reducing problem size and enhancing numerical stability. Effective preprocessing can simplify the model by eliminating redundancies and reducing overall complexity. In the third instance, adjusting PreDepRow significantly reduced computational time, noting the importance of proper model management. These adjustments underscore the importance of tuning parameters to enhance the efficiency solver, enabling faster and more accurate results.

4.2. Benchmarking Results for Optimizers

Table 4 presents the benchmarking results of optimizers across 34 instances. The instances were organized considering the production target, as an increase in computational time (Tc) was noted as this target increased. The results were compared between the default model (PMSPOHO-D), the tuned model (PMSPOHO-T), and the model with the free optimizer (PMSPOHO-CBC). The critical parameters for comparison were Tc and GAP, which measure the complexity model and the efficiency solver. In this study, the GAP value is provided directly by the Gurobi optimizer as part of its solution output.

Table 4. Benchmarking results for optimizers per instances.

				PMSPOHO-D			PMSPOHO-T			PMSPOHO-CBC
Instance	$\mathit{P}$	$\mathit{v}$	$\mathit{m}$	${\mathit{C}}_{\mathit{max}}$	Tc	GAP	${\mathit{C}}_{\mathit{max}}$	Tc	GAP	${\mathit{C}}_{\mathit{max}}$	Tc	GAP
1	20	20	2	29	14.52	0.00%	29	9.73	0.00%	30	3600	4.58%
2	20	16	2	29	9.51	0.00%	29	5.92	0.00%	30	3600	4.64%
3	20	10	2	29	3.82	0.00%	29	2.91	0.00%	31	3600	5.21%
4	20	8	2	29	2.51	0.00%	29	1.85	0.00%	30	3600	4.82%
5	20	6	2	31	1.6	0.00%	31	1.58	0.00%	32	3600	3.77%
6	20	5	2	34	1.41	0.00%	34	1.03	0.00%	35	3600	2.36%
7	20	4	2	40	1.13	0.00%	40	1.01	0.00%	41	3600	2.56%
8	20	3	2	51	0.9	0.00%	51	1.82	0.00%	51	1846	0.00%
9	81	20	4	55	28.25	0.00%	55	26.74	0.00%	60	3600	8.52%
10	81	16	4	55	18.34	0.00%	55	18.61	0.00%	60	3600	8.20%
11	81	10	4	64	49.23	0.00%	64	46.08	0.00%	68	3600	6.45%
12	81	8	4	78	69.59	0.00%	78	50.86	0.00%	82	3600	5.50%
13	81	6	4	100	66.54	0.00%	100	63.01	0.00%	106	3600	5.72%
14	81	4	4	147	76.29	0.00%	147	59.78	0.00%	152	3600	3.27%
15	81	20	6	38	42.12	0.00%	38	42.26	0.00%	42	3600	10.25%
16	81	16	6	42	318.67	0.00%	42	130.11	0.00%	46	3600	9.86%
17	81	10	6	63	94.3	0.00%	63	76.82	0.00%	70	3600	10.52%
18	81	8	6	77	100.46	0.00%	77	100.13	0.00%	85	3600	10.73%
19	81	6	6	98	145.77	0.00%	98	90.32	0.00%	110	3600	12.72%
20	90	5	3	130	42.98	0.00%	130	26.41	0.00%	163	3600	25.32%
21	90	4	3	161	83.77	0.00%	161	40.36	0.00%	202	3600	25.47%
22	90	3	3	212	44.52	0.00%	212	30.78	0.00%	259	3600	22.23%
23	200	19	4	125	1784.21	0.00%	125	1627.21	0.00%	161	3600	29.03%
24	200	18	4	125	1693.64	0.00%	125	1437.64	0.00%	161	3600	28.53%
25	200	17	4	125	1634.63	0.00%	125	1463.63	0.00%	161	3600	28.93%
26	200	16	4	125	1640.24	0.00%	125	1400.24	0.00%	161	3600	28.73%
27	200	15	4	125	1584.04	0.00%	125	1437.04	0.00%	164	3600	31.45%
28	200	14	4	125	1554.43	0.00%	125	1291.43	0.00%	159	3600	27.32%
29	200	13	4	125	1532.23	0.00%	125	1349.23	0.00%	161	3600	29.05%
30	200	12	4	151	1524.64	0.00%	151	1372.64	0.00%	194	3600	28.63%
31	200	11	4	151	1279.45	0.00%	151	1019.45	0.00%	189	3600	25.43%
32	200	10	4	151	1017.6	0.00%	151	746.6	0.00%	186	3600	23.23%
33	200	9	4	166	865.6	0.00%	166	615.6	0.00%	203	3600	22.01%
34	200	8	4	183	798.8	0.00%	183	671.8	0.00%	229	3600	24.93%

The tuned model (PMSPOHO-T) consistently handles lower computational times than the other models. This indicates that parameter tuning has significantly improved the solver efficiency. The GAP, which is the difference between the best-known solution and the best lower bound found by the solver, is 0.00% for both PMSPOHO-D and PMSPOHO-T, indicating that the solutions found are optimal. However, PMSPOHO-CBC shows a higher GAP in several instances, reflecting lower precision and highlighting the limitations of a commercial optimizer.

PMSPOHO-T stands out with the best results in terms of Tc, solving instances faster while maintaining solution precision. This starkly contrasts with the model with the free optimizer (PMSPOHO-CBC), which shows a higher GAP in many cases, thereby highlighting its limitations. It also demonstrates that the problem’s complexity is NP-Hard, meaning that as instances increase, optimal results could be obtained after significantly longer times, making a free optimizer an inefficient option for field applications.

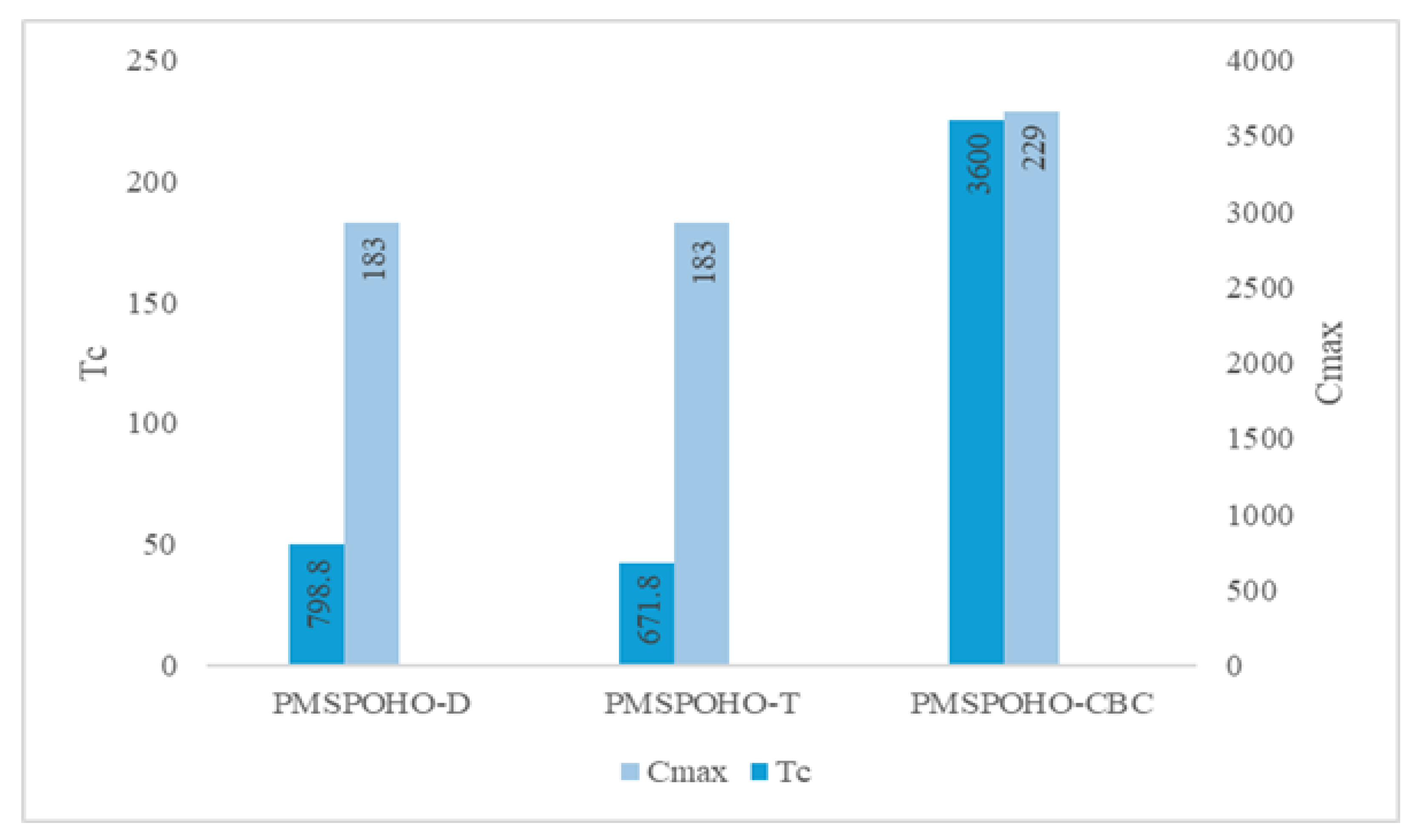
Figure 3 compares the computational time ($Tc$) and $C_{\max }$ for the PMSPOHO-D, PMSPOHO-T, and PMSPOHO-CBC optimizers for instance 34. PMSPOHO-D and PMSPOHO-T achieve the same $C_{\max }$ of 183, but PMSPOHO-T is more efficient in terms of computational time, with 671.8 compared to 798.8 for PMSPOHO-D. On the other hand, PMSPOHO-CBC shows the worst performance, with a $C_{\max }$ of 229 and a computational time of 3600. This indicates that PMSPOHO-T is the most efficient among the three evaluated optimizers, achieving a good balance between computational time and $C_{\max }$.

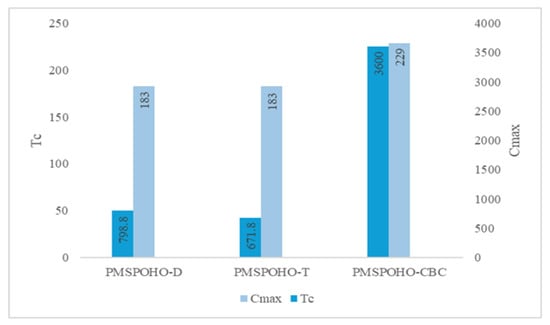
Figure 3. Comparison of computational time and $C_{max}$ for instance 34.

4.3. Tactical Approach Insights

Table 5 shows the efficiency of the applied algorithms. Algorithm 1 calculates the minimum number of hauling equipment, resulting in eight equipment. On the other hand, Algorithm 2 performs a k-$C_{max}$ evaluation, allowing for a more appropriate analysis between these two variables. This improves tactical decision-making by showing how varying $C_{max}$ impacts k and vice-versa. Minimizing $C_{max}$ results in significantly reduced values (between 33 and 49), although an increase in k enables planners to balance temporal efficiency and operational costs. Algorithm 2 provides a more comprehensive and balanced perspective for tactical decision-making and is supported by Algorithm 1, which defines the number of resources needed to meet the production target.

Table 5. Results of optimizing the proposed algorithms.

			Minimize k			Minimize ${\mathit{C}}_{\mathit{max}}$
$\mathit{v}$	$\mathit{m}$	$\mathit{P}$	${{\mathit{C}}_{\mathit{max}} }_{\mathit{ub}}$	$\mathit{k}$	$\mathit{Tc}$	${{\mathit{C}}_{\mathit{max}} }_{\mathit{lb}}$	$\mathit{k}$	$\mathit{Tc}$
19	4	200	51	2350	151.46	33	6998	54.97
18	4	200	51	2350	219.68	33	6648	46.31
17	4	200	51	2350	117.08	33	6298	38.57
16	4	200	51	2350	99.44	33	5948	33.81
15	4	200	51	2350	125.16	33	5598	31.16
14	4	200	51	2350	162.80	33	5248	26.78
13	4	200	51	2350	75.34	34	4898	24.63
12	4	200	51	2350	58.55	35	4548	20.73
11	4	200	51	2350	111.22	37	4198	21.40
10	4	200	51	2350	103.30	40	3848	32.76
9	4	200	50	2350	44.62	44	3498	19.40
8	4	200	51	2350	76.94	49	3148	15.93

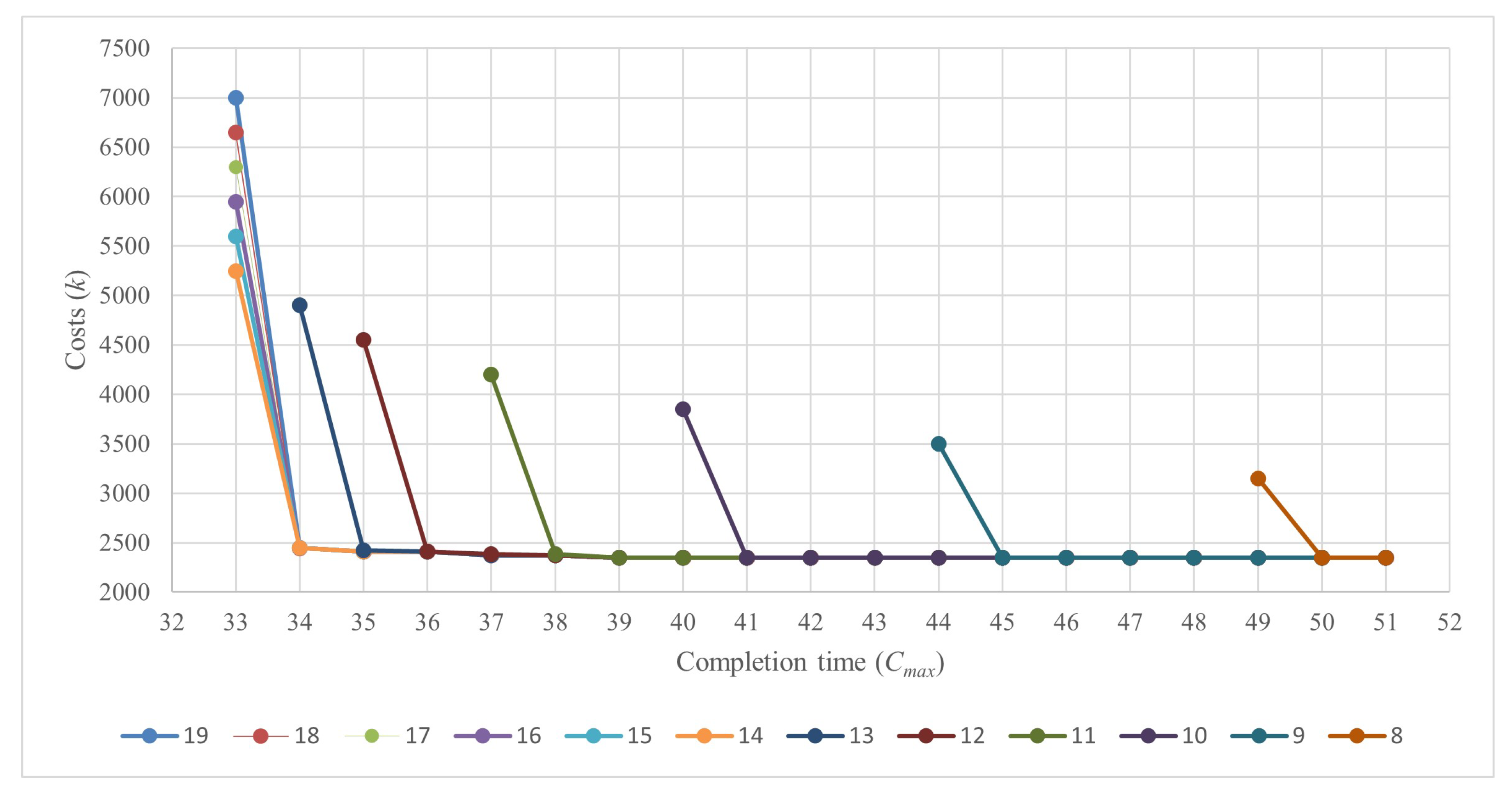
As completion times shorten, costs rise disproportionately, indicating a trade-off between time and cost efficiency in ore hauling operations. The steeper curves at lower completion times imply significant cost increases for faster operations, while the flatter slopes at higher times suggest a minimum cost threshold. The broader range of completion times with more hauling equipment means that, although additional equipment can speed up operations, it also incurs higher costs, highlighting the importance of balancing budgetary limitations with operational urgency in scheduling mining operations.

Figure 4 shows the relationship between costs and completion time for different numbers of hauling equipment. There is a marked cost decrease with only a slight increase in completion time. A tactical approach to determining the minimum amount of hauling equipment needed to meet production targets should consider not only cost and completion time but also the slope of each line, which supports the application of the algorithms proposed in this paper. For instance, moving from nine to eight hauling units marginally increases completion time while significantly reducing cost. This suggests that operating with eight hauling units could be an effective tactical decision if the additional time does not compromise other priorities of the ore hauling operation.

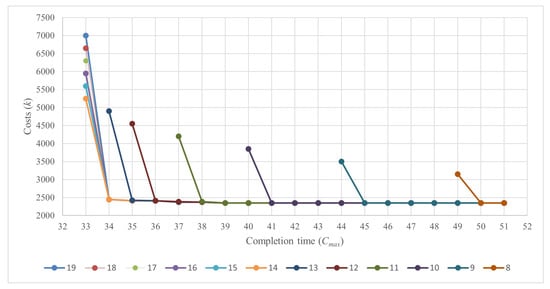
Figure 4. Costs k vs. completion time $C_{max}$ for the instances proposed in Table 5.

Decision-makers must weigh the cost increase associated with using more equipment against reducing hauling time. Beyond a certain point, adding more hauling units diminishes the benefit of lowering completion time but incurs substantially higher costs. Pinpointing the moment when the additional cost no longer justifies the decrease in hauling time is critical for optimizing operations and managing resources efficiently.

4.4. Operational Approach Insights

Figure 5 shows the schedule, for instance 34, which considers eight hauling and four loading equipment. This visualizes the ore loading program for a mining operation during the first 50 trips of the production target. It is interesting to see how the allocation is organized to ensure that the minimum necessary amount of hauling equipment is kept in constant motion, indicating a careful assessment of loading times and intervals between tasks. This strategy ensures that no loading equipment remains idle and that the hauling equipment is effectively distributed to meet the production target.

Figure 5. Schedule for instance 34 considering minimize completion time $C_{max}$.

By minimizing the amount of hauling equipment, the operation can become more cost-effective and improve logistics by reducing congestion and potential bottlenecks in the ore hauling operation. This balanced approach between efficiency and effectiveness in scheduling is crucial for a successful operation that adapts to the dynamic and often unpredictable demands of mining.

Table 6 provides a detailed distribution of loading and hauling equipment utilization in a mining operation, highlighting the allocation and usage of these resources in production. It is observed that loading equipment two and three are the most utilized, with utilization percentages of 32% and 30%, respectively, indicating high demand and frequent use. In contrast, loading vehicle four is the least utilized, operating at only 12% utilization. This suggests that resources are not being fully optimized, particularly considering that loading vehicle four might be the most costly to operate, as less frequently used equipment typically requires regular maintenance and occupies valuable space that could be better utilized.

Table 6. Loading and hauling equipment utilization.

	Loading Equipment
Hauling Equipment	1	2	3	4	Total	Utilization
0	3	2	1	0	6	12%
1	3	2	1	1	7	14%
2	1	1	3	0	5	10%
3	1	1	2	2	6	12%
4	1	4	2	0	7	14%
5	2	2	3	0	7	14%
6	1	1	2	2	6	12%
7	1	3	1	1	6	12%
Total	13	16	15	6	50
Utilization	26%	32%	30%	12%

The under-utilization of the costly loading equipment fourraises significant cost management and operational efficiency considerations. The high cost of this equipment may be due to specialized features that necessitate more sophisticated maintenance or a higher initial investment. However, its sub-optimal utilization implies that this investment needs to yield the expected returns, which is critical in operations aiming to maximize efficiency and profitability. This situation underscores the urgent need to reassess task distribution and resource allocation to ensure that all loading equipment are utilized in a manner that justifies their cost, thereby optimizing the entire operation and reducing potential resource wastage.

The results demonstrate that the proposed model is efficient in terms of computational time and that the proposed algorithms are useful tactical tools for more effective decision-making regarding the allocation of hauling equipment necessary to achieve the targets set in ore transport operations. However, it is essential to acknowledge that analyzing more significant instances as a mathematical model could complicate the time required to obtain results, even with the optimizer parameters finely tuned. Therefore, it will be essential to extend the solution search periods and develop approximate methods to reduce these times and attain practical and executable solutions.

5. Conclusions

The proposed model demonstrates significant efficiency in terms of computational time, effectively balancing cost and completion time in ore hauling operations. Applying the two algorithms provided tactical tools that enhance decision-making regarding the allocation of hauling equipment. The model efficiency is evident in the computational results, showing that parameter tuning can significantly improve solver performance. The tuned model consistently handled lower computational times than default settings, highlighting the importance of careful parameter adjustments. Furthermore, incorporating dynamic release times and different speeds of hauling equipment in the model adds a layer of realism, ensuring that the scheduling reflects actual operational conditions. This aspect further optimizes the allocation process, making the model computationally robust.

Despite the results, the model has limitations. A primary limitation is its scalability. As the size of the instances increases, the time required to obtain results can become prohibitive, even with optimized parameters. This issue is inherent in mathematical models dealing with complex, NP-hard problems. Additionally, the reliance of the model on exact optimization methods may only sometimes be practical for real-time decision-making in dynamic environments where quick responses are essential.

Future work should focus on extending solution search periods and developing approximate methods to address these limitations. These methods, including heuristic or metaheuristic approaches, can reduce computational times and provide near-optimal practical and executable solutions in real-world scenarios. Additionally, integrating machine learning techniques to predict and dynamically adjust parameters could enhance the model’s performance and adaptability [58].