Allometric Models for Predicting Aboveground Biomass of Trees in the Dry Afromontane Forests of Northern Ethiopia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
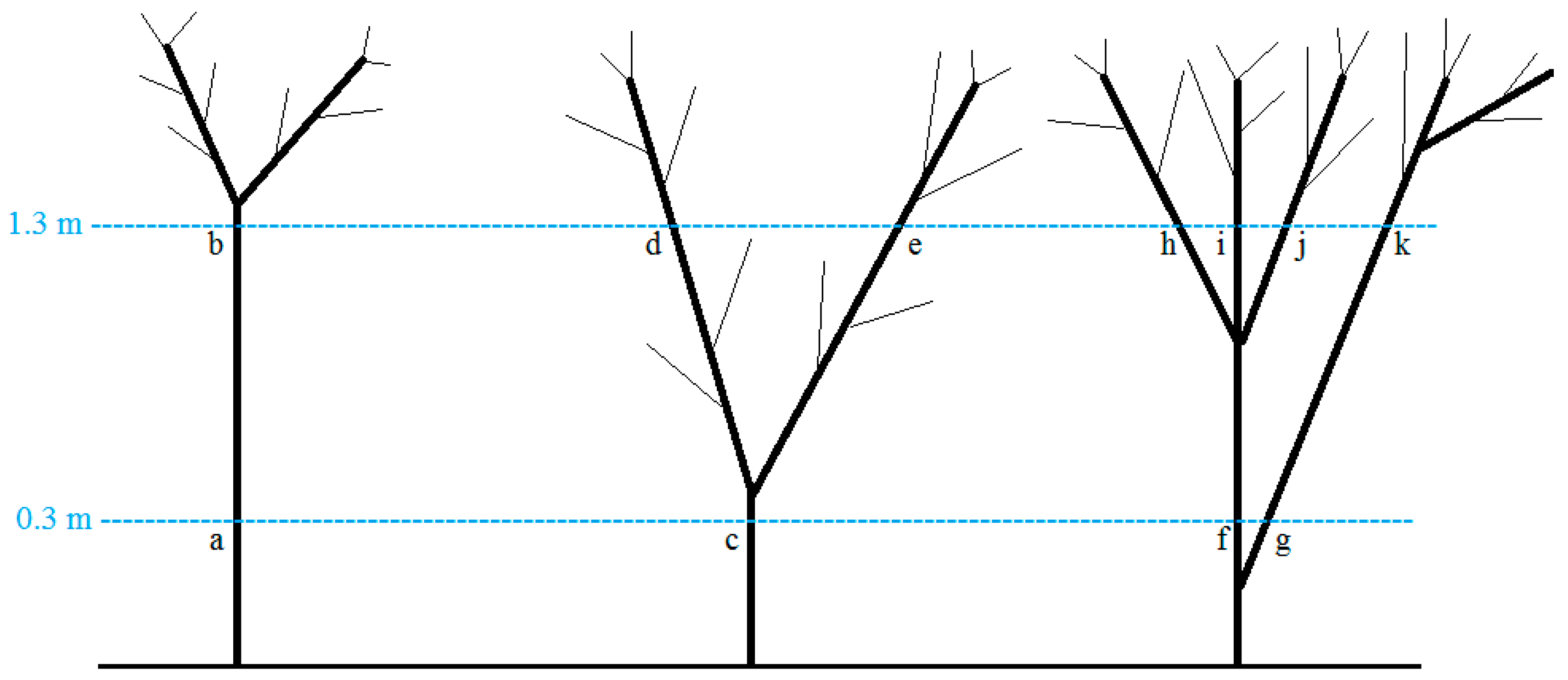
2.2. Data Collection
2.3. Analyses
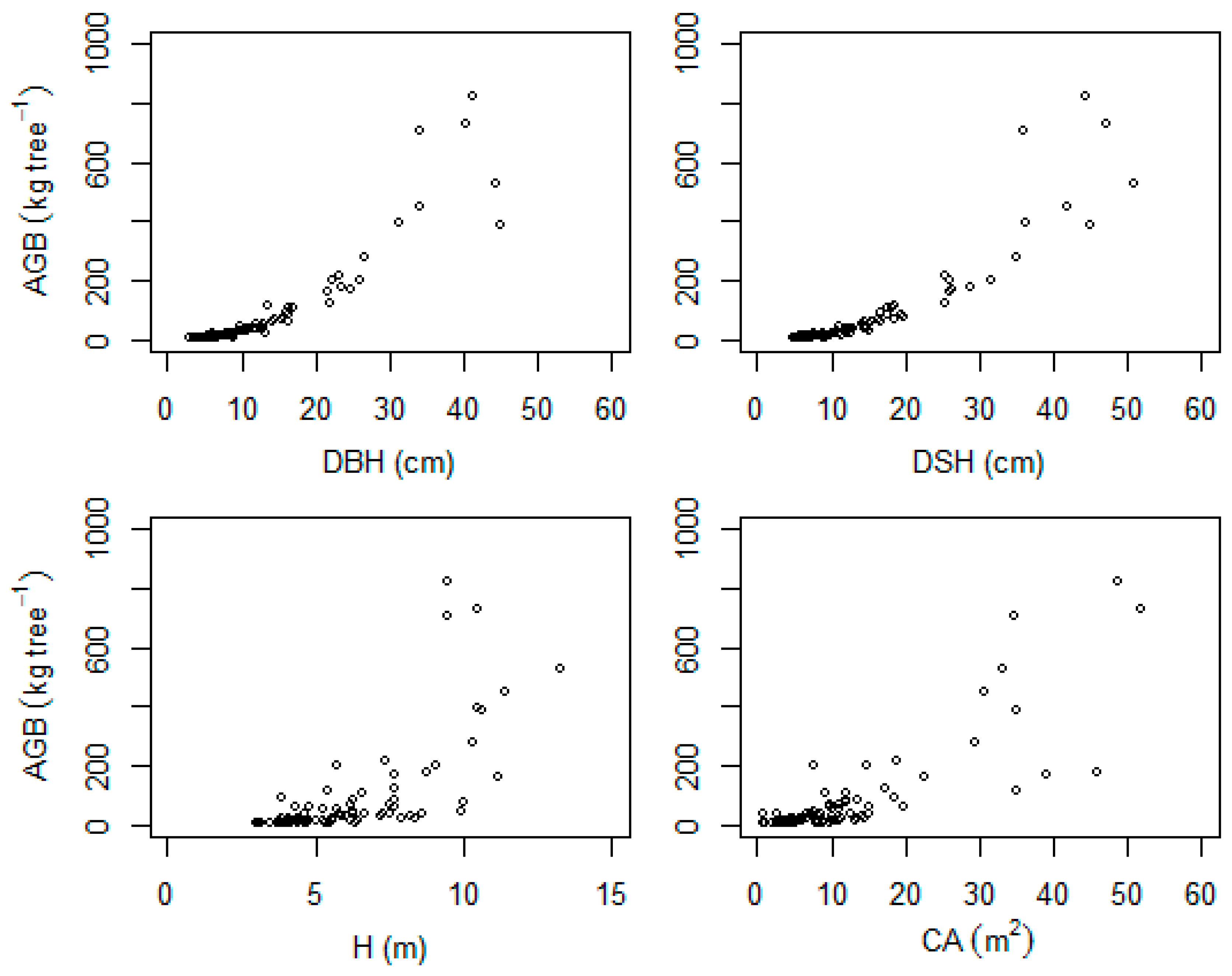
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shirima, D.D.; Munishi, P.K.T.; Lewis, S.L.; Burgess, N.D.; Marshall, A.R.; Balmford, A.; Swetnam, R.D.; Zahabu, E.M. Carbon storage, structure and composition of miombo woodlands in Tanzania’s Eastern Arc Mountains. Afr. J. Ecol. 2011, 49, 332–342. [Google Scholar] [CrossRef]
- Mokria, M.; Mekuria, W.; Gebrekirstos, A.; Aynekulu, E.; Belay, B.; Gashaw, T.; Bräuning, A. Mixed-species allometric equations and estimation of aboveground biomass and carbon stocks in restoring degraded landscape in northern Ethiopia. Environ. Res. Lett. 2018, 13, 24022. [Google Scholar] [CrossRef]
- Chidumayo, E.N. Is charcoal production in Brachystegia-Julbernardia woodlands of Zambia sustainable? Biomass Bioenergy 2019, 125, 1–7. [Google Scholar] [CrossRef]
- Ngugi, M.R.; Neldner, V.J.; Ryan, S.; Lewis, T.; Li, J.; Norman, P.; Mogilski, M. Estimating potential harvestable biomass for bioenergy from sustainably managed private native forests in Southeast Queensland, Australia. For. Ecosyst. 2018, 5. [Google Scholar] [CrossRef]
- Dube, T.; Gara, T.W.; Mutanga, O.; Sibanda, M.; Shoko, C.; Murwira, A.; Masocha, M.; Ndaimani, H.; Hatendi, C.M. Estimating forest standing biomass in savanna woodlands as an indicator of forest productivity using the new generation WorldView-2 sensor. Geocarto Int. 2016, 33, 178–188. [Google Scholar] [CrossRef]
- Worbes, M.; Raschke, N. Carbon allocation in a Costa Rican dry forest derived from tree ring analysis. Dendrochronologia 2012, 30, 231–238. [Google Scholar] [CrossRef]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; Volume 134 of FAO Forestry Paper; Food and Agriculture Organization A Forest Resources Assessment publication: Rome, Italy, 1997. [Google Scholar]
- Henry, M.; Besnard, A.; Asante, W.A.; Eshun, J.; Adu-Bredu, S.; Valentini, R.; Bernoux, M.; Saint-André, L. Wood density, phytomass variations within and among trees, and allometric equations in a tropical rainforest of Africa. For. Ecol. Manag. 2010, 260, 1375–1388. [Google Scholar] [CrossRef]
- Basuki, T.M.; van Laake, P.E.; Skidmore, A.K.; Hussin, Y.A. Allometric equations for estimating the above-ground biomass in tropical lowland Dipterocarp forests. For. Ecol. Manag. 2009, 257, 1684–1694. [Google Scholar] [CrossRef]
- Chave, J.; Kira, T.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Higuchi, N.; Andalo, C.; Cairns, M.A.; Ogawa, H.; Fromard, F.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Chave, J.; Chidumayo, E.; Ploton, P.; Saldarriaga, J.G.; Mencuccini, M.; Ortiz-Malavassi, E.; Vieilledent, G.; Muller-Landau, H.C.; Búrquez, A.; Eid, T.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Conti, G.; Enrico, L.; Casanoves, F.; Díaz, S. Shrub biomass estimation in the semiarid Chaco forest: A contribution to the quantification of an underrated carbon stock. Ann. For. Sci. 2013, 70, 515–524. [Google Scholar] [CrossRef] [Green Version]
- Vashum, K.T.; Jayakumar, S. Methods to Estimate Above-Ground Biomass and Carbon Stock in Natural Forests—A Review. J. Ecosyst. Ecography 2012, 2. [Google Scholar] [CrossRef]
- Chave, J.; Condit, R.; Lao, S.; Caspersen, J.P.; Foster, R.B.; Hubbell, S.P. Spatial and temporal variation of biomass in a tropical forest: Results from a large census plot in Panama. J. Ecol. 2003, 91, 240–252. [Google Scholar] [CrossRef]
- Ngomanda, A.; Obiang, N.L.E.; Lebamba, J.; Mavouroulou, Q.M.; Gomat, H.; Mankou, G.S.; Loumeto, J.; Iponga, D.M.; Ditsouga, F.K.; Koumba, R.Z.; et al. Site-specific versus pantropical allometric equations: Which option to estimate the biomass of a moist central African forest? For. Ecol. Manag. 2013, 312, 1–9. [Google Scholar] [CrossRef]
- Mokria, M.; Gebrekirstos, A.; Aynekulu, E.; Bräuning, A. Tree dieback affects climate change mitigation potential of a dry afromontane forest in northern Ethiopia. For. Ecol. Manag. 2015, 344, 73–83. [Google Scholar] [CrossRef]
- Wondrade, N.; Dick, O.B.; Tveite, H. Estimating above Ground Biomass and Carbon Stock in the Lake Hawassa Watershed, Ethiopia by Integrating Remote Sensing and Allometric Equations. For. Res. Open Access 2015, 4. [Google Scholar] [CrossRef] [Green Version]
- Tesfaye, M.A.; Bravo-Oviedo, A.; Bravo, F.; Ruiz-Peinado, R. Aboveground biomass equations for sustainable production of fuelwood in a native dry tropical afro-montane forest of Ethiopia. Ann. For. Sci. 2016, 73, 411–423. [Google Scholar] [CrossRef] [Green Version]
- Ubuy, M.H.; Eid, T.; Bollandsås, O.M.; Birhane, E. Aboveground biomass models for trees and shrubs of exclosures in the drylands of Tigray, northern Ethiopia. J. Arid Environ. 2018, 156, 9–18. [Google Scholar] [CrossRef]
- Feyisa, K.; Beyene, S.; Megersa, B.; Said, M.Y.; Angassa, A. Allometric equations for predicting above-ground biomass of selected woody species to estimate carbon in East African rangelands. Agrofor. Syst. 2016, 92, 599–621. [Google Scholar] [CrossRef]
- Yuen, J.Q.; Fung, T.; Ziegler, A.D. Review of allometric equations for major land covers in SE Asia: Uncertainty and implications for above- and below-ground carbon estimates. For. Ecol. Manag. 2016, 360, 323–340. [Google Scholar] [CrossRef]
- Henry, M.; Picard, N.; Trotta, C.; Manlay, R.J.; Valentini, R.; Bernoux, M.; Saint-André, L. Estimating tree biomass of sub-Saharan African forests: A review of available allometric equations. Silva Fenn. 2011, 45, 477–569. [Google Scholar] [CrossRef] [Green Version]
- Giday, K. Management Interventions to Assist Restoration of Degraded Dry Afromontane Forest N. Ethiopia. Ph.D. Thesis, KU Leuven University, Leuven, Belgium, 2013. [Google Scholar]
- Worku, E.; Soromessa, T. Allometric Equation for Biomass Determination in Juniperus procera Endl. and Podocarpus falcatus Mirb of Wof-Washa Forest: Implication for Climate Change Mitigation. Am. J. Life Sci. 2015, 3, 190–202. [Google Scholar] [CrossRef] [Green Version]
- Kebede, B.; Soromessa, T. Allometric equations for aboveground biomass estimation of Olea europaea L. subsp. cuspidata in Mana Angetu Forest. Ecosyst. Health Sustain. 2018, 4, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Solomon, N.; Birhane, E.; Tadesse, T.; Treydte, A.C.; Meles, K. Carbon stocks and sequestration potential of dry forests under community management in Tigray, Ethiopia. Ecol. Process. 2017, 6, 20. [Google Scholar] [CrossRef]
- Woldemichael, L.; Bekele, T.; Nemomissa, S. Vegetation Composition in Hugumbirda-Gratkhassu National Forest Priority Area, South Tigray. Momona Ethiop. J. Sci. 2011, 2, 27–48. [Google Scholar] [CrossRef]
- BirdLife International. Available online: http://datazone.birdlife.org/site/factsheet/dessaa-forest-iba-ethiopia (accessed on 2 March 2019).
- Berihu, T.; Girmay, G.; Sebhatleab, M.; Berhane, E.; Zenebe, A.; Sigua, G.C. Soil carbon and nitrogen losses following deforestation in Ethiopia. Agron. Sustain. Dev. 2017, 37. [Google Scholar] [CrossRef] [Green Version]
- Hishe, H.; Giday, K.; Neka, M.; Soromessa, T.; Van Orshoven, J.; Muys, B. Detection of Olea europaea subsp. cuspidata and Juniperus procera in the dry Afromontane forest of northern Ethiopia using subpixel analysis of Landsat imagery. J. Appl. Remote Sens. 2015, 9, 95975. [Google Scholar] [CrossRef] [Green Version]
- WeForest. Available online: https://www.weforest.org/project/ethiopia-desaa (accessed on 14 March 2019).
- Wiemann, M.C.; Williamson, G.B. Density and Specific Gravity Metrics in Biomass Research; General Technical Report, FPL-GTR-208; USDA Forest Service, Forest Products Laboratory: Madison, WI, USA, 2012. [Google Scholar]
- Williamson, G.B.; Wiemann, M.C. Measuring wood specific gravity...correctly. Am. J. Bot. 2010, 97, 519–524. [Google Scholar] [CrossRef] [Green Version]
- Ubuy, M.H.; Eid, T.; Bollandsås, O.M. Variation in wood basic density within and between tree species and site conditions of exclosures in Tigray, northern Ethiopia. Trees 2018, 32, 967–983. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Kachamba, D.J.; Eid, T.; Gobakken, T. Above- and belowground biomass models for trees in the miombo woodlands of Malawi. Forests 2016, 7, 38. [Google Scholar] [CrossRef] [Green Version]
- Eshete, G.; Ståhl, G. Functions for multi-phase assessment of biomass in acacia woodlands of the Rift Valley of Ethiopia. For. Ecol. Manag. 1998, 105, 79–90. [Google Scholar] [CrossRef]
- Giday, K.; Eshete, G.; Barklund, P.; Aertsen, W.; Muys, B. Wood biomass functions for Acacia abyssinica trees and shrubs and implications for provision of ecosystem services in a community managed exclosure in Tigray, Ethiopia. J. Arid Environ. 2013, 94, 80–86. [Google Scholar] [CrossRef]
- Birhane, E.; Treydte, A.C.; Eshete, A.; Solomon, N.; Hailemariam, M. Can rangelands gain from bush encroachment? Carbon stocks of communal grazing lands invaded by Prosopis juliflora. J. Arid Environ. 2017, 141, 60–67. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2000; Volume 7, ISBN 9780387781884. [Google Scholar]
- Van Breugel, M.; Ransijn, J.; Craven, D.; Bongers, F.; Hall, J.S. Estimating carbon stock in secondary forests: Decisions and uncertainties associated with allometric biomass models. For. Ecol. Manag. 2011, 262, 1648–1657. [Google Scholar] [CrossRef]
- Roxburgh, S.H.; Poul, K.I.; Clifford, D.; England, J.R.; John Raison, R. Guidelines for constructing allometric models for the prediction of woody biomass: How many individuals to harvest? Ecosphere 2015, 6, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Guedes, B.S.; Sitoe, A.A.; Olsson, B.A. Allometric models for managing lowland miombo woodlands of the Beira corridor in Mozambique. Glob. Ecol. Conserv. 2018, 13, e00374. [Google Scholar] [CrossRef]
- Feldpausch, T.R.; Lloyd, J.; Lewis, S.L.; Brienen, R.J.W.; Gloor, M.; Monteagudo Mendoza, A.; Lopez-Gonzalez, G.; Banin, L.; Abu Salim, K.; Affum-Baffoe, K.; et al. Tree height integrated into pantropical forest biomass estimates. Biogeosciences 2012, 9, 3381–3403. [Google Scholar] [CrossRef] [Green Version]
- Rutishauser, E.; Noor’an, F.; Laumonier, Y.; Halperin, J.; Hergoualch, K.; Verchot, L. Generic allometric models including height best estimate forest biomass and carbon stocks in Indonesia. For. Ecol. Manag. 2013, 307, 219–225. [Google Scholar] [CrossRef]
- Aynekulu, E. Forest Diversity in Fragmented Landscapes of Northern Ethiopia and Implications for Conservation. Ph. D. Thesis, Bonn-University, Bonn, Germany, 2011. [Google Scholar]
- Correia, A.C.; Faias, S.P.; Ruiz-Peinado, R.; Chianucci, F.; Cutini, A.; Fontes, L.; Manetti, M.C.; Montero, G.; Soares, P.; Tome, M. Generalized biomass equations for Stone pine (Pinus pinea L.) across the Mediterranean basin. For. Ecol. Manag. 2018, 429, 425–436. [Google Scholar] [CrossRef]
- Ploton, P.; Barbier, N.; Momo, S.T.; Rejou-Mechain, M.; Boyemba Bosela, F.; Chuyong, G.; Dauby, G.; Droissart, V.; Fayolle, A.; Calisto Goodman, R.; et al. Closing a gap in tropical forest biomass estimation: Taking crown mass variation into account in pantropical allometries. Biogeosciences 2016, 13, 1571–1585. [Google Scholar] [CrossRef] [Green Version]
- Goodman, R.C.; Phillips, O.L.; Baker, T.R. The importance of crown dimensions to improve tropical tree biomass estimates. Ecol. Appl. 2014, 24, 680–698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error propagation and sealing for tropical forest biomass estimates. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2004, 359, 409–420. [Google Scholar] [CrossRef] [PubMed]
- Vieilledent, G.; Vaudry, R.; Andriamanohisoa, S.F.D.; Rakotonarivo, O.S.; Randrianasolo, H.Z.; Razafindrabe, H.N.; Bidaud Rakotoarivony, C.; Ebeling, J.; Rasamoelina, M. A universal approach to estimate biomass and carbon stock in tropical forests using generic allometric models. Ecol. Appl. 2012, 22, 572–583. [Google Scholar] [CrossRef] [PubMed]
- Mugasha, W.A.; Manyanda, B.J.; Nzunda, E.F.; Malimbwi, R.E. Biomass and volume models based on stump diameter for assessing degradation of miombo woodlands in Tanzania. Int. J. For. Res. 2019, 2019, 1876329. [Google Scholar]
- Mugasha, W.A.; Eid, T.; Bollandsas, O.M.; Malimbwi, R.E.; Chamshama, S.; Zahabu, E.; Katani, J.Z. Allometric models for prediction of above- and belowground biomass of trees in the miombo woodlands of Tanzania. For. Ecol. Manag. 2013, 310, 87–101. [Google Scholar] [CrossRef]

| Species | n | DSH (cm) | DBH (cm) | H (m) | CA (m2) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Range | Mean | Range | Mean | Range | Mean | Range | ||
| Juniperus procera Hochst. ex Endl. | 23 | 21.2 | 5.2–51.0 | 18.1 | 4.2–45.2 | 8.5 | 5.4–13.3 | 17.1 | 0.7–69.2 |
| Olea europaea L. subsp. Cuspidata (Wall. ex DC.) Ciffieri | 16 | 21.6 | 5.1–47.3 | 19.3 | 4.6–41.2 | 6.6 | 3.5–10.5 | 17.0 | 2.7–51.9 |
| Acacia etbaica Schweinf | 3 | 11.6 | 7.4–16.8 | 10 | 5.7–16.0 | 3.7 | 3.0–4.1 | 8.8 | 3.3–18.7 |
| Cadia purpurea Ait | 8 | 7.8 | 4.9–11.0 | 6.5 | 2.9–9.8 | 4.6 | 3.7–6.3 | 7.9 | 2.7–13.2 |
| Tarchonanthus camphorantus L. | 7 | 10.1 | 5.7–16.7 | 9.3 | 5.3–16.3 | 4.8 | 3.9–7.7 | 11.0 | 5.9–19.9 |
| Calpurnia aurea Benth. | 6 | 9.3 | 5.7–12.8 | 8.4 | 4.7–11.8 | 6.0 | 4.4–8.6 | 9.6 | 5.9–15.2 |
| Euclea racemose Murray subsp. Schimperi (A. DC) F. White | 4 | 6.1 | 5.1–7.8 | 5.4 | 3.6–8.1 | 3.7 | 3.2–4.4 | 7.6 | 2.9–14.4 |
| Acokanthera schimperi (A. DC.) Benth. & Hook.f. ex Schweinf. | 4 | 10.7 | 8.8–15.0 | 7.5 | 5.6–12 | 4.4 | 3.8–5.7 | 6.6 | 4.5–11.0 |
| Rhus natalensis Bernh. ex Krauss | 7 | 9.4 | 5.4–14.4 | 8.4 | 4.3–12.2 | 4.5 | 3.1–5.6 | 9.0 | 3.6–15.2 |
| Dodonaea angustifolia L. F. | 8 | 10.2 | 5.3–18.6 | 8.6 | 4.8–16.5 | 5.2 | 3.8–6.6 | 9.6 | 1.2–35.2 |
| All | 86 | 14.8 | 4.9–51.0 | 12.8 | 2.9–45.2 | 6.1 | 3.0–13.3 | 12.6 | 0.7–69.2 |
| Model Type | Expression | Reference |
|---|---|---|
| General multispecies (pan-tropical) | AGB = 0.112 × (DBH2 × H × ρ)0.916 | Chave et al. [10] |
| General multispecies (pan-tropical) | AGB = 0.0673 × (DBH2 × H × ρ)0.976 | Chave et al. [11] |
| General multispecies (Ethiopia) | AGB = 0.3102 × DSH1.5155 × CW0.6453 | Ubuy et al. [19] |
| General multispecies (Ethiopia) | AGB = 0.2451 × (DSH2 × H)0.7038 | Mokria et al. [2] |
| Local species-specific (Ethiopia) | ln(AGB) = ln(−2.48) + 2.32 × ln(DBH) | Worku and Soromessa [24] |
| Local species-specific (Ethiopia) | AGB = 1.12 × DBH1.54 | Solomon et al. [26] |
| Local species-specific (Ethiopia) | AGB = 0.866 × DBH1.432 × H0.608 × ρ1.067 | Kebede and Soromessa [25] |
| Model | Model Expression | Parameter Estimates | adj-R2 | rRMSE (%) | rBias (%) | AIC | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | B | c | d | e | ||||||
| M1 | AGB = a × DBHb | 0.298 | 2.034 | 0.935 | 74.6 | 4.4 | 64.2 | |||
| M2 | AGB = a × DBHb × Hc | 0.334 | 2.112 | −0.170 ns | 0.935 | 74.0 | 4.4 | 65.3 | ||
| M3 | AGB = a × DBHb × CAc | 0.310 | 1.859 | 0.168 | 0.940 | 69.3 | 3.5 | 58.8 | ||
| M4 | AGB = a × DBHb × ρc | 0.336 | 2.041 | 0.473 | 0.938 | 62.6 | 3.9 | 61.0 | ||
| M5 | AGB = a × DBHb × Hc × CAd | 0.327 | 1.902 | −0.080 ns | 0.163 | 0.940 | 69.3 | 3.6 | 60.6 | |
| M6 | AGB = a × DBHb × Hc × ρd | 0.327 | 2.016 | 0.055 ns | 0.505 | 0.938 | 62.3 | 3.8 | 62.9 | |
| M7 | AGB = a × DBHb × CAc × ρd | 0.350 | 1.864 | 0.171 | 0.485 | 0.943 | 56.9 | 3.0 | 54.8 | |
| M8 | AGB = a × DBHb × Hc × CAd × ρe | 0.317 | 1.760 | 0.199 ns | 0.185 | 0.600 | 0.943 | 54.6 | 2.6 | 55.9 |
| M9 | AGB = a × DSHb | 0.170 | 2.128 | 0.941 | 71.2 | 2.4 | 55.9 | |||
| M10 | AGB = a × DSHb × Hc | 0.178 | 2.170 | −0.087 ns | 0.941 | 70.3 | 2.4 | 57.7 | ||
| M11 | AGB = a × DSHb × CAc | 0.184 | 1.951 | 0.165 | 0.956 | 66.8 | 1.6 | 50.1 | ||
| M12 | AGB = a × DSHb × ρc | 0.196 | 2.141 | 0.625 | 0.957 | 54.7 | 1.8 | 47.7 | ||
| M13 | AGB = a × DSHb × Hc × CAd | 0.185 | 1.957 | −0.011 ns | 0.164 | 0.945 | 66.8 | 1.6 | 52.1 | |
| M14 | AGB = a × DSHb × Hc × ρd | 0.179 | 2.045 | 0.209 ns | 0.738 | 0.957 | 54.3 | 1.4 | 48.4 | |
| M15 | AGB = a × DSHb × CAc × ρd | 0.213 | 1.965 | 0.164 | 0.624 | 0.952 | 50.4 | 0.9 | 40.9 | |
| M16 | AGB = a × DSHb × Hc × CAd × ρe | 0.187 | 1.799 | 0.316 ns | 0.182 | 0.795 | 0.953 | 49.7 | 0.2 | 39.7 |
| Model | Species | n | Model Expression | Parameter Estimates | adj-R2 | rRMSE (%) | rBias (%) | AIC | |
|---|---|---|---|---|---|---|---|---|---|
| a | b | ||||||||
| M17 | Juniperus procera | 23 | AGB = a × DBHb | 0.161 | 2.199 | 0.966 | 74.1 | −10.7 | 5.6 |
| M18 | Juniperus procera | 23 | AGB = a × DSHb | 0.095 | 2.250 | 0.982 | 37.2 | −5.6 | −8.8 |
| M19 | Olea europaea | 16 | AGB = a × DBHb | 0.173 | 2.250 | 0.968 | 43.7 | −11.8 | 8.6 |
| M20 | Olea europaea | 16 | AGB = a × DSHb | 0.125 | 2.279 | 0.948 | 44.7 | 3.1 | 16.3 |
| M21 | Other species | 47 | AGB = a × DBHb | 0.454 | 1.848 | 0.815 | 13.3 | 1.0 | 42.6 |
| M22 | Other species | 47 | AGB = a × DSHb | 0.190 | 2.100 | 0.846 | 9.9 | 0.9 | 33.9 |
| Model | Option/Model | Observed Mean (kg) | Predicted Mean (kg) | rRMSE (%) | rBias (%) |
|---|---|---|---|---|---|
| System I | DBH/M7 | 88.7 | 86.4 | 52.0 | 2.6 ns |
| DSH/M15 | 88.7 | 88.3 | 46.5 | 0.4 ns | |
| System II | DBH/M17, M19, M21 | 88.7 | 89.0 | 55.8 | −0.4 ns |
| DSH/M18, M20, M22 | 88.7 | 88.9 | 47.4 | −0.2 ns |
| Model Type | References | n | Observed Mean (kg) | Predicted Mean (kg) | rRMSE (%) | rBias (%) |
|---|---|---|---|---|---|---|
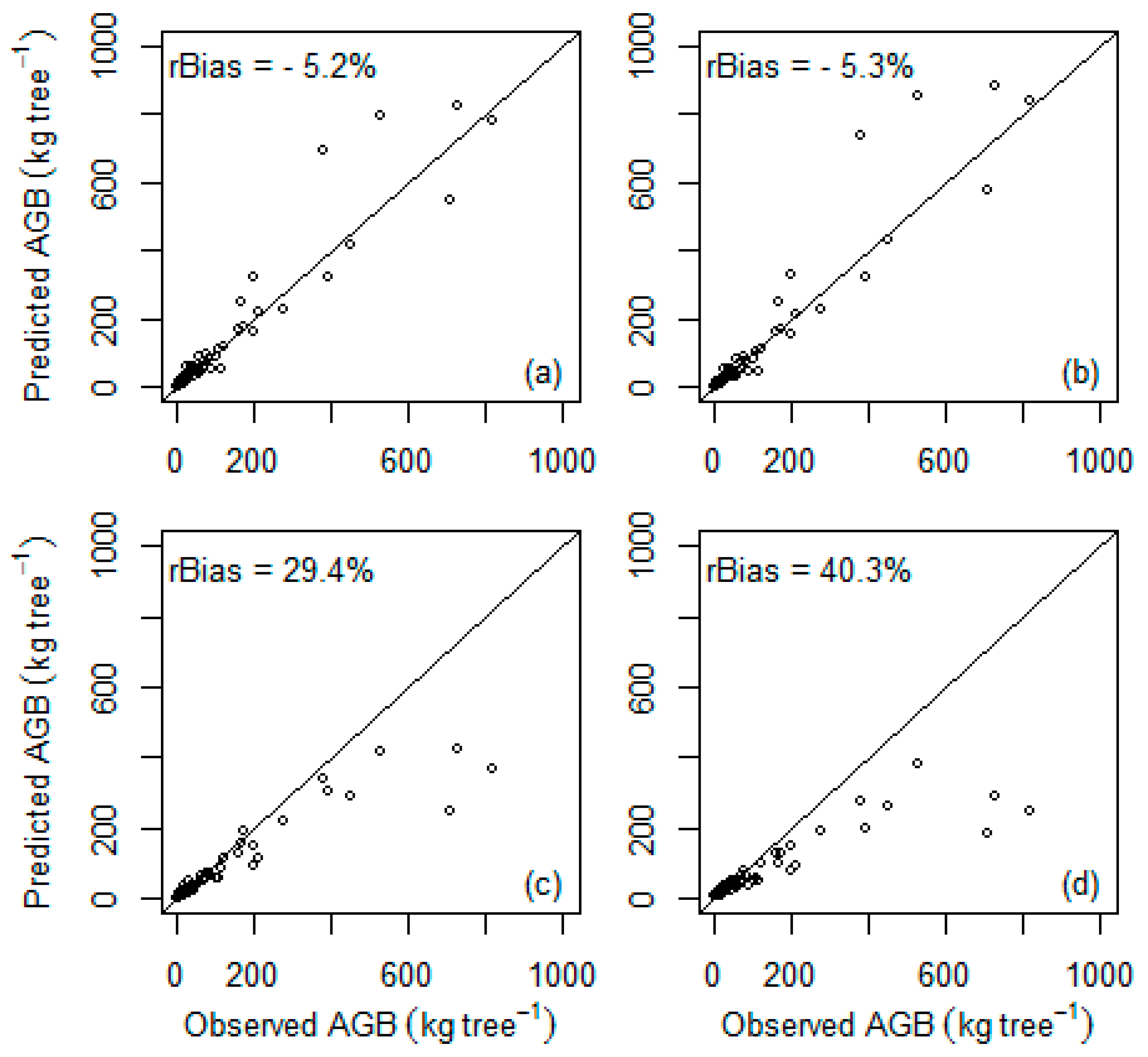
| General multispecies | Chave et al. [10] | 86 | 88.7 | 93.3 | 60.1 | −5.2 ns |
| General multispecies | Chave et al. [11] | 86 | 88.7 | 93.5 | 68.3 | −5.3 ns |
| General multispecies | Ubuy et al. [19] | 86 | 88.7 | 62.6 | 93.2 | 29.4 ** |
| General multispecies | Mokria et al. [2] | 86 | 88.7 | 52.9 | 118.7 | 40.3 ** |
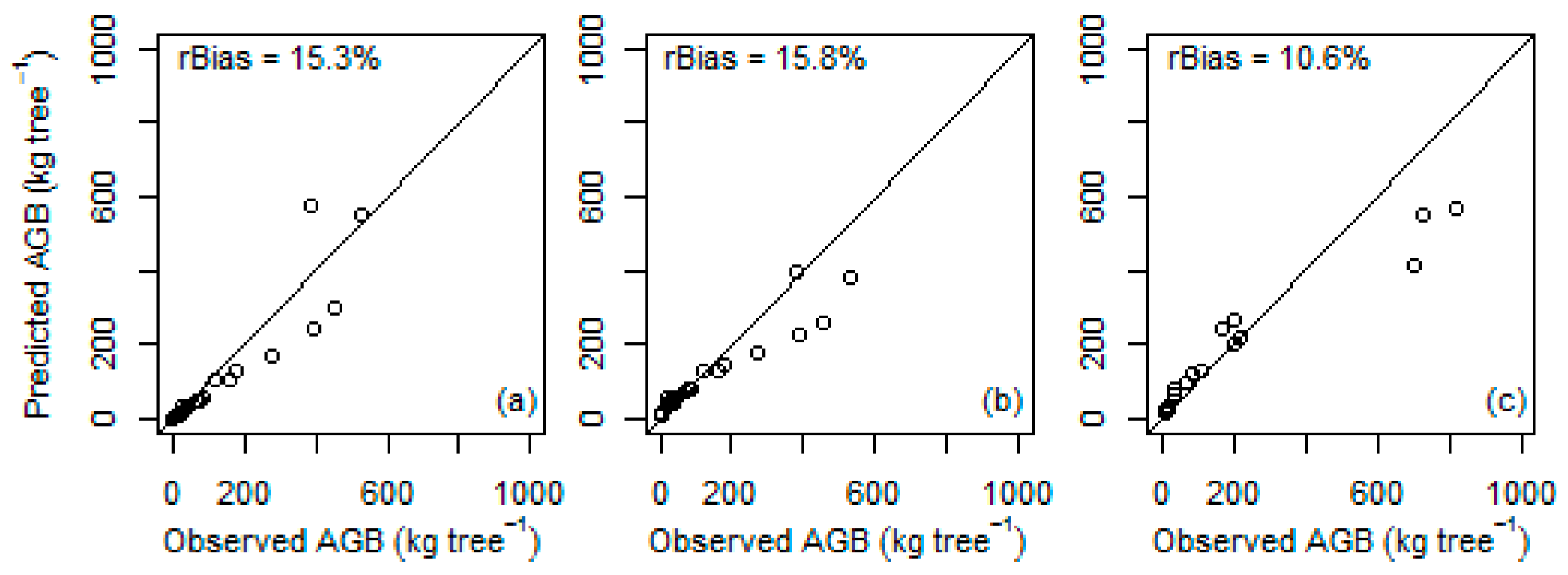
| Local species-specific | Worku and Soromessa [24] | 23 | 132.1 | 112.0 | 50.9 | 15.3 ns |
| Local species-specific | Solomon et al. [26] | 23 | 132.1 | 178.6 | 50.6 | 15.8 ns |
| Local species-specific | Kebede and Soromessa [25] | 16 | 213.3 | 190.7 | 51.5 | 10.6 ns |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tetemke, B.A.; Birhane, E.; Rannestad, M.M.; Eid, T. Allometric Models for Predicting Aboveground Biomass of Trees in the Dry Afromontane Forests of Northern Ethiopia. Forests 2019, 10, 1114. https://doi.org/10.3390/f10121114
Tetemke BA, Birhane E, Rannestad MM, Eid T. Allometric Models for Predicting Aboveground Biomass of Trees in the Dry Afromontane Forests of Northern Ethiopia. Forests. 2019; 10(12):1114. https://doi.org/10.3390/f10121114
Chicago/Turabian StyleTetemke, Buruh Abebe, Emiru Birhane, Meley Mekonen Rannestad, and Tron Eid. 2019. "Allometric Models for Predicting Aboveground Biomass of Trees in the Dry Afromontane Forests of Northern Ethiopia" Forests 10, no. 12: 1114. https://doi.org/10.3390/f10121114
APA StyleTetemke, B. A., Birhane, E., Rannestad, M. M., & Eid, T. (2019). Allometric Models for Predicting Aboveground Biomass of Trees in the Dry Afromontane Forests of Northern Ethiopia. Forests, 10(12), 1114. https://doi.org/10.3390/f10121114





