“Diminishing Returns” in the Scaling between Leaf Area and Twig Size in Three Forest Communities Along an Elevation Gradient of Wuyi Mountain, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Leaf and Twig Sampling
2.3. Data Analysis
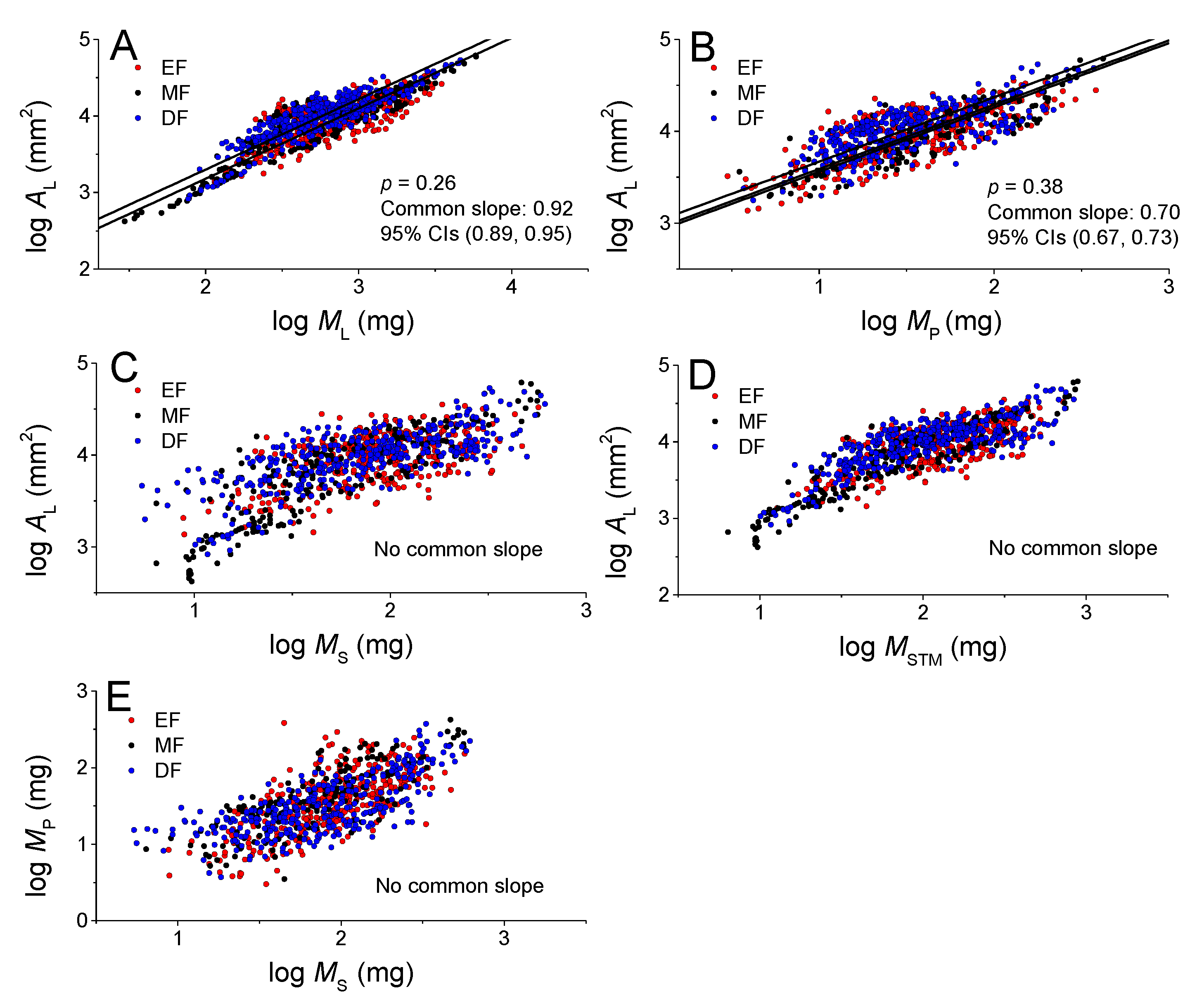
3. Results
3.1. Variation in Lamina Size, Petiole and Stem Mass at the Leaf and Twig Levels
3.2. Scaling Relationships at the Leaf Level among Lamina Area and Mass, and Petiole Mass
3.3. Scaling Relationships at the Twig Level among Lamina Areaand Petiole and Stem Mass
4. Discussion
4.1. Thelamina Area vs. Lamina Mass Scaling Relationship
4.2. Scaling Relationships of Lamina Area and Petiole Mass
4.3. Scaling Relationships of Petiole and Stem Biomass Along an Elevation Gradient
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Niklas, K.J.; Enquist, B.J. On the vegetative biomass partitioning of seed plant leaves, stems, and roots. Am. Nat. 2002, 59, 482–497. [Google Scholar] [CrossRef]
- Reich, P.B.; Tjoelker, M.G.; Walters, M.B.; Vanderklein, D.W.; Buschena, C. Close association of RGR, leaf and root morphology, seed mass and shade tolerance in seedlings of nine boreal tree species in high and low light. Funct. Ecol. 1998, 12, 327–338. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant Allometry: The Scaling of Form and Process; The University of Chicago Press: Chicago, IL, USA, 1994. [Google Scholar]
- Cheng, D.L.; Niklas, K.J. Above-and below-ground biomass relationships across 1534 forested communities. Ann. Bot. 2007, 99, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Niklas, K.J.; Cobb, E.D.; Niinemets, Ü.; Reich, P.B.; Sellin, A.; Shipley, B.; Wright, I.J. “Diminishing returns” in the scaling of functional leaf traits across and within species groups. Proc. Natl. Acad. Sci. USA 2007, 104, 8891–8896. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shipley, B. Structured interspecific determinants of specific leaf area in 34 species of herbaceous angiosperms. Funct. Ecol. 1995, 9, 312–319. [Google Scholar] [CrossRef]
- Milla, R.; Reich, P.B.; Niinemets, Ü.; Castro-Díez, P. Environmental and developmental controls on specific leaf area are little modified by leaf allometry. Funct. Ecol. 2010, 22, 565–576. [Google Scholar] [CrossRef]
- Niinemets, Ü.; Kull, O. Biomass investment in leaf lamina versus lamina support in relation to growth irradiance and leaf size in temperate deciduous trees. Tree Physiol. 1999, 19, 349–358. [Google Scholar] [CrossRef] [Green Version]
- Niinemets, Ü.; Portsmuth, A.; Tena, D.; Tobias, M.; Matesanz, S.; Valladares, F. Do we underestimate the importance of leaf size in plant economics? Disproportional scaling of support costs within the spectrum of leaf physiognomy. Ann. Bot. 2007, 100, 283–303. [Google Scholar] [CrossRef]
- Pickup, M.; Westoby, M.; Basden, A. Dry mass costs of deploying leaf area in relation to leaf size. Funct. Ecol. 2005, 19, 88–97. [Google Scholar] [CrossRef]
- Sun, J.; Fan, R.; Niklas, K.J.; Zhong, Q.; Yang, F.; Li, M.; Chen, X.; Sun, M.; Cheng, D. “Diminishing returns” in the scaling of leaf area vs. dry mass in Wuyi Mountain bamboos, Southeast China. Am. J. Bot. 2017, 104, 993–998. [Google Scholar] [CrossRef] [Green Version]
- Niklas, K.J.; Enquist, B.J. Invariant scaling relationships for interspecific plant biomass production rates and body size. Proc. Natl. Acad. Sci. USA 2001, 98, 2922–2927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milla, R.; Reich, P.B. The scaling of leaf area and mass: the cost of light in terception increases with leaf size. Proceedings of the Royal Society B: Biological Sciences 2007, 274, 2109–2114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, S.; Liu, C.; Zhang, W.; Xu, S.; Wang, N.; Li, Y.; Gao, J.; Wang, Y.; Wang, G. The scaling relationships between leaf mass and leaf area of vascular plant species change with elevation. PLoS ONE 2013, 8, e76872. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.F.; Freschet, G.T.; Pan, X.; Cornelissen, J.; Li, Y.; Dong, M. Coordinated variation in leaf and root traits across multiple spatial scales in Chinese semi-arid and arid ecosystems. New Phytologist 2010, 188, 543–553. [Google Scholar] [CrossRef]
- Li, M.; Zheng, Y.; Fan, R.R.; Zhong, Q.L.; Cheng, D.L. Scaling relationships of twig biomass allocation in Pinus hwangshanensis along an altitudinal gradient. PLoS ONE 2017, 12, e0178344. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M.T.; Lyu, M.; Niklas, K.J.; Zhong, Q.L.; Li, M.; Cheng, D.L. Stem Diameter (and Not Length)Limits Twig Leaf Biomass. Frontiers in Plant Science 2019, 10, 185. [Google Scholar] [CrossRef]
- Warton, D.I.; Duursma, R.A.; Falster, D.S.; Taskinen, S. Smatr 3-an Rpackage for estimation and inference about allometric lines. Methods Ecol. Evol. 2012, 3, 257–259. [Google Scholar] [CrossRef]
- Niklas, K.J.; Cobb, E.D. Evidence for “diminishing returns” from the scaling of stem diameter and specific leaf area. Am. J. Bot. 2008, 95, 549–557. [Google Scholar] [CrossRef]
- Givnish, T.J.; McDiarmid, R.W.; Buck, W.R. Fire adaptation in Neblinariaceliae (Theaceae), a high-elevation rosette shrub endemic to a wet equatorial tepui. Oecologia 1986, 70, 481–485. [Google Scholar] [CrossRef] [Green Version]
- Niinemets, Ü. Global-scale climatic controls of leaf dry mass per area, density, and thickness in trees and shrubs. Ecology 2001, 82, 453–469. [Google Scholar] [CrossRef]
- Ogawa, K.; Adu-Bredu, S.; Yokota, T.; Hagihara, A. Leaf biomass changes with stand development in Hinoki cypress (Chamaecyparis obtusa [Sieb. & Zucc.] Endl.). Plant Ecol. 2010, 211, 79–88. [Google Scholar] [CrossRef]
- Drake, J.E.; Davis, S.C.; Raetz, L.M.; Delucia, E.H. Mechanisms of age-related changes in forest production: The influence of physiological and successional changes. Glob. Chang. Biol. 2011, 17, 1522–1535. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant Biomechanics: An Engineering Approach to Plant Form and Function; The University of Chicago Press: Chicago, IL, USA, 1992. [Google Scholar]
- Niinemets, Ü.; Portsmuth, A.; Tobias, M. Leaf size modifies support biomass distribution among stems, petioles and mid-ribs in temperate plants. New Phytol. 2006, 171, 91–104. [Google Scholar] [CrossRef] [PubMed]
- Li, G.Y.; Yang, D.M.; Sun, S.C. Allometric relationships between lamina area, lamina mass and petiole mass of 93 temperate woody species vary with leaf habit, leaf form and altitude. Funct. Ecol. 2008, 22, 557–564. [Google Scholar] [CrossRef]
- Niklas, K.J. The evolution of leaf form and function. In Leaf Development and Canopy Growth; Marshall, B., Roberts, J.A., Eds.; Scheffield Academic Press: Scheffield, UK, 2000. [Google Scholar]
- Niklas, K.J. A mechanical perspective on foliage leaf form and function. New Phytol. 1999, 143, 19–31. [Google Scholar] [CrossRef]
- Zhu, J.D.; Meng, T.T.; Ni, J.; Su, H.X.; Xie, Z.Q.; Zhang, S.R.; Zheng, Y.R.; Xiao, C.W. Within-leaf allometric relationships of mature forests in different bioclimatic zones vary with plant functional types. Chin. J. Plant Ecol. 2011, 35, 687–698. [Google Scholar] [CrossRef]
- Sun, S.C.; Jin, D.M.; Shi, P.L. The leaf size-twig size spectrum of temperate woody species along an altitudinal gradient: An invariant allometric scaling relationship. Ann. Bot. 2006, 97, 97–107. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.; Wu, N.; Sun, S. Within-twig biomass allocation in subtropical evergreen broad-leaved species along an altitudinal gradient: Allometric scaling analysis. Trees 2009, 23, 637–647. [Google Scholar] [CrossRef]
- Woodward, F.I.; Lomas, M.R.; Kelly, C.K. Global climate and the distribution of plant biomes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 1465–1476. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; He, X.; Xu, X.; Yang, D. Scaling relationships among twig components are affected by sex in the dioecious tree Populus cathayana. Trees 2015, 29, 737–746. [Google Scholar] [CrossRef]

| Forest Type | PFTS | Family | Genus | Species | Lifeform | Family | Genus | Species |
|---|---|---|---|---|---|---|---|---|
| EF | arbor | 9 | 15 | 18 | evergreen | 8 | 13 | 22 |
| shrub | 10 | 11 | 14 | deciduous | 9 | 10 | 10 | |
| MF | arbor | 9 | 10 | 12 | evergreen | 8 | 10 | 13 |
| shrub | 4 | 5 | 8 | deciduous | 5 | 5 | 7 | |
| DF | arbor | 8 | 8 | 9 | evergreen | 5 | 5 | 6 |
| shrub | 12 | 13 | 14 | deciduous | 14 | 16 | 17 |
| Type | Leaf-level | Twig-Level | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | mp (g) | ml (g) | al (mm2) mL (g) | ML (g) | MP (g) | MS (g) | AL (mm2) | MSTM (g) | ||
| EF | 335 | 0.011 ± 0.52b | 0.2 ± 8.19a | 2286 ± 66.83a | 0.21 ± 8.66a | 0.91 ± 34.59a | 0.051 ± 2.71b | 0.111 ± 4.51a | 10983 ± 349.75a | 0.162 ± 6.17a |
| MF | 205 | 0.014 ± 0.93a | 0.173 ± 11.77b | 2135 ± 115.14a | 0.184 ± 12.45b | 0.808 ± 69.04a | 0.063 ± 5.54a | 0.088 ± 7.85b | 9509 ± 677.66b | 0.137 ± 12.07b |
| DF | 375 | 0.009 ± 0.42c | 0.138 ± 5.61c | 2228 ± 72.10a | 0.145 ± 5.94c | 0.755 ± 36.67b | 0.048 ± 2.86b | 0.114 ± 5.57a | 11816 ± 413.51a | 0.156 ± 7.74a |
| All | 915 | 0.010 ± 0.33 | 0.168 ± 4.69 | 2228 ± 46.21 | 0.178 ± 4.96 | 0.824 ± 25.08 | 0.052 ± 1.92 | 0.107 ± 3.33 | 10994 ± 262.39 | 0.154 ± 4.75 |
| log y vs. log x | Forests | n | α (95%CIs) | log β (95%CIs) | r2 | p |
|---|---|---|---|---|---|---|
| al vs. ml | EF | 335 | 0.79 (0.74, 0.84) | 1.57 (1.45, 1.68) | 0.62 | <0.001 |
| MF | 205 | 1.00 (0.96, 1.03) | 1.13 (1.06, 1.20) | 0.94 | <0.001 | |
| DF | 375 | 0.92 (0.87, 0.96) | 1.40 (1.31, 1.49) | 0.77 | <0.001 | |
| All | 915 | 0.94 (0.92, 0.97) | 1.28 (1.23, 1.34) | 0.83 | <0.001 | |
| al vs. mp | EF | 335 | 0.68 (0.63, 0.73) | 2.70 (2.65, 2.75) | 0.52 | <0.001 |
| MF | 160 | 0.65 (0.60, 0.71) | 2.72 (2.66, 2.78) | 0.67 | <0.001 | |
| DF | 330 | 0.74 (0.68, 0.80) | 2.72 (2.67, 2.77) | 0.43 | <0.001 | |
| All | 825 | 0.68(0.65, 0.72) | 2.72(2.69, 2.75) | 0.51 | <0.001 | |
| ml vs. mp | EF | 335 | 0.86 (0.82, 0.90) | 1.44 (1.40, 1.48) | 0.81 | <0.001 |
| MF | 160 | 0.82 (0.77, 0.87) | 1.42 (1.37, 1.48) | 0.85 | <0.001 | |
| DF | 330 | 0.89 (0.83, 0.94) | 1.36(1.31, 1.41) | 0.67 | <0.001 | |
| All | 825 | 0.86(0.83, 0.89) | 1.40(1.38, 1.43) | 0.77 | <0.001 | |
| al vs. mL | EF | 335 | 0.79 (0.74, 0.84) | 1.55 (1.43, 1.67) | 0.62 | <0.001 |
| MF | 160 | 0.99 (0.96, 1.02) | 1.12 (1.05, 1.19) | 0.94 | <0.001 | |
| DF | 330 | 0.91 (0.87, 0.96) | 1.39 (1.30, 1.48) | 0.77 | <0.001 | |
| All | 825 | 0.94 (0.91,0.96) | 1.27 (1.22, 1.33) | 0.83 | <0.001 |
| log y vs. Log x | Forests | n | α (95%CIs) | log β (95%CIs) | r2 | p |
|---|---|---|---|---|---|---|
| AL vs. ML | EF | 335 | 0.90 (0.84, 0.96) | 1.40 (1.22,1.57) | 0.60 | <0.001 |
| MF | 160 | 0.95(0.90, 0.99) | 1.27(1.15,1.39) | 0.88 | <0.001 | |
| DF | 330 | 0.90(0.86, 0.94) | 1.52(1.40, 1.64) | 0.78 | <0.001 | |
| All | 825 | 0.92 (0.90, 0.95) | 1.37(1.29, 1.45) | 0.76 | <0.001 | |
| AL vs. MP | EF | 335 | 0.71 (0.66, 0.76) | 2.87 (2.79, 2.95) | 0.56 | <0.001 |
| MF | 160 | 0.72 (0.66, 0.78) | 2.83(2.73, 2.92) | 0.73 | <0.001 | |
| DF | 330 | 0.67(0.62, 0.72) | 3.01 (2.93, 3.09) | 0.54 | <0.001 | |
| All | 825 | 0.70 (0.67, 0.73) | 2.91(2.86, 2.96) | 0.57 | <0.001 | |
| AL vs. MS | EF | 335 | 0.85(0.78, 0.92) | 2.32 (2.18, 2.47) | 0.33 | <0.001 |
| MF | 160 | 1.03 (0.96, 1.10) | 2.02(1.89, 2.15) | 0.74 | <0.001 | |
| DF | 330 | 0.71(0.66, 0.76) | 2.67 (2.57, 2.76) | 0.53 | <0.001 | |
| All | 825 | 0.85 (0.81, 0.89) | 2.35(2.28, 2.42) | 0.54 | <0.001 | |
| AL vs. MSTM | EF | 335 | 0.85(0.79, 0.92) | 2.17 (2.03, 2.31) | 0.48 | <0.001 |
| MF | 160 | 0.93 (0.88, 0.98) | 2.03(1.94, 2.13) | 0.86 | <0.001 | |
| DF | 330 | 0.75 (0.71, 0.80) | 2.47 (2.37, 2.56) | 0.64 | <0.001 | |
| All | 825 | 0.85 (0.82, 0.88) | 2.22(2.16, 2.28) | 0.67 | <0.001 | |
| MP vs. MS | EF | 335 | 1.19 (1.10, 1.30) | –0.76 (–0.95, –0.58) | 0.47 | <0.001 |
| MF | 160 | 1.06 (0.97, 1.16) | –0.37(–0.56, –0.18) | 0.64 | <0.001 | |
| DF | 330 | 0.88(0.81, 0.94) | –0.15 (–0.27, –0.02) | 0.52 | <0.001 | |
| All | 825 | 0.92 (0.90, 0.95) | 1.37(1.29, 1.45) | 0.76 | <0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, G.; Niklas, K.J.; Li, M.; Sun, J.; Lyu, M.; Chen, X.; Wang, M.; Zhong, Q.; Cheng, D. “Diminishing Returns” in the Scaling between Leaf Area and Twig Size in Three Forest Communities Along an Elevation Gradient of Wuyi Mountain, China. Forests 2019, 10, 1138. https://doi.org/10.3390/f10121138
Zhu G, Niklas KJ, Li M, Sun J, Lyu M, Chen X, Wang M, Zhong Q, Cheng D. “Diminishing Returns” in the Scaling between Leaf Area and Twig Size in Three Forest Communities Along an Elevation Gradient of Wuyi Mountain, China. Forests. 2019; 10(12):1138. https://doi.org/10.3390/f10121138
Chicago/Turabian StyleZhu, Guojie, Karl Joseph Niklas, Man Li, Jun Sun, Min Lyu, Xiaoping Chen, Mantang Wang, Quanlin Zhong, and Dongliang Cheng. 2019. "“Diminishing Returns” in the Scaling between Leaf Area and Twig Size in Three Forest Communities Along an Elevation Gradient of Wuyi Mountain, China" Forests 10, no. 12: 1138. https://doi.org/10.3390/f10121138




