Growth and Yield Models for Balsa Wood Plantations in the Coastal Lowlands of Ecuador
Abstract
:1. Introduction
2. Materials and Methods
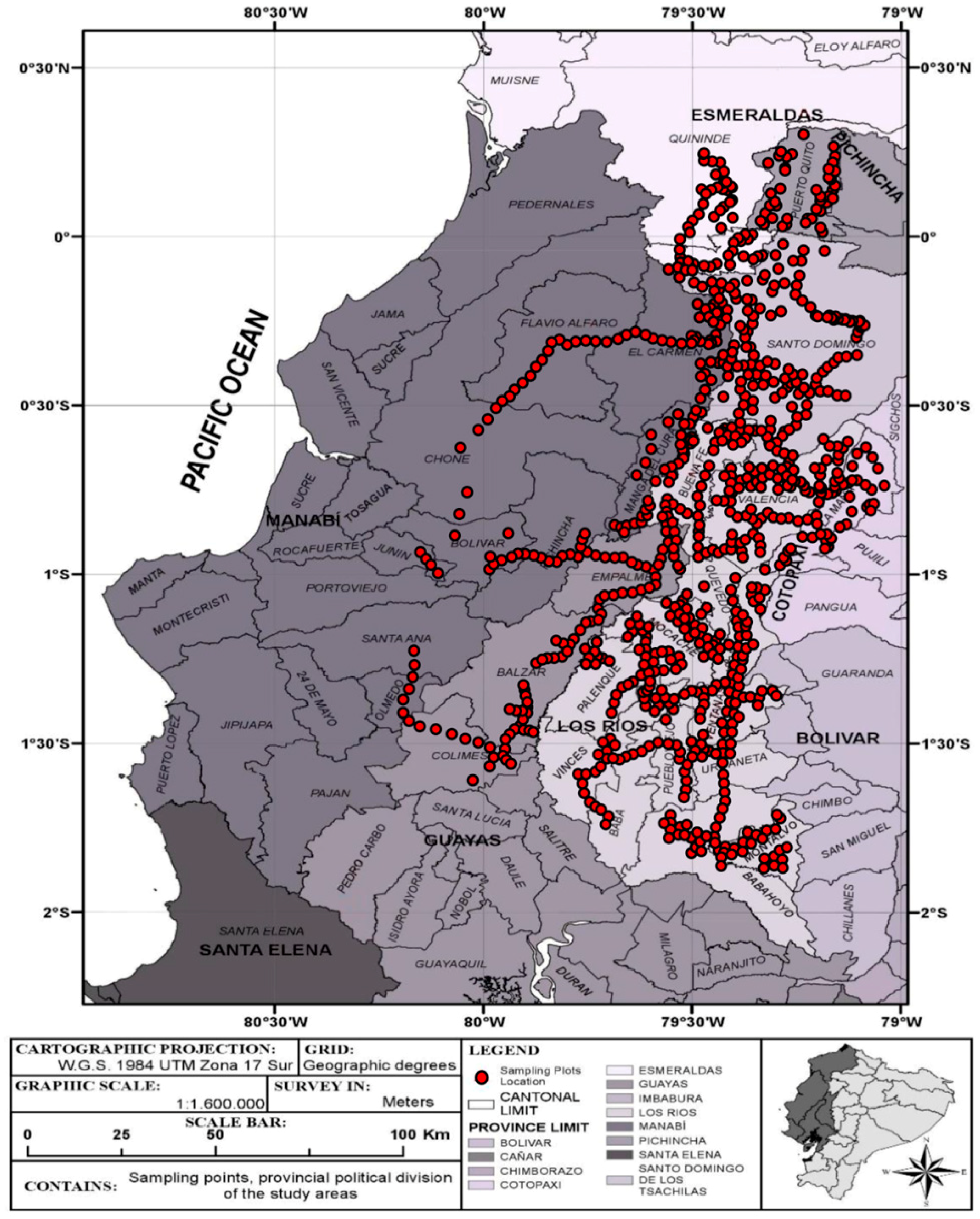
2.1. Study Area
2.2. Data Collection
2.3. Site Index Assessment
2.4. Tree Volume Assessment
2.5. Assessment of Balsa Production
3. Results
3.1. Balsa Site Index
3.2. Volume Models
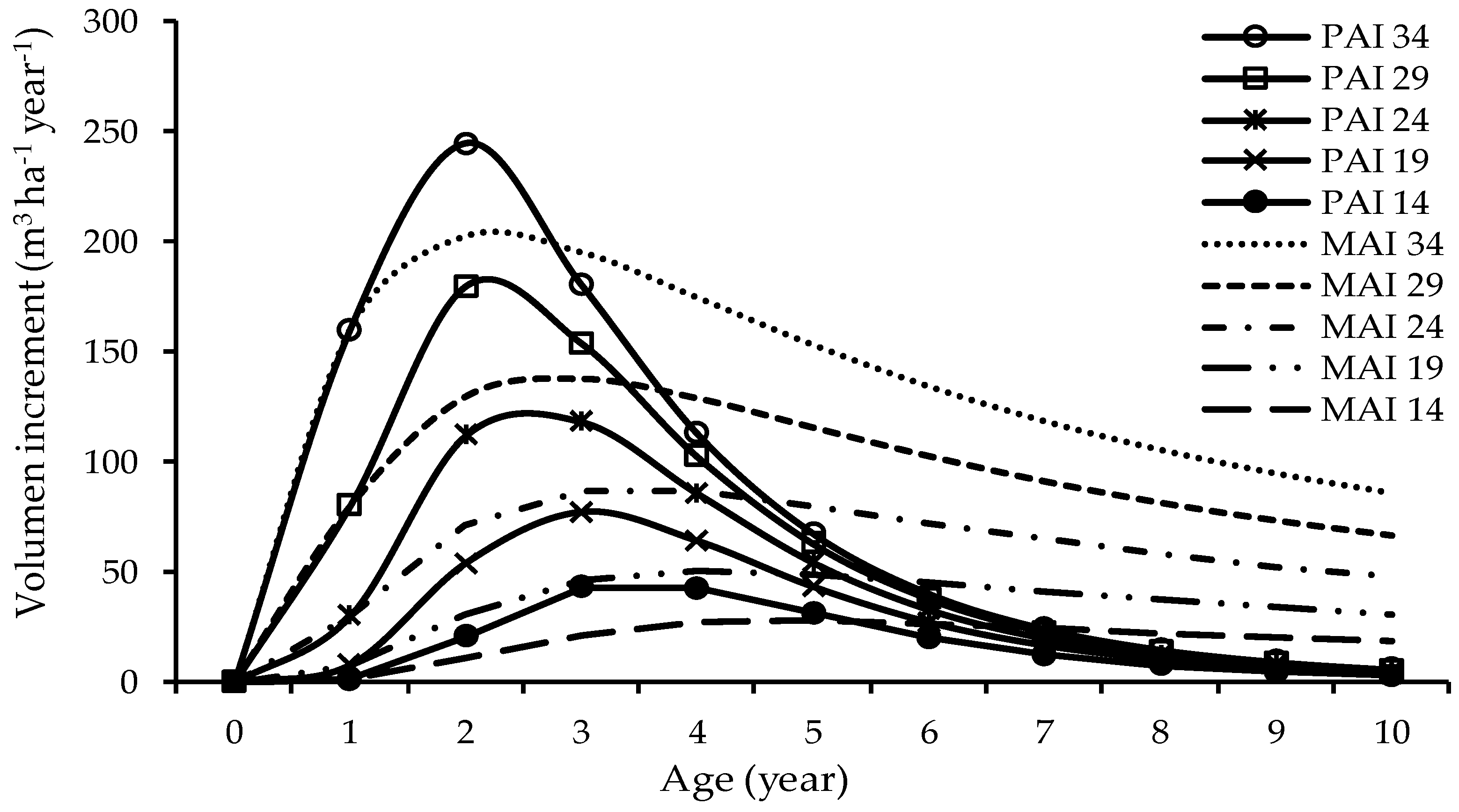
3.3. Mean Annual Increment
4. Discussion
4.1. Site Index Assessment of Height and Diameter
4.2. Tree Volume Assessment
4.3. Mean Annual Increment in Volume
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Castro-Díez, P.; Vaz, A.S.; Silva, J.S.; van Loo, M.; Alonso, Á.; Aponte, C.; Bayón, Á.; Bellingham, P.J.; Chiuffo, M.C.; DiManno, N.; et al. Global effects of non-native tree species on multiple ecosystem services. Biol. Rev. 2019. [Google Scholar] [CrossRef]
- Douterlungne, D.; Thomas, E.; Levy-Tacher, S.I. Fast-growing pioneer tree stands as a rapid and effective strategy for bracken elimination in the Neotropics. J. Appl. Ecol. 2013, 50, 1257–1265. [Google Scholar] [CrossRef]
- Levy-Tacher, S.; Vleut, I.; Román-Dañobeytia, F.; Aronson, J. Natural regeneration after long-term bracken fern control with balsa (Ochroma pyramidale) in the Neotropics. Forests 2015, 6, 2163–2177. [Google Scholar] [CrossRef]
- Midgley, S.; Blyth, M.; Howcroft, N.; Midgley, D.; Brown, A. Balsa: Biology, Production and Economics in Papua New Guinea, 1st ed.; ACIAR Technical Report Series; ACIAR: Canberra, Australia, 2010; pp. 98–99. [Google Scholar]
- Cañadas, L. El mapa ecológico y bioclimático del Ecuador; Editores Asociados Cia. Ltd.: Quito, Ecuador, 1983; pp. 50–120. ISBN 978-9942-09360-8. [Google Scholar]
- Vleut, I.; Levy-Tacher, S.I.; de Boer, F.; Galindo-González, J.; Ramírez-Marcial, N. Can a fast-growing early successional tree (Ochroma pyramidale, Malvaceae) accelerate forest succession? J. Trop. Ecol. 2013, 29, 173–180. [Google Scholar] [CrossRef]
- Cañadas-López, A.; Rade-Loor, D.; Cevallos, G.F.; Andrade, J.M.D.; Murillo-Hernández, I.; Molina-Hidrovo, C.M.; Castro, H.Q. Ecuaciones generales de diámetro-altura para Ochroma pyramidale, Región Costa-Ecuador. Bosques. Latitud. Cero. 2016, 6, 1–14. [Google Scholar]
- Goosem, S.P.; Tucker, N.I.J. Repairing the Rainforest-Theory and Practice of Rainforest Re-Establishment in North Queensland’s Wet Tropics; Casswary Publication: Cairns, Australia, 1995; pp. 71–80. [Google Scholar]
- Martínez-Garza, C.; Campo, J.; Ricker, M.; Tobón, W. Effect of initial soil properties on six-year growth of 15 tree species in tropical restoration plantings. Ecol. Evol. 2016, 6, 8686–8694. [Google Scholar] [CrossRef] [PubMed]
- Cañadas, A.; Rade, D.; Domínguez, J.M.; Murillo, I.; Molina, C. Modelación forestal como Innovación tecnológica para el manejo silvicultural y aprovechamiento económico de la Balsa, Región Costa-Ecuador; Abya Yala: Quito, Ecuador, 2016; pp. 10–50. ISBN 978-9942-09-360-8. [Google Scholar]
- Haggar, J.; Sosa, M.; Días, B.; Hernández, G.; Contreras, J.A.; Uc, C. Integración de factores biofísicos, económicos y sociales en el diseño de sistemas agroforestales en la península de Yucatán. In Los Sistemas Agroforestales de Latinoamérica y de la Selva Baja Caducifolia en México; Monroy, R., Colin, H., Boyas, J., Eds.; IICA; INIFAP; UAEM: Estado de Morales, México, 1998; pp. 71–85. [Google Scholar]
- Vincent, A.B. Is height/age a reliable index of site? For. Chron. 1961, 37, 144–150. [Google Scholar] [CrossRef]
- Montoro Girona, M.; Morin, H.; Lussier, J.-M.; Walsh, D. Radial growth response of black spruce stands ten years after experimental shelter woods and seed-tree cuttings in boreal forest. Forests 2016, 7, 240. [Google Scholar] [CrossRef]
- Kleinn, C. Überlegungen zur Berechnung von Einzelbaumvolumen mittels kubischer Spline Interpolation. AFZ 1989, 47, 1246–1247. [Google Scholar]
- Diéguez-Aranda, U.; Castedo-Dorado, F.; Álvarez-González, J.G.; Rojo, A. Compatible taper function for Scots pine plantations in northwestern Spain. Can. J. For. Res. 2006, 5, 1190–1205. [Google Scholar] [CrossRef]
- Wehenkel, C.; Cruz-Cobos, F.; Carrillo, A.; Lujan-Soto, J.E. Estimating bark volumes for 16 native tree species on the Sierra Madre Occidental, Mexico. Scand. J. For. Res. 2012, 27, 578–585. [Google Scholar] [CrossRef]
- Simental-Cano, B.; López-Sánchez, C.A.; Wehenkel, C.; Vargas-Larreta, B.; Álvarez-González, J.G.; Corral-Rivas, J.J. Species-specific and regional volume models for 12 forest species in Durango, Mexico. RCHSCFA 2017, 23, 155–171. [Google Scholar] [CrossRef]
- MAGAP. La política Agropecuaria Ecuatoriana. Hacia un Desarrollo Territorial Sostenible 2015–2025; I Parte; MAGAP: Quito, Ecuador, 2016; pp. 328–330. [Google Scholar]
- De-Miguel, S.; Pukkala, T.; Morales, M. Using optimization to solve tree misidentification and uneven measurement interval problems in individual-tree modeling of Balsa stand dynamics. Ecol. Eng. 2014, 69, 232–236. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A., Jr.; Vanclay, J.K. Forest Growth and Yield Modeling, 1st ed.; John Wiley & Sons: Noida, India, 2011; pp. 40–98. [Google Scholar]
- INAMHI. Boletines Hidrometeorológicos. Available online: http://www.serviciometeorologico.gob.ec/boletines-avisos-y-alertas/ (accessed on 16 April 2019).
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Peschel, W. Die mathematischen Methoden zur Herleitung der Wachstumsgesetze von Baun und Bestand und die Ergebnisse ihrer Anwendung. Tharandter. Forstl. Jahrb. 1938, 169–247. [Google Scholar]
- Cieszewski, C.J. Three methods of deriving advanced dynamic site equations demonstrated on inland Douglas-fir site curves. Can. J. For. Res. 2001, 31, 165–173. [Google Scholar] [CrossRef]
- Shater, Z.; de-Miguel, S.; Kraid, B.; Pukala, T.; Palahi, M. A growth and yield model for eveng-aged Pinus brutia Ten. stands in Syria. Ann. For. Sci. 2011, 68, 149–157. [Google Scholar] [CrossRef]
- Cieszewski, C.J. Comparing fixed- and variable-base-age site equations having single versus multiple asymptotes. For. Sci. 2002, 48, 7–23. [Google Scholar] [CrossRef]
- Cieszewski, C.J. Developing a well-behaved dynamic site equation using a modified Hossfeld IV function Y3 = (axm)/(c + xm−1), a simplified mixed-model and scant subapline fir data. For. Sci. 2003, 49, 539–554. [Google Scholar] [CrossRef]
- Colbert, J.J.; Schuckers, M.; Fekedulegn, D.; Rentch, J.; Mac Siúrtáin, M.; Gottschalk, K. Individual tree basal-area growth parameter estimates for four models. Ecol. Model. 2004, 174, 115–126. [Google Scholar] [CrossRef]
- Burkhart, H.; Tomé, M. Modeling Forest Trees and Stands, 1 st ed.; Springer: Dordrecht, The Nederland, 2012; pp. 45–70. [Google Scholar]
- Pienaar, L.V.; Turnbull, K.J. The Chapman-Richards generalization of von Bertalanffy’s growth model for basal area growth and yield in even-aged stands. For. Sci. 1973, 19, 2–22. [Google Scholar] [CrossRef]
- Tjørve, E.; Tjørve, K.M. A unified approach to the Richards-model family for use in growth analyses: Why we need only two model forms. J. Theor. Biol. 2010, 267, 417–425. [Google Scholar] [CrossRef]
- Palahí, M.; Grau, J.M. Preliminary site index model and individual-tree growth and mortality models for black pine (Pinus nigra Arn.) in Catalonia (Spain). Forest Syst. 2003, 12, 137–148. [Google Scholar]
- Panik, M.J. Growth Curve Modeling: Theory and Applications, 1st ed.; John Wiley & Sons: Noida, India, 2013; pp. 56–89. [Google Scholar]
- Cieszewski, C.J. GADA Derivation of Dynamic Site Equations with Polymorphism and Variable Asymptotes from Richards, Weibull, and Other Exponential Functions; PMRC-Technical Report 2004–20045; Daniel N. Warnell School of Forest Resources, University of Georgia: Athens, GA, USA, 2004; p. 16. [Google Scholar]
- Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: http://www.R-project.org/ (accessed on 18 January 2019).
- Cañadas-López, Á.; Andrade-Candell, J.; Domínguez-A, J.; Molina-Hidrovo, C.; Schnabel-Delgado, O.; Vargas-Hernández, J.; Wehenkel, C. Growth and yield models for teak planted as living fences in coastal Ecuador. Forests 2018, 9, 55. [Google Scholar] [CrossRef]
- SAS Institute Inc. SAS/ETS® 9.2 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2008. [Google Scholar]
- Schumacher, F.X.; Hall, F.S. Logarithmic expression of timber-tree volume. J. Agric. Res. 1933, 47, 719–734. [Google Scholar]
- Spurr, S.H. Forest Inventory; Ronald Press Co.: New York, NY, USA, 1952; p. 476. [Google Scholar]
- Avery, T.E.; Burkhart, H.E. Forest Measurements, 5th ed.; McGraw-Hill: New York, NY, USA, 2002; p. 456. ISBN 1478629088. [Google Scholar]
- Ruiz, R.M.; Martínez, G.E.R.; Mata, J.J. Análisis del crecimiento y producción de látex en plantaciones forestales comerciales de hule (Hevea brasiliensis Muell Arg.) en el estado de Oaxaca, México. RaXimhai 2007, 3, 565–578. [Google Scholar]
- Honer, T.G. A new total cubic foot volume function. For. Chron. 1965, 41, 476–493. [Google Scholar] [CrossRef]
- Newnham, R.M. Variable-form taper functions for four Alberta tree species. Can. J. For. Res. 1992, 22, 210–223. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike; Parzen, A., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Snipes, M.; Taylor, D.C. Model selection and Akaike Information Criteria: An example from wine ratings and prices. Wine Econ. Policy 2014, 3, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Pukkala, T.; von Gadow, K. Continuous Cover Forestry; Springer Verlag: Dordrecht, Holland, 2012; pp. 85–128. ISBN 978-94-007-2201-9. [Google Scholar]
- Rodríguez-Carrillo, A.; Cruz-Cobos, F.; Vargas-Larreta, B.; Hernández, F.J. Compatible dominant height-site index model for juniper (Juniperus deppeana Steud.). Rev. Chapingo Ser. Cie. 2015, 21, 97–108. [Google Scholar] [CrossRef]
- Díaz-Maroto, I.J.; Fernández-Parajes, J.; Vila-Lameiro, P. Site index model for natural stands of rebollooak (Quercus pyrenaica Willd.) in Galicia, NW Iberian Peninsula. Cienc. For. 2010, 20, 57–68. [Google Scholar] [CrossRef]
- Diéguez-Aranda, U.; Grandas-Árias, J.A.; Álvarez-González, J.G.; Gadow, K. Site quality curves for birch stands in North Western Spain. Silva Fenn. 2006, 40, 631–644. [Google Scholar] [CrossRef]
- Stankova, T.; Diéguez-Aranda, U. A tentative dynamic site index model for Scots pine (Pinus sylvestris L.) plantations in Bulgaria. Silva Balcanica 2012, 13, 5–19. [Google Scholar]
- Gräfe, W. Struktur-und Dynamikuntersuchungen in jungen Zweitwuchsbeständen der westlichen Llanos Venezuelas. Ph.D. dissertation, Georg-August-Universität zu Göttingen, Göttigen, Germany, 1981. [Google Scholar]
- Lamprecht, H. Silviculture in the Tropics—Tropical Forest Ecosystems and Their Tree Species-Possibilities and Methods for Their Long-Term Utilization; GTZ: Eschborn, Germany, 1989; pp. 297–298. [Google Scholar]
- Wishnie, M.H.; Dent, D.H.; Mariscal, E.; Deago, J.; Cedeño, N.; Ibarra, D.; Condit, R.; Ashton, P.M.S. Initial performance and reforestation potential of 24 tropical tree species planted across a precipitation gradient in the Republic of Panama. For. Ecol. Manag. 2007, 243, 39–49. [Google Scholar] [CrossRef]
- Butterfield, R.P. Early species selection for tropical reforestation: A consideration of stability. For. Ecol. Manag. 1996, 81, 161–168. [Google Scholar] [CrossRef]
- Dalling, J.W.; Lovelock, C.E.; Hubbell, S.P. Growth responses of seedlings of two neotropical pioneer species to simulated forest gap environments. J. Tro. Eco. 1999, 15, 827–839. [Google Scholar] [CrossRef] [Green Version]
- Pearson, T.R.H.; Burslem, D.F.R.P.; Goeriz, R.E.; Dalling, J.W. Regeneration niche partitioning in neotropical pioneers: Effects of gap size, seasonal drought and herbivory on growth and survival. Oecologia 2003, 137, 456–465. [Google Scholar] [CrossRef]
- Healy, C.; Gotelli, N.J.; Potvin, C. Partitioning the effects of biodiversity and environmental heterogeneity for productivity and mortality in a tropical tree plantation. J. Ecol. 2008, 96, 903–913. [Google Scholar] [CrossRef]
- Van Breugel, M.; Hall, J.S.; Craven, D.; Bailon, M.; Hernández, A.; Abbene, M.; van Breugel, P. Succession of ephemeral secondary forests and their limited role for the conservation of floristic diversity in a human-modified tropical landscape. PloS ONE 2013, 8, e82433. [Google Scholar] [CrossRef]
- Azambuja Magalhães, W.; da Silva Freddi, O.; Lange, A.; Wruck, F.J.; Silva, W.M.; Soares, M.B. Atributos físico-hídricos do solo em sistema integrado de produção com diferentes arranjos do componente florestal paricá. Pesq Agropec Bras 2018, 53, 351–360. [Google Scholar] [CrossRef]
- De Souza, F.M.; Batista, J.L.F. Restoration of seasonal semideciduous forests in Brazil: Influence of age and restoration design on forest structure. For. Ecol. Manag. 2004, 191, 185–200. [Google Scholar] [CrossRef]
- Román-Dañobeytia, F.J.; Levy-Tacher, S.I.; Aronson, J.; Rodrigues, R.R.; Castellanos-Albores, J. Testing the performance of fourteen native tropical tree species in two abandoned pastures of the Lacandon rainforest region of Chiapas, Mexico. Restor. Ecol. 2012, 20, 378–386. [Google Scholar] [CrossRef]
- Montoro Girona, M.; Rossi, S.; Lussier, J.M.; Walsh, D.; Morin, H. Understanding tree growth responses after partial cuttings: A new approach. PLoS ONE 2017, 12, e0172653. [Google Scholar] [CrossRef]
- Hernández-Ramos, J.; Santos-Posadas, H.M.; Valdéz-Lazalde, J.R.; Tamarit-Urias, J.C.; Ángeles-Pérez, G.; Hernández-Ramos, A.; Méndez-López, B.; Peduzzi, A. Estimación del volumen comercial en plantaciones de Eucalyptus urophylla con modelos de volumen total y de razón. Agrociencia-Mexico 2017, 51, 561–580. [Google Scholar]
- Sautunce-Cunuhay, P.; Coronel, T.G.D.; García-Cruzatty, L. Crecimiento de especies arbóreas tropicales en la colección de la Universidad Técnica Estatal de Quevedo. Revista Ciencia y Tecnología 2009, 2, 21–27. [Google Scholar]
- Mora-Yela, R.V. Valoración económica de las plantaciones de teca (Tectona grandis) y balsa (Ochroma pyramidale) en tres cantones del Litoral Ecuatoriano. Tesis de Ingeniería, Universidad Técnica Estatal de Quevedo, Quevedo, Ecuador, 2011. [Google Scholar]
- Murillo-Lince, J.C. Tablas de volumen y porcentaje de aprovechamiento en el aserrado de Ochroma pyramidale (BALSA) en el recinto El Vergel, Cantón Valencia, Provincia de Los Ríos. Tesis de Ingeniería, Universidad Técnica Estatal de Quevedo, Quevedo, Ecuador, 2012. [Google Scholar]
- Barragán-Márquez, M.S. Evaluación de la calidad de plantaciones de balsa Ochroma pyramidale (Cav. ex Lam.) Urb. de un año de edad, en los cantones Valencia y Mocache. Tesis de Ingeniería, Universidad Técnica Estatal de Quevedo, Quevedo, Ecuador, 2015. [Google Scholar]
- Rueda, R.; Williamson, G.B. Radial and vertical wood specific gravity in Ochroma pyramidale (Cav. ex Lam.) Urb. (Bombacaceae). Biotropica 1992, 24, 4–512. [Google Scholar] [CrossRef]
- Longwood, F. Present and Potential Commercial Timbers of the Caribbean; U.S. Department of Agriculture Agric. Handb: Washington, DC, USA, 1962; pp. 36–38.
- Webb, D.B.; Wood, P.J.; Smith, J.P.; Henman, G.S. A Guide to Species Selection for Tropical and Sub-Tropical Plantations; Commonwealth Forestry Institute: Oxford, UK, 1980; pp. 34–54. [Google Scholar]
- González-Osorio, B.G.; Molina, X.C.; Navarrete, E.T.; Fonseca, C.S.; Ochoa, L.S. Caracterización del cultivo de balsa (Ochroma pyramidale) en la Provincia de los Ríos-Ecuador. Revista Ciencia y Tecnología 2010, 3, 7–11. [Google Scholar]
- Wycherley, P.R.; Mitchell, B.A. Growth of Balsa trees Ochroma lagopus Sw. at the Rubber Research Institute Experiment Station. Mal. Forest. 1962, 25, 140–149. [Google Scholar]
- Howcroft, N.H.S. The Balsa Manual: Techniques for Establishment and the Management of Balsa (Ochroma lagopus) plantations in Papua New Guinea; ITTO: Keravat, Papua New Guinea, 2002; pp. 28–44. [Google Scholar]


| Province | Density of Plantation (Trees ha−1) | Age (Year) | Diameter at Breast Height (cm) | Total Height (m) | Basal Area (m2 ha−1) | Mean Annual Increment * (m3 ha−1) | |
|---|---|---|---|---|---|---|---|
| Los Ríos | Average | 334.4 | 4.4 | 22.4 | 22.4 | 13.0 | 29.2 |
| Maximum | 1506.0 | 10.9 | 44.1 | 40.6 | 26.0 | 228.1 | |
| Minimum | 90.0 | 1.1 | 2.9 | 2.5 | 0.3 | 2.2 | |
| Stand Err | ±712.5 | ±0.1 | ±1.1 | ±1.3 | ±0.6 | ±5.1 | |
| Santo Domingo de los Tsáchilas | Average | 343.2 | 4.1 | 22.5 | 22.7 | 14.1 | 33.0 |
| Maximum | 856.0 | 9.4 | 44.6 | 35.0 | 26.9 | 198.4 | |
| Minimum | 100.0 | 1.3 | 3.8 | 7.4 | 2.0 | 2.3 | |
| Stand Err | ±777.4 | ±0.1 | ±1.4 | ±1.6 | ±0.8 | ±9.9 | |
| Cotopaxi | Average | 390.5 | 3.9 | 23.3 | 23.9 | 15.8 | 39.2 |
| Maximum | 760.0 | 7.2 | 37.5 | 34.6 | 28.1 | 99.5 | |
| Minimum | 190.0 | 1.5 | 8.8 | 10.7 | 4.8 | 10.4 | |
| Stand Err | ±892.2 | ±0.2 | ±2.8 | ±2.9 | ±1.8 | ±15.3 | |
| Manabí | Average | 280.7 | 5.1 | 21.9 | 23.1 | 11.6 | 22.9 |
| Maximum | 800.0 | 10.8 | 35.2 | 34.3 | 22.5 | 43.9 | |
| Minimum | 90.0 | 1.4 | 6.8 | 7.4 | 2.2 | 3.0 | |
| Stand Err | ±280.7 | ±0.6 | ±3.8 | ±4.9 | ±1.7 | ±6.4 | |
| Guayas | Average | 408.5 | 3.6 | 19.2 | 20.6 | 11.9 | 29.4 |
| Maximum | 599.0 | 6.8 | 33.6 | 28.6 | 22.0 | 52.1 | |
| Minimum | 194.0 | 1.8 | 10.9 | 10.8 | 4.6 | 7.1 | |
| Stand Err | ±881.9 | ±0.2 | ±4.2 | ±3.4 | ±2.3 | ±13.4 | |
| Esmeraldas | Average | 361.4 | 3.8 | 21.8 | 20.5 | 13.4 | 16.3 |
| Maximum | 569.0 | 6.5 | 32.5 | 27.8 | 30.0 | 38.9 | |
| Minimum | 155.0 | 1.5 | 13.7 | 11.4 | 6.0 | 18.3 | |
| Stand Err | ±2842.5 | ±0.3 | ±4.2 | ±4.2 | ±4.9 | ±28.4 | |
| Pichincha | Average | 337.0 | 3.9 | 24.6 | 20.2 | 11.6 | 23.1 |
| Maximum | 493.0 | 6.8 | 32.6 | 27.6 | 19.2 | 37.4 | |
| Minimum | 210.0 | 1.8 | 15.3 | 9.9 | 4.0 | 7.4 | |
| Stand Err | ±1160.5 | ±0.6 | ±5.9 | ±5.7 | ±3.3 | ±9.8 |
| Province | Total Annual Precipitation (mm) | Mean Annual Temperature (°C) | Elevation (Meters above Sea Level) | Number of Plots | Life Zone * |
|---|---|---|---|---|---|
| Los Ríos | 2000 | 25.2 | 30–300 | 1300 | TwF-TrF |
| Santo Domingo de los Tsáchilas | 2280 | 23.5 | 200–700 | 529 | Twf-TrF |
| Cotopaxi | 3019 | 24.0 | 300–600 | 117 | TmF-TrF |
| Manabí | 1000 | 24.6 | 20–300 | 100 | TdF-TrF |
| Guayas | 1189 | 26.7 | 30–100 | 56 | TdF-TrF |
| Esmeraldas | 2646 | 25.6 | 100–300 | 32 | TwF-TrF |
| Pichincha | 1998 | 25.0 | 300–700 | 27 | TwF-TrF |
| Model | Expression | |
|---|---|---|
| Schumacher-Hall (allometric) [38] | (6) | |
| Spurr [39] | (7) | |
| Spurr potential [40] | (8) | |
| Spurr with independent term [40] | (9) | |
| Incomplete generalized combined variable [40] | (10) | |
| Australian formula [41] | (11) | |
| Honer [42] | (12) | |
| Newnham [43] | (13) |
| Parameter | Model | Parameter | Estimated Value | Standard Error | p Value | RMSE |
|---|---|---|---|---|---|---|
| Height–Age | Equation (1) | a1 | 31.844 | 0.6646 | <0.001 | 13.79 |
| a2 | 0.2973 | 0.0247 | <0.001 | |||
| a3 | 1.0767 | 0.0662 | <0.001 | |||
| Equation (2) | a1 | 0.8036 | 0.0065 | <0.001 | 6.43 | |
| a2 | −0.1382 | 0.0001 | <0.001 | |||
| a3 | 0.1331 | 0.001 | <0.001 | |||
| Equation (3) | b1 | 0.4207 | 0.1483 | <0.001 | 4.27 | |
| b2 | −4.6136 | 0.2719 | <0.001 | |||
| b3 | 20.395 | 5.4538 | <0.001 | |||
| Diameter–Age | Equation (1) | a1 | 33.607 | 0.7364 | <0.001 | 23.06 |
| a2 | 0.3108 | 0.0372 | <0.001 | |||
| a3 | 0.7876 | 0.0696 | <0.001 | |||
| Equation (2) | a1 | 1.3090 | 0.00003 | <0.0000001 | 8.53 | |
| a2 | −0.1886 | 0.00001 | <0.001 | |||
| a3 | 0.1792 | 0.00004 | <0.0000001 | |||
| Equation (3) | b1 | 0.7989 | 0.0791 | <0.0000001 | 5.61 | |
| b2 | −9.7819 | 2.3562 | <0.0000001 | |||
| b3 | 41.234 | 0.2583 | <0.0000001 |
| Model | MSE | R2Adj | Parameter | Estimator | SE | AIC |
|---|---|---|---|---|---|---|
| Newnham | 0.028 | 0.909 | a | 0.349727 | 0.0198 | −392 |
| b | 0.000024 | 0.000005 | ||||
| c | 2.343151 | 0.0629 | ||||
| d | 0.760481 | 0.0518 | ||||
| Spurr with independent term | 0.028 | 0.907 | a | 0.322645 | 0.0124 | −380 |
| b | 0.000042 | 0.0000003 | ||||
| Incomplete generalized combined variable | 0.028 | 0.907 | a | 0.279241 | 0.0528 | −379 |
| b | 0.00375 | 0.00379 | ||||
| c | 0.000041 | 0.0000008 | ||||
| Australiana formula | 0.028 | 0.907 | a | 0.282614 | 0.0572 | −378 |
| b | −0.00006 | 0.000050 | ||||
| c | 0.004089 | 0.00382 | ||||
| d | 0.000043 | 0.000002 | ||||
| Schumacher-Hall (allometric) | 0.046 | 0.849 | a | 0.002402 | 0.000331 | −122 |
| b | 1.100958 | 0.0465 | ||||
| c | 0.819285 | 0.0738 | ||||
| Spurr potential | 0.046 | 0.848 | a | 0.002264 | 0.000281 | −121 |
| b | 0.980555 | 0.0181 | ||||
| Honer | 0.058 | 0.809 | a | 973.3571 | 38.4457 | 1.56 |
| b | −1995.99 | 822.1 | ||||
| Spurr | 0.081 | 0.733 | a | 0.000055 | 0.0000004 | 177 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cañadas-López, Á.; Rade-Loor, D.; Siegmund-Schultze, M.; Moreira-Muñoz, G.; Vargas-Hernández, J.J.; Wehenkel, C. Growth and Yield Models for Balsa Wood Plantations in the Coastal Lowlands of Ecuador. Forests 2019, 10, 733. https://doi.org/10.3390/f10090733
Cañadas-López Á, Rade-Loor D, Siegmund-Schultze M, Moreira-Muñoz G, Vargas-Hernández JJ, Wehenkel C. Growth and Yield Models for Balsa Wood Plantations in the Coastal Lowlands of Ecuador. Forests. 2019; 10(9):733. https://doi.org/10.3390/f10090733
Chicago/Turabian StyleCañadas-López, Álvaro, Diana Rade-Loor, Marianna Siegmund-Schultze, Geovanny Moreira-Muñoz, J. Jesús Vargas-Hernández, and Christian Wehenkel. 2019. "Growth and Yield Models for Balsa Wood Plantations in the Coastal Lowlands of Ecuador" Forests 10, no. 9: 733. https://doi.org/10.3390/f10090733
APA StyleCañadas-López, Á., Rade-Loor, D., Siegmund-Schultze, M., Moreira-Muñoz, G., Vargas-Hernández, J. J., & Wehenkel, C. (2019). Growth and Yield Models for Balsa Wood Plantations in the Coastal Lowlands of Ecuador. Forests, 10(9), 733. https://doi.org/10.3390/f10090733





