Image Data Acquisition for Estimating Individual Trees Metrics: Closer Is Better
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Sampling and Reference Data Collection
2.3. Image Data Acquisition
2.4. Image Processing and Metric Estimation
2.5. Data Analysis
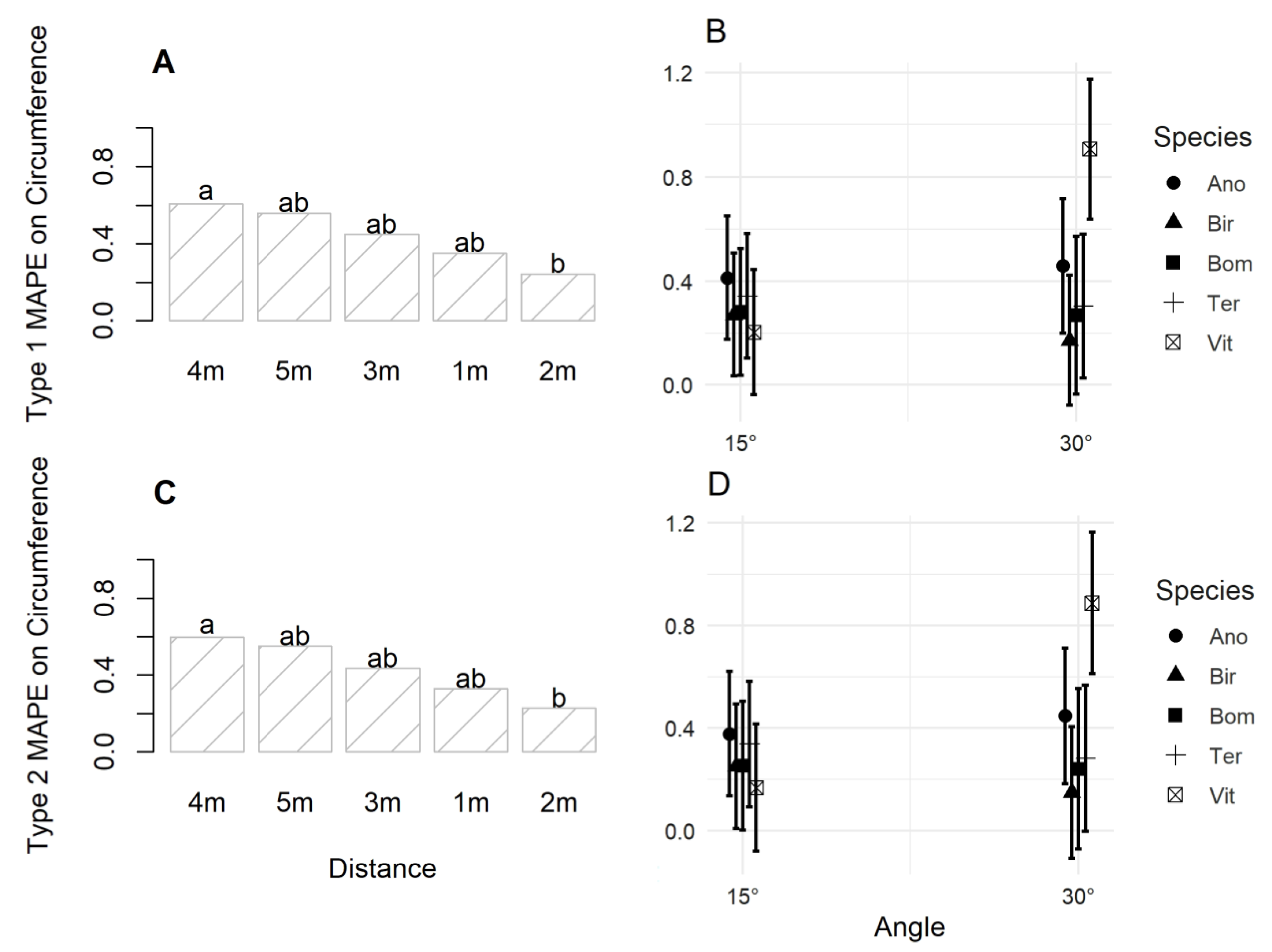
3. Results
3.1. Individual Tree Model Reconstruction
3.2. Accuracy of Image Acquisition Scenarios
4. Discussion
4.1. Individual Tree Model Reconstruction by SFM-MVS
4.2. Accuracy of Image Capture Scenarios for Individual Tree Metric Estimation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gatziolis, D.; Lienard, J.F.; Vogs, A.; Strigul, N.S. 3D Tree Dimensionality Assessment Using Photogrammetry and Small Unmanned Aerial Vehicles. PLoS ONE 2015, 10, e0137765. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, X.; Wang, Y.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Hyyppä, J.; Honkavaara, E.; Liu, J. Forest Data Collection Using Terrestrial Image-Based Point Clouds From a Handheld Camera Compared to Terrestrial and Personal Laser Scanning. IEEE Trans. Geosci. Remote. Sens. 2015, 53, 5117–5131. [Google Scholar] [CrossRef]
- Morgenroth, J.; Gomez, C. Assessment of tree structure using a 3D image analysis technique—A proof of concept. Urban For. Urban Green. 2014, 13, 198–203. [Google Scholar] [CrossRef]
- Miller, J.; Morgenroth, J.; Gomez, C. 3D modelling of individual trees using a handheld camera: Accuracy of height, diameter and volume estimates. Urban For. Urban Green. 2015, 14, 932–940. [Google Scholar] [CrossRef]
- Surový, P.; Yoshimoto, A.; Panagiotidis, D. Accuracy of Reconstruction of the Tree Stem Surface Using Terrestrial Close-Range Photogrammetry. Remote Sens. 2016, 8, 123. [Google Scholar] [CrossRef] [Green Version]
- Mokroš, M.; Výbošt’ok, J.; Tomaštík, J.; Grznárová, A.; Valent, P.; Slavík, M.; Merganĭc, J. High Precision Individual Tree Diameter and Perimeter Estimation from Close-Range Photogrammetry. Forests 2018, 9, 696. [Google Scholar] [CrossRef] [Green Version]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Zhang, H.; Chen, C.; Tang, L. Three-dimensional digitization of the arid land plant Haloxylon ammodendron using a consumer-grade camera. Ecol. Evol. 2018, 8, 5891–5899. [Google Scholar] [CrossRef] [PubMed]
- Piermattei, L.; Karel, W.; Wang, D.; Wieser, M.; Mokroš, M.; Surový, P.; Koreň, M.; Tomaštík, J.; Pfeifer, N.; Hollaus, H. Terrestrial Structure from Motion Photogrammetry for Deriving Forest Inventory Data. Remote Sens. 2019, 11, 950. [Google Scholar] [CrossRef] [Green Version]
- Koeser, A.K.; Roberts, J.; Miesbauer, J.W.; Lopes, A.B.; Kling, G.J.; Lo, M.; Morgenroth, J. Testing the Accuracy of Imaging Software for Measuring Tree Root Volumes. Urban For. Urban Green. 2016, 18, 95–99. [Google Scholar] [CrossRef]
- Forsman, M.; Börlin, N.; Holmgren, J. Estimation of Tree Stem Attribute Using Terrestrial Photogrammetry with a Camera Rig. Forests 2016, 7, 61. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Z.; Yang, L.; Mannan, A.; Khan, T.U.; Zhao, Z.; Cheng, Z. Extraction of sample plot parameters from 3D point cloud reconstruction based on combined RTK and CCD continuous photography. Remote Sens. 2018, 10, 1299. [Google Scholar] [CrossRef] [Green Version]
- Mokroš, M.; Liang, X.; Surový, P.; Valent, P.; Černăva, J.; Chudý, F.; Tunák, D.; Salon, S.; Merganič, J. Evaluation of Close-Range Photogrammetry Image Collection Methods for Estimating Tree Diameters. ISPRS Int. J. Geoinf. 2018, 7, 93. [Google Scholar] [CrossRef] [Green Version]
- Iglhaut, K.; Cabo, C.; Puliti, S.; Piermatteit, L.; O’Connor, J.; Rosette, J. Structure from Motion Photogrammetry in Forestry: A Review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Strimbu, B.M. Stem Measurement and Taper Modeling Using Photogrammetric Point Clouds. Remote Sens. 2017, 9, 716. [Google Scholar] [CrossRef] [Green Version]
- Roberts, J.W.; Koeser, A.K.; Abd-Elrahman, A.H.; Hansen, G.; Landryd, S.M.; Wilkinson, E. Terrestrial photogrammetric stem mensuration for street trees. Urban For. Urban Green. 2018, 35, 66–71. [Google Scholar] [CrossRef]
- Mulverhill, C.; Coops, N.C.; Tompalski, P.; Bater, C.W.; Dick, A.R. The utility of terrestrial photogrammetry for assessment of tree volume and taper in boreal mixedwood forests. Ann. For. Sci. 2019, 76, 83. [Google Scholar] [CrossRef] [Green Version]
- Zakari, S.; Tente, B.A.H.; Yabi, I.; Toko, I.I. Evolution hydroclimatique, perceptions et adaptation des agroéleveurs dans l’extrême nord du Bénin (Afrique de l’Ouest). In Actes Du 28ème Colloque De L’AIC; Liège: Wallonie, Belgique, 2015; pp. 399–405. [Google Scholar]
- Picard, N.; Saint-André, L.; Henry, M. Manual for Building Tree Volumes and Biomass Allometric Equations: From Field Measurement to Prediction; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2012; pp. 1–215. [Google Scholar]
- Agisoft, L.L.C. Agisoft Metashape User Manual: Professional Edition, Version 1.5; Agisoft LLC: St. Petersburg, Russia, 2019; Available online: https://www.agisoft.com/pdf/metashape-pro_1_5_en.pdf (accessed on 31 December 2019).
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing forest metrics with a ground-based scanning lidar. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef] [Green Version]







| Metric | Species | Mean | S.D | CV % | Minimum | Maximum |
|---|---|---|---|---|---|---|
| A. leiocarpa | 135.40 | 78.70 | 58.14 | 46.50 | 275.00 | |
| B. costatum | 127.30 | 60.30 | 47.36 | 44.00 | 198.00 | |
| CBH (cm) | S. birrea | 130.50 | 72.80 | 55.79 | 51.00 | 239.00 |
| T. laxiflora | 131.10 | 53.30 | 40.63 | 61.50 | 202.00 | |
| V. paradoxa | 125.60 | 53.90 | 42.93 | 43.70 | 195.00 | |
| Total | 130.10 | 60.40 | 46.62 | 43.70 | 274.90 | |
| A. leiocarpa | 2.28 | 0.94 | 41.36 | 1.32 | 3.97 | |
| B. costatum | 3.60 | 0.97 | 26.84 | 2.34 | 4.65 | |
| HStem (m) | S. birrea | 2.49 | 0.79 | 31.60 | 1.48 | 3.75 |
| T. laxiflora | 2.56 | 0.93 | 36.23 | 1.33 | 4.02 | |
| V. paradoxa | 2.86 | 0.34 | 12.01 | 2.50 | 3.35 | |
| Total | 2.78 | 0.91 | 32.69 | 1.32 | 4.80 | |
| A. leiocarpa | 10.00 | 2.62 | 26.2 | 5.89 | 13.78 | |
| B. costatum | 10.10 | 3.70 | 36.7 | 4.91 | 14.64 | |
| HT (m) | S. birrea | 10.14 | 3.23 | 31.87 | 6.20 | 13.00 |
| T. laxiflora | 9.54 | 2.02 | 21.14 | 6.30 | 11.50 | |
| V. paradoxa | 9.34 | 2.06 | 22.11 | 6.46 | 12.60 | |
| Total | 9.82 | 2.63 | 26.73 | 4.91 | 14.64 |
| Df | Deviance | Resid. Df | Pr(>Chi) | |
|---|---|---|---|---|
| NULL | 599 | |||
| d | 4 | 7.02 | 595 | 0.135 |
| α | 3 | 348.80 | 592 | <0.001 *** |
| s | 4 | 74.98 | 588 | <0.001 *** |
| α × s | 12 | 30.63 | 576 | 0.002 ** |
| d × α | 12 | 10.90 | 564 | 0.538 |
| d × s | 16 | 17.95 | 548 | 0.327 |
| d × α × s | 48 | 16.39 | 500 | >0.999 |
| α | ||||||
|---|---|---|---|---|---|---|
| 15° | 30° | 45° | 60° | Mean ± SEM | ||
| d (m) | 1 | 1.6 ± 0.5 aA | 1.8 ± 0.6 aA | 7.7 ± 17.8 bA | 1.7 ± 13.3 aA | 2.1 ± 0.9 A |
| 2 | 1.6 ± 0.4 aA | 2.2 ± 0.7 aA | 8.1 ± 11.5 bA | 7.4 ± 51.4 bB | 2.5 ± 0.8 A | |
| 3 | 10.4 ± 2.9 aB | 10.6 ± 4.0 aB | 10.2 ± 2.6 aB | 7.5 ± 4.7 aB | 10.3 ± 1.9 B | |
| 4 | 14.5 ± 4.3 aC | 15.5 ± 5.1 aC | 18.2 ± 13.1 aC | 20.8 ± 23.7 aC | 15.7 ± 2.9 C | |
| 5 | 15.4 ± 3.1 aC | 15.5 ± 3.8 aC | 13.2 ± 12.2 aC | 15.9 ± 0.0 aC | 15.3 ± 2.1 C | |
| Mean ± SEM | 8.3 ± 1.5 a | 9.2 ± 1.9 a | 11.2 ± 3.1 a | 11.6 ± 7.0 a | 9.0 ± 1.1 | |
| α | ||||||
|---|---|---|---|---|---|---|
| 15° | 30° | 45° | 60° | Mean ± SE | ||
| d (m) | 1 | 3.0 ± 0.7 aA | 2.0 ± 0.6 aA | 22.6 ± 45.2 bA | 3.7 ± 16.6 aA | 4.2 ± 2.4 A |
| 2 | 2.5 ± 0.6 aA | 2.6 ± 0.7 aA | 7.9 ± 14.4 aA | 6.6 ± 46.3 aA | 3.1 ± 0.8 A | |
| 3 | 12.6 ± 3.7 aB | 15.8 ± 5.9 aB | 14.3 ± 6.6 aA | 11.2 ± 4.1 aA | 13.9 ± 2.8 B | |
| 4 | 22.4 ± 7.0 aC | 18.8 ± 5.0 aBC | 22.1 ± 35.8 aA | 36.5 ± 48.7 aA | 22.0 ± 4.6 C | |
| 5 | 24.6 ± 5.0 aC | 25.0 ± 6.20 aC | 26.2 ± 12.6 aA | 33.7 ± 0.0 aA | 25.0 ± 3.40 C | |
| Mean ± SEM | 12.2 ± 2.3 a | 12.9 ± 2.6 a | 17.5 ± 6.9 a | 19.5 ± 13.9 a | 13.3 ± 1.70 | |
| Significance (ANOVA Summary) | |||||||
|---|---|---|---|---|---|---|---|
| d | α | s | d × α Interaction | d × s Interaction | α × s Interaction | d × α × s Interaction | |
| MAPEC1 | 0.010 * | 0.108 | 0.087 | 0.666 | 0.974 | 0.007 ** | 0.774 |
| MAPEC2 | 0.011 * | 0.103 | 0.113 | 0.643 | 0.976 | 0.007 ** | 0.755 |
| MAPEV1 | 0.756 | 0.039 * | 0.073 | 0.191 | 0.913 | 0.023 * | 0.913 |
| MAPEV2 | 0.652 | 0.037 * | 0.049 * | 0.202 | 0.868 | 0.030 * | 0.912 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akpo, H.A.; Atindogbé, G.; Obiakara, M.C.; Adjinanoukon, A.B.; Gbedolo, M.; Lejeune, P.; Fonton, N.H. Image Data Acquisition for Estimating Individual Trees Metrics: Closer Is Better. Forests 2020, 11, 121. https://doi.org/10.3390/f11010121
Akpo HA, Atindogbé G, Obiakara MC, Adjinanoukon AB, Gbedolo M, Lejeune P, Fonton NH. Image Data Acquisition for Estimating Individual Trees Metrics: Closer Is Better. Forests. 2020; 11(1):121. https://doi.org/10.3390/f11010121
Chicago/Turabian StyleAkpo, Hospice A., Gilbert Atindogbé, Maxwell C. Obiakara, Arios B. Adjinanoukon, Madaï Gbedolo, Philippe Lejeune, and Noël H. Fonton. 2020. "Image Data Acquisition for Estimating Individual Trees Metrics: Closer Is Better" Forests 11, no. 1: 121. https://doi.org/10.3390/f11010121
APA StyleAkpo, H. A., Atindogbé, G., Obiakara, M. C., Adjinanoukon, A. B., Gbedolo, M., Lejeune, P., & Fonton, N. H. (2020). Image Data Acquisition for Estimating Individual Trees Metrics: Closer Is Better. Forests, 11(1), 121. https://doi.org/10.3390/f11010121





