Strategies for Modeling Regeneration Density in Relation to Distance from Adult Trees
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Spatial Pattern of Pinus Sylvestris Saplings and Adult Trees
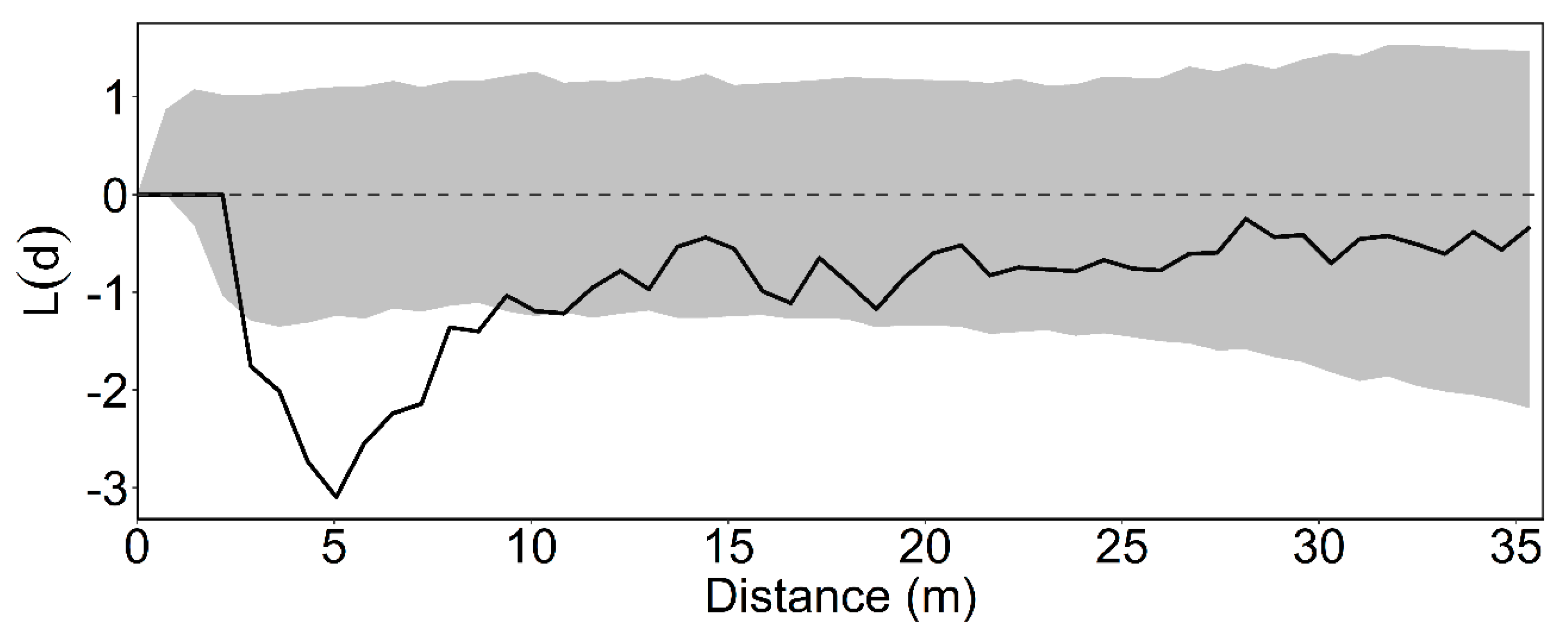
2.3. Intertype Krx(d) Function
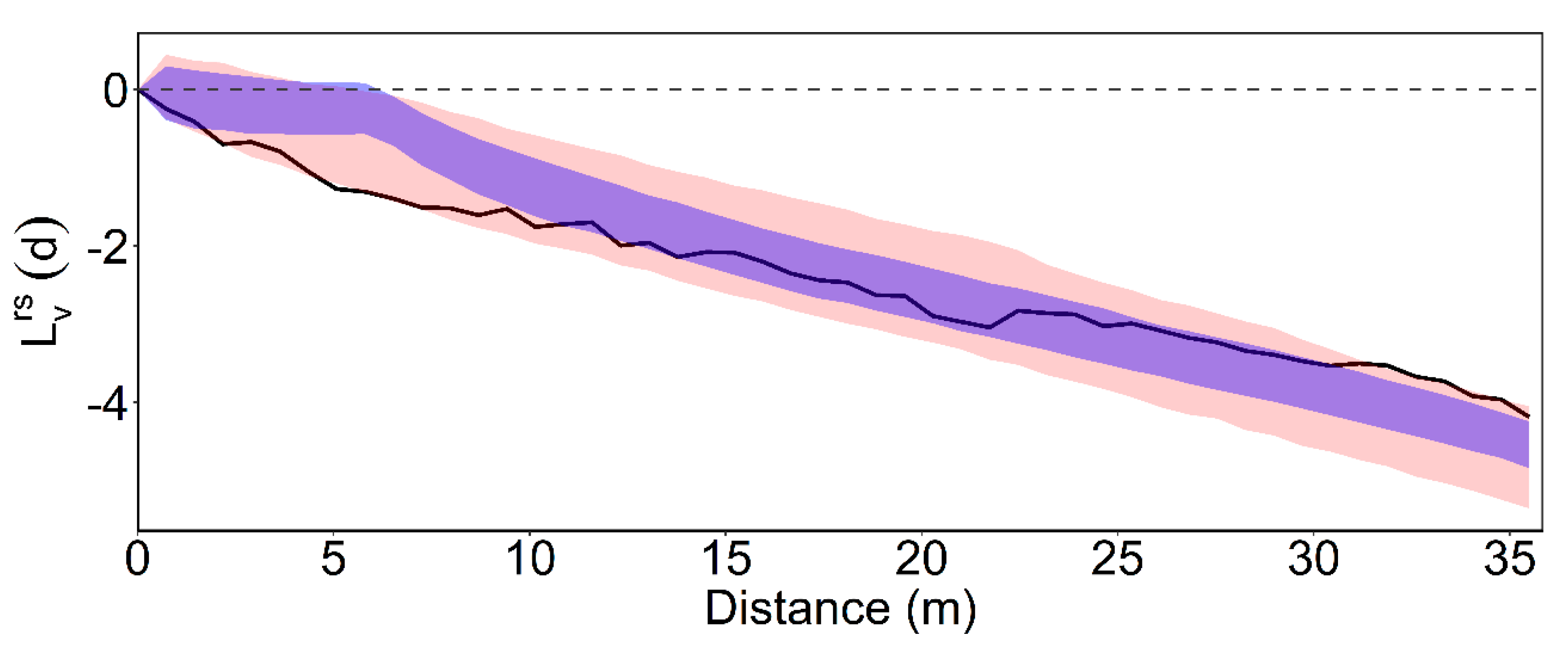
2.4. Intertype Mark Correlation Function
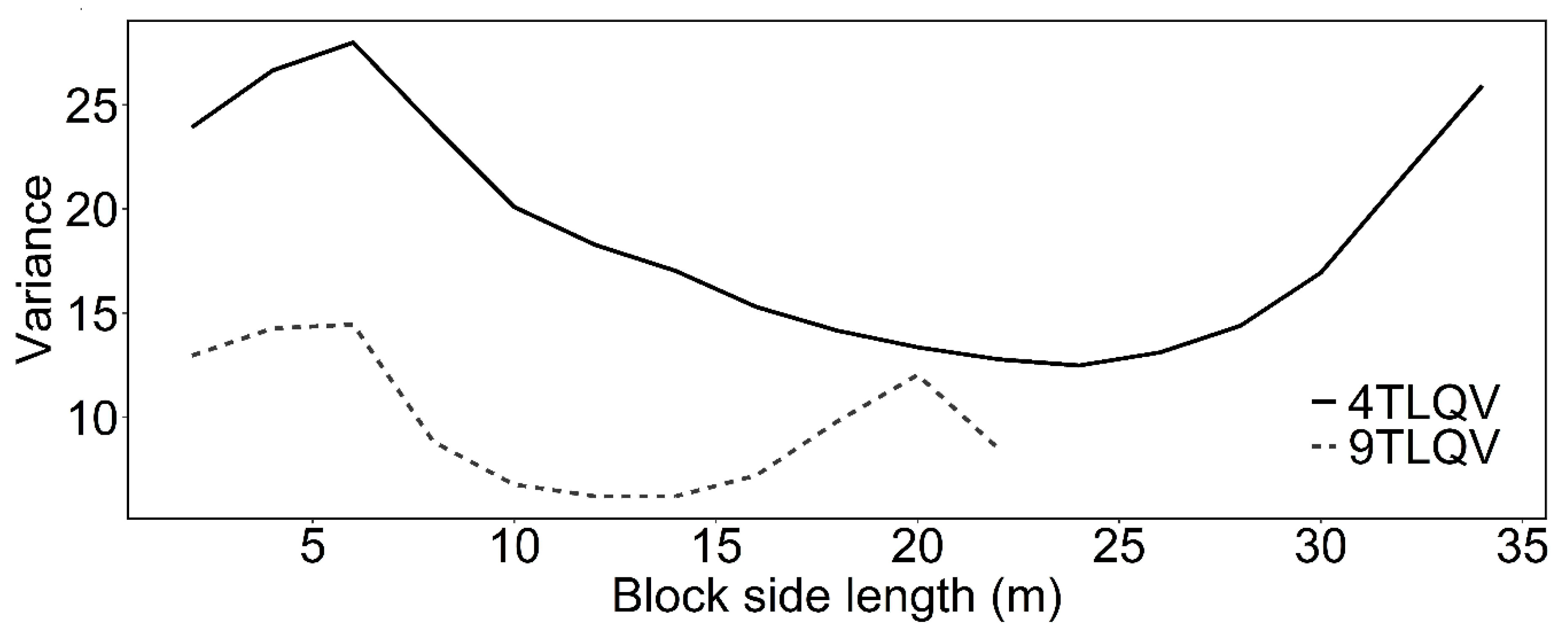
2.5. Disentangling the Spatial Pattern from the Mark Correlation: Intertype Mark Variance Function
2.6. Functional Predictor within a Generalized Additive Model Framework
3. Results
3.1. Spatial Pattern of P. Sylvestris Saplings and Adult Trees over the Regeneration Fellings of the Uniform Shelterwood System
3.2. Intertype Functions
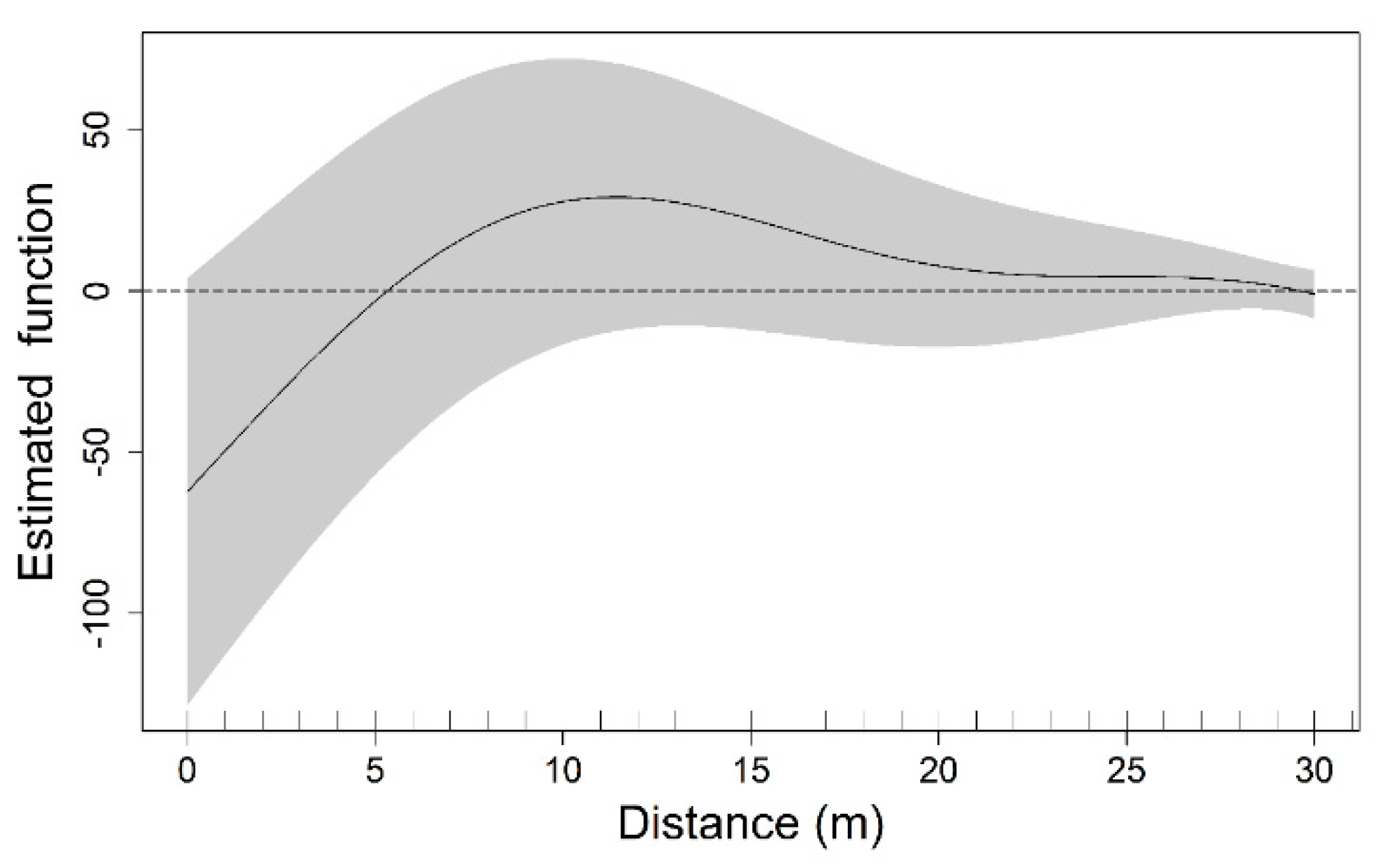
3.3. Functional Predictor within a Generalized Additive Model Framework
4. Discussion
4.1. Pinus sylvestris Sapling Distribution over the Fellings of the Uniform Shelterwood Method
4.2. Method Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lucas-Borja, M.E. Climate change and forest natural regeneration in mediterranean mountain areas. For. Res. 2014, 3, 2–3. [Google Scholar] [CrossRef] [Green Version]
- Simon, A.; Katzensteiner, K.; Gratzer, G. Drivers of forest regeneration patterns in drought prone mixed-species forests in the northern calcareous alps. For. Ecol. Manag. 2019, 453, 117589. [Google Scholar] [CrossRef]
- Petersson, L.K.; Milberg, P.; Bergstedt, J.; Dahlgren, J.; Felton, A.M.; Götmark, F.; Salk, C.; Löf, M. Changing land use and increasing abundance of deer cause natural regeneration failure of oaks: Six decades of landscape-scale evidence. For. Ecol. Manag. 2019, 444, 299–307. [Google Scholar] [CrossRef]
- Munck, I.A.; Morin, R.S.; Ostrofsky, W.D.; Searles, W.; Smith, D.R.; Stanosz, G.R. Impact of Sirococcus shoot blight (Sirococcus tsugae) and other damaging agents on eastern hemlock (Tsuga canadensis) regeneration in Northeastern USA. For. Ecol. Manag. 2018, 429, 449–456. [Google Scholar] [CrossRef]
- Lavoie, J.; Montoro Girona, M.; Morin, H. Vulnerability of conifer regeneration to spruce budworm outbreaks in the eastern canadian boreal forest. Forests 2019, 10, 850. [Google Scholar] [CrossRef] [Green Version]
- Clark, J.S.; Iverson, L.; Woodall, C.W.; Allen, C.D.; Bell, D.M.; Bragg, D.C.; D’Amato, A.W.; Davis, F.W.; Hersh, M.H.; Ibanez, I.; et al. The impacts of increasing drought on forest dynamics, structure, and biodiversity in the United States. Glob. Chang. Biol. 2016, 22, 2329–2352. [Google Scholar] [CrossRef] [Green Version]
- Hansen, W.D.; Braziunas, K.H.; Rammer, W.; Seidl, R.; Turner, M.G. It takes a few to tango: Changing climate and fire regimes can cause regeneration failure of two subalpine conifers. Ecology 2018, 99, 966–977. [Google Scholar] [CrossRef]
- Montoro Girona, M.; Lussier, J.M.; Morin, H.; Thiffault, N. Conifer regeneration after experimental shelterwood and seed-tree treatments in boreal forests: Finding silvicultural alternatives. Front. Plant Sci. 2018, 9. [Google Scholar] [CrossRef]
- Kuuluvainen, T.; Pukkala, T. Simulation of within-tree and between-tree shading of direct-radiation in a forest canopy: Effect of crown shape and sun elevation. Ecol. Modell. 1989, 49, 89–100. [Google Scholar] [CrossRef]
- Woods, K.D.; Acer, K. Patterns of tree replacement: Canopy effects on understory pattern in hemlock-northern hardwood forests. Vegetatio 1984, 56, 87–107. [Google Scholar]
- Pardos, M.; Montes, F.; Aranda, I.; Cañellas, I. Influence of environmental conditions on germinant survival and diversity of scots pine (Pinus sylvestris L.) in central Spain. Eur. J. For. Res. 2007, 126, 37–47. [Google Scholar] [CrossRef]
- Batllori, E.; Camarero, J.J.; Gutiérrez, E. Current regeneration patterns at the tree line in the Pyrenees indicate similar recruitment processes irrespective of the past disturbance regime. J. Biogeogr. 2010, 37, 1938–1950. [Google Scholar] [CrossRef]
- Ledo, A.; Cayuela, L.; Manso, R.; Condés, S. Recruitment patterns and potential mechanisms of community assembly in an Andean Cloud Forest. J. Veg. Sci. 2015, 26, 876–888. [Google Scholar] [CrossRef]
- LeMay, V.; Pommerening, A.; Marshall, P. Spatio-temporal structure of multi-storied, multi-aged interior douglas fir (Pseudotsuga menziesii var. glauca) stands. J. Ecol. 2009, 97, 1062–1074. [Google Scholar] [CrossRef]
- Ripley, B. Modelling spatial patterns (with discussion). J. R. Stat. Soc. 1977, 39, 172–212. [Google Scholar]
- Stoyan, D.; Stoyan, H. Non-homogeneous gibbs process models for forestry—A case study. Biom. J. 1998, 40, 521–531. [Google Scholar] [CrossRef]
- Pommerening, A.; Stoyan, D. Edge-correction needs in estimating indices of spatial forest structure. Can. J. For. Res. 2006, 36, 1723–1739. [Google Scholar] [CrossRef] [Green Version]
- Lotwick, H.W.; Silverman, B.W. Methods for analysing spatial processes of several types of points. J. R. Stat. Soc. Ser. B 1982, 44, 406–413. [Google Scholar] [CrossRef]
- Goreaud, F.; Pélissier, R. Avoiding misinterpretation of biotic interactions with the intertype K12-function: Population independence vs. random labelling hypotheses. J. Veg. Sci. 2003, 14, 681–692. [Google Scholar] [CrossRef]
- Montes, F.; Cañellas, I. The spatial relationship between post-crop remaining trees and the establishment of saplings in Pinus sylvestris stands in Spain. Appl. Veg. Sci. 2007, 10, 151. [Google Scholar] [CrossRef]
- Moreno-Fernández, D.; Augustin, N.H.; Montes, F.; Cañellas, I.; Sánchez-González, M. Modeling sapling distribution over time using a functional predictor in a generalized additive model. Ann. For. Sci. 2018, 75, 9. [Google Scholar] [CrossRef] [Green Version]
- Mason, W.; Alía, R. Current and future status of scots pine (Pinus sylvestris L.) forests in Europe. For. Syst. 2000, 9, 317–335. [Google Scholar]
- Martínez-Vilalta, J.; Cochard, H.; Mencuccini, M.; Sterck, F.; Herrero, A.; Korhonen, J.F.J.; Llorens, P.; Nikinmaa, E.; Nolè, A.; Poyatos, R.; et al. Hydraulic adjustment of scots pine across Europe. New Phytol. 2009, 184, 353–364. [Google Scholar] [CrossRef] [PubMed]
- Sterck, F.J.; Martínez-Vilalta, J.; Mencuccini, M.; Cochard, H.; Gerrits, P.; Zweifel, R.; Herrero, A.; Korhonen, J.F.J.; Llorens, P.; Nikinmaa, E.; et al. Understanding trait interactions and their impacts on growth in scots pine branches across Europe. Funct. Ecol. 2012, 26, 541–549. [Google Scholar] [CrossRef] [Green Version]
- Taeger, S.; Zang, C.; Liesebach, M.; Schneck, V.; Menzel, A. Impact of climate and drought events on the growth of scots pine (Pinus sylvestris L.) provenances. For. Ecol. Manag. 2013, 307, 30–42. [Google Scholar] [CrossRef]
- Barbeito, I.; LeMay, V.; Calama, R.; Cañellas, I. Regeneration of Mediterranean Pinus sylvestris under two alternative shelterwood systems within a multiscale framework. Can. J. For. Res. 2011, 41, 341–351. [Google Scholar] [CrossRef]
- Coban, S.; Colak, A.H.; Rotherham, I.D. Interactions between canopy cover density and regeneration cores of older saplings in scots pine (Pinus sylvestris L.) stands. For. Syst. 2016, 25. [Google Scholar] [CrossRef] [Green Version]
- Herrero, A.; Zamora, R.; Castro, J.; Hódar, J.A. Limits of pine forest distribution at the treeline: Herbivory matters. Plant Ecol. 2012, 213, 459–469. [Google Scholar] [CrossRef]
- Ledo, A.; Condés, S.; Montes, F. Intertype mark correlation function: A new tool for the analysis of species interactions. Ecol. Modell. 2011, 222, 580–587. [Google Scholar] [CrossRef]
- Tíscar, P.A.; Candel-Pérez, D.; Estrany, J.; Balandier, P.; Gómez, R.; Lucas-Borja, M.E. Regeneration of three pine species in a Mediterranean forest: A study to test predictions from species distribution models under changing climates. Sci. Total Environ. 2017, 584, 78–87. [Google Scholar] [CrossRef]
- Montero, G.; del Río, M.; Roig, S.; Rojo, A. Selvicultura de Pinus sylvestris L. In Compendio de Selvicultura Aplicada en España2; Serrada, R., Montero, G., Reque, J., Eds.; INIA & Ministerio de Educación y Ciencia: Torrejón de Ardoz (Madrid), Spain, 2008; pp. 503–534. [Google Scholar]
- García López, J. Short description of the Navafría pine forest and its management history. In Mountain Silviculture; Montero, G., Elena Roselló, R., Eds.; Sistemas y Recursos Forestales: Madrid, Spain, 1994. [Google Scholar]
- Moreno-Fernández, D.; Cañellas, I.; Barbeito, I.; Sánchez-González, M.; Ledo, A. Alternative approaches to assessing the natural regeneration of Scots pine in a mediterranean forest. Ann. For. Sci. 2015, 72, 569–583. [Google Scholar] [CrossRef] [Green Version]
- Dale, M. Spatial Pattern Analysis in Plant Ecology; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Fortin, M.-J.; Dale, M.R.T.; ver Hoef, J. Spatial analysis in ecology. In Encyclopedia of Environmetrics; El-Shaarawi, A., Piegorsch, W., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2002; pp. 2051–2058. [Google Scholar]
- Goreaud, F.; Pélissier, R. On explicit formulas of edge effect correction for Ripley’s K -function. J. Veg. Sci. 1999, 10, 433–438. [Google Scholar] [CrossRef]
- Montes, F.; Barbeito, I.; Rubio, A.; Cañellas, I. Evaluating height structure in Scots pine forests using marked point processes. Can. J. For. Res. 2008, 38, 1924–1934. [Google Scholar] [CrossRef]
- Wood, S.N. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 3–36. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R. Generalized additive models. Stat. Sci. 1989, 10, 297–318. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman and Hall/CRC: Chapman, CA, USA, 2017; ISBN 9781498728331. [Google Scholar]
- Venables, W.; Ripley, R. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Augustin, N.H.; Musio, M.; von Wilpert, K.; Kublin, E.; Wood, S.N.; Schumacher, M. Modeling spatiotemporal forest health monitoring data. J. Am. Stat. Assoc. 2009, 104, 899–911. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, P.J.; Diggle, P.J. GeoR: Analysis of Geostatistical Data. 2016. Available online: http://www.leg.ufpr.br/geoR (accessed on 23 September 2019).
- R Core Team. R: A Language and Environment for Statistical Computing 2019; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Pardos, M.; Montes, F.; Cañellas, I. Spatial dynamics of natural regeneration in two differently managed pinus sylvestris stands before and after silvicultural intervention using replicated spatial point patterns. For. Sci. 2008, 54, 260–272. [Google Scholar]
- Beghin, R.; Lingua, E.; Garbarino, M.; Lonati, M.; Bovio, G.; Motta, R.; Marzano, R. Pinus sylvestris forest regeneration under different post-fire restoration practices in the northwestern Italian Alps. Ecol. Eng. 2010, 36, 1365–1372. [Google Scholar] [CrossRef]
- Carrer, M.; Soraruf, L.; Lingua, E. Convergent space-time tree regeneration patterns along an elevation gradient at high altitude in the Alps. For. Ecol. Manag. 2013, 304, 1–9. [Google Scholar] [CrossRef]
- Malone, S.L.; Fornwalt, P.J.; Battaglia, M.A.; Chambers, M.E.; Iniguez, J.M.; Sieg, C.H. Mixed-severity fire fosters heterogeneous spatial patterns of conifer regeneration in a dry conifer forest. Forests 2018, 9, 45. [Google Scholar] [CrossRef] [Green Version]
- Augustin, N.H.; Trenkel, V.M.; Wood, S.N.; Lorance, P. Space-time modelling of blue ling for fisheries stock management. Environmetrics 2013, 24, 109–119. [Google Scholar] [CrossRef] [Green Version]
- Eickenscheidt, N.; Augustin, N.H.; Wellbrock, N. Spatio-temporal modelling of forest monitoring data: Modelling German tree defoliation data collected between 1989 and 2015 for trend estimation and survey grid examination using GAMMs. IForest Biogeosciences For. 2019, 12, 338. [Google Scholar] [CrossRef]
- Augustin, N.H.; Mattocks, C.; Faraway, J.J.; Greven, S.; Ness, A.R. Modelling a response as a function of high-frequency count data: The association between physical activity and fat mass. Stat. Methods Med. Res. 2015, 26, 2210–2226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Montoro Girona, M.; Morin, H.; Lussier, J.-M.; Walsh, D. Radial growth response of black spruce stands ten years after experimental shelterwoods and seed-tree cuttings in boreal forest. Forests 2016, 7, 240. [Google Scholar] [CrossRef] [Green Version]
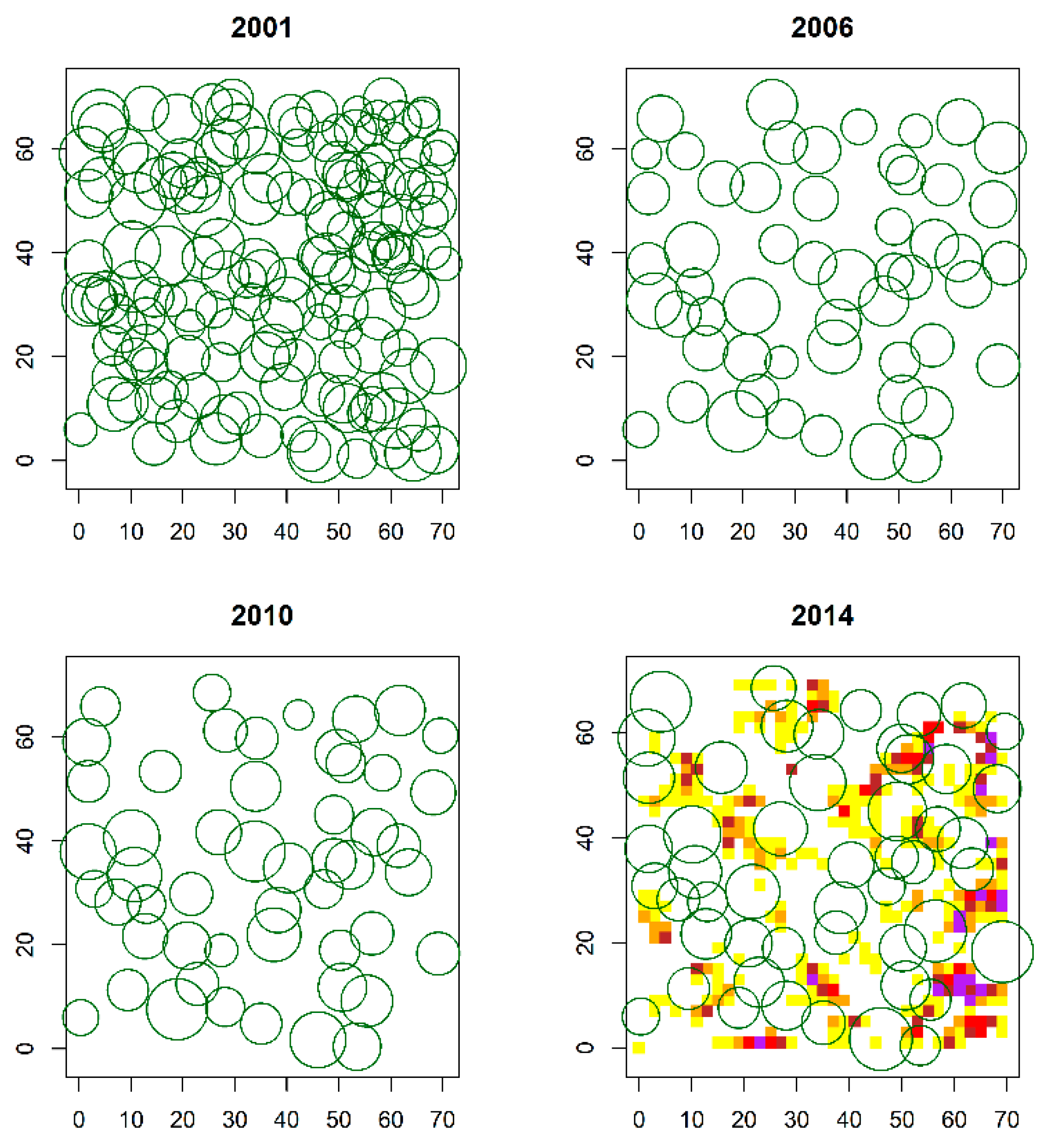


| Feature | 2001 | 2006 | 2010 | 2014 |
|---|---|---|---|---|
| Adult trees (stems with dbh ≥ 10 cm) | ||||
| Nmt (trees ha−1) | 306 | 108 | 102 | 100 |
| Dmt (cm) | 42.5 (6.7) | 44.1 (6.1) | 45.6 (6.1) | 46.2 (6.4) |
| Gmt (m2 ha−1) | 44.2 | 16.8 | 16.9 | 17.1 |
| Hmt (m) | 22.1 (2.0) | 21.6 (2.0) | 22.2 (1.9) | 22.7 (2.1) |
| Saplings (stems with height ≥ 1.30 m and dbh < 10 cm) | ||||
| Ns (saplings ha−1) | 0 | 0 | 0 | 4684 |
| Ds (cm) | 0 | 0 | 0 | 0.8 (0.3) |
| Gs (m2 ha−1) | 0 | 0 | 0 | 0.3 |
| Hs (m) | 0 | 0 | 0 | 1.5 (0.2) |
| Variables Included in the Model during the Selection Process | AIC | Percentage of Deviance Explained (%) |
|---|---|---|
| α | 3327.3 | 0 |
| 3294.9 | 5.8 | |
| 3013.0 | 47.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno-Fernández, D.; Ledo, A.; Cañellas, I.; Montes, F. Strategies for Modeling Regeneration Density in Relation to Distance from Adult Trees. Forests 2020, 11, 120. https://doi.org/10.3390/f11010120
Moreno-Fernández D, Ledo A, Cañellas I, Montes F. Strategies for Modeling Regeneration Density in Relation to Distance from Adult Trees. Forests. 2020; 11(1):120. https://doi.org/10.3390/f11010120
Chicago/Turabian StyleMoreno-Fernández, Daniel, Alicia Ledo, Isabel Cañellas, and Fernando Montes. 2020. "Strategies for Modeling Regeneration Density in Relation to Distance from Adult Trees" Forests 11, no. 1: 120. https://doi.org/10.3390/f11010120
APA StyleMoreno-Fernández, D., Ledo, A., Cañellas, I., & Montes, F. (2020). Strategies for Modeling Regeneration Density in Relation to Distance from Adult Trees. Forests, 11(1), 120. https://doi.org/10.3390/f11010120






