Seemingly Unrelated Mixed-Effects Biomass Models for Young Silver Birch Stands on Post-Agricultural Lands
Abstract
:1. Introduction
2. Material and Methods
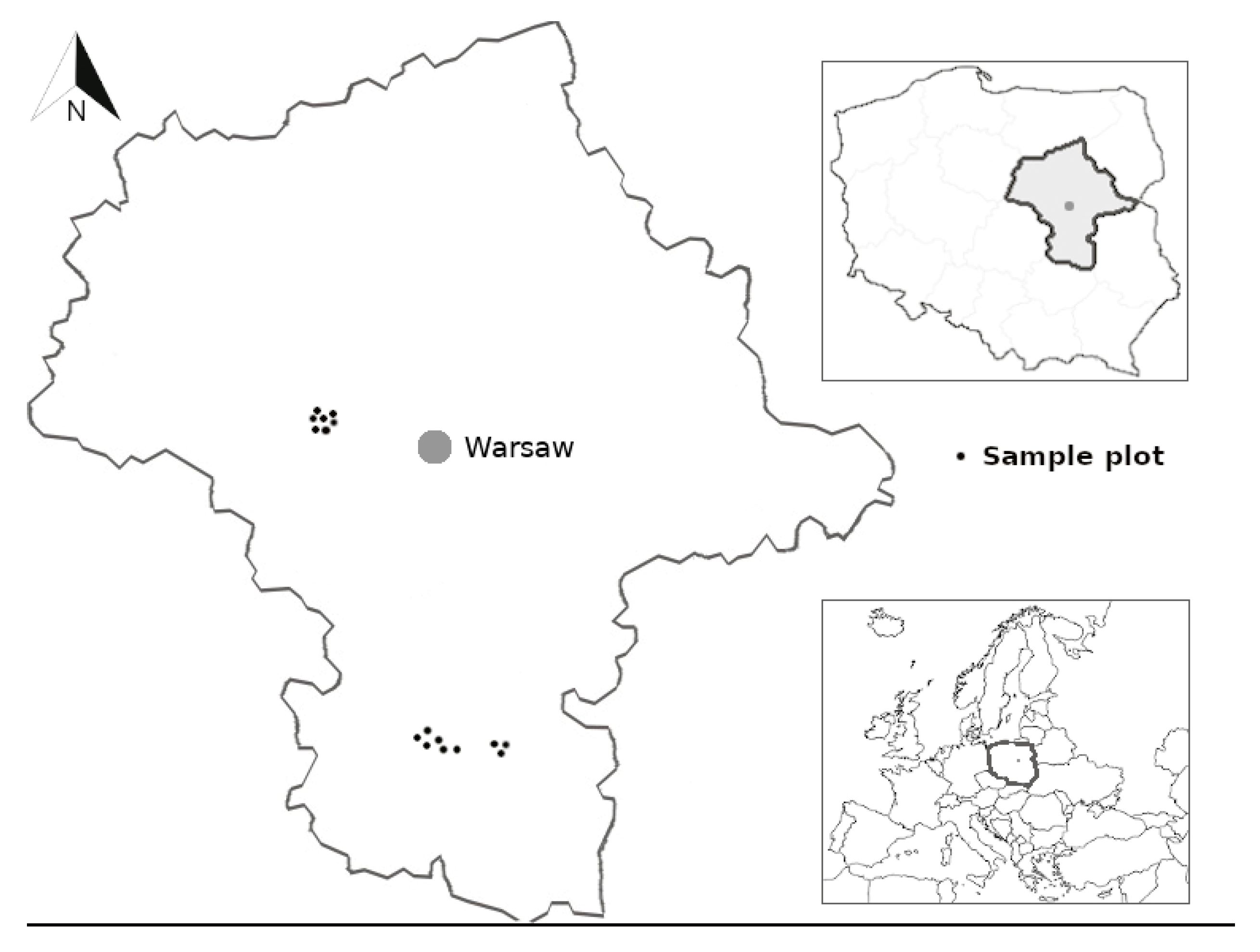
2.1. Study Sites
2.2. Uprooted Trees
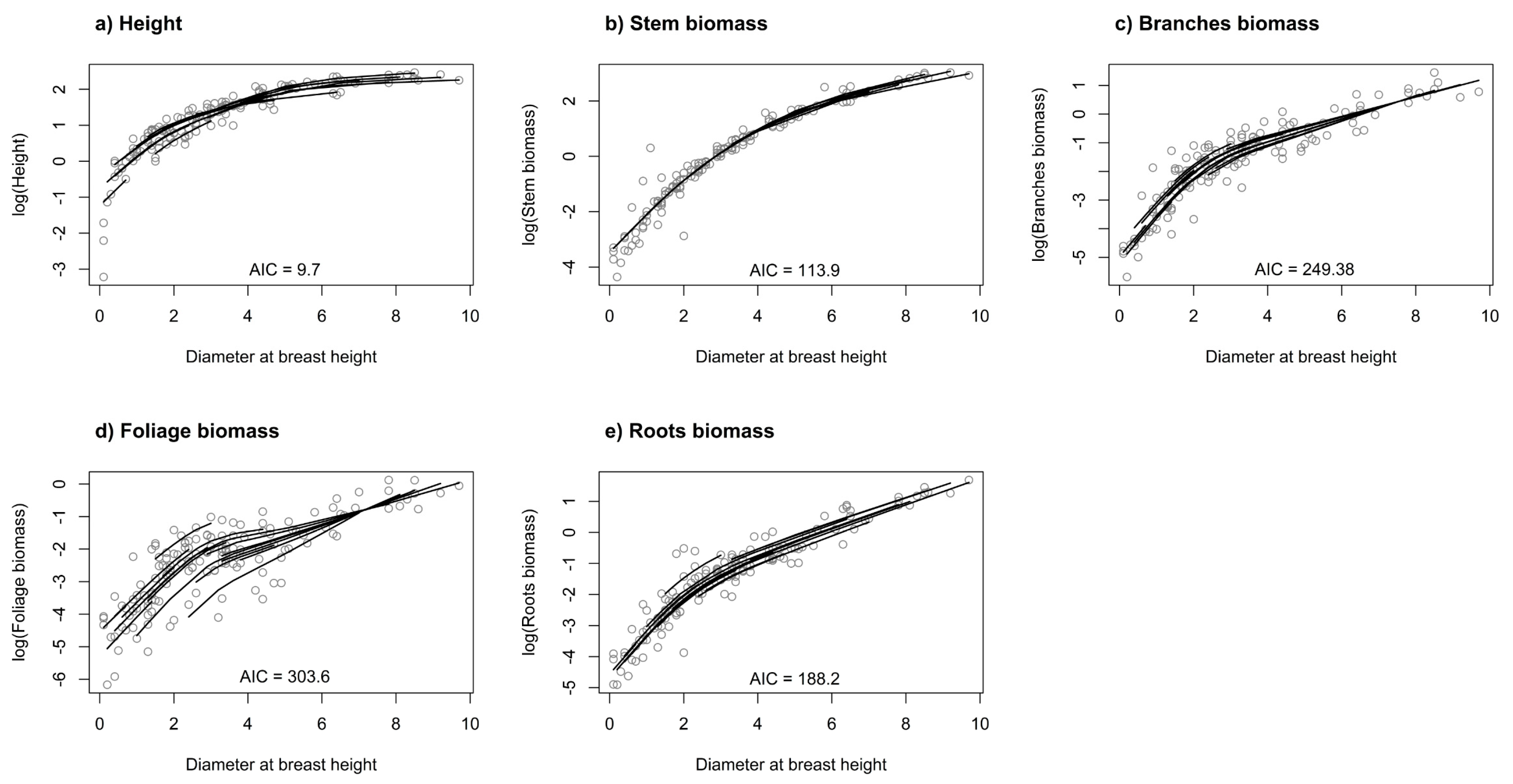
2.3. Separate Mixed-Effect Models
2.4. Multivariate Seemingly Unrelated Mixed-Effects Model System
2.5. Fixed and Cross-Model Random-Effect Prediction
3. Results
Fixed and Cross-Model Random Effects Prediction
4. Discussion and Conclusions
Author Contributions
Funding

Conflicts of Interest
References
- Raport o stanie lasów w Polsce 2017 (Annual Report on the Condition of Forests in Poland 2017); State Forests Information Center: Warsaw, Poland, 2018. (In Polish)
- Raport o stanie lasów w Polsce 2018 (Annual Report on the Condition of Forests in Poland 2018); State Forests Information Center: Warsaw, Poland, 2019. (In Polish)
- Van Kooten, G.C.; Eagle, A.J.; Manley, J.; Smolak, T. How costly are carbon offsets? A meta-analysis of carbon forest sinks. Environ. Sci. Policy 2004, 7, 239–251. [Google Scholar] [CrossRef] [Green Version]
- Fahey, T.J.; Woodbury, P.B.; Battles, J.J.; Goodale, C.L.; Hamburg, S.P.; Ollinger, S.V.; Woodall, C.W. Forest carbon storage: Ecology, management, and policy. Front. Ecol. Environ. 2009, 8, 245–252. [Google Scholar] [CrossRef] [Green Version]
- Rittenhouse, C.D.; Rissman, A.R. Forest cover, carbon sequestration, and wildlife habitat: Policy review and modeling of tradeoffs among land-use change scenarios. Environ. Sci. Policy 2012, 21, 94–105. [Google Scholar] [CrossRef]
- Karlsson, A.; Albrektson, A.; Forsgren, A.; Svensson, L. An analysis of successful natural regeneration of downy and silver birch on abandoned farmland in Sweden. Silva Fenn. 1998, 32, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Uri, V.; Lõhmus, K.; Ostonen, I.; Tullus, H.; Lastik, R.; Vildo, M. Biomass production, foliar and root characteristics and nutrient accumulation in young silver birch (Betula pendula Roth.) stand growing on abandoned agricultural land. Eur. J. For. Res. 2007, 126, 495–506. [Google Scholar] [CrossRef]
- Zasada, M.; Bijak, S.; Bronisz, K.; Bronisz, A.; Gawęda, T. Biomass dynamics in young silver birch stands on post-agricultural lands in central Poland. Drewno: Prace nauk. doniesienia komun. 2014, 57, 29–40. [Google Scholar]
- Cardellini, G.; Valada, T.; Cornillier, C.; Vial, E.; Dragoi, M.; Goudiaby, V.; Mues, V.; Lasserre, B.; Gruchała, A.; Rørstad, P.K.; et al. EFO-LCI: A New Life Cycle Inventory Database of Forestry Operations in Europe. Environ. Manag. 2018, 61, 1031–1047. [Google Scholar] [CrossRef]
- Lehtonen, A.; Mäkipää, R.; Heikkinen, J.; Sievänen, R.; Liski, J. Biomass expansion factors (BEFs) for Scots pine, Norway spruce and birch according to stand age for boreal forests. For. Ecol. Manag. 2004, 188, 211–224. [Google Scholar] [CrossRef]
- Teobaldelli, M.; Somogyi, Z.; Migliavacca, M.; Usoltsev, V.A. Generalized functions of biomass expansion factors for conifers and broadleaved by stand age, growing stock and site index. For. Ecol. Manag. 2009, 257, 1004–1013. [Google Scholar] [CrossRef]
- Jagodziński, A.M.; Zasada, M.; Bronisz, K.; Bronisz, A.; Bijak, S. Biomass conversion and expansion factors for a chronosequence of young naturally regenerated silver birch (Betula pendula Roth) stands growing on post-agricultural sites. For. Ecol. Manag. 2017, 384, 208–220. [Google Scholar] [CrossRef]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe; Silva Fenn. Monographs; Finnish Society of Forest Science, Finnish Forest Research Institute: Tampere, Finland, 2005. [Google Scholar]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Bronisz, K.; Zasada, M. Uproszczone wzory empiryczne do określania suchej biomasy nadziemnej części drzew i ich komponentów dla sosny zwyczajnej (Simplified empirical formulas to determine the dry biomass of aboveground components of trees for Scots pine). Sylwan 2016, 160, 277–283. (In Polish) [Google Scholar]
- Kuznetsova, T.; Lukjanova, A.; Mandre, M.; Lõhmus, K. Aboveground biomass and nutrient accumulation dynamics in young black alder, silver birch and Scots pine plantations on reclaimed oil shale mining areas in Estonia. For. Ecol. Manag. 2011, 262, 56–64. [Google Scholar] [CrossRef]
- Adegbidi, H.G.; Jokela, E.J.; Comerford, N.B.; Barros, N.F. Biomass development for intensively managed loblolly pine plantations growing on Spodosols in the southeastern USA. For. Ecol. Manag. 2002, 167, 91–102. [Google Scholar] [CrossRef]
- Pajtík, J.; Konôpka, B.; Lukac, M. Individual biomass factors for beech, oak and pine in Slovakia: A comparative study in young naturally regenerated stands. Trees 2011, 25, 277–288. [Google Scholar] [CrossRef]
- Smith, A.; Granhus, A.; Astrup, R.; Bollandsås, O.M.; Petersson, H. Functions for estimating aboveground biomass of birch in Norway. Scan. J. For. Res. 2014, 29, 565–578. [Google Scholar] [CrossRef]
- Mälkönen, E. Annual primary production and nutrient cycle in a birch stand: Seloste. Environ. Sci. 1977, 91. [Google Scholar]
- Johansson, T. Biomass production of Norway spruce (Picea abies (L.) Karst.) growing on abandoned farmland. Silva Fenn. 1999, 33, 261–280. [Google Scholar] [CrossRef] [Green Version]
- Bronisz, K.; Strub, M.; Cieszewski, C.; Bijak, S.; Bronisz, A.; Tomusiak, R.; Wojtan, R.; Zasada, M. Empirical equations for estimating aboveground biomass of Betula pendula growing on former farmland in central Poland. Silva Fenn. 2016, 50, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Bijak, S.; Zasada, M.; Bronisz, A.; Bronisz, K.; Czajkowski, M.; Ludwisiak, Ł.; Tomusiak, R.; Wojtan, R. Estimating coarse roots biomass in young silver birch stands on post-agricultural lands in central Poland. Silva Fenn. 2013, 47, 1–14. [Google Scholar] [CrossRef]
- Varik, M.; Aosaar, J.; Ostonen, I.; Lõhmus, K.; Uri, V. Carbon and nitrogen accumulation in belowground tree biomass in a chronosequence of silver birch stands. For. Ecol. Manag. 2013, 302, 62–70. [Google Scholar] [CrossRef]
- Smith, A.; Granhus, A.; Astrup, R. Functions for estimating belowground and whole tree biomass of birch in Norway. Scan. J. For. Res. 2016, 31, 568–582. [Google Scholar] [CrossRef]
- Kozak, A. Methods for Ensuring Additivity of Biomass Components by Regression Analysis. For. Chron. 1970, 46, 402–405. [Google Scholar] [CrossRef]
- Chiyenda, S.S.; Kozak, A. Additivity of component biomass regression equations when the underlying model is linear. Can. J. For. Res. 1984, 14, 441–446. [Google Scholar] [CrossRef]
- Cunia, T.; Briggs, R.D. Forcing Additivity of Biomass Tables-Some Empirical Results. Can. J. For. Res. 1984, 14, 376–384. [Google Scholar] [CrossRef]
- Parresol, B.R. Assessing tree and stand biomass: A review with examples and critical comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar]
- Bi, H.; Turner, J.; Lambert, M. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Developing Two Additive Biomass Equations for Three Coniferous Plantation Species in Northeast China. Forests 2016, 7, 136. [Google Scholar] [CrossRef] [Green Version]
- Lambert, M.-C.; Ung, C.-H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- Ruiz-Peinado, R.; Montero, G.; Del Rio, M. Biomass models to estimate carbon stocks for hardwood tree species. For. Syst. 2012, 21, 42–52. [Google Scholar] [CrossRef]
- Zasada, M.; Bronisz, K.; Bijak, S.; Wojtan, R.; Tomusiak, R.; Dudek, A.; Michalak, K.; Wróblewski, L. Wzory empiryczne do określania suchej biomasy nadziemnej części drzew i ich komponentów (Empirical formulae for determination of the dry biomass of aboveground parts of the tree). Sylwan 2008, 152, 27–39. (In Polish) [Google Scholar]
- Mehtätalo, L.; Lappi, J. Forest Biometrics with examples in R; Chapman & Hall/CRC: London, UK, 2020; Available online: http://cs.uef.fi/~lamehtat/documents/TreeSize20190612.pdf (accessed on 12 June 2019).
- Fehrmann, L.; Lehtonen, A.; Kleinn, C.; Tomppo, E. Comparison of linear and mixed-effect regression models and a k-nearest neighbour approach for estimation of single-tree biomass. Can. J. For. Res. 2008, 38, 1–9. [Google Scholar] [CrossRef]
- De-Miguel, S.; Mehtätalo, L.; Durkaya, A. Developing generalized, calibratable, mixed-effects meta-models for large-scale biomass prediction. Can. J. For. Res. 2014, 44, 648–656. [Google Scholar] [CrossRef]
- Huy, B.; Kralicek, K.; Poudel, K.P.; Phuong, V.T.; Khoa, P.V.; Hung, N.D.; Temesgen, H. Allometric equations for estimating tree aboveground biomass in evergreen broadleaf forests of Viet Nam. For. Ecol. Manag. 2016, 382, 193–205. [Google Scholar] [CrossRef]
- Ou, G.; Wang, J.; Xu, H.; Chen, K.; Zheng, H.; Zhang, B.; Sun, X.; Xu, T.; Xiao, Y. Incorporating topographic factors in nonlinear mixed-effects models for aboveground biomass of natural Simao pine in Yunnan, China. J. For. Res. 2016, 27, 119–131. [Google Scholar] [CrossRef]
- Pearce, H.G.; Anderson, W.R.; Fogarty, L.G.; Todoroki, C.L.; Anderson, S.A.J. Linear mixed-effects models for estimating biomass and fuel loads in shrublands. Can. J. For. Res. 2010, 40, 2015–2026. [Google Scholar] [CrossRef]
- Harrell, F.E. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis; Springer Series in Statistics, 2nd ed.; Springer: New York, NY, USA, 2015; ISBN 978-3-319-19424-0. [Google Scholar]
- De-Miguel, S.; Mehtätalo, L.; Shater, Z.; Kraid, B.; Pukkala, T. Evaluating marginal and conditional predictions of taper models in the absence of calibration data. Can. J. For. Res. 2012, 42, 1383–1394. [Google Scholar] [CrossRef]
- Lappi, J. Calibration of Height and Volume Equations with Random Parameters. For. Sci. 1991, 37, 781–801. [Google Scholar]
- Bronisz, K.; Mehtätalo, L. Mixed-effects generalized height–diameter model for young silver birch stands on post-agricultural lands. For. Ecol. Manag. 2020, 460, 117901. [Google Scholar] [CrossRef]
- Martyn, D. Klimaty kuli ziemskiej (Climates of the Earth); PWN: Warsaw, Poland, 2000. (In Polish) [Google Scholar]
- Snowdon, P.; Raison, J.; Keith, H.; Ritson, P.; Grierson, P.; Adams, M.A.; Montagu, K.; Hui-quan, B.; Burrows, W.; Eamus, D. Protocol for Sampling Tree and Stand Biomass; Australian Greenhouse Office: Canberra, Australia, 2002. [Google Scholar]
- Samuelsson, R.; Burvall, J.; Jirjis, R. Comparison of different methods for the determination of moisture content in biomass. Biomass Bioenergy 2006, 30, 929–934. [Google Scholar] [CrossRef]
- Mehtätalo, L. lmfor: Functions for Forest Biometrics; 2019. Available online: https://cran.r-project.org/web/packages/lmfor (accessed on 22 October 2019).
- Baskerville, G.L. Use of logarithmic regression in the estimation of plant biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- Pukelsheim, F. Optimal Design of Experiments; Classics in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006; ISBN 978-0-89871-604-7. [Google Scholar]
- Pinheiro, J.; Bates, D.; Saikat, D.; Deepayan, S. nlme: Linear and Nonlinear Mixed Effects Models; 2020. Available online: https://cran.r-project.org/web/packages/nlme (accessed on 4 March 2020).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- RStudio Team. RStudio: Integrated Development for R.; RStudio Inc.: Boston, MA, USA, 2015. [Google Scholar]
- Maltamo, M.; Mehtätalo, L.; Vauhkonen, J.; Packalén, P. Predicting and calibrating tree attributes by means of airborne laser scanning and field measurements. Can. J. For. Res. 2012, 42, 1896–1907. [Google Scholar] [CrossRef]
- Ung, C.-H.; Bernier, P.; Guo, X.-J. Canadian national biomass equations: New parameter estimates that include British Columbia data. Can. J. For. Res. 2008, 38, 1123–1132. [Google Scholar] [CrossRef]
- Vonderach, C.; Kändler, G.; Dormann, C.F. Consistent set of additive biomass functions for eight tree species in Germany fit by nonlinear seemingly unrelated regression. Ann. For. Sci. 2018, 75, 49. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, J.P.; Parresol, B.R. Additivity in tree biomass components of Pyrenean oak (Quercus pyrenaica Willd.). For. Ecol. Manag. 2003, 179, 269–276. [Google Scholar] [CrossRef]
- Parresol, B.R. Additivy of nonlinear biomass equations. Can. J. For. Res. 2001, 31, 865–878. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Wang, G.; Tang, S. Modelling a system of nonlinear additive crown width models applying seemingly unrelated regression for Prince Rupprecht larch in northern China. For. Ecol. Manag. 2017, 386, 71–80. [Google Scholar] [CrossRef]
- Mehtätalo, L. Localizing a Predicted Diameter Distribution Using Sample Information. For. Sci. 2005, 51, 292–303. [Google Scholar]
- Siipilehto, J. Methods and applications for improving parameter prediction models for stand structures in Finland. Diss. For. 2011, 124, 56. [Google Scholar] [CrossRef] [Green Version]
- Repola, J. Biomass equations for birch in Finland. Silva Fenn. 2008, 42, 605–624. [Google Scholar] [CrossRef] [Green Version]
- Tsutsumi, M.; Shiyomi, M.; Sato, S.; Sugawara, K. Use of Gamma Distribution Aboveground Biomass of Plant Species in Grazing Pasture. Grassland Sci. 2002, 47, 615–618. [Google Scholar]
- Bollandsås, O.M.; Gregoire, T.G.; Næsset, E.; Øyen, B.-H. Detection of biomass change in a Norwegian mountain forest area using small footprint airborne laser scanner data. Stat. Methods Appl. 2013, 22, 113–129. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2013; ISBN 978-1-4757-8144-1. [Google Scholar]



| Plots | Trees | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Age | Area | N | BA | DBH | H | ST | BR | FL | RT | |
| Min | 3 | 0.001 | 2987 | 0.21 | 0.1 | 1.41 | 0.0128 | 0.003 | 0.002 | 0.007 |
| Mean | 9 | 0.018 | 46,486 | 12.76 | 3.22 | 5.57 | 2.982 | 0.443 | 0.174 | 0.575 |
| Median | 9 | 0.019 | 12,572 | 12.73 | 2.9 | 4.85 | 1.078 | 0.241 | 0.108 | 0.26 |
| SD | 4 | 0.015 | 60,547 | 9.06 | 2.17 | 2.96 | 4.687 | 0.644 | 0.211 | 0.924 |
| Max | 16 | 0.05 | 198,095 | 28.82 | 9.7 | 13.08 | 20.627 | 4.256 | 1.133 | 5.42 |
| Dependent Variable | H | ST | BR | FL | RT |
|---|---|---|---|---|---|
| −0.873 (0.177) | −3.543 (0.224) | −5.281 (0.246) | −5.649 (0.394) | −4.894 (0.198) | |
| 1.041 (0.116) | 1.463 (0.175) | 1.705 (0.189) | 1.461 (0.252) | 1.573 (0.158) | |
| −0.079 (0.019) | −0.052 (0.029) | −0.086 (0.036) | −0.056 (0.045) | −0.075 (0.030) | |
| 0.171 (0.049) | 0.083 (0.076) | 0.124 (0.099) | 0.038 (0.121) | 0.104 (0.081) | |
| −0.119 (0.043) | −0.035 (0.066) | 0.007 (0.095) | 0.1 (0.112) | 0.013 (0.077) | |
| −0.491 | −0.705 | −0.147 | −0.147 | −0.3 | |
| 0.2242 | 0.42 | 0.4742 | 0.5282 | 0.4052 |
| Dependent Variable | H | ST | BR | FL | RT | ||||||
| H | 0.4162 | −0.963 | 0.715 | −0.859 | −0.435 | 0.518 | −0.656 | 0.952 | −0.682 | −0.357 | |
| - | 0.1162 | −0.795 | 0.951 | 0.219 | −0.386 | 0.477 | −0.866 | 0.497 | 0.52 | ||
| ST | - | - | 0.2412 | −0.922 | −0.228 | 0.408 | −0.484 | 0.699 | −0.486 | −0.43 | |
| - | - | - | 0.0962 | 0.093 | −0.289 | 0.378 | −0.756 | 0.395 | 0.615 | ||
| BR | - | - | - | - | 0.4422 | −0.902 | 0.954 | −0.677 | 0.937 | −0.617 | |
| - | - | - | - | - | 0.0732 | −0.895 | 0.747 | −0.849 | 0.568 | ||
| FL | - | - | - | - | - | - | 1.012 | −0.846 | 0.995 | −0.366 | |
| - | - | - | - | - | - | - | 0.2222 | −0.854 | −0.076 | ||
| RT | - | - | - | - | - | - | - | - | 0.2952 | −0.305 | |
| - | - | - | - | - | - | - | - | - | 0.0612 | ||
| Dependent Variable | H | ST | BR | FL |
|---|---|---|---|---|
| ST | 0.256 | |||
| BR | −0.151 | 0.478 | - | - |
| FL | −0.054 | 0.495 | 0.638 | - |
| RT | −0.013 | 0.579 | 0.552 | 0.496 |
| Dependent Variable | H | ST | BR | FL | RT | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of trees | (m) | (%) | (kg) | (%) | (kg) | (%) | (kg) | (%) | (kg) | (%) |
| 2 | 0.005 | 0.6 | 0.006 | 1.1 | 0.003 | 1.8 | 0.038 | 29.5 | 0.002 | 1.1 |
| 3 | 0.007 | 0.8 | 0.012 | 2.2 | 0.01 | 8.5 | 0.051 | 39.5 | 0.008 | 4.4 |
| 4 | 0.045 | 5.4 | 0.037 | 6.7 | 0.03 | 17.6 | 0.053 | 41.1 | 0.02 | 11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bronisz, K.; Mehtätalo, L. Seemingly Unrelated Mixed-Effects Biomass Models for Young Silver Birch Stands on Post-Agricultural Lands. Forests 2020, 11, 381. https://doi.org/10.3390/f11040381
Bronisz K, Mehtätalo L. Seemingly Unrelated Mixed-Effects Biomass Models for Young Silver Birch Stands on Post-Agricultural Lands. Forests. 2020; 11(4):381. https://doi.org/10.3390/f11040381
Chicago/Turabian StyleBronisz, Karol, and Lauri Mehtätalo. 2020. "Seemingly Unrelated Mixed-Effects Biomass Models for Young Silver Birch Stands on Post-Agricultural Lands" Forests 11, no. 4: 381. https://doi.org/10.3390/f11040381
APA StyleBronisz, K., & Mehtätalo, L. (2020). Seemingly Unrelated Mixed-Effects Biomass Models for Young Silver Birch Stands on Post-Agricultural Lands. Forests, 11(4), 381. https://doi.org/10.3390/f11040381





