Taper Function for Pinus nigra in Central Italy: Is a More Complex Computational System Required?
Abstract
:1. Introduction
2. Materials and Methods
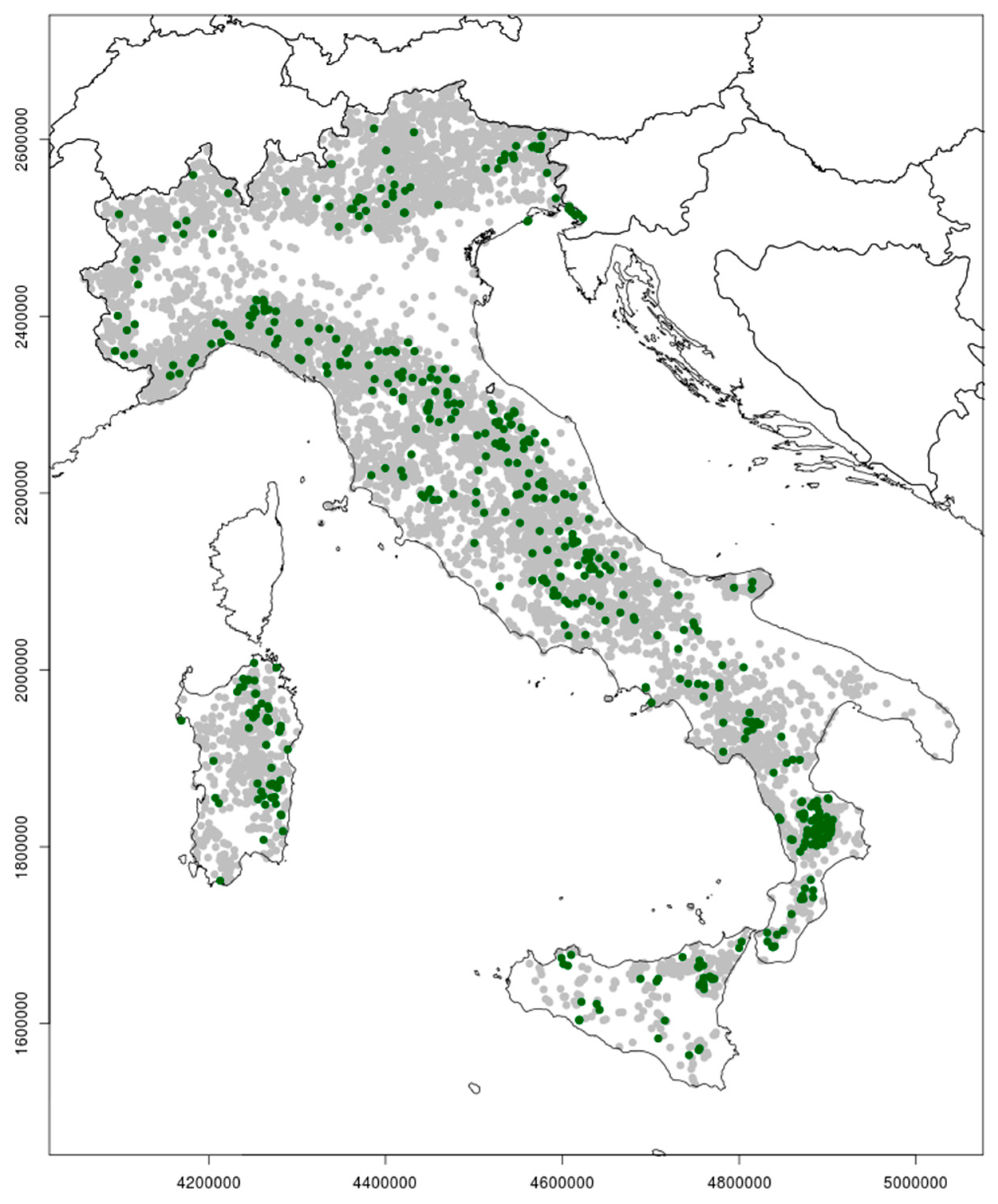
2.1. Sampling Method
2.2. Stem Taper Functions
2.3. Measurement Technique
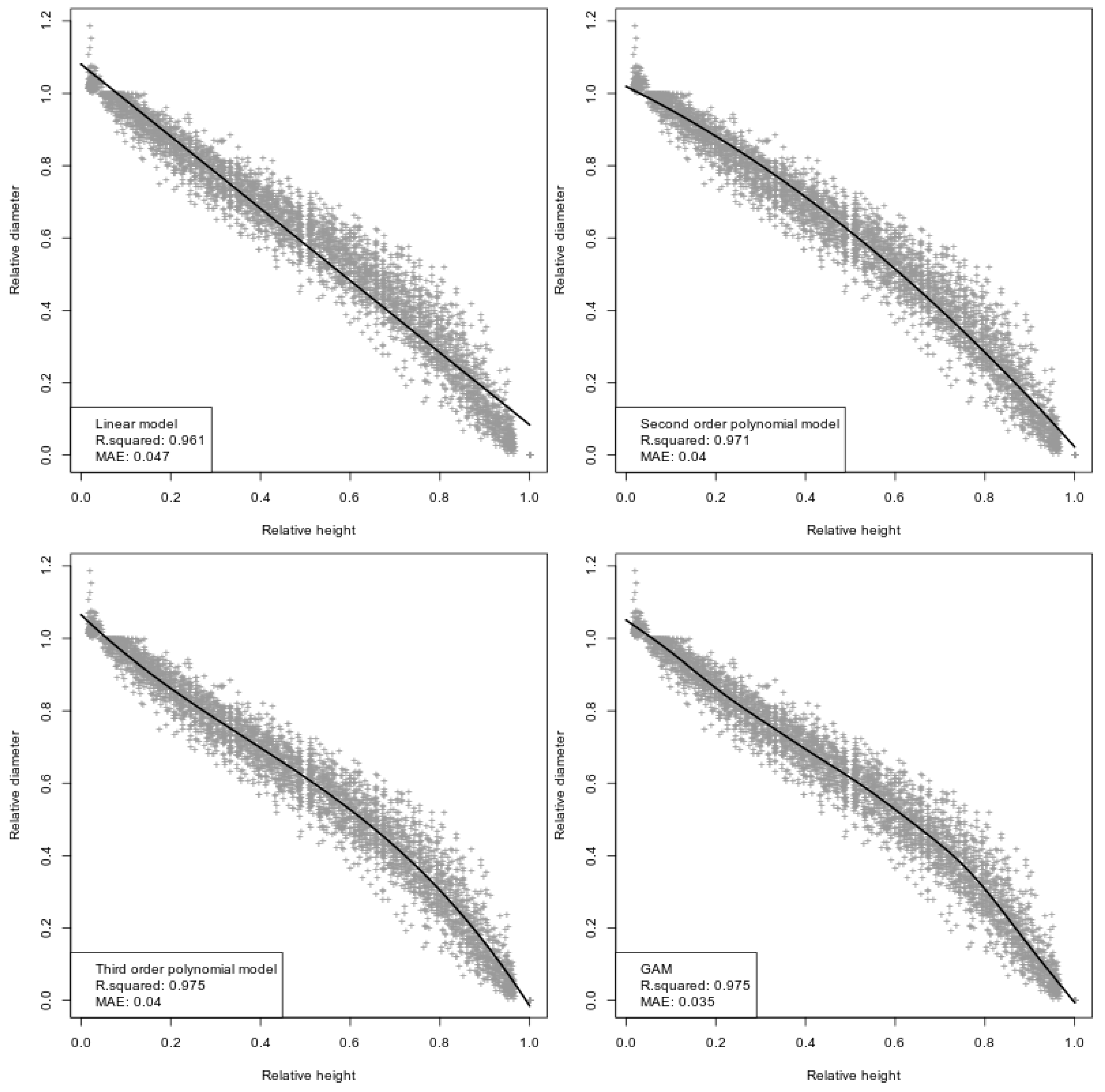
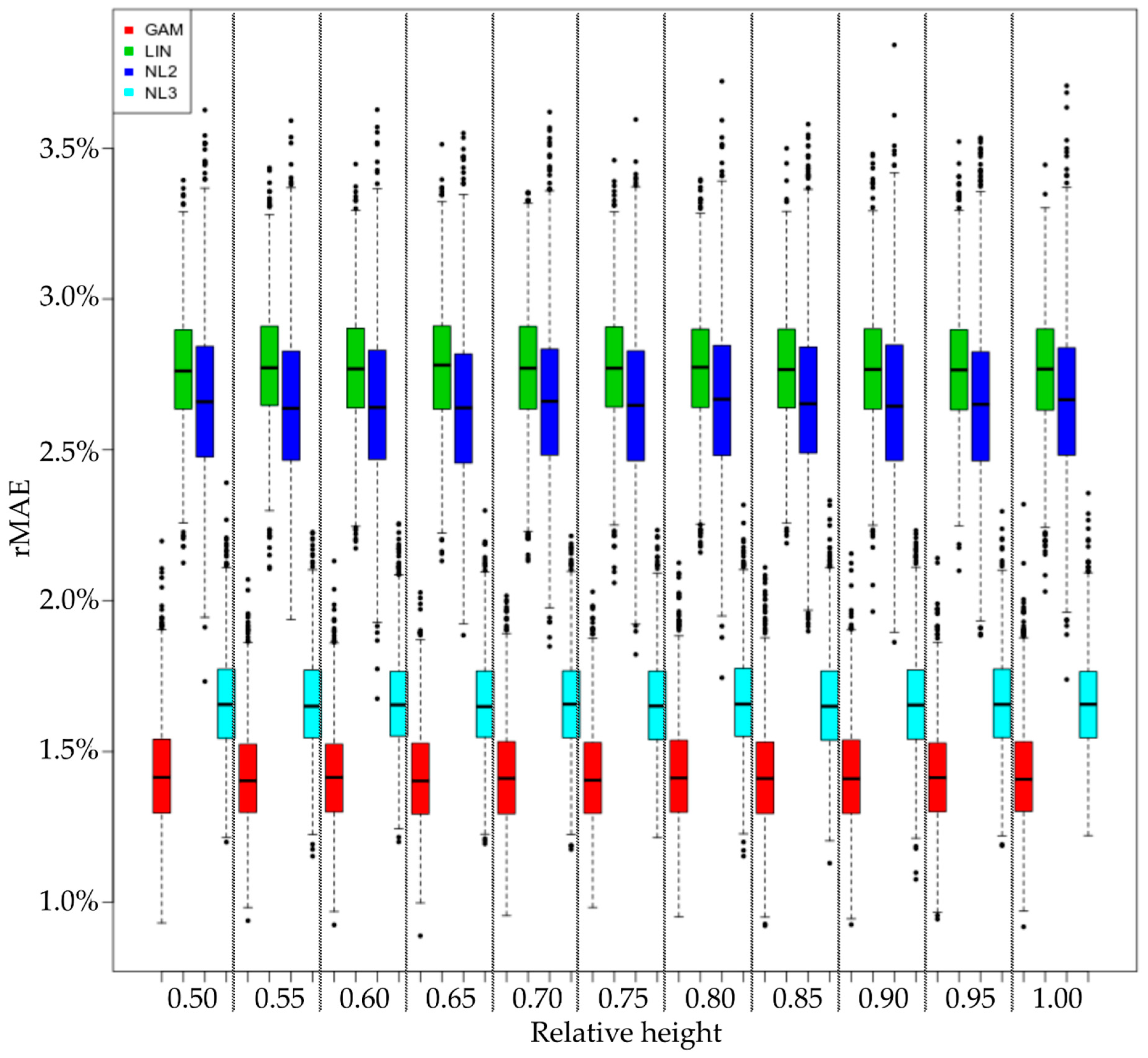
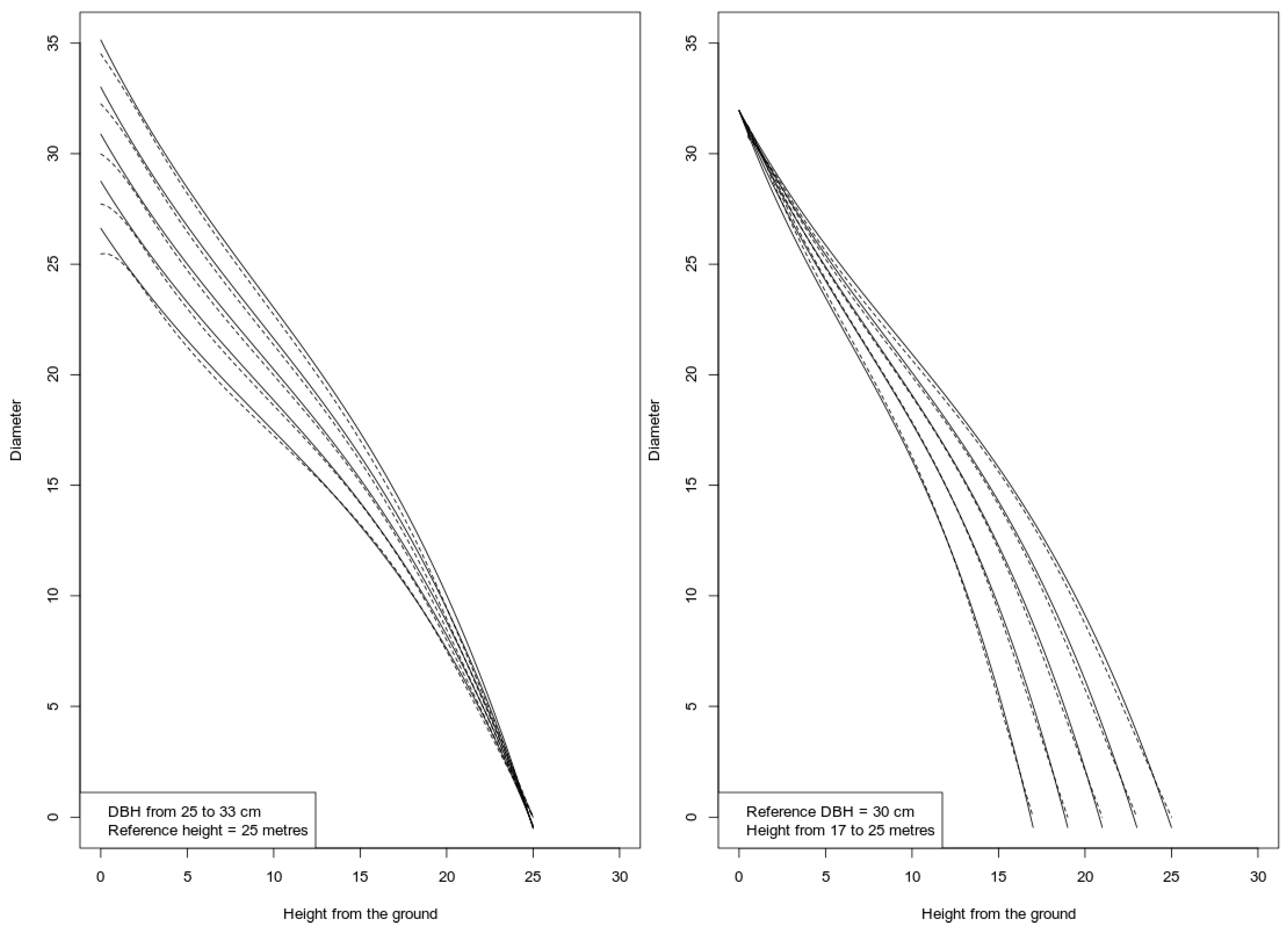
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Isajev, V.; Fady, B.; Semerci, H.; Andonovski, V. EUFORGEN Technical Guidelines for Genetic Conservation and Use for European Black Pine (Pinus nigra); International Plant Genetic Resources Institute: Rome, Italy, 2014; ISBN 92-9043-659-X. [Google Scholar]
- Piermattei, A.; Renzaglia, F.; Urbinati, C. Recent expansion of Pinus nigra Arn. above the timberline in the central Apennines, Italy. Ann. For. Sci. 2012, 69, 509–517. [Google Scholar] [CrossRef] [Green Version]
- Cantiani, P.; Chiavetta, U. Estimating the mechanical stability of Pinus nigra Arn. using an alternative approach across several plantations in central Italy. iFor. Biogeosci. For. 2015, 8, 846–852. [Google Scholar] [CrossRef] [Green Version]
- Barbati, A.; Corona, P.; Salvati, L.; Gasparella, L. Natural forest expansion into suburban countryside: Gained ground for a green infrastructure? Urban For. Urban Green. 2013, 12, 36–43. [Google Scholar] [CrossRef] [Green Version]
- Marchi, M.; Paletto, A.; Cantiani, P.; Bianchetto, E.; De Meo, I. Comparing Thinning System Effects on Ecosystem Services Provision in Artificial Black Pine (Pinus nigra J. F. Arnold) Forests. Forests 2018, 9, 188. [Google Scholar] [CrossRef] [Green Version]
- Tabacchi, G.; De Natale, F.; Di Cosmo, L.; Floris, A.; Gagliano, C.; Gasparini, P.; Genchi, L.; Scrinzi, G.; Tosi, V. Le Stime di Superficie 2005. Inventario Nazionale delle Foreste e dei Serbatoi Forestali di Carbonio; CRA-ISAFA: Trento, Italy, 2007. [Google Scholar]
- Santini, F.; Serrano, L.; Kefauver, S.C.; Abdullah-Al, M.; Aguilera, M.; Sin, E.; Voltas, J. Morpho-physiological variability of Pinus nigra populations reveals climate-driven local adaptation but weak water use differentiation. Environ. Exp. Bot. 2019, 166, 103828. [Google Scholar] [CrossRef]
- Ciancio, O.; Iovino, F.; Menguzzato, G.; Nicolaci, A.; Nocentini, S. Structure and growth of a small group selection forest of calabrian pine in Southern Italy: A hypothesis for continuous cover forestry based on traditional silviculture. For. Ecol. Manag. 2006, 224, 229–234. [Google Scholar] [CrossRef]
- Ivetić, V.; Škorić, M. The impact of seeds provenance and nursery production method on Austrian pine (Pinus nigra Arn.) seedlings quality. Ann. For. Res. 2013, 56, 297–305. [Google Scholar]
- Cantiani, P.; Marchi, M. A spatial dataset of forest mensuration collected in black pine plantations in central Italy. Ann. For. Sci. 2017, 74, 50. [Google Scholar] [CrossRef]
- Marchi, M.; Castaldi, C.; Merlini, P.; Nocentini, S.; Ducci, F. Stand structure and influence of climate on growth trends of a Marginal forest population of Pinus nigra spp. nigra. Ann. Silvic. Res. 2015, 39, 100–110. [Google Scholar]
- Puletti, N.; Grotti, M.; Scotti, R. Evaluating the Eccentricities of Poplar Stem Profiles with Terrestrial Laser Scanning. Forests 2019, 10, 239. [Google Scholar] [CrossRef] [Green Version]
- Neumann, M.; Starlinger, F. The significance of different indices for stand structure and diversity in forests. For. Ecol. Manag. 2001, 145, 91–106. [Google Scholar] [CrossRef]
- Pommerening, A.; Särkkä, A. What mark variograms tell about spatial plant interactions. Ecol. Model. 2013, 251, 64–72. [Google Scholar] [CrossRef]
- Marchi, M. Nonlinear versus linearised model on stand density model fitting and stand density index calculation: Analysis of coefficients estimation via simulation. J. For. Res. 2019, 30, 1595–1602. [Google Scholar] [CrossRef] [Green Version]
- Crookston, N.L.; Rehfeldt, G.E.; Dixon, G.E.; Weiskittel, A.R. Addressing climate change in the forest vegetation simulator to assess impacts on landscape forest dynamics. For. Ecol. Manag. 2010, 260, 1198–1211. [Google Scholar] [CrossRef]
- Holopainen, M.; Vastaranta, M.; Hyyppä, J. Outlook for the next generation’s precision forestry in Finland. Forests 2014, 5, 1682–1694. [Google Scholar] [CrossRef] [Green Version]
- Fardusi, M.J.; Chianucci, F.; Barbati, A. Concept to practices of geospatial information tools to assist forest management & planning under precision forestry framework: A review. Ann. Silvic. Res. 2017, 41, 3–14. [Google Scholar]
- Scotti, R.; Mura, M.; Piredda, I.; Campus, S.; Lovreglio, R. Gestione forestale sostenibile in Sardegna: Dal legno al legname, le funzioni di profilo. In Atti del II Congresso Internazionale di Selvicoltura. Progettare il Futuro per il Settore Forestale; Accademia Italiana di Scienze Forestali: Florence, Italy, 2014; Volume 2, pp. 1056–1061. [Google Scholar]
- Paletto, A.; De Meo, I.; Grilli, G.; Nikodinoska, N. Selective and traditional forest management options for black pine forests in Central Italy: Effects on ecosystem services. Ann. For. Res. 2017, 60, 313–326. [Google Scholar] [CrossRef] [Green Version]
- Cantiani, P.; De Meo, I.; Becagli, C.; Bianchetto, E.; Cazau, C.; Mocali, S.; Salerni, E. EffEcts of thinnings on plants and fungi biodiversity in a Pinus nigra plantation: A case study in central Italy. For. Ideas 2015, 21, 149–162. [Google Scholar]
- Barbato, D.; Perini, C.; Mocali, S.; Bacaro, G.; Tordoni, E.; Maccherini, S.; Marchi, M.; Cantiani, P.; De Meo, I.; Bianchetto, E.; et al. Teamwork makes the dream work: Disentangling cross-taxon congruence across soil biota in black pine plantations. Sci. Total Environ. 2019, 656, 659–669. [Google Scholar] [CrossRef]
- Ciccarese, L.; Mattsson, A.; Pettenella, D. Ecosystem services from forest restoration: Thinking ahead. New For. 2012, 43, 543–560. [Google Scholar] [CrossRef]
- Salerni, E.; D’Aguanno, M.; Leonardi, P.; Perini, C. Ectomycorrhizal communities above and below ground and truffle productivity in a Tuber aestivum orchard. For. Syst. 2014, 23, 329–338. [Google Scholar] [CrossRef] [Green Version]
- García-Montero, L.G.; Manjón, J.L.; Martín-Fernández, S.; Di Massimo, G. Problems of using pines in Tuber melanosporum culture: Soils and truffle harvest associated with Pinus nigra and P. sylvestris. Agrofor. Syst. 2007, 70, 243–249. [Google Scholar] [CrossRef]
- Jäghagen, K.; Lageson, H. Timber quality after thinning from above and below in stands of pinus sylvestris. Scand. J. For. Res. 1996, 11, 336–342. [Google Scholar] [CrossRef]
- Kublin, E.; Breidenbach, J.; Kändler, G. A flexible stem taper and volume prediction method based on mixed-effects B-spline regression. Eur. J. For. Res. 2013, 132, 983–997. [Google Scholar] [CrossRef]
- Marchi, M.; Ferrara, C.; Bertini, G.; Fares, S.; Salvati, L. A sampling design strategy to reduce survey costs in forest monitoring. Ecol. Indic. 2017, 81, 182–191. [Google Scholar] [CrossRef]
- R Development Core Team. R: A language and environment for statistical computing. R Found. Stat. Comput. 2019. [Google Scholar]
- Miehle, P.; Battaglia, M.; Sands, P.J.; Forrester, D.I.; Feikema, P.M.; Livesley, S.J.; Morris, J.D.; Arndt, S.K. A comparison of four process-based models and a statistical regression model to predict growth of Eucalyptus globulus plantations. Ecol. Model. 2009, 220, 734–746. [Google Scholar] [CrossRef]
- Simpson, D.; Fagerli, H.; Hellsten, S.; Knulst, J.C.; Westling, O. Comparison of modelled and monitored deposition fluxes of sulphur and nitrogen to ICP-forest sites in Europe. Biogeosciences 2006, 3, 335–337. [Google Scholar] [CrossRef] [Green Version]
- Di Biase, R.M.; Fattorini, L.; Marchi, M. Statistical inferential techniques for approaching forest mapping. A review of methods. Ann. Silvic. Res. 2018, 42, 46–58. [Google Scholar]
- Marchi, M.; Chiavetta, U.; Castaldi, C.; Ducci, F. Does complex always mean powerful ? A comparison of eight methods for interpolation of climatic data in Mediterranean area. Ital. J. Agrometeorol. 2017, 1, 59–72. [Google Scholar]
- Wang, T.; Wang, G.; Innes, J.; Nitschke, C.; Kang, H. Climatic niche models and their consensus projections for future climates for four major forest tree species in the Asia-Pacific region. For. Ecol. Manag. 2016, 360, 357–366. [Google Scholar] [CrossRef]
- Dickson, M.M.; Giuliani, D.; Espa, G.; Bee, M.; Taufer, E.; Santi, F. Design-based estimation in environmental surveys with positional errors. Environ. Ecol. Stat. 2018, 25, 155–169. [Google Scholar] [CrossRef]
- Pagliarella, M.C.; Corona, P.; Fattorini, L. Spatially-balanced sampling versus unbalanced stratified sampling for assessing forest change: Evidences in favour of spatial balance. Environ. Ecol. Stat. 2018, 25, 111–123. [Google Scholar] [CrossRef]
- Pecchi, M.; Marchi, M.; Burton, V.; Giannetti, F.; Moriondo, M.; Bernetti, I.; Bindi, M.; Chirici, G. Species distribution modelling to support forest management. A literature review. Ecol. Model. 2019, 411, 108817. [Google Scholar] [CrossRef]
- Barbet-Massin, M.; Jiguet, F.; Albert, C.H.; Thuiller, W. Selecting pseudo-absences for species distribution models: How, where and how many? Methods Ecol. Evol. 2012, 3, 327–338. [Google Scholar] [CrossRef]
- Leroy, B.; Delsol, R.; Hugueny, B.; Meynard, C.N.; Barhoumi, C.; Barbet-Massin, M.; Bellard, C. Without quality presence–absence data, discrimination metrics such as TSS can be misleading measures of model performance. J. Biogeogr. 2018, 45, 1994–2002. [Google Scholar] [CrossRef]
- Marchetti, M.; Vizzarri, M.; Lasserre, B.; Sallustio, L.; Tavone, A. Natural capital and bioeconomy: Challenges and opportunities for forestry. Ann. Silvic. Res. 2014, 38, 62–73. [Google Scholar]
- Profft, I.; Mund, M.; Weber, G.-E.; Weller, E.; Schulze, E.-D. Forest management and carbon sequestration in wood products. Eur. J. For. Res. 2009, 128, 399–413. [Google Scholar] [CrossRef] [Green Version]
- Ray, D.; Petr, M.; Mullett, M.; Bathgate, S.; Marchi, M.; Beauchamp, K. A simulation-based approach to assess forest policy options under biotic and abiotic climate change impacts: A case study on Scotland’s National Forest Estate. For. Policy Econ. 2019, 103, 17–27. [Google Scholar] [CrossRef]
- Pacheco, A.; Camarero, J.J.; Ribas, M.; Gazol, A.; Gutierrez, E.; Carrer, M. Disentangling the climate-driven bimodal growth pattern in coastal and continental Mediterranean pine stands. Sci. Total Environ. 2018, 615, 1518–1526. [Google Scholar] [CrossRef]
| Relative Height Class | Mean Relative Diameter | Standard Deviation | CV | Number of Samples |
| 0.00–0.05 | 1.028 | 0.023 | 0.022 | 1 |
| 0.05–0.10 | 0.988 | 0.020 | 0.021 | 1 |
| 0.10–0.15 | 0.941 | 0.035 | 0.037 | 2 |
| 0.15–0.20 | 0.890 | 0.035 | 0.039 | 2 |
| 0.20–0.25 | 0.842 | 0.040 | 0.047 | 3 |
| 0.25–0.30 | 0.798 | 0.043 | 0.055 | 5 |
| 0.30–0.35 | 0.758 | 0.047 | 0.063 | 6 |
| 0.35–0.40 | 0.716 | 0.049 | 0.068 | 7 |
| 0.40–0.45 | 0.680 | 0.051 | 0.075 | 9 |
| 0.45–0.50 | 0.635 | 0.052 | 0.082 | 10 |
| 0.50–0.55 | 0.594 | 0.058 | 0.098 | 15 |
| 0.55–0.60 | 0.552 | 0.057 | 0.104 | 17 |
| 0.60–0.65 | 0.504 | 0.064 | 0.126 | 24 |
| 0.65–0.70 | 0.456 | 0.067 | 0.146 | 33 |
| 0.70–0.75 | 0.404 | 0.075 | 0.185 | 52 |
| 0.75–0.80 | 0.345 | 0.072 | 0.209 | 67 |
| 0.80–0.85 | 0.278 | 0.077 | 0.277 | 118 |
| 0.85–0.90 | 0.194 | 0.070 | 0.363 | 207 |
| 0.90–0.95 | 0.105 | 0.056 | 0.536 | 441 |
| 0.95–1.00 | 0.017 | 0.030 | 1.783 | 4885 |
| Iteration | DF | t | Number of Samples to Be Measured | |
| 1 | 79 | 1.9905 | 206 | |
| 2 | 205 | 1.9716 | 202 | |
| 3 | 201 | 1.9718 | 202 | |
| Model | Mean Relative Absolute Error | Explained Variance |
|---|---|---|
| Linear | 0.03273 (±0.96 × 10–3) | 96.1% (±0.60 × 10–3) |
| Second order polynomial | 0.03195 (±0.85 × 10–3) | 97.1% (±0.55 × 10–3) |
| Third order polynomial | 0.01362 (±0.83 × 10–3) | 97.4% (±0.49 × 10–3) |
| GAM | 0.01254 (±0.84 × 10–3) | 97.5% (±0.50 × 10–3) |
| Coefficient | Estimate | Standard Error | t value | Pr(>|t|) | |
|---|---|---|---|---|---|
| α | 0.590 | 0.00072 | 817.57 | < 2.2 × 10−16 | *** |
| β | −1.265 | 0.03827 | −25.92 | < 2.2 × 10−16 | *** |
| γ | −2.075 | 0.04882 | −42.50 | < 2.2 × 10−16 | *** |
| δ | −20.44 | 0.02213 | −418.71 | < 2.2 × 10−16 | *** |
| p-value: < 2.2 × 10−16 - R-squared: 0.9749 - Residuals Standard error: 0.04882 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marchi, M.; Scotti, R.; Rinaldini, G.; Cantiani, P. Taper Function for Pinus nigra in Central Italy: Is a More Complex Computational System Required? Forests 2020, 11, 405. https://doi.org/10.3390/f11040405
Marchi M, Scotti R, Rinaldini G, Cantiani P. Taper Function for Pinus nigra in Central Italy: Is a More Complex Computational System Required? Forests. 2020; 11(4):405. https://doi.org/10.3390/f11040405
Chicago/Turabian StyleMarchi, Maurizio, Roberto Scotti, Giulia Rinaldini, and Paolo Cantiani. 2020. "Taper Function for Pinus nigra in Central Italy: Is a More Complex Computational System Required?" Forests 11, no. 4: 405. https://doi.org/10.3390/f11040405
APA StyleMarchi, M., Scotti, R., Rinaldini, G., & Cantiani, P. (2020). Taper Function for Pinus nigra in Central Italy: Is a More Complex Computational System Required? Forests, 11(4), 405. https://doi.org/10.3390/f11040405






