Monitoring Broadscale Vegetational Diversity and Change across North American Landscapes Using Land Surface Phenology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Polar Coordinate Transformation and Phenology Metrics
2.3. Dimensional Reduction and Phenological Classification
3. Results and Discussion
3.1. Phenology Metrics
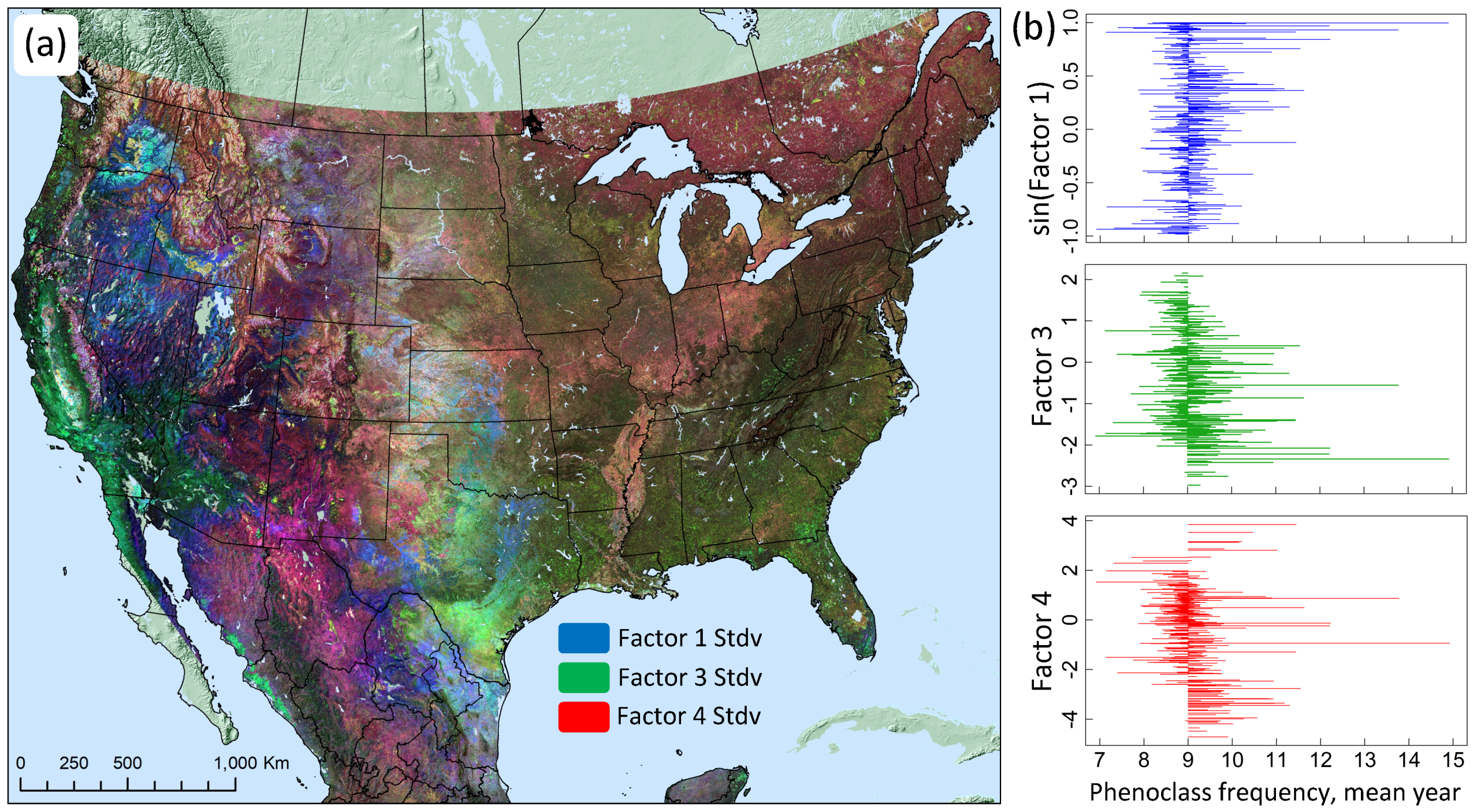
3.2. Dimensional Reduction
3.3. Phenological Classification
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Morisette, J.T.; Richardson, A.D.; Knapp, A.K.; Fisher, J.I.; Graham, E.A.; Abatzoglou, J.; Wilson, B.E.; Breshears, D.D.; Henebry, G.M.; Hanes, J.M. Tracking the rhythm of the seasons in the face of global change: Phenological research in the 21st century. Front. Ecol. Environ. 2009, 7, 253–260. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.; Schwartz, M.D.; Fei, S. Validating satellite phenology through intensive ground observation and landscape scaling in a mixed seasonal forest. Remote Sens. Environ. 2011, 115, 143–157. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Dash, J.; Atkinson, P.M. Intercomparison of satellite sensor land surface phenology and ground phenology in Europe. Geophys. Res. Lett. 2015, 42, 2253–2260. [Google Scholar] [CrossRef] [Green Version]
- Hargrove, W.W.; Spruce, J.P.; Gasser, G.E.; Hoffman, F.M. Toward a national early warning system for forest disturbances using remotely sensed canopy phenology. Photogramm. Eng. Remote Sens. 2009, 75, 1150–1156. [Google Scholar]
- Kennedy, R.E.; Townsend, P.A.; Gross, J.E.; Cohen, W.B.; Bolstad, P.; Wang, Y.Q.; Adams, P. Remote sensing change detection tools for natural resource managers: Understanding concepts and tradeoffs in the design of landscape monitoring projects. Remote Sens. Environ. 2009, 113, 1382–1396. [Google Scholar] [CrossRef]
- Cleland, E.E.; Chuine, I.; Menzel, A.; Mooney, H.A.; Schwartz, M.D. Shifting plant phenology in response to global change. Trends Ecol. Evol. 2007, 22, 357–365. [Google Scholar] [CrossRef]
- Polgar, C.A.; Primack, R.B. Leaf-out phenology of temperate woody plants: From trees to ecosystems. New Phytol. 2011, 191, 926–941. [Google Scholar] [CrossRef]
- Norman, S.P.; Hargrove, W.W.; Christie, W.M. Spring and autumn phenological variability across environmental gradients of Great Smoky Mountains National Park, USA. Remote Sens. 2017, 9, 407. [Google Scholar] [CrossRef] [Green Version]
- Van Leeuwen, J.D.W. Monitoring the Effects of Forest Restoration Treatments on Post-Fire Vegetation Recovery with MODIS Multitemporal Data. Sensors 2008, 8, 2017–2042. [Google Scholar] [CrossRef] [Green Version]
- Kleynhans, W.; Olivier, J.C.; Wessels, K.J.; Salmon, B.P.; van den Bergh, F.; Steenkamp, K. Detecting Land Cover Change Using an Extended Kalman Filter on MODIS NDVI Time-Series Data. IEEE Geosci. Remote Sens. Lett. 2011, 8, 507–511. [Google Scholar] [CrossRef] [Green Version]
- De Beurs, K.M.; Townsend, P.A. Estimating the effect of gypsy moth defoliation using MODIS. Remote Sens. Environ. 2008, 112, 3983–3990. [Google Scholar] [CrossRef]
- Hicke, J.A.; Allen, C.D.; Desai, A.R.; Dietze, M.C.; Hall, R.J.; Hogg, E.H.; Kashian, D.M.; Moore, D.; Raffa, K.F.; Sturrock, R.N.; et al. Effects of biotic disturbances on forest carbon cycling in the United States and Canada, Global Change Biology. Glob. Chang. Biol. 2012, 18, 7–34. [Google Scholar] [CrossRef]
- Spruce, J.P.; Hicke, J.A.; Hargrove, W.W.; Grulke, N.E.; Meddens, A.J.H. Use of MODIS NDVI Products to Map Tree Mortality Levels in Forests Affected by Mountain Pine Beetle Outbreaks. Forests 2019, 10, 811. [Google Scholar] [CrossRef] [Green Version]
- Van Mantgem, P.J.; Stephenson, N.L.; Byrne, J.C.; Daniels, L.D.; Franklin, J.F.; Fule, P.Z.; Harmon, M.E.; Larson, A.J.; Smith, J.M.; Taylor, A.H.; et al. Widespread Increase of Tree Mortality Rates in the Western United States. Science 2009, 323, 521–524. [Google Scholar] [CrossRef] [Green Version]
- White, M.A.; Hoffman, F.M.; Hargrove, W.W.; Nemani, R.R. A global framework for monitoring phenological responses to climate change. Geophys. Res. Lett. 2005, 32, 4. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Brown, J.F.; Miura, T.; Van Leeuwen, W.J.D.; Reed, B.C. Phenological Classification of the United States: A Geographic Framework for Extending Multi-Sensor Time-Series Data. Remote Sens. 2010, 2, 526–544. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Hepner, G.F.; Dennison, P.E. Delineation of Phenoregions in Geographically Diverse Regions Using k-means++ Clustering: A Case Study in the Upper Colorado River Basin. Gisci. Remote Sens. 2012, 49, 163–181. [Google Scholar] [CrossRef]
- Kumar, J.; Mills, R.T.; Hoffman, F.M.; Hargrove, W.W. Parallel k-Means Clustering for Quantitative Ecoregion Delineation Using Large Data Sets. Procedia Comput. Sci. 2011, 4, 1602–1611. [Google Scholar] [CrossRef] [Green Version]
- Mills, R.T.; Kumar, J.; Hoffman, F.M.; Hargrove, W.W.; Spruce, J.P.; Norman, S.P. Identification and Visualization of Dominant Patterns and Anomalies in Remotely Sensed Vegetation Phenology Using a Parallel Tool for Principal Components Analysis. Procedia Comput. Sci. 2013, 18, 2396–2405. [Google Scholar] [CrossRef] [Green Version]
- Bolton, D.K.; Gray, J.M.; Melaas, E.K.; Moon, M.; Eklundh, L.; Friedl, M.A. Continental-scale land surface phenology from harmonized Landsat 8 and Sentinel-2 imagery. Remote Sens. Environ. 2020, 240. [Google Scholar] [CrossRef]
- Morellato, L.P.C.; Alberti, L.F.; Hudson, I.L. Applications of Circular Statistics in Plant Phenology: A Case Studies Approach. In Phenological Research: Methods for Environmental and Climate Change Analysis; Hudson, I.L., Keatley, M.R., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 339–359. [Google Scholar] [CrossRef]
- Brooks, B.J.; Lee, D.C.; Pomara, L.Y.; Hargrove, W.W.; Desai, A.R. Quantifying Seasonal Patterns in Disparate Environmental Variables Using the PolarMetrics R Package. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 296–302. [Google Scholar] [CrossRef]
- Spruce, J.P.; Gasser, G.E.; Hargrove, W.W. MODIS NDVI Data, Smoothed and Gap-Filled, for the Conterminous US: 2000–2015; ORNL DAAC: Oak Ridge, TN, USA, 2016. [Google Scholar] [CrossRef]
- Prados, D.; Ryan, R.E.; Ross, K.W. Remote Sensing Time Series Product Tool. In Proceedings of the American Geophysical Union, Fall Meeting 2006, San Francisco, CA, USA, 11–15 December 2006. abstract id. IN33B-1341. [Google Scholar]
- McKellip, R.D.; Spruce, J.P.; Smoot, J.C.; Gasser, G.E.; Ryan, R.E.; Holekamp, K.; Ross, K. Time Series Product Tool (TSPT) Version 2.0. Available online: https://www.techbriefs.com/component/content/article/ntb/tech-briefs/information-sciences/20965 (accessed on 5 April 2020).
- McKellip, R.D.; Ross, K.W.; Spruce, J.P.; Smoot, J.C.; Ryan, R.E.; Gasser, G.E.; Prados, D.L.; Vaughan, R.D. Phenological Parameters Estimation Tool. Available online: https://www.techbriefs.com/component/content/article/ntb/tech-briefs/software/8481 (accessed on 5 April 2020).
- Burgan, R.; Hardy, C.; Ohlen, D.; Fosnight, G.; Treder, R. Ground sample data for the Conterminous U.S. Land Cover Characteristics Database; General Technical Report RMRS-GTR-41; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 1999; Volume 13. [Google Scholar] [CrossRef]
- Melendez-Pastor, I.; Navarro-Pedreno, J.; Koch, M.; Gomez, I.; Hernandez, E.I. Land-Cover Phenologies and Their Relation to Climatic Variables in an Anthropogenically Impacted Mediterranean Coastal Area. Remote Sens. 2010, 2, 2072–4292. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org (accessed on 26 May 2020).
- Sokal, R.R. The Principles and Practice of Numerical Taxonomy. Taxon 1963, 12, 190–199. [Google Scholar] [CrossRef]
- Hartigan, J.A. Clustering Algorithms, 99th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1975; ISBN 047135645X. [Google Scholar]
- Forgy, E. Cluster Analysis of Multivariate Data: Efficiency versus Interpretability of Classifications. Biometrics 1965, 21, 768–780. [Google Scholar]
- MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Mills, R.T.; Hoffman, F.M.; Kumar, J.; Hargrove, W.W. Cluster Analysis-Based Approaches for Geospatiotemporal Data Mining of Massive Data Sets for Identification of Forest Threats. Procedia Comput. Sci. 2011, 4, 1612–1621. [Google Scholar] [CrossRef] [Green Version]
- SAS Institute Inc. SAS/STAT® 14.2 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2016. [Google Scholar]





| Type | Variable Name | Descriptive Name | Units | Polar Description |
|---|---|---|---|---|
| Timing Variables | GSbegin | Beginning of growing season | Days | Number of days (or radial angle) corresponding to 15% of cumulative annual NDVI |
| GSmid_early | Middle of early growing season | Days | Number of days (or radial angle) corresponding to 32.5% of cumulative annual NDVI | |
| GSmid | Middle of entire growing season | Days | Number of days (or radial angle) corresponding to 50% of cumulative annual NDVI | |
| GSmid_late | Middle of late growing season | Days | Number of days (or radial angle) corresponding to 65% of cumulative annual NDVI | |
| GSend | End of growing season | Days | Number of days (or radial angle) corresponding to 80% of cumulative annual NDVI | |
| Greenness & Seasonality Variables | LOS | Length of growing season | Days | Number of days between early and late growing season thresholds |
| mean_NDVI_grw | Average growing season greenness | NDVI | Average NDVI during the growing season (GSbegin to GSend) | |
| std_NDVI_grw | Variability in growing season greenness | NDVI | Standard deviation of NDVI during the growing season | |
| AVearly | Magnitude of early growing season seasonality | NDVI | Length of the average vector during early growing season (GSbegin to GSmid) | |
| AVgrw | Magnitude of entire growing season seasonality | NDVI | Length of the average vector during entire growing season (GSbegin to GSend) | |
| AVlate | Magnitude of late growing season seasonality | NDVI | Length of the average vector during late growing season (GSmid to GSend) | |
| Theta (Offset) 1 | Offset between calendar year and start of phenological year | Days | Number of days between the beginning of the calendar year (1 January) and the start of the phenological year (defined by when the average minimum in NDVI occurs) |
| Factor 1 | Factor 2 | Factor 3 | Factor 4 | ||
|---|---|---|---|---|---|
| Timing Variables | GSbegin sin | −0.892 | 0.311 | 0.244 | |
| GSbegin cos | 0.283 | 0.911 | |||
| GSmid_early sin | 0.959 | ||||
| GSmid_eary cos | 0.927 | −0.245 | 0.202 | ||
| GSmid sin | 0.675 | 0.702 | |||
| GSmid cos | 0.672 | −0.662 | 0.241 | ||
| GSmid_late sin | 0.936 | −0.231 | 0.215 | ||
| GSmid_late cos | −0.939 | 0.304 | |||
| GSend sin | 0.568 | −0.689 | 0.392 | ||
| GSend cos | −0.764 | −0.579 | |||
| Greenness & Seasonality Variables | LOS | 0.898 | |||
| mean_NDVI_grw | −0.209 | 0.964 | |||
| std_NDVI_grw | 0.321 | −0.836 | |||
| AVearly | 0.960 | ||||
| AVgrw | −0.247 | 0.838 | −0.457 | ||
| AVlate | −0.274 | 0.859 | −0.367 | ||
| Factor 1 | Factor 2 | Factor 3 | Factor 4 | ||
| Proportional Variance | 0.294 | 0.282 | 0.231 | 0.145 | |
| Cumulative Variance | 0.294 | 0.576 | 0.807 | 0.953 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brooks, B.-G.J.; Lee, D.C.; Pomara, L.Y.; Hargrove, W.W. Monitoring Broadscale Vegetational Diversity and Change across North American Landscapes Using Land Surface Phenology. Forests 2020, 11, 606. https://doi.org/10.3390/f11060606
Brooks B-GJ, Lee DC, Pomara LY, Hargrove WW. Monitoring Broadscale Vegetational Diversity and Change across North American Landscapes Using Land Surface Phenology. Forests. 2020; 11(6):606. https://doi.org/10.3390/f11060606
Chicago/Turabian StyleBrooks, Bjorn-Gustaf J., Danny C. Lee, Lars Y. Pomara, and William W. Hargrove. 2020. "Monitoring Broadscale Vegetational Diversity and Change across North American Landscapes Using Land Surface Phenology" Forests 11, no. 6: 606. https://doi.org/10.3390/f11060606
APA StyleBrooks, B.-G. J., Lee, D. C., Pomara, L. Y., & Hargrove, W. W. (2020). Monitoring Broadscale Vegetational Diversity and Change across North American Landscapes Using Land Surface Phenology. Forests, 11(6), 606. https://doi.org/10.3390/f11060606






