The Effects of Combining the Variables in Allometric Biomass Models on Biomass Estimates over Large Forest Areas: A European Beech Case Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Calibration Datasets
2.1.2. Inventory Dataset
2.2. Data Analysis
2.2.1. Fitting Allometric Models to Calibration Datasets
- (a)
- separate variable model (Equation (1));
- (b)
- combined variable model (Equation (2)).
2.2.2. Prediction of Biomass
- (a)
- the separate variable model:where , , and are the parameter estimates of Equation (1) fitted to Datasets Q1–Q5; is the diameter at breast height of the ith tree from the jth plot in the inventory dataset; is the height of the ith tree from the jth plot in the inventory dataset; RSE1 is the residual standard error of Equation (1) that was used to calculate the back transformation correction factor [23].
- (b)
- the combined variable model:where and are the parameter estimates of Equation (2); is the combined predictor variable for the ith tree in the jth plot in the inventory dataset (it was calculated by multiplication of squared D with H); RSE2 is the residual standard error of Equation (2); exp(RSE22/2) is the correction factor [23].
2.3. Data Processing
3. Results
3.1. The Effects at the Level of Large Forest Area Estimates
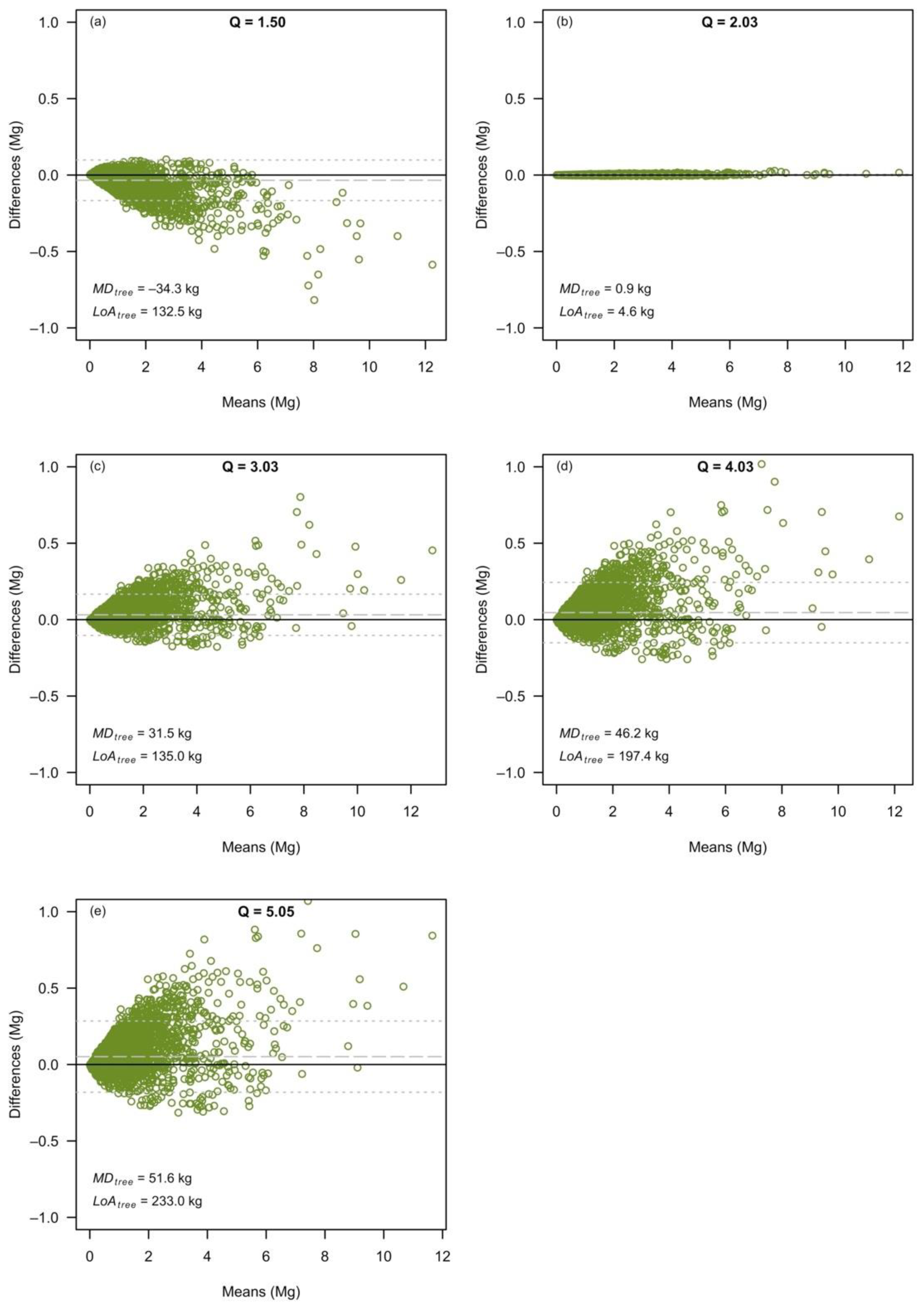
3.2. The Effects at the Level of Individual Tree Predictions
3.3. The Effects at the Level of Plot Estimates
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Dataset | Q-Ratio | Separate Variable model (Equation (1)) | Combined Variable Model (Equation (2)) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Q1 | 1.50 | −3.808 (0.287) | 1.850 (0.083) | 1.231 (0.169) | 0.212 | 0.978 | −3.437 (0.139) | 0.982 (0.015) | 0.214 | 0.977 |
| Q2 | 2.03 | −3.409 (0.257) | 1.966 (0.077) | 0.970 (0.149) | 0.223 | 0.977 | −3.425 (0.139) | 0.980 (0.015) | 0.222 | 0.978 |
| Q3 | 3.03 | −3.068 (0.179) | 2.127 (0.059) | 0.702 (0.106) | 0.172 | 0.986 | −3.452 (0.113) | 0.990 (0.012) | 0.177 | 0.986 |
| Q4 | 4.03 | −2.804 (0.207) | 2.187 (0.068) | 0.543 (0.126) | 0.190 | 0.983 | −3.394 (0.127) | 0.982 (0.014) | 0.200 | 0.981 |
| Q5 | 5.05 | −2.515 (0.186) | 2.204 (0.057) | 0.436 (0.107) | 0.159 | 0.987 | −3.282 (0.118) | 0.971 (0.012) | 0.174 | 0.984 |
References
- Yanai, R.D.; Wayson, C.; Lee, D.; Espejo, A.B.; Campbell, J.L.; Green, M.B.; Zukswert, J.M.; Yoffe, S.B.; Aukema, J.E.; Lister, A.J.; et al. Improving uncertainty in forest carbon accounting for REDD+ mitigation efforts. Environ. Res. Lett. 2020, 15, 124002. [Google Scholar] [CrossRef]
- Xu, L.; Saatchi, S.S.; Yang, Y.; Yu, Y.; Pongratz, J.; Bloom, A.A.; Bowman, K.; Worden, J.; Liu, J.; Yin, Y.; et al. Changes in global terrestrial live biomass over the 21st century. Sci. Adv. 2021, 7, eabe9829. [Google Scholar] [CrossRef]
- Brown, S. Measuring carbon in forests: Current status and future challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
- Grassi, G.; House, J.; Dentener, F.; Federici, S.; den Elzen, M.; Penman, J. The key role of forests in meeting climate targets requires science for credible mitigation. Nat. Clim. Chang. 2017, 7, 220–226. [Google Scholar] [CrossRef]
- Nabuurs, G.-J.; Lindner, M.; Verkerk, P.J.; Gunia, K.; Deda, P.; Michalak, R.; Grassi, G. First signs of carbon sink saturation in European forest biomass. Nat. Clim. Chang. 2013, 3, 792–796. [Google Scholar] [CrossRef]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
- Stephenson, N.L.; Das, A.J.; Condit, R.; Russo, S.E.; Baker, P.J.; Beckman, N.G.; Coomes, D.A.; Lines, E.R.; Morris, W.K.; Rüger, N.; et al. Rate of tree carbon accumulation increases continuously with tree size. Nature 2014, 507, 90–93. [Google Scholar] [CrossRef] [PubMed]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and Stem Volume Equations for Tree Species in Europe; Finnish Society of Forest Science, Finnish Forest Research Institute: Helsinki, Finland, 2005. [Google Scholar]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci. 2003, 49, 12–35. [Google Scholar]
- McRoberts, R.E.; Moser, P.; Zimermann Oliveira, L.; Vibrans, A.C. A general method for assessing the effects of uncertainty in individual-tree volume model predictions on large-area volume estimates with a subtropical forest illustration. Can. J. For. Res. 2015, 45, 44–51. [Google Scholar] [CrossRef]
- Rutishauser, E.; Noor’an, F.; Laumonier, Y.; Halperin, J.; Rufi’ie; Hergoualch, K.; Verchot, L. Generic allometric models including height best estimate forest biomass and carbon stocks in Indonesia. For. Ecol. Manag. 2013, 307, 219–225. [Google Scholar] [CrossRef]
- Dutcă, I.; Mather, R.; Blujdea, V.N.; Ioraș, F.; Olari, M.; Abrudan, I.V. Site-effects on biomass allometric models for early growth plantations of Norway spruce (Picea abies (L.) Karst.). Biomass Bioenergy 2018, 116, 8–17. [Google Scholar] [CrossRef]
- Dutcă, I. The Variation Driven by Differences between Species and between Sites in Allometric Biomass Models. Forests 2019, 10, 976. [Google Scholar] [CrossRef] [Green Version]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.C.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C.; et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Chang. Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef] [PubMed]
- Ducey, M.J. Evergreenness and wood density predict height–diameter scaling in trees of the northeastern United States. For. Ecol. Manag. 2012, 279, 21–26. [Google Scholar] [CrossRef]
- Vizcaíno-Palomar, N.; Ibáñez, I.; Benito-Garzón, M.; González-Martínez, S.C.; Zavala, M.A.; Alía, R. Climate and population origin shape pine tree height-diameter allometry. New For. 2017, 48, 363–379. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Dutcă, I.; McRoberts, R.E.; Næsset, E.; Blujdea, V.N.B. A practical measure for determining if diameter (D) and height (H) should be combined into D2H in allometric biomass models. For. Int. J. For. Res. 2019, 92, 627–634. [Google Scholar] [CrossRef] [Green Version]
- Schepaschenko, D.; Shvidenko, A.; Usoltsev, V.; Lakyda, P.; Luo, Y.; Vasylyshyn, R.; Lakyda, I.; Myklush, Y.; See, L.; McCallum, I.; et al. A dataset of forest biomass structure for Eurasia. Sci. Data 2017, 4, 170070. [Google Scholar] [CrossRef]
- Bouriaud, O.; Don, A.; Janssens, I.A.; Marin, G.; Schulze, E.-D. Effects of forest management on biomass stocks in Romanian beech forests. For. Ecosyst. 2019, 6, 19. [Google Scholar] [CrossRef] [Green Version]
- Marin, G.; Strimbu, V.C.; Abrudan, I.V.; Strimbu, B.M. Regional variability of the Romanian main tree species growth using national forest inventory increment cores. Forests 2020, 11, 409. [Google Scholar] [CrossRef] [Green Version]
- Bouriaud, O.; Marin, G.; Hervé, J.-C.; Riedel, T.; Lanz, A. Estimation Methods in the Romanian National Forest Inventory; Nova Science Publishers, Inc.: Haupauge, NY, USA, 2020. [Google Scholar]
- Baskerville, G.L. Use of Logarithmic Regression in the Estimation of Plant Biomass. Can. J. For. Res. 1972, 2, 49–53. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Westfall, J.A. Effects of Uncertainty in Model Predictions of Individual Tree Volume on Large Area Volume Estimates. For. Sci. 2014, 60, 34–42. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Domke, G.M.; Ståhl, G.; Saarela, S.; Westfall, J.A. Hybrid estimators for mean aboveground carbon per unit area. For. Ecol. Manag. 2016, 378, 44–56. [Google Scholar] [CrossRef]
- Cochran, W. Sampling Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Särndal, C.-E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer Series in Statistics: New York, NY, USA, 1992. [Google Scholar]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Wallenius, T.; Laamanen, R.; Peuhkurinen, J.; Mehtätalo, L.; Kangas, A. Analysing the agreement between an airborne laser scanning based forest inventory and a control inventory-a case study in the state owned forests in Finland. Silva Fenn. 2012, 46, 111–129. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- RStudio Team. RStudio: Integrated Development for R; RStudio, Inc.: Boston, MA, USA, 2016. [Google Scholar]
- Dutcă, I.; Mather, R.; Ioraș, F. Sampling trees to develop allometric biomass models: How does tree selection affect model prediction accuracy and precision? Ecol. Indic. 2020, 117, 106553. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, X.; Ouyang, Z.; Lu, F.; Feng, L.; Tao, J. A review of biomass equations for China’s tree species. Earth Syst. Sci. Data 2020, 12, 21–40. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Xu, W.; Tang, Z.; Xie, Z. A biomass equation dataset for common shrub species in China. Earth Syst. Sci. Data 2020, 12, 21–40. [Google Scholar]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
- Picard, N.; Boyemba Bosela, F.; Rossi, V. Reducing the error in biomass estimates strongly depends on model selection. Ann. For. Sci. 2015, 72, 811–823. [Google Scholar] [CrossRef] [Green Version]
- Canadell, J.G.; Raupach, M.R. Managing forests for climate change mitigation. Science 2008, 320, 1456–1457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ziegler, A.D.; Phelps, J.; Yuen, J.Q.; Webb, E.L.; Lawrence, D.; Fox, J.M.; Bruun, T.B.; Leisz, S.J.; Ryan, C.M.; Dressler, W.; et al. Carbon outcomes of major land-cover transitions in SE Asia: Great uncertainties and REDD+ policy implications. Glob. Chang. Biol. 2012, 18, 3087–3099. [Google Scholar] [CrossRef] [PubMed]

| Dataset Name | Q-Ratio | Sample Size | D-Range (cm) | H-Range (m) | AGB-Range (kg) |
|---|---|---|---|---|---|
| Q1 | 1.50 | 100 | 5.6–60.1 | 7.91–35.80 | 8.3–3456.6 |
| Q2 | 2.03 | 100 | 5.6–86.3 | 8.54–40.30 | 8.3–8447.1 |
| Q3 | 3.03 | 100 | 6.1–86.3 | 8.20–40.30 | 10.1–8447.1 |
| Q4 | 4.03 | 100 | 6.0–86.3 | 5.64–40.30 | 11.3–8447.1 |
| Q5 | 5.05 | 100 | 6.2–86.3 | 9.39–40.30 | 11.4–8447.1 |
| Dataset | Q-Ratio | SE | |||||
|---|---|---|---|---|---|---|---|
| Relative Difference (%) | Relative Difference (%) | ||||||
| Q1 | 1.50 | 289.30 | 278.09 | –3.9 | 10.54 | 9.91 | –6.0 |
| Q2 | 2.03 | 276.71 | 277.00 | 0.1 | 9.84 | 9.86 | 0.2 |
| Q3 | 3.03 | 287.03 | 297.63 | 3.7 | 10.08 | 10.66 | 5.8 |
| Q4 | 4.03 | 274.99 | 290.44 | 5.6 | 9.50 | 10.35 | 9.0 |
| Q5 | 5.05 | 270.28 | 287.34 | 6.3 | 9.19 | 10.18 | 10.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osewe, E.O.; Dutcă, I. The Effects of Combining the Variables in Allometric Biomass Models on Biomass Estimates over Large Forest Areas: A European Beech Case Study. Forests 2021, 12, 1428. https://doi.org/10.3390/f12101428
Osewe EO, Dutcă I. The Effects of Combining the Variables in Allometric Biomass Models on Biomass Estimates over Large Forest Areas: A European Beech Case Study. Forests. 2021; 12(10):1428. https://doi.org/10.3390/f12101428
Chicago/Turabian StyleOsewe, Erick O., and Ioan Dutcă. 2021. "The Effects of Combining the Variables in Allometric Biomass Models on Biomass Estimates over Large Forest Areas: A European Beech Case Study" Forests 12, no. 10: 1428. https://doi.org/10.3390/f12101428
APA StyleOsewe, E. O., & Dutcă, I. (2021). The Effects of Combining the Variables in Allometric Biomass Models on Biomass Estimates over Large Forest Areas: A European Beech Case Study. Forests, 12(10), 1428. https://doi.org/10.3390/f12101428






