Genetic Parameters of Stem and Wood Traits in Full-Sib Silver Birch Families

Abstract

This study investigated heritability of stem and wood traits to improve Swedish silver birch (Betula pendula Roth.) through breeding. Birch is 12% of Sweden’s forest area but mainly used for low value pulp or firewood. This paper applied non-destructive test (NDT) methods, and estimated traits’ heritability (h²), to help breed birch for high value solid wood products. Two trials of 22 families were assessed at age 19 for stem diameter (DBH), stem straightness, rough brown bark height (BH), grain angle (GA), Pilodyn penetration depth (Pilo) and acoustic velocity (AV). X-ray densitometry was performed on a subsample of radial cores taken at 1.3 m from the ground to get an average benchmark density. The h² values were moderate for GA (0.20 and 0.21) and Pilo (0.53 and 0.48) at the two sites, but the h² values for AV were low (0.05 and 0.30). There were moderate genotypic correlations between BH and DBH (0.51–0.54). There were low genotypic and phenotypic correlations between NDT measurements and other traits so including NDT in birch breeding efforts should not inadvertently reduce size, stem or wood quality. The high genetic correlations between sites suggest that GA, Pilo and AV values were determined more by genotype than by environment.

1. Introduction

Over 12% of Sweden’s productive forest volume is composed of birch (Betula spp.) [1]. The majority of harvested birch is used for pulp [2] or firewood production as it is considered to be low quality. The volume of high quality wood is presumably insufficient to sustainably supply a domestic wood products industry. Birch regularly occurs in forests managed for Norway spruce or Scots pine production [3] where there is limited interest in managing birch for high quality wood. These birches are scattered in pure or mixed softwood stands and naturally regenerated from unimproved material, especially during early succession stages, such as after clear-cutting or storm damage [3,4]. The current recommendations are to plant improved material and adopt specialized silvicultural practices to produce high-quality birch wood and increase the value of Sweden’s birch stands.

The two main species of birch in Swedish forests are silver birch (B. pendula Roth.) and downy birch (B. pubescens Ehrh.), and are commonly treated as a single species for inventory and harvest [1]. Of these two species, downy birch is able to grow on compact or wet sites, while silver birch requires relatively fertile sites with appropriate levels of water for vigorous growth [5,6]. Silver birch has been found to have higher volume production [7], straighter form [8], and higher wood density [9]. Therefore, silver birch is of interest to the Swedish tree breeding program. The breeding program for silver birch started in the 1980s with the main intention to improve volume production, and then to improve stem form traits, e.g., straightness, and branch properties [10,11]. Currently, the genetic gain in volume production per hectare is about 12–15%, with significant improvement of stem form traits.

The selection of superior genotypes in the birch breeding program occurs in the first quarter of a full rotation, which is usually 40 years long. Few studies wait until a stand is mature to assess trial performance [12], especially as size and growth rate can be measured in young stands. Height and diameter can be the selection criteria when the breeding objective is to improve volume growth [13]. Wood quality traits important for sawn lumber production have not been considered in the birch breeding program, apart from single studies regarding wood density and fiber traits important for pulp production [10,14]. A minor genotypic correlation was observed by Stener and Hedenberg [10] between diameter and density for silver birch. Unfavorable genotypic correlations like this have necessitated the inclusion of multiple selection traits in some conifer breeding programs [15,16,17]. Faster growth rates have also been found to reduce birch strength [18] and wood density [19,20] in unimproved material.

Birch breeding programs have previously not included solid wood traits due to labor intensive measurements, limited resources, the requirement for destructive assessment methods [10,21], and a preference for selection at young ages [22]. Modern non-destructive testing (NDT) tools have been commonly used to measure density [23,24,25,26,27] stiffness [27,28,29,30], and grain angle [31,32] in coniferous and Eucalyptus species, yet are seldom applied to birch. These NDT tools are convenient for the measurement of genetic field trials [33] as measurements can occur at early ages, accelerating breeding cycles without felling the trees [22,34,35]. These tools also tend to be rapid and easy to use [36,37,38] compared to lab based methods allowing for larger sample size, and in some cases save time and money.

Wood density is frequently used as a key predictor of lumber strength and stability [36,39]. Wood density and wood hardness in silver birch have been found to be strongly correlated [9]. Wood hardness can be rapidly and non-distractively assessed with the Pilodyn densitometer [40,41] and the measurement value indicates wood density [40]. The depth of Pilodyn penetration (Pilo) has been found to be heritable for Eucalyptus spp. [42,43], coniferous species [25,27] and Betula spp. [41]. Estimates of heritability are population specific and vary by site, so need to be assessed separately for each trial of interest. Heritability estimates for density tend to be higher than for size or stem quality traits, and generally above 0.3 [44], showing there is the potential to improve birch wood density through breeding. There are numerous studies comparing the ability of NDT tools to assess wood density [36,39,45], and densitometry is commonly mentioned as a rapid and accurate contemporary method to gather detailed information on radial density variation. Although a single density value per stem is often sufficient to compare stands or families [19,46], densitometry allows researchers to rapidly obtain high resolution density data [47].

Grain angle (GA), or the “slope of grain”, is known to cause sawn lumber deformation during drying [48] and negatively influence wood strength [49,50]. The angle can be positive or negative depending on the alignment of the cells to the stem axis or along a piece of wood, where more extreme values are worse. GA can be assessed on standing trees by applying the scribe method on a large bark window [51], using a wedge grain angle gauge [52,53], or with laboratory based methods on core samples [38,54]. Heritability of grain angle can vary dramatically, from 0.0 to 1.0 between two species of Eucalyptus [43].

Stiffness, as described by the modulus of elasticity (MOE), can also have an impact on sawing and drying so it is an important wood quality trait for lumber producers [55]. Measuring acoustic velocity (AV) in the tree stem has been used for MOE prediction in conifers, and is correlated with lumber strength [56,57,58]. AV may also be related to GA [59] and seems to be correlated with the angle of the cellulose microfibrals (MFA) in the S2 layer of the cell wall [60,61]. Time-of-flight (ToF) tools are common forestry field tools, which can be used to test standing tree AV [58,61]. Measurements of resonance-based AV on logs and solid timber are strongly correlated with ToF measurements [62,63], and fairly well correlated with bending strength [37]. For Eucalyptus spp. there have been a wide range of heritability values for AV; from 0.16 to 0.74 [28] for E. nitens, 0.20 for E. pilularis [43] and 0.62 for E. dunnii [43].

The aim of this study was to investigate phenotypic and genetic variation in growth and wood properties in two clonal experiments at the mid-harvest age, established with clones from 22 full-sib silver birch families produced in the Swedish birch breeding program. Relationships between birch growth traits, external quality traits, and wood properties measured with NDT, were studied to find if an external trait were highly correlated with wood properties, and could then be used in the breeding program as selection criteria. Wood density was estimated by means of indirect and direct methods to determine if birch wood density can be measured indirectly by means of the Pilodyn. The hypothesis tested were that there is no relationship between average family diameter and wood density, i.e., selection for diameter is not decreasing biomass production, and that there is a strong relationship between Pilodyn measurements and wood densities determined from cores. Determining if NDT values are heritable, and that there is sufficient variation in values, was also a key objective in this study, as this relates to the hypothesis that wood quality traits can be included in the birch breeding programs.

2. Materials and Methods

The material used for this study was collected in two clonal trials with silver birch located in Hyssna (57°29′40″ N, 12°33′55″ E) and Brunsberg (61°28′45″ N, 13°92′77″ E), south to mid Sweden (Figure 1). Hyssna is generally considered to be the superior site for growth as average monthly temperatures range from −4 to 21 °C and the average monthly rainfall varies from 39 to 80 mm. Brunsberg has a slightly shorter growing season, average monthly temperatures ranging from −8 to 22 °C, and the average monthly rainfall fluctuates between 19 and 82 mm [64]. Both trials were fenced before planting to eliminate browsing. Both trials were planted in a 2 × 2 m spacing in spring 1999 with one-year old material. The experimental design was a single-tree plot design where each tree is randomly assigned to a planting spot. Each tree’s ID code, genotype and parent information was then associated with its location: tree number within row, row number within block, and block number. Not all genotypes were present in each block due to the incomplete blocking design. There was a buffer zone surrounding the trial. A total of 3534 and 2479 trees were planted in Hyssna and Brunsberg, respectively.

The planted material included clones from 22-full-sib families produced by crossing trees in the Swedish elite birch population. The elite population contains the 20 “best birch” clones for a deployment zone below 59.5° latitude. The elite population was established to increase the genetic gain over four birch breeding populations delimited in southern Sweden. There were seven unique mother trees and ten unique father trees in the crosses, with no reciprocal crosses (see Appendix A

Table A1. Parents which were crossed to produce offspring. The ‘X’ mark indicates mother and father ID for the resulting offspring used in this study. Unique genotype IDs and names have been substituted for numbers. Tree 66 was used both as a mother and a father tree.

Parental Crosses		Mother Unique ID Code
		01	02	03	04	05	66	07
Father unique ID code	10	X	X
	11	X		X
	12	X		X
	13	X			X	X
	14		X	X	X
	15		X	X			X
	16		X		X
	66			X
	17					X		X
	18						X	X

). Any tree could be used as a mother and a father tree. One mother tree was used five times, two mothers were used four times, one mother was used three times, and three mothers were used twice. Three fathers were used three times, six fathers two times, and one father one time. There were between 28 and 35 planted genotypes per family/cross in Hyssna and between 8 and 34 in Brunsberg. There were between 2 and 9 individuals (ramets) per clone with an average of 4.6 individuals per clone. In addition, there were seedlings from two half-sib families and seedlings from three reference locations planted in the experiment.

The field measurements were performed on all stems at ages 6, 12 and 19 years for both sites. Diameter (DBH) was measured in the north–south direction at a height of 1.3 m from the stem base (breast height) for all trees. Height was measured at age 6 for all trees in both experiments. Hyssna was thinned between at 12 years and 19 years, reducing the number of stems by 30% during the first thinning. A summary of all measured traits are in

Table 1. Measurements and units for manual, visual and non-destructive field assessments.

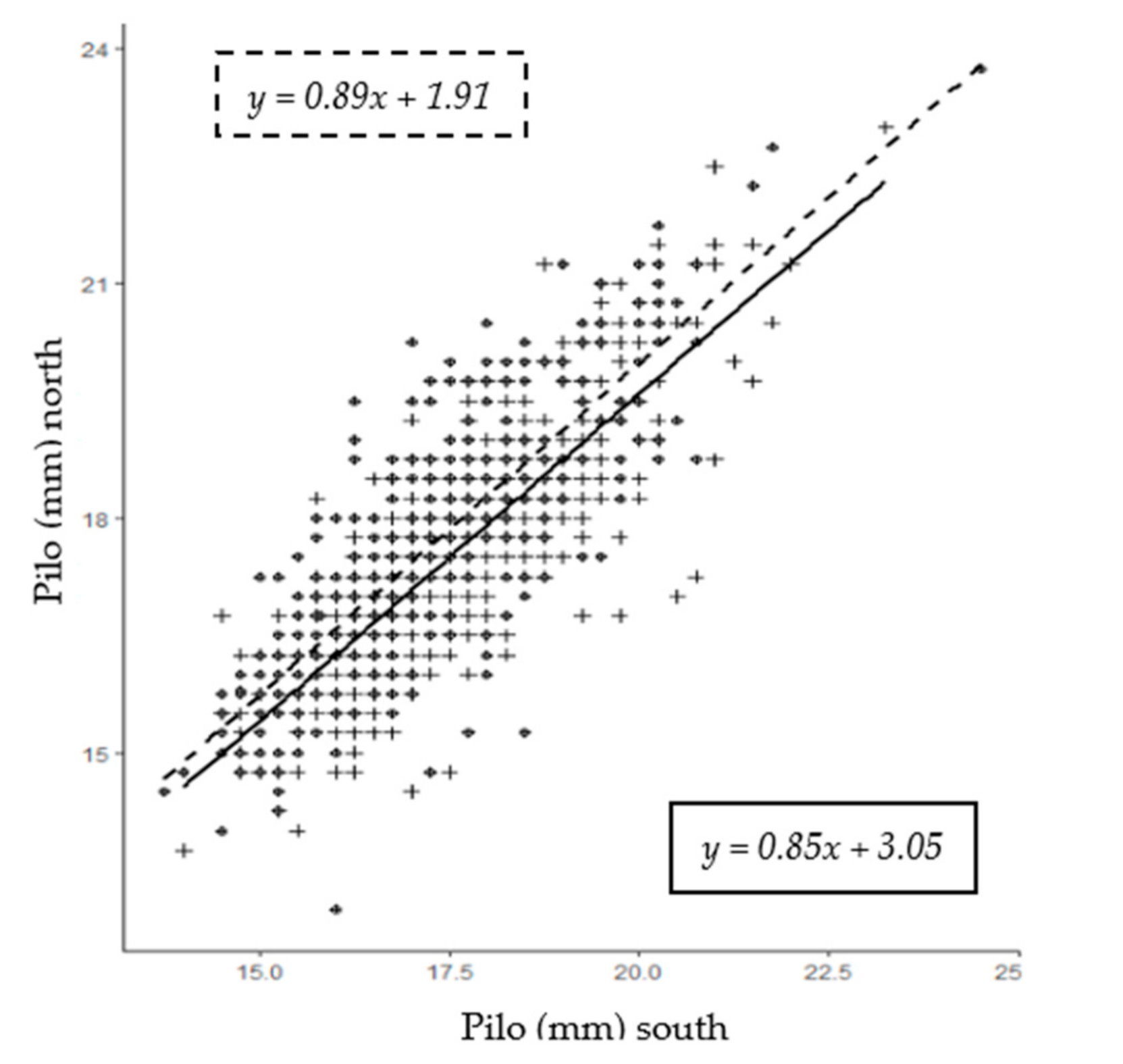
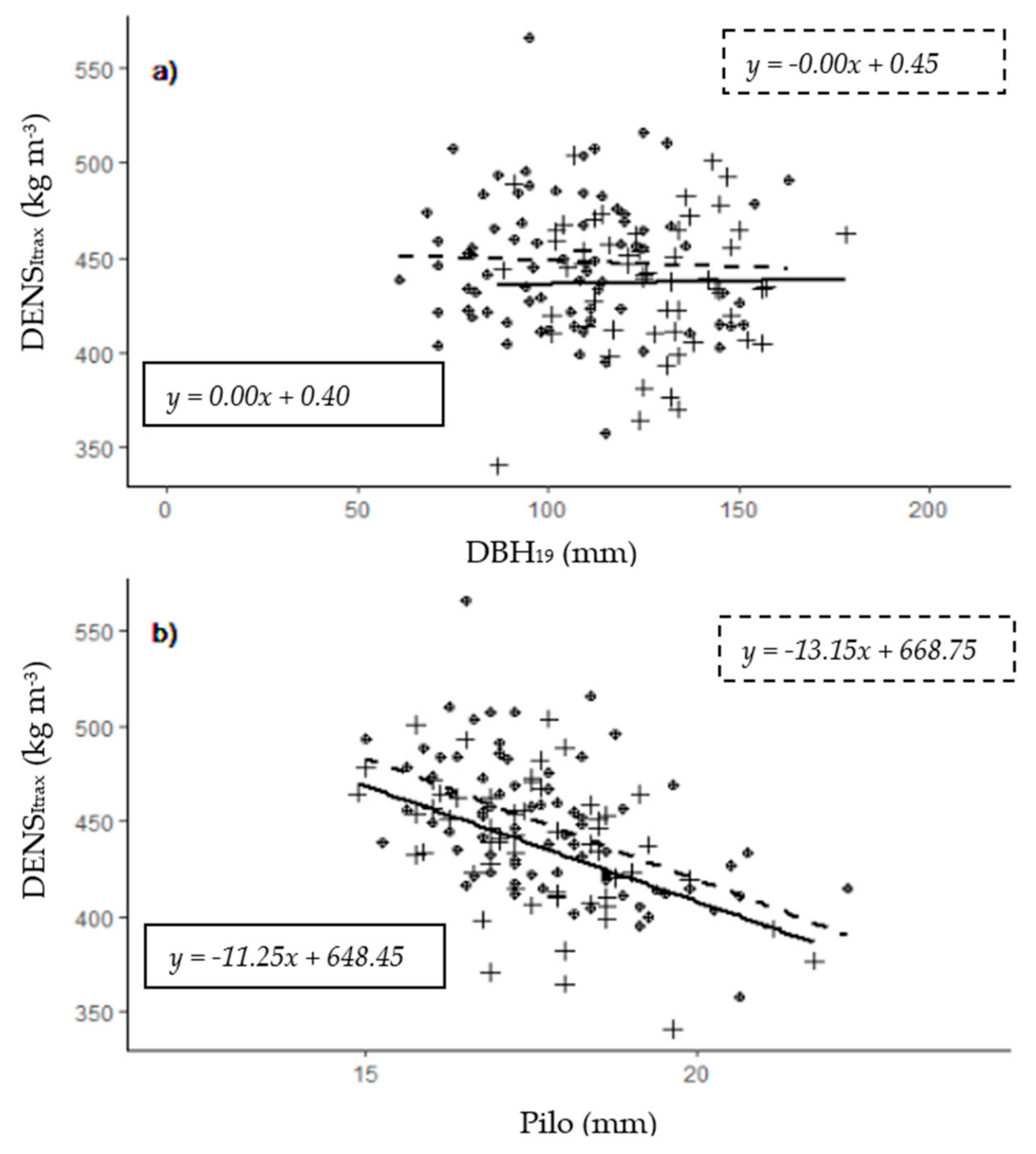
Measured Traits	Code	Description (units)
Size traits
Height age 6	H6	Length of main stem (cm)
Diameter age 6	DBH6	Stem diameter at 1.3 m height (mm) age 6
Diameter age 12	DBH12	Stem diameter at 1.3 m height (mm) age 12
Diameter age 19	DBH19	Stem diameter at 1.3 m height (mm) age 19
Stem form traits
Straightness	STR	Straightness score for stem below 8 m high (1–9)
Bark height	BH	Height at which smooth bark dominates (cm)
Wood quality traits
Grain angle	GA	Average grain angle measurement for north and south face at 1.3 m (°)
Pilodyn penetration	Pilo	Penetration depth by Pilodyn at 1.3 m height (mm)
Acoustic velocity	AV	1,000,000 divided by Fakopp (ToF) value (μs to travel 1 m) is AV (m s−1)
Itrax benchmark wood density	DENSItrax	1.3 m core average wood density from Itrax densitometer and LignoVisionTM (kg m−3)

, alongside units and trait descriptions.

Stem properties of all remaining trees were assessed in May 2018 when stems were 19 years old from the date of planting. Straightness was ranked on a scale from one to nine, where a score of nine indicated the best quality. This method has been a standard assessment tool for straightness in the birch breeding program [10,53,65]. The assessment of straightness considered any deviation from a cylinder in the bottom 8 m stem section, with a score of 5 considered by the assessor to be a stem representative of the site. A total of 1123 stems at Hyssna and 1410 stems at Brunsberg were ranked for straightness. The height of brown rough bark was measured from the stump base up to the height at which smooth silver bark dominated. Any defects or damages to the stem were recorded, and included features such as scars, breakages and stem lean. In addition, ramicorns (also referred to as epicornic branches) and multileaders were counted for each stem.

A subsample of trees was selected from the 22 control pollinated families, which had more than 20 individuals at both sites. Trees with severe defects, a DBH below 60 mm, or with a rough bark height above 140 cm, were excluded from the subsample. The 22 families then had 20 individuals selected randomly. The identity of the trees was tracked. If the tree has been damaged since the original assessment, it was not sampled, and then the next suitable stem was sampled if available. In this sense the sampling was not random, and some families had less than 20 trees sampled (at least 15 at both sites).

The subsample of stems was measured using NDT methods between August and September 2018. The grain angle, Pilodyn penetration depth, and AV along the stems were measured (Table 1). The Pilodyn 6J Forest (PROCEQ, Zurich, Switzerland) densitometer was applied twice to the north and south stem faces without bark removal [27] at breast height. The second Pilodyn measurement was taken a few centimeters to the left of the initial measurement, and both were averaged to get north and south values. A wedge grain angle gauge (grain angle meter) was used at breast height to measure grain angle on the north and south sides [52,53]. These values were averaged to get a single grain angle value per stem. Stem AV in the longitudinal direction was measured using the Fakopp TreeSonic Timer (FAKOPP Enterprise, Agfalva, Hungary) and converted from ToF (μs m⁻¹) to AV (m s⁻¹) [66]. The TreeSonic timer was applied to the southern stem face between 0.8 and 1.8 m, so that the 1 m length was centered on breast height. If there were any issues or uncertainties for any of the NDT tools, measurements were repeated and sometimes shifted a few centimeters to avoid defects and reduce operator error.

Average family diameters were used to select twelve families to take cores from; four families with the highest average, four with lowest average, and the four families with mid-range diameters. For each family, five trees per site were randomly selected. A 5 mm diameter core was taken at breast height from the south through to the north face of these trees. In total, 58 cores were collected from Hyssna and 72 cores from Brunsberg, and prepared using the method outlined by Hallingbäck et al. [67].

The Itrax scanning densitometer (Cox Analytical Systems, Mölndal, Sweden) was used to create x-ray images of all the cores as described in Bergsten et al. [68]. Later, the images were analysed using the computer program LIGNOVISION™ (Rinntech, Heidelberg, Germany). The program provided average light intensity (LI) values for a user defined area, which included a single annual ring. LI was then converted to wood density by using a function that included temperature, relative humidity, LI values for a calibration sample, and sample thickness [67]. Average wood density (DENS_Itrax) was used for the remaining analysis, and is the average density value of all rings identified in LIGNOVISION™ for a given stem.

Variance and covariance components for the genetic analysis were estimated separately for each site using ASReml 4.0 [69] with a univariate linear mixed model in the following equation:

$$y= Xb+ Z_{\alpha }\alpha +Z_{c}c+Z_{f}f+\epsilon$$

(1)

where $y$ is a vector of observed values, b is a vector of fixed effects (i.e., blocks, plots), α is a vector of random additive genetic effects, c is a vector of random effects of a clone within a full-sib family, f is a vector of random effects of a full-sib family and ε is a vector of random residuals. X, Z_α, Z_c and Z_f, are design matrices linking phenotypic observations to fixed and random effects. The first-order autocorrelation for parameters was tested in the model and kept if the model converged and the log likelihood improved.

Estimates of the individual tree narrow-sense heritability (h²) were calculated for each trait from the variance components obtained in the univariate analysis. Standard errors were estimated with the Taylor series expansion method.

$$h_i^2=\frac{{\widehat{\sigma }}_A^2}{{\widehat{\sigma }}_P^2}= \frac{{\widehat{\sigma }}_A^2}{{\widehat{\sigma }}_A^2+{\widehat{\sigma }}_c^2+{\widehat{\sigma }}_f^2+{\widehat{\sigma }}_{\epsilon }^2}$$

(2)

where for any trait i: $h_i^2$ is the narrow-sense heritability, ${\widehat{\sigma }}_A^2$ is the additive genetic variance, ${\widehat{\sigma }}_P^2$ is the total phenotypic variance (${\widehat{\sigma }}_A^2+{\widehat{\sigma }}_c^2+{\widehat{\sigma }}_f^2$), and ${\widehat{\sigma }}_{\epsilon }^2$ is the total error variance. This value is often used to indicate the proportion of variation in a trait that cannot be attributed to site or phenotypic factors.

Phenotypic coefficients of variation (PCV) and genotypic coefficients of variation (GCV) were calculated for each trait using the following formulas:

$$\mathrm{PCV}= \frac{\sqrt{{\sigma }_p^2}}{\overline{x}}\times 10$$

(3)

$$\mathrm{GCV}= \frac{\sqrt{{\sigma }_A^2}}{\overline{x}}\times 100$$

(4)

where $\overline{x}$ is the general mean, ${\sigma }_p^2$ is the phenotypic variance and ${\sigma }_A^2$ is the additive genetic variance.

To estimate genetic correlations, the trait variance components and covariance components between pairs of traits were estimated using bivariate analysis. The bivariate model was an expansion of the univariate model to include a vector of values for two traits and matrices corresponding to fixed effect design and random effect design for each trait, respectively.

Variances and covariances of the random effects were estimated as:

$$Var\left[\begin{array}{c}a\\ c\\ f\\ \epsilon \end{array}\right]= \left[\begin{array}{cccc}G⨂A& 0& 0& 0\\ 0& C⨂I & 0& 0\\ 0& 0& F⨂I& 0\\ 0& 0& 0& R⨂I\end{array}\right]$$

(5)

where A is the numerator relationship matrix, G is the additive genetic (co)variance matrix, C is the clone (co)variance matrix, F is the family co(variance) matrix, R is the residual (co)variance matrix, and I is an identity matrix.

The n × n symmetric numerator relationship matrix A in was structured as:

$$A= \left[\begin{array}{ccc}{p}_{11}& \dots & p_{1n}\\ ⋮& \ddots & ⋮\\ p_{n1}& \dots & p_{nn}\end{array}\right]$$

(6)

where p_ij is the additive pedigree-based relationship between any pair of tree individuals i and j for all n individuals included in the analysis. The 2 × 2 order symmetric matrices G, C, F and R, are in turn structured as:

$$G= \left[\begin{array}{cc}{\sigma }_{a1}^2& {\sigma }_{a12}\\ {\sigma }_{a12}& {\sigma }_{a2}^2\end{array}\right]$$

(7)

$$C= \left[\begin{array}{cc}{\sigma }_{c1}^2& {\sigma }_{c12}\\ {\sigma }_{c12}& {\sigma }_{c2}^2\end{array}\right]$$

(8)

$$F= \left[\begin{array}{cc}{\sigma }_{f1}^2& {\sigma }_{f12}\\ {\sigma }_{f12}& {\sigma }_{f2}^2\end{array}\right]$$

(9)

$$R= \left[\begin{array}{cc}{\sigma }_{\epsilon 1}^2& {\sigma }_{\epsilon 12}\\ {\sigma }_{\epsilon 12}& {\sigma }_{\epsilon 2}^2\end{array}\right]$$

(10)

where ${\sigma }_{a1}^2, {\sigma }_{c1}^2, {\sigma }_{f1}^2,{\sigma }_{\epsilon 1}^2$ and ${\sigma }_{a2}^2, {\sigma }_{c2}^2, {\sigma }_{f2}^2,{\sigma }_{\epsilon 2}^2$ are additive genetic, clone within family, full-sib family and residual variances for trait 1 and 2, respectively. The ${\sigma }_{a12}, {\sigma }_{c12}, {\sigma }_{f12}$, and ${\sigma }_{\epsilon 12}$, are additive genetic, clonal within family, full-sib family and residual covariances between trait 1 and 2.

Phenotypic (cor_P) and genotypic (cor_G) correlations between traits and age–age genotypic correlations ($R_{\left(x, y\right)}$) were calculated as:

$$R_{\left(x, y\right)}= \frac{{\widehat{cov}}_{\left(1,2\right)}}{\sqrt{{\widehat{\sigma }}_{\left(1\right)}^2 x {\widehat{\sigma }}_{\left(2\right)}^2}}$$

(11)

where ${\widehat{\sigma }}_{\left(1\right)}^2$ and ${\widehat{\sigma }}_{\left(2\right)}^2$ are the estimated phenotypic or genotypic variances for traits 1 and 2 or the same trait variances at two different ages, respectively, and ${\widehat{cov}}_{\left(1, 2\right)}$ is the estimated phenotypic or genotypic covariance (${\sigma }_{a12}$) between traits 1 and 2 or between two different ages. These correlations indicate how similar two traits are, so that as one trait changes the other is likely to also change if the phenotype or genotype are linked. Values were recorded with a negative symbol if the correlation was negative.

The between site genetic correlations were estimated by compound variances for the linear mixed model and heterogeneous genetic variance within each site. The model used covariance parameterization [70] and was of the same general form as Equation (5) with the addition of random genetic site effects $Z_{s}s$; where s is a vector of site random effects, and Z_s is a design matrix linking the phenotypic observation to fixed and random effects.

A between-site genetic correlation of one is expected if the genetic influences on the trait are identical between sites, whereas a value of zero implies that the genetic effects on the trait are independent of the site. These are consistently referred to as genetic correlations to avoid confusion with the above genotypic correlations (cor_G).

Graphs were produced using the statistics software R (version 3.6.3, R Core Team, Vienna, Austria) for Pilodyn north against Pilodyn south measurements, Itrax density against stem diameter, and Itrax density against Pilodyn penetration depth. R was also used to plot linear trend lines between the variables. Correlations between variables were calculated using the cor() function and the Pearson’s correlation method, which assumes a linear relationship between variables and indicates the strength and direction of this relationship (from −1 to +1).

3. Results

3.1. Descriptive Statistics, Heritability and Variability of Traits

The average height of trees measured at age six was 71 cm for Hyssna and 47 cm for Brunsberg, with respective average diameters of 56 and 36 mm (

Table 2. Measurements and units for manual, visual and non-destructive field assessments.

Traits	N		Mean		Min		Max		PCV (%)		h2		SE (%)		GCV (%)
Site	H	B	H	B	H	B	H	B	H	B	H	B	H	B	H	B
H6 (mm)	3360	2279	71	47	27	8	105	80	15	28	0.2	0.07	0.02	0.01	6.3	6.3
DBH6 (mm)	3360	2262	56	36	11	2	111	82	27	42	0.19	0.04	0.02	0.01	11.1	7.8
DBH12 (mm)	3320	2230	83	65	17	7	157	163	25	32	0.28	0.05	0.02	0.01	13.5	7.6
DBH19 (mm)	2362	1409	110	98	17	20	211	194	25	28	0.21	0.09	0.04	0.03	10.6	7.1
STR (1–9)	1123	1410	5	4.6	1	1	8	8	18.1	20.1	0.23	0.22	0.03	0.03	8.4	9.4
BH (cm)	1141	1390	67	46	0	10	280	240	65	74	0.44	0.39	0.04	0.03	2.4	45.4
GA (°)	440	393	−1.8	−1.5	−6.3	−6.3	2.5	2.8	63	74	0.20	0.21	0.03	0.03	31	51.9
Pilo (mm)	442	453	17.6	17.2	13.8	8.3	23.2	24.1	7.7	10.2	0.53	0.48	0.06	0.07	5.8	7.1
AV (m s−1)	450	453	4184	4237	6135	4717	3636	3165	4.8	5.5	0.05	0.3	0.04	0.08	0.6	1.6
DENSItrax (kg m−3)	115	151	431	444	329	358	520	566	8	7.1	NA	NA	NA	NA	NA	NA

). At 19 years old the diameters in Hyssna and Brunsberg were 110 and 98 mm, respectively. These size traits (height and diameters) had heritability estimates around 0.2 for Hyssna and below 0.1 for Brunsberg. PCVs were higher for Brunsberg (maximum 42%) than for Hyssna (maximum 27%), yet Hyssna had higher GCVs (maximum 13.5%) than Brunsberg (maximum 7.8%). Height at age 6 had the lowest coefficients of variation for any size trait, with PCV values of 15% at Hyssna and 28% at Brunsberg, and a GCV of 6.3% at both sites.

The mean score for stem straightness (STR) was 5 at Hyssna and 4.6 at Brunsberg. The related PCVs were 18.1 and 20.1% and GCVs were 8.4 and 9.4%. Heritability for STR was 0.23 at Hyssna and 0.22 at Brunsberg. The average bark height (BH) was 67 cm at Hyssna and 46 cm and Brunsberg, with PCVs of 65 and 74%, and GCVs of 2.4 and 45.4%. Heritability estimates for BH were 0.44 at Hyssna and 0.39 at Brunsberg. For these stem form traits, coefficients of variation were lower at Hyssna and heritibilities were slightly lower at Brunsberg.

Wood quality trait (GA, Pilo, AV and DENS_Itrax) average values were poorer at Hyssna than Brunsberg: GA was −1.8° and −1.3°, Pilo was 17.6 and 17.2 mm, AV was 4184 and 4237 m s⁻¹, and DENS_Itrax was 431 and 444 kg m⁻³ (for Hyssna and Brunsberg, respectively). GA had PCVs above 60% and GCVs above 30% at both sites, and heritabilities were 0.20 at Hyssna and 0.21 at Brunsberg. Pilo had a PCV of 7.7% and GCV of 5.8% at Hyssna, and a PCV of 10.2% and GCV of 7.1% at Brunsberg. Heritability for Pilo was around 0.50 at both sites. Heritability for AV was non-existant at Hyssna (0.05) but moderate at Brunsberg (0.30), which also had PCVs around 5% and GCVs below 2%, the lowest of all wood quality traits. DENS_Itrax had too few measurements to calculate genetic parameters.

3.2. Phenotypic and Genotypic Correlations between Traits

Phenotypic correlations (cor_P) were above 0.83 between diameters (DBH₆, DBH₁₂, and DBH₁₉), and above 0.7 between H₆ and diameters (

Table 3. Phenotypic (above the diagonal) and additive genotypic (below the diagonal) correlations between traits. H is Hyssna and B is for Brunsberg.

Traits	H6		DBH6		DBH12		DBH19		BH		GA		Pilo		AV
Site	H	B	H	B	H	B	H	B	H	B	H	B	H	B	H	B
H6	1		0.84	0.93	0.80	0.82	0.70	0.76	0.32	0.38	−0.04	−0.01	−0.04	−0.01	−0.18	−0.27
DBH6	0.68	0.67	1		0.92	0.90	0.84	0.83	0.54	0.51	0.03	−0.03	0.17	0.02	0.10	−0.10
DBH12	0.71	0.55	0.95	0.90	1		0.94	0.94	0.51	0.51	−0.03	−0.04	0.12	0.12	0.03	−0.07
DBH19	0.73	0.61	0.90	0.99	0.98	0.99	1		0.53	0.51	−0.16	−0.12	0.08	0.18	0.00	−0.11
BH	0.08	−0.11	0.5	0.35	0.42	0.23	0.37	0.25	1		−0.15	−0.07	0.04	−0.12	0.25	0.09
GA	0.67	0.28	0.85	0.24	0.97	0.45	0.99	0.49	0.29	0.05	1		0.15	0.06	−0.16	−0.12
Pilo	−0.22	−0.19	−0.03	−0.19	−0.15	−0.07	−0.34	0.02	−0.17	−0.36	−0.18	−0.04	1		0.16	0.09
AV	0.37	−0.61	−0.16	−0.25	−0.06	−0.11	−0.11	0.04	−0.11	0.29	−0.46	−0.07	−0.12	−0.10	1

). Genotypic correlations (cor_G) were above 0.9 between diameters (DBH₆, DBH₁₂, and DBH₁₉), and above 0.55 between H₆ and diameters (Table 3).

Diameters had high cor_P with BH (above 0.5), and moderate cor_G with BH (0.23–0.5). Other cor_P values were low between size traits, bark height and wood quality traits, with most cor_P values close to ±0.1, and the largest cor_P (−0.27) between AV and H₆ at Brunsberg.

The cor_P between BH and wood quality traits were low, ranging from 0.04 for Pilo at Brunsberg to 0.25 for AV at Hyssna. BH had slightly higher cor_G values with Pilo (−0.17 and −0.36) and AV (−0.11 and 0.29), for Hyssna and Brunsberg, respectively.

Wood quality traits (GA, Pilo, and AV) generally had low cor_P (−0.03 to 0.16) and cor_G (around 0.1) with other wood quality traits. There was a moderate (−0.46) cor_G between GA and AV at Hyssna, but a low cor_G value for Brunsberg (−0.07). GA had low to high (0.24 to 0.99) cor_G with size traits.

3.3. Correlations between Sites and Measurements

The between site correlation for H6 was 0.76 the highest for any size trait (

Table 4. Genetic correlations between the same traits measured at two sites (Hyssna and Brunsberg). SE is standard error.

Trait	Genetic Correlation between Hyssna and Brunsberg	SE
H6	0.757	0.104
DBH6	0.444	0.149
DBH12	0.466	0.127
DBH19	0.350	0.13
STR	0.824	0.113
BH	0.673	0.069
GA	0.956	0.117
Pilo	0.815	0.098
AV	0.998	<0.001

). The same correlation for DBH6 was 0.44, DBH12 was 0.47, and DBH19 0.35. The between-site correlations were higher for stem form traits (above 0.6) than for size traits (Table 4). Wood quality traits had high between-site correlations; 0.96 for GA, 0.82 for Pilo, and 1.00 for AV.

The average Pilodyn readings for the north and south stem faces had a correlation of 0.809 for Hyssna and 0.823 for Brunsberg (Figure 2). Given the strong correlation, an average of the north and south Pilodyn readings for each stem (Pilo) is used elsewhere in this paper. DENS_Itrax was moderately correlated with DBH19 (Figure 3a) at Brunsberg (−0.29) but not Hyssna (0.04). DENS_Itrax was negatively correlated with Pilo (−0.36 and −0.46), for Hyssna and Brunsberg, respectively (Figure 3b).

4. Discussion

Since the 1980s, the Swedish breeding program has managed to increase volume production per area (m³ ha⁻¹) by 15% and improved overall stem quality, compared to unimproved silver birch regeneration [13]. Unfortunately, the annual birch seedling production is less than 1% of the Norway spruce or Scots pine seedling production [71], reflecting the still limited interest in planting improved birch. This gap can be reduced if opportunities and markets are developed, and product education occurs, to encourage the use of birch wood [72]. Birch is believed to have lower production than the planted spruce and pine [73,74] and be too low quality for solid products, so any activity to improve growth rates, form or perception, could increase the amount of birch planted. As the use of broadleaved species is increasingly promoted in Sweden to meet goals for biodiversity [75], plantation management will need to focus on maximizing production value from broadleaf trees, both in mixtures and pure stands. For birch, this will include silvicultural choices such as improved genetic material and establishment methods.

It is important to test planting material across sites (GxE correlation) located in different conditions [76]. In our study, there were between site differences indicating that variables not related to genetics might influence the performance of genotypes. Phenotypic coefficients of variation were higher at Brunsberg than Hyssna. Brunsberg stem form traits and wood quality traits had higher genotypic coefficients of variation, while the reverse was true for size traits; diameters and height had lower genotypic variation at Hyssna. Higher genotypic variation is desirable in breeding programs as it indicates these traits have potential for improvement, and higher variability can make selection progress rapidly [77]. There were also high genetic correlations between sites for height, stem form, and wood quality traits, while diameters had moderate (below 0.5) between site genetic correlations. High between-site genetic correlations suggest that the best families will perform well at both sites as family performance rankings were stable.

The heritabilities for size traits reported here were slightly lower than in other genetics studies of silver birch in Sweden. In the study by Stener and Jansson [78], average heritibilities for diameter (0.29) and height (0.32) of open-pollinated silver birch trees at age 7 were similar to those in this study (0.04–0.28) and varied between sites. Gailis et al. [79] studied open-pollinated silver birch in Latvia at ages 10 and 14 years [79], and had heritibilities above 0.12 for diameter and 0.30 for height. This paper’s heritabilities were much lower than those found by Skrøppa and Solvin [80] at age 16 for height (0.38) and diameter (0.81) for full and half-sib families in Norway. The genotypes used by Skroppa and Solvin were produced from a 9 × 9 diallel mating design [80], which may explain the relatively large differences in heritabilities compared to our study. Here, the moderately high heritability, and reasonable variability, indicate that selection for size traits is possible in the studied population.

Of the stem form traits, straightness has been more frequently assessed [78,79] than any bark metric [81]. For these other studies of silver birch [78,79], heritability for straightness ranged from 0.02 to 0.45 and was generally lower than for size traits. The heritibilities for straightness at Hyssna and Brunsberg, were above 0.2 in our study and would fit within this range of values. Viherä-Aarnio and Velling [81] measured bark thickness of 22-year-old silver birch in a provenance trial. They found that seed origin latitude was related to bark thickness, yet, unfortunately, did not provide heritabilities. In our study, heritability for bark height was very high at both Hyssna and Brunsberg, but genetic variation was very low at Hyssna. The results of this study suggest stem form traits can be improved through breeding. Stem straightness has previously been considered in the breeding program for birch [10,78]. The high genotypic variation and heritability of rough bark height makes this trait interesting and relatively easy to include in breeding, if there is enough commercial interest.

Grain angle heritability using the wedge grain angle meter has been commonly assessed for conifer species [31,32,52,82], yet it is difficult to find any hardwood species genetics trials which considered grain angle [83]. For 9-year-old open-pollinated family trials of Eucalyptus in Australia, E. dunnii had a heritability for grain angle of 1.0 [83] compared to 0.0 for E. pilularis [43], which is a large range of heritability estimates between species. The heritability for silver birch wood density in an 11-year-old Swedish clonal trial [10] was 0.73, which was higher than for Pilo in this study. Liang et al., studied 60 half-sib B. platyphylla families in China [84] and found heritability estimates of 0.30 and 0.37 for air-dry and oven-dry wood density, respectively. The same paper reported heritability values for flexural strength (0.37) and elastic modulus (0.15), which could be comparable to this study’s AV measurements but included the influence of wood density on stiffness [37]. It is common for wood quality traits to have higher heritability estimates than size traits [85] as size traits tend to be under strong environmental influence.

The NDT tools used in this study to indirectly assess wood quality traits had fairly high heritabilities. Pilo had high heritability estimates at both sites, but Pilo had less variation than GA, which had low-moderate (0.2) heritability values. AV heritability was moderate at Brunsberg but extremely low at Hyssna, and had the lowest genetic coefficients of variation for any trait. Therefore, the results of this study should be complemented with more observations of B. pendula solid wood quality traits to see if these results are species or population specific, and to confirm that they are not unusual. One benefit of this work, is that the sampled trees are still growing, and could be assessed again later to see how well early performance relates to log mechanical properties, or how relationships vary with age [31,86]. The assessment of wood mechanical properties with NDT tools was also rapid, so the methodology should be easy for other researchers to apply.

The phenotypic correlations between bark height and wood quality traits were moderate, and genotypic correlations were slightly stronger. The rough bark height could affect the NDT measurements despite stems with rough bark at 1.3 m being excluded from the sample. It would be worth exploring these relationships further as rough bark height can be rapidly measured. Viherä-Aarnio and Velling [81] related bark thickness to seed origin latitude in a 22-year-old silver birch progeny trial in Finland. Phenotypic and genotypic correlations between wood quality traits were low to moderate, and varied by site. For wood quality traits this means that a single value is not representative, and that selection for one trait will not impact another.

Pilodyn’s north and south values were highly correlated, and a single value should be sufficient for later assessment in silver birch field trails. Practical issues meant that taking two measurements per stem face was helpful, especially as the tool sometimes slipped or misfired. A second value can help to identify errors and provide more accurate estimates. Hyssna had higher growth, and lower Pilo and AV values, in agreement with studies of birch wood properties where faster growth rates reduced density [19,20] and strength [18]. However, the plots of diameter against density showed a poor relationship and a low correlation (phenotypic correlations were also low) meaning this difference is likely due to site conditions. In agreement with other studies, growth rate seemingly had no effect on wood density [87,88], but did vary by site. Itrax density and Pilodyn penetration were moderately correlated, although this relationship could be improved with more observations. The level of accuracy provided by Pilodyn has been sufficient for genetics trials comparing families, but not for comparing individuals within families [40]. Selection for the best trees to clone may be improved by using detailed density information, as provided by core scanning or destructive sampling.

The average DENS_Itrax values were 431 kg m⁻³ at Hyssna and 444 kg m⁻³ at Brunsberg. Some comparable studies of juvenile silver birch [10,19,81] had average density values of: 478 kg m⁻³ for 22-year-old Finnish provenance trials [81], 455 kg m⁻³ for Latvian plantation-grown birch for ages 11 to 15 years [19], and of 429 kg m⁻³ for 11-year-old Swedish birch clones [10]. The density values obtained in this report are similar to other studies, yet there is variation within families, and often even within a stem [20,89], which is ignored when average values are used.

5. Conclusions

Pilodyn penetration was under strong genetic control, and grain angle had moderate heritabilities with high genotypic variation. This indicates that there is the potential to improve grain angle through breeding. However, low genotypic variation for Pilodyn measurements indicate that it will be harder to improve Pilodyn penetration through breeding, and consequently harder to influence wood density. Genotypic and phenotypic correlations between growth traits measured at different ages were high, indicating that early selection is possible for size traits. Low genotypic and phenotypic correlations between NDT measurements and growth traits indicate that wood quality traits cannot be improved by indirect selection. The high genetic correlations between sites suggest that grain angle, Pilodyn penetration and acoustic velocity values are determined by genotype rather than by environment. The results of the study indicate that NDT tools can be applied to silver birch genetics programs, yet more studies are needed to confirm their usefulness. The measurements for grain angle seem to have the greatest potential for improvement, while Pilodyn penetration also shows promise for inclusion. Pilodyn penetration was moderately correlated with wood density. The measurement was relatively quick and can be applied to a large number of individuals. No unfavorable correlations were observed between wood density and diameter, as are often observed in coniferous species. A broader study is needed to identify and quantify the effects of variables which could influence NDT measurements in birch genetics trials. Further work should also explore the possible relationships between bark height and size/wood quality traits. High between site genetic correlations support the use of NDT tools for comparing traits between families, but more accurate or destructive methods may be required to select individual trees.