The Possibility of Using the Chapman–Richards and Näslund Functions to Model Height–Diameter Relationships in Hemiboreal Old-Growth Forest in Estonia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Site
2.2. Data Collection
2.3. Model Type Selection to Describe the H-D Relationship in Naturally Developing Forest
2.4. Modeling of H-D Relationship
2.5. Comparative Analysis of H-D Modeling Results
3. Results
3.1. Modeling Results of the Old Growth Forest
3.2. Modeling Results of the Managed Forest
3.3. Model Selection and Comparison
3.4. A Comparison of Old-Growth Height Curve Modeling Results with Managed Forests Height Curves
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kangur, A.; Sims, A.; Jõgiste, K.; Kiviste, A.; Korjus, H.; von Gadow, K. Comparative modeling of stand development in Scots pine dominated forests in Estonia. For. Ecol. Manag. 2007, 250, 109–118. [Google Scholar] [CrossRef]
- Bravo, F.; Fabrika, M.; Ammer, C.; Barreiro, S.; Bielak, K.; Coll, L.; Fonseca, T.; Kangur, A.; Löf, M.; Merganičová, K.; et al. Modelling approaches for mixed forests dynamics prognosis. Research gaps and opportunities. For. Syst. 2019, 28, eR002. [Google Scholar] [CrossRef] [Green Version]
- Kangur, A.; Korjus, H.; Jõgiste, K.; Kiviste, A. A conceptual model of forest stand development based on permanent sample-plot data in Estonia. Scand. J. For. Res. 2005, 20, 94–101. [Google Scholar] [CrossRef]
- Shorohova, E.; Kuuluvainen, T.; Kangur, A.; Jõgiste, K. Natural stand structures, disturbance regimes and successional dynamics in the Eurasian boreal forests: A review with special reference to Russian studies. Ann. For. Sci. 2009, 66, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Sharma, M.; Parton, J. Height–diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. For. Ecol. Manag. 2007, 249, 187–198. [Google Scholar] [CrossRef]
- Motallebi, A.; Kangur, A. Are allometric relationships between tree height and diameter dependent on environmental conditions and management? Trees Struct. Funct. 2016, 30. [Google Scholar] [CrossRef]
- Padari, A.; Metslaid, S.; Kangur, A.; Sims, A.; Kiviste, A. Modelling stand mean height in young naturally regenerated stands—A case study in järvselja, estonia. Balt. For. 2009, 15, 226–236. [Google Scholar]
- Pretzsch, H. Standard Analysis of Long-Term Experimental Plots. In Forest Dynamics, Growth and Yield: From Measurement to Model; Pretzsch, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 181–222. ISBN 978-3-540-88307-4. [Google Scholar]
- Laarmann, D.; Korjus, H.; Sims, A.; Stanturf, J.A.; Kiviste, A.; Köster, K. Analysis of forest naturalness and tree mortality patterns in Estonia. IUFRO Conf. Biodivers. For. Ecosyst. Landsc. 2009, 258, S187–S195. [Google Scholar] [CrossRef]
- Laarmann, D.; Korjus, H.; Sims, A.; Kangur, A.; Stanturf, J.A. Initial effects of restoring natural forest structures in Estonia. For. Ecol. Manag. 2013, 304. [Google Scholar] [CrossRef]
- Jõgiste, K.; Frelich, L.E.; Laarmann, D.; Vodde, F.; Baders, E.; Donis, J.; Jansons, A.; Kangur, A.; Korjus, H.; Köster, K.; et al. Imprints of management history on hemiboreal forest ecosystems in the Baltic States. Ecosphere 2018, 9. [Google Scholar] [CrossRef] [Green Version]
- Jõgiste, K.; Korjus, H.; Stanturf, J.A.; Frelich, L.E.; Baders, E.; Donis, J.; Jansons, A.; Kangur, A.; Köster, K.; Laarmann, D.; et al. Hemiboreal forest: Natural disturbances and the importance of ecosystem legacies to management. Ecosphere 2017, 8. [Google Scholar] [CrossRef]
- Vanclay, J. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; CAB International: Wallingford, UK, 1994; ISBN 0-85198-913-6. [Google Scholar]
- Gschwantner, T.; Alberdi, I.; Balázs, A.; Bauwens, S.; Bender, S.; Borota, D.; Bosela, M.; Bouriaud, O.; Cañellas, I.; Donis, J.; et al. Harmonisation of stem volume estimates in European National Forest Inventories. Ann. For. Sci. 2019, 76, 24. [Google Scholar] [CrossRef] [Green Version]
- Adekunle, V.A.J.; Nair, K.N.; Srivastava, A.K.; Singh, N.K. Models and form factors for stand volume estimation in natural forest ecosystems: A case study of Katarniaghat Wildlife Sanctuary (KGWS), Bahraich District, India. J. For. Res. 2013, 24, 217–226. [Google Scholar] [CrossRef]
- Padari Assessment of forest stands. Assortments and damages. Kasvava metsa hindamine. Sortimendid ja rikked. In Pidev Metsakorraldus; Estonian Agricultural University: Tartu, Estonia, 1999; Volume 32, pp. 37–43.
- Padari, A. Mathematical analysis and modification possibilities of Ozolinš’ taper curve on the example of Hiiumaa pines. For. Stud. 2020, 72, 34–53. [Google Scholar] [CrossRef]
- Nilson, A. Weight function for non-linear transformation of regression equations. For. Stud. Metsanduslikud Uurim. 2002, XXXVII, 89–112. [Google Scholar]
- Schmidt, M.; Kiviste, A.; von Gadow, K. A spatially explicit height–diameter model for Scots pine in Estonia. Eur. J. For. Res. 2011, 130, 303–315. [Google Scholar] [CrossRef] [Green Version]
- Kiviste, K.; Kiviste, A. Algebraic Difference Equations of Stand Height, Diameter, and Volume Depending on Stand Age and Site Factors for Estonian State Forests. Math. Comput. For. Nat. Resour. Sci. 2009, 1, 67–77. [Google Scholar]
- Kängsepp, V.; Kangur, A.; Kiviste, A. Tree height distribution dynamics in young naturally regenerated study plots. For. Stud. 2015, 63. [Google Scholar] [CrossRef] [Green Version]
- Laas, E.; Tattar, T.; Teppo, P.; Paal, T. Järvselja Looduskaitseala Kaitsekorralduskava 2012–2021 [Nature Protection Management Plan 2012–2021 for Järvselja Nature Reserve]; Republic of Estonia Environmental Board: Tallinn, Estonia, 2007. [Google Scholar]
- Kollom, M. Development of Primeval Forest Structure in Järvselja, Estonia: A Research Based on National Forest Inventory Data. Master’s Thesis, Agricultural Sciences (Forestry), Estonian University of Life Sciences, Tartu, Estonia, 2011. [Google Scholar]
- Lõhmus, E. Forest site types in the Järvselja protected compartment. [(Järvselja looduskaitsekvartali metsakasvukohatüübid]. In Kasesalu, H. (toim.). Järvselja Ürgmetsa Loodusest; Eesti Looduseuurijate Seltsi Aastaraamat; Valgus: Tallinn, Estonia, 1993; pp. 261–283. [Google Scholar]
- Kiviste, A.; Hordo, M.; Kangur, A.; Kardakov, A.; Laarmann, D.; Lilleleht, A.; Metslaid, S.; Sims, A.; Korjus, H. Monitoring and modeling of forest ecosystems: The Estonian Network of Forest Research Plots. For. Stud. 2015, 62. [Google Scholar] [CrossRef] [Green Version]
- Lõhmus, E. Estonian Forest Site Types. Second Edition. [Eesti Metsakasvukohatüübid. Teine Trükk]; Loodusfoto: Tartu, Estonia, 2004. [Google Scholar]
- Kiviste, A.; Hordo, M. Network of permanent forest growth plots in Estonia. Metsanduslikud Uurim. For. Stud. 2002, XXXVII, 43–58. [Google Scholar]
- Gove, J.H.; Lynch, T.B.; Ducey, M.J. The Chapman-Richards Distribution and its Relationship to the Generalized Beta. For. Ecosyst. 2019, 6, 27. [Google Scholar] [CrossRef]
- Von Bertalanffy, L. Quantitative Laws in Metabolism and Growth. Q. Rev. Biol. 1957, 32, 217–231. [Google Scholar] [CrossRef]
- RICHARDS, F.J. A Flexible Growth Function for Empirical Use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Zhao-gang, L.; Feng-ri, L. The generalized Chapman-Richards function and applications to tree and stand growth. J. For. Res. 2003, 14, 19–26. [Google Scholar] [CrossRef]
- Pienaar, L.V.; Turnbull, K.J. The Chapman-Richards Generalization of Von Bertalanffy’s Growth Model for Basal Area Growth and Yield in Even—Aged Stands. For. Sci. 1973, 19, 2–22. [Google Scholar] [CrossRef]
- Štícha, V.; Sharma, R.P.; Vacek, Z.; Vacek, S.; Nuhlíček, O. Timber and Branch Volume Prediction: Effects of Stand and Site Characteristics on Dendromass and Timber-To-Branch Volume Ratio of Norway Spruce in Managed Forests. Forests 2019, 10, 144. [Google Scholar] [CrossRef] [Green Version]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D. Nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 2006, 3, 109. [Google Scholar]
- Hölttä, T.; Mäkinen, H.; Nöjd, P.; Mäkelä, A.; Nikinmaa, E. A physiological model of softwood cambial growth. Tree Physiol. 2010, 30, 1235–1252. [Google Scholar] [CrossRef] [PubMed]
- Hölttä, T.; Lintunen, A.; Chan, T.; Mäkelä, A.; Nikinmaa, E. A steady-state stomatal model of balanced leaf gas exchange, hydraulics and maximal source–sink flux. Tree Physiol. 2017, 37, 851–868. [Google Scholar] [CrossRef]
- Näslund, M. Skogsförsöksanstaltens gallringsförsök i tallskog. Meddelanden från Statens Skogsförsöksanstalt 29, no 1., Stockholm. Swed. Inst. Exp. For 1936, 29, 169. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Interence. A practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Wood, S.N. Generalized Additive Models. An Introduction with R; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Hanewinkel, M.; Pretzsch, H. Modelling the conversion from even-aged to uneven-aged stands of Norway spruce (Picea abies L. Karst.) with a distance-dependent growth simulator. For. Ecol. Manag. 2000, 134, 55–70. [Google Scholar] [CrossRef]
- Rouvinen, S.; Kuuluvainen, T. Tree diameter distributions in natural and managed old Pinus sylvestris-dominated forests. For. Ecol. Manag. 2005, 208, 45–61. [Google Scholar] [CrossRef]
- Metslaid, S.; Sims, A.; Kangur, A.; Hordo, M.; Jõgiste, K.; Kiviste, A.; Hari, P. Growth patterns from different forest generations of Scots pine in Estonia. J. For. Res. 2011, 16, 237–243. [Google Scholar] [CrossRef]
- Kangur, A.; Kiviste, A.; Hynynen, J.; Korjus, H.; Kaimre, P. Preface: Temporal and spatial validation of forest models. Eessõna Metsa Mudelite Ruumilise Ja Ajalise Usaldatavuse Hindamine 2011, 55, 5–10. [Google Scholar]
- Metslaid, S.; Hordo, M.; Korjus, H.; Kiviste, A.; Kangur, A. Spatio-temporal variability in Scots pine radial growth responses to annual climate fluctuations in hemiboreal forests of Estonia. Agric. For. Meteorol. 2018, 252, 283–295. [Google Scholar] [CrossRef]
- Rebane, S.; Jõgiste, K.; Kiviste, A.; Stanturf, J.A.; Kangur, A.; Metslaid, M. C-exchange and balance following clear-cutting in hemiboreal forest ecosystem under summer drought. For. Ecol. Manag. 2020, 472, 118249. [Google Scholar] [CrossRef]



| Variable | Live Trees | Standing Dead Wood | Snags | Downed Dead Wood | ||||
|---|---|---|---|---|---|---|---|---|
| Järvselja | Laeva | Järvselja | Laeva | Järvselja | Laeva | Järvselja | Laeva | |
| Number of measured, (N) | 6008 | 1702 | 263 | 256 | 1097 | 188 | 2983 | 116 |
| Number estimated trees per compartment | 15,480 | - | 1060 | - | 2661 | - | 6112 | - |
| Dominating species * | SP, LI, BAR, BI, NOM | SP, BI, CA, LI | SP, LI, SP | SP, BI, CA | SP, SP, AH | SP, BI, CA | BI, SP, BAR, LI, | SP, BI |
| Mean diameter, D (cm) | 19.0 | 27.3 | 19.6 | 24.0 | 26.9 | 22.6 | 25.1 | 17.9 |
| Mean height/length, H/L (m) | 17.3 | 25.6 | 8.1 | 25.4 | 4.4 | 6.6 | 8.6 | 16.9 |
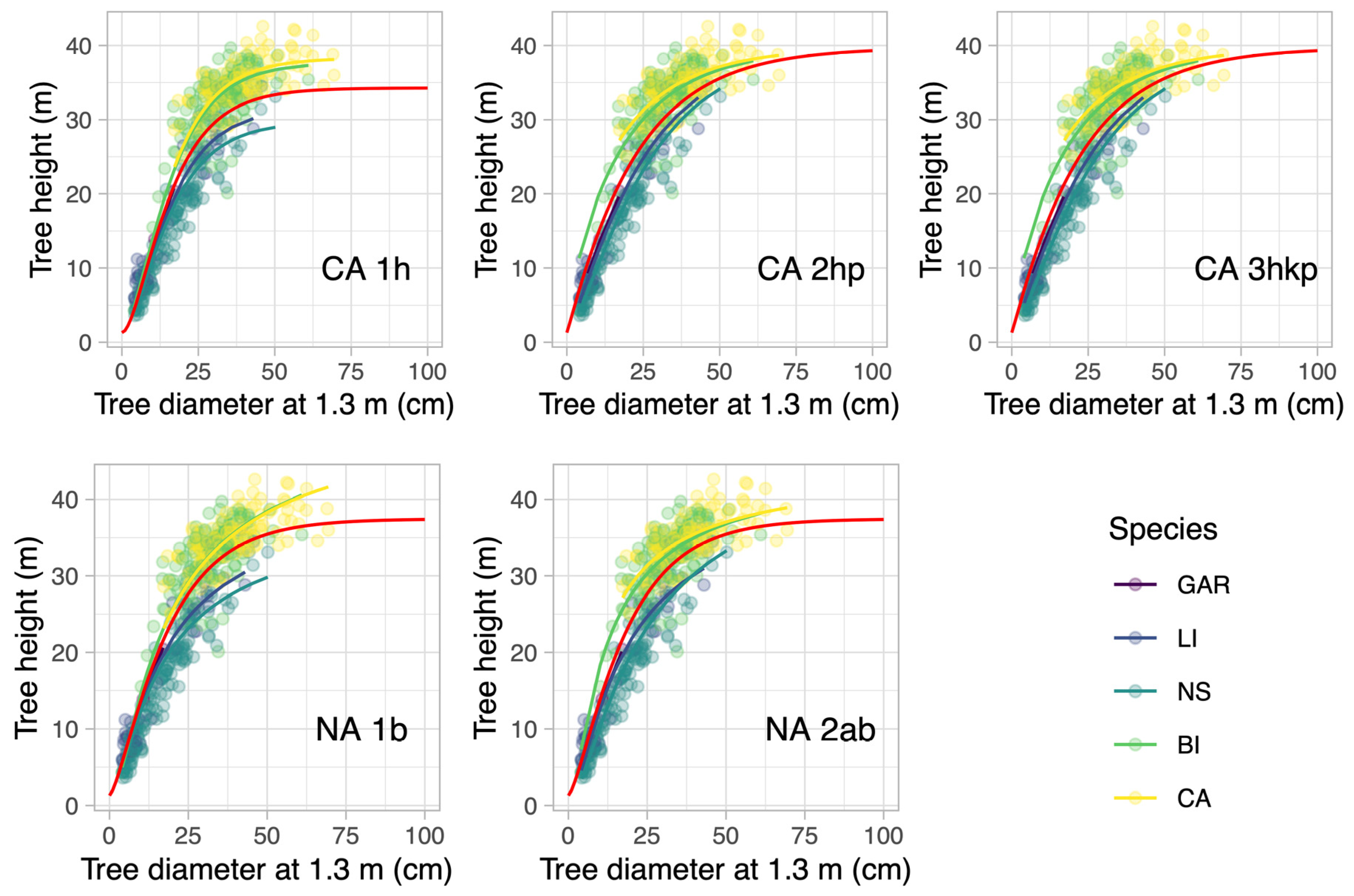
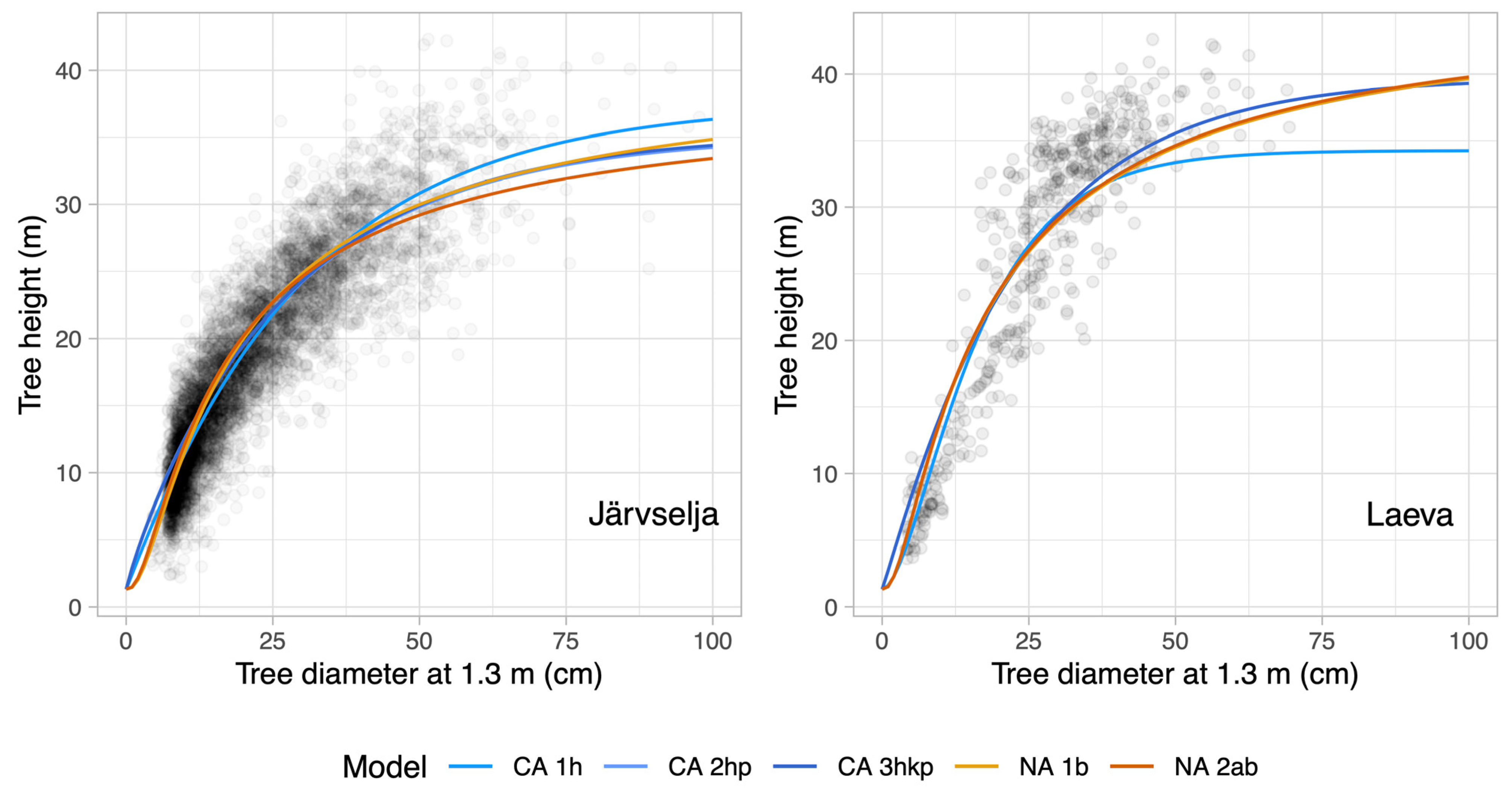
| Location | Equation | AIC | hmx | k | p | a | hmx |
|---|---|---|---|---|---|---|---|
| Järvselja | CA 1h | 26,515.46 | 36.27 ± 1.26 | 0.034 ± 0.002 | 1.027 ± 0.024 | - | - |
| CA 2hp | 25,974.98 | 33.89 ± 1.41 | 0.035 ± 0.002 | 0.900 ± 0.064 | - | - | |
| CA 3hkp | 25,974.84 | 34.06 ± 1.43 | 0.035 ± 0.004 | 0.911 ± 0.075 | - | - | |
| NA 1b | 26,662.17 | - | - | - | 1.794 ± 0.015 | 42.09 ± 1.54 | |
| NA 2ab | 26,089.33 | - | - | - | 1.519 ± 0.123 | 38.57 ± 2.02 | |
| Laeva | CA 1h | 2300.34 | 32.96 ± 1.78 | 0.085 ± 0.005 | 1.898 ± 0143 | - | - |
| CA 2hp | 2232.85 | 38.43 ± 0.65 | 0.046 ± 0.003 | 1.070 ± 0.157 | - | - | |
| CA 3hkp | 2234.85 | 38.43 ± 0.65 | 0.046 ± 0.003 | 1.069 ± 0.157 | - | - | |
| NA 1b | 2352.55 | - | - | - | 1.514 ± 0.052 | 46.33 ± 2.90 | |
| NA 2ab | 2243.96 | - | - | - | 1.454 ± 0.0206 | 46.06 ± 1.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nigul, K.; Padari, A.; Kiviste, A.; Noe, S.M.; Korjus, H.; Laarmann, D.; Frelich, L.E.; Jõgiste, K.; Stanturf, J.A.; Paluots, T.; et al. The Possibility of Using the Chapman–Richards and Näslund Functions to Model Height–Diameter Relationships in Hemiboreal Old-Growth Forest in Estonia. Forests 2021, 12, 184. https://doi.org/10.3390/f12020184
Nigul K, Padari A, Kiviste A, Noe SM, Korjus H, Laarmann D, Frelich LE, Jõgiste K, Stanturf JA, Paluots T, et al. The Possibility of Using the Chapman–Richards and Näslund Functions to Model Height–Diameter Relationships in Hemiboreal Old-Growth Forest in Estonia. Forests. 2021; 12(2):184. https://doi.org/10.3390/f12020184
Chicago/Turabian StyleNigul, Kristi, Allar Padari, Andres Kiviste, Steffen M. Noe, Henn Korjus, Diana Laarmann, Lee E. Frelich, Kalev Jõgiste, John A. Stanturf, Teele Paluots, and et al. 2021. "The Possibility of Using the Chapman–Richards and Näslund Functions to Model Height–Diameter Relationships in Hemiboreal Old-Growth Forest in Estonia" Forests 12, no. 2: 184. https://doi.org/10.3390/f12020184
APA StyleNigul, K., Padari, A., Kiviste, A., Noe, S. M., Korjus, H., Laarmann, D., Frelich, L. E., Jõgiste, K., Stanturf, J. A., Paluots, T., Põldveer, E., Kängsepp, V., Jürgenson, H., Metslaid, M., & Kangur, A. (2021). The Possibility of Using the Chapman–Richards and Näslund Functions to Model Height–Diameter Relationships in Hemiboreal Old-Growth Forest in Estonia. Forests, 12(2), 184. https://doi.org/10.3390/f12020184









