Rheological Properties of Wood–Plastic Composites by 3D Numerical Simulations: Different Components
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of Composites
2.3. Rheological Parameters
2.4. Polyflow Software Numerical Analysis
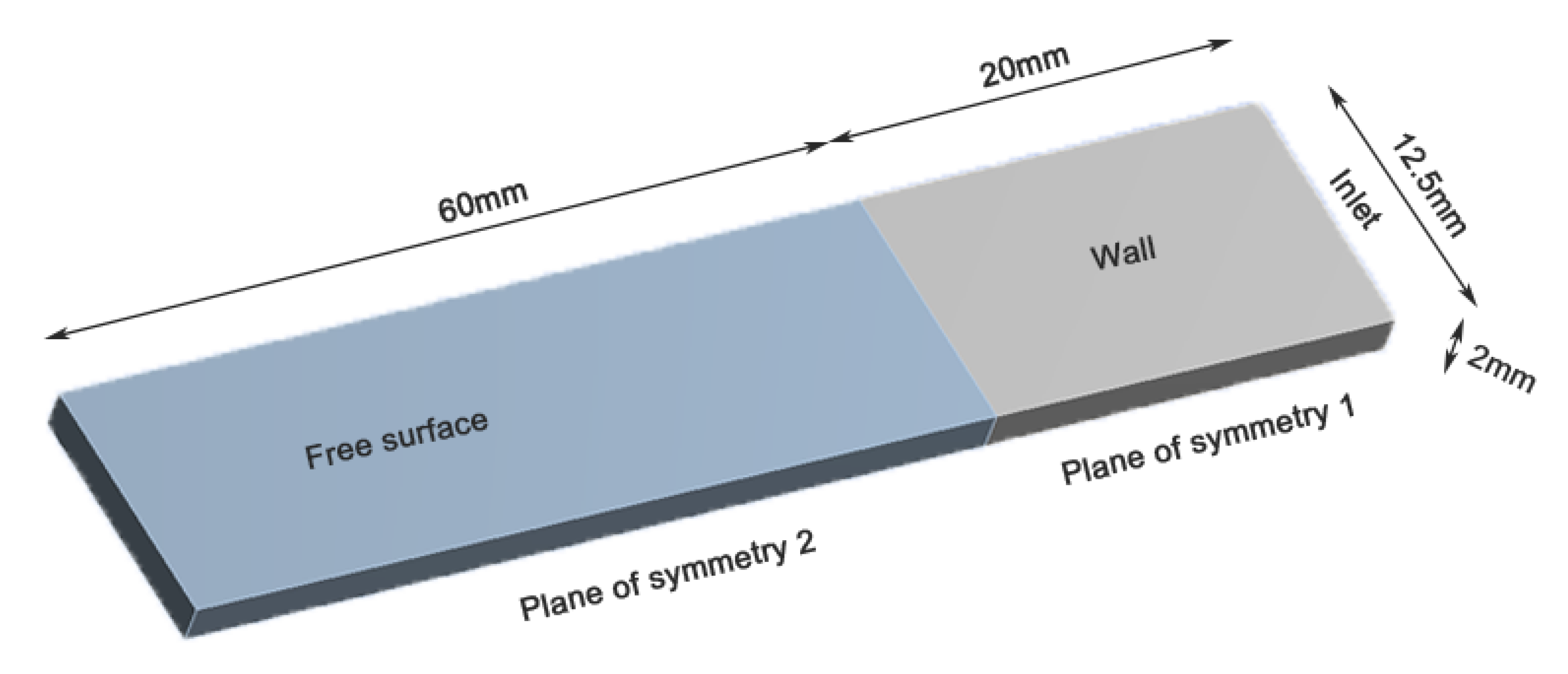
2.4.1. Finite Element Model
2.4.2. Simulation Condition
- (1)
- The material used for extrusion was an incompressible, highly viscous, non-Newtonian fluid.
- (2)
- The material fully filled the mold and underwent isothermal, steady, and laminar flow in the flow channel.
- (3)
- Inertia and gravity were neglected due to the slow flow velocity and high viscosity.
- (4)
- There was no slip between the material and the channel wall during extrusion [25].
2.4.3. Details of the Finite Element Calculations
2.4.4. Simulation Scheme
3. Results
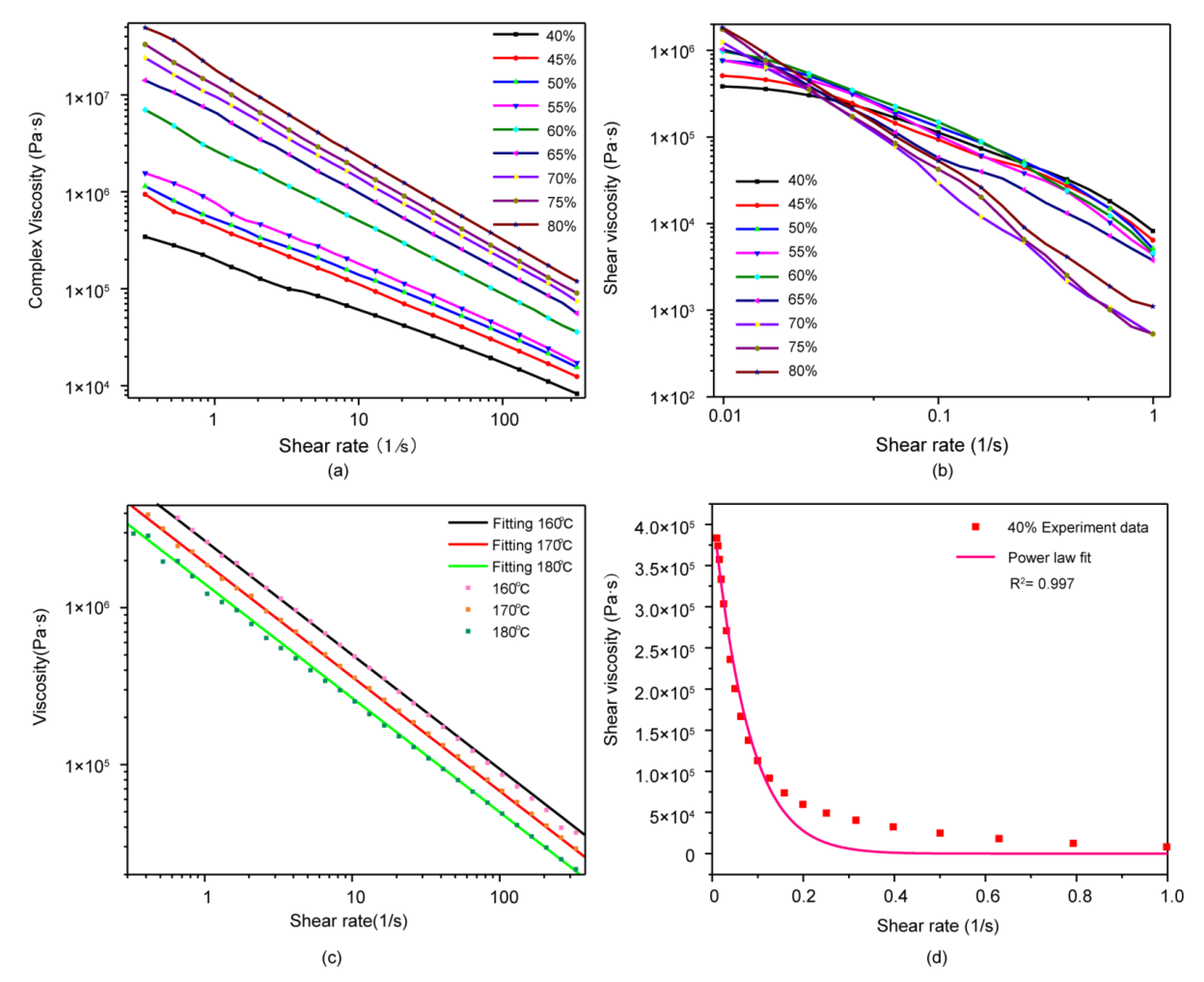
3.1. Rheological Behavior of Materials
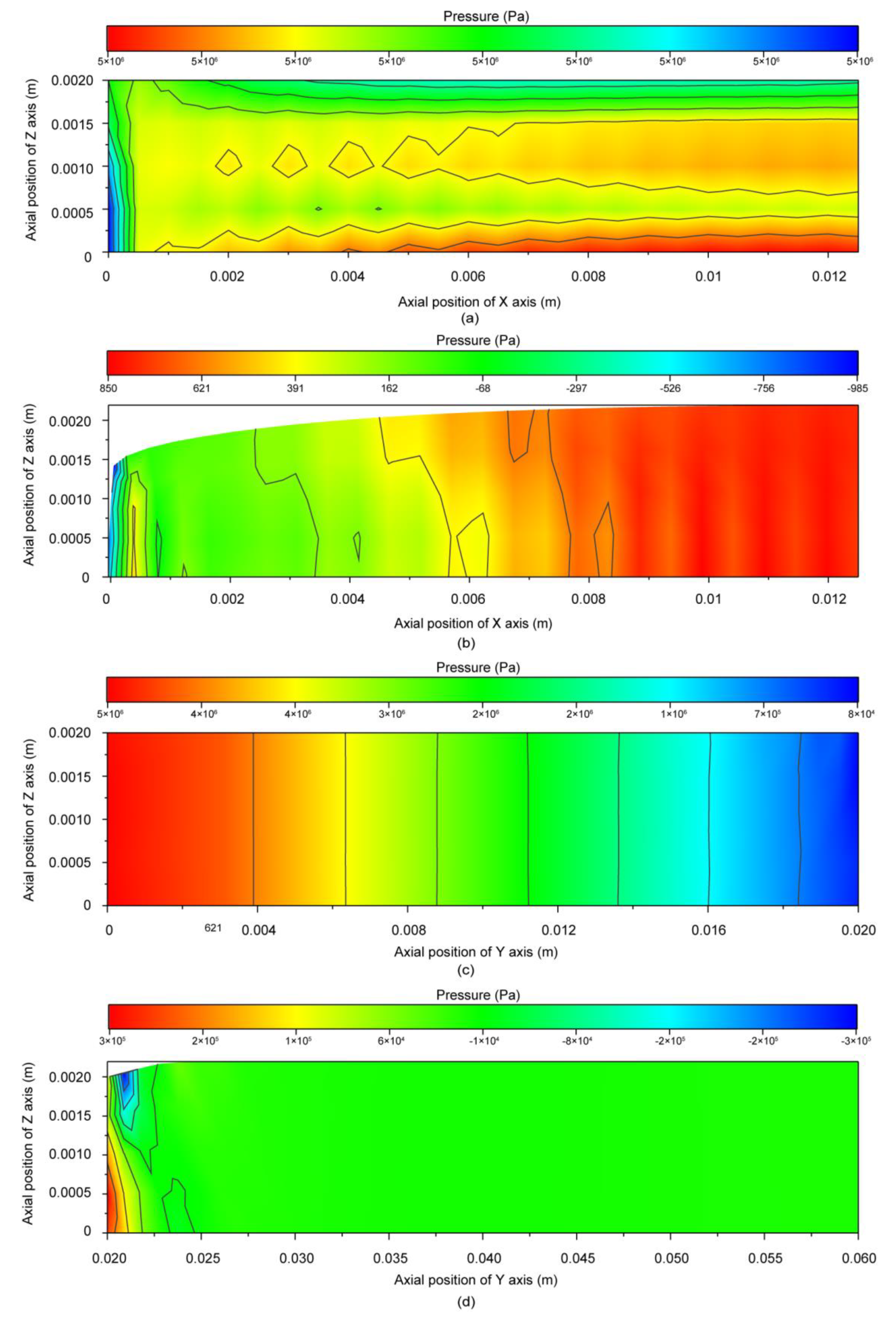
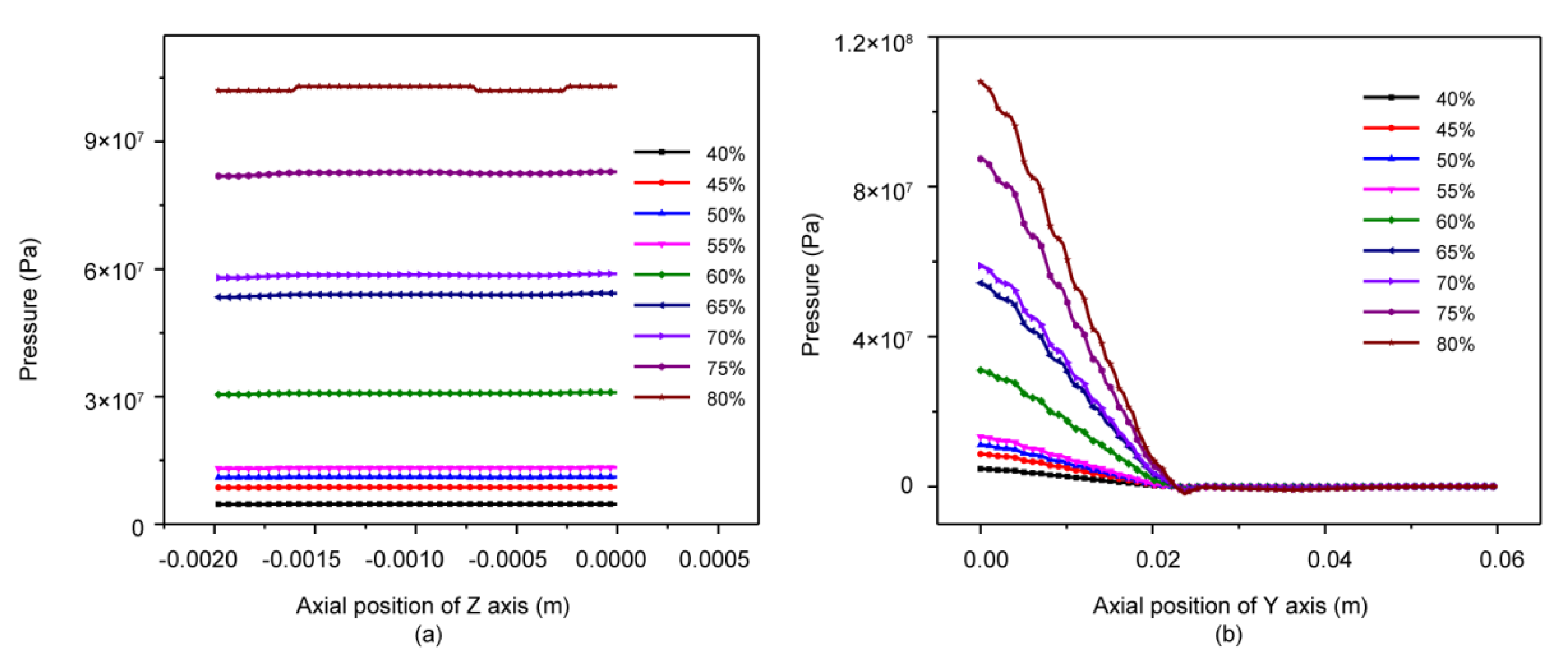
3.2. Pressure Distribution Field Analysis
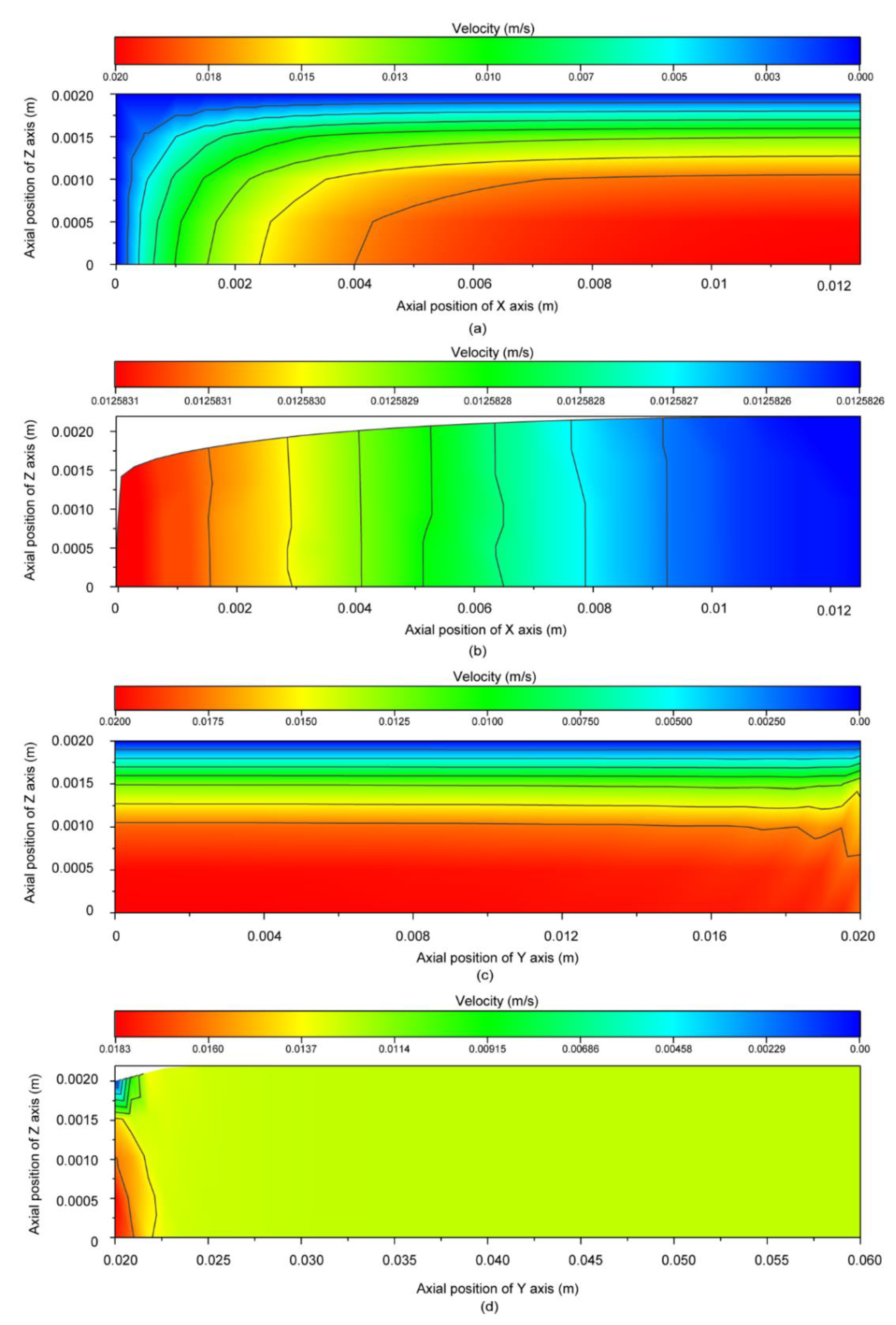
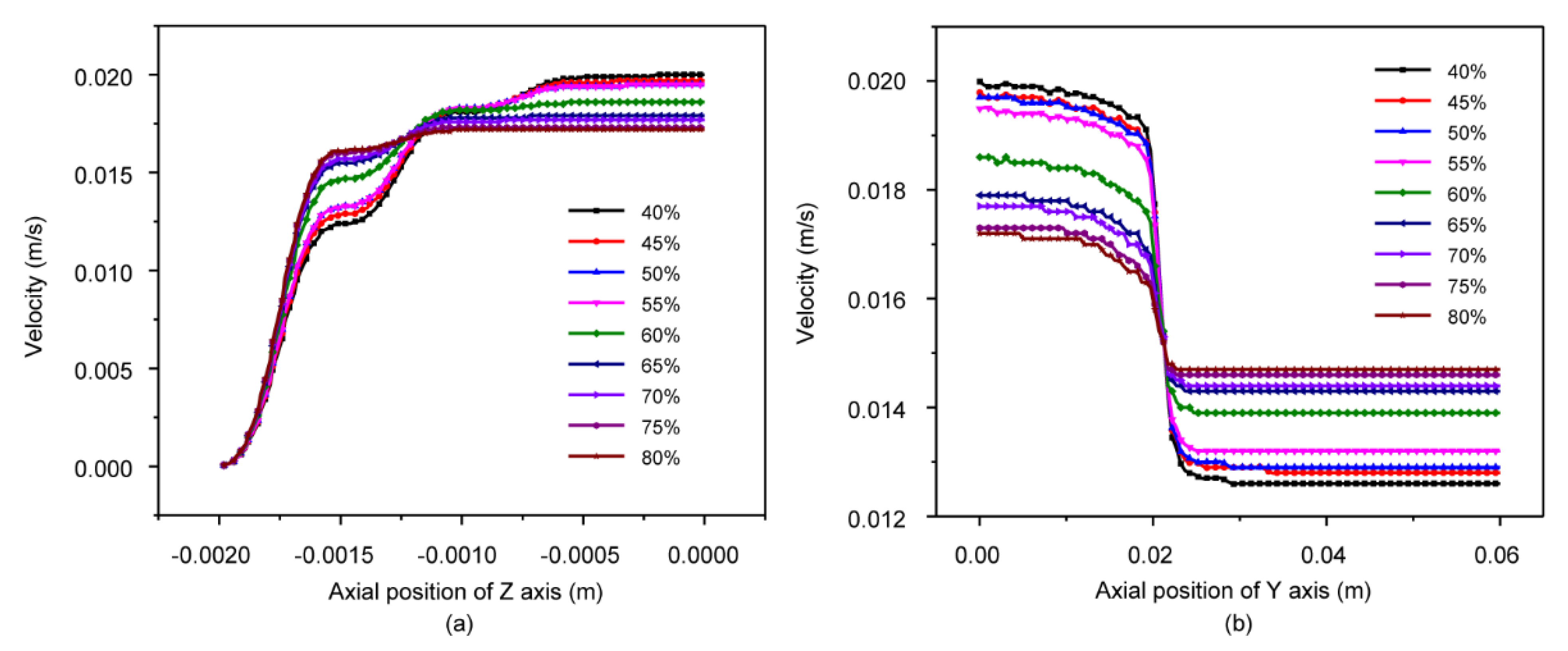
3.3. Velocity Distribution Field Analysis
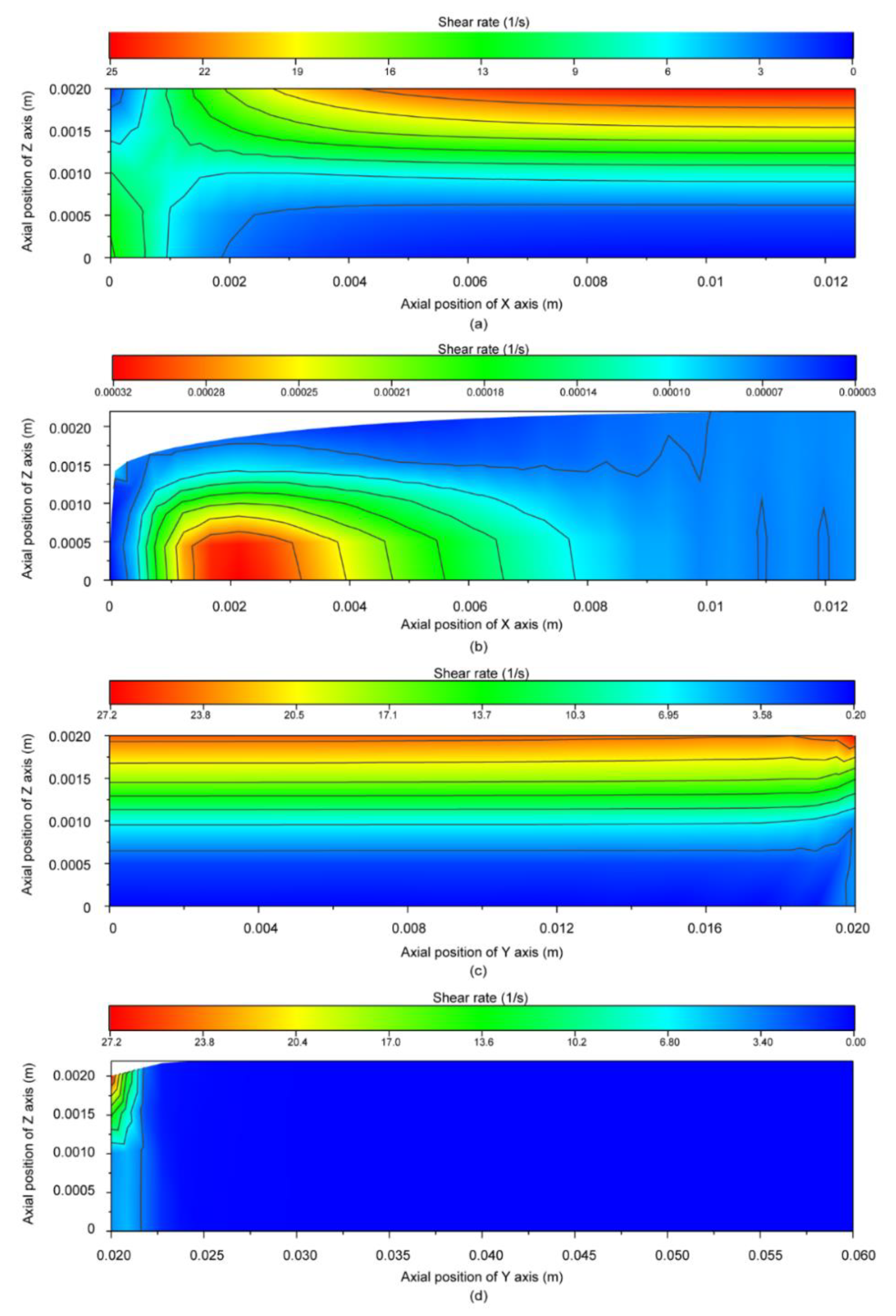
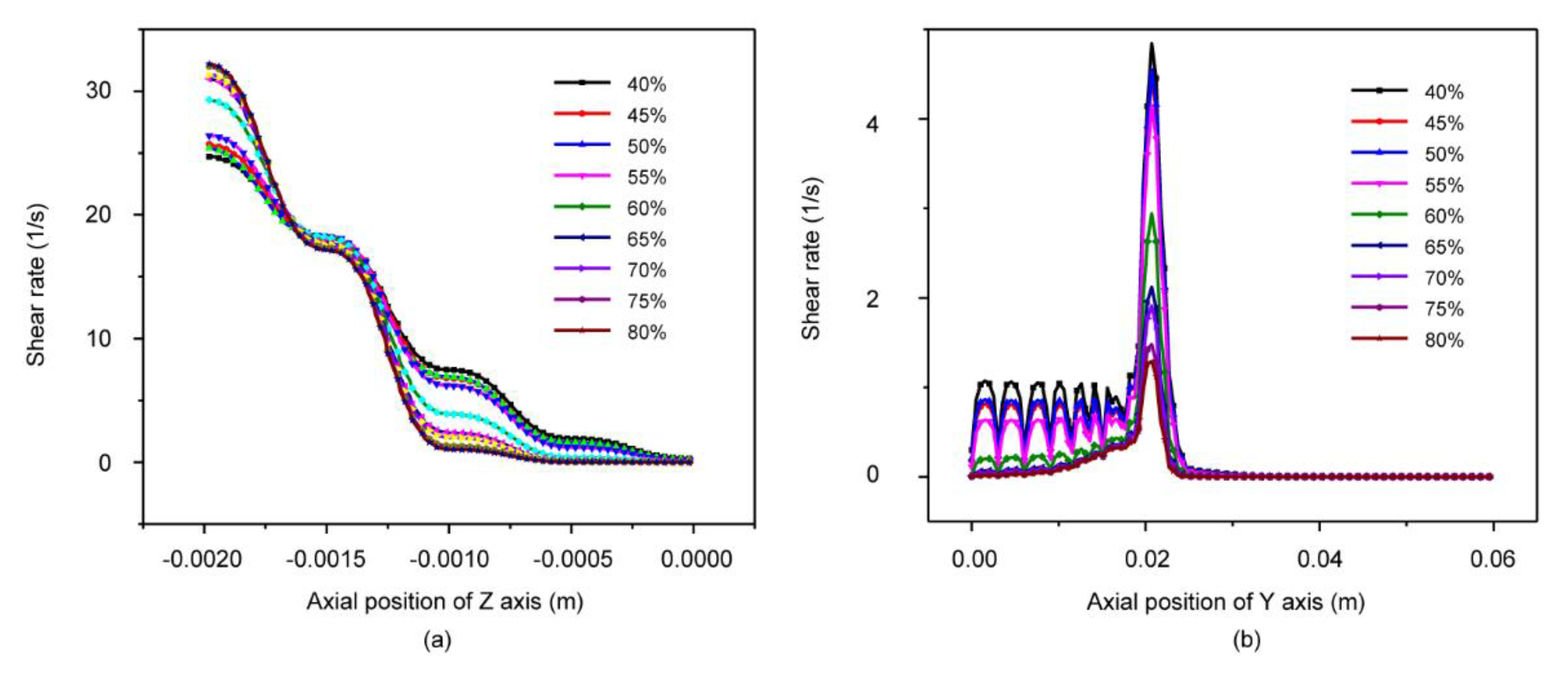
3.4. Shear Rate Distribution Field Analysis
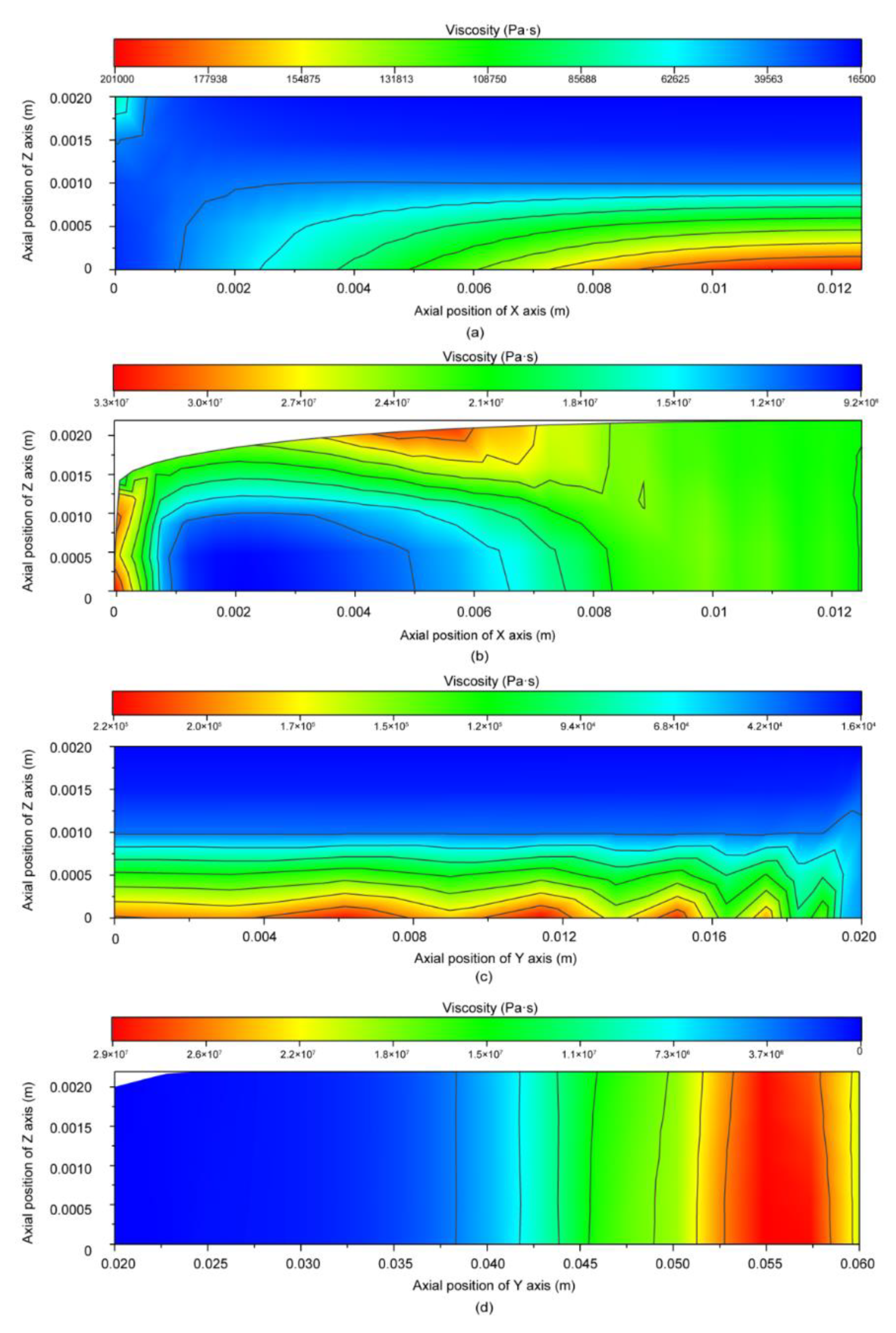
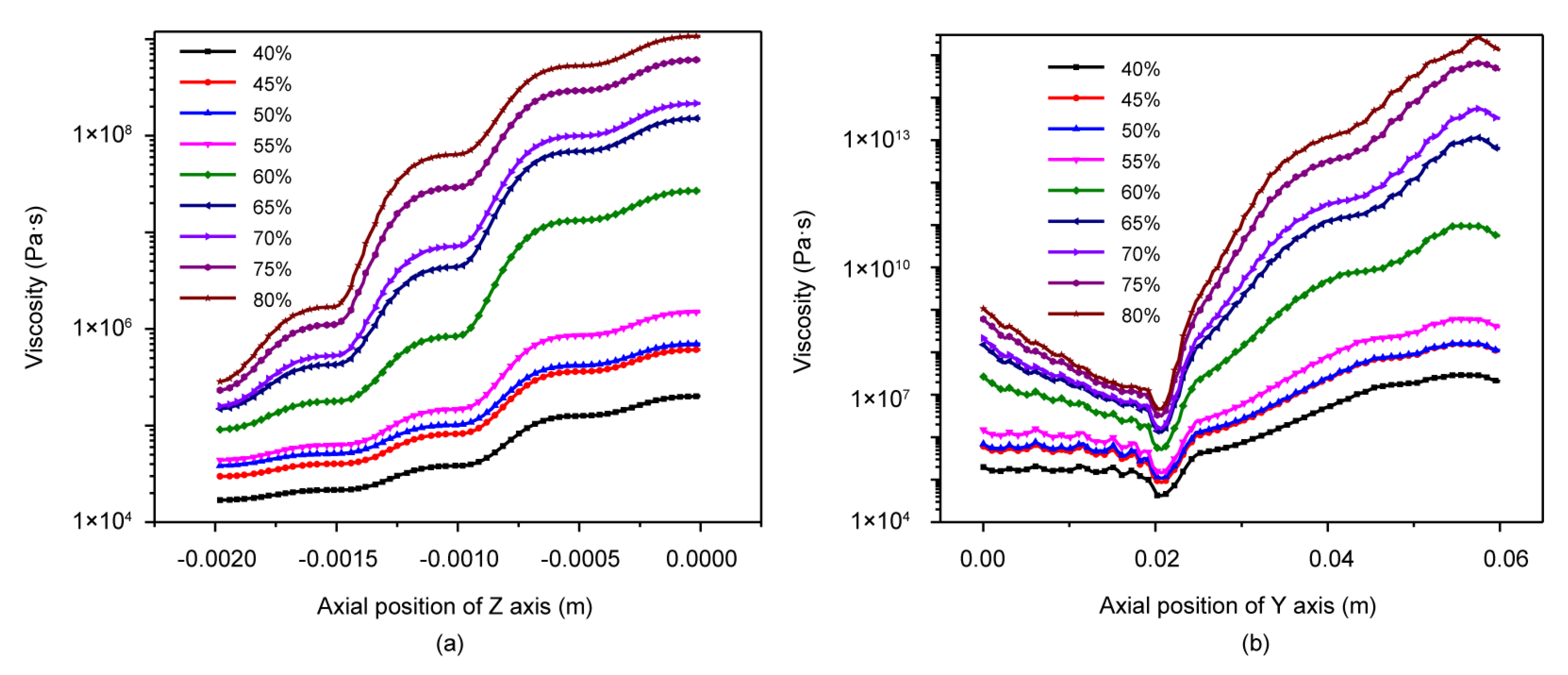
3.5. Viscosity Distribution Field Analysis
4. Discussion
4.1. Effect of Different Components on Pressure Field Distribution
4.2. Effect of Different Components on Viscosity Field Distribution
4.3. Effect of Different Components on Velocity and Shear Rate Field Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yatigala, N.S.; Bajwa, D.S.; Bajwa, S.G. Compatibilization improves physico-mechanical properties of biodegradable biobased polymer composites. Compos. Part A Appl. Sci. Manuf. 2018, 107, 315–325. [Google Scholar] [CrossRef]
- Uitterhaegen, E.; Parinet, J.; Labonne, L.; Merian, T.; Ballas, S.; Veronese, T.; Merah, O.; Talou, T.; Stevens, C.V.; Chabert, F.; et al. Performance, durability and recycling of thermoplastic biocomposites reinforced with coriander straw. Compos. Part A Appl. Sci. Manuf. 2018, 113, 254–263. [Google Scholar] [CrossRef]
- Kirchhoff, N.; Schröder, C.; Stute, D.; Moritzer, E.; Schmid, H. Wood-Plastic-Composites: Rheologische Charakterisierung und Füllverhalten im Spritzgießprozess. Chem. Ing. Tech. 2012, 84, 1584–1589. [Google Scholar] [CrossRef]
- Sarabi, M.T.; Behravesh, A.H.; Shahi, P.; Daryabari, Y. Effect of polymeric matrix melt flow index in reprocessing extruded wood-plastic composites. J. Thermoplast. Compos. 2014, 27, 881–894. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Faruk, O. Wood fiber reinforced polypropylene composites: Compression and injection molding process. Polym. Plast. Technol. 2004, 43, 871–888. [Google Scholar] [CrossRef]
- Ou, R.; Wang, Q.; Wolcott, M.P.; Sui, S.; Xie, Y.; Song, Y. Effects of Chemical Modification of Wood Flour on the Rheological Properties of High-Density Polyethylene Blends. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Mazzanti, V.; Mollica, F. In-line rheometry of polypropylene based Wood Polymer Composites. Polym. Test. 2015, 47, 30–35. [Google Scholar] [CrossRef]
- Cheung, H.; Ho, M.; Lau, K.; Cardona, F.; Hui, D. Natural fibre-reinforced composites for bioengineering and environmental engineering applications. Compos. Part B Eng. 2009, 40, 655–663. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of HDPE-wood composites. I. Steady state shear and extensional flow. Compos. Part A Appl. Sci. Manuf. 2004, 35, 303–311. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of wood plastics melt, part 2: Effects of lubricating systems in HDPE/maple composites. Polym. Eng. Sci. 2006, 46, 464–473. [Google Scholar] [CrossRef]
- Laufer, N.; Hansmann, H.; Koch, M. Rheological Characterisation of the Flow Behaviour of Wood Plastic Composites in Consideration of Different Volume Fractions of Wood. J. Phys. Conf. 2017, 790, 12017. [Google Scholar] [CrossRef]
- Mazzanti, V.; Mollica, F.; El Kissi, N. Rheological and mechanical characterization of polypropylene-based wood plastic composites. Polym. Compos. 2016, 37, 3460–3473. [Google Scholar] [CrossRef]
- Godard, F.; Vincent, M.; Agassant, J.F.; Vergnes, B. Rheological behavior and mechanical properties of sawdust/polyethylene composites. J. Appl. Polym. Sci. 2009, 112, 2559–2566. [Google Scholar] [CrossRef]
- Mazzanti, V.; Mollica, F. Rheological behavior of wood flour filled poly(lactic acid): Temperature and concentration dependence. Polym. Compos. 2019, 401, E169–E176. [Google Scholar] [CrossRef]
- Altug, M.; Kaya, S.; Guldas, A.; Zeyveli, M. Investigation of rheological and mechanical properties of wood flour reinforced polypropylene. Mater. Werkst. 2018, 49, 73–88. [Google Scholar] [CrossRef]
- Yilmaz, O.; Gunes, H.; Kirkkopru, K. Optimization of a profile extrusion die for flow balance. Fibers Polym. 2014, 15, 753–761. [Google Scholar] [CrossRef]
- Sun, D.; Zhu, X.; Gao, M. 3D Numerical Simulation of Reactive Extrusion Processes for Preparing PP/TiO2 Nanocomposites in a Corotating Twin Screw Extruder. Materials 2019, 12, 671. [Google Scholar] [CrossRef]
- Tang, D.; Marchesini, F.H.; D’Hooge, D.R.; Cardon, L. Isothermal flow of neat polypropylene through a slit die and its die swell: Bridging experiments and 3D numerical simulations. J. Non-Newton. Fluid 2019, 266, 33–45. [Google Scholar] [CrossRef]
- Sun, Y.D.; Chen, Q.R.; Sun, W.J. Numerical simulation of extrusion process and die structure optimization for a complex magnesium doorframe. Int. J. Adv. Manuf. Technol. 2015, 80, 495–506. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, N.; Wei, W.; Hu, X.; Tan, Y.; Yu, Y.; Deng, Y.; Bi, C.; Zhang, L.; Zhang, H. Assessing the dynamic extrusion-based 3D printing process for power-law fluid using numerical simulation. J. Food Eng. 2020, 275. [Google Scholar] [CrossRef]
- Wen, J.S.; Yang, M.K.; Fan, D.J. Numerical simulation of energy consumption in the melt conveying section of eccentric rotor extruders. Adv. Polym. Technol. 2018, 37, 3335–3347. [Google Scholar] [CrossRef]
- Díaz, J.J.D.C.; Nieto, P.J.G.; García, A.B.; Mu Oz, J.G.; Meré, J.O. Finite volume modeling of the non-isothermal flow of a non-Newtonian fluid in a rubber’s extrusion die. J. Non-Cryst. Solids 2008, 354, 5334–5336. [Google Scholar] [CrossRef]
- Chen, Z. Research on the Impact of 3D Printing on the International Supply Chain. Adv. Mater. Sci. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Yang, F.; Guo, C.; Zhang, M.; Bhandari, B.; Liu, Y. Improving 3D printing process of lemon juice gel based on fluid flow numerical simulation. LWT Food Sci. Technol. 2019, 102, 89–99. [Google Scholar] [CrossRef]
- Mazzanti, V.; Mollica, F. Pressure dependent wall slip of wood flour filled polymer melts. J. Non-Newton. Fluid 2017, 247, 178–187. [Google Scholar] [CrossRef]
- Mompean, G.; Thais, L.; Tomé, M.F.; Castelo, A. Numerical prediction of three-dimensional time-dependent viscoelastic extrudate swell using differential and algebraic models. Comput. Fluids 2011, 44, 68–78. [Google Scholar] [CrossRef]
- Han, C.D. What is the role of “pressure” in the use of capillary and slit flows to determine the shear-rate dependent viscosity of a viscoelastic fluid? Polym. Eng. Sci. 2008, 48, 1126–1140. [Google Scholar] [CrossRef]
- Zhang, J.; Rizvi, G.M.; Park, C.B.; Hasan, M.M. Study on cell nucleation behavior of HDPE–wood composites/supercritical CO2 solution based on rheological properties. J. Mater. Sci. 2011, 46, 3777–3784. [Google Scholar] [CrossRef]
- Garcia-Rejon, A.; Diraddo, R.W.; Ryan, M.E. Effect of die geometry and flow characteristics on viscoelastic annular swell. J. Non-Newton. Fluid 1995, 60, 107–128. [Google Scholar] [CrossRef]
- Tang, D.; Marchesini, F.H.; Cardon, L.; D’Hooge, D.R. The impact of upstream contraction flow on three-dimensional polymer extrudate swell from slit dies. J. Non-Newton. Fluid 2020, 282, 104337. [Google Scholar] [CrossRef]
- Gleissle, W.; Hochstein, B. Validity of the Cox–Merz rule for concentrated suspensions. J. Rheol. 2003, 47, 897–910. [Google Scholar] [CrossRef]
- Touloupidis, V.; Wurnitsch, C.; Albunia, A.; Galgali, G. Connecting Linear Polymers Molecular Structure to Viscoelastic Properties and Melt Flow Index. Macromol. Theory Simul. 2016, 25, 392–402. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Z.; Wang, Z.; Wang, B.; Feng, C. Optimizing torque rheometry parameters for assessing the rheological characteristics and extrusion processability of wood plastic composites. J. Thermoplast. Compos. 2019, 32, 123–140. [Google Scholar]
- Wu, G.; Song, Y.; Zheng, Q.; Du, M.; Zhang, P. Dynamic rheological properties for HDPE/CB composite melts. J. Appl. Polym. Sci. 2003, 88, 2160–2167. [Google Scholar] [CrossRef]
- Habibi, M.; Najafi, S.K.; Ghasemi, I. Rheological and mechanical properties of composites made from wood flour and recycled LDPE/HDPE blend. Iran. Polym. J. 2017, 26, 949–956. [Google Scholar] [CrossRef]
- Habib, M.A.; Said, S.A.M.; Badr, H.M.; Hussaini, I.; Al Bagawi, J.J. Effect of geometry on flow field and oil/water separation in vertical deadlegs. Int. J. Numer. Methods Heart 2005, 15, 348–362. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, S.; Li, F.; Wu, F.; Yao, T. The chain scission extent of polystyrene in different shear flow fields. Polym. Eng. Sci. 2018, 58, 913–919. [Google Scholar] [CrossRef]
| WF/wt% | HDPE/wt% | MAPE/wt% | Lubricant/wt% |
|---|---|---|---|
| 40 | 55 | 3 | 2 |
| 45 | 50 | 3 | 2 |
| 50 | 45 | 3 | 2 |
| 55 | 40 | 3 | 2 |
| 60 | 35 | 3 | 2 |
| 65 | 30 | 3 | 2 |
| 70 | 25 | 3 | 2 |
| 75 | 20 | 3 | 2 |
| 80 | 15 | 3 | 2 |
| WF/wt% | R2 | |||
|---|---|---|---|---|
| 40 | 53,087 | 0.440 | 0.312 | 0.977 |
| 45 | 97,483 | 0.411 | 0.275 | 0.981 |
| 50 | 127,732 | 0.401 | 0.293 | 0.981 |
| 55 | 169,396 | 0.356 | 0.308 | 0.987 |
| 60 | 498,320 | 0.246 | 0.327 | 0.996 |
| 65 | 957,822 | 0.186 | 0.320 | 0.988 |
| 70 | 1,076,080 | 0.171 | 0.322 | 0.981 |
| 75 | 1,569,410 | 0.143 | 0.295 | 0.981 |
| 80 | 1,918,580 | 0.131 | 0.284 | 0.985 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, X.; Hao, X.; Ou, R.; Liu, T.; Guo, C.; Wang, Q.; Yi, X.; Sun, L. Rheological Properties of Wood–Plastic Composites by 3D Numerical Simulations: Different Components. Forests 2021, 12, 417. https://doi.org/10.3390/f12040417
Lv X, Hao X, Ou R, Liu T, Guo C, Wang Q, Yi X, Sun L. Rheological Properties of Wood–Plastic Composites by 3D Numerical Simulations: Different Components. Forests. 2021; 12(4):417. https://doi.org/10.3390/f12040417
Chicago/Turabian StyleLv, Xingcong, Xiaolong Hao, Rongxian Ou, Tao Liu, Chuigen Guo, Qingwen Wang, Xin Yi, and Lichao Sun. 2021. "Rheological Properties of Wood–Plastic Composites by 3D Numerical Simulations: Different Components" Forests 12, no. 4: 417. https://doi.org/10.3390/f12040417
APA StyleLv, X., Hao, X., Ou, R., Liu, T., Guo, C., Wang, Q., Yi, X., & Sun, L. (2021). Rheological Properties of Wood–Plastic Composites by 3D Numerical Simulations: Different Components. Forests, 12(4), 417. https://doi.org/10.3390/f12040417






