Analysis of the Structure and Hydraulic Function of Bordered Pits Using the Lattice Boltzman Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Lattice Boltzmann Method
2.2. Curved Boundary Treatment for LBM of Micro-Scale Liquid Flow in Pits
2.3. Materials and Numerical Parameters
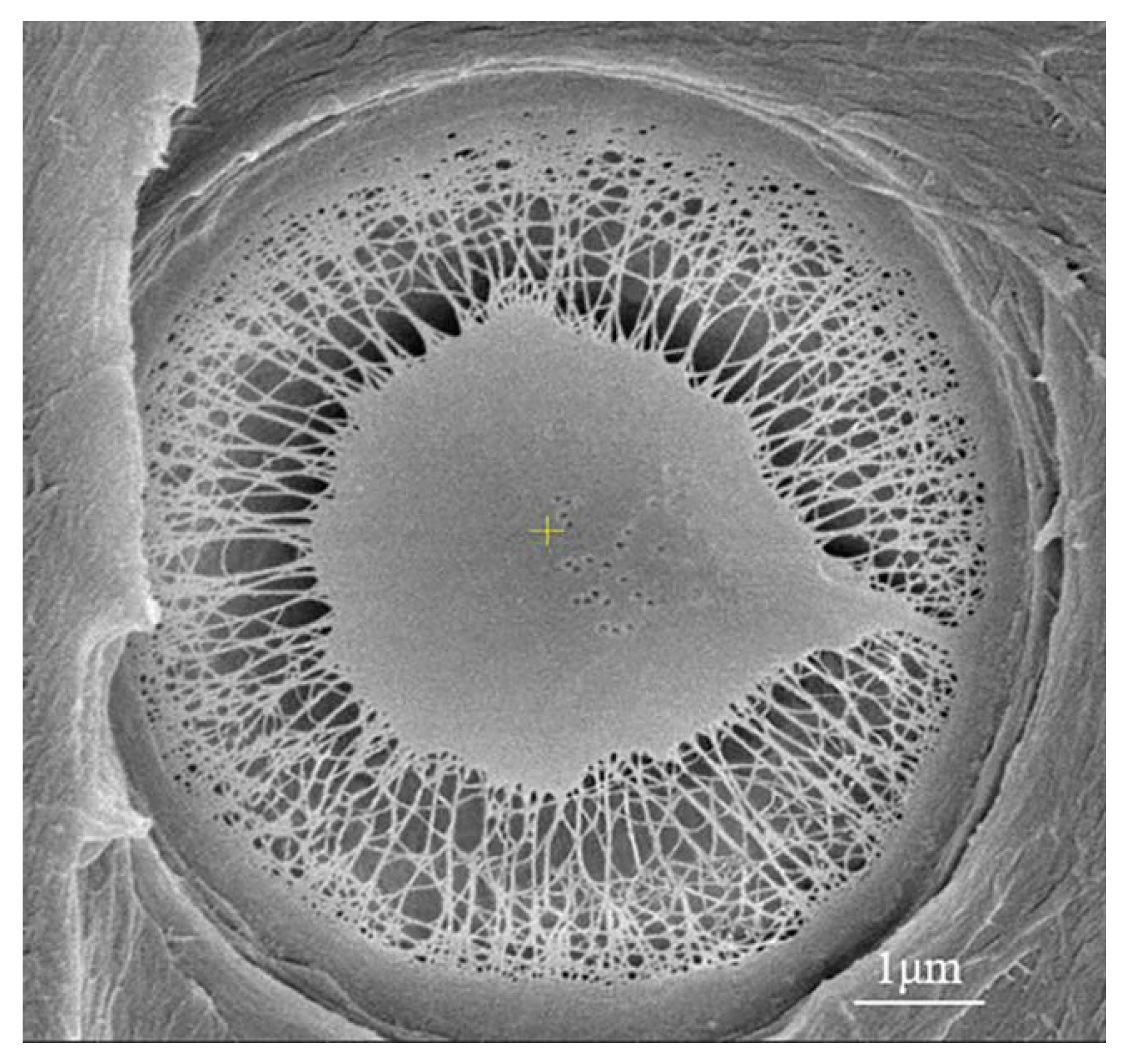
3. Results and Discussion
3.1. Simulations of the Water Flow through Different Components of the Bordered Pits
3.2. Influence of Pit Structure on Flow Rate and Pressure Drop
3.3. Flow Analysis of Margo Pores
3.4. Verification and Analysis of Flow Resistance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Bonetti, S.; Breitenstein, D.; Fatichi, S.; Domec, J.; Or, D. Persistent decay of fresh xylem hydraulic conductivity varies with pressure gradient and marks plant responses to injury. Plant Cell Environ. 2021, 44, 371–386. [Google Scholar] [CrossRef]
- Rakefet, D.-S.; Indira, P.; Maayan, M.; Sylvain, D.; Cochard, H.; Victor, L.; Eric, B.; Gaelle, C.; Galina, S.; Shabtai, C. Indirect evidence for genetic differentiation in vulnerability to embolism in pinus halepensis. Front. Plant Sci. 2016, 7, 768–782. [Google Scholar]
- Liu, Y.-Y.; Wang, A.-Y.; An, Y.-N.; Lian, P.-Y.; Wu, D.-D.; Zhu, J.-J.; Meinzer, F.C.; Hao, G.-Y. Hydraulics play an important role in causing low growth rate and dieback of aging Pinus sylvestris var. mongolica trees in plantations of Northeast China. Plant Cell Environ. 2018, 41, 1500–1511. [Google Scholar] [CrossRef]
- Gevú, K.V.; Lima, H.R.P.; Kress, J.; Da Cunha, M. Morphological analysis of vessel elements for systematic study of three Zingiberaceae tribes. J. Plant Res. 2017, 130, 527–538. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schulte, P.J.; Hacke, U.G. Solid mechanics of the torus-margo in conifer inter-tracheid bordered pits. New Phytol. 2020, 229, 1431–1439. [Google Scholar] [CrossRef]
- Medeiros, J.S.; Frederic, L.; Maherali, H.; Steven, J. Vestured pits and scalariform perforation plate morphology modify the relationships between angiosperm vessel diameter, climate and maximum plant height. New Phytol. 2018, 221, 1802–1813. [Google Scholar] [CrossRef] [PubMed]
- Brodersen, C.; Jansen, S.; Choat, B.; Rico, C.; Pittermann, J. Cavitation resistance in seedless vascular plants: The structure and function of interconduit pit membranes. Plant Physiol. 2014, 165, 895–904. [Google Scholar] [CrossRef] [Green Version]
- Jansen, S.; Lamy, J.-B.; Burlett, R.; Cochard, H.; Gasson, P.; Delzon, S. Plasmodesmatal pores in the torus of bordered pit membranes affect cavitation resistance of conifer xylem. Plant Cell Environ. 2012, 35, 1109–1120. [Google Scholar] [CrossRef]
- Schulte, P.J.; Gibson, A.C. Hydraulic conductance and tracheid anatomy in six species of extant seed plants. Can. J. Bot. Rev. Can. Bot. 1988, 66, 1073–1079. [Google Scholar] [CrossRef]
- Choat, B.; Cobb, A.R.; Jansen, S. Structure and function of bordered pits: New discoveries and impacts on whole-plant hydraulic function. New Phytol. 2008, 177, 608–626. [Google Scholar] [CrossRef] [PubMed]
- Choat, B.; Brodie, T.W.; Cobb, A.R.; Zwieniecki, M.A.; Holbrook, N.M. Direct measurements of intervessel pit membrane hydraulic resistance in two angiosperm tree species. Am. J. Bot. 2006, 93, 993–1000. [Google Scholar] [CrossRef] [Green Version]
- Lancashire, J.R.; Ennos, A.R. Modelling the hydrodynamic resistance of bordered pits. J. Exp. Bot. 2002, 373, 1485–1493. [Google Scholar] [CrossRef]
- Schoonmaker, A.L.; Hacke, U.G.; Landhäusser, S.M.; Lieffers, V.J.; Tyree, M.T. Hydraulic acclimation to shading in boreal conifers of varying shade tolerance. Plant Cell Environ. 2010, 33, 382–393. [Google Scholar] [CrossRef]
- Valli, A.; Koponen, A.; Vesala, T.; Timonen, J. Simulations of water flow through bordered pits of conifer xylem. J. Stat. Phys. 2002, 107, 121–142. [Google Scholar] [CrossRef]
- Schulte, P.J. Computational fluid dynamics models of conifer bordered pits show how pit structure affects flow. New Phytol. 2011, 193, 721–729. [Google Scholar] [CrossRef]
- Schulte, P.J.; Hacke, U.G.; Schoonmaker, A.L. Pit membrane structure is highly variable and accounts for a major resistance to water flow through tracheid pits in stems and roots of two boreal conifer species. New Phytol. 2015, 208, 102–113. [Google Scholar] [CrossRef] [PubMed]
- Jithin, M.; Kumar, N.; De, A.; Das, M.K. Pore-scale simulation of shear thinning fluid flow using lattice boltzmann method. Transp. Porous Media 2017, 121, 753–782. [Google Scholar] [CrossRef]
- Kim, Y.H.; Xu, X.; Lee, J.S. The effect of stent porosity and strut shape on saccular aneurysm and its numerical analysis with lattice boltzmann method. Ann. Biomed. Eng. 2010, 38, 2274–2292. [Google Scholar] [CrossRef]
- Eshghinejadfard, A.; Daróczy, L.; Janiga, G.; Thévenin, D. Calculation of the permeability in porous media using the lattice Boltzmann method. Int. J. Heat Fluid Flow 2016, 62, 93–103. [Google Scholar] [CrossRef]
- Filippova, O.; Hänel, D. Lattice-boltzmann simulation of gas-particle flow in filters. Comput. Fluids 1997, 26, 697–712. [Google Scholar] [CrossRef]
- Mei, R.; Yu, D.; Shyy, W.; Luo, L.-S. Force evaluation in the lattice Boltzmann method involving curved geometry. Phys. Rev. E 2002, 65, 041203. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Tao, S.; Meng, X.; Zhang, K.; Lu, G. Discrete effects on boundary conditions of the lattice Boltzmann method for fluid flows with curved no-slip walls. Phys. Rev. E. 2020, 101, 063307. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C. Biomechanics: Circulation; Springer: New York, NY, USA, 1997. [Google Scholar]
- Kvist, P.; Therning, A.; Gebäck, T.; Rasmuson, A. Lattice Boltzmann simulations of diffusion through native and steam-exploded softwood bordered pits. Wood Sci. Technol. 2017, 51, 1261–1276. [Google Scholar] [CrossRef] [Green Version]
- Kotowska, M.M.; Thom, R.; Zhang, Y.; Schenk, H.J.; Jansen, S. Within-tree variability and sample storage effects of bordered pit membranes in xylem of Acer pseudoplatanus. Trees 2019, 34, 61–71. [Google Scholar] [CrossRef]
- Lazzarin, M.; Crivellaro, A.; Williams, C.B.; Dawson, T.E.; Mozzi, G.; Anfodillo, T. Tracheid and pit anatomy vary in tandem in a tall sequoiadendron giganteum tree. IAWA J. 2016, 37, 172–185. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Xu, F.; Ai, Q.; Zhang, L. Hydrodynamics modeling and flow resistance characteristics simulation of plant tracheid pit. Trans. Chin. Soc. Agric. Mach. 2016, 6, 303–310. [Google Scholar]
- Pittermann, J.; Choat, B.; Jansen, S.; Stuart, S.A.; Lynn, L.; Dawson, T.E. The relationships between xylem safety and hydraulic efficiency in the Cupressaceae: The evolution of pit membrane form and function. Plant Physiol. 2010, 153, 1919–1931. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Zhang, L.; Li, Z. Computational fluid dynamics model and flow resistance characteristics of Jatropha curcas L xylem vessel. Sci. Rep. 2020, 10, 14728. [Google Scholar] [CrossRef] [PubMed]
- Pittermann, J.; Sperry, J.S.; Hacke, U.G.; Wheeler, J.K.; Sikkema, E.H. Torus-Margo Pits Help Conifers Compete with Angiosperms. Science 2005, 310, 1924. [Google Scholar] [CrossRef] [Green Version]
- Hacke, U.G.; Sperry, J.S.; Pittermann, J. Analysis of circular bordered pit function. II. Gymnosperm tracheids with torus-margo pit membranes. Am. J. Bot. 2004, 91, 386–400. [Google Scholar] [CrossRef] [Green Version]
- Sperry, J.S.; Hacke, U.G.; Wheeler, J.K. Comparative analysis of end wall resistivity in xylem conduits. Plant Cell Environ. 2005, 28, 456–465. [Google Scholar] [CrossRef]
- Hacke, U.G.; Sperry, J.S. Functional and ecological xylem anatomy. Perspect. Plant Ecol. Evol. Syst. 2013, 4, 97–115. [Google Scholar] [CrossRef] [Green Version]
- Choat, B.; Pittermann, J. New insights into bordered pit structure and cavitation resistance in angiosperms and conifers. New Phytol. 2009, 182, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Tixier, A.; Herbette, S.; Jansen, S.; Capron, M.; Tordjeman, P.; Cochard, H.; Badel, E. Modelling the mechanical behavior of pit membranes in bordered pits with respect to cavitation resistance in angiosperms. Ann. Bot. 2014, 114, 175–178. [Google Scholar] [CrossRef] [PubMed] [Green Version]









| Component | ΔP (Pa) | Resistance (Pa s m−3) | Fraction of Resistance (%) |
|---|---|---|---|
| No Border | 0.573 | 1.747 × 1013 | 0.116 |
| Border | 31.21 | 9.515 × 1014 | 6.36 |
| Torus | 127.4 | 3.884 × 1015 | 25.97 |
| Margo | 331.3 | 1.009 × 1016 | 67.55 |
| Sections | Resistance LBM-C (%) | Resistance MA-C (%) |
|---|---|---|
| Aperture | 15.07 | 12.02 |
| Torus | 20.42 | 19.59 |
| Margo | 64.51 | 68.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, W.; Yang, C.; Ma, Y.; Yu, W.; Qin, G.; Jin, Y. Analysis of the Structure and Hydraulic Function of Bordered Pits Using the Lattice Boltzman Method. Forests 2021, 12, 526. https://doi.org/10.3390/f12050526
Qu W, Yang C, Ma Y, Yu W, Qin G, Jin Y. Analysis of the Structure and Hydraulic Function of Bordered Pits Using the Lattice Boltzman Method. Forests. 2021; 12(5):526. https://doi.org/10.3390/f12050526
Chicago/Turabian StyleQu, Wen, Chunmei Yang, Yan Ma, Wenji Yu, Guangyi Qin, and Yufei Jin. 2021. "Analysis of the Structure and Hydraulic Function of Bordered Pits Using the Lattice Boltzman Method" Forests 12, no. 5: 526. https://doi.org/10.3390/f12050526
APA StyleQu, W., Yang, C., Ma, Y., Yu, W., Qin, G., & Jin, Y. (2021). Analysis of the Structure and Hydraulic Function of Bordered Pits Using the Lattice Boltzman Method. Forests, 12(5), 526. https://doi.org/10.3390/f12050526





