Global Tree Taper Modelling: A Review of Applications, Methods, Functions, and Their Parameters
Abstract
:1. Introduction
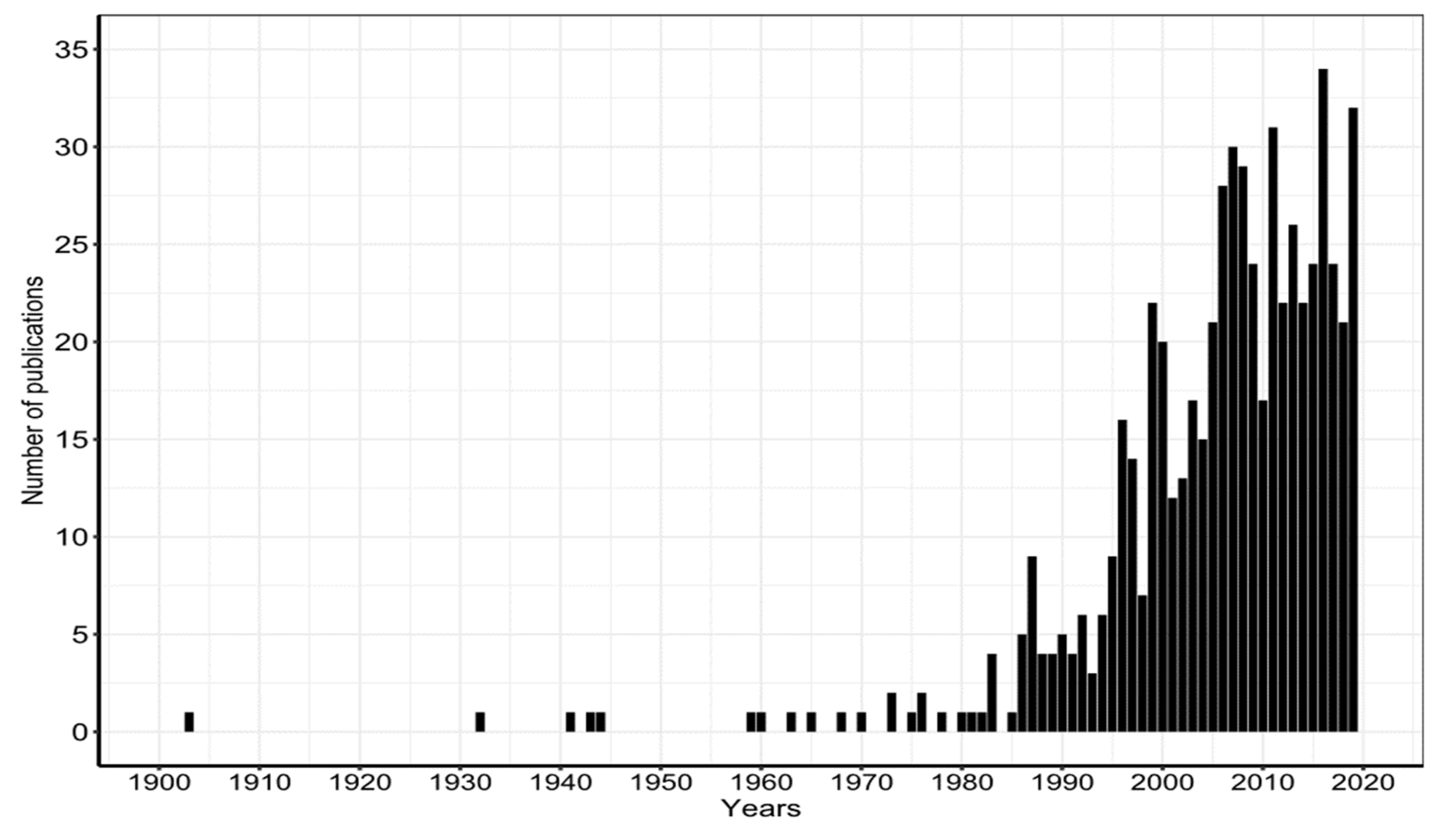
2. Literature Search and Compilation
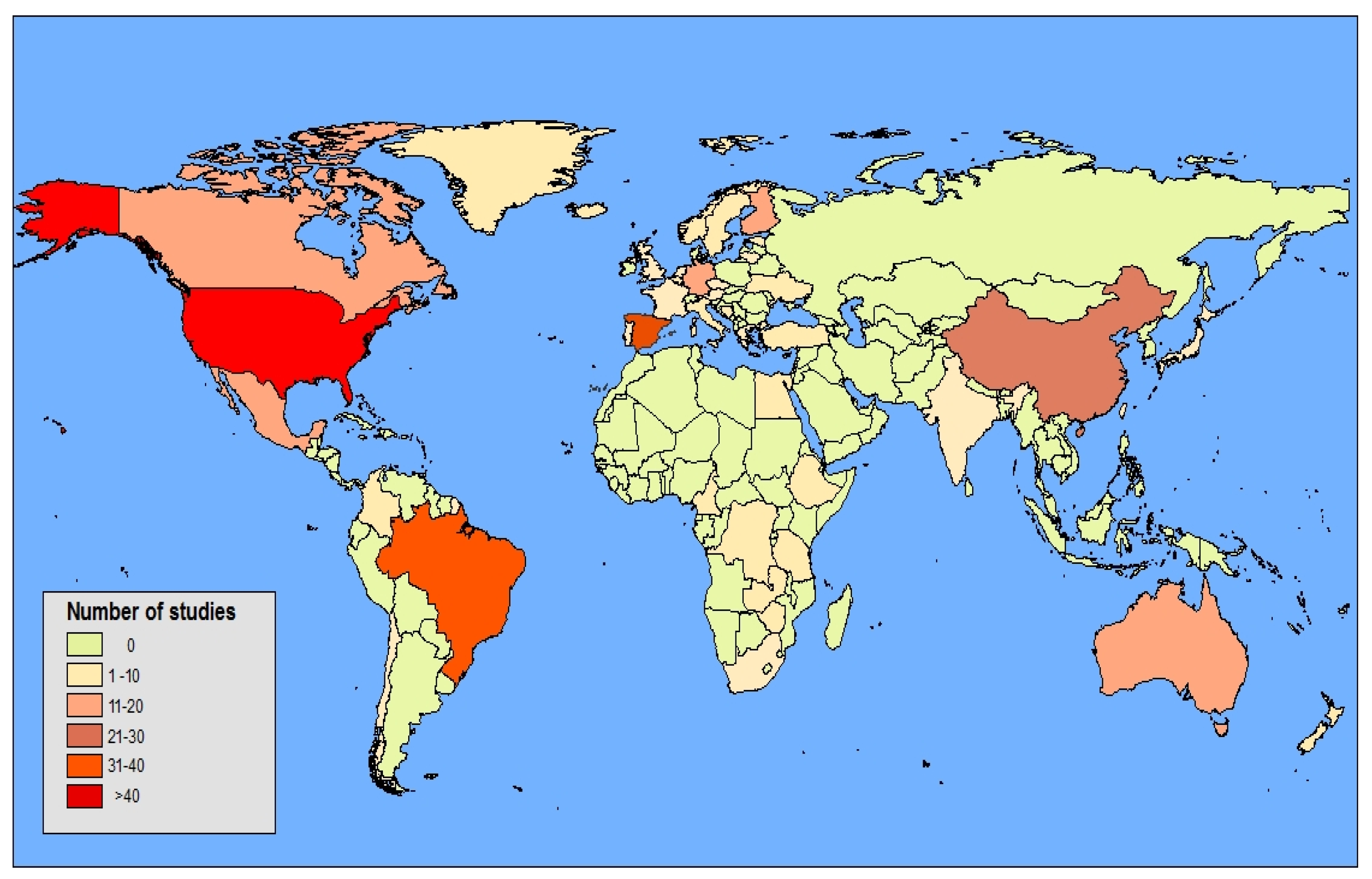
3. Frequency and Geographic Distribution of Taper Functions
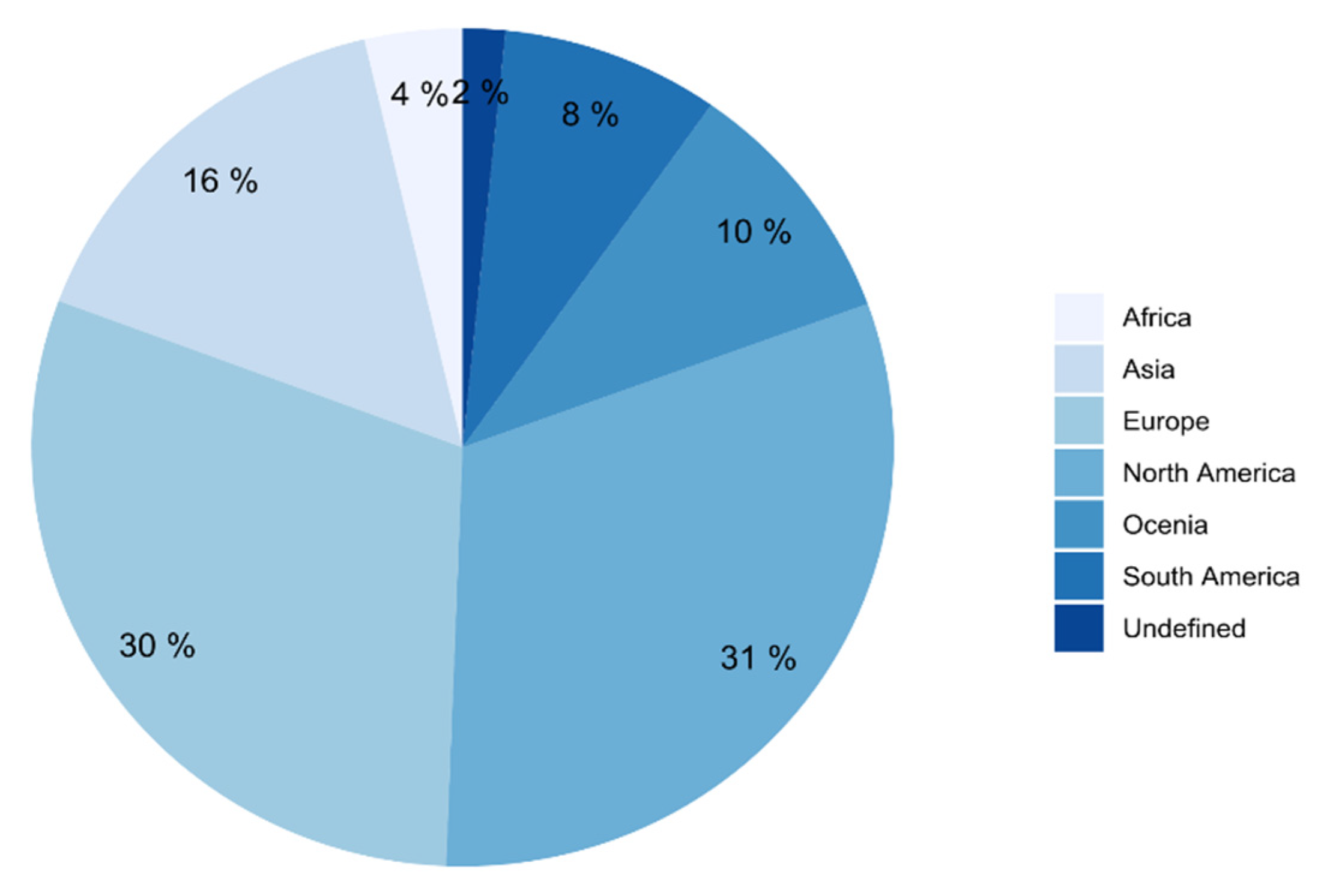
4. Forest Types of Studied Taper Functions
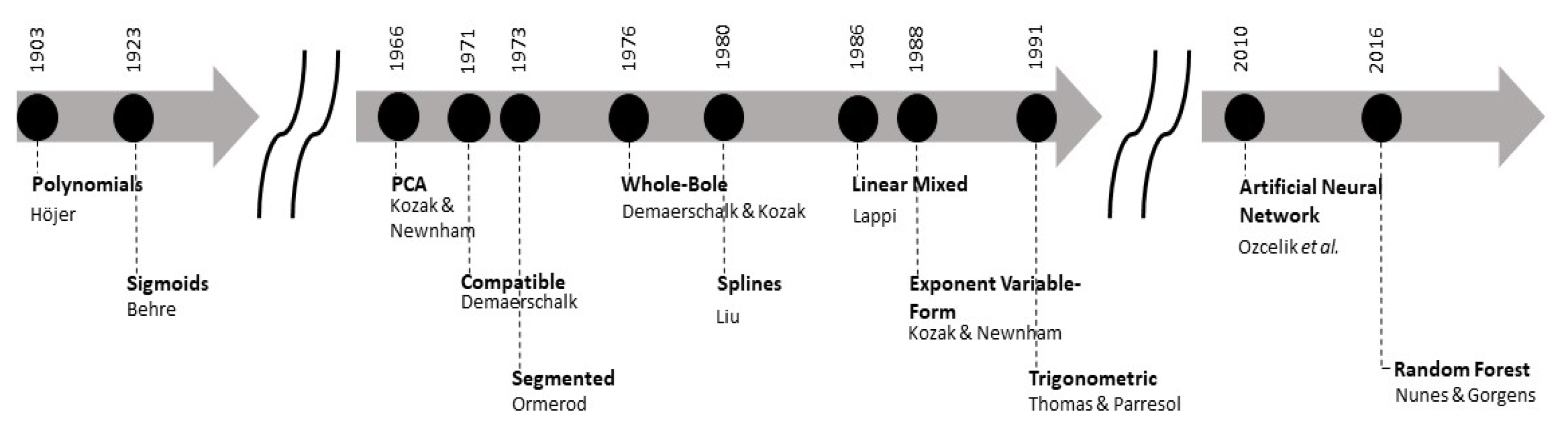
5. A Brief History of Taper Functions
6. Types of Taper Function
6.1. Parametric Taper Equations
6.1.1. Static Taper Equations
Polynomial Form Models
Sigmoid Taper Equations
Segmented Polynomial Taper Equations
Variable Exponent Form Models
Trigonometric Models
6.1.2. Complex Taper Functions
Compatible Taper Models
Whole-Bole Systems Models
Dynamic Taper Models
Other Complex Taper Models
Contemporary Taper Models
6.2. Non-Parameric Taper Equations
7. Parameters and Accuracy of Taper Functions
| Types of Taper Functions | Species | Country | Reference |
|---|---|---|---|
| Non-parametric (ML) | Acacia mearnsii (De Wild.) | BRA | Schikowski, et al. [62] |
| Static, segmented polynomial, and variable-exponent | Abies nordmanniana (subsp. bornmulleriana Mattf.) | TUR | Sakici, et al. [63] |
| Variable-exponent equation | Alnus rubra (Bong.) | USA, CAN | Hibbs, et al. [64] |
| Static polynomial equation | Araucaria cunninghamii (Ait. ex D. Don) | AUS | Allen, et al. [65] |
| Segmented polynomial | Betula platyplhylla (Sukaczev) | CHN | Shahzad, et al. [66] |
| Single and segmented polynomial | Betula alnoides | CHN | Tang, et al. [67] |
| Segmented polynomial | Calocedrus formosana | TWN | Wang, et al. [68] |
| Non-parametric (AI) | Cryptomeria japónica | BRA | Sanquetta, et al. [69] |
| Sigmoid equation | Cryptomeria japónica. D. Don. | JPN | Hada [70] |
| Segmented polynomial | Eucalyptus grandis × E. urophylla (Hybrid) E. grandis × E. camaldulensis (Hybrid) | ZAF | Morley and Little [71] |
| Static polynomial | Eucalyptus grandis × Eucalyptus urophylla (Hybrid) | BRA | Da Silva, et al. [72] |
| Compatible taper equation | Eucalyptus pilularis; E. obliqua; E. andrewsii; E.saligna; Corymbia maculata | AUS | Muhairwe [30] |
| Static polynomial | Eucalyptus cloeziana (f. Muell.) | ZMB | Eerikäinen, et al. [73] |
| Variable-exponent equation | Eucalyptus saligna | CMR | Fonweban [74] |
| Non-parametric (ANN) | Fagus orientalis Abies nordmanniana | TUR | Sakici and Ozdemir [75] |
| Segmented polynomial | Larix gmelinii (Rupr.) | CHN | Liu, et al. [76] |
| Dynamic taper equation | Nothofagus spp. | CHL | Valenzuela, et al. [77] |
| Segmented polynomial | Picea abies (L.) H. Karst. | CZE | Adamec, et al. [78] |
| Sigmoid (Spline) taper equation | Picea abies (L. Karst.) | CZE | Kuželka and Marušák [79] |
| Variable-exponent | Picea sitchensis (Bong. Carr.) Pinus sylvestris (L.) | GBR | Fonweban, et al. [10] |
| Variable-exponent equation | Picea glauca (Moench. Voss) | CAN | Huang, et al. [80] |
| Polynomial | Pinus nigra (J.F. Arnold) | ITA | Marchi, et al. [81] |
| Segmented polynomial | Pinus elliottii × P. caribaea var. hondurensis (Pexc) | ZAF | Algera, et al. [82] |
| Compatible taper equation | Pinus cooperi Pinus durangensis | MEX | Corral-Rivas, et al. [83] |
| Mixed segmented compatible | Pinus brutia (Ten.) Pinus nigra (Arnold.) | TUR | Özçelik, et al. [84] |
| Segmented polynomial | Pinus sylvestris (L.); Pinus pinaster (Ait.); Quercus pyrenaica (Willd.); Populus x euramericana (Dode); Pinus pinea (L.); Juniperus thurifera (L.); Pinus nigra (Arnold.); Fagus sylvatica (L.) | ESP | Rodríguez, et al. [85] |
| Semi-parametric | Pinus spp. and Quercus spp. | MEX | Návar [86] |
| Variable-exponent equation | Pinus banksiana (Lamb.) Picea mariana (Mill. BSP) | CAN | Subedi, et al. [87] |
| Segmented polynomial | Pinus contorta Larix sibirica | ISL | Heidarsson and Pukkala [88] |
| Segmented polynomial | Pinus sylvestris (L.) | TUR | Özçelik [89] |
| Compatible taper equation | Pinus taeda (L.) | USA | Coble and Hilpp [90] |
| Variable-exponent equation | Pinus pinaster (Ait.) | ESP | Rojo, et al. [91] |
| Variable-exponent equation | Pinus taeda (L.) | USA | Bullock and Burkhart [92] |
| Static polynomial equation | Pinus kesiya, Pinus oocarpa, Pinus merkusii, Pinus michoacana, Eucalyptus grandis, Eucalyptus doeziana | ZMB | Heinonen, et al. [93] |
| Segmented polynomial | Populus hybrids (P. trichocarpa/P. deltoids) | FRA | Benbrahim and Gavaland [94] |
| Segmented polynomial | Pseudotsuga menziesii | ESP | López-Sánchez, et al. [95] |
| Compatible taper equation | Quercus variabilis | CHN | Zheng, et al. [96] |
| Dynamic taper equation | Quercus robur (L.) | ESP | Gómez-García, et al. [97] |
| Segmented polynomial | Quercus fagaceae | MEX | Pompa-García, et al. [98] |
| Compatible taper equation | Quercus robur L. Q petraea (Matt) Liebl | DNK | Tarp-Johansen, et al. [99] |
| Compatible taper equation | Quercus robur (L.) | ZAF | Trincado, et al. [100] |
| Compatible taper equations | Salix schwerinii (E. L. Wolf) | FIN | Salam, et al. [101] |
| Segmented polynomial | Taiwania cryptomerioides | TWN | Wang, et al. [102] |
| Mixed polynomial | Tectona grandis (L.f.) | BRA | Lanssanova, et al. [103] |
| Non-parametric (ANN) | Tectona grandis (Linn.) | BRA | Leite, da Silva, Binoti, Fardin and Takizawa [31] |
| Spline regression | Not defined | DEU | Kublin, et al. [104] |
8. Applications of Taper Functions
9. Opportunities for Taper Function Development
10. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Gray, H.R. The Form and Taper of Forest-Tree Stems; Imperial Forestry Institute, University of Oxford: Oxford, UK, 1956. [Google Scholar]
- Kershaw, J.A., Jr.; Ducey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Clutter, J.L.; Fortson, J.C.; Pienaar, L.V.; Brister, G.H.; Bailey, R.L. Timber Management: A Quantitative Approach; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1983. [Google Scholar]
- Trincado, G.; Burkhart, H.E. A generalized approach for modeling and localizing stem profile curves. For. Sci. 2006, 52, 670–682. [Google Scholar] [CrossRef]
- Scolforo, H.F.; McTague, J.P.; Raimundo, M.R.; Weiskittel, A.; Carrero, O.; Scolforo, J.R.S. Comparison of taper functions applied to eucalypts of varying genetics in Brazil: Application and evaluation of the penalized mixed spline approach. Can. J. For. Res. 2018, 48, 568–580. [Google Scholar] [CrossRef] [Green Version]
- Bruce, D.; Curtis, R.O.; Vancoevering, C. Development of a system of taper and volume tables for red alder. For. Sci. 1968, 14, 339–350. [Google Scholar] [CrossRef]
- Byrne, J.C.; Reed, D.D. Complex compatible taper and volume estimation systems for red and loblolly pine. For. Sci. 1986, 32, 423–443. [Google Scholar] [CrossRef]
- Kozak, A. My last words on taper equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef] [Green Version]
- Fonweban, J.; Gardiner, B.; Macdonald, E.; Auty, D. Taper functions for Scots pine (Pinus sylvestris L.) and Sitka spruce (Picea sitchensis (Bong.) Carr.) in Northern Britain. Forestry 2011, 84, 49–60. [Google Scholar] [CrossRef]
- Li, R.; Weiskittel, A.; Dick, A.R.; Kershaw, J.A., Jr.; Seymour, R.S. Regional stem taper equations for eleven conifer species in the Acadian region of North America: Development and assessment. North. J. Appl. For. 2012, 29, 5–14. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Weiskittel, A.R. Comparison of model forms for estimating stem taper and volume in the primary conifer species of the North American Acadian region. Ann. For. Sci. 2010, 67, 302. [Google Scholar] [CrossRef] [Green Version]
- Kozak, A.; Smith, J.H.G. Standards for evaluating taper estimating systems. For. Chron. 1993, 69, 438–444. [Google Scholar] [CrossRef] [Green Version]
- Pang, L.; Ma, Y.; Sharma, R.P.; Rice, S.; Song, X.; Fu, L. Developing an improved parameter estimation method for the segmented taper equation through combination of constrained two-dimensional optimum seeking and least square regression. Forests 2016, 7, 194. [Google Scholar] [CrossRef] [Green Version]
- Assis, A.L.; Scolforo, J.R.S.; Mello, J.M.; Acerbi, F.W.; Oliveira, A.D. Comparison between segmented and non-segmented polynomial models in the estimates of diameter and merchantable volume of Pinuse taeda. Ciência Florest. 2001, 12, 89–107. [Google Scholar] [CrossRef] [Green Version]
- McTague, J.P.; Weiskittel, A.R. Evolution, history, and use of stem taper equations: A review of their development, application, and implementation. Can. J. For. Res. 2021, 51, 210–235. [Google Scholar] [CrossRef]
- Behre, E.C. Preliminary notes on studies of tree form. J. For. 1923, 21, 507–511. [Google Scholar] [CrossRef]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1363–1368. [Google Scholar] [CrossRef]
- Lappi, J. Mixed Linear Models for Analyzing and Predicting Stem Form Variation of Scots Pine; Metsäntutkimuslaitos: Helsinki, Finland, 1986. [Google Scholar]
- Ormerod, D.J. A simple bole model. For. Chron. 1973, 49, 136–138. [Google Scholar] [CrossRef] [Green Version]
- Demaerschalk, J.P. Converting volume equations to compatible taper equations. For. Sci. 1972, 18, 241–245. [Google Scholar] [CrossRef]
- de Rosayro, R.A. Field characters in the identification of tropical forest trees. Emp. For. Rev. 1953, 32, 124–141. [Google Scholar]
- Baker, P.J.; Bunyavejchewin, S.; Oliver, C.D.; Ashton, P.S. Disturbance and historical stand dynamics of a seasonal tropical forest in western Thailand. Ecol. Monogr. 2005, 75, 317–343. [Google Scholar] [CrossRef]
- Young, T.P.; Perkocha, V. Treefalls, crown asymmetry, and buttresses. J. Ecol. 1994, 82, 319–324. [Google Scholar] [CrossRef]
- Nunes, M.H.; Görgens, E.B. Artificial intelligence procedures for tree taper estimation within a complex vegetation mosaic in Brazil. PLoS ONE 2016, 11, e0154738. [Google Scholar] [CrossRef] [Green Version]
- Recknagel, F. Applications of machine learning to ecological modelling. Ecol. Model. 2001, 146, 303–310. [Google Scholar] [CrossRef]
- Perry, D.R.; Williams, J. The tropical rain forest canopy: A method providing total access. Biotropica 1981, 13, 283–285. [Google Scholar] [CrossRef]
- Sohngen, B.; Mendelsohn, R.; Sedjo, R. Forest management, conservation, and global timber markets. Am. J. Agric. Econ. 1999, 81, 1–13. [Google Scholar] [CrossRef]
- Cushman, K.C.; Muller-Landau, H.C.; Condit, R.S.; Hubbell, S.P. Improving estimates of biomass change in buttressed trees using tree taper models. Methods Ecol. Evol. 2014, 5, 573–582. [Google Scholar] [CrossRef]
- Muhairwe, C.K. Bark thickness equations for five commercial tree species in regrowth forests of Northern New South Wales. Aust. For. 2000, 63, 34–43. [Google Scholar] [CrossRef]
- Leite, H.G.; da Silva, M.L.M.; Binoti, D.H.B.; Fardin, L.; Takizawa, F.H. Estimation of inside-bark diameter and heartwood diameter for Tectona grandis Linn. trees using artificial neural networks. Eur. J. For. Res. 2011, 130, 263–269. [Google Scholar] [CrossRef]
- Höjer, A.G. Bihang till fr. lovén: Om vära Barrskogar; Department of Agriculture, Forest Service: Stockholm, Sweden, 1903.
- Jonson, T. Taxatoriska undersökningar om skogsträdens form, I, granens stamform. Sknogsvårdsför Tidskr 1910, 8, 285–328. [Google Scholar]
- Fries, J. Eigenvector analyses show that Birch and Pine have similar form in Sweden and British Columbia. For. Chron. 1965, 41, 135–139. [Google Scholar] [CrossRef] [Green Version]
- Fries, J.; Matern, B. On the use of multivariate methods for the construction of tree taper curves. In Proceedings of the IUFRO Advisory Group of Forest Statisticians Conference, Stockholm, Sweden, 27 September–1 October 1965; p. 33. [Google Scholar]
- Kozak, A.; Smith, J.H.G. Critical analysis of multivatiate techniques for estimating tree taper suggests that simpler methods are best. For. Chron. 1966, 42, 458–463. [Google Scholar] [CrossRef] [Green Version]
- Grosenbaugh, L.R. Tree form: Definition, interpolation, extrapolation. For. Chron. 1966, 42, 444–457. [Google Scholar] [CrossRef]
- Demaerschalk, J.P. Integrated systems for the estimation of tree taper and volume. Can. J. For. Res. 1973, 3, 90–94. [Google Scholar] [CrossRef]
- Zhao, D.; Lynch, T.B.; Westfall, J.; Coulston, J.; Kane, M.; Adams, D.E. Compatibility, development, and estimation of taper and volume equation systems. For. Sci. 2018, 65, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Husch, B.; Beers, T.W.; Kershaw, J.A., Jr. Forest Mensuration, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Max, T.A.; Burkhart, H.E. Segmented polynomial regression applied to taper equations. For. Sci. 1976, 22, 283–289. [Google Scholar] [CrossRef]
- Bi, H. Trigonometric variable-form taper equations for Australian Eucalypts. For. Sci. 2000, 46, 397–409. [Google Scholar] [CrossRef]
- Lappi, J. A multivariate, nonparametric stem-curve prediction method. Can. J. For. Res. 2006, 36, 1017–1027. [Google Scholar] [CrossRef]
- Kublin, E.; Breidenbach, J.; Kändler, G. A flexible stem taper and volume prediction method based on mixed-effects B-spline regression. Eur. J. For. Res. 2013, 132, 983–997. [Google Scholar] [CrossRef]
- Robinson, A.P.; Lane, S.E.; Thérien, G. Fitting forestry models using generalized additive models: A taper model example. Can. J. For. Res. 2011, 41, 1909–1916. [Google Scholar] [CrossRef]
- Özçelik, R.; Diamantopoulou, M.J.; Brooks, J.R.; Wiant, H.V. Estimating tree bole volume using artificial neural network models for four species in Turkey. J. Environ. Manag. 2010, 91, 742–753. [Google Scholar] [CrossRef]
- Harrell, F.E. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis; Springer: Berlin, Germany, 2015. [Google Scholar]
- Pedan, A. Smoothing with SAS® Proc Mixed. In Proceedings of the SAS Users Group International Proceedings, Seattle, WA, USA, 30 March–2 April 2003; pp. 268–328. [Google Scholar]
- Kozak, A.; Munro, D.D.; Smith, J.H.G. Taper functions and their application in forest inventory. For. Chron. 1969, 45, 278–283. [Google Scholar] [CrossRef]
- Goodwin, A.N. A cubic tree taper model. Aust. For. 2009, 72, 87–98. [Google Scholar] [CrossRef]
- Forslund, R.R. The power function as a simple stem profile examination tool. Can. J. For. Res. 1991, 21, 193–198. [Google Scholar] [CrossRef]
- Newnham, R. A Variable-Form Taper Function; PI-X-83; Forestry Canada Petawawa National Forestry Institute: Mattawa, ON, Canada, 1988. [Google Scholar]
- Newnham, R. Variable-form taper functions for four Alberta tree species. Can. J. For. Res. 1992, 22, 210–223. [Google Scholar] [CrossRef]
- Thomas, C.E.; Parresol, B.R. Simple, flexible, trigonometric taper equations. Can. J. For. Res. 1991, 21, 1132–1137. [Google Scholar] [CrossRef]
- Demaerschalk, J.P.; Kozak, A. The whole-bole system: A conditioned dual-equation system for precise prediction of tree profiles. Can. J. For. Res. 1977, 7, 488–497. [Google Scholar] [CrossRef]
- Muhairwe, C.K. Tree form and taper variation over time for interior lodgepole pine. Can. J. For. Res. 1994, 24, 1904–1913. [Google Scholar] [CrossRef]
- Laasasenaho, J. Taper Curve and Volume Functions for Pine, Spruce and Birch; Communicationes Instituti Forestalis Fenniae, Metsäntutkimuslaitos: Helsinki, Finland, 1982. [Google Scholar]
- Feng, G.; Huang, G.; Lin, Q.; Gay, R. Error minimized extreme learning machine with growth of hidden nodes and incremental learning. IEEE Trans. Neural Netw. 2009, 20, 1352–1357. [Google Scholar] [CrossRef]
- Yang, S.-I.; Burkhart, H.E. Robustness of parametric and nonparametric fitting procedures of tree-stem taper with alternative definitions for validation data. J. For. 2020, 118, 576–583. [Google Scholar] [CrossRef]
- Breuer, L.; Eckhardt, K.; Frede, H.-G. Plant parameter values for models in temperate climates. Ecol. Model. 2003, 169, 237–293. [Google Scholar] [CrossRef]
- Nicoletti, M.F.; e Carvalho, S.D.P.C.; do Amaral Machado, S.; Costa, V.J.; Silva, C.A.; Topanotti, L.R. Bivariate and generalized models for taper stem representation and assortments production of loblolly pine (Pinus taeda L.). J. Environ. Manag. 2020, 270, 110865. [Google Scholar] [CrossRef]
- Schikowski, A.B.; Corte, A.P.D.; Ruza, M.S.; Sanquetta, C.R.; Montaño, R.A. Modeling of stem form and volume through machine learning. An. Acad. Bras. Cienc. 2018, 90, 3389–3401. [Google Scholar] [CrossRef]
- Sakici, O.E.; Misir, N.; Yavuz, H.; Misir, M. Stem taper functions for Abies nordmanniana subsp. bornmulleriana in Turkey. Scand. J. For. Res. 2008, 23, 522–533. [Google Scholar] [CrossRef]
- Hibbs, D.; Bluhm, A.A.; Garber, S. Stem taper and volume of managed red alder. West. J. Appl. For. 2007, 22, 61–66. [Google Scholar] [CrossRef] [Green Version]
- Allen, P.J.; Henry, N.B.; Gordon, P. Polynomial taper model for Queensland plantation hoop pine. Aust. For. 1992, 55, 9–14. [Google Scholar] [CrossRef]
- Shahzad, M.K.; Hussain, A.; Burkhart, H.E.; Li, F.; Jiang, L. Stem taper functions for Betula platyphylla in the Daxing’an Mountains, northeast China. J. For. Res. 2020, 32, 529–541. [Google Scholar] [CrossRef]
- Tang, C.; Wang, C.S.; Pang, S.J.; Zhao, Z.G.; Guo, J.J.; Lei, Y.C.; Zeng, J. Stem taper equations for Betula alnoides in South China. J. Trop. For. Sci. 2017, 29, 80–92. [Google Scholar]
- Wang, D.H.; Chung, C.H.; Hsiech, H.C.; Tang, S.C. Taper modeling on Calocedrus formosana plantations in Lienhuachih, Central Taiwan. Taiwan J. For. Sci. 2018, 33, 163–171. [Google Scholar]
- Sanquetta, C.R.; Piva, L.R.O.; Wojciechowski, J.; Corte, A.P.D.; Schikowski, A.B. Volume estimation of Cryptomeria japonica logs in southern Brazil using artificial intelligence models. South. For. 2018, 80, 29–36. [Google Scholar] [CrossRef]
- Hada, S. On the taper of the Sugi (Cryptomeria japónica. D. Don.) bole by the form quotient. J. Jpn. For. Soc. 1958, 40, 379–382. [Google Scholar]
- Morley, T.; Little, K. Comparison of taper functions between two planted and coppiced eucalypt clonal hybrids, South Africa. New For. 2012, 43, 129–141. [Google Scholar] [CrossRef]
- Da Silva, L.M.S.; Rodriguez, L.C.E.; Caixeta Filho, J.V.; Bauch, S.C. Fitting a taper function to minimize the sum of absolute deviations. Sci. Agric. 2006, 63, 460–470. [Google Scholar] [CrossRef]
- Eerikäinen, K.P.A.; Mabvurira, D.; Saramäki, J. Alternative taper curve estimation methods for Eucalyptus cloeziana (f. Muell.). South. Afr. For. J. 1999, 184, 12–24. [Google Scholar] [CrossRef]
- Fonweban, J.N. An evaluation of numerical integration of taper functions for volume estimation in Eucalyptus saligna stands. J. Trop. For. Sci. 1999, 11, 410–419. [Google Scholar]
- Sakici, O.E.; Ozdemir, G. Stem taper estimations with artificial neural networks for mixed oriental beech and kazdaği fir stands in Karabük region, Turkey. Cerne 2018, 24, 439–451. [Google Scholar] [CrossRef]
- Liu, Y.; Yue, C.; Wei, X.; Blanco, J.A.; Trancoso, R. Tree profile equations are significantly improved when adding tree age and stocking degree: An example for Larix gmelinii in the Greater Khingan Mountains of Inner Mongolia, Northeast China. Eur. J. For. Res. 2020, 139, 443–458. [Google Scholar] [CrossRef]
- Valenzuela, C.; Acuña, E.; Ortega, A.; Quiñonez-Barraza, G.; Corral-Rivas, J.; Cancino, J. Variable-top stem biomass equations at tree-level generated by a simultaneous density-integral system for second growth forests of roble, raulí, and coigüe in Chile. J. For. Res. 2019, 30, 993–1010. [Google Scholar] [CrossRef]
- Adamec, Z.; Adolt, R.; Drápela, K.; Závodský, J. Evaluation of different calibration approaches for merchantable volume predictions of norway spruce using nonlinear mixed effects model. Forests 2019, 10, 1104. [Google Scholar] [CrossRef] [Green Version]
- Kuželka, K.; Marušák, R. Input point distribution for regular stem form spline modeling. For. Syst. 2015, 24. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Titus, S.; Price, D.; Morgan, D. Validation of ecoregion-based taper equations for white spruce in Alberta. For. Chron. 1999, 75, 281–292. [Google Scholar] [CrossRef]
- Marchi, M.; Scotti, R.; Rinaldini, G.; Cantiani, P. Taper function for Pinus nigra in central Italy: Is a more complex computational system required? Forests 2020, 11, 405. [Google Scholar] [CrossRef] [Green Version]
- Algera, M.; Kätsch, C.; Chirwa, P.W. Developing a taper model for the Pinus elliottii × P. caribaea var. hondurensis hybrid in South Africa. South. For. 2019, 81, 141–150. [Google Scholar] [CrossRef]
- Corral-Rivas, J.J.; Vega-Nieva, D.J.; Rodríguez-Soalleiro, R.; López-Sánchez, C.A.; Wehenkel, C.; Vargas-Larreta, B.; Álvarez-González, J.G.; Ruiz-González, A.D. Compatible system for predicting total and merchantable stem volume over and under bark, branch volume and whole-tree volume of pine species. Forests 2017, 8, 417. [Google Scholar] [CrossRef] [Green Version]
- Özçelik, R.; Karatepe, Y.; Gürlevik, N.; Cañellas, I.; Crecente-Campo, F. Development of ecoregion-based merchantable volume systems for Pinus brutia Ten. and Pinus nigra Arnold. in southern Turkey. J. For. Res. 2016, 27, 101–117. [Google Scholar] [CrossRef]
- Rodríguez, F.; Lizarralde, I.; Bravo, F. Comparison of stem taper equations for eight major tree species in the Spanish Plateau. For. Syst. 2015, 24. [Google Scholar] [CrossRef] [Green Version]
- Návar, J. A stand-class growth and yield model for Mexico’s northern temperate, mixed and multi-aged forests. Forests 2014, 5, 3048–3069. [Google Scholar] [CrossRef]
- Subedi, N.; Sharma, M.; Parton, J. Effects of sample size and tree selection criteria on the performance of taper equations. Scand. J. For. Res. 2011, 26, 555–567. [Google Scholar] [CrossRef]
- Heidarsson, L.; Pukkala, T. Taper functions for lodgepole pine (Pinus contorta) and siberian larch (Larix sibirica) in Iceland. Icel. Agric. Sci. 2011, 24, 3–11. [Google Scholar]
- Özçelik, R. Comparison of formulae for estimating tree bole volumes of Pinus sylvestris. Scand. J. For. Res. 2008, 23, 412–418. [Google Scholar] [CrossRef]
- Coble, D.W.; Hilpp, K. Compatible cubic-foot stem volume and upper-stem diameter equations for semi-intensive plantation grown loblolly pine trees in East Texas. South. J. Appl. For. 2006, 30, 132–141. [Google Scholar] [CrossRef] [Green Version]
- Rojo, A.; Perales, X.; Sánchez-Rodríguez, F.; Álvarez-González, J.G.; von Gadow, K. Stem taper functions for maritime pine (Pinus pinaster Ait.) in Galicia (Northwestern Spain). Eur. J. For. Res. 2005, 124, 177–186. [Google Scholar] [CrossRef]
- Bullock, B.P.; Burkhart, H.E. Equations for predicting green weight of loblolly pine trees in the South. South. J. Appl. For. 2003, 27, 153–159. [Google Scholar] [CrossRef]
- Heinonen, J.; Saramäki, J.; Sekeli, P.M. A polynomial taper curve function for Zambian exotic tree plantations. J. Trop. For. Sci. 1996, 8, 339–354. [Google Scholar]
- Benbrahim, M.; Gavaland, A. A new stem taper function for short-rotation poplar. Scand. J. For. Res. 2003, 18, 377–383. [Google Scholar] [CrossRef]
- López-Sánchez, C.A.; Rodríguez-Soalleiro, R.; Castedo-Dorado, F.; Corral-Rivas, S.; Álvarez-González, J.G. A taper function for Pseudotsuga menziesii plantations in Spain. South. For. 2016, 78, 131–135. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, Y.; Jia, L.; Mason, E.; We, S.; Sun, C.; Duan, J. Compatible taper-volume models of Quercus variabilis Blume forests in north China. iForest Biogeosci. For. 2017, 10, 567–575. [Google Scholar] [CrossRef] [Green Version]
- Gómez-García, E.; Crecente-Campo, F.; Barrio-Anta, M.; Diéguez-Aranda, U. A disaggregated dynamic model for predicting volume, biomass and carbon stocks in even-aged pedunculate oak stands in Galicia (NW Spain). Eur. J. For. Res. 2015, 134, 569–583. [Google Scholar] [CrossRef]
- Pompa-García, M.; Corral-Rivas, J.J.; Hernández-Díaz, J.C.; Alvarez-González, J.G. A system for calculating the merchantable volume of oak trees in the northwest of the state of Chihuahua, Mexico. J. For. Res. 2009, 20, 293–300. [Google Scholar] [CrossRef]
- Tarp-Johansen, M.J.; Skovsgaard, J.P.; Madsen, S.F.; Johannsen, V.K.; Skovgaard, I. Compatible stem taper and stem volume functions for oak (Quercus robur L and Q petraea (Matt) Liebl) in Denmark. Ann. Sci. For. 1997, 54, 577–595. [Google Scholar] [CrossRef]
- Trincado, G.; Gadow, K.V.; Tewari, V.P. Comparison of three stem profile equations for Quercus robur L. S. Afr. For. J. 1996, 177, 23–28. [Google Scholar] [CrossRef]
- Salam, M.M.A.; Pelkonen, P.; Mehtätalo, L.; Gong, J. Using stem analysis data for modelling the volume of Kinuyanagi willow (Salix schwerinii E. L. Wolf). Balt. For. 2015, 21, 259–271. [Google Scholar]
- Wang, D.H.; Hsieh, H.C.; Tang, S.C. Taper modeling on Taiwania plantation trees in the Liukuei area. Taiwan J. For. Sci. 2007, 22, 339–353. [Google Scholar]
- Lanssanova, L.R.; Machado, S.D.A.; Garrett, A.T.D.A.; Bonete, I.P.; Pelissari, A.L.; Filho, A.F.; da Silva, F.A.; Ciarnoschi, L.D. Mixed-effect non-linear modelling for diameter estimation along the stem of Tectona grandis in mid-western Brazil. South. For. 2019, 81, 167–173. [Google Scholar] [CrossRef]
- Kublin, E.; Augustin, N.H.; Lappi, J. A flexible regression model for diameter prediction. Eur. J. For. Res. 2008, 127, 415–428. [Google Scholar] [CrossRef]
- Gomat, H.Y.; Deleporte, P.; Moukini, R.; Mialounguila, G.; Ognouabi, N.; Saya, A.R.; Vigneron, P.; Saint-Andre, L. What factors influence the stem taper of Eucalyptus: Growth, environmental conditions, or genetics? Ann. For. Sci. 2011, 68, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Mehtätalo, L.; Lappi, J. Taper curves. In Biometry for Forestry and Environmental Data: With Examples in R; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2020; pp. 377–378. [Google Scholar]
- Larsen, D.R. Simple taper: Taper equations for the field forester. In General Technical Report NRS-P-167, Proceedings of the 20th Central Hardwood Forest Conference, Columbia, MO, USA, 28 March–1 April 2016; Kabrick, J.M., Dey, D.C., Knapp, B.O., Larsen, D.R., Shifley, S.R., Stelzer, H.E., Eds.; US Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2016; pp. 265–278. [Google Scholar]
- Cremer, K.; Borough, C.; McKinnell, F.; Carter, P. Effects of stocking and thinning on wind damage in plantations. N. Zeal. J. For. Sci. 1982, 12, 244–268. [Google Scholar]
- Olofsson, E.; Blennow, K. Decision support for identifying spruce forest stand edges with high probability of wind damage. For. Ecol. Manag. 2005, 207, 87–98. [Google Scholar] [CrossRef]
- Grossman, G.H.; Potter-Witter, K. Economics of red pine management for utility pole timber. North. J. Appl. For. 1991, 8, 22–25. [Google Scholar] [CrossRef]
- Salam, M.; Pelkonen, P. Applying taper function in standard volume equation for the past volume increment analysis of Kinuyanagi Willow. J. Basic Appl. Sci. Res. 2012, 2, 6084–6097. [Google Scholar]
- Mulverhill, C.; Coops, N.C.; Tompalski, P.; Bater, C.W.; Dick, A.R. The utility of terrestrial photogrammetry for assessment of tree volume and taper in boreal mixedwood forests. Ann. For. Sci. 2019, 76, 83. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Morgenroth, J.; Manley, B. Integrating data from discrete return airborne LiDAR and optical sensors to enhance the accuracy of forest description: A review. Curr. For. Rep. 2015, 1, 206–219. [Google Scholar] [CrossRef] [Green Version]
- Chianucci, F.; Puletti, N.; Grotti, M.; Ferrara, C.; Giorcelli, A.; Coaloa, D.; Tattoni, C. Nondestructive Tree stem and crown volume allometry in hybrid poplar plantations derived from terrestrial laser scanning. For. Sci. 2020, 66, 737–746. [Google Scholar] [CrossRef]
- Yrttimaa, T.; Luoma, V.; Saarinen, N.; Kankare, V.; Junttila, S.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Structural changes in boreal forests can be quantified using terrestrial laser scanning. Remote Sens. 2020, 12, 2672. [Google Scholar] [CrossRef]
- Eliopoulos, N.J.; Shen, Y.; Nguyen, M.L.; Arora, V.; Zhang, Y.; Shao, G.; Woeste, K.; Lu, Y.-H. Rapid tree diameter computation with terrestrial stereoscopic photogrammetry. J. For. 2020, 118, 355–361. [Google Scholar] [CrossRef]
- Benson, A.R.; Koeser, A.K.; Morgenroth, J. Estimating conductive sapwood area in diffuse and ring porous trees with electronic resistance tomography. Tree Physiol. 2018, 39, 484–494. [Google Scholar] [CrossRef] [PubMed]

| Equation | Coefficients | Species | Stat., Unit | Value | Country | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | - | - | - | ||||||||
| 2 | * * * * Form class = 75 | Picea abies (L.) Karst. | - | - | USA | |||||||
| 3 | * * * Form class = 75 | Picea abies (L.) Karst. | SEE vol. (%) | ±13.74 | USA | |||||||
| 4 | Tsuga heterophylla (Raf.) Sarg. | - | - | USA | ||||||||
| 5 | , −1.976 8.238, −4.964 , −7.417 | Alnus rubra (Bong.) | SEE, in | 0.0704 | USA | |||||||
| 6 | Pinus resinosa Sol. Ex Aiton | SSE, D (cm) | 446.634 | USA | ||||||||
| Pinus taeda L. | SSE, D (cm) | 526.285 | USA | |||||||||
| 7 | Not available | Populus tremuloides Michx. | - | - | CAN | |||||||
| 8 | Populus tremuloides Michx. (Coastal) | SEE, D (inch) | 0.59 | CAN | ||||||||
| Pseudotsuga menziesii (Mirbel) Franco (Interior) | SEE, D (inch) | 1.33 | CAN | |||||||||
| 9 | , , , | Pinus taeda L. | MAD, D (cm) | 0.53–0.86 | USA | |||||||
| 10 | , , 0.914280, | Pinus resinosa Sol. Ex Aiton | SSE, D (inch) | 268.918 | USA | |||||||
| , , , | Pinus taeda L. | SSE, D (inch) | 294.163 | |||||||||
| 11 | Pinus resinosa Sol. Ex AitonPicea mariana (Mill.) Britton | ME % Vol. | 3.92 | CAN | ||||||||
| 12 | , , , , | Pinus contorta | SEE, D (cm) | 1.39 | CAN | |||||||
| , , , , | Thuja plicata | SEE, D (cm | 6.67 | |||||||||
| 13 | Quercus phellos (L.) | SEE d (cm) | 1.284 | USA | ||||||||
| 14 | Species | Region | K1 × 102 | K2 | Mixed Species | Bias % vol. | −8.2 | USA | ||||
| Cottonwood | C + I | 0.20302 | 0.37223 | |||||||||
| Douglas-Fir | C | 0.167216 | 0.306585 | |||||||||
| Douglas-Fir | I | 0.181694 | 0.33313 | Bias % vol. | −12.2 | |||||||
| Lodgepole pine | C + I | 0.226124 | 0.41459 | |||||||||
| Yellow cedar | C + I | 0.219329 | 0.402132 | |||||||||
| Yellow pine | C + I | 0.208576 | 0.382417 | Bias % vol. | −7.7 | |||||||
| Region: C= Coastal, I = Interior | ||||||||||||
| 19 | , −44.310 26.708, −3.5452 , 0.33021 17.070 | Pinus radiata D.Don | SEE, D (cm) | 1.43 | NZL | |||||||
| 20/21 | Not available | Pseudotsuga menziesii (Mirbel) Franco; Acer spp. (L.) | SEE D (inch) | 0.72/0.49 | CAN | |||||||
| 22 | , , , | Pinus contorta | SEE, D (cm) | 0.6468 | CAN | |||||||
| 23 | , , , , | Pinus spp. | SEE, D (%) | 3.63 | CAN | |||||||
| 24 | u | Coefficient | Pinus sylvestris (L.) | RMSE, vol. (%) | 3.5 | FIN | ||||||
| a0 | a1 | a2 | a3 | |||||||||
| 1 | 0.784 | 0.958 | 0.034 | −0.118 | ||||||||
| 2 | 0.793 | 0.897 | 0.043 | −0.123 | ||||||||
| 3 | 0.746 | 0.853 | 0.052 | −0.124 | ||||||||
| 4 | 0.558 | 0.933 | 0.033 | −0.111 | ||||||||
| 5 | 0.521 | 0.903 | 0.038 | −0.101 | ||||||||
| 6 | 0.483 | 0.862 | 0.046 | −0.09 | ||||||||
| 7 | 318 | 0.866 | 0.042 | −0.057 | ||||||||
| 8 | 0.065 | 0.939 | 0.019 | −0.011 | ||||||||
| 9 | −0.313 | 1.054 | −0.018 | 0.056 | ||||||||
| 10 | −0.644 | 1.12 | −0.044 | 0.113 | ||||||||
| 11 | −1.141 | 1.194 | −0.073 | 0.169 | ||||||||
| 12 | −1.798 | 1.23 | −0.093 | 0.206 | ||||||||
| 13 | −0.63 | 1.276 | −0.108 | 0.23 | ||||||||
| 14 | −2.168 | 1.396 | −0.162 | 0.524 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salekin, S.; Catalán, C.H.; Boczniewicz, D.; Phiri, D.; Morgenroth, J.; Meason, D.F.; Mason, E.G. Global Tree Taper Modelling: A Review of Applications, Methods, Functions, and Their Parameters. Forests 2021, 12, 913. https://doi.org/10.3390/f12070913
Salekin S, Catalán CH, Boczniewicz D, Phiri D, Morgenroth J, Meason DF, Mason EG. Global Tree Taper Modelling: A Review of Applications, Methods, Functions, and Their Parameters. Forests. 2021; 12(7):913. https://doi.org/10.3390/f12070913
Chicago/Turabian StyleSalekin, Serajis, Cristian Higuera Catalán, Daniel Boczniewicz, Darius Phiri, Justin Morgenroth, Dean F. Meason, and Euan G. Mason. 2021. "Global Tree Taper Modelling: A Review of Applications, Methods, Functions, and Their Parameters" Forests 12, no. 7: 913. https://doi.org/10.3390/f12070913
APA StyleSalekin, S., Catalán, C. H., Boczniewicz, D., Phiri, D., Morgenroth, J., Meason, D. F., & Mason, E. G. (2021). Global Tree Taper Modelling: A Review of Applications, Methods, Functions, and Their Parameters. Forests, 12(7), 913. https://doi.org/10.3390/f12070913







