Abstract
The aim of this paper is to analyze the effect of different degrees of mixing on the diversity structure in stands left to spontaneous development. The research included two communities of species endemic to the Balkan Peninsula—the Serbian spruce (Picea omorika Pančić Purk.) and the Macedonian pine (Pinus peuce Griseb). Data from eight sample plots were used in the research. The changes in diameter and height structure, spatial arrangement of trees, and diameter differentiation were analyzed. The analyzed parameters of structural diversity show relatively low to moderate values. Results showed an increase in mixing was reflected in the width and shape of distributions. A spatial analysis of stands with a higher degree of mixing showed a tendency towards a random to regular distribution of individuals, in contrast to stands with a lower degree of mixing which showed a tendency towards a clump distribution. The pronounced species’ dimensional and spatial diversity confirms their importance to the condition of modern forest management. Significant differences in the change of structure are shown by stands with a share of admixed species of above 20% by volume. The obtained results refer to stands left to spontaneous development, suggesting than an active research and management approach must be assumed to realize the goal of protecting rare forest ecosystems.
1. Introduction
The diversity of vegetation of the Balkan Peninsula, in a broader context, can be explained by its position where diametrically opposed climatic influences meet and affect the area [1]. The most important relict-endemic forest ecosystems of the Balkan Peninsula are the communities of Serbian spruce (Picea omorika) and Macedonian pine (Pinus peuce). Anthropogenic impacts in the past have reduced the range of Serbian spruce to small and inaccessible habitats along the middle course of the Drina River (Bosnia and Herzegovina, Serbia) and Macedonian pine to habitats of the highland region (Bulgaria, Serbia, Macedonia, Montenegro, Albania, and Greece) (Figure 1) [2]. The character of habitats in which these communities develop, the passive approach to their protection, as well as the absence of economic interests, have resulted in poor research of these ecosystems [3,4].
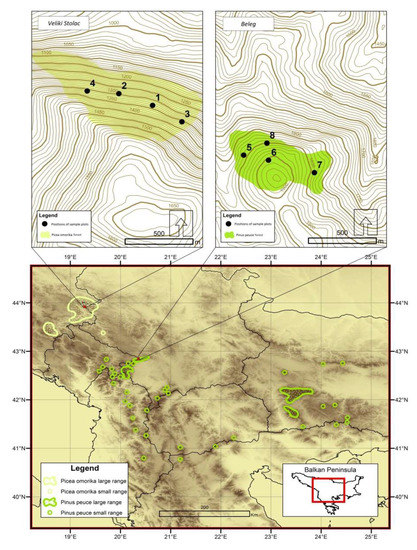
Figure 1.
An overview of spatial distribution of the sample plots with the range of the investigated relict-endemic forest communities of the Balkan Peninsula [20]. The sample plots of Serbian spruce are located in the Bosnian municipality of Višegrad (Veliki Stolac) and the Macedonian pine in the Serbian municipality of Tutin (Beleg).
Structural parameters have been assessed as very good indicators of biodiversity and are recommended as its direct measure [4,5]. Whittaker [6] defines different categories of biodiversity. The proposed division at the stand level implies a variety of tree positions, tree species, and their dimensions [7,8,9]. The study of these characteristics does not neglect the significant three-dimensional structure of stands [8,10,11,12,13].
Today, unlike in the past when monocultures were of great importance in Europe, ever more attention is paid to heterogeneous mixed stands [4]. The heterogeneity of natural spontaneously developed stands is higher than in those managed by man [4,14]. Given their structural complexity, the nature of their research is very complex [15,16]. Conventional approaches to stand condition analysis based on data such as mean diameter, dominant height, volume per hectare, etc. ignore the complex nature of the stand and are predominantly economic in nature. The observing of a stand as a structurally functional community of individual trees gives us the opportunity to better understand the complex relationships between individuals in it.
The aim of this research is to evaluate the effect of mixing on the diversity of dimensions and horizontal and vertical structures of stands in relict-endemic communities of Serbian spruce and Macedonian pine in the area of the Balkan Peninsula. The starting hypothesis is that an increase in mixing causes an increase in structural differentiation, or the structural diversity of stands [4,5,17,18,19].
2. Materials and Methods
2.1. Research Area
During 2019, four sample plots (SP) were established in the stands of Piceaomorika and another four in the stands of Pinus peuce (Figure 1). The sample plots were located in homogeneous, dense and preserved parts of the studied forest community of different degrees of mixing. The plots are equal in area (0.30 ha) and of regular square shape (54.8 m × 54.8 m).
The mixed stands of Piceo-OmorikaeAbieti fagetum Čol.1965 occupy the edges and lower areas of the investigated locality (Veliki Stolac), where they spatially lean on mixed communities of spruce, fir, beech, and Austrian pine. The altitude ranges from 1300 m (SP 2) to 1370 m (SP 3). The exposure is north, and the slope is 30–42°. The parent rock is limestone with shallowly developed black soils on it [21]. The average annual rainfall is 977 mm with an average annual temperature of 5 °C.
The Macedonian pine stands at the investigated locality (Beleg) form a vegetation belt above the forests of spruce and the forests of spruce and Macedonian pine Piceo-Pinetum peuces Lakš. 1965 [20]. They are located at an altitude ranging from 1825 m (SP 5) to 1910 m (SP 6). The exposures are different (SP 5 W-NW; SP 6 N-NW; SP 7 E; SP 8 N), and the slope of the terrain is 15–30°. The parent rock is limestone, and the soil is shallow dystric humus-silicate soil. The average annual rainfall is 749 mm, and the average annual temperature is 5.2 °C.
The share of other tree species in the stands of Serbian spruce (SP 1–4) and Macedonian pine (SP 5–8), expressed as % of volume per hectare (V × ha−1), is shown in Table 1.

Table 1.
The shares of admixed tree species in the investigated stands expressed in percentage of volume per admixed species.
The stands included in this research have the character of strictly protected natural communities that have not been exposed to direct anthropogenic influences that could have compromised their natural character. The preservation of these relict-endemic ecosystems has been contributed to by the difficult-to-access terrain, distance of the locality from populated areas, and lack of forest roads.
2.2. Data Collection
The positions of the sample plots were recorded with a GPS device. The diameters at breast height (dhb) and the total heights (h) of all trees with a diameter greater than 10 cm were measured in the sample plots. The trees were marked with numbers at breast height and their coordinates were recorded. The coordinates were recorded using a WILD T05 theodolite and a laser distance meter from the defined angles of the sample plots.
2.3. Data Processing
Complex structural analysis based on the spatial relationships of neighboring trees requires the use of the edge-correction method [22]. In order to obtain unbiased data, the plus-sampling method [23,24] was used. Trees from 44.7 m × 44.7 m (0.2 ha) subsamples from sample plots’ centers were used to avoid the edge effect. All parameters of spatial analysis were calculated on the basis of a defined subsample.
2.3.1. The Mixing Effect
The mixing effect by the number of trees in the sample plots was defined by the measure of evenness E [25], the percentage ratio of (H) (the species diversity index [26]), and the maximum diversity (Hmax = lnS), where S is the number of different tree species in the sample plot. The mixing effect is also defined according to the percentage share of species by volume (Table 1). Tree volumes were calculated according to the local models V = f(dbh, h) for the analyzed tree species [27,28,29,30,31]. Volume was calculated for each individual tree based on input values of diameter and total height according to two-way volume tables. The volume thus obtained on the sample plots was calculated per hectare.
The measure of spatial segregation of species used is the mingling index M [32]. A structural group of four neighboring trees was used to determine this index [8,33,34,35]. The index of structural groups is calculated according to the following formula:
At the level of the sample plot, index M was calculated as the arithmetic mean of the individual values of the Mi index of structural groups. The designations used in the function have the following meaning: i is the ordinal number of the reference tree (1…N), N is the number of trees in the plot, j is the number of the neighboring tree (1… 4), n is the observed number of neighboring trees (4), and mj is a parameter (1 if the reference and neighboring species are different, 0 if they are the same).
2.3.2. Horizontal Structure
The Clark–Evans aggregation index R [36] was used to analyze the spatial pattern of trees in the sample plots. The index was used according to the adjusted calculation method [37] of real (rA) and expected average distance between individuals (rE), as follows:
Letters in the formula have the following meaning: A is the area (m2), N is the number of trees, P is the perimeter (m), and ri is the distance from the i-th tree to the nearest neighbor.
The spatial pattern of trees was determined based on the Ripley’s K(r) function [38]. The edge-correction effect [23,39,40,41] implies an unbiased way of calculating the K(r) function:
Interpretation of the results was performed using the L(r) function, in a form that in the simplest way shows the change in the L value with an increasing distance r. In the graphical representation of the spatial pattern of trees, we used the adapted form of the L (r) function [40,42].
The letters in the previous two functions have the following meanings: A is the area (m2), N is the number of trees, uij is the distance between the i-th tree and the j-th tree, Ir(uij) is the indicator of the function that equals 1 if uij ≤ r (or 0 vice versa), wij is the edge-correction factor for the i-th tree and its neighboring j-th tree, and r is the analyzed reference distance.
2.3.3. Vertical Structure
The height structure by sample plots is shown graphically based on the percentage of trees (N%) by height classes of 3.0 m width. In order to simplify the comparative analysis of the height structure of individual sample plots, statistical measures of central tendency (average height), dispersion (standard deviation, variation width), and distribution (skewness, kurtosis) were used.
Species profile index A [43] was used as a unique measure of the height structure of the sample plots, based on the adapted method of calculating diversity index H [26]. The comparatively significant relative value of the species profile index Arel was obtained from the ratio of absolute A and maximum Amax value, as follows:
The letters used have the following meanings: S is the number of tree species, Z is the number of vertical layers (3), pij is the share of species in vertical layers (nij/N), nij is the number of trees of a certain species in the vertical layer, and N is the total number of trees.
2.3.4. Diameter Structure
The diameter structure of trees in the sample plots is graphically shown on the basis of the percentage of trees (N%) by diameter classes of 5 cm width. In order to facilitate the comparative analysis of diameter distributions in the sample plots, the statistical parameters listed for the vertical structure were used.
The diameter differentiation index Td [32] was used to analyze diameter diversity. The index quantifies the diversity of reference tree diameters and their nearest neighboring trees [5,32,44]. A structural group of four neighboring trees was used to determine this index [8,32,33,45]. Structural group indices were calculated according to the following equation:
At sample plot level, the Td index is calculated as the arithmetic mean of the individual values of the Tdi index of structural groups. The letters used in the formula have the following meaning: i is the number of the reference tree (1…N), j is the number of the nearest tree (1…n), n is the number of nearest trees (4), and N is the total number of trees in the plot.
In addition to the above parameters and indices, the Gini coefficient (GC) was used to estimate the structural unevenness of the sample plots [46,47]:
The letters used have the following meaning: j is the rank of trees according to the diameter expressed in ascending order from 1 to n, n is the total number of trees in the sample plot, bаj is the basal area of the j-th tree by rank (m2).
The hyperbolic tangent index S [48] was used to define the relationships between the species in the sample plot. The relationship between the diameters of reference trees of admixed species and dominant species that are spatially closest to the observed reference trees was analyzed. A structural group with four neighboring trees was used [48]. The structural group index Si is calculated as follows:
The sample plot index S was calculated as the arithmetic mean of the structural group indices Si without edge-correction [22,46]. The letters in the previous formula have the following meaning: i is the number of the reference tree of the admixed species (1…N), j is the number of the nearest dominant tree (1… k), k is the number of nearest dominant trees to the reference tree (4), mi is the reference tree (observed characteristic-dbhi), mj is the neighboring tree (observed characteristic- dbhj), factor a ranges from 0.0 to 1.5 (the most appropriate is 1.0), and N is the total number of trees of admixed species in the sample plot.
2.4. Statistical Analysis
Testing of the distribution of the investigated characteristics of trees in relation to their normal distribution was performed using the Shapiro–Wilk test of normality. The empirical data of the distribution and normal distribution were compared. The Levene test was used to test the homogeneity of variance. A comparison of the empirical distributions of the analyzed characteristics was done based on the Mann–Whitney U test. The acceptance (rejection) of the hypotheses about the normality of data distribution, i.e., their mutual differences, was tested at the significance level of 0.05. The analysis of the relationship between the used structure parameters was performed using the Spearman’s rank-order correlation. The testing of the spatial patterns was conducted with 199 Monte Carlo simulations of the null hypothesis of complete spatial randomness. The parts of the L (r) function above, below, and within confidence the intervals indicate clumped, regular, and random spatial patterns.
Different software packages [49,50] were used in the data processing, analysis, and testing. The spatial analysis of trees was performed using the “spatstat” [51] package in the R-3.5.1 program [52].
3. Results
3.1. Dendrometric Characteristics of the Investigated Forest Communities
Forest communities of relict-endemic species, according to the basic dendrometric values (Table 2), have the following characteristics. In the stands of Serbian spruce, the mean diameter per basal area ranges from 24.7 (SP 2) to 29.9 cm (SP 3), and the mean height ranges from 25.8 (SP 2) to 27.9 m (SP 3). The number of trees ranges from 810 (SP 3) to 1285 pcs × ha−1 (SP 4). The basal area values range from 52.9 (SP 1) to 65.1 m2 × ha−1 (SP 4), and volumes from 649 (SP 1) to 794 m3 × ha−1 (SP 4). There is an obvious trend of increasing volume with an increasing degree of mixing of stands of this community (Va%). In the Macedonian pine stands, the mean diameter per basal area ranges from 31.8 (SP 5) to 44.2 cm (SP 8) and the height ranges from 17.6 (SP 5) to 20.7 m (SP 8). The number of trees ranges from 326 (SP 8) to 1015 pcs × ha−1 (SP 5), the basal area ranges from 50.1 (SP 8) to 80.0 m2 × ha−1 (SP 5), and the volume ranges from 511 (SP 8) to 700 m3 × ha−1 (SP 5). There is an evident decrease in the number of trees and volume, as well as an increase in the mean diameter and height with an increase in the mixing of Macedonian pine stands.

Table 2.
Basic numerical characteristics of the sample plots.
Differences at the community level are expressed in all parameters. The average values of heights (HQMD; HDo) and slenderness (HQMD/QMD) are higher for 35% (32%) and 100%, and average value of diameters (QMD; Do) are lower for 48% (52%) in the community of Serbian spruce. The average number of trees (1079 pcs × ha−1) and volume (728 m3 × ha−1) are higher by 82% and 28%, respectively, in the Serbian spruce community compared to the Macedonian pine community. In contrast, the average value of basal area in the Macedonian pine community (63.2 m2 × ha−1) is higher by 8% than in the Serbian spruce community (58.4 m2 × ha−1). The different ratios of volume and basal area in these two forest communities are a consequence of large differences in slenderness, i.e., the height structure of the stands.
3.2. Spatial Pattern of Tree Distribution in the Investigated Stands
The average distance between neighboring trees (Table 3) in the community of Serbian spruce ranges from 1.44 m (SP 2) to 1.84 m (SP 3). The aggregation indices R have values close to the reference random distribution. The test results indicate that only the trees in the sample plot with the highest degree of mixing (SP 4) have a regular distribution (p < 0.05). The average distance between neighboring Macedonian pine trees ranges from 1.14 m (SP 1) to 3.41 m (SP 4). The aggregation indices R differ significantly in the sample plots. The testing indicates that only the trees from sample plot 7 are randomly distributed in space. In the sample plots with the lowest degree of mixing (SP 5, SP 6), a statistically significant clumping was found (p < 0.001, p < 0.01), while the trees in the sample plot with the highest degree of mixing (SP 8) had a regular distribution (p < 0.05).

Table 3.
Basic spatial characteristics. Mean distance between individuals (m) and aggregation index (R).
The spatial pattern of tree distribution in the studied communities was determined based on the Ripley’s L(r) function (Figure 2). In the community of Serbian spruce in the first two sample plots with a lower degree of mixing (SP 1, SP 2), the distribution of trees with a change in distance has different values. Based on the conducted Monte Carlo simulations of the null hypothesis of complete spatial randomness, at distances of up to 2.0 m (SP 1) the trees are randomly arranged, and at over 2.0 m the arrangement has a clump character. In sample plot 2, the random distribution of trees is at distances of up to 4.0 m, from 4.0 to 8.0 m the distribution is clumped, and at over 8.0 m it is at the upper limit of statistical randomness. In the other two sample plots (SP 3, SP 4) with a higher degree of mixing, the distribution of trees is within the limits of statistical significance of random distribution at all distances.
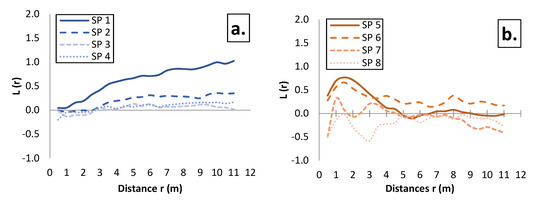
Figure 2.
Ripley’s L(r) function of the spatial pattern of tree locations in the Serbian spruce (a) and Macedonian pine (b) forest communities. The values of the function higher than expected (positive values) show a tendency towards clumping, values lower than expected (negative values) show a tendency towards a regular distribution at the observed distance. For simplicity’s sake, lines that indicate a 99% confidence interval based on 199 Monte Carlo simulations of the null hypothesis of complete spatial randomness were not interpreted in this figure.
In the Macedonian pine community, in sample plots with a lower degree of mixing (SP 5, SP 6), the distribution of trees has different values with a change in distance. At distances of up to 3.0 m (SP 5) and 2.5 m (SP 6), the trees are clumped in space. As these distances increase, the trees have a random arrangement. In the sample plots with a higher degree of mixing (SP 7, SP 8), the arrangement of trees is within the limits of statistical significance of random distribution at all distances, with a significantly wider confidence level.
In the stands of Serbian spruce the values of Ripley’s L(r) function increase with an increasing distance, while with increasing mixing they have smaller absolute values at the observed distances. As the mixing increases, the spatial pattern of trees tends to change from a clumped to a random distribution. In the stands of Macedonian pine, the functions have slightly more complex relationships, but it is clear that with increasing mixing, the arrangement of trees has a trend from a clumped to a regular distribution.
3.3. Vertical Structure
The distributions of trees by height classes in the sample plots in the investigated forest communities are graphically presented in Figure 3. Based on the testing of empirical height distributions (Mann–Whitney U test), a statistically significant difference (p < 0.05) was found between the distributions in the sample plots.
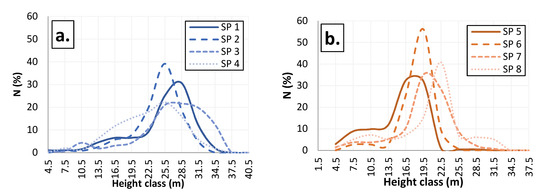
Figure 3.
Distribution of trees by height classes in the Serbian spruce (a) and Macedonian pine (b) stands.
The arithmetic mean height (hA) in the Serbian spruce stands ranges from 22.4 (SP 4) to 27.1 m (SP 3). The variation width of heights (hV) is even across the sample plots and ranges from 29.4 m (SP 1) to 31.7 m (SP 4), with a higher standard deviation in sample plots with a higher degree of mixing (SP 3, SP 4). The height structure in all sample plots shows a negative (right) skewness (α3 < 0), while the values of the kurtosis coefficient α4 < 3 in SP 1, SP 3, and SP 4 indicate kurtosis from above, and in SP 2 lateral kurtosis (α4 > 3). The concentration of the number of trees of 30% (SP 1) and 40% (SP 2) in one height class and lower values of deviation from the arithmetic mean indicate a slightly different structure compared to the sample plots with a higher degree of mixing (SP 3, SP 4). The height structures in these sample plots do not have such clearly expressed maximums and have a slightly larger variation width.
In the Macedonian pine stands, hA values are lower than in the stands of Serbian spruce. They range from 15.5 (SP 5) to 20.5 m (SP 8) and increase with the degree of mixing in the stand. Thestandard deviation hV also shows higher values with increased mixing. In all Macedonian pine sample plots, height structures have a negative (right) skewness (α3 < 0), while in SP 5, SP 6, and SP 8 α4 < 3, and in SP 7 α4 > 3. Like in the Serbian spruce stands, stands with a lower degree of mixing (SP 5, SP 6) are clearly separated from stands with a higher degree of mixing (SP 7, SP 8) in terms of height structure.
The differentiation of the vertical structure is also expressed on the basis of the results of vertical profile fulfillment Arel (Table 4). In the stands of Serbian spruce, Arel values range from 43.5% (SP 1) to 58.9% (SP 4), and in the Macedonian pine stands from 45.8% (SP 5) to 68.6% (SP 8). The growing trend of Arel in stands of both tree species is positively correlated with the increase in the degree of mixing. The increase in mixing directly affected the complexity of vertical form of the investigated stands.

Table 4.
Values of the relative species profile index (Arel).
3.4. Diameter Structure
Based on the testing of empirical diameter distributions (Mann–Whitney U test), a statistically significant difference (p < 0.05) was found between the sample plots. In the Serbian spruce stands, the arithmetic mean diameter (dbhA) ranges from 23.6 (SP 4) to 28.7 cm (SP 3). A significantly higher variation width (dbhV) and standard deviation were found in the sample plots with a higher degree of mixing (SP 3, SP 4). The diameter distribution in the sample plot with the lowest degree of mixing has a negative skewness (α3 = −0.16) and kurtosis (α4 = −0.45), while in other plots the values of α3 are positive at 0.73 (SP 2), 0.42 (SP 3), 1.30 (SP 4), along withα4 at 1.69 (SP 2), 0.07 (SP 3), 2.07 (SP 4). According to the shape of distributions (Figure 4), the sample plots with a lower degree of mixing (SP 1, SP 2) show a narrower diameter distribution and a more pronounced concentration of trees within one diameter class. The shapes of distributions focused on thinner diameter classes indicate pronounced processes of selection and differentiation of higher diameter classes. Tree differentiation (SP 3, SP 4) becomes more intense with an increase in mixing in stands (low right part of distribution).
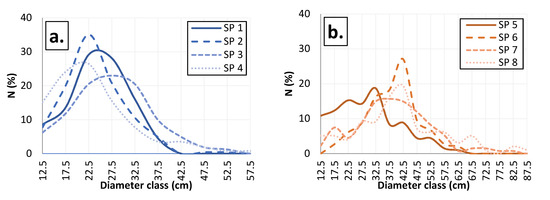
Figure 4.
Distribution of trees by diameter classes in the stands of Serbian spruce (a) and Macedonian pine (b).
In the stands of Macedonian pine, dbhA grows with an increase in mixing from 29.6 cm (SP 5) to 41.2 cm (SP 8). Like in the case of Serbian spruce, the sample plots with a higher degree of mixing (SP 7, SP 8) with a significantly higher dbh and standard deviation are clearly differentiated. Diameter distributions in all sample plots have positive α3 values of 0.44 (SP 5), 0.09 (SP 6), 0.58 (SP 7), and 0.48 (SP 8). The value of α4 in the sample plot with the lowest share of admixed species (SP 5) is negative (−0.39), while the values in other fields are positive at 0.14 (SP 6), 1.04 (SP 7), and 0.26 (SP 8). Compared to the normal distribution (SP 6), the forms with the highest concentration of trees in lower diameter classes (SP 5) and a significantly wider distribution and laid down right part of the diagram (SP 7, SP 8) reveal more complex relationships in the Macedonian pine stands (Figure 4). The forms indicate the processes of selection (SP 5), initiated (SP 6), and pronounced (SP 7, SP 8) tree differentiation. The diameter structure in all sample plots has a clearly expressed single maximum. The appearance of several less pronounced peaks along the variation width indicates a more complex structural form of these stands compared to the classical structure of even-aged stands.
3.5. Parameters of Diameter Diversity
The spatial measure of mixing M clearly distinguishes between two categories of species segregation in stands (Table 5). The first category with a higher degree of segregation is below 0.20 (SP 1, SP 2, SP 5, SP 6) and the lower one is above 0.20 (SP 3, SP 4, SP 7, SP 8). Mean values of the diameter differentiation index Td in the stands of Serbian spruce range from 0.24 (SP 2) to 0.31 (SP 4). The index shows a weak (SP 1, SP 2, SP 3) to medium (SP 4) level of diameter differentiation. In Macedonian pine stands. The index ranges from 0.22 (SP 6) to 0.33 (SP 8) and has a weak (SP 6) to medium (SP 5, SP 7, SP 8) intensity of diameter differentiation. The differentiation index Td is the highest in the stands with the highest degree of mixing (SP 4, SP 8), but it does not show a clear correlation with the change of mixing. Values of the Gini coefficient GC in Serbian spruce range from 0.26 (SP 1) to 0.41 (SP 4), and Macedonian pine from 0.25 (SP 6) to 0.41 (SP 5).

Table 5.
Parameters of diameter diversity in the investigated stands.
The Gini coefficient of homogeneity in the stands of Serbian spruce shows a clear increasing trend with an increasing degree of mixing, while in the stands of Macedonian pine this trend deviates in the sample plot with the lowest degree of mixing (SP 5). The hyperbolic tangent index S of admixed species in the community of Serbian spruce is from 0.41 (SP 1) to 0.78 (SP 4), and has an increasing trend with increasing mixing, while in the community of Macedonian pine it has values from 0.40 (SP 8) to 0.57 (SP 7) and does not show a clear correlation with increasing mixing.
3.6. Spearman’s Correlation Coefficient ρ
Based on the established relationship between stand characteristics and mixing, a correlation analysis was performed using the Spearman’s correlation coefficient ρ (Table 6). A strong positive correlation was found between the mixing index M and the aggregation index R (ρ = 0.87, p < 0.01), the mixing index M and the relative species profile index Arel (ρ = 0.86, p < 0.05), the aggregation index R and the relative species profile index Arel(ρ = 0.74, p < 0.05), and the diameter differentiation index Td and the Gini coefficient GC (ρ = 0.85, p < 0.01). A weak to moderately strong correlation, without statistical significance, was found among the other parameters of stand structure.

Table 6.
Matrix of Spearman’s correlation coefficient ρ between the species mixing index (M), aggregation index (R), relative species profile index (Arel), diameter differentiation index (Td), Gini coefficient (GC), and hyperbolic tangent index (S).
4. Discussion
4.1. Differences in the Basic Characteristics between the Researched Stands and Other Stands of the Same Species
In previous studies of mixed stands of Serbian spruce in Serbia [53,54], lower values of all numerical (dendrometric) variables were found at a locality in the immediate vicinity of the investigated stands except for the number of trees per unit area. The structure of these stands is much more complex than in the investigated stands and ranges from uneven-aged stands to structures close to selection stands. The increase in total volume with increasing mixing was also confirmed by these studies.
Available research on Macedonian pine stands in Macedonia (Pelister) [27,55] and Serbia (Šar Mountain) [56,57], higher values of the mean diameter and height of trees were found, while the basal area and volumes are smaller than in the investigated stands resulting from the smaller number of trees. These differences are a consequence of different ecological conditions of stand development. The stands of Macedonian pine [27,55,56,57] are located in optimal conditions of development [58], while the investigated stands are located on the border of the vertical (1825 to 1910 m above sea level) and horizontal (north) range of the species (Figure 1).
4.2. Effect of Mixing on the Spatial Pattern of Tree Distribution
The spatial distribution of trees in stands is influenced by numerous factors. It is most influenced by the management system, the origin and structure of stands, the composition of the species that build them, developmental stages, natural disturbances, habitat conditions and abiotic conditions to which they have adapted their development. In intensively managed stands, the distribution of trees tends towards a regular (random) distribution [59,60]. In stands that are not subjected to management treatments, active selection and differentiation processes influence the regulation of tree distribution with a tendency toward a regular distribution [40,41], i.e., random distribution [60,61], which was confirmed by this research. These pronounced processes in mixed stands of the studied species affected the random distribution of trees. The regularity of distribution is especially pronounced in trees with larger diameters [40,41], which is also the trend observed in this research (SP 7, SP 8).
The tendency towards clumping of trees at lower distances in the stands of Serbian spruce (SP 1, SP 2) can be explained by microhabitat conditions (form of the micro-relief conditioned by the parent rock, a mosaic shallow initial phase of the soil) and the relative absence of other species with different bio-ecological characteristics which would contribute to the process of intensive competition and differentiation. The formed homogeneous groups in the coves and at the crossings between ridges, which intersect the entire locality, condition the clumping of trees at relatively larger distances. The clumping of Macedonian pine trees at lower distances (SP 5, SP 6) can be explained by the specifics of the species development in high mountain climatic conditions. The relations of the spatial distribution of the trees can be divided into two groups; I. with a lower degree of mixing (SP 1, SP 2; SP 5, SP 6), where the trees tend to clump (group) and II. with a higher degree of mixing (SP 3, SP 4; SP 7, SP 8), where the trees tend to be randomly to regularly distributed. Wider distributions of dimension (Figure 3 and Figure 4) indicate an increasingly pronounced influence of the separation of ecological niches of different species in mixed stands and the dimensional unevenness and intensive separation of taller and shorter trees into strata. This fact also affected the spatial arrangement of the trees.
4.3. Diversity Indices as an Appropriate Measure of Stand Differences (Td, GC)
The diameter differentiation index Td based on the researched references shows different values in different stand situations. The lowest values are typical of even-aged stands that are actively managed, 0.11 in taigas [62], 0.13–0.21 in pine cultures of different ages [41], 0.21 in an even-aged beech stand [8], 0.25 in young Douglas fir culture [8], 0.30 [59], and 0.34 [60] in even-aged stands of different forest types. Slightly higher average values of Td were found in uneven-aged stands of beech 0.27–0.42 [63], 0.36 [64], and 0.42 [8] in mixed stands of beech. In a series of permanent research plots in the Czech Republic [65,66,67,68] on a similar sample in protected mixed stands of spruce, fir and beech values were determined to be from 0.41 to 0.55 [67] and in managed mixed stands of beech of different origin they were from 0.36–0.49 [68]. In relict pure stands of Scots pine lower values (0.20–0.33) were found [65]. In research on mixed stands of Scots pine without management treatment [66], a trend of decreasing the degree of diameter differentiation (from 0.37–0.48 to 0.36–0.42) was determined in the analyzed period of 15 years on all permanent research plots. The inventory of different forest types in the Austrian Alps determined the average value of the Td index in stands of 0.37, and values significantly above this average (0.50) were found in two-story (multi-story) stands [69]. In the selected stands, the determined mean values of the Td index are 0.43 [64] and 0.42 [59]. The highest Td values are typical of virgin forests, and they range from 0.47 [70] to 0.76–0.78 [60].
By comparing the presented Td indices, the differentiation of diameters has characteristic higher or lower values in relation to the developmental and structural type of stands. These differences indicate, but do not determine, the stand type. In non-managed forests, the differences are the result of competition between species and within the species during development, and in forests that are regularly managed, they are a direct consequence of these relationships and the nature of applied management treatments.
The determined values of the index from 0.24 to 0.33 indicate a simpler type of stand, which only confirms the previous analysis of the height and diameter structure.
In the practical use of the Td index, it is important to pay attention to the distribution of index values of structural groups, as well as the use of appropriate measures of central tendency. The approximately normal values of the Td index distribution indicate the possibility of using mean values [62] as a representative parameter in the analysis of the relationship, which is the case here. For significant deviations from the normal distribution, the use of mode [62] or median [69] is adequate.
The Gini coefficient GC has the lowest values in young even-aged stands of 0.15–0.30 [71], 0.22 [60], and 0.25 in two-story stands [69]. Higher values are typical of mixed and uneven-aged stands of different compositions (e.g., 0.37–0.54 [19], 0.50–0.58 [71], 0.49–0.57 [72], and 0.35–0.52 [73]). Values above 0.60 [71] are characteristic of selective stands and virgin forests. The mean values in the selection stands of the Austrian Alps are 0.63 [59]. The highest values of the index were found in beech and spruce reserves and virgin forests of the southeastern Carpathians 0.69–0.71 [74], beech and hornbeam in the Czech Republic 0.67–0.75 [60], beech, fir, spruce in Bosnia and Herzegovina 0.67 [70], and beech in Serbia 0.45–0.52 [72]. The values presented in different stands justify the use of GC as an adequate measure of stand inequality, which also indicates but does not determine the stand type.
In relation to the distribution of the analyzed dimensions, the indices show certain regularities. Stands with a normal distribution have lower GC values compared to stands with the inverse J-shape [46,59] and regular distributions [46]. In this research, two stands with a statistically significant normal distribution (SP 1, SP 6) have the lowest GC values. This confirms the assumption that GC values increase with the deviation of the distribution from the normal shape [47,75]. The diameter distribution in uneven-aged stands is reflected in higher and more constant index values compared to even-aged stands [47]. In the research of different forms of pure and mixed stands of spruce, fir, and beech of the Eastern Carpathians [75] GC has been shown to be a useful tool in differentiating different structural types of stands. Regardless of the established justification and superiority in relation to other indices [46], the possibility of obtaining the same values in different structures (as with the previous index) limits its application [76]. That shortcoming requires the analysis of the flows of the Lorentz curve on which the index is based or the use of adequate additional parameters in determining the differences of the analyzed stands [76].
In the practical use of this index, as a useful tool in forest management, it is necessary to pay attention to the impact of the callipering threshold on its value [75], the type and size of the sample used [77], as well as the index value in the structures of transitional forms in the process of stand regeneration [47].
4.4. Impact of Admixed Species on Stand Structure
In order to determine the causes of changes in structure parameters with an increasing degree of mixing, the ratio of diameters between admixed and dominant species was analyzed in the investigated stands. The hyperbolic tangent index S in the stands of Serbian spruce has a growing trend in relation to mixing. The parameter shows that, with an increase in their share, admixed species have larger dimensions compared to the neighboring (competing) trees of dominant species. This fact can explain the almost regular changes in the analyzed parameters of the structure of Serbian spruce stands with an increase in the degree of mixing. The S index in Macedonian pine stands does not show a high dependence on the degree of mixing, but still there are small changes in structural parameters with its increase. The index determines the cause of the change in diversity well and determines equally well the competitive status of the relationships among the species. Serbian spruce in mixed stands can be characterized as extremely endangered by the competition of admixed tree species. The determined impact of mixing, considering the priority goal of the survival of this tree species (generally of species diversity), compromises the justification of establishing the strictest protection regimes of these stands, allowing them to develop spontaneously.
4.5. Correlation of the Investigated Parameters of Structural Diversity
There is not much literature data on the impact of mixing on the aggregation index. Contrary to the obtained results (Table 6), in stands with active management, the established ratio has a negative character of low intensity [62].
The pronounced link between the vertical fulfillment of the Arel profile and the mixing of stands is based on their mathematical correlation. The obtained values confirm the advantage of using the index in stands with different numbers of species [5], as well as the impact of deviation of structure from pure single-story stands on the growth of index values [78].
The impact of mixing on dimensional diversity indices is indirectly expressed through the impact on stand structure. Differences in the distributions of the investigated stands with increasing mixing had a positive effect on diameter differentiation indices (Td, GC). A study of different empirical and theoretical stand situations [46] found a strong impact of mixing on GC values. Significant differences in GC values were found between the pure and mixed even-aged stands of the most common species of Central Europe [79]. Mixed stands had on average significantly higher GC values (0.46) than pure stands (0.36), with an established correlation of medium strength.
The moderately strong positive correlation found in studies of the impact of mixing on the M and Td differentiation indices in virgin forests [70] and actively managed different forest types [62] was also confirmed by this study.
Prior research in stands of even-aged and almost even-aged structure found a strong correlation between Td and GC [80], which is also confirmed by this study. In contrast, the weak correlation of these indices in stands of more complex structure, virgin forests [70], diverse stands [80], and stands of different types [71], emphasizes the impact of structure on the change in their relationship. The reason for this should be sought in various mathematical assumptions of the above indices.
Since the hyperbolic tangent index S is a new index, no research has been performed on its correlation with other structural parameters. In addition to the tree characteristics diversity index, it has also been proposed as a useful tool for researching absolute and relative growth rates [48]. Considering the concept of using the index, the relationship between the S index and the mixing index M depends on the distribution of the observed characteristics of the admixed species in stands with different degrees of mixing. In this research, it has a weak positive correlation with the stand mixing index.
5. Conclusions
The structural diversity of the studied relict-endemic communities confirms their great importance in terms of biodiversity and reifies their need for protection and conservation in the Balkans.
Structural indices, whose values clearly vary in different stand situations, have proven to be useful and reliable indicators for defining stand characteristics, as well as for differentiating stands on the basis of them. Their mutual correlation was observed, as well as their correlation with the mixing of stands, which implies an increase in structural diversity with an increase in the degree of mixing in stands.
Compared to pure stands, mixed stands have a more pronounced skewness and kurtosis of the diameter structure, significantly wider variation widths of diameters and heights, a more pronounced vertical development, and higher values of structural indices, which all together result in a greater structural heterogeneity (diversity). These differences are significantly more pronounced in stands with a higher degree of mixing.
According to the obtained results, a 20% share of admixed species by volume and the spatial mixing of species M of 0.20, can be considered the lower limit of the impact of mixing on the change in structural characteristics of stands, with changes reflected in all parameters of horizontal and vertical structures.
The past development of the investigated stands without direct anthropogenic influence caused the formation of the initial phases of virgin stand forms. The established experiments contribute to a better understanding of structural relationships in the conditions of spontaneous stand development. The obtained low to medium values of structural diversity do not justify the existing management concept. In addition, they point to the need for an active management approach in order to preserve the biodiversity of rare and endangered forest communities. The dialectical principle of the development of forest communities, from the initial to the terminal phase, makes the establishment of permanent and strict protection regimes debatable from the aspect of biodiversity conservation. Finally, forest communities left to spontaneous development will certainly not go in the direction of conservation.
Author Contributions
Conceptualization, A.P. and M.M.; methodology, A.P. and D.P.; software, A.P.; writing—original draft preparation, A.P., B.Š. and S.O.; writing—review and editing, all authors; visualization, A.P., B.Š. and S.O.; supervision, M.M. and D.P.; project administration, S.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education, Science, and Technological Development of the Republic of Serbia within the project “Sustainable management of total forest potentials in the Republic of Serbia”-EVBR 37008.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Acknowledgments
The authors also acknowledge the support of the State Enterprise for Forest Management “Srbija šume” and State Enterprise National Park “Tara” for providing accommodation during the field data collection.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stevanović, V.; Jovanović, S.; Lakušić, D.; Niketić, M. Diversity of the vascular flora of Yugoslavia with an overview of species of international importance. In Biodiversity of Yugoslavia-with an Overview of Species of International Importance; Faculty of Biology: Belgrade, Serbia, 1995; pp. 183–217. [Google Scholar]
- Janković, M. Phytogeography, 2nd ed.; Science Book: Belgrade, Serbia, 1990. [Google Scholar]
- Pommerening, A.; Murphy, S.T. A review of the history, definitions and methods of continuous cover forestry with special attention to afforestation and restocking. Forestry 2004, 77, 27–44. [Google Scholar] [CrossRef] [Green Version]
- Río, M.; Pretzsch, H.; Alberdi, I.; Bielak, K.; Bravo, F.; Brunner, A.; Condés, S.; Ducey, M.J.; Fonseca, T.; von Lüpke, N.; et al. Characterization of the structure, dynamics, and productivity of mixed-species stands: Review and perspectives. Eur. J. For. Res. 2015, 135, 23–49. [Google Scholar] [CrossRef]
- Pretzsch, H. Standard Analysis of Long-Term Experimental Plots. In Forest Dynamics, Growth and Yield: From Measurement to Model; Springer: Berlin/Heidelberg, Germany, 2009; pp. 181–222. [Google Scholar] [CrossRef]
- Whittaker, R.H. Evolution and measurement of species diversity. Taxon 1972, 21, 213–251. [Google Scholar] [CrossRef] [Green Version]
- Gadow, K.V. Forest structure and diversity. Allg. Forst Jagdztg. 1999, 170, 117–122. [Google Scholar]
- Pommerening, A. Approaches to quantifying forest structures. Forestry 2002, 75, 305–324. [Google Scholar] [CrossRef]
- Aguirre, O.; Hui, G.Y.; Gadow, K.; Jimenez, J. An analysis of spatial forest structure using neighbourhood-based variables. For. Ecol. Manag. 2003, 183, 137–145. [Google Scholar] [CrossRef]
- Neumann, M.; Starlinger, F. The significance of different indices for stand structure and diversity in forests. For. Ecol. Manag. 2001, 145, 91–106. [Google Scholar] [CrossRef]
- Gadow, K.V.; Hui, G. Characterising forest spatial structure and diversity. In Sustainable Forestry in Temperate Regions; Proceeding of JUFRO International Workshop Sustainable Forestry in Temperate Regions; Bjoerk, L., Ed.; University of Lund: Lund, Sweden, 2002; pp. 20–30. [Google Scholar]
- McElhinny, C.; Gibbons, P.; Brack, C.; Bauhus, J. Forest and woodland stand structural complexity: Its definition and measurement. For. Ecol. Manag. 2005, 218, 1–24. [Google Scholar] [CrossRef]
- Pommerening, A. Evaluating structural nearest neighbor summary statistics by reversing forest structural analysis. For. Ecol. Manag. 2006, 224, 266–277. [Google Scholar] [CrossRef]
- Hansen, A.J.; Spies, T.A.; Swanson, F.J.; Ohmann, J.L. Conserving biodiversity in managed forests. BioScience 1991, 41, 382–392. [Google Scholar] [CrossRef] [Green Version]
- Kuuluvainen, T.; Penttinen, A.; Leinonen, K.; Nygren, M. Statistical opportunities for comparing stand structural heterogeneity in managed and primeval forests: An example from boreal spruce forest in southern Finland. Silva Fenn. 1996, 30, 315–328. [Google Scholar] [CrossRef] [Green Version]
- Paillet, Y.; Bergès, L.; Hjältén, J.; Ódor, P.; Avon, C.; Bernhardt-Römermann, M.; Bijlsma, R.; de Bruyn, L.; Fuhr, M.; Grandin, U.; et al. Biodiversity differences between managed and unmanaged forests: Meta-analysis of species richness in Europe. Conserv. Biol. 2010, 24, 101–112. [Google Scholar] [CrossRef]
- Pretzsch, H.; Rio, M.; Schutze, G.; Ammer, C.; Annighöfer, P.; Avdagic, A.; Barbeito, I.; Bielak, K.; Brazaitis, G.; Coll, L.; et al. Mixing of Scots pine (Pinus sylvestris L.) and European beech (Fagus sylvatica L.) enhances structural heterogeneity, and the effect increases with water availability. For. Ecol. Manag. 2016, 373, 149–166. [Google Scholar] [CrossRef] [Green Version]
- Pretzsch, H.; Biber, P. Tree species mixing can increase maximum stand density. Can. J. For. Res. 2016, 46, 1179–1193. [Google Scholar] [CrossRef] [Green Version]
- Bravo-Oviedo, A.; Pretzsch, H.; del Río, M. Dynamics, Silviculture and Management of Mixed Forests. In Growth and Structure in Mixed-Species Stands Compared with Monocultures: Review and Perspectives; Bravo-Oviedo, A., Pretzsch, H., Río, M., Eds.; Springer: Cham, Switzerland, 2018; Volume 31, pp. 131–184. [Google Scholar] [CrossRef]
- EUFORGEN. Available online: http://www.euforgen.org/species/picea-omorika/+/pinus-peuce/ (accessed on 17 April 2021).
- Tomić, Z. Forestry Phytocenology; Faculty of Forestry, University of Belgrade: Belgrade, Serbia, 2004. [Google Scholar]
- Pommerening, A.; Stoyan, D. Edge-correction needs in estimating indices of spatial forest structure. Can. J. For. Res. 2006, 36, 1723–1739. [Google Scholar] [CrossRef] [Green Version]
- Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. Statistical Analysis and Modelling of Spatial Point Patterns; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Motz, K.; Sterba, H.; Pommerening, A. Sampling measures of tree diversity. For. Ecol. Manag. 2010, 260, 1985–1996. [Google Scholar] [CrossRef]
- Magurran, A. Ecological Diversity and Its Measurement; Princeton University Press: Princeton, NJ, USA, 1988. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Pariško, Ž. Wood Productivity of Macedonian Pine (Pinus peuce-Griseb) in Dependence on Habitat Conditions in Pelister. Ph.D. Thesis, Faculty of Agriculture and Forestry, University of Kiril and Metodij, Skopje, North Macedonia, 1962. [Google Scholar]
- Banković, S.; Stojanović, L.J. Two-way volume table for Serbian spruce in SR Serbia. Bull. Fac. For. 1976, 50, 55–66. [Google Scholar]
- Banković, S.; Jović, D.; Medarević, M. Volume tables for beech (Fagus moesiaca Czeczott). Bull. Fac. For. 1989, 71–72, 343–358. [Google Scholar]
- Banković, S. Volume tables for fir (Abies alba Mill.) and spruce (Picea excelsa Link.) in forests of National park Tara. Bull. Fac. For. 1991, 1, 106. [Google Scholar]
- Banković, S.; Medarević, M.; Pantić, D.; Filipović, M. Volume Tables for Spruce in the Region of National Park of Kopaonik, Forestry; Association of Forestry Engineers and Technicians: Belgrade, Serbia, 2003; Volume 3–4, pp. 51–60. [Google Scholar]
- Füldner, K. Describing Forest Structures in Mixed Beech-Ash-Maple-Sycamore Stands. Ph.D. Thesis, University of Göttingen, Göttingen, Germany, 1995. [Google Scholar]
- Albert, M.; Gadow, K. Assessing Biodiversity with New Neighborhood-Based Parameters. In Proceedings of the International Conference on Data Management and Modelling Using Remote Sensing and GIS for Tropical Forest Land Inventory, Jakarta, Indonesia, 26–29 October 1998; pp. 433–445. [Google Scholar]
- Gadow, K.; Zhang, X.H.; Wehenkel, C.; Pommerening, A.; Corral-Rivas, J.; Koral, M.; Myklush, S.; Hui, G.Y.; Kiviste, A.; Zhao, X.H. Forest structure and diversity. In Continuous Cover Forestry; Pukkala, T., Gadow, K., Eds.; Springer Science + Business Media: Berlin/Heidelberg, Germany, 2012; pp. 29–84. [Google Scholar]
- Pommerening, A.; Uria-Diez, J. Do large forest trees tend towards high species mingling? Ecol. Inform. 2017, 42, 139–147. [Google Scholar] [CrossRef]
- Clark, P.J.; Evans, F.C. Distance to nearest neighbour as a measure of spatial relationships in populations. Ecology 1954, 35, 445–453. [Google Scholar] [CrossRef]
- Donnelly, K. Simulations to determine the variance and edge-effect of total nearest neighbour distance. In Simulation Studies in Archaeology; Hodder, I., Ed.; Cambridge University Press: London, UK, 1978; pp. 91–95. [Google Scholar]
- Ripley, B.D. Modelling spatial patterns. J. R. Stat. Soc. Ser. B 1977, 39, 172–192; discussion 192–212. [Google Scholar] [CrossRef]
- Diggle, P.J. Statistical Analysis of Spatial Point Patterns; Hodder Arnold: London, UK, 2003. [Google Scholar]
- Gray, L.; He, F. Spatial point-pattern analysis for detecting density-dependent competition in a boreal chronosequence of Alberta. For. Ecol. Manag. 2009, 259, 98–106. [Google Scholar] [CrossRef]
- Szmyt, J. Spatial pattern of trees of different diameter classes in managed pine stands (Pinus sylvestris L.) of different age. Acta Sci. Pol. Silv. Colendar. Rat. Ind. Lignar. 2010, 9, 37–49. [Google Scholar]
- Ripley, B.D. Tests of randomness for spatial point patterns. J. Roy. Stat. Soc. B 1979, 41, 358–374. [Google Scholar] [CrossRef]
- Pretzsch, H. Analysis and Reproduction of Spatial Stand Structures. Methodic Thoughts on the basis ofMixed Beech-Larch Stands in Lawer Saxony. Cent. Forstwes. 1995, 112, 91–117. [Google Scholar]
- Gadow, K.V. Stand description in the forest management. ForstHolz 1993, 48, 602–606. [Google Scholar]
- Wang, H.; Zhang, G.; Hui, G.; Li, Y.; Hu, Y.; Zhao, Z. The influence of sampling unit size and spatial arrangement patterns on neighborhood-based spatial structure analyses of forest stands. For. Syst. 2016, 25, 4. [Google Scholar] [CrossRef] [Green Version]
- Lexerod, N.L.; Eid, T. An evaluation of different diameter diversity indices based on criteria related to forest management planning. For. Ecol. Manag. 2006, 222, 17–28. [Google Scholar] [CrossRef]
- O’Hara, K.L.; Hasenauer, H.; Kindermann, G. Sustainability in multi-aged stands: An analysis of long-term plenter system. Forestry 2007, 80, 163–181. [Google Scholar] [CrossRef] [Green Version]
- Pommerening, A.; Szmyt, J.; Zhang, G. A new nearest-neighbour index for monitoring spatial size diversity: The hyperbolic tangent index. Ecol. Model. 2020, 435, 109232. [Google Scholar] [CrossRef]
- JASP, Version 0.9.0.1. JASP Team. 2018. Available online: https://jasp-stats.org/ (accessed on 5 February 2021).
- GraphPad Prism. Version 9.0.0 for Windows. GraphPad Software: San Diego, CA, USA; Available online: https://graphpad.com/ (accessed on 20 January 2021).
- Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Patterns. Methodology and Applications with R; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.r-project.org/ (accessed on 19 November 2020).
- Stojanović, L.J. Investigation of the Influence of Some Habitat and Stand Factors on the Dynamics of the Development of serbian Spruce Trees in Characteristic Sites in SR Serbia. Master’s Thesis, Faculty of Forestry, University of Belgrade, Belgrade, Serbia, 1972. [Google Scholar]
- Ostojić, D. Ecological Factors of Natural Maintenance and Renewal of Cenopopulations of Serbian Spruce in NP Tara. Ph.D. Thesis, Faculty of Forestry, University of Belgrade, Belgrade, Serbia, 2005. [Google Scholar]
- Velkovski, N.; Krstić, M.; Govedar, Z.; Vasilevski, K.; Bjelanović, I.; Keren, S. Natural regeneration processes in old-growth Pinus peuce forest in the National park “Pelister” on Mt. Baba. Forestry 2013, 1–2, 67–80. [Google Scholar]
- Tomanić, L.; Stojanović, L.J.; Karadžić, D.; Stefanović, V.; Ostojić, D. Phytocenological and stand characteristics of Macedonian pine forests in the reserve Jažinačko lake on Mt. Šara. Nat. Prot. 1998, 50, 305–318. [Google Scholar]
- Ostojić, D.; Krstić, M. Structure, stand productivity and tree development in a mixed Macedonian and Scotch pine forest. In Proceedings of the VII International congress of ecology (INTECOL), Florence, Italy, 19–25 July 1998. [Google Scholar]
- Em, H.; Džekov, S. Macedonian pine forests on Mt. Pelister. In Proceedings of the Symposiumabout Macedonian Pine; Faculty of Agriculture and Forestry, University of “Kiril and Metodij”: Skopje, North Macedonia, 1969; pp. 49–61. [Google Scholar]
- Sterba, H.; Zingg, A. Distance-dependent and distance-independent stand structure description. Allg. Forst Jagdztg. 2006, 177, 169–176. [Google Scholar]
- Bilek, L.; Reemes, J.; Zahradnik, D. Managed vs. unmanaged. Structure of beech forest stands (Fagus sylvatica L.) after 50 years of development, Central Bohemia. For. Syst. 2011, 20, 122–138. [Google Scholar] [CrossRef] [Green Version]
- Szwagrzyk, J.; Czerwezak, M. Spatial Patterns of Trees in Natural Forests of East-Central Europe. J. Veg. Sci. 1993, 4, 469–476. [Google Scholar] [CrossRef]
- Seidling, W.; Travaglini, D.; Meyer, P.; Waldner, P.; Fischer, R.; Granke, O.; Chirici, G.; Corona, P. Dead wood and stand structure–Relationships for forest plots across Europe. iForest 2014, 7, 269–381. [Google Scholar] [CrossRef]
- Matovic, B. Relationship between Structure, Species and Ecosystem Diversity of High Beech Forests in Serbia. Ph.D. Thesis, Faculty of Biology, University of Belgrade, Belgrade, Serbia, 2012; p. 247. [Google Scholar]
- Pommerening, A.; Stoyan, D. Reconstructing spatial tree point patterns from nearest neighbour summary statistics measured in small subwindows. Can. J. For. Res. 2008, 38, 1110–1122. [Google Scholar] [CrossRef] [Green Version]
- Vacek, S.; Vacek, Z.; Bílek, L.; Simon, J.; Remeš, J.; Hůnová, I.; Král, J.; Putalová, T.; Mikeska, M. Structure, regeneration and growth of Scots pine (Pinus sylvestris L.) stands with respect to changing climate and environmental pollution. Silva Fenn. 2016, 50, 1564. [Google Scholar] [CrossRef] [Green Version]
- Vacek, S.; Vacek, Z.; Remeš, J.; Bílek, L.; Hůnová, I.; Bulušek, D.; Putalová, T.; Král, J.; Simon, J. Sensitivly of unmanaged relict pine forest in the Czech Republic to climate change and air pollution. Trees 2017, 31, 1599–1617. [Google Scholar] [CrossRef]
- Vacek, Z. Structure and dynamics of spruce-beech-fir forests in Nature Reserves of the Orlickéhory Mts. in relation to ungulate game. Cent. Eur. For. J. 2017, 63, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Hájek, H.; Vacek, Z.; Vacek, S.; Bílek, L.; Prausovám, R.; Linda, R.; Bulušek, D.; Králíček, I. Changes in diversity of protected scree and herb-rich beech forest ecosystems over 55 years. Cent. Eur. For. J. 2020, 66, 202–217. [Google Scholar] [CrossRef]
- Sterba, H. Diversity indices based on angle count sampling and their interrelationships when used in forest inventories. Forestry 2008, 81, 587–597. [Google Scholar] [CrossRef] [Green Version]
- Keren, S.; Svoboda, M.; Janda, P.; Negel, T. Relationships between Structural Indices and Conventional Stand Attributes in an Old-Growth Forest in Southest Europe. Forests 2020, 11, 4. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.K.; Gadow, V.K.; Akca, A. Forest structure and Lorenz model. Allg. ForstJagdztg. 1999, 170, 220–223. [Google Scholar]
- Matović, B.; Koprivica, M.; Kisin, B.; Stojanović, D.; Kneginjić, I.; Stjepanović, S. Comparison of Stand Structure in Managed and Virgin European Beech Forests in Serbia. Šumarski List 2018, 1–2, 47–57. [Google Scholar] [CrossRef]
- Klopcic, M.; Boncina, A. Stand dynamics of silver fir (Abies alba Mill.)-European beech (Fagus sylvatica L.) forests during the past century: A decline of silver fir? Forestry 2011, 84, 259–271. [Google Scholar] [CrossRef] [Green Version]
- Cristea, V.; Leca, S.; Ciceu, A.; Chivulescu, S.; Badea, O. Structural Features of Old Growth Forest from South EasternCharpathians, Romania. South-East Eur. For. 2019, 10, 159–164. [Google Scholar] [CrossRef]
- Duduman, G. A forest management planning tool to create highly diverse uneven-aged stands. Forestry 2011, 84, 301–314. [Google Scholar] [CrossRef]
- Weiner, J.; Solbring, O. The meaning and measurement of size hierarchies in plant populations. Oecologia 1984, 61, 334–336. [Google Scholar] [CrossRef] [PubMed]
- Dixon, P.M.; Weiner, J.; Mitchell-Olds, T.; Woodley, R. Bootstrapping the Gini coefficient of inequality. Ecology 1987, 68, 1548–1551. [Google Scholar] [CrossRef]
- Hanewinkel, M.; Pretzsch, H. Modelling the conversion from even-aged to uneven-aged sstands of Norway spruce (Piceaabies L. Karst.) with a distance-depadent growth simulator. For. Ecol. Manag. 2000, 134, 55–70. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schutze, G. Effect of tree species mixing on the size structure, density, and yield of forest stands. Eur. J. For. Res. 2015, 135, 1–22. [Google Scholar] [CrossRef]
- Peck, J.E.; Zenner, E.K.; Brang, P.; Zingg, A. Tree size distribution and abundance explain structural complexity differentially within stands of even-aged and uneven-aged structure types. Eur. J. For. Res. 2014, 133, 335–346. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).