Comparison between Empirical Models and the CBM-CFS3 Carbon Budget Model to Predict Carbon Stocks and Yields in Nova Scotia Forests
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Permanent Sample Plot Measurement
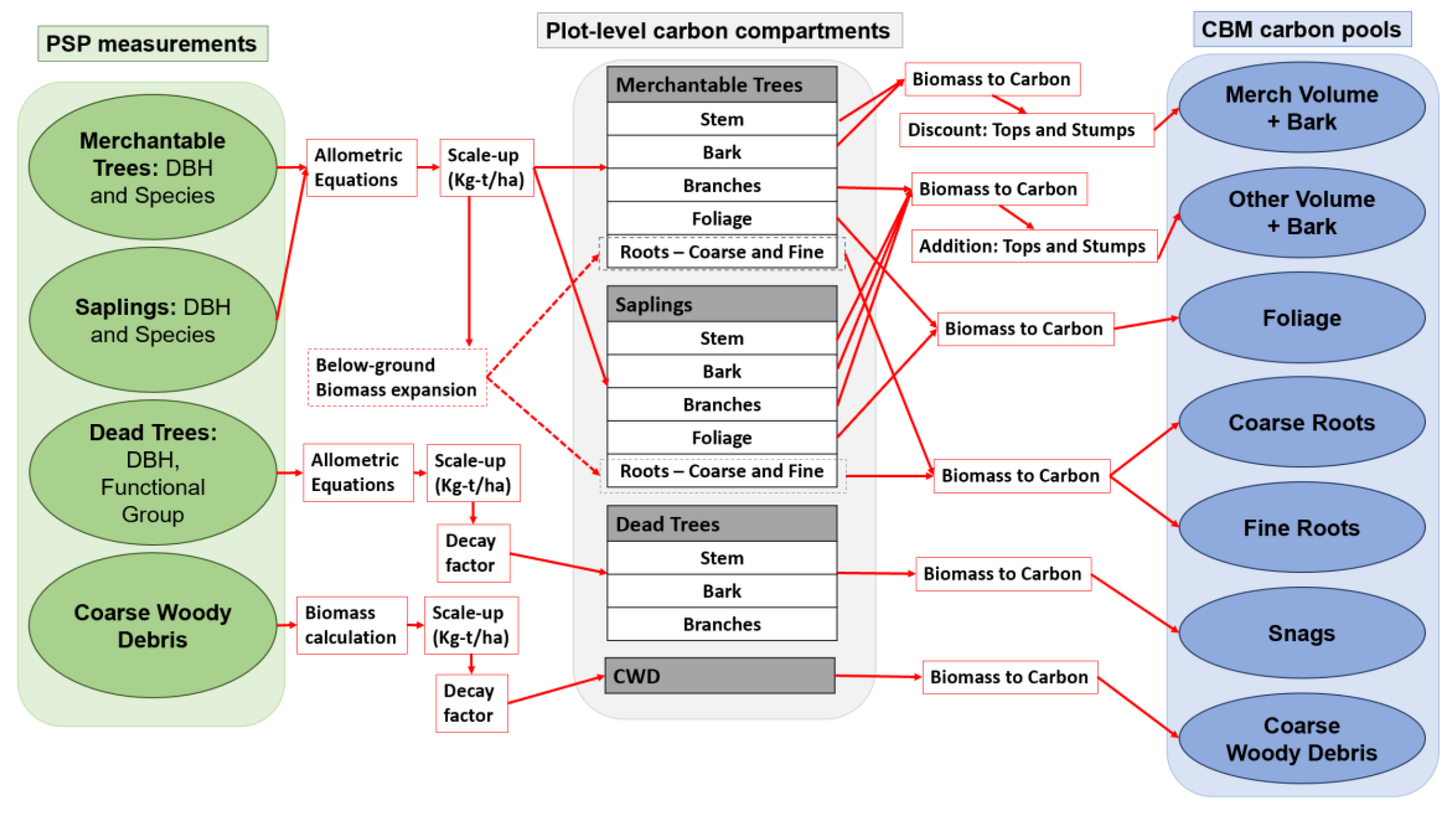
2.3. PSP Measurement Processing
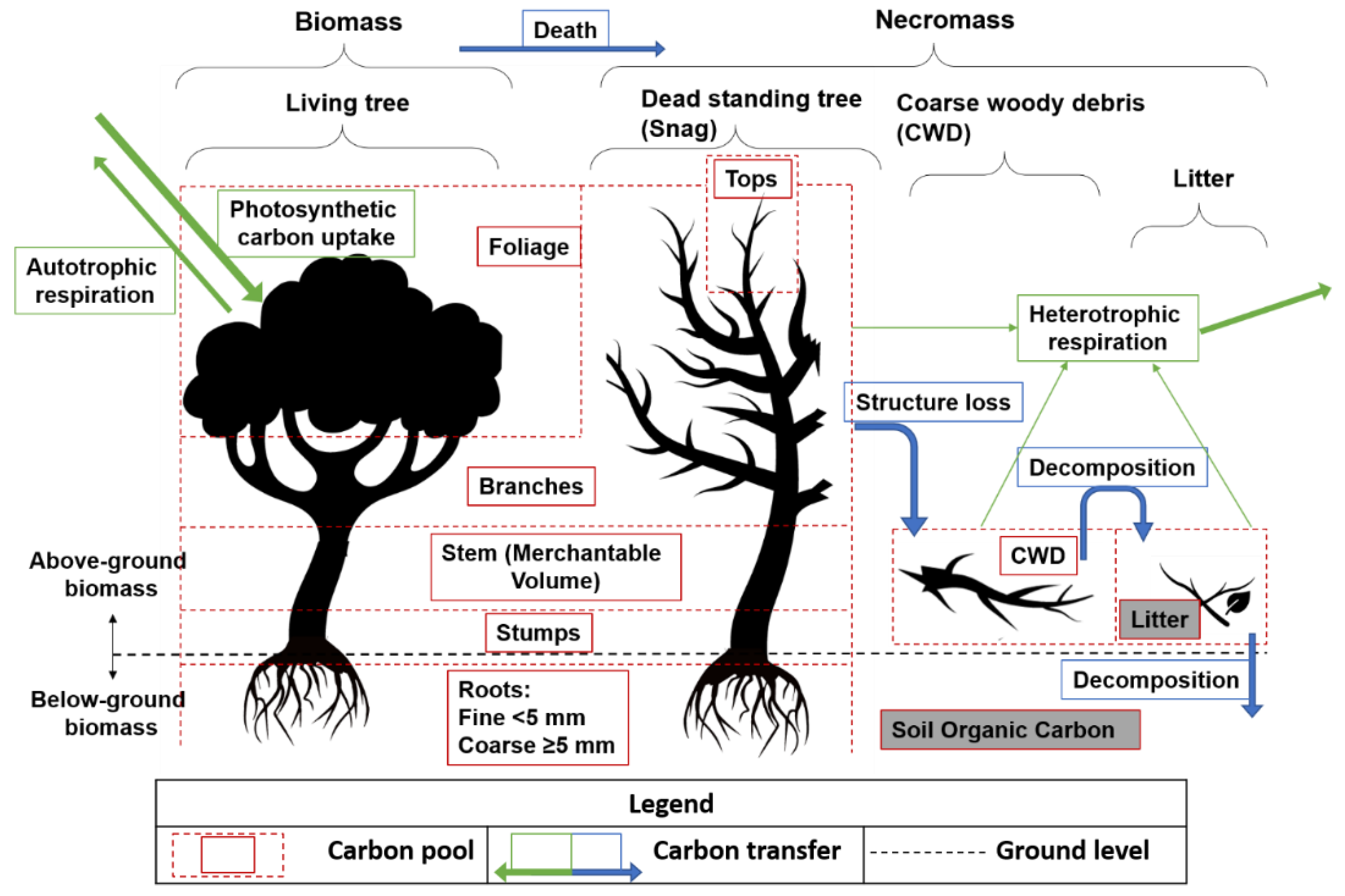
2.3.1. Carbon Calculation from PSP Data
Forest Communities
Age
2.4. Empirical Model Development
2.5. Carbon Budget Model of the Canadian Forest Sector
2.6. CBM-CFS3 Estimations
2.7. PSP Model vs. CBM-CFS3 Estimation Comparison
2.7.1. Pool and Plot-Level Comparison
2.7.2. Stand and Landscape-Level Comparison
3. Results
3.1. Empirical Model Development
Comparison of Estimations against Independent Observations
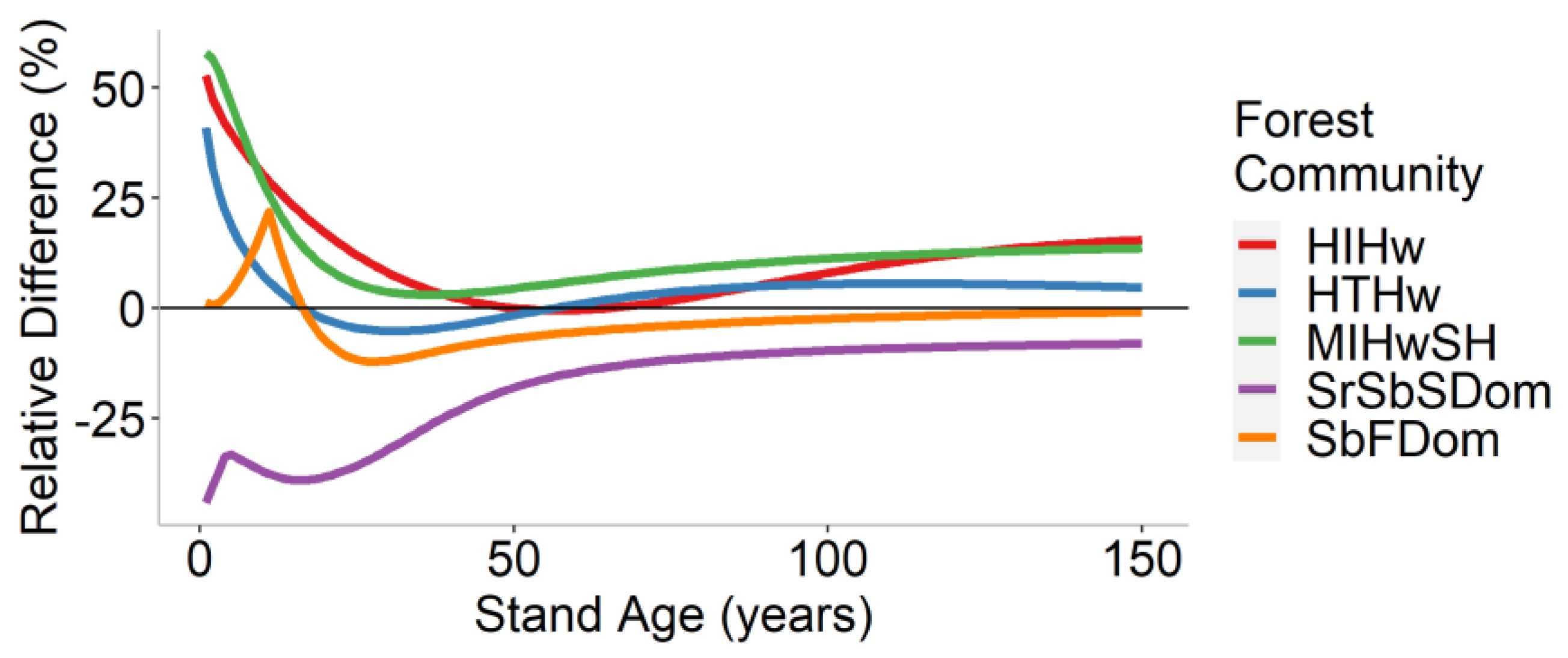
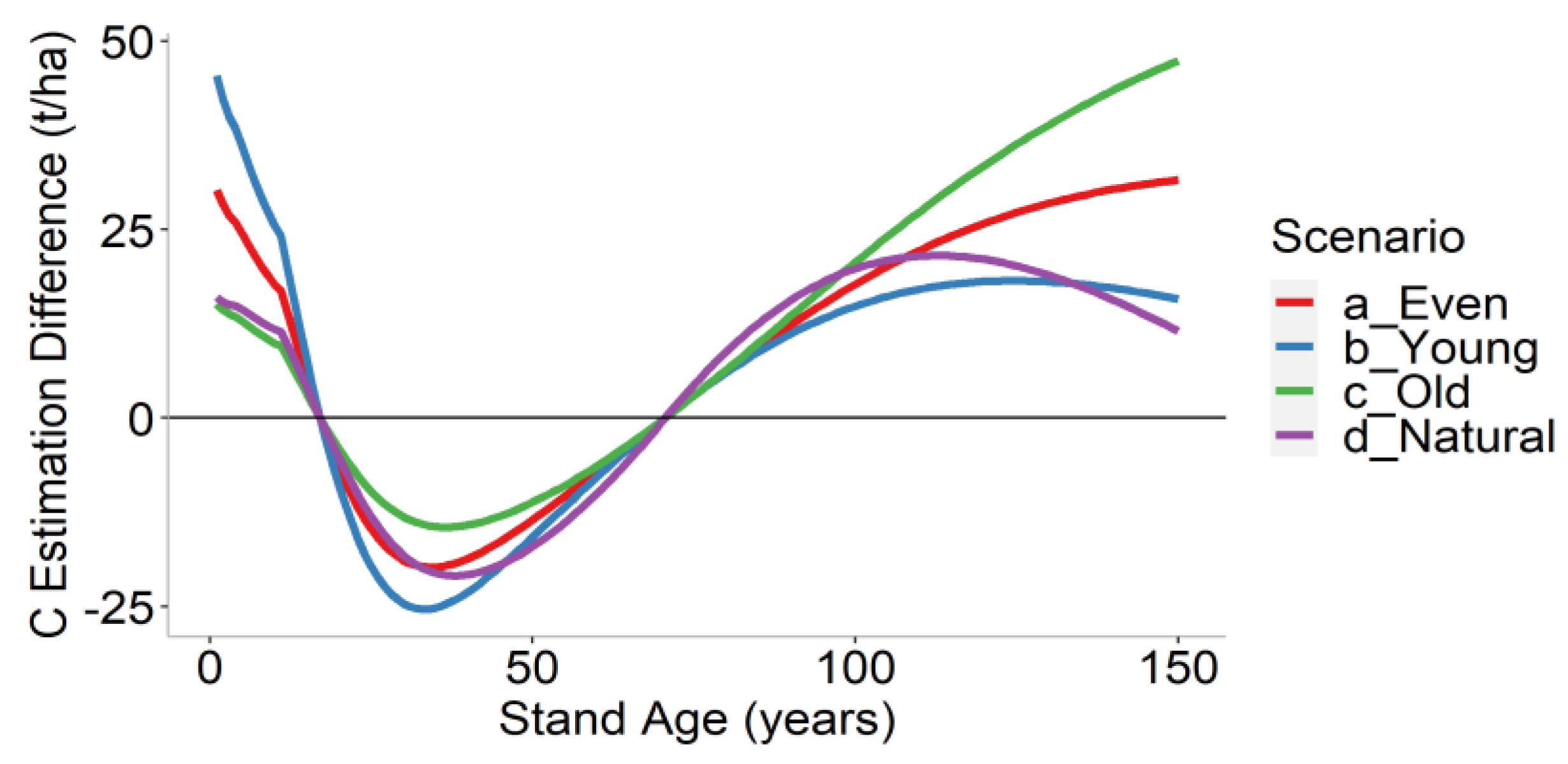
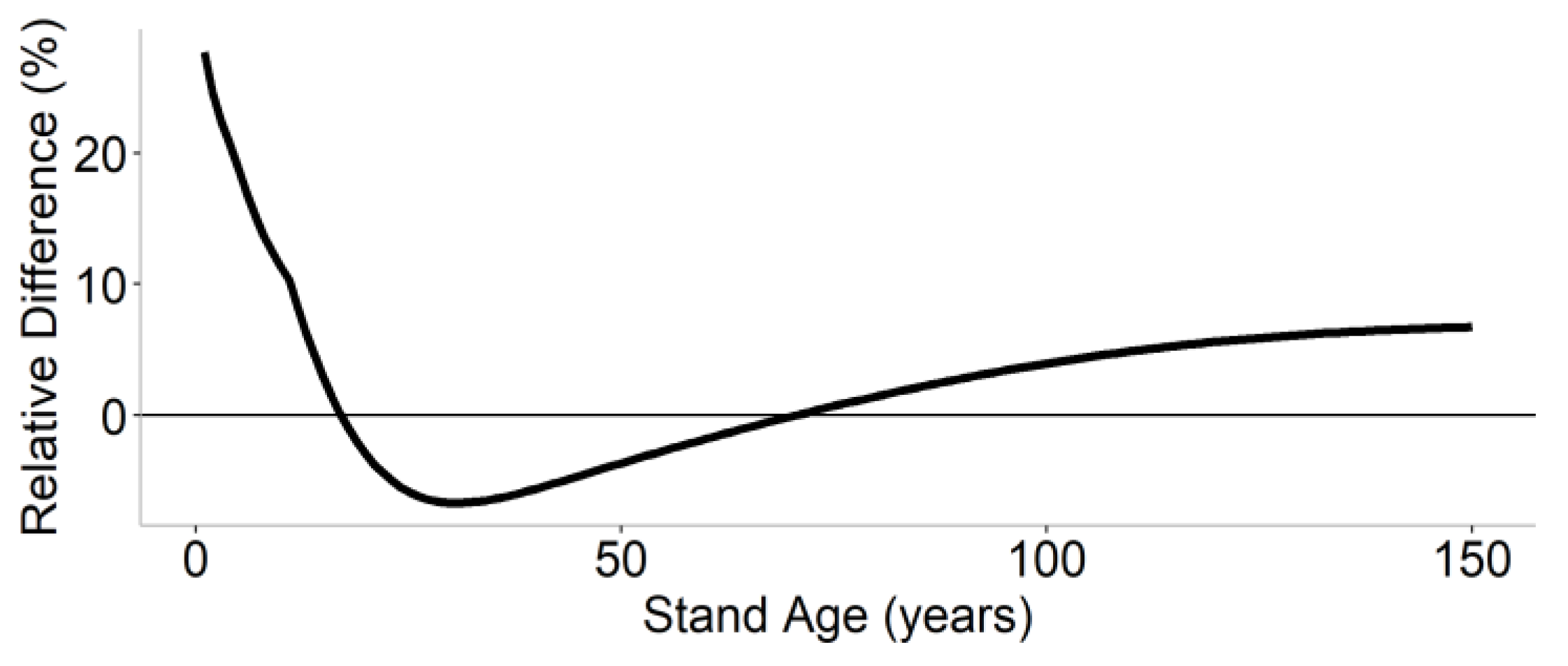
3.2. Stand-Level Method Comparison
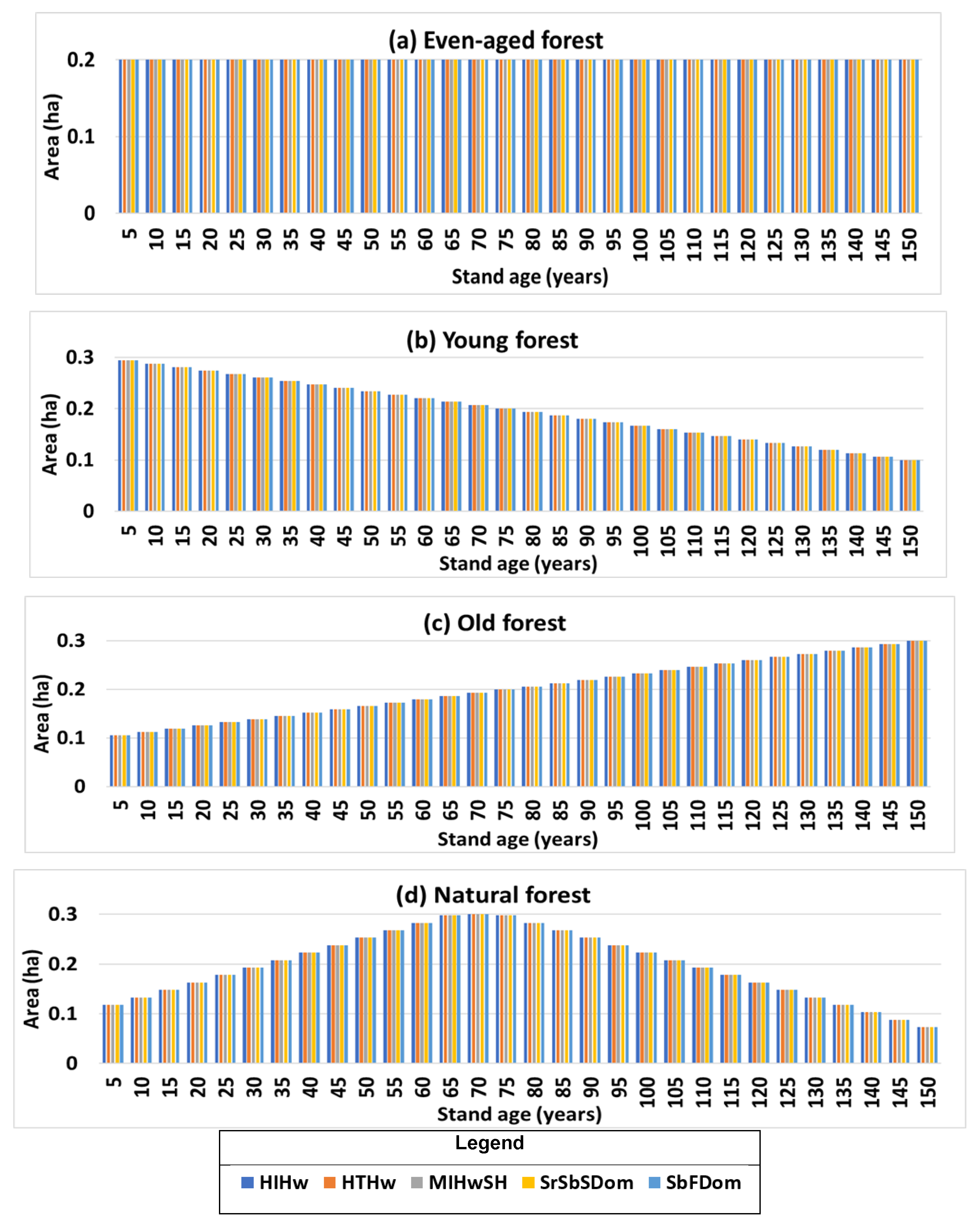
3.3. Landscape-Level Method Comparison
4. Discussion
4.1. Tree and Plot-Level Biomass
4.2. Stand- and Landscape-Level Comparison
4.3. Further Considerations
- The 50% carbon assumption. The CBM-CFS3 assumes a 50% carbon ratio to oven-dried biomass, consequently used in this analysis. This general rule is not valid when looking at individual tree tissues or individual species, as softwood trees often contain slightly greater than 50% carbon content and hardwood species slightly below 50% [44]. Local estimations could therefore be improved if species- and tissue-specific carbon ratios were used.
- Forest community classification. The use of remote sensing data (i.e., aerial photography) to classify forest communities was chosen as this is how the NSDLF classifies stands for management planning. As the PSP data offers a breakdown of species composition for every plot, it would be possible to classify stands based on the percent composition of species, which could reduce the error associated with remotely- sensed classification. Moreover, the Boudewyn et al. [34] equations rely on a single leading species to be used when converting merchantable volume to biomass at the stand level, which may further explain some of the differences in the results of this study. Forest community was a broad enough classification to maintain large sample sizes post-stratification. Other variables considered included land capability, which is often used in forest models as an indicator of site quality. The land capability was not used here as it is a derivative of age, and therefore could be confounding in this analysis where age is necessary to compare against CBM-CFS3 output. It would also further reduce sample sizes between groups. Site index or other types of site-describing variables that influence forest growth and yield were not included in this analysis, which is a limitation of this study and an area for future research. However, the reason for not having the site in the regression analysis was because this study aimed to compare empirical models to the CBM-CFS3 model at multiple scales as parsimoniously as possible. The purpose was not to develop the most accurate predictions and yield curves for carbon or merchantable volume. This was also why merchantable volume curves were developed from the same PSP data as were used for carbon and the existing NSDLF yield curves (which include several site metrics) were not used.
- Age. Age is a subjective variable to assess natural forests, especially in more mature or uneven-aged stands, but it is necessary in this analysis for CBM-CFS3 comparison. This analysis assumes forest stands are a uniform age when actual forest stands can contain several cohorts of trees and variable mortality. Forest plots can be difficult to assign an age to; they can maintain different levels of regeneration even after disturbance or harvest resets the age to zero. A protocol should be established to apply these methods to stands of varying successional stages. Moreover, Nova Scotia is moving towards a model of forestry that relies more on partial harvests with multi/all-aged silviculture systems, which will further challenge the prominent use of stand age in forest (and forest carbon) modelling.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Decay Classes
| Nova Scotia | USDA | ||||
|---|---|---|---|---|---|
| Number | Snags | CWD | Number | Snags | CWD |
| 1 | Recently Dead. Branches and twigs intact, bark on. | Bark on, hard bole, round, twigs and branches present and supporting log partially off the ground. | 1 | All limbs and branches are present; the top of the crown is still present; all bark remains; sapwood is intact, with minimal decay; heartwood is sound and hard. | Sound, freshly fallen, intact logs with no rot, no conks present indicating a lack of decay, original wood color, no invading roots, fine twigs attached with tight bark. |
| 2 | Moderate decay. Dead for a number of years, shedding fine twigs and branches, bark loose and flaking, fairly sound/wind firm, bole has signs of decay/rot in sapwood or heartwood that was sound at the time of mortality. | Bark flaking, mostly hard bole (little decay), round, few branch stubs, flat on the ground. | 3 | Only limb stubs exist; the top is broken; a variable amount of bark remains; sapwood is sloughing; heartwood has advanced decay in upper bole and is beginning at the base. | Heartwood is still sound with piece supporting its own weight, sapwood can be pulled apart by hand or is missing, wood color is the reddish-brown or original color, roots may be invading sapwood, only branch stubs are remaining which cannot be pulled out of the log. |
| 3 | Advanced Decay. Decay/rot in bole is advanced, most of the bark being flaking off or absent, the stability is declining. | Bark mostly gone, soft bole, oval, sinking into the ground. | 4 | Few or no limb stubs remain; the top is broken; a variable amount of bark remains; sapwood is sloughing; heartwood has advanced decay at the base and is sloughing in the upper bole. | Heartwood is rotten with pieces unable to support own weight, rotten portions of the piece are soft and/or blocky in appearance, a metal pin can be pushed into heartwood, wood color is reddish or light brown, invading roots may be found throughout the log, branch stubs can be pulled out. |
| 5 | No evidence of branches remains; the top is broken; <20 percent of the bark remains; sapwood is gone; heartwood is sloughing throughout. | There is no remaining structural integrity to the piece with a lack of circular shape as rot spreads out across the ground, the rotten texture is soft and can become powder when dry, wood color is red-brown to dark brown, invading roots are present throughout, branch stubs and pitch pockets have usually rotten down. | |||
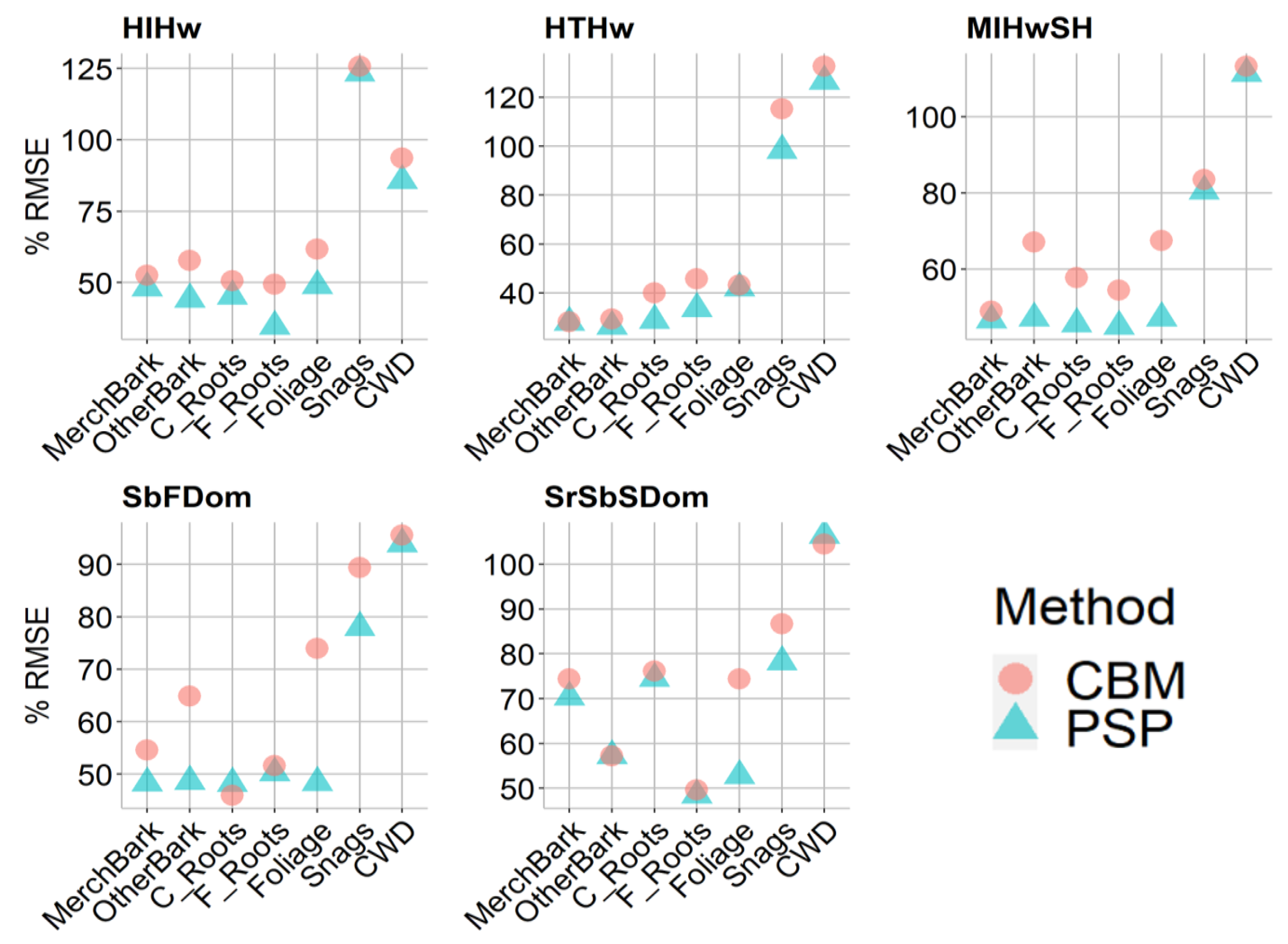
Appendix B. Root Mean Square Error and Bias
| Forest Community | Carbon Pool | RMSE (t/ha) | % RMSE | ||
|---|---|---|---|---|---|
| PSP | CBM | PSP | CBM | ||
| HIHw | Merch + Bark | 19.3 | 21 | 48.1 | 52.4 |
| Other + Bark | 7.2 | 9.4 | 44.2 | 57.7 | |
| Coarse Roots | 4.6 | 5.1 | 45.2 | 50.6 | |
| Fine Roots | 0.5 | 0.8 | 34.6 | 49.3 | |
| Foliage | 1.7 | 2.2 | 48.9 | 61.7 | |
| Snags | 4.9 | 5.0 | 123.4 | 125.7 | |
| CWD | 2.3 | 2.5 | 85.7 | 93.6 | |
| HTHw | Merch + Bark | 16.3 | 16.4 | 27.9 | 28.1 |
| Other + Bark | 6.0 | 6.7 | 26.3 | 29.3 | |
| Coarse Roots | 3.6 | 5.0 | 28.8 | 40.0 | |
| Fine Roots | 0.5 | 0.7 | 33.6 | 45.8 | |
| Foliage | 1.4 | 1.4 | 42.1 | 43.2 | |
| Snags | 4.5 | 5.2 | 98.3 | 115.3 | |
| CWD | 4.7 | 4.9 | 126.6 | 132.6 | |
| MIHwSH | Merch + Bark | 17.1 | 18.0 | 46.7 | 48.9 |
| Other + Bark | 7.2 | 10.3 | 47.1 | 67.1 | |
| Coarse Roots | 4.2 | 5.3 | 45.7 | 57.7 | |
| Fine Roots | 0.7 | 0.8 | 45.0 | 54.4 | |
| Foliage | 2.0 | 2.9 | 47.2 | 67.5 | |
| Snags | 4.6 | 4.8 | 80.5 | 83.5 | |
| CWD | 4.4 | 4.5 | 111.4 | 113.2 | |
| SbFDom | Merch + Bark | 14.1 | 15.9 | 48.3 | 54.6 |
| Other + Bark | 5.9 | 7.9 | 48.6 | 64.8 | |
| Coarse Roots | 3.5 | 3.4 | 48.2 | 46.0 | |
| Fine Roots | 0.8 | 0.8 | 50.2 | 51.6 | |
| Foliage | 2.5 | 3.9 | 48.4 | 73.9 | |
| Snags | 4.2 | 4.9 | 77.9 | 89.4 | |
| CWD | 3.7 | 3.8 | 93.9 | 95.5 | |
| SrSbSDom | Merch + Bark | 23.3 | 24.7 | 70.3 | 74.3 |
| Other + Bark | 6.5 | 6.5 | 57.2 | 57.1 | |
| Coarse Roots | 6.3 | 6.5 | 74.5 | 76.1 | |
| Fine Roots | 0.7 | 0.7 | 48.4 | 49.6 | |
| Foliage | 2.4 | 3.3 | 52.8 | 74.3 | |
| Snags | 4.0 | 4.4 | 78.2 | 86.7 | |
| CWD | 2.7 | 2.7 | 106.4 | 104.5 | |
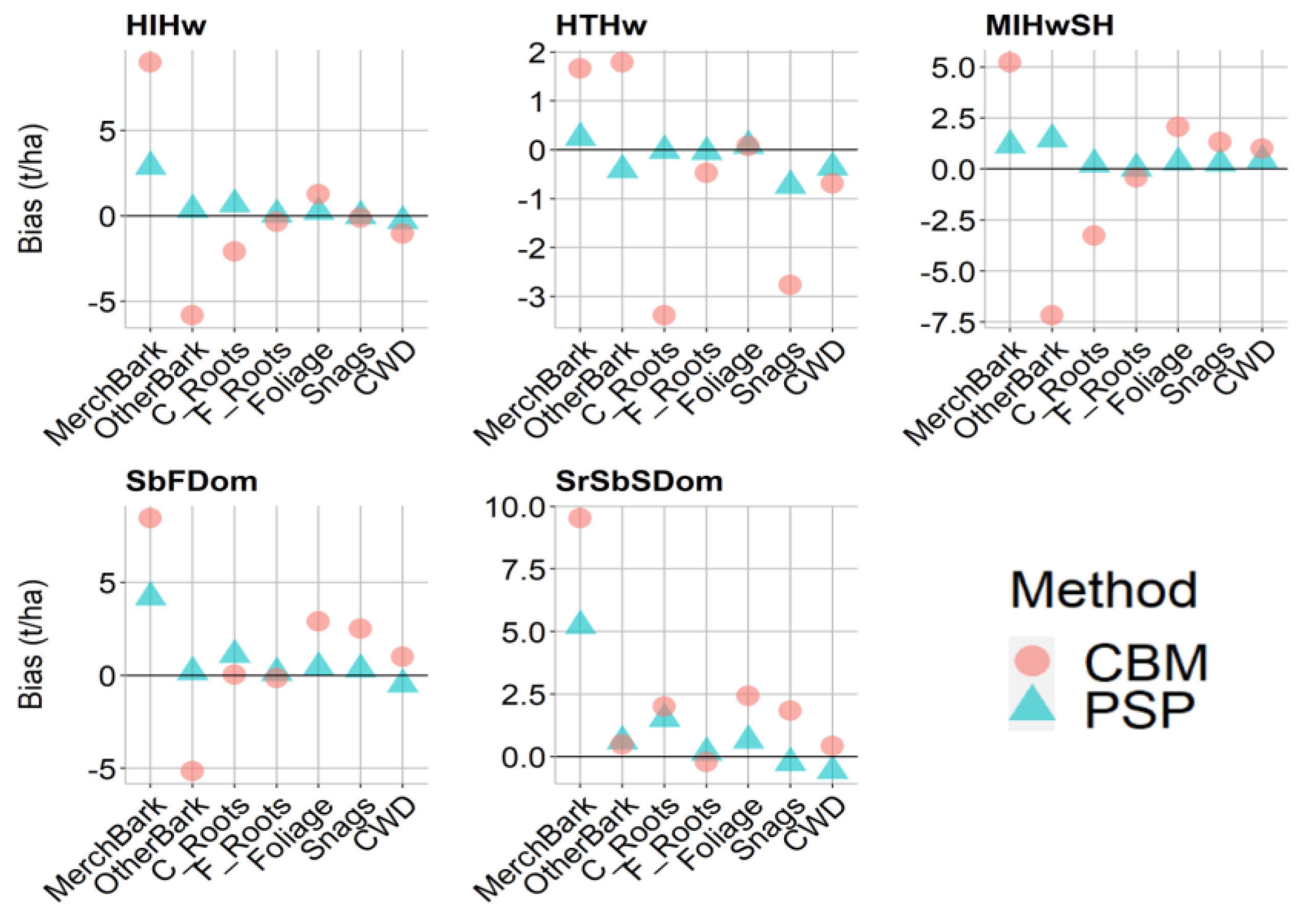
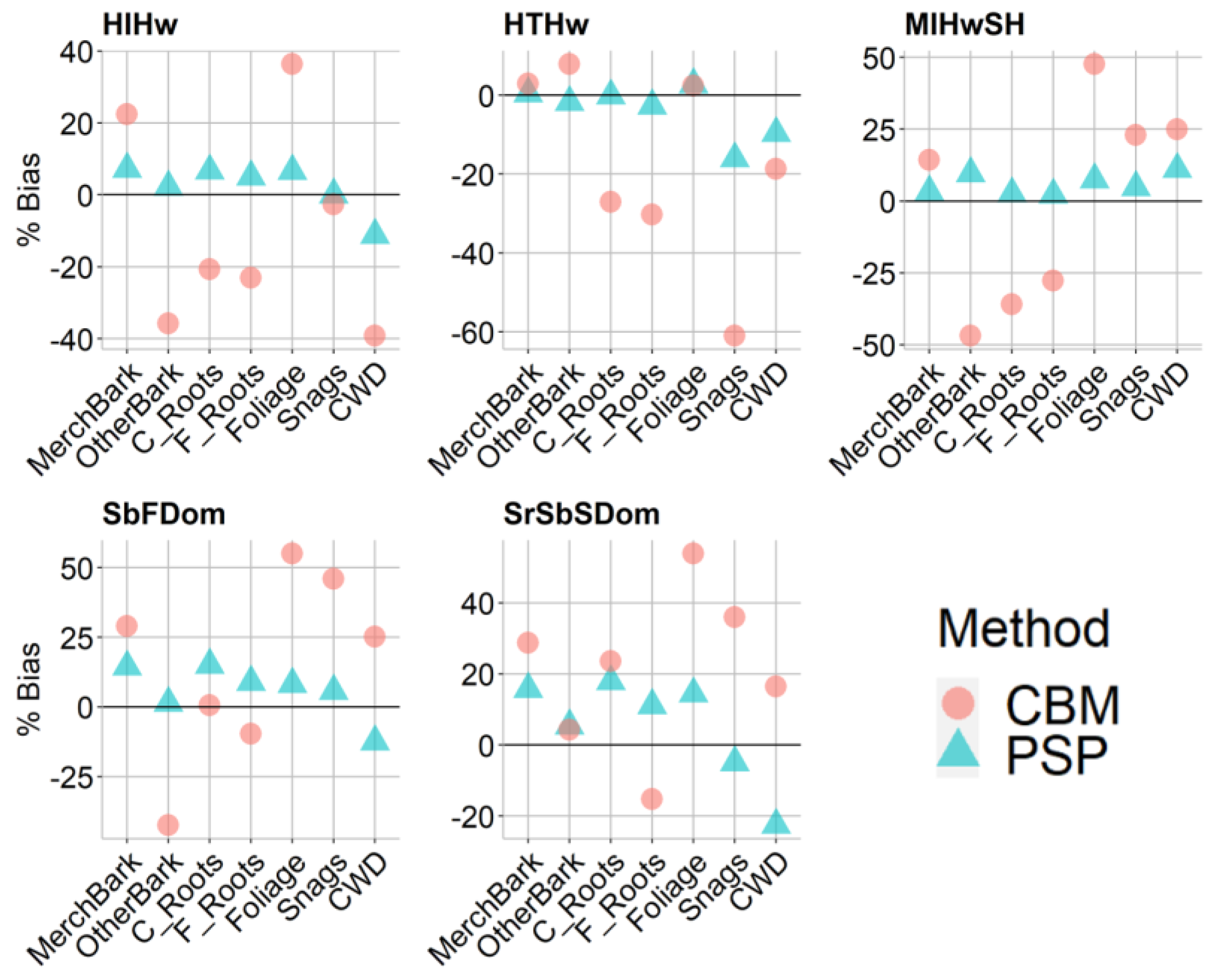
| Forest Community | Carbon Pool | Bias | % Bias | ||
|---|---|---|---|---|---|
| PSP | CBM | PSP | CBM | ||
| HIHw | Merch + Bark | 2.9 | 9.0 | 7.2 | 22.4 |
| Other + Bark | 0.4 | −5.8 | 2.2 | −35.8 | |
| Coarse Roots | 0.7 | −2.1 | 6.7 | −20.7 | |
| Fine Roots | 0.1 | −0.4 | 5.0 | −23.1 | |
| Foliage | 0.2 | 1.3 | 6.6 | 36.3 | |
| Snags | 0.0 | −0.1 | 0.0 | −2.6 | |
| CWD | −0.3 | −1.0 | −11.2 | −39.2 | |
| HTHw | Merch + Bark | 0.3 | 1.7 | 0.4 | 2.9 |
| Other + Bark | −0.4 | 1.8 | −1.8 | 7.9 | |
| Coarse Roots | 0.0 | −3.4 | −0.1 | −27.1 | |
| Fine Roots | 0.0 | −0.5 | −2.7 | −30.3 | |
| Foliage | 0.1 | 0.1 | 2.7 | 2.4 | |
| Snags | −0.7 | −2.8 | −16.1 | −61.0 | |
| CWD | −0.4 | −0.7 | −9.7 | −18.8 | |
| MIHwSH | Merch + Bark | 1.2 | 5.2 | 3.2 | 14.2 |
| Other + Bark | 1.5 | −7.2 | 9.6 | −46.9 | |
| Coarse Roots | 0.2 | −3.3 | 2.6 | −36.0 | |
| Fine Roots | 0.0 | −0.4 | 2.1 | −27.7 | |
| Foliage | 0.3 | 2.1 | 7.4 | 47.6 | |
| Snags | 0.3 | 1.3 | 4.7 | 23.0 | |
| CWD | 0.4 | 1.0 | 11.1 | 24.9 | |
| SbFDom | Merch + Bark | 4.2 | 8.4 | 14.4 | 29.0 |
| Other + Bark | 0.2 | −5.1 | 1.4 | −42.4 | |
| Coarse Roots | 1.1 | 0.0 | 15.1 | 0.5 | |
| Fine Roots | 0.1 | −0.1 | 8.9 | −9.7 | |
| Foliage | 0.4 | 2.9 | 8.2 | 55.0 | |
| Snags | 2.5 | 5.7 | 45.9 | ||
| CWD | 1.0 | −12.4 | 25.2 | ||
| SrSbSDom | Merch + Bark | 5.2 | 9.5 | 15.7 | 28.7 |
| Other + Bark | 0.6 | 0.5 | 5.5 | 4.3 | |
| Coarse Roots | 1.5 | 2 | 17.9 | 23.5 | |
| Fine Roots | 0.2 | −0.2 | 11.1 | −15.2 | |
| Foliage | 0.6 | 2.4 | 14.4 | 53.9 | |
| Snags | −0.2 | 1.8 | −4.9 | 36.0 | |
| CWD | −0.6 | 0.4 | −22.5 | 16.4 | |
References
- Kurz, W.A.; Dymond, C.C.; White, T.M.; Stinson, G.; Shaw, C.H.; Rampley, G.J.; Smyth, C.; Simpson, B.N.; Neilson, E.T.; Trofymow, J.A.; et al. CBM-CFS3: A model of carbon-dynamics in forestry and land-use change implementing IPCC standards. Ecol. Model. 2009, 220, 480–504. [Google Scholar] [CrossRef]
- Eggleston, S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. IPCC Guidelines for National Greenhouse Gas. Inventories; Intergovernmental Panel on Climate Change; Institute for Global Environmental Strategies: Hayama, Japan, 2006; Volume 5. [Google Scholar]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making a reality. Environ. Res. Lett. 2007, 2, 45023. [Google Scholar] [CrossRef]
- Hamburg, S. Simple rules for measuring changes in ecosystem carbon in forestry-offset projects. Mitig. Adapt. Strateg. Glob. Chang. 2000, 5, 25–37. [Google Scholar] [CrossRef]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; FAO Forestry Paper-134; Food and Agriculture Organization of the United Nations: Rome, Italy, 1997. [Google Scholar]
- Lambert, M.-C.; Ung, C.; Raulier, F. Canadian national tree above-ground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- Stark, H.; Nothdurft, A.; Bauhus, J. Allometries for Widely Spaced Populus ssp. and Betula ssp. in Nurse Crop Systems. Forests 2013, 4, 1003–1031. [Google Scholar] [CrossRef]
- Suchomel, C.; Pyttel, P.; Becker, G.; Bauhus, J. Biomass equations for sessile oak (Quercus petraea (Matt.) Liebl.) and hornbeam (Carpinus betulus L.) in aged coppiced forests in southwest Germany. Biomass Bioenergy 2012, 46, 722–730. [Google Scholar] [CrossRef]
- Mokany, K.; Raison, R.J.; Prokushkin, A.S. Critical analysis of root: Shoot ratios in terrestrial biomes. Glob. Chang. Biol. 2006, 12, 84–96. [Google Scholar] [CrossRef]
- Paul, K.I.; Roxburgh, S.H.; Chave, J.; England, J.R.; Zerihun, A.; Specht, A.; Lewis, T.; Bennett, L.T.; Baker, T.G.; Adams, M.A.; et al. Testing the generality of above-ground biomass allometry across plant functional types at the continent scale. Glob. Chang. Biol. 2016, 22, 2106–2124. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhang, Q.; Cihlar, J.; Bauhus, J.; Price, D. Estimating fine-root biomass and production of boreal and cool temperate forests using above-ground measurements: A new approach. Plant. Soil 2004, 265, 31–46. [Google Scholar] [CrossRef]
- Penman, J.; Gytarsky, M.; Hiraishi, T.; Krug, T.; Kruger, D.; Pipatti, R.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K.; et al. Good practice guidance for land use, land-use change and forestry. In Good Practice Guidance for Land Use, Land-Use Change and Forestry; IPCC Institute for Global Environmental Strategies: Kanagawa, Japan, 2003. [Google Scholar]
- Domke, G.M.; Woodall, C.W.; Smith, J.E. Accounting for density reduction and structural loss in standing dead trees: Implications for forest biomass and carbon stock estimates in the United States. Carbon Balance Manag. 2011, 6, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harmon, M.; Woodall, C.; Fasth, B.; Sexton, J.; Yatkov, M. Differences between Standing and Downed Dead Tree Wood Density Reduction Factors; Res. Pap. NRS-15. U.S. Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2011; 40p. Available online: https://permanent.access.gpo.gov/gpo14619/rp-nrs15.pdf (accessed on 10 August 2020).
- Kull, S.; Rampley, G.; Morken, S.; Metsaranta, J.; Neilson, E.; Kurz, W. Operational-Scale Carbon Budget Model of the Canadian Forest Sector (CBM-CFS3) Version 1.2: User’s Guide; Canadian Forest Service; Norther Forestry Centre: Edmonton, AB, Canada, 2019; 348p. [Google Scholar]
- NSDNR. Nova Scotia Data File: Inventory Permanent Sample Plots Data; Department of Lands and Forestry: Truro, NS, Canada, 2019; Available for research purposes upon request of the Department. [Google Scholar]
- NSDNR. State of the Forest Report; Department of Lands and Forestry: Truro, NS, Canada, 2016; 90p, Available online: https://novascotia.ca/natr/forestry/reports/State_of_the_Forest_2016.pdf (accessed on 15 August 2020).
- Metsaranta, J.M.; Shaw, C.H.; Kurz, W.A.; Boisvenue, C.; Morken, S. Uncertainty of inventory-based estimates of the carbon dynamics of Canada’s managed forest (1990–2014). Can. J. For. Res. 2017, 47, 1082–1094. [Google Scholar] [CrossRef]
- Environment and Climate Change Canada. Environment Canada Weather Records, Nova Scotia Average Temperature. 2020. Available online: https://climate.weather.gc.ca/historical_data/search_historic_data_e.html?hlyRange=1960-10-01%7C1986-12-31&dlyRange=1960-10-01%7C2002-10-31&mlyRange=1960-01-01%7C2002-10-01&urlExtension=_e.html&searchType=stnProv&optLimit=yearRange&StartYear=1980&EndYear=2020&selRowPerPage=25&Line=186&Month=12&Day=7&lstProvince=NS&timeframe=3&Year=2002 (accessed on 4 May 2020).
- Wein, R.W.; Speer, J.E. Lichen Biomass in Acadian and Boreal Forests of Cape Breton Island, Nova Scotia. Bryologist 1975, 78, 328–333. Available online: http://www.jstor.org/stable/3241889 (accessed on 15 August 2020). [CrossRef]
- McGrath, T. Nova Scotia Forest Management Guide; FRR # 100, Report FOR 2018-001; Department of Lands and Forestry: Truro, NS, Canada, 2018; 158p. [Google Scholar]
- Canada’s National Forest Inventory Website. Available online: https://nfi.nfis.org/en/maps (accessed on 15 July 2020).
- Townsend, P. Nova Scotia Forest Inventory Based on Permanent Sample Plots Measured between 1999 and 2003; Report FOR 2004-3; Department of Natural Resources, Forestry Division: Truro, NS, Canada, 2004; 31p. [Google Scholar]
- NSDNR. Forest Inventory Permanent Sample Plot Field Measurement Methods and Specifications; Nova Scotia Department of Natural Resources, Forestry Division: Truro, NS, Canada, 2004; 66p, Available online: https://novascotia.ca/natr/forestry/reports/InvReport2004.pdf (accessed on 5 September 2021).
- R Core Team. R: A Language and Environment for Statistical Computing, version 1.3.1093; R Core Team: 2019. Available online: https://www.r-project.org/ (accessed on 1 March 2020).
- Microsoft Core Team. Excel Version 16.0.13328.20210; Microsoft Corporation: Redmond, WA, USA, 2019. [Google Scholar]
- Li, Z.; Kurz, W.A.; Apps, M.J.; Beukema, S.J. Belowground biomass dynamics in the Carbon Budget Model of the Canadian Forest Sector: Recent improvements and implications for the estimation of NPP and NEP. Can. J. For. Res. 2003, 33, 126–136. [Google Scholar] [CrossRef]
- Marshall, P.L.; Davis, G.; LeMay, V.M. Using Line Intersect Sampling for Coarse Woody Debris; Technical Report TR-003; BC Ministry of Forests, Nanaimo Research Section, Vancouver Forest Region: Vancouver, BC, Canada, 2000; 34p. [Google Scholar]
- Nova Scotia Data File: Crown Land Forest Model Data; Department of Lands and Forestry: Truro, NS, Canada, 2019.
- Harrel, F. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis; Springer: New York, NY, USA, 2015; Volume 3, pp. 72–114. [Google Scholar]
- Florent, B.; Christian, R.; Sandrine, C.; Martin, B.; Jean-Pierre, F.; Marie-Laure, D.-M. A Toolbox for Nonlinear Regression in R: The Package nlstools. J. Stat. Softw. 2015, 66, 1–21. Available online: http://www.jstatsoft.org/v66/i05/ (accessed on 1 March 2020).
- Fekedulegn, D.; Mac Siurtain, M.P.; Colbert, J.J. Parameter estimation of non-linear growth models in forestry. Silva. Fenn. 1999, 33, 327–336. Available online: https://www.researchgate.net/publication/241321199_Parameter_Estimation_of_Nonlinear_Growth_Models_in_Forestry (accessed on 15 August 2020). [CrossRef] [Green Version]
- Stinson, G.; Kurz, W.A.; Smyth, C.E.; Neilson, E.T.; Dymond, C.C.; Metsaranta, J.M.; Boisvenue, C.; Rampley, G.J.; Li, Q.; White, T.M.; et al. An inventory-based analysis of Canada’s managed forest carbon dynamics, 1990 to 2008. Glob. Chang. Biol. 2011, 17, 2227–2244. [Google Scholar] [CrossRef] [Green Version]
- Boudewyn, P.; Song, X.; Magnussen, S.; Gillis, M.D. Model-Based, Volume-to-Biomass Conversion for Forested and Vegetated Land in Canada; Information Report BC-X-411; Canadian Forest Service, Pacific Forestry Centre: Victoria, BC, Canada, 2007; 112p. [Google Scholar]
- Moroni, M.T.; Shaw, C.H.; Kurz, W.A.; Rampley, G.J. Forest carbon stocks in Newfoundland boreal forests of harvest and natural disturbance origin II: Model evaluation. Can. J. For. Res. 2010, 40, 2146–2163. [Google Scholar] [CrossRef]
- Vorster, A.; Evangelista, P.H.; Stovall, A.E.L.; Ex, S. Variability and uncertainty in forest biomass estimates from the tree to landscape scale: The role of allometric equations. Carbon Balance Manag. 2020, 15, 1–20. Available online: https://cbmjournal.biomedcentral.com/articles/10.1186/s13021-020-00143-6#citeas (accessed on 19 August 2020). [CrossRef]
- Hennigar, C.R.; MacLean, D.A.; Amos-Binks, L.J. A novel approach to optimize management strategies for carbon stored in both forests and wood products. For. Ecol. Manag. 2008, 256, 786–797. [Google Scholar] [CrossRef]
- Seeberg-Elverfeldt, C. Carbon Finance Possibilities for Agriculture, Forestry and Other Land Use Projects in a Smallholder Context; Food and Agriculture Organization of the United Nations: Rome, Italy, 2010. [Google Scholar]
- Picard, N.; Bosela, F.B.; Rossi, V. Reducing the error in biomass estimates strongly depends on model selection. Ann. For. Sci. 2015, 72, 811–823. [Google Scholar] [CrossRef] [Green Version]
- Kozak, A.; Kozak, R.A. Notes on regression through the origin. For. Chron. 1995, 71, 326–330. [Google Scholar] [CrossRef] [Green Version]
- Reyes, G.P.; Kneeshaw, D.; Grandpré, L.D.; Leduc, A. Changes in woody vegetation abundance and diversity after natural disturbances causing different levels of mortality. J. Veg. Sci. 2010, 21, 406–417. Available online: http://www.jstor.org/stable/40925497 (accessed on 12 August 2020). [CrossRef]
- Power, K.; Gillis, M.D. Canada’s Forest Inventory 2001–2006; Information Report BC-X-408E; Canadian Forest Service, Pacific Forestry Centre: Victoria, BC, Canada, 2006; 100p. [Google Scholar]
- Holdaway, R.; McNeill, S.; Mason, N.; Carswell, F. Propagating Uncertainty in Plot-Based Estimates of Forest Carbon Stock and Carbon Stock Change. Ecosystems 2014, 17, 627–640. [Google Scholar] [CrossRef]
- Thomas, S.; Martin, A. Carbon Content of Tree Tissues: A Synthesis. Forests 2012, 3, 332–352. Available online: https://www.mdpi.com/1999-4907/3/2/332/htm (accessed on 20 August 2020). [CrossRef] [Green Version]
- NSDNR. Forest Inventory Permanent Sample Plot Field Measurement Methods and Specifications, Version 2006-1.3; 2006 update, not published; Department of Lands and Forestry, Forestry Division: Truro, NS, Canada, 2006; 66p. [Google Scholar]

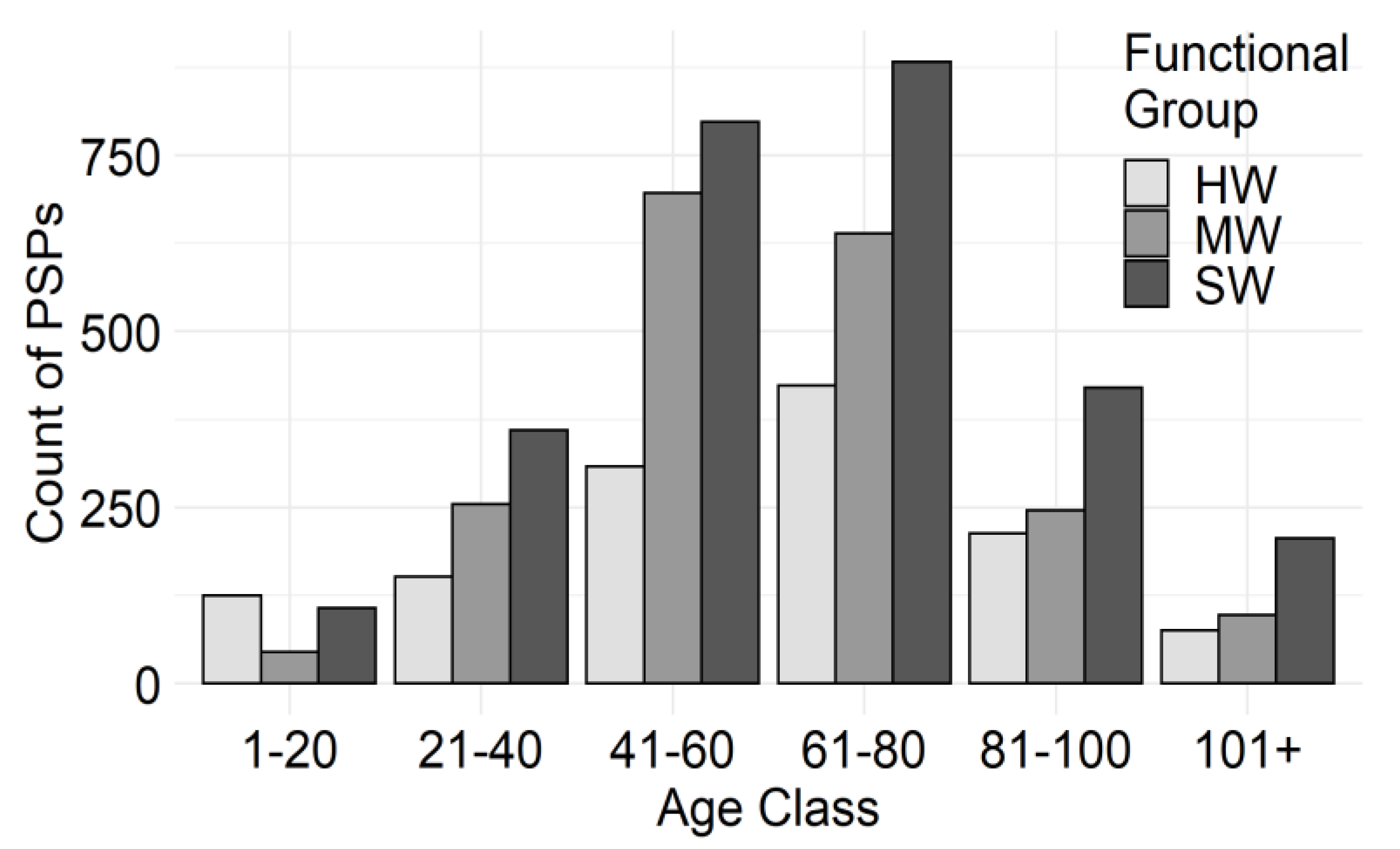

| Functional Group | Forest Community | Description | Number of PSP Records Used | % of Functional Group | % of PSP Dataset |
|---|---|---|---|---|---|
| Hardwood | HTHw | Tolerant HW dominated | 533 | 40.3 | 8.4 |
| HIHw | Intolerant HW dominated | 531 | 42.5 | 8.8 | |
| Mixedwood | MIHwSH | Intolerant HW and Softwood dominated | 1081 | 51.6 | 18.2 |
| Softwood | SrSbDom | Red and Black Spruce dominated | 1423 | 53.4 | 23.4 |
| SbFDom | Balsam fir dominated | 450 | 17.8 | 7.8 | |
| Total | 4018 | 66.7 |
| Forest Community | Carbon Pool | Function (*) | β0 | β1 | β2 | RSE (t/ha) | |
|---|---|---|---|---|---|---|---|
| i | Description | ||||||
| HIHw | 1 | Merch + Bark | 1 | 0.0436 | 9.524 | 0.139 | 17.20 |
| 2 | Other + Bark | 2 | 7.0415 | 0.216 | - | 7.73 | |
| 3 | Coarse roots | 1 | 0.0476 | 2.6 | 0.171 | 4.23 | |
| 4 | Fine roots | 1 | 0.0958 | 0.272 | 0.152 | 0.69 | |
| 5 | Foliage | 2 | 0.864 | 0.350 | - | 1.72 | |
| 6 | Snags | 1 | 0.0246 | 1.422 | 0.0891 | 5.20 | |
| 7 | CWD | 1 | 0.0734 | −4.345 | −1.597 | 3.06 | |
| HTHw | 1 | Merch + Bark | 1 | 0.0485 | 16.0533 | 0.234 | 16.90 |
| 2 | Other + Bark | 2 | 9.33 | 0.214 | - | 7.15 | |
| 3 | Coarse roots | 1 | 0.0814 | 2.524 | 0.193 | 3.58 | |
| 4 | Fine roots | 1 | 0.1357 | 0.234 | 0.145 | 0.54 | |
| 5 | Foliage | 1 | 0.0893 | 1.719 | 0.527 | 1.40 | |
| 6 | Snags | 2 | 0.468 | 0.569 | - | 5.02 | |
| 7 | CWD | 1 | 0.0167 | 2.580 | 0.337 | 4.15 | |
| MIHwSH | 1 | Merch + Bark | 1 | 0.0612 | 7.668 | 0.166 | 17.23 |
| 2 | Other + Bark | 1 | 0.153 | 4.383 | 0.308 | 6.60 | |
| 3 | Coarse roots | 1 | 0.0706 | 1.625 | 0.147 | 4.16 | |
| 4 | Fine roots | 1 | 0.119 | 0.146 | 0.0886 | 0.64 | |
| 5 | Foliage | 1 | 0.112 | 0.948 | 0.222 | 1.81 | |
| 6 | Snags | 1 | 0.0329 | 3.383 | 0.445 | 4.67 | |
| 7 | CWD | 2 | 5.613 | −0.12 | - | 3.83 | |
| SrSbSDom | 1 | Merch + Bark | 1 | 0.099 | 2.934 | 0.0973 | 17.91 |
| 2 | Other + Bark | 1 | 0.129 | 4.637 | 0.425 | 5.85 | |
| 3 | Coarse roots | 1 | 0.0973 | 0.711 | 0.0944 | 4.57 | |
| 4 | Fine roots | 1 | 0.125 | 0.136 | 0.102 | 0.69 | |
| 5 | Foliage | 1 | 0.110 | 0.803 | 0.201 | 1.98 | |
| 6 | Snags | 1 | 0.0378 | 6.628 | 1.136 | 4.90 | |
| 7 | CWD | 1 | 0.0493 | −4.614 | −1.557 | 3.84 | |
| SbFDom | 1 | Merch + Bark | 1 | 0.123 | 1.343 | 0.0452 | 12.60 |
| 2 | Other + Bark | 1 | 0.188 | 1.702 | 0.135 | 6.77 | |
| 3 | Coarse roots | 1 | 0.126 | 0.319 | 0.0434 | 3.18 | |
| 4 | Fine roots | 1 | 0.159 | 0.0401 | 0.0268 | 0.695 | |
| 5 | Foliage | 1 | 0.166 | 0.320 | 0.0607 | 2.40 | |
| 6 | Snags | 2 | 2.691 | 0.169 | - | 4.67 | |
| 7 | CWD | 1 | −0.0017 | 1.102 | −0.835 | 5.01 | |
| Forest Community | β0 | β1 | β2 | RSE (m3/ha) |
|---|---|---|---|---|
| HIHw | 0.03562 | 28.0787 | 0.1002 | 57.5 |
| HTHw | 0.0524 | 28.6933 | 0.1582 | 52.2 |
| MIHwSH | 0.06097 | 18.8199 | 0.1232 | 61.6 |
| SrSbSDom | 0.09794 | 6.132 | 0.05929 | 71.6 |
| SbFDom | 0.1281 | 2.9188 | 0.0313 | 46.5 |
| Forest Community | Mean Difference (t/ha) | Mean Relative Difference (%) |
|---|---|---|
| HIHw | 8.0 | 10.3 |
| HTHw | 3.3 | 3.4 |
| MIHwSH | 7.7 | 11.9 |
| SrSbSDom | −8.4 | −17.6 |
| SbFDom | −2.2 | −3.1 |
| Scenario | Forest Structure | Mean Difference (t/ha) | Mean Relative Difference (%) |
|---|---|---|---|
| a | Even age structure | 8.4 | 2.4 |
| b | Young forest | 5.0 | 2.4 |
| c | Old forest | 11.8 | 2.4 |
| d | Natural forest | 5.0 | 2.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heffner, J.; Steenberg, J.; Leblon, B. Comparison between Empirical Models and the CBM-CFS3 Carbon Budget Model to Predict Carbon Stocks and Yields in Nova Scotia Forests. Forests 2021, 12, 1235. https://doi.org/10.3390/f12091235
Heffner J, Steenberg J, Leblon B. Comparison between Empirical Models and the CBM-CFS3 Carbon Budget Model to Predict Carbon Stocks and Yields in Nova Scotia Forests. Forests. 2021; 12(9):1235. https://doi.org/10.3390/f12091235
Chicago/Turabian StyleHeffner, Jason, James Steenberg, and Brigitte Leblon. 2021. "Comparison between Empirical Models and the CBM-CFS3 Carbon Budget Model to Predict Carbon Stocks and Yields in Nova Scotia Forests" Forests 12, no. 9: 1235. https://doi.org/10.3390/f12091235
APA StyleHeffner, J., Steenberg, J., & Leblon, B. (2021). Comparison between Empirical Models and the CBM-CFS3 Carbon Budget Model to Predict Carbon Stocks and Yields in Nova Scotia Forests. Forests, 12(9), 1235. https://doi.org/10.3390/f12091235






