Evaluation of NASA’s GEDI Lidar Observations for Estimating Biomass in Temperate and Tropical Forests
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. GEDI Data
- (1)
- GEDI01_B_2019112201147_O02034_T01337_02_003_01
- (2)
- GEDI01_B_2019165230622_O02859_T04183_02_003_01
- (3)
- GEDI01_B_2019191095142_O03254_T00065_02_003_01
2.3. LVIS Data
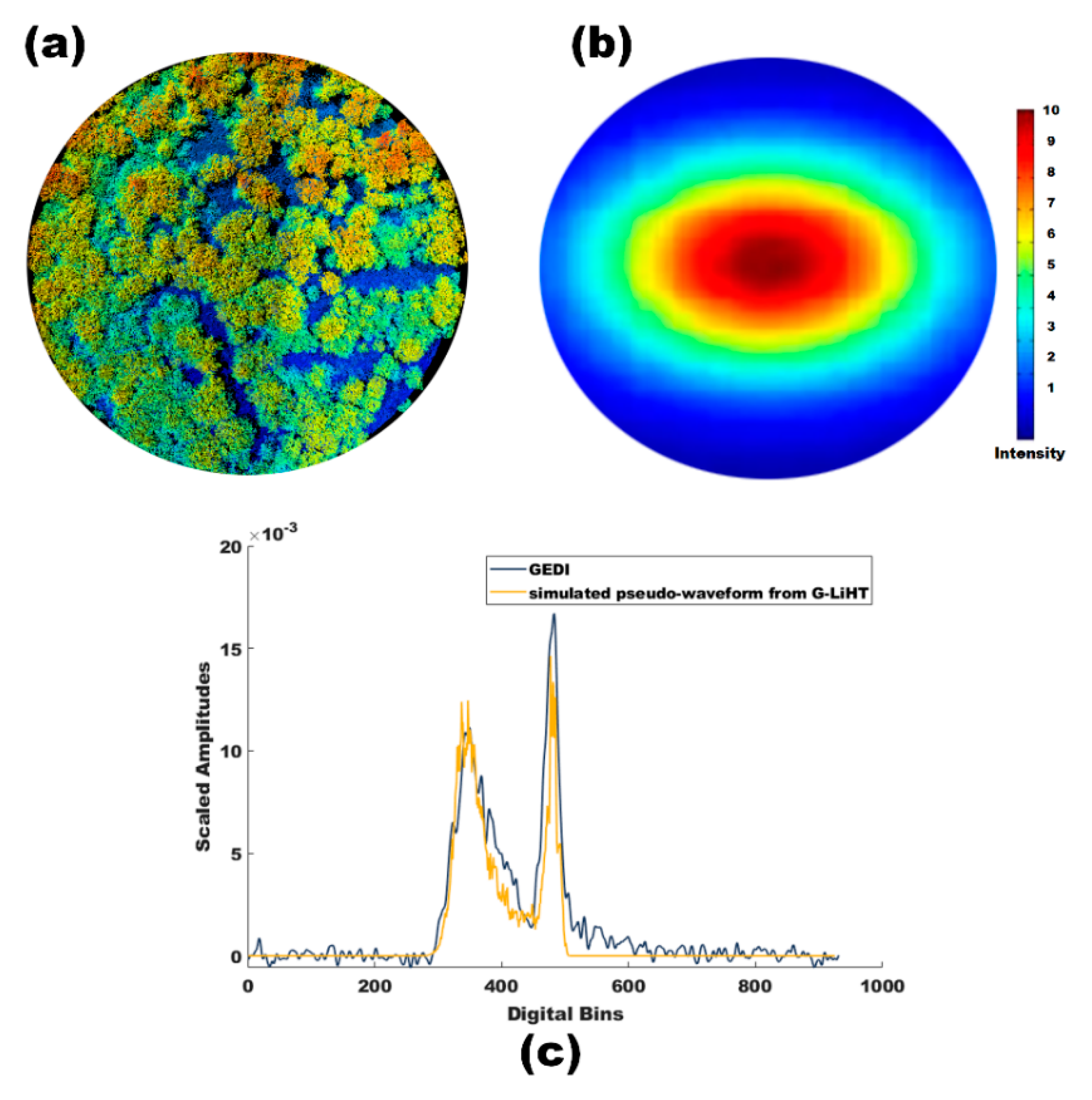
2.4. G-LiHT Data
2.5. SRTM Data
2.6. GlobeLand30 Land Cover Product
2.7. Carbon Monitoring System
3. Methods
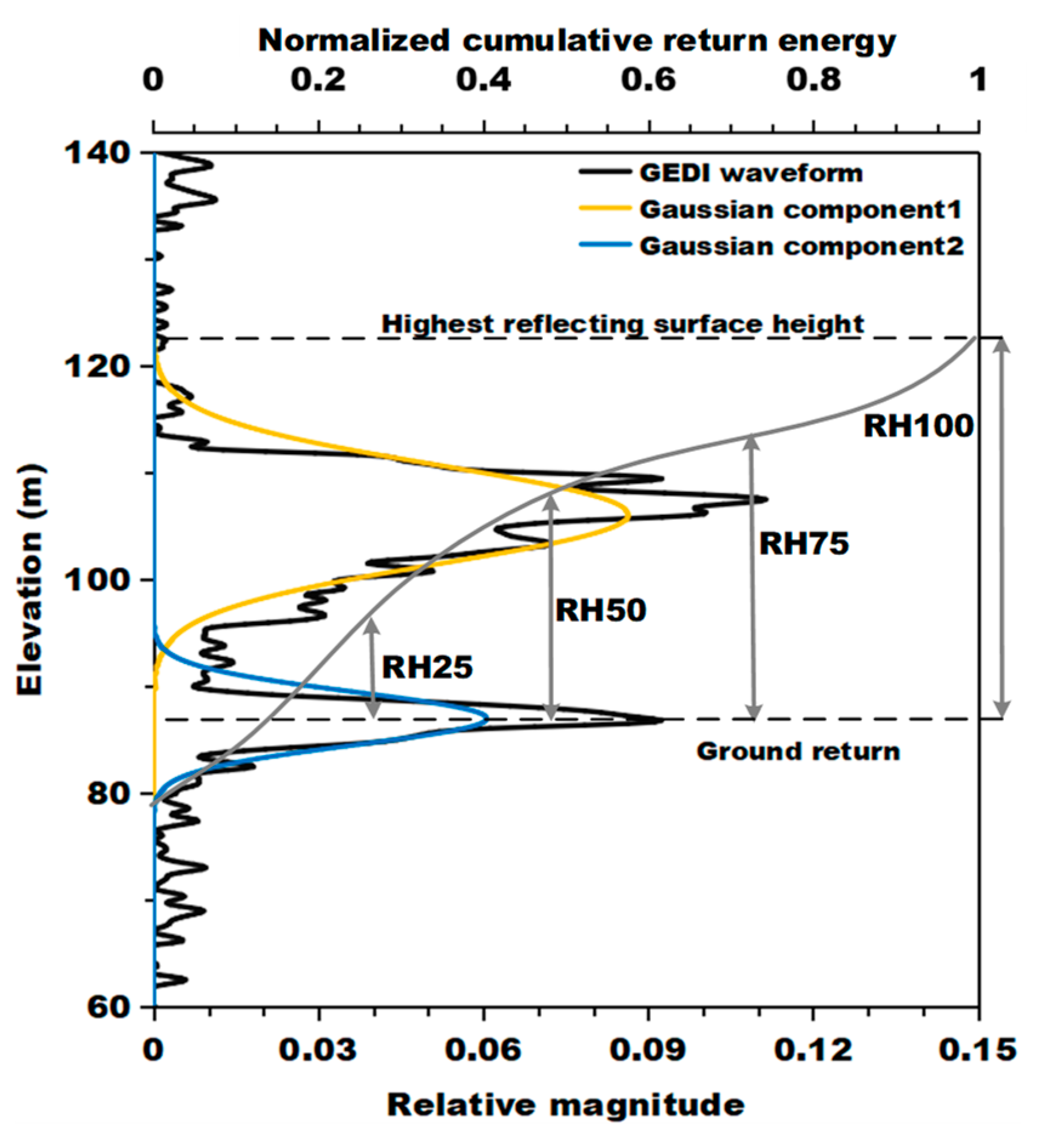
3.1. GEDI and LVIS Data Processing
3.2. G-LiHT Lidar Data Processing
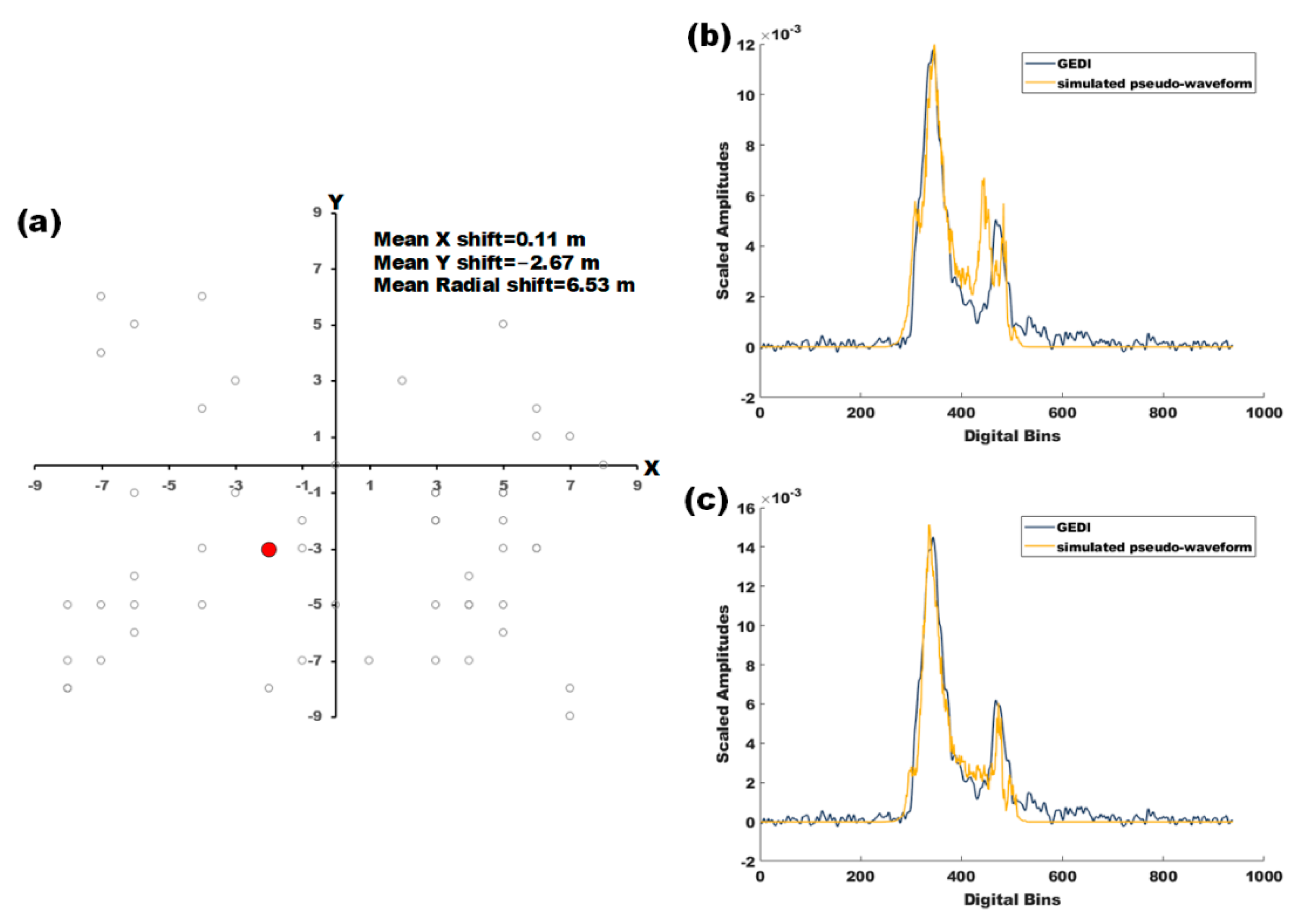
3.3. Assessing the Uncertainty of GEDI Geolocation Information
3.4. Estimating AGB Using Random Forests
3.5. Accuracy Assessment
4. Results
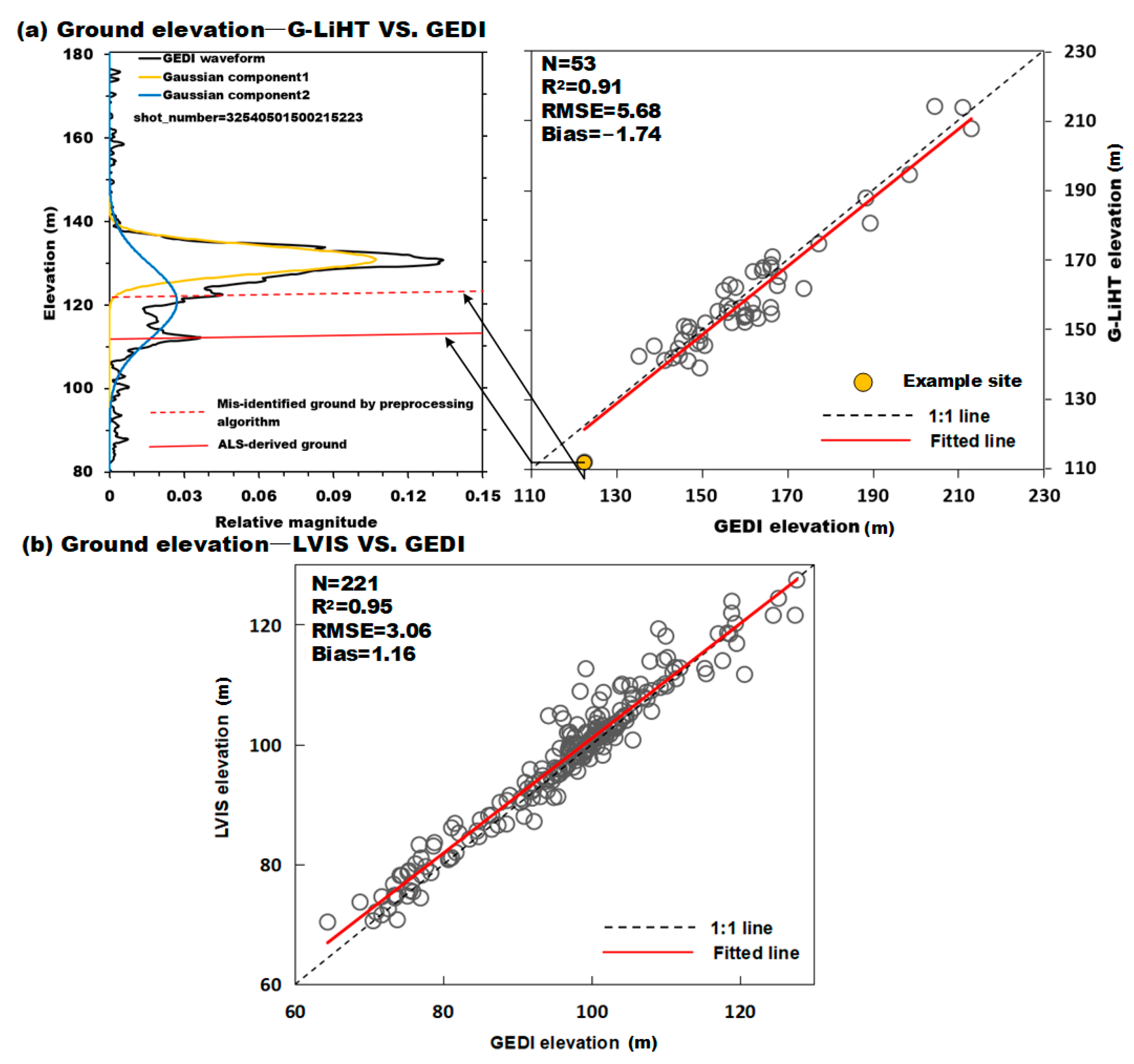
4.1. Ground Elevation Assessment
4.2. Percentile Height Assessment
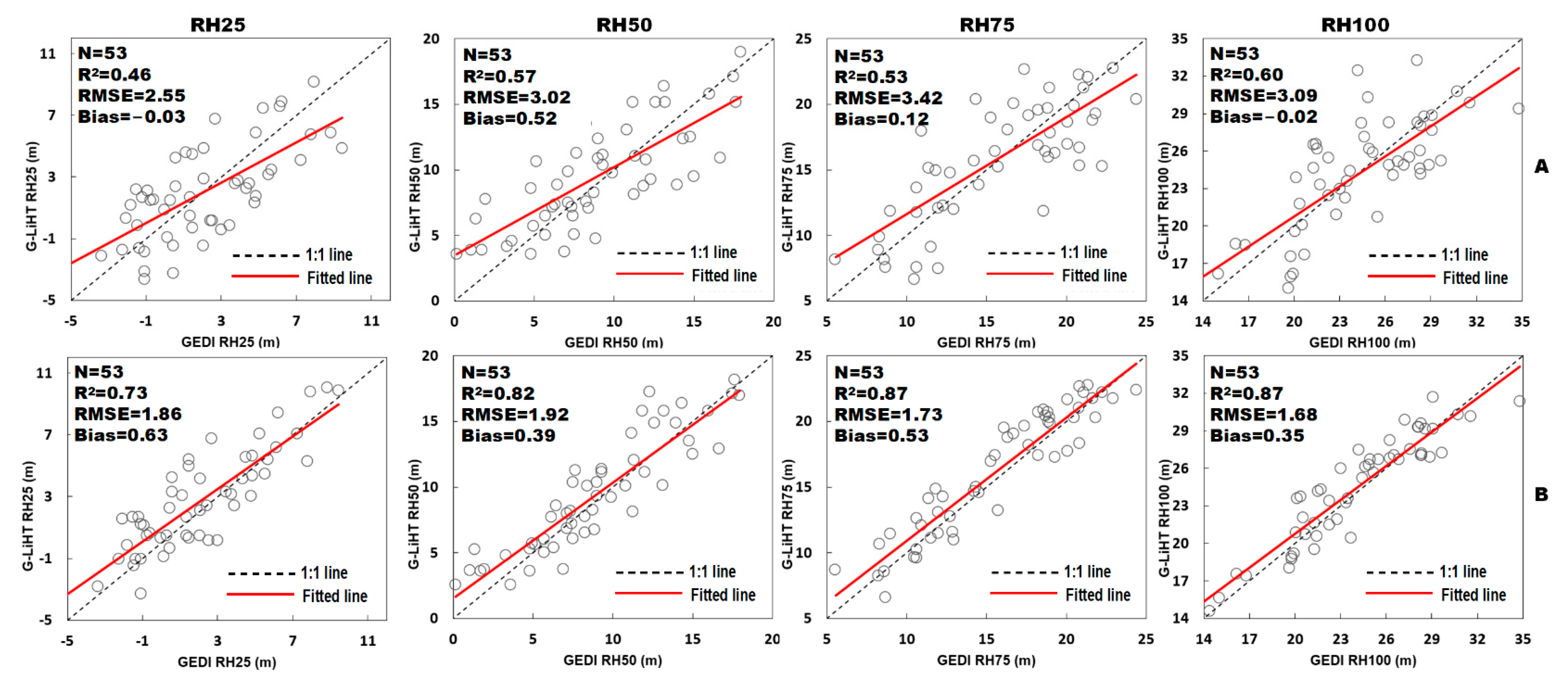
4.2.1. Comparisons of Percentile Heights between GEDI and G-LiHT
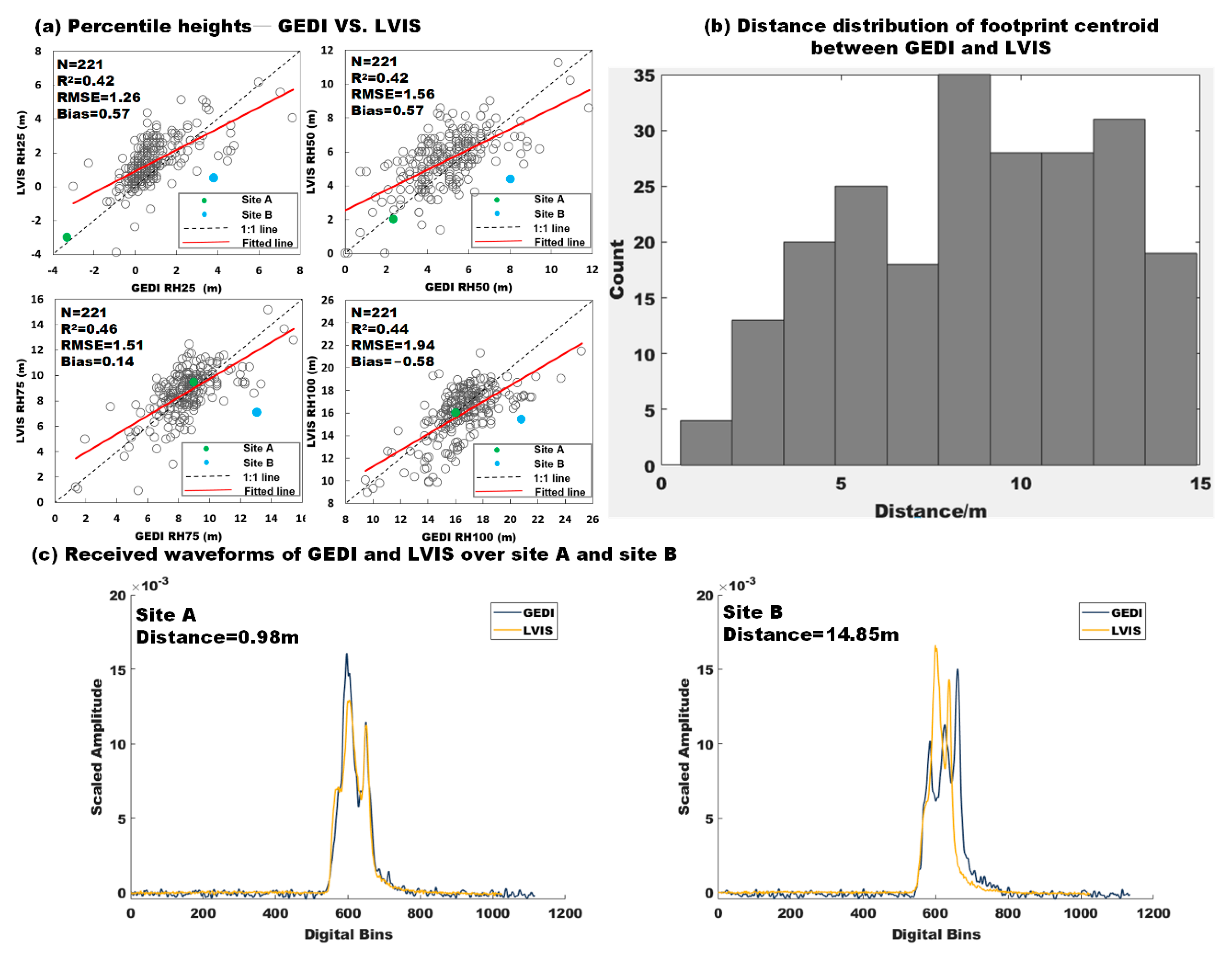
4.2.2. Comparisons of Percentile Heights between GEDI and LVIS
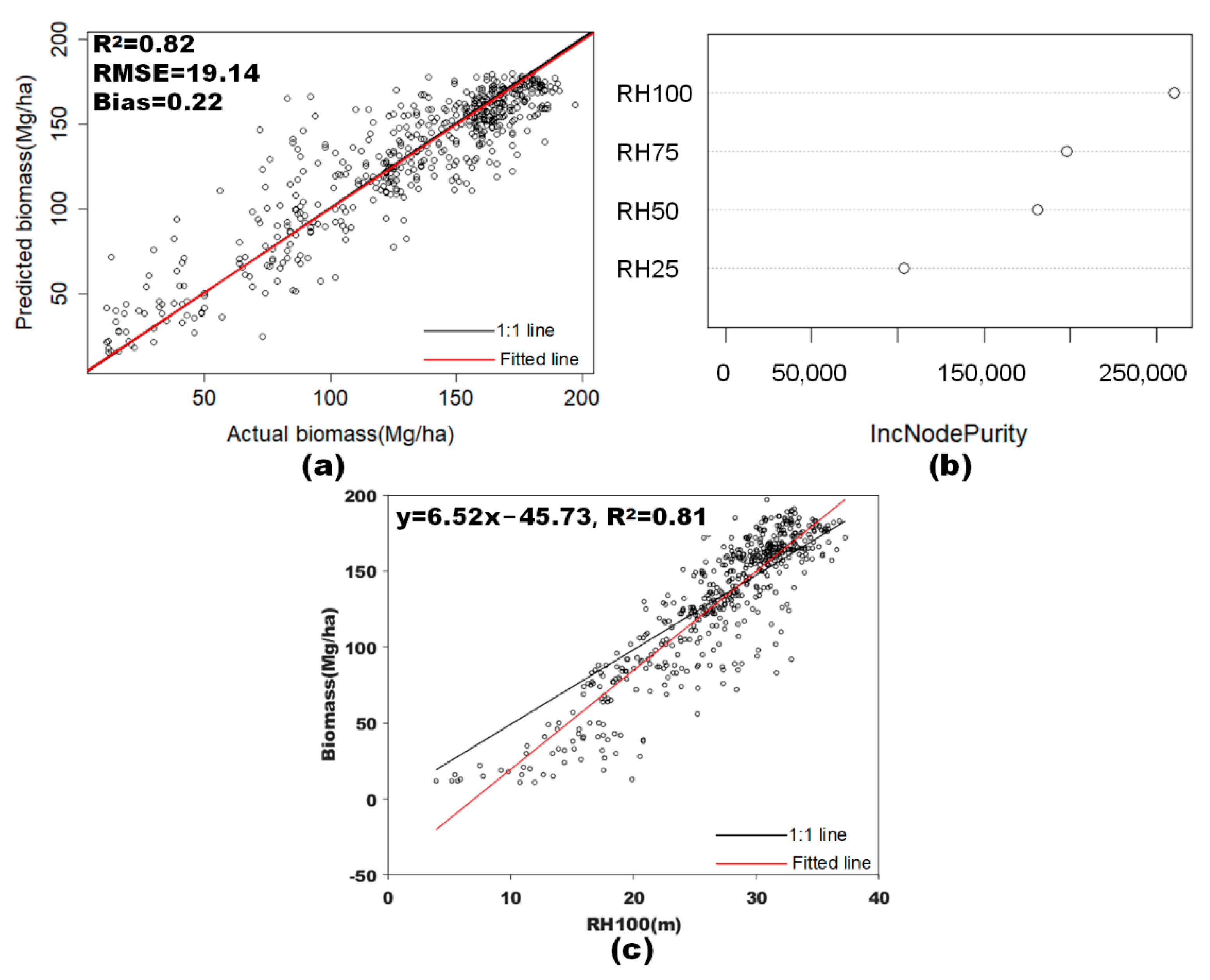
4.3. Aboveground Biomass Estimation
5. Discussion
5.1. Limitations of the Current Lidar Waveform Processing Method for Ground Detection
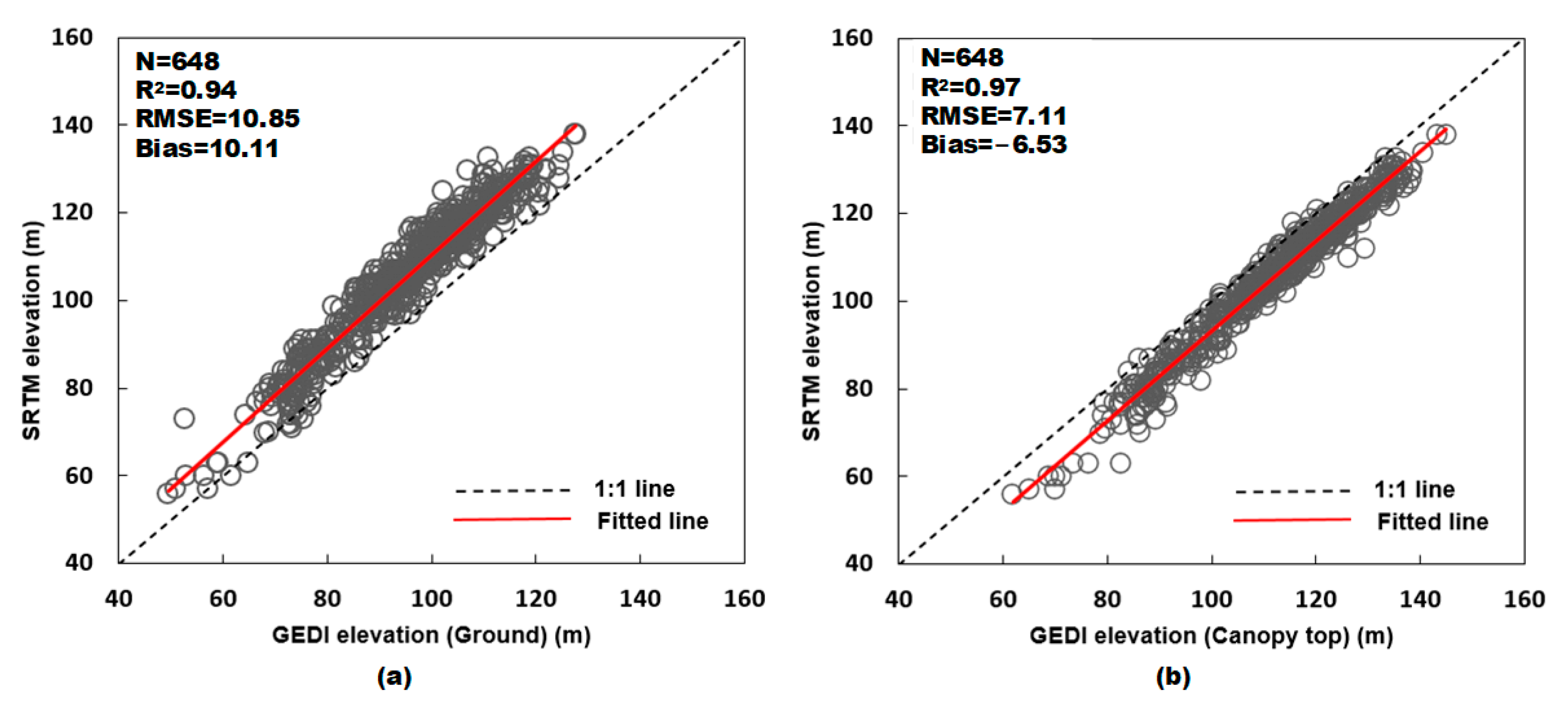
5.2. Difference in Ground Elevation between SRTM and GEDI
5.3. Role of Lidar Emitted Energy for Canopy Detection
5.4. Selection of Percentile Heights in Biomass Prediction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, J.M. Carbon Neutrality: Toward a Sustainable Future. Innovation 2021, 2, 100127. [Google Scholar] [CrossRef] [PubMed]
- Nunes, L.J.R.; Meireles, C.I.R.; Pinto Gomes, C.J.; Almeida Ribeiro, N.M.C. Forest Contribution to Climate Change Mitigation: Management Oriented to Carbon Capture and Storage. Climate 2020, 8, 21. [Google Scholar] [CrossRef]
- Loaiza Usuga, J.C.; Rodriguez Toro, J.A.; Ramirez Alzate, M.V.; Lema Tapias, A.D.J. Estimation of Biomass and Carbon Stocks in Plants, Soil and Forest Floor in Different Tropical Forests. Forest. Ecol. Manag. 2010, 260, 1906–1913. [Google Scholar] [CrossRef]
- Qi, W.; Saarela, S.; Armston, J.; Stahl, G.; Dubayah, R. Forest Biomass Estimation Over Three Distinct Forest Types Using TanDEM-X InSAR Data and Simulated GEDI Lidar Data. Remote Sens. Environ. 2019, 232, 111283. [Google Scholar] [CrossRef]
- Stark, S.C.; Leitold, V.; Wu, J.L.; Hunter, M.O.; de Castilho, C.V.; Costa, F.R.C.; McMahon, S.M.; Parker, G.G.; Shimabukuro, M.T.; Lefsky, M.A.; et al. Amazon Forest Carbon Dynamics Predicted by Profiles of Canopy Leaf Area and Light Environment. Ecol. Lett. 2012, 15, 1406–1414. [Google Scholar] [CrossRef] [PubMed]
- Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-Destructive Tree Volume Estimation through Quantitative Structure Modelling: Comparing UAV Laser Scanning with Terrestrial LIDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
- Zhao, K.; Suarez, J.C.; Garcia, M.; Hu, T.; Wang, C.; Londo, A. Utility of Multitemporal Lidar for Forest and Carbon Monitoring: Tree Growth, Biomass Dynamics, and Carbon Flux. Remote Sens. Environ. 2018, 204, 883–897. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of Tropical Forest Height and Biomass Dynamics Using Lidar Remote Sensing at La Selva, Costa Rica. J. Geophys. Res.-Biogeosci. 2010, 115, G00E09. [Google Scholar] [CrossRef]
- Cook, B.D.; Corp, L.A.; Nelson, R.F.; Middleton, E.M.; Morton, D.C.; McCorkel, J.T.; Masek, J.G.; Ranson, K.J.; Vuong, L.; Montesano, P.M. NASA Goddard’s LiDAR, Hyperspectral and Thermal (G-LiHT) Airborne Imager. Remote Sens. 2013, 5, 4045–4066. [Google Scholar] [CrossRef]
- Xing, Y.; Huang, J.; Gruen, A.; Qin, L. Assessing the Performance of ICESat-2/ATLAS Multi-Channel Photon Data for Estimating Ground Topography in Forested Terrain. Remote Sens. 2020, 12, 2084. [Google Scholar] [CrossRef]
- Corp, L.A.; Cook, B.D.; McCorkel, J.; Middleton, E.M. Data products of NASA Goddard’s LiDAR, Hyperspectral, and Thermal Airborne Imager (G-LiHT). Next-Gener. Spectrosc. Technol. VIII 2015, 9482, 333–344. [Google Scholar]
- Marrs, J.; Ni-Meister, W. Machine Learning Techniques for Tree Species Classification Using Co-Registered LiDAR and Hyperspectral Data. Remote Sens. 2019, 11, 819. [Google Scholar] [CrossRef]
- Nelson, R.; Margolis, H.; Montesano, P.; Sun, G.; Cook, B.; Corp, L.; Andersen, H.; DeJong, B.; Paz Pellat, F.; Fickel, T.; et al. Lidar-Based Estimates of Aboveground Biomass in the Continental US and Mexico Using Ground, Airborne, and Satellite Observations. Remote Sens. Environ. 2017, 188, 127–140. [Google Scholar] [CrossRef]
- Blair, J.B.; Rabine, D.L.; Hofton, M.A. The Laser Vegetation Imaging Sensor: A Medium-Altitude, Digitisation-Only, Airborne Laser Altimeter for Mapping Vegetation and Topography. ISPRS J. Photogramm. 1999, 54, 115–122. [Google Scholar] [CrossRef]
- Cui, L.; Jiao, Z.; Dong, Y.; Sun, M.; Zhang, X.; Yin, S.; Ding, A.; Chang, Y.; Guo, J.; Xie, R. Estimating Forest Canopy Height Using MODIS BRDF Data Emphasizing Typical-Angle Reflectances. Remote. Sens. 2019, 11, 2239. [Google Scholar] [CrossRef]
- Silva, C.A.; Saatchi, S.; Garcia, M.; Labriere, N.; Klauberg, C.; Ferraz, A.; Meyer, V.; Jeffery, K.J.; Abernethy, K.; White, L.; et al. Comparison of Small- and Large-Footprint Lidar Characterization of Tropical Forest Aboveground Structure and Biomass: A Case Study From Central Gabon. IEEE J.-Stars 2018, 11, 3512–3526. [Google Scholar] [CrossRef]
- Huang, W.; Sun, G.; Dubayah, R.; Cook, B.; Montesano, P.; Ni, W.; Zhang, Z. Mapping Biomass Change After Forest Disturbance: Applying LiDAR Footprint-Derived Models at Key Map Scales. Remote. Sens. Environ. 2013, 134, 319–332. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K.J.; Kimes, D.S.; Blair, J.B.; Kovacs, K. Forest Vertical Structure From GLAS: An Evaluation Using LVIS and SRTM Data. Remote Sens. Environ. 2008, 112, 107–117. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Ding, J.; Guo, Z.; Tang, S.; Wang, C.; Huang, Q.; Liu, R.; Chen, J.M. A Combined GLAS and MODIS Estimation of the Global Distribution of Mean Forest Canopy Height. Remote Sens. Environ. 2016, 174, 24–43. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping Forest Canopy Height Globally with Spaceborne Lidar. J. Geophys. Res.-Biogeosci. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X.; Zhou, X.; Gong, P. Integration of Multi-Resource Remotely Sensed Data and Allometric Models for Forest Aboveground Biomass Estimation in China. Remote Sens. Environ. 2019, 221, 225–234. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Espirito-Santo, F.D.; Hunter, M.O.; de Oliveira, R. Estimates of Forest Canopy Height and Aboveground Biomass Using ICESat. Geophys. Res. Lett. 2005, 32, L22S02. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-Resolution Mapping of Forest Canopy Height Using Machine Learning by Coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 Data. Int. J. Appl. Earth. Obs. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S.; Harbeck, K. Estimating Aboveground Biomass and Forest Canopy Cover with Simulated ICESat-2 Data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhou, T.; Nelson, R.; Neuenschwande, A.; Sheridan, R.; Narine, L.; Walsh, K.M. Photon Counting LiDAR: An Adaptive Ground and Canopy Height Retrieval Algorithm for ICESat-2 Data. Remote Sens. Environ. 2018, 208, 154–170. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-Resolution Laser Ranging of the Earth’S Forests and Topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Puliti, S.; Breidenbach, J.; Schumacher, J.; Hauglin, M.; Klingenberg, T.F.; Astrup, R. Above-Ground Biomass Change Estimation Using National Forest Inventory Data with Sentinel-2 and Landsat. Remote Sens. Environ. 2021, 265, 112644. [Google Scholar] [CrossRef]
- Silva, C.A.; Duncanson, L.; Hancock, S.; Neuenschwander, A.; Thomas, N.; Hofton, M.; Fatoyinbo, L.; Simard, M.; Marshak, C.Z.; Armston, J.; et al. Fusing Simulated GEDI, ICESat-2 and NISAR Data for Regional Aboveground Biomass Mapping. Remote Sens. Environ. 2021, 253, 112234. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M.; et al. Biomass Estimation From Simulated GEDI, ICESat-2 and NISAR Across Environmental Gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Leite, R.V.; Silva, C.A.; Broadbent, E.N.; Do Amaral, C.H.; Liesenberg, V.; Alves De Almeida, D.R.; Mohan, M.; Godinho, S.; Cardil, A.; Hamamura, C.; et al. Large Scale Multi-Layer Fuel Load Characterization in Tropical Savanna Using GEDI Spaceborne Lidar Data. Remote Sens. Environ. 2022, 268, 112764. [Google Scholar] [CrossRef]
- Rishmawi, K.; Huang, C.; Zhan, X. Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sens. 2021, 13, 442. [Google Scholar] [CrossRef]
- Goetz, S.; Dubayah, R. Advances in Remote Sensing Technology and Implications for Measuring and Monitoring Forest Carbon Stocks and Change. Carbon. Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K.; Neuenschwander, A.; Lin, C. Satellite Lidar Vs. Small Footprint Airborne Lidar: Comparing the Accuracy of Aboveground Biomass Estimates and Forest Structure Metrics at Footprint Level. Remote Sens. Environ. 2011, 115, 2786–2797. [Google Scholar] [CrossRef]
- GEDI Project Science Office. GEDI Instrument Overview. 2022. Available online: https://gedi.umd.edu/instrument/instrument-overview/ (accessed on 1 February 2022).
- Huang, W.; Dolan, K.A.; Swatantran, A.; Johnson, K.D.; Tang, H.; ONeil-Dunne, J.; Dubayah, R.; Hurtt, G. High-Resolution Mapping of Aboveground Biomass for Forest Carbon Monitoring System in the Tri-State Region of Maryland, Pennsylvania and Delaware, USA. Environ. Res. Lett. 2019, 14, 95002. [Google Scholar] [CrossRef]
- Cowan, D.; Cooper, G. The Shuttle Radar Topography Mission-a New Source of Near-Global Digital Elevation Data. Explor. Geophys. 2005, 36, 334–340. [Google Scholar] [CrossRef]
- Sarabandi, K.; Lin, Y.C. Simulation of Interferometric SAR Response for Characterizing the Scattering Phase Center Statistics of Forest Canopies. IEEE Trans. Geosci. Remote 2000, 38, 115–125. [Google Scholar] [CrossRef]
- Chen, J.; Cao, X.; Peng, S.; Ren, H. Analysis and Applications of GlobeLand30: A Review. Isprs. Int. J. Geo.-Inf. 2017, 6, 230. [Google Scholar] [CrossRef]
- Jun, C.; Ban, Y.; Li, S. Open Access to Earth Land-Cover Map. Nature 2014, 514, 434. [Google Scholar] [CrossRef]
- Dubayah, R.O.A.S. LiDAR Derived Biomass, Canopy Height and Cover for Tri-State (MD, PA, DE) Region, V2; ORNL DAAC: Oak Ridge, TN, USA, 2018. [Google Scholar]
- Yang, X.; Wang, C.; Pan, F.; Nie, S.; Xi, X.; Luo, S. Retrieving Leaf Area Index in Discontinuous Forest Using ICESat/GLAS Full-Waveform Data Based On Gap Fraction Model. Isprs. J. Photogramm. 2019, 148, 54–62. [Google Scholar] [CrossRef]
- Hofton, M.; Blair, J.B.; Story, S.; Yi, D. Algorithm Theoretical Basis Document (ATBD) for GEDI Transmit and Receive Waveform Processing for L1 and L2 Products. 2019. Available online: https://lpdaac.usgs.gov/documents/581/GEDI_WF_ATBD_v1.0.pdf (accessed on 1 February 2022).
- Cui, L.; Jiao, Z.; Zhao, K.; Sun, M.; Dong, Y.; Yin, S.; Zhang, X.; Guo, J.; Xie, R.; Zhu, Z.; et al. Retrieving Forest Canopy Elements Clumping Index Using ICESat GLAS Lidar Data. Remote Sens. 2021, 13, 948. [Google Scholar] [CrossRef]
- Blair, J.B.; Hofton, M.A. Modeling Laser Altimeter Return Waveforms Over Complex Vegetation Using High-Resolution Elevation Data. Geophys. Res. Lett. 1999, 26, 2509–2512. [Google Scholar] [CrossRef]
- Hancock, S.; Armston, J.; Hofton, M.; Sun, X.; Tang, H.; Duncanson, L.I.; Kellner, J.R.; Dubayah, R. The GEDI Simulator: A Large-Footprint Waveform Lidar Simulator for Calibration and Validation of Spaceborne Missions. Earth Space Sci. 2019, 6, 294–310. [Google Scholar] [CrossRef] [PubMed]
- Karlson, M.; Ostwald, M.; Reese, H.; Sanou, J.; Tankoano, B.; Mattsson, E. Mapping Tree Canopy Cover and Aboveground Biomass in Sudano-Sahelian Woodlands Using Landsat 8 and Random Forest. Remote Sens. 2015, 7, 10017–10041. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest Biomass Estimation From Airborne LiDAR Data Using Machine Learning Approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Estimating Above-Ground Biomass in Sub-Tropical Buffer Zone Community Forests, Nepal, Using Sentinel 2 Data. Remote Sens. 2018, 10, 601. [Google Scholar] [CrossRef]
- Meko, D.; Cook, E.R.; Stahle, D.W.; Stockton, C.W.; Hughes, M.K. Spatial Patterns of Tree-Growth Anomalies in the United States and Southeastern Canada. J. Clim. 1993, 6, 1773–1786. [Google Scholar] [CrossRef]
- Zhao, X.; Su, Y.; Hu, T.; Chen, L.; Gao, S.; Wang, R.; Jin, S.; Guo, Q. A Global Corrected SRTM DEM Product for Vegetated Areas. Remote Sens. Lett. 2018, 9, 393–402. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q. A Practical Method for SRTM DEM Correction Over Vegetated Mountain Areas. Isprs. J. Photogramm. 2014, 87, 216–228. [Google Scholar] [CrossRef]
- Hofton, M.; Dubayah, R.; Blair, J.B.; Rabine, D. Validation of SRTM Elevations Over Vegetated and Non-Vegetated Terrain Using Medium Footprint Lidar. Photogramm. Eng. Rem. Sens. 2006, 72, 279–285. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Ma, Q.; Li, W. SRTM DEM Correction in Vegetated Mountain Areas through the Integration of Spaceborne LiDAR, Airborne LiDAR, and Optical Imagery. Remote Sens. 2015, 7, 11202–11225. [Google Scholar] [CrossRef]
- Wang, C.; Glenn, N.F. Integrating LiDAR Intensity and Elevation Data for Terrain Characterization in a Forested Area. IEEE Geosci. Remote Sens. 2009, 6, 463–466. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Harding, D.J. SRTM C-band and ICESat Laser Altimetry Elevation Comparisons as a Function of Tree Cover and Relief. Photogramm. Eng. Rem. Sens. 2006, 72, 287–298. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Lahssini, K. An Assessment of the GEDI Lasers’ Capabilities in Detecting Canopy Tops and their Penetration in a Densely Vegetated, Tropical Area. Remote Sens. 2022, 13, 2969. [Google Scholar] [CrossRef]
- Drake, J.B.; Dubayah, R.O.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Chazdon, R.L.; Weishampel, J.F.; Prince, S.D. Estimation of Tropical Forest Structural Characteristics Using Large-Footprint Lidar. Remote Sens. Environ. 2002, 79, 305–319. [Google Scholar] [CrossRef]


| Products | Attributes | Record Name in GEDI File |
|---|---|---|
| L1B | Unique shot identifier | shot_number |
| Latitude | latitude_bin0 | |
| Longitude | longitude_bin0 | |
| Number of sample intervals of received waveform | rx_sample_count | |
| Starting address of received waveform | rx_sample_start_index | |
| Record file of received waveform | rxwaveform | |
| Height of start of received waveform, relative to WGS-84 ellipsoid (ellipsoidal height) | elevation_bin0 | |
| Quality level—indicates that a “stale” cue point from the coarse search algorithm is being used | stale_return_flag | |
| Quality level—greater than zero if shot occurs during a degrade period, zero otherwise | degrade | |
| Starting address of transmitted waveform | tx_sample_start_index | |
| Number of sample intervals of transmitted waveform | tx_sample_count | |
| Starting address of transmitted waveform | txwaveform |
| GEDI-Derived RH | a | b | R2 | t-Test |
|---|---|---|---|---|
| RH25 | 4.42 | 97.03 | 0.35 | 0.00 |
| RH50 | 4.81 | 59.95 | 0.56 | 0.00 |
| RH75 | 5.24 | 29.77 | 0.67 | 0.00 |
| RH100 | 6.52 | −45.73 | 0.81 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Cui, L.; Park, J.; García, M.; Zhou, Y.; Silva, C.A.; He, L.; Zhang, H.; Zhao, K. Evaluation of NASA’s GEDI Lidar Observations for Estimating Biomass in Temperate and Tropical Forests. Forests 2022, 13, 1686. https://doi.org/10.3390/f13101686
Sun M, Cui L, Park J, García M, Zhou Y, Silva CA, He L, Zhang H, Zhao K. Evaluation of NASA’s GEDI Lidar Observations for Estimating Biomass in Temperate and Tropical Forests. Forests. 2022; 13(10):1686. https://doi.org/10.3390/f13101686
Chicago/Turabian StyleSun, Mei, Lei Cui, Jongmin Park, Mariano García, Yuyu Zhou, Carlos Alberto Silva, Long He, Hu Zhang, and Kaiguang Zhao. 2022. "Evaluation of NASA’s GEDI Lidar Observations for Estimating Biomass in Temperate and Tropical Forests" Forests 13, no. 10: 1686. https://doi.org/10.3390/f13101686
APA StyleSun, M., Cui, L., Park, J., García, M., Zhou, Y., Silva, C. A., He, L., Zhang, H., & Zhao, K. (2022). Evaluation of NASA’s GEDI Lidar Observations for Estimating Biomass in Temperate and Tropical Forests. Forests, 13(10), 1686. https://doi.org/10.3390/f13101686








