Biomass Estimation and Carbon Storage of Taxodium Hybrid Zhongshanshan Plantations in the Yangtze River Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites Description
2.2. Destructive Tree Sampling
2.3. Forest Inventory and Measurements
2.4. Height-Diameter at Breast Height Function Development
2.5. Tree Biomass Model Development
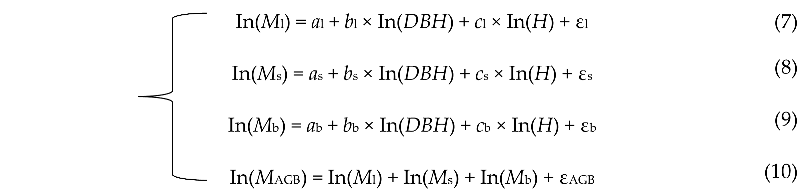 where the subscripts l, s, b and AGB stand for leaf, stem, branch and aboveground, respectively. ε is the model correction factor.
where the subscripts l, s, b and AGB stand for leaf, stem, branch and aboveground, respectively. ε is the model correction factor.2.6. Estimation of Ecosystem Carbon Storage
2.7. Statistical Analyses
3. Results
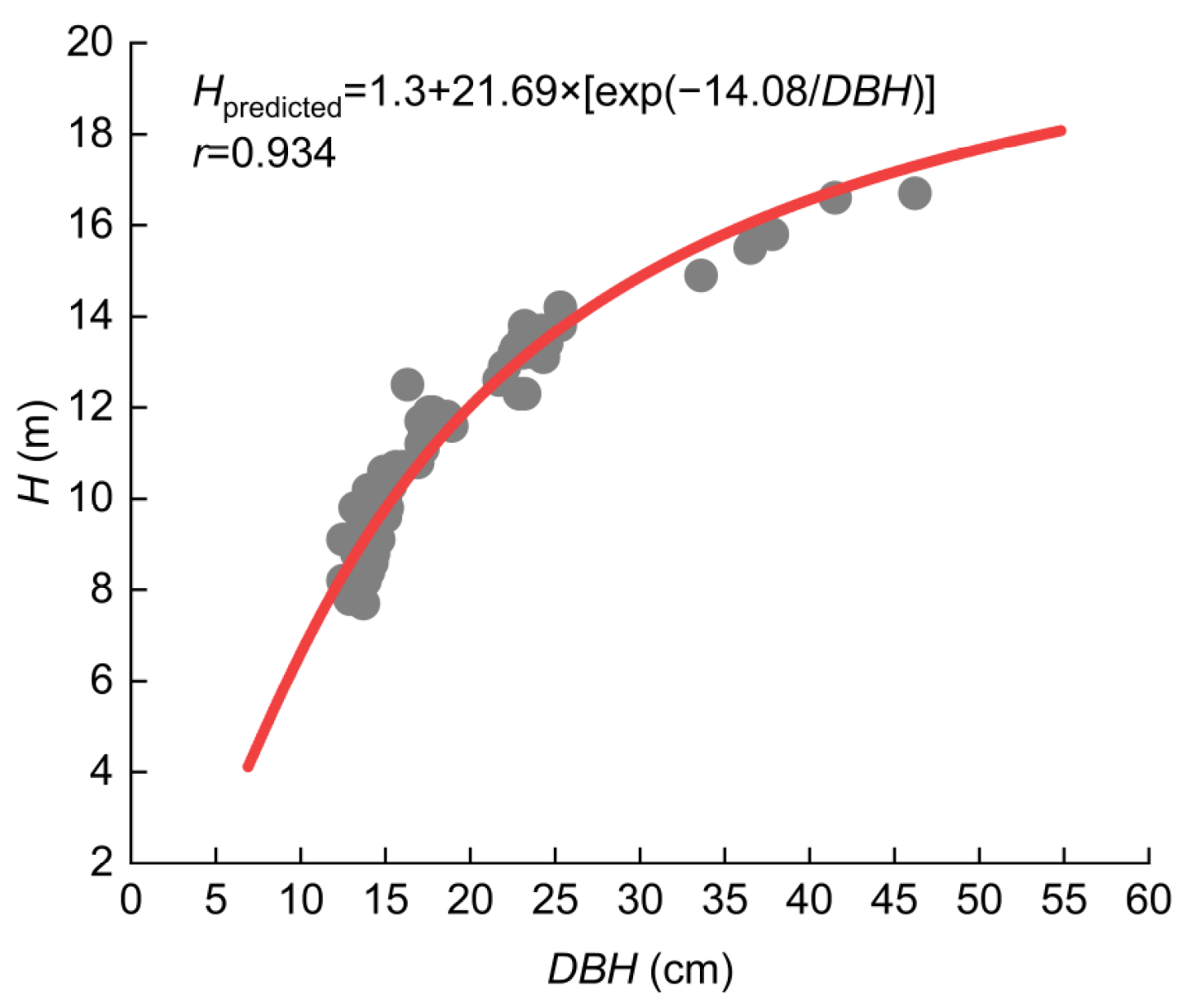
3.1. Height-Diameter at Breast Height Function
3.2. Each Component Biomass Model Selection
3.3. Additive Biomass Equations
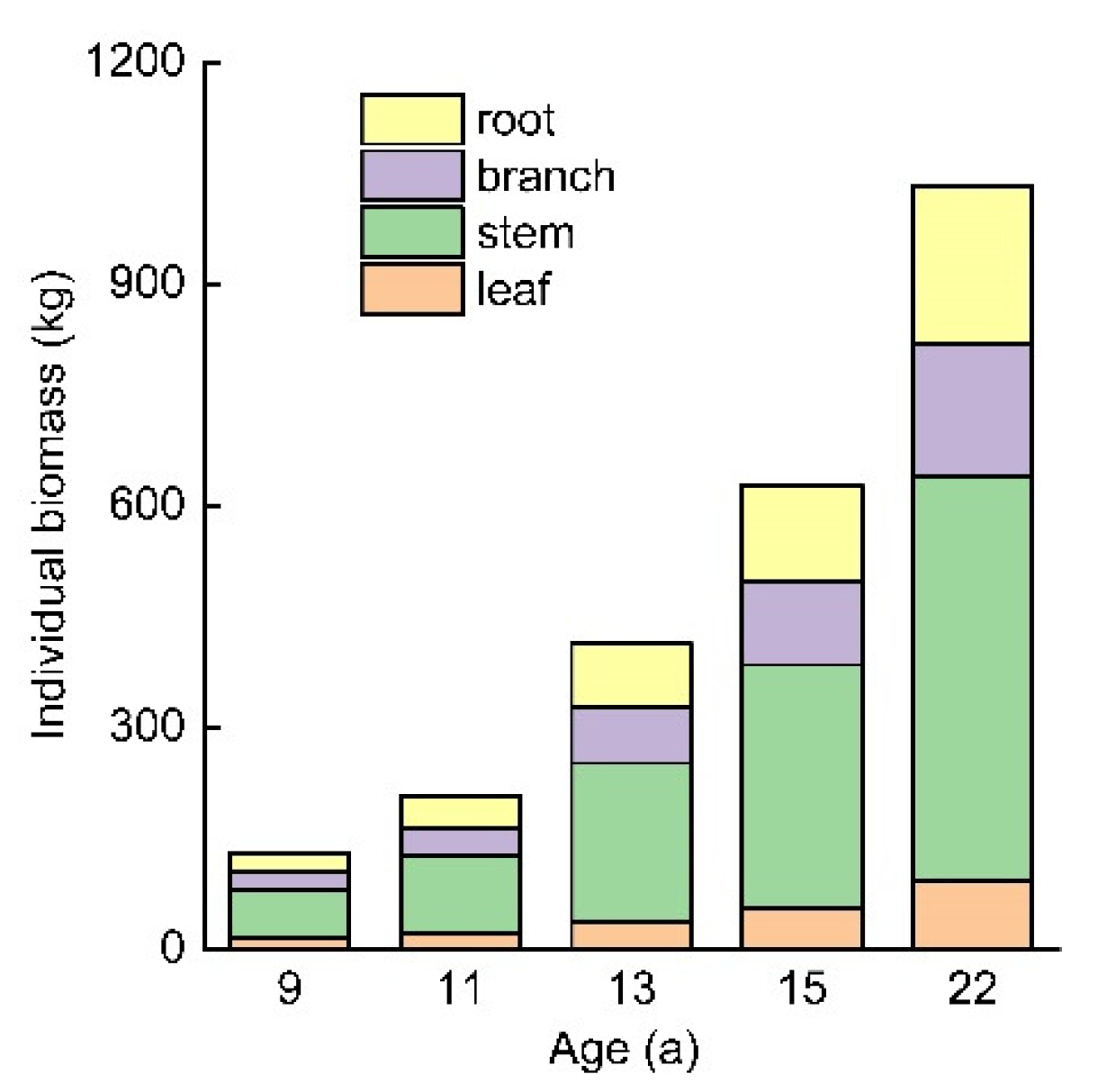
3.4. Individual Tree Biomass and Allocation
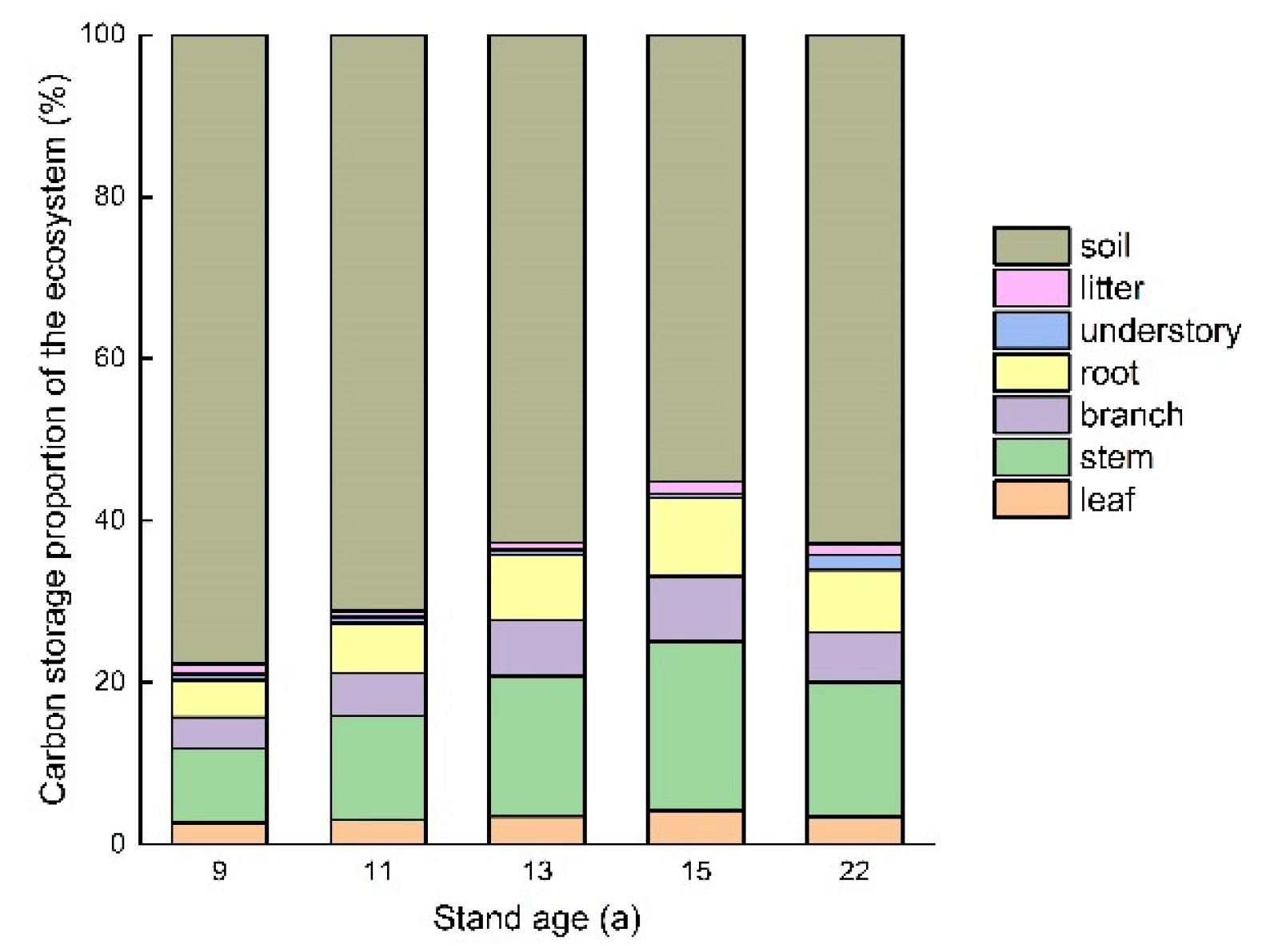
3.5. Ecosystem Carbon Storage and Allocation
4. Discussion
4.1. Tree Biomass Development
4.2. Biomass Distribution
4.3. Ecosystem Carbon Storage
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pugh, T.A.; Lindeskog, M.; Smith, B.; Poulter, B.; Arneth, A.; Haverd, V.; Calle, L. Role of forest regrowth in global carbon sink dynamics. Proc. Natl. Acad. Sci. USA 2019, 116, 4382–4387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muttaqin, M.Z.; Alviya, I.; Lugina, M.; Hamdani, F.A.U. Developing community-based forest ecosystem service management to reduce emissions from deforestation and forest degradation. For. Policy Econ. 2019, 108, 101938. [Google Scholar] [CrossRef]
- Daba, D.E.; Soromessa, T. The accuracy of species-specific allometric equations for estimating aboveground biomass in tropical moist montane forests: Case study of Albizia grandibracteata and Trichilia dregeana. Carbon Bal. Manag. 2019, 14, 18. [Google Scholar] [CrossRef] [PubMed]
- Hirigoyen, A.; Resquin, F.; Cerrillo, R.N.; Franco, J.; Casnati, C.R. Stand biomass estimation methods for Eucalyptus grandis and Eucalyptus dunnii in Uruguay. BOSQUE 2021, 42, 53–66. [Google Scholar] [CrossRef]
- Brandeis, T.J.; Delaney, M.; Parresol, B.R.; Royer, L. Development of equations for predicting Puerto Rican subtropical dry forest biomass and volume. For. Ecol. Manag. 2006, 233, 133–142. [Google Scholar] [CrossRef]
- Zhao, D.; Kane, M.; Markewitz, D.; Teskey, R.; Clutter, M. Additive tree biomass equations for midrotation loblolly pine plantations. For. Sci. 2015, 61, 613–623. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Fu, L.; Widagdo, F.R.A.; Dong, L.H.; Li, F.R. Improving the accuracy of tree biomass estimations for three coniferous tree species in Northeast China. Trees 2022, 36, 451–469. [Google Scholar] [CrossRef]
- Huang, H.; Li, Z.; Gong, P.; Cheng, X.; Clinton, N.; Cao, C.; Ni, W.; Wang, L. Automated methods for measuring DBH and tree heights with a commercial scanning lidar. Photogramm. Eng. Remote Sens. 2011, 77, 219–227. [Google Scholar] [CrossRef]
- Hua, J.F.; Han, L.W.; Wang, Z.Q.; Gu, C.S.; Yin, Y.L. Morpho-anatomical and photosynthetic responses of Taxodium hybrid ‘Zhongshanshan’ 406 to prolonged flooding. Flora 2017, 231, 29–37. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Yin, Y.L.; Hua, J.F.; Fan, W.C.; Yu, C.G.; Xuan, L.; Yu, F.Y. Cloning and characterization of ThSHRs and ThSCR transcription factors in Taxodium hybrid ‘Zhongshanshan 406’. Genes 2017, 8, 185. [Google Scholar] [CrossRef]
- Xuan, L.; Hua, J.F.; Zhang, F.; Wang, Z.Q.; Pei, X.X.; Yang, Y.; Yin, Y.L.; Creech, D.L. Identification and functional analysis of ThADH1 and ThADH4 genes involved in tolerance to waterlogging stress in Taxodium hybrid ‘Zhongshanshan 406’. Genes 2021, 12, 225. [Google Scholar] [CrossRef] [PubMed]
- Shi, Q.; Yin, Y.L.; Wang, Z.Q.; Creech, D.; Hua, J.F. Influence of soil properties on the performance of the Taxodium hybrid ‘Zhongshanshan 407’ in a short-term pot experiment. Soil Sci. Plant Nutr. 2017, 63, 145–152. [Google Scholar] [CrossRef] [Green Version]
- Buford, M. Height-diameter relationships at age 15 in loblolly pine seed sources. For. Sci. 1986, 32, 812–818. [Google Scholar]
- Huang, S.; Titus, S.J.; Wiens, D.P. Comparison of nonlinear height–diameter functions for major Alberta tree species. Can. J. For. Res. 1992, 22, 1297–1304. [Google Scholar] [CrossRef]
- Ravindranath, N.H.; Ostwald, M. Carbon Inventory Methods: Handbook for Greenhouse Gas Inventory, Carbon Mitigation and Roundwood Production Projects; Springer Science and Business Media: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Dong, L.; Zhang, L.; Li, F.R. Developing additive systems of biomass equations for nine hardwood species in Northeast China. Trees 2015, 29, 1149–1163. [Google Scholar] [CrossRef]
- Brandt, J.S.; Butsic, V.; Schwab, B.; Kuemmerle, T.; Radeloff, V.C. The relative effectiveness of protected areas, a logging ban, and sacred areas for old-growth forest protection in southwest China. Biol. Conserv. 2015, 181, 1–8. [Google Scholar] [CrossRef]
- Liu, N.; Sun, P.; Caldwell, P.V.; Harper, R.; Liu, S.; Sun, G. Trade-off between watershed water yield and ecosystem productivity along elevation gradients on a complex terrain in southwestern China. J. Hydrol. 2020, 590, 125449. [Google Scholar] [CrossRef]
- Xue, Y.; Yang, Z.; Wang, X.; Lin, Z.; Li, D.; Su, S. Tree biomass allocation and its model additivity for Casuarina equisetifolia in a tropical forest of Hainan Island, China. PLoS ONE 2016, 11, e0151858. [Google Scholar] [CrossRef] [Green Version]
- Mugasha, W.A.; Mwakalukwa, E.E.; Luoga, E.; Malimbwi, R.E.; Zahabu, E.; Silayo, D.S.; Sola, G.; Crete, P.; Henry, M.; Kashindye, A. Allometric models for estimating tree volume and aboveground biomass in lowland forests of Tanzania. Inter. J. For. Res. 2016, 2016, 8076271. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, X.L.; Han, H.; Shi, Z.J.; Yang, X.H. Biomass accumulation and carbon sequestration in an age-sequence of Mongolian pine plantations in Horqin sandy land, China. Forests 2019, 10, 197. [Google Scholar] [CrossRef] [Green Version]
- Segura, M.; Kanninen, M. Allometric models for tree volume and total aboveground biomass in a tropical humid forest in Costa Rica. Biotropica 2005, 37, 2–8. [Google Scholar] [CrossRef]
- Cao, J.; Wang, X.; Tian, Y.; Wen, Z.; Zha, T. Pattern of carbon allocation across three different stages of stand development of a Chinese pine (Pinus tabulaeformis) forest. Ecol. Res. 2012, 27, 883–892. [Google Scholar] [CrossRef]
- Xiang, W.H.; Li, L.H.; Ouyang, S.; Xiao, W.F.; Zeng, L.X.; Chen, L.; Lei, P.F.; Deng, X.W.; Zeng, Y.L.; Fang, J.P. Effects of stand age on tree biomass partitioning and allometric equations in Chinese fir (Cunninghamia lanceolata) plantations. Eur. J. For. Res. 2021, 140, 317–332. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Mensah, S.; Veldtman, R.; Seifert, T. Allometric models for height and aboveground biomass of dominant tree species in South African Mistbelt forests. South. For. 2017, 79, 19–30. [Google Scholar] [CrossRef]
- Picard, N.; Rutishauser, E.; Ploton, P.; Ngomanda, A.; Henry, M. Should tree biomass allometry be restricted to power models? For. Ecol. Manag. 2015, 353, 156–163. [Google Scholar] [CrossRef]
- Ganamé, M.; Bayen, P.; Ouédraogo, I.; Larba, H.B.; Adjima, T. Allometric models for improving aboveground biomass estimates in West African savanna ecosystems. Trees For. People 2021, 4, 100077. [Google Scholar] [CrossRef]
- Mbow, C.; Verstraete, M.M.; Sambou, B.; Diaw, A.T.; Neufeldt, H. Allometric models for aboveground biomass in dry savanna trees of the Sudan and Sudan-Guinean ecosystems of Southern Senegal. J. For. Res. 2014, 19, 340–347. [Google Scholar] [CrossRef]
- Baral, S.; Neumann, M.; Basnyat, B.; Sharma, R.P.; Silwal, R.; Shrestha, H.L.; Subedi, T.; Vacik, H. Volume functions for Shorea robusta Gaertn. in Nepal. Forestry 2022, 95, 405–415. [Google Scholar] [CrossRef]
- Claus, A.; George, E. Effect of stand age on fine-root biomass and biomass distribution in three European forest chronosequences. Can. J. For. Res. 2005, 35, 1617–1625. [Google Scholar] [CrossRef]
- Du, H.; Zeng, F.; Peng, W.; Wang, K.; Zhang, H.; Liu, L.; Song, T. Carbon storage in a Eucalyptus plantation chronosequence in Southern China. Forests 2015, 6, 1763–1778. [Google Scholar] [CrossRef]
- Panzoua, G.J.L.; Fayolle, A.; Feldpausch, T.R.; Ligot, G.; Doucet, J.L.; Forni, E.; Zombo, I.; Mazengue, M.; Loumeto, J.J.; Gourlet-Fleury, S. What controls local-scale aboveground biomass variation in central Africa? Testing structural, composition and architectural attributes. For. Ecol. Manag. 2018, 429, 570–578. [Google Scholar] [CrossRef]
- Peichl, M.; Arain, M.A. Above- and belowground ecosystem biomass and carbon pools in an age-sequence of temperate pine plantation forests. Agric. For. Meteorol. 2006, 140, 51–63. [Google Scholar] [CrossRef]
- Xu, M.P.; Lu, X.Q.; Xu, Y.D.; Zhong, Z.K.; Zhang, W.; Ren, C.J.; Han, X.H.; Yang, G.H.; Feng, Y.Z. Dynamics of bacterial community in litter and soil along a chronosequence of Robinia pseudoacacia plantations. Sci. Total Environ. 2020, 703, 135613. [Google Scholar] [CrossRef] [PubMed]
- Nunes, M.H.; Camargo, J.L.C.; Vincent, G.; Calders, K.; Oliveira, R.S.; Huete, A.; Mendes de Moura, Y.; Nelson, B.; Smith, M.N.; Stark, S.C. Forest fragmentation impacts the seasonality of Amazonian evergreen canopies. Nat. Commun. 2022, 13, 917. [Google Scholar] [CrossRef]
- Chen, Z. Effects of stand density on the biomass and productivity of Pinus massoniana air-sowing stands. J. Cent. South For. Univ. 2001, 21, 44–47, (In Chinese with English Summary). [Google Scholar]
- Moriondo, M.; Leolini, L.; Brilli, L.; Dibari, C.; Tognetti, R.; Giovannelli, A.; Rapi, B.; Battista, P.; Caruso, G.; Gucci, R. A simple model simulating development and growth of an olive grove. Eur. J. Agron. 2019, 105, 129–145. [Google Scholar] [CrossRef]
- Wang, J.; Delang, C.O.; Hou, G.; Gao, L.; Yang, X.; Lu, X. Carbon sequestration in biomass and soil following reforestation: A case study of the Yangtze River Basin. J. For. Res. 2022, 33, 1663–1690. [Google Scholar] [CrossRef]
- Eslamdoust, J.; Sohrabi, H. Carbon storage in biomass, litter, and soil of different native and introduced fast-growing tree plantations in the South Caspian Sea. J. For. Res. 2018, 29, 449–457. [Google Scholar] [CrossRef]
- Yu, D.S.; Shi, X.Z.; Wang, H.J.; Sun, W.X.; Warner, E.D.; Liu, Q.H. National scale analysis of soil organic carbon storage in China based on Chinese soil taxonomy. Pedosphere 2007, 17, 11–18. [Google Scholar] [CrossRef]
- Wang, X.G.; Zhu, B.; Hua, K.K.; Luo, Y.; Zhang, J.; Zhang, A.B. Assessment of soil organic carbon stock in the upper Yangtze River basin. J. Mt. Sci. 2013, 10, 866–872. [Google Scholar] [CrossRef]
- Dignac, M.F.; Derrien, D.; Barre, P.; Barot, S.; Cécillon, L.; Chenu, C.; Chevallier, T.; Freschet, G.T.; Garnier, P.; Guenet, B. Increasing soil carbon storage: Mechanisms, effects of agricultural practices and proxies. A review. Agron. Sustain. Dev. 2017, 37, 14. [Google Scholar] [CrossRef]
- Vesterdal, L.; Rosenqvist, L.; Salm, C.; Hansen, K.; Groenenberg, B.J.; Johansson, M.B. Carbon sequestration in soil and biomass following afforestation: Experiences from oak and Norway spruce chronosequences in Denmark, Sweden and the Netherlands. In Environmental Effects of Afforestation in North-Western Europe; Springer: Berlin/Heidelberg, Germany, 2007; pp. 19–51. [Google Scholar]
- Lü, X.; Yin, J.; Jepsen, M.R.; Tang, J. Ecosystem carbon storage and partitioning in a tropical seasonal forest in Southwestern China. For. Ecol. Manag. 2010, 260, 1798–1803. [Google Scholar] [CrossRef]
- Gogoi, A.; Ahirwal, J.; Sahoo, U.K. Evaluation of ecosystem carbon storage in major forest types of Eastern Himalaya: Implications for carbon sink management. J. Environ. Manag. 2022, 302, 113972. [Google Scholar] [CrossRef]



| Age (a) | Site | Location | Altitude (m) | H (m) | DBH (cm) | Density (Stems ha−1) |
|---|---|---|---|---|---|---|
| 9 | Nanjing | 118°49′35″ E 32°10′59″ N | 15 | 8.4 | 13.6 | 1111 |
| 11 | Jingzhou | 112°13′37″ E 30°19′34″ N | 34 | 9.6 | 14.1 | 1111 |
| 13 | Chonqing | 108°27′3″ E 30°45′58″ N | 245 | 11.6 | 17.6 | 920 |
| 15 | Yunnan | 102°46′41″ E 24°49′43″ N | 1891 | 12.9 | 23.2 | 830 |
| 22 | Nanjing | 118°47′40″ E 32°20′13″ N | 17 | 14.6 | 33.1 | 410 |
| Equation | Model | Component | Estimated Coefficients | R2 | MAPE | ||
|---|---|---|---|---|---|---|---|
| a | b | c | |||||
| (4) | In(M) = a + b × In(DBH) | leaf | −2.08 | 1.52 | - | 0.847 | 0.0999 |
| stem | −1.88 | 2.15 | - | 0.972 | 0.0255 | ||
| branch | −2.95 | 2.22 | - | 0.971 | 0.0278 | ||
| (5) | In(M) = a + b × In(DBH) + c × In(H) | leaf | −3.57 | 0.16 | 2.47 | 0.853 | 0.0970 |
| stem | −4.02 | 0.18 | 3.57 | 0.979 | 0.0225 | ||
| branch | −5.63 | 0.01 | 4.01 | 0.980 | 0.0276 | ||
| (6) | InM = a + b × In[(DBH)2 × H)] | leaf | −2.45 | 0.59 | - | 0.850 | 0.0992 |
| stem | −2.40 | 0.84 | - | 0.975 | 0.0247 | ||
| branch | −3.49 | 0.87 | - | 0.975 | 0.0275 | ||
| Component | Estimated Coefficients | R2 | MAPE | ||
|---|---|---|---|---|---|
| a | b | c | |||
| leaf | −3.66 | 0.69 | 2.15 | 0.892 | 0.0927 |
| stem | −3.92 | 0.18 | 3.57 | 0.981 | 0.0197 |
| branch | −4.62 | 0.05 | 3.59 | 0.953 | 0.0495 |
| Components | Biomass (t ha−1) | ||||
|---|---|---|---|---|---|
| 9-Year-Old | 11-Year-Old | 13-Year-Old | 15-Year-Old | 22-Year-Old | |
| Leaf | 6.28 | 8.60 | 12.50 | 17.12 | 14.12 |
| Stem | 26.39 | 42.95 | 72.99 | 100.86 | 82.75 |
| Branch | 9.74 | 15.81 | 26.19 | 34.97 | 27.46 |
| Root | 11.03 | 17.51 | 29.00 | 39.77 | 32.32 |
| Total tree | 53.43 | 84.87 | 140.67 | 192.71 | 156.65 |
| Total understories | 1.82 | 1.99 | 2.21 | 2.22 | 8.15 |
| Litter | 3.27 | 2.14 | 3.12 | 6.22 | 6.12 |
| Total | 58.52 | 88.99 | 146.01 | 201.15 | 170.92 |
| Components | Carbon Storage (t ha−1) | ||||
|---|---|---|---|---|---|
| 9-Year-Old | 11-Year-Old | 13-Year-Old | 15-Year-Old | 22-Year-Old | |
| Leaf | 3.26 | 4.47 | 6.50 | 8.90 | 7.34 |
| Stem | 11.59 | 18.85 | 32.04 | 44.28 | 36.33 |
| Branch | 4.74 | 7.70 | 12.75 | 17.03 | 13.37 |
| Root | 5.73 | 9.11 | 15.08 | 20.68 | 16.81 |
| Total tree | 25.32 | 40.13 | 66.37 | 90.89 | 73.85 |
| Understory | 0.91 | 0.99 | 1.11 | 1.11 | 4.07 |
| Litter | 1.63 | 1.07 | 1.56 | 3.11 | 3.06 |
| Soil | 96.89 | 104.36 | 116.32 | 117.12 | 136.66 |
| Total ecosystem | 120.08 | 156.68 | 211.74 | 263.11 | 231.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Q.; Hua, J.; Creech, D.; Yin, Y. Biomass Estimation and Carbon Storage of Taxodium Hybrid Zhongshanshan Plantations in the Yangtze River Basin. Forests 2022, 13, 1725. https://doi.org/10.3390/f13101725
Shi Q, Hua J, Creech D, Yin Y. Biomass Estimation and Carbon Storage of Taxodium Hybrid Zhongshanshan Plantations in the Yangtze River Basin. Forests. 2022; 13(10):1725. https://doi.org/10.3390/f13101725
Chicago/Turabian StyleShi, Qin, Jianfeng Hua, David Creech, and Yunlong Yin. 2022. "Biomass Estimation and Carbon Storage of Taxodium Hybrid Zhongshanshan Plantations in the Yangtze River Basin" Forests 13, no. 10: 1725. https://doi.org/10.3390/f13101725
APA StyleShi, Q., Hua, J., Creech, D., & Yin, Y. (2022). Biomass Estimation and Carbon Storage of Taxodium Hybrid Zhongshanshan Plantations in the Yangtze River Basin. Forests, 13(10), 1725. https://doi.org/10.3390/f13101725






