Comparing the Building Code Sawn Lumber’s Wet Service Factors (C_M) with Four Commercial Wood Species Laboratory Tests

Abstract

Indonesian Wooden Building Code (SNI 7973-2013) has adopted the National Design Specification (NDS) for Wood Construction since 2013. A periodic harmonization of the building-code-designated values (i.e., reference design values and adjustment factors) with the experimental data of commercial wood species is necessary. This study aimed to compare the building code’s wet service factors (C_M) with the laboratory test of some commercial wood species. Since wood is weaker when its moisture content is high, the wet service factor (C_M) must adjust the sawn lumber reference design values if the building serves in wet or aquatic environments. Four commercial wood species, namely pine (Pinus merkusii), agathis (Agathis dammara), red meranti (Shorea leprosula), and mahogany (Swietenia mahagoni), were subjected to mechanical property tests. To calculate the empirical C_M values, the mechanical properties tests were conducted on air-dry and wet wood. Instead of testing the full-sized timber, which contains the growth characteristics and defects, this study chose clear-wood specimens to resemble the boundary condition of the ceteris paribus (other things being equal). The wet (water-saturated) specimens were immersed in water for 65 days, and the test was carried out when the specimen was still immersed. The test arrangement imitated the submerged wood as the worst-case scenario of the wet environment where the construction serves, rather than green or partially immersed timber. As many as 40 specimens were tested to compare each mechanical property’s wet service factor; thus, this study reported 200 specimens’ laboratory test results. The empirical C_M values to adjust the modulus of elasticity, modulus of rupture, shear strength parallel-to-grain, tensile strength parallel-to-grain, and maximum crushing strength (C_M = 0.59, 0.76, 0.65, 0.73, and 0.67, respectively) were significantly lower than SNI 7973-2013 designated values (C_M = 0.9, 0.85, 0.97, 1, and 0.8, respectively). The empirical C_M for the compression stress perpendicular-to-grain at the proportional limit and that at the 0.04″ deformation (C_M = 0.66) were slightly lower than the designated values (C_M = 0.67), although they were not significantly different. This study resulted in lower empirical C_M values than the designated ones, which found that the building code lacked conservativeness. The lacked conservativeness is mainly attributed to the building code’s recent choices, e.g., (1) the wet service environment basis is the green timber rather than the fully water-saturated one, and (2) the ratio of near minimum (5% lower) distribution value is chosen as the C_M value rather than the average of wet timber’s mechanical property divided by the air-dry one. This study proposes changing both recent choices to alternative ones to develop more safe and reliable designated C_M values.

1. Introduction

Wood is a widespread construction material that has served in various environmental conditions in many past and contemporary cultures. Wood’s earliest use in construction was likely to provide shelter and build vehicles (ships) for transportation. Selecting wood as an environmentally benign material for green building would greatly help achieve global resources sustainability. In addition to their renewable properties, modern wood products have a high recycling potential value, indicating their closed-loop material flow to increase efficiency during their life cycle [1]. Life cycle analysis justifies that mass timber buildings commonly have lower global warming potential and life cycle primary energy than reinforced concrete and steel buildings [2]. Wood products and wooden construction practices (such as timber frames [3], timber formwork [4], and prefabricated timber houses [5]) continuously develop to reduce potential environmental impacts.

Indonesian Wooden Building Code (SNI 7973-2013) [6] has adopted the National Design Specification (NDS) for Wood Construction [7] since 2013. The designated reference design values of structural timber were appointed from the bending test of 1094 pieces of local commercial wood measuring 6 × 12 × 300 cm reported by Firmanti et al. [8]. The allowable stresses determined by machine-assisted grading procedure have considered the species (group of species), the fifth percentile and characteristic values, the timber dimension, and the growth characteristics and defects. Since the 1980s, the practice of reference stress determination in the U.S. and Canada has commonly changed from small-clear wood specimens to full-sized timbers testing. However, the engineering community does not entirely abandon the previous practice because the sequential standard procedures to determine the reference design value from the small-clear wood specimen testing are still legally current. The reference design values of bending strength (F_b), tensile strength parallel-to-grain (F_t), shear strength parallel-to-grain (F_v), compressive strength perpendicular-to-grain (F_c⊥), compressive strength parallel-to-grain (F_c), modulus of elasticity (E), and minimum modulus of elasticity (E_min) must be corrected by some corresponding adjustment factors following

Table 1. Adjustment factors application for correcting the sawn lumber’s reference resistance [6,7].

		ASD Only	ASD and LRFD										LRFD Only
		Load Duration Factor	Wet Service Factor	Temperature Factor	Beam Stability Factor	Size Factor	Flat Use Factor	Incising Factor	Repetitive Member Factor	Column Stability Factor	Buckling Stiffness Factor	Bearing Area Factor	Format Conversion Factor	Resistance Factor	Time Effect Factor
		CD	CM	Ct	CL	CF	Cfu	Ci	Cr	CP	CT	Cb	KF	ϕ	λ
Fb’ = Fb	×	CD	CM	Ct	CL	CF	Cfu	Ci	Cr	-	-	-	2.54	0.85	λ
Ft’ = Ft	×	CD	CM	Ct	-	CF	-	Ci	-	-	-	-	2.70	0.80	λ
Fv’ = Fv	×	CD	CM	Ct	-	-	-	Ci	-	-	-	-	2.88	0.75	-
Fc⊥’ = Fc⊥	×	-	CM	Ct	-	-	-	Ci	-	-	-	Cb	1.67	0.90	λ
Fc’ = Fc	×	CD	CM	Ct	-	CF	-	Ci	-	CP	-	-	2.40	0.90	-
E’ = E	×	-	CM	Ct	-	-	-	Ci	-	-	-	-	-	-	-
Emin’ = Emin	×	-	CM	Ct	-	-	-	Ci	-	-	CT	-	1.76	0.85	-

. The adjustment factors consider the service environment conditions’ effects on the member strength and elasticity and shall be unbiasedly estimated.

Although the Building Code thoroughly governs wooden building construction, the existing procedures should be investigated and refined based on independent and trustworthy scientific testing. A periodic harmonization of the building-code-designated values (i.e., reference design values and adjustment factors) with the laboratory tests of commercial wood available in the building material market is necessary. ASTM D5536:94(1999) [9], ASTM D143:2014 [10], ASTM D2555:2005 [11], ASTM D2915:2017 [12], and ASTM D245:2000 [13] are sequence procedures to obtain the allowable stress of full-sized structural lumber from the small clear-wood specimen laboratory tests. If the full-sized sawn lumber sample taken from the market is tested in the laboratory, the sequence procedures to obtain the allowable stress are ASTM D198:2021 [14], ASTM D2555:2005 [11], and ASTM D2915:2017 [12]. The ASTM D5457:2019 [15] replaces the ASTM D2915:2017 [12] if the designer prefers to follow the load and resistance factor design (LRFD) methodology than the allowable stress design (ASD). Those sequence procedures provide a basis for statistical estimates that need further adjustments to determine design values for use with an accepted design methodology. However, they do not purport to address the adjustment factors needed to adjust test data to standardized mechanical and environmental conditions. The building engineers (users) are responsible for seeking the appropriate adjustment factors for specific conditions that the wooden building serves.

The adjustment factor is the ratio of mechanical properties in the relevant service environment to the standardized laboratory test results. Since the allowable stress values (F_b, F_t, F_c, F_v, and E_min) (Table 1) determination has calculated the near minimum value to consider the 95% confidence of safety, their related adjustment factors shall be the unbiased estimation values to avoid redundancy. The unbiased estimations of adjustment values are the average of the ratio of mechanical properties at the relevant service environments to those of the standardized laboratory test results. When an adjustment factor is evaluated, the specimen conditions and test procedures should be well arranged so that the other factors are assumed to be in the boundary condition of the ceteris paribus (all other things being equal). The ceteris paribus condition is necessary to ascertain the independency of the evaluated adjustment factor from the other affecting factors during the experiment processes. Hayatunnufus et al. [16] and Bahtiar et al. [17] measured the bending stress of sawn lumber subjected to concentrated loads at one and several points, respectively. Their laboratory test data on the beam stability factor (C_L), defined as the ratio of each edge-wise bending specimen’s modulus of rupture (MOR, S_Ri) to the standardized straight-grain small-clear wood specimen’s average MOR value (${{\displaystyle \overline{S}}}_R$), is in harmony with the beam stability factor (C_L) designated by SNI 7973-2013. The $S_{Ri}/{{\displaystyle \overline{S}}}_R$ ratio, which was curve fitted as the function of beam slenderness ratio (R_B) following the Ylinen formula, is the unbiased estimation for the beam stability factor (C_L).

Since the wood’s moisture content substantially influences its mechanical properties and their relationship is relatively straightforward, most of the wood usage problem is related to its moisture content. The moisture content effects must be considered when using timber for structural purposes [18]. Temperature and relative humidity daily cycles raise the moisture content daily changes and further affect the wood’s mechanical properties, such as creep deflection [19]. Timber, which frequently receives wet–dry cycles, may degrade faster than constantly wet or dry ones. Wood is composed of anatomical elements whose lumens are connected by different pit types. The cell walls’ behavior naturally affects the wood’s properties as it responds to moisture content change. The moisture content change leads to shrinkage–swelling and the adjustment of wood strength and stiffness [20]. Air-dried wood with an average value of 12%–18% has stronger mechanical properties than wood with more than 20% moisture content. Wood should be conditioned to the dry condition (15%–19% moisture content) for general structural application rather than using it in the green state. When the wood has dried, the free water in the lumens is evaporated first, and further drying increases the wood’s strength with the bound water loss. A negative correlation between wood mechanical properties and the 10%–30% moisture content is reported [21,22,23]. Madsen [24] conducted the full-sized sawn lumber mechanical properties test at the green and air-dry conditions (moisture content between 10%–25%), measured the mechanical properties change per 1% moisture content difference, and extrapolated the data to the fiber saturation point (FPS). Madsen [24] calculated C_M as the ratio of the FPS extrapolated mechanical property to that at air-dry conditions, where he chose the fifth percentile values as the numerator and denominator (C_M = R_w0.05/R_d0.05) (Figure 1). Choosing the near minimum values as the basis for C_M calculation, Madsen [24] reported that timber’s shear strength parallel-to-grain, compressive strength parallel-to-grain, and compressive stress perpendicular-to-grain are sensitive to the moisture content change; meanwhile, bending strength, tensile strength parallel-to-grain, and stiffness are insensitive.

The mechanical properties of wood measured on dry specimens are significantly greater than on green wood [25,26,27,28,29,30]. The branch and trunk of the living tree or the freshly sawn wood are examples of green wood. The green wood moisture content ranges from 31% to 239% [31,32,33], generally higher than the fiber saturation point (FSP). Researchers proposed various methods to measure the FSP value, which resulted in varied result values [34]. Stamm [35] measured the FSP as around 30%, while some researchers [36,37,38,39,40] proposed the FSP as around 40% (38.5%–42.5%). FSP is the moisture content at which the cell walls are entirely saturated, but water does not exist in cell lumina. Above the fiber saturation point, the cell walls are entirely water-saturated, and some free water is located in the lumina. If its moisture content is above the fiber saturation point, the wood’s mechanical properties are constant at the weakest value and do not significantly change with the moisture content change [41].

In addition to terrestrial construction, wood is also a popular material for a building that serves aquatic and wet environments (e.g., ships [42], harbor ports at marine facilities [43], fishing huts [44], and cooling towers [45,46,47,48]). As hygroscopic materials, wood absorbs and desorbs water from its environment to reach its equilibrium moisture content. The higher moisture content of wood resulted in its strength and stiffness reduction. Eurocode 5:2004 [49] and New Zealand Timber Standard NZS: 3603:1993 [50] accommodate the moisture content exchanged between the material and the environment by governing the concept of service class, which represents the air humidity and temperature which will affect the material’s properties during the structure’s service lifetime [51]. Many countries’ building codes for wood construction (i.e., NDS:2018 [52], CSA-086:2019 [53], and SNI 7973:2013 [6]) govern that wet service factor (C_M) is mandatory to adjust the sawn lumber reference design values when the building serves in the wet or aquatic environments. Wood construction designers apply wet service factor (C_M) adjustments to ensure the wooden building’s safety and serviceability in a wet environment. When the timber serves the condition where its moisture content exceeds 19% for an extended time, its strength and stiffness are reduced; thus, its design values must be adjusted by the wet service factor (C_M) [6,52,53].

SNI 7973:2013 [6] lists the designated C_M values (

Table 2. Wet service factor (C_M) for sawn lumber [6,7].

	Fb	Ft	Fv	Fc⊥	Fc	E and Emin
CM	0.85 *	1.0	0.97	0.67	0.8 **	0.9

Note: *: if F_b ≤ 8 MPa, C_M = 1.0; **: if F_c ≤ 5.2 MPa, C_M = 1.0.

). SNI 7973:2013 does not specify C_M for different species nor the timber’s size and quality, but a different type of material property. In contrast, NDS:2018 [52] provides six tables to accommodate the C_M value of different sizes and qualities of timber, such as

Table 4. Physical properties of air-dry and wet clear-wood specimens.

	Pine		Agathis		Red Meranti		Mahogany
	Dry	Wet	Dry	Wet	Dry	Wet	Dry	Wet
Moisture content (w, %)	17.1	131.1	16.5	118.3	16.5	74.1	15.9	95.6
Density (ρ, g/cm3)	0.50	1.08	0.56	0.92	0.73	0.95	0.65	1.00
Specific gravity (SG)	0.42	0.48	0.48	0.41	0.61	0.53	0.55	0.51

A–F. The C_M values provided by NDS in Table 4A–C,E,F are the same as seen in Table 2. Only NDS’s Table 4D for visually graded timber (5” × 5” and larger) provides the different C_M values.

Because the moisture content generally raises the biggest usage problem of wood as a hygroscopic material, this study encourages investigating the wet service factor (C_M). Some occurrences proved the necessity to investigate the wet service factor (C_M). A wooden cooling tower that served in a wet environment for 13 years in Pangalengan (ID) was reported to be in a dangerous condition per ISO 10816-3:2009 [54] because it suffered from the high vibration symptom. In addition to the deterioration in the maximum depth of 2.5 mm [45], the vibration amplitude was high because of the decreasing modulus of elasticity (E) value in the high temperature, water-saturated, and immersed conditions. The 13 years of service life is much shorter than the 50 years in the planned design; thus, structural modification following the triangle bracing system is recommended [46].

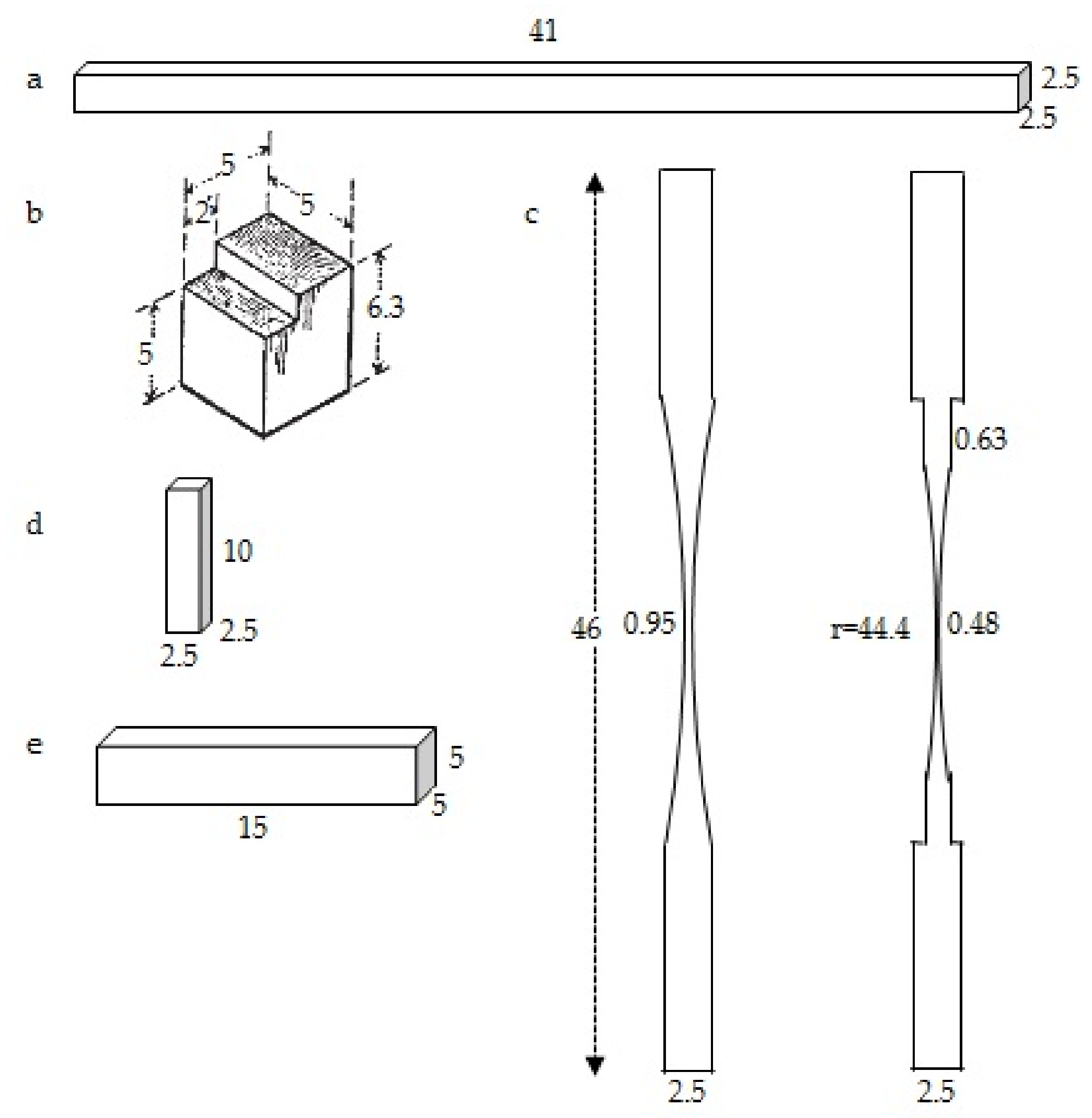
This study’s objective is to compare and harmonize the experimental C_M value with the tabulated one in the building code; thus, wooden construction designers can confidently apply it to design wooden constructions that serve in the wet or aquatic environment. Although small clear-wood properties may differ from the full-sized sawn lumber, small clear-wood specimen test results are the traditional basis to generate the lumber’s allowable stresses associated with the adjustment factors [24]. When comparing the mechanical properties of wet to air-dry wood, the pair of specimens being compared shall have similar properties before the treatment is applied. The defects and growth characteristics, which are variedly contained in every full-sized timber, disturb the assumption of the boundary condition of the ceteris paribus when determining the ratio of the wet to air-dry wood’s mechanical properties. Since the effect of growth characteristics and defects on the full-sized timber’s mechanical properties have been calculated in the structural grading as the strength ratio for determining the allowable stresses (F_b, F_c, F_t, F_c⊥, F_v, E, and E_min) and the size effect factor (C_F) has considered the effects of sawn lumber’s dimension (Table 1), the traditional small clear-wood is a well representative specimen to develop the other adjustment factors, such as C_D, C_M, C_t, C_i, K_F, ϕ, and λ. This study tests the mechanical properties of clear-wood in dry and wet conditions to harmonize the building-code-designated wet service factor (C_M) with the laboratory test of commercial wood species available in the building material market. Laboratory tests of several commercially available wood species are necessary to calibrate the tabulated values periodically. Four wood species which abundantly available in the building material market, namely, pine (Pinus merkusii), agathis (Agathis dammara), red meranti (Shorea leprosula), and mahogany (Swietenia mahagoni), are selected in this study as the sample for the mechanical properties tests in the dry and wet conditions. The mechanical properties tests included static bending, shear parallel-to-grain, tension-parallel-to-grain, compression-parallel-to-grain, and compression-perpendicular-to-grain. The empirical C_M is the ratio of each mechanical property value in the wet (water-saturated) condition to that in the air-dry condition. Instead of comparing green and air-dry wood, however, this study compared wet (re-saturated) and air-dry wood, and the mechanical test of the wet specimen was conducted when the specimen was immersed in a water bath. These submerged specimen test arrangements imitate the worst-case scenario of what would happen if a wooden building got wet for any reason than comparing green to air-dry wood.

2. Methods

2.1. Physical and Mechanical Properties Test

The 400 × 12 × 6 cm size of some commercially available timbers, including pine, agathis, red meranti, and mahogany, were cut into the size of several small clear specimens following ASTM D143-2014 [10]. Instead of sampling and cutting the tree following ASTM D5536-94 (1999) [9], the timbers were bought randomly from the building material shops to represent the available commercial sawn lumber in the market. The mechanical properties tests were static bending, shear-parallel-to-grain, tension-parallel-to-grain, compression-parallel-to-grain, and compression-perpendicular-to-grain. The static bending tests were made on 2.5 × 2.5 × 41 cm secondary method specimens (Figure 2a). A digital caliper measures the actual height (h) and width (b) at the center and the length (l). The shear-parallel-to-grain tests were applied on 5 × 5 × 6.3 cm specimens notched about 1.3 cm in length and 2 cm in depth to produce failure on a 5 × 5 cm surface (Figure 2b). The shearing surface’s actual dimensions were measured. Figure 2c shows the specimen’s shape and size for the tension-parallel-to-grain tests. The actual cross-sectional dimensions at the smallest part were measured. The compression-parallel-to-grain tests were applied on 2.5 × 2.5 × 10 cm secondary method specimens (Figure 2d). Measurements of the actual length and cross-sectional dimensions were conducted. The specimens having a size of 5 × 5 × 15 cm were prepared for the compression-perpendicular-to-grain tests (Figure 2e). The actual height (h), width (b), and length (l) were measured.

As many as 40 specimens were tested to compare and harmonize the wet service factor (C_M) corresponding to each mechanical property. Therefore, 200 specimens were prepared for five mechanical properties tests, such as 100 pieces for the air-dry specimens and 100 for the wet specimens. Each mechanical properties test was conducted on 40 specimens: 20 specimens were tested at the air-dry condition in an indoor room (24–27 °C temperature and 80% relative air humidity), and 20 others were tested in the wet (water-saturated) condition. The mechanical properties test arrangements (e.g., specimen size, lying position, and loading rate) were carefully conducted following ASTM D 143-2014 [10] using Universal Testing Machine (UTM) 30-ton capacity (SATEC/Baldwin, Grove City, PA, USA). The periodically calibrated load cell, linear variable displacement transducers (LVDT), and multipurpose digital indicator (MPDI) data acquisition machine (installed by PT Testindo—Jakarta and calibrated by PT Global Quality Indonesia—Bandung, ID) were set at the UTM to measure and record the load and displacement. The MDPI periodically recorded the test data every 0.5 s.

Meanwhile, the wet (water-saturated) specimens were first immersed in water for 65 days. Then their mechanical properties tests were conducted when the specimen was immersed in a pool of water at around 10 cm depth (Figure 3) to mimic the worst-case scenario of the relevant wet and aquatic environment conditions. The water was obtained from the Ciapus river (6°33′03.2′ S 106°43′37.4″ E) and processed for daily use at the IPB University-Darmaga Campus.

Each specimen’s mass (m₁) and dimensions (length (l), width (b), and depth (h)) were measured not long before every mechanical property test. The moisture content, density, and specific gravity were also measured soon after the mechanical property test. After the failure, the specimen’s stringy parts were cleaned, the specimen was weighed (m₂), and then put in the 103 ± 2 °C oven for 48 h. After 48 h, the specimen was taken out from the oven, weighed, and put again in the oven. This process was repeated every three hours until three consecutive weights were constant. The constant weight is the oven-dry weight (m_o). The moisture content (w) is the percentage of the water mass (m₂-m_o) to the oven-dry wood mass (m_o) (Equation (1)). The density (ρ) is the ratio of air-dry mass (m₁) to the air-dry volume (v₁) (Equation (2)). Air-dry volume is v₁ = l × b × h. Specific gravity (S_G) is the ratio of oven-dry mass (m_o) to the air-dry volume (v₁) and divided by the water density at standard conditions (ρ_w = 1000 kg/m³) (Equation (3)). All test procedures were conducted in the Forest Products Department—Faculty of Forestry and Environment—IPB University, accredited by The Society of Wood Science and Technology (SWST) since 2014.

$$w=\frac{m_2-m_o}{m_o}\times 100\%$$

(1)

$$\rho =\frac{m_1}{v_1}=\frac{m_1}{lbh}$$

(2)

$$S_G=\frac{\rho }{\left(w\%+1\right){\rho }_w}$$

(3)

2.2. Data Analysis

2.2.1. The Mechanical Properties Difference

Table 3. Modified t-test procedures to analyze: (1) the dry to wet wood’s mechanical properties differences and (2) the empirical C_M to SNI 7973:2013′s tabulated value.

ith Species	jth Replication	kth Condition		$\mathbf{Error} ({\mathit{\epsilon }}_{\mathit{i}\mathit{j}\mathit{k}}={\mathit{x}}_{\mathit{i}\mathit{j}\mathit{k}}-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{i}\mathit{k}})$		Empirical Wet Service Factor (CME)
		1 = Wet	2 = Dry	1 = Wet	2 = Dry	xi11/xij2	xi21/xij2	xi31/xij2	xi41/xij2	xi51/xij2
1 = meranti	1	x111	x112	x111$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{1}}$	x112$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{2}}$	x111/x112	x121/x112	x131/x112	x141/x112	x151/x112
	2	x121	x122	x121$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{1}}$	x122$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{2}}$	x111/x122	x121/x122	x131/x122	x141/x122	x151/x122
	3	x131	x132	x131$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{1}}$	x132$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{2}}$	x111/x132	x121/x132	x131/x132	x141/x132	x151/x132
	4	x141	x142	x141$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{1}}$	x142$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{2}}$	x111/x142	x121/x142	x131/x142	x141/x142	x151/x142
	5	x151	x152	x151$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{1}}$	x151$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{2}}$	x111/x152	x121/x152	x131/x152	x141/x152	x151/x152
	Average	${{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{1}}$	${{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{2}}$
	Difference	$D_{\mathit{1}j}={{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{1}}-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{1}\mathit{j}\mathit{2}}$
2 = mahogany	1	x211	x212	x211$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{1}}$	x212$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{2}}$	x211/x212	x221/x212	x231/x212	x241/x212	x251/x212
	2	x221	x222	x221$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{1}}$	x222$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{2}}$	x211/x222	x221/x222	x231/x222	x241/x222	x251/x222
	3	x231	x232	x231$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{1}}$	x232$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{2}}$	x211/x232	x221/x232	x231/x232	x241/x232	x251/x232
	4	x241	x242	x241$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{1}}$	x242$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{2}}$	x211/x242	x221/x242	x231/x242	x241/x242	x251/x242
	5	x251	x252	x251$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{1}}$	x251$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{2}}$	x211/x252	x221/x252	x231/x252	x241/x252	x251/x252
	Average	${{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{1}}$	${{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{2}}$
	Difference	$D_{\mathit{2}j}={{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{1}}-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{2}\mathit{j}\mathit{2}}$
3 = agathis	1	x311	x312	x311$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{1}}$	x312$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{2}}$	x311/x312	x321/x312	x331/x312	x341/x312	x351/x312
	2	x321	x322	x321$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{1}}$	x322$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{2}}$	x311/x322	x321/x322	x331/x322	x341/x322	x351/x322
	3	x331	x332	x331 −${ \mathit{x} ¯}_{\mathit{3}\mathit{j}\mathit{1}}$	x332$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{2}}$	x311/x332	x321/x332	x331/x332	x341/x332	x351/x332
	4	x341	x342	x341$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{1}}$	x342$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{2}}$	x311/x342	x321/x342	x331/x342	x341/x342	x351/x342
	5	x351	x352	x351$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{1}}$	x351$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{2}}$	x311/x352	x321/x352	x331/x352	x341/x352	x351/x352
	Average	${{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{1}}$	${{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{2}}$
	Difference	$D_{\mathit{3}j}={{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{1}}-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{3}\mathit{j}\mathit{2}}$
4 = pine	1	x411	x412	x411$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{1}}$	x412$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{2}}$	x411/x412	x421/x412	x431/x412	x441/x412	x451/x412
	2	x421	x422	x421$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{1}}$	x422$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{2}}$	x411/x422	x421/x422	x431/x422	x441/x422	x451/x422
	3	x431	x432	x431$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{1}}$	x432$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{2}}$	x411/x432	x421/x432	x431/x432	x441/x432	x451/x432
	4	x441	x442	x441$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{1}}$	x442$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{2}}$	x411/x442	x421/x442	x431/x442	x441/x442	x451/x442
	5	x451	x452	x451$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{1}}$	x451$-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{2}}$	x411/x452	x421/x452	x431/x452	x441/x452	x451/x452
	Average	${{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{1}}$	${{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{2}}$
	Difference	$D_{\mathit{4}j}={{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{1}}-{{\displaystyle \overline{\mathit{x}}}}_{\mathit{4}\mathit{j}\mathit{2}}$

will summarize each type of mechanical test result. The Kolmogorov–Smirnov, Liliefors, and Shapiro–Wilk test the normality of the error (ε). The errors are the difference of each specimen measurement (x_ijk) to the average value of the same species and condition specimen (${{\displaystyle \overline{x}}}_{ik}$) calculated per Equation (4). The differences between mechanical properties in the wet condition (σ_w) with that in the dry condition (σ_d) were evaluated using the modified t-Student test (paired-group t-test), following Table 3 procedures. The t-Student formula is Equation (5).

$${\epsilon }_{ijk}=x_{ijk}-{{\displaystyle \overline{x}}}_{ik}$$

(4)

$$t=\frac{{{\displaystyle \overline{D}}}_i-0}{s_D/\sqrt{n}}$$

(5)

• where
• x_ijk = mechanical properties of the ith species (1 = meranti, 2 = mahogany, 3 = agathis, 4 = pine), jth replication (1, 2, 3, 4, and 5), and kth conditions (1 = wet, 2 = air dry)
• ${{\displaystyle \overline{x}}}_{ik}$ = average value of the same species and condition specimen
• ${{\displaystyle \overline{D}}}_i={{\displaystyle \overline{x}}}_{ij2}-{{\displaystyle \overline{x}}}_{ij1}$
• 0 = hypothetical difference
• $s_D=\sqrt{\sum \frac{{\epsilon }_{ijk}{}^2}{n-8}}$
• n = number of specimens (40 units)
• 8 = number of cells (species × conditions).

The null hypothesis (H₀) is ${{\displaystyle \overline{\mathit{D}}}}_{\mathit{i}}=0$, while the alternative hypothesis (H₁) is ${{\displaystyle \overline{\mathit{D}}}}_{\mathit{i}} \ne 0$. If the calculated absolute t_value (|t_value|) (Equation (5)) is greater than the two-tail tabulated t-Student [t_{(α/2, ν)} = t_{(0.025, n−8)}], H₀ is rejected and H₁ is accepted. The accepted H₁ indicates that the wood’s mechanical properties in the dry condition are significantly different from those in the wet condition.

2.2.2. Wet Service Factor

The experimental wet service factor value of each specimen ($C_{M{E}_{ij}}$) is calculated as the ratio of measured mechanical properties in the wet conditions (σ_ij1) to those at the dry conditions of the same species (σ_ij2) (Equation (6)). The C_M values from all possible combinations of the same species’ mechanical properties at wet to air-dry conditions are listed in Table 3. Every species results in 25 combinations; therefore, 100 combinations are listed for four species (Table 3). Since normal approximation [55] was assumed to fit the ratio of wood’s mechanical properties at the wet condition to the air-dry ones, the modified t-Student test (one-point t-Student test) was conducted following Equation (7) to analyze whether the experimental wet service factor (C_ME) value is different compared to the tabulated value in the building code (C_M(SNI)).

$$C_{M{E}_{ij}}=\frac{{\mathsf{\sigma }}_{ij1}}{{\mathsf{\sigma }}_{ij2}}$$

(6)

$$t=\frac{{{\displaystyle \overline{C}}}_{ME}-C_{M\left(SNI\right)}}{s_{C_{ME}}/\sqrt{n}}$$

(7)

• where:
• $C_{M{E}_{ij}}$ = empirical wet service factor for the ith species (1 = meranti, 2 = mahogany, 3 = agathis, 4 = pine) at the jth combination within species (1, 2, 3, …, 25),
• ${{\displaystyle \overline{C}}}_{ME}$ = average empirical wet service factor
• C_M(SNI) = SNI 7973:2013-tabulated C_M
• $s_{C_{ME}}$ = standard deviation of empirical wet service factor
• n = total number of combination data (100 units)

The formula for the one-point t-Student test is Equation (7), while the null hypothesis (H₀) is ${{\displaystyle \overline{C}}}_{ME}=C_{M\left(SNI\right)}$ versus the alternative hypothesis (H₁) is ${{\displaystyle \overline{C}}}_{ME} C_{M\left(SNI\right)}$. If the calculated absolute t_value (|t_value|) resulting in Equation (7) is greater than the two-tail tabulated t-Student (t_{(α/2, ν)} = t_{(0.025, 99)}), H₀ is rejected and H₁ is accepted. The accepted H₁ indicates that the experimental wet service factor (C_ME) is significantly different from the tabulated C_M in the building code (C_M(SNI)). The significantly different C_M values will propose to revise the building code tabulated C_M.

3. Results and Discussion

3.1. The Physical Properties

The climates in Bogor, West Java, Indonesia are 19.3 °C–34.2 °C temperature, 62.2%–95.4% humidity, and 4212 mm yearly rainfall. The warm, humid, and rainy environments result in wood’s high equilibrium moisture content. This study measured that the specimen’s average air-dry moisture contents ranged from 15.92% to 17.13%, in line with some research reports on wood [17,56,57,58,59] or bamboo [60,61,62,63,64,65] located in Bogor (ID), but wetter than the equilibrium moisture content (EMC) in the subtropical region such as Coventry (UK) [66,67]. The air-dry timber is wetter than mortar [68]. The air-dry specimen’s moisture content is compatible with the timber under dry service conditions, such as indoor structures, where the moisture content does not exceed 19%. The wood’s strength and stiffness are relatively constant when it exceeds the fiber saturation point [41]. When immersed in the water pool for 65 days, the specimen’s moisture content range was 74.13%–131.13% (Table 4). The specimens exceeded the fiber saturation point; thus, their mechanical properties were expectedly constant at the weakest state. The ratio of the mechanical properties of the wood wetter than the fiber saturation point to those in the air-dry conditions resulted in the empirical wet service factor (C_M) value. The immersion in the water bath during the mechanical property tests guaranteed the water-saturated condition of the specimen’s whole parts.

The wood densities (ρ) vary within and between species, and the moisture content affects it too. The wet wood always has a higher density than the air-dry ones (Table 4) because the water directly contributes to the mass measurement. All specimens’ specific gravity (S_G) was measured and transformed into oven-dry mass per air-dry volume basis, and this study resulted in a value of between 0.41 and 0.61. The density strongly correlates with the mechanical properties, and air-dry density was the basis for structural timber’s strength grading following PKKI NI-5:1961 [69]. Pine and agathis have a similar specific gravity (0.41–0.48). Mahogany is denser (0.51–0.55), while red meranti is the densest among others (0.53–0.61).

3.2. The Mechanical Properties

3.2.1. The Mechanical Properties Difference between Wet and Dry Wood

The wet wood, which has a high moisture content, is lower in strength than the dry wood because of the decrease of the portion of woody material and the density of cell walls. The cell walls’ stiffness also decreases when they bind more water [70]; thus, the wood strength and stiffness also reduce. Madsen [71] reported that the wood stiffness increases as the moisture content decreases and the strength of initially strong wood would also increase.

This study proposed the wet wood mechanical properties test to be conducted on the re-saturated specimen immersed in the water bath. Due to load distribution along the specimen, there might be significantly different mechanical properties resulting from the immersed and non-immersed specimens. In non-immersed specimens, micro-analysis may observe the drier region at the differential part that received the higher stress and strain. Some regions’ higher stress and strain will squeeze more water than other parts. This critical region, which receives the highest load, becomes drier, and its strength increases. The critical region’s increasing strength may improve the whole specimen’s strength. This phenomenon has a lower probability of happening in the immersed specimen.

Several publications provide mechanical properties of pine, agathis, meranti, and mahogany wood at air-dry conditions similar to this study’s results (

Table 5. This study’s mechanical properties of wood at air-dry conditions compared to several previous reports.

Mechanical Properties	This Study’s Laboratory Test				$\mathbf{Previous} \mathbf{Report} ({\displaystyle {\displaystyle \overline{\mathit{x}}}}\pm \mathit{s}) \mathbf{or} (\mathbf{min}–\mathbf{max})$
	Pine	Agathis	Meranti	Mahogany	Pine	Agathis	Meranti	Mahogany
Modulus of rupture (σb, MPa)	62.73	56.49	86.94	81.58	55.15 ± 10.18 [17]	52.03 ± 4.46 [16]	72.42 ± 12.15 [17]	70.47 ± 11.37 [17]
					55.57 ± 10.76 [16]	49.0–71.1 [69]	75.33 ± 15.95 [16]	70.83 ± 12.52 [16]
					49.0–71.1 [69]	49.3 [76]	35.3–107.9 [69]	49.0–107.9 [69]
					63 [78]		87.6 [75]
Shear strength parallel-to-grain (τ, MPa)	9.76	9.88	10.53	12.11	8.55 [77]		10 [75]	7.0 [76]
Maximum crushing strength (σc, MPa)	28.54	26.09	54.21	46.17	29.4–41.7 [69]	29.4–41.7 [69]	21.1–63.7 [69]	29.4–61.3 [69]
					23.0–29.4 [79]	32.8 [76]	50.7 [75]	36.9 [76]
Modulus of elasticity (E, MPa)	7278	9113	10523	8158	7218 ± 1837 [17]	6976 ± 618 [17]	11001 ± 1379 [17]	8033 ± 1079 [17]
					7341 ± 2069 [16]	7407 ± 639 [16]	10372 ± 1559 [16]	8013 ± 1449 [16]
					7845 [69]	7845 [69]	5884–9806 [69]	7845–9806 [69]
					7597 [78]		12200 [75]	9562 [76]

). Similar to many reports [18,72,73,74], this study also finds that the mechanical properties of wet wood are consistently weaker than those of dry ones (

Table 6. The average mechanical properties of wood in wet (water-saturated) and air-dry conditions.

Mechanical Properties	Wet (Water-Saturated)				Air-Dry
	Pine	Agathis	Meranti	Mahogany	Pine	Agathis	Meranti	Mahogany
Modulus of rupture (σb, MPa)	36.89	43.24	77.91	57.60	62.73	56.49	86.94	81.58
Shear strength parallel-to-grain (τ, MPa)	6.23	7.66	5.20	8.07	9.76	9.88	10.53	12.11
Tensile strength parallel-to-grain (σt, MPa)	51.82	24.10	115.38	46.33	71.14	44.57	135.10	63.69
Maximum crushing strength (σc, MPa)	17.63	16.81	31.51	37.69	28.54	26.09	54.21	46.17
Compressive stress perpendicular-to-grain at the proportional limit (σc⊥pl, MPa)	1.83	3.75	5.61	4.47	5.05	4.82	8.55	5.75
Compressive stress perpendicular-to-grain at the 0.04″ deformation (σc⊥0.04, MPa)	1.75	3.86	5.84	4.90	5.20	5.12	8.60	6.18
Modulus of elasticity (E, MPa)	4070	5096	5922	4786	7278	9113	10,523	8158

). A similar phenomenon is valid for modulus of rupture (σ_b), shear strength parallel-to-grain (τ), tensile strength parallel-to-grain (σ_t), maximum crushing strength (σ_c), compression stress perpendicular-to-grain at the proportional limit (σ_c⊥pl), compression stress perpendicular-to-grain at the 0.04″ deformation (σ_c⊥0.04), and modulus of elasticity (E) (Figure 4). This study’s re-saturated wood’s mechanical properties are generally lower than the several published green wood’s mechanical properties [75,76,77]. The reason for the discrepancy is the moisture history of the specimens. The properties of the green specimens are not always the same as those saturated with water after drying.

In addition to the moisture history, the water-immersed condition during the mechanical property test is expected to affect the testing results. When loading is applied to the wet specimen at non-immersed conditions, the specimen part near the loading point may be dryer than the other part, and the hydrogen bonds between cellulose chains at this portion have the probability of returning. The loading point is the most critical portion, where its increasing strength will improve the specimen’s overall strength. When an immersed specimen is subjected to load, every portion is still water-saturated; thus, it has less probability for the hydrogen bond to return.

The dimension deformation during load application to the water-immersed specimen is expected to be higher than the non-immersed specimen because of its lesser hardness. The dimension deformation at the loading point of an immersed specimen is the highest among other portions. The smaller actual cross-sectional dimensions at the loading point because of the indentation of the loading block and support during load application decrease the area, moment of inertia, and stiffness; therefore, the load-carrying capacity and bending-moment-bearing capacity weaken. The measurement of just-harvested (green) lumber’s dimensions usually results in higher values than the re-saturated specimens because the measurements are conducted at the green and air-dry conditions, respectively. In construction practice, the sawn lumber’s actual dimensions are more often measured in dry conditions.

Kolmogorov–Smirnov test indicated that all data distributions are normal. Lilliefors test indicated the normal distribution for almost all data except for tensile strength parallel-to-grain. The Shapiro–Wilk test found the non-normal distribution of the error of three mechanical properties (modulus of rupture, shear strength parallel-to-grain, and tensile strength parallel-to-grain); in contrast, the others (modulus of elasticity, maximum crushing strength, compressive strength perpendicular-to-grain at the proportional limit, and the 0.04″ deformation) are normal (

Table 7. The normality test of the error of mechanical properties test results.

Mechanical Properties	Kolmogorov–Smirnov			Lilliefors		Shapiro–Wilk
	d	p	Normality	p	Normality	W	p	Normality
Modulus of rupture (σb)	0.11925	>0.20	normal	<0.20	normal	0.89851	0.00173	not normal
Shear strength parallel-to-grain (τ)	0.11753	>0.20	normal	<0.20	normal	0.92898	0.01492	not normal
Tensile strength parallel-to-grain (σt)	0.14497	>0.20	normal	<0.05	not normal	0.93596	0.02533	not normal
Maximum crushing strength (σc)	0.10496	>0.20	normal	>0.20	normal	0.95468	0.10992	normal
Compressive stress perpendicular-to-grain at the proportional limit (σc⊥pl)	0.06086	>0.20	normal	>0.20	normal	0.99137	0.98821	normal
Compressive stress perpendicular-to-grain at the 0.04″ deformation (σc⊥0.04)	0.11445	>0.20	normal	>0.20	normal	0.97774	0.60605	normal
Modulus of elasticity (E)	0.13437	>0.20	normal	<0.10	normal	0.97572	0.53438	normal

).

Table 8. Paired-group t-test results for the mechanical properties difference of air-dry and wet wood.

Properties	Sample Size (n)	Average ± Standard Deviation			t-Value	t Table	p
		Wet	Dry	Dry–Wet
Modulus of rupture (σb, MPa)	40	53.91±6.03	71.93±11.85	18.02±10.25	11.1259	2.3518	0.0000 **
Shear strength parallel-to-grain (τ, MPa)	40	6.79±1.04	10.57±1.12	3.78±1.18	20.2947	2.3518	0.0000 **
Tensile strength parallel-to-grain (σt, MPa)	40	59.41±14.04	78.62±12.38	19.22±14.42	8.4282	2.3518	0.0000 **
Maximum crushing strength (σc, MPa)	40	25.91±1.75	38.75±2.62	12.84±2.43	33.4706	2.3518	0.0000 **
Compressive stress perpendicular-to-grain at the proportional limit (σc⊥pl, MPa)	40	3.92±0.70	6.04±0.75	2.13±0.79	17.0042	2.3518	0.0000 **
Compressive stress perpendicular-to-grain at 0.04″ (σc⊥0.04, MPa)	40	4.09±0.91	6.28±0.87	2.19±0.97	14.2766	2.3518	0.0000 **
Modulus of elasticity (E, MPa)	40	4969±983	8768±1577	3799±1432	16.7834	2.3518	0.0000 **

Note: ** very significantly different.

shows that the coefficient of variation (CV) of wet and air-dry wood’s mechanical properties ranges are 6.76%–23.63% and 6.75%–17.98%, respectively. The CV of the differences between wet and air-dry wood’s mechanical properties increases to become 18.90%–75.04% because the average values (μ_(d-w)) are smaller than the original average value of wet and air-dry wood’s mechanical properties (μ_w and μ_d), and the standard deviation (s_(d-w)) is higher than wet and air-dry ones (s_w and s_d) (Figure 1). The paired-group t-test results in Table 8 indicate that the wet wood mechanical properties are significantly different compared to the air-dry’s one.

3.2.2. Wet Service Factor (C_M)

The designated reference design value for sawn lumber assumes a maximum moisture content of 19%. Wood with a moisture content of 19% or less is dry, while it with more than 19% is considered wet [6,7,53]. Significant differences in the strength of wet with dry wood require the application of the wet service factor (C_M) to adjust the reference design value, especially for the wood member that tends to be wet. Examples of these situations are the green wood that has just been felled, wood used to build scaffolding that is exposed to the weather, wood used for decking, floor joists suspended above the ground that is prone to splashing, wood that is not protected from the weather, and wood near a potential water leak.

The reference design values of wooden members of aquatic environment constructions are subject to this C_M adjustment. SNI 7973:2013 [6] does not specify C_M for different species but a different type of material property. C_M adjusts the mechanical (structural) properties’ reference design values (F_b, F_t, F_c, F_v, F_c⊥, E, and E_min). The reference design values have considered the 5% lower confidence values and the safety factor adjustments. The reference design values have already considered the mechanical property near minimum values; thus, the adjustment factors, including C_M, are the ratio of estimated mechanical properties in the actual relevant environment conditions to that measured in the standardized laboratory test conditions. If the minimum C_M values among wood species are chosen, the C_M adjustment to the reference design may result in a very conservative value. Madsen [24] proposed C_M as the ratio of wet to air-dry mechanical properties; both wet and air-dry mechanical properties are the fifth percentile values. In contrast, this study sustains C_M as the average ratio of all within a species’ possible combinations of wet mechanical properties to that of air-dry. Suppose both wet and air-dry wood’s mechanical properties (σ_w and σ_d, respectively) can be assumed to fit normal distributions. In that case, the distribution of the C_M values (σ_w/σ_d ratio) can be analyzed using normal approximation following Francés and Rubio [55]. This study proposes straightforward and conservative procedures for determining the empirical C_M. The water immersion usually results in the wood’s weakest strength and stiffness; thus, the minimum C_M value, ensuring safety, is obtained.

The experimental C_M values for each mechanical property show the general trend, although they vary between species (

Table 9. The wet service factor (C_M) of four wood species compared to the tabulated C_M in SNI 7973:2013.

Properties	Wood Species				Average	SNI
	Pine	Agathis	Meranti	Mahogany
Modulus of rupture (σb)	0.64	0.77	0.90	0.72	0.76	0.85
Shear strength parallel-to-grain (τ)	0.64	0.78	0.50	0.67	0.65	0.97
Tensile strength parallel-to-grain (σt)	0.74	0.55	0.87	0.75	0.73	1.00
Maximum crushing strength (σc)	0.62	0.65	0.58	0.82	0.67	0.80
Compressive stress perpendicular-to-grain at the proportional limit (σc⊥pl)	0.36	0.82	0.66	0.79	0.66	0.67
Compressive stress perpendicular-to-grain at 0.04″ (σc⊥0.04)	0.34	0.79	0.69	0.80	0.66	0.67
Modulus of elasticity (E)	0.58	0.59	0.57	0.61	0.59	0.90

). The tensile strength sustained in the direction of parallel-to-grain is severely reduced when the wood is soaked in the water. The experimental C_M value for tensile strength parallel-to-grain indicates that the ratio of tensile strength of wet to air-dry wood ranges from 0.55 to 0.87. This value shows that wet wood’s tensile-load-bearing capacity weakens to become almost half. Madsen [24] reported a 25% and 35% increase in allowable tensile strength parallel-to-grain above that of green lumber when maximum moisture contents are 19% and 15%, respectively. The 25%–35% additional values are equivalent to a green to air-dry allowable tensile strength ratio of 0.74 to 0.80, which is still comparable to this study’s range results. However, Madsen [24] recommended that C_M was equal to 1 because the fifth percentile line was at about the same level for tension. The SNI 7973:2013′s tabulated C_M value for tensile strength parallel-to-grain is 1 (one), indicating that the decrease in tensile strength due to wet conditions is not recognized. The building code revision must recognize the wooden member tensile reduction because of wet service conditions. The average empirical C_M for tensile strength parallel-to-grain resulting in this study (C_M = 0.73) may be safely chosen as the designated C_M to recognize the tensile strength parallel-to-grain reduction because of its high moisture content.

In contrast with C_M for tensile parallel-to-grain, the building code accommodates the wet wood carrying capacity adjustment to resist bending moment, shear load parallel-to-grain, and compressive load parallel-to-grain (Table 2). However, its tabulated C_M values are still too high. The tabulated C_M values for modulus of rupture, shear strength parallel-to-grain, maximum crushing strength, and modulus of elasticity are 0.85, 0.97, 0.80, and 0.90, respectively, significantly higher than this experiment’s results; thus, harmonization is necessary. The C_M empirical value for modulus of rupture, shear strength parallel-to-grain, maximum crushing strength, and modulus of elasticity are 0.76, 0.65, 0.67, and 0.59, respectively (Table 6). These C_M values statistically differ from the SNI 7973:2013-tabulated C_M value (

Table 10. One-point t-test result for the difference between empirical and tabulated wet service factor.

Properties	Sample Size (n, Combination)	Wet Service Factor (CM)			|t-value|	t-table	p
		Empiric	Standard Error	SNI 7973:2013
Modulus of rupture (σb)	100	0.76	0.17	0.85	5.5739	2.276	0.0000 **
Shear strength parallel-to-grain (τ)	100	0.65	0.15	0.97	20.8549	2.276	0.0000 **
Tensile strength parallel-to-grain (σt)	100	0.73	0.21	1	13.0702	2.276	0.0000 **
Maximum crushing strength (σc)	100	0.67	0.12	0.8	11.3755	2.276	0.0000 **
Compressive stress perpendicular-to-grain at the proportional limit (σc⊥pl)	100	0.66	0.24	0.67	0.5070	2.276	0.6133 ns
Compressive stress perpendicular-to-grain at 0.04″ (σc⊥0.04)	100	0.66	0.25	0.67	0.5898	2.276	0.5567 ns
Modulus of elasticity (E)	100	0.59	0.15	0.85	17.2010	2.276	0.0000 **

Note: **: very significant, ns: not significant.

). Due to its high value, the tabulated C_M application to adjust the reference design value needs to be more safe, and the building probability of failure is underestimated. The experimental C_M values for compressive stress perpendicular-to-grain at the proportional limit and the 0.04″ deformation (C_M = 0.66) are a bit lower than the designated values (C_M = 0.67), although they are not statistically different.

Madsen [24] reported an 8% to 75% increase in allowable properties above that of green lumber when the maximum moisture content is 19% or 15% (

Table 11. The ratio of green to air-dry allowable properties of lumber 4” (10 cm) and less in nominal thickness when the maximum moisture content is 19% or 15% following Madsen [24] data (recalculated).

Properties	Percentage Increase in Allowable Properties above That of Green Lumber When Maximum Moisture Content Is [24]		Ratio of Green to Air-Dry Allowable Properties When Maximum Moisture Content Is
	19%	15%	19%	15%
Modulus of rupture (σb)	25	35	0.80	0.74
Modulus of elasticity (E)	14	20	0.88	0.83
Tensile strength parallel-to-grain (σt)	25	35	0.80	0.74
Maximum crushing strength (σc)	50	75	0.67	0.57
Shear strength parallel-to-grain (τ)	8	13	0.93	0.88
Compressive stress perpendicular-to-grain (σc⊥)	50	50	0.67	0.67

). Then, Equation (8) calculates the ratio of green to air-dry allowable properties (C_M) using his data and finds that the C_M ranges are 0.57–0.88 and 0.67–0.93 when the maximum moisture content is 15% and 19%, respectively. Madsen’s [24,71] mechanical properties ratio of full-sized timber at air dry (15% MC) conditions to that of fiber saturation point (30% MC) (Figure 5) is similar to that of lumber 4” (10 cm) and less in nominal thickness (Table 11). Figure 5 indicates that the ratios of average full-sized timber’s mechanical properties at air-dry to the average of that at the fiber saturation point are 0.77 for Hem-Fir and 0.76 for Spruce-Pine-Fir (S-P-F), similar with this study’s results on small-clear wood specimens (C_M=0.76, Figure 6). Instead of choosing the ratio of the 50% percentile values representing the average values as the unbiased estimations, Madsen chose the ratio of 5% lower percentile values for calculating the C_M values (R_w0.05/R_d0.05). His biased choices resulted in high C_M values for the modulus of rupture (1.07 for Hem-Fir and 0.94 for S-P-F) and did not recognize the decreasing modulus of rupture of wet timber. The near minimum values have been considered when determining the timber’s allowable stress; thus, choosing the near minimum values as the basis for C_M calculation is redundant.

$$C_M=\frac{1}{1+{\Delta }_{\sigma }/100}$$

(8)

Wood Handbook [75] also provides functions relating mechanical properties to the specific gravity of small clear-wood specimens at the green and 12% moisture content conditions, based on 43 softwood and 66 hardwood species. Substituting the average specific gravity of pines, agathis, red meranti, and mahogany in Table 4, the approximated mechanical properties at the green and 12% moisture content are in

Table 12. The mechanical properties of green and 12% moisture content of small clear specimens were calculated following the function relating mechanical properties to specific gravity [75], and their ratio.

Properties	Softwood						Hardwood						Average CM
	Pine			Agathis			Meranti			Mahogany
	Green	12% MC	CM	Green	12% MC	CM	Green	12% MC	CM	Green	12% MC	CM
Modulus of rupture (σb)	48.9	76.2	0.64	48.38	75.3	0.64	61.8	90.8	0.68	56.8	83.6	0.68	0.66
Shear strength parallel-to-grain (τ)	6.1	8.4	0.73	6.1	8.3	0.73	8.9	11.6	0.76	8.1	10.7	0.76	0.75
Maximum crushing strength (σc)	23.5	43.2	0.54	23.2	42.7	0.54	26.3	46.1	0.57	24.2	43.2	0.56	0.55
Compressive stress perpendicular-to-grain (σc⊥)	2.6	4.7	0.55	2.5	4.6	0.55	4.6	6.7	0.69	3.8	5.7	0.67	0.61
Modulus of elasticity (E)	8.8	10.5	0.84	8.7	10.4	0.84	9.3	11.1	0.83	8.8	10.6	0.83	0.83

. Table 12 also lists the ratio of mechanical properties at green to that at 12% moisture content, and the value range is 0.55–0.83.

The current C_M values designated by NDS 2018 [52], ASTM D1990-19:2019 [80], and SNI 7973:2013 are not equivalent to the ratio of the green small clear-wood to the dry ones given in ASTM D2555:2005 [11] or wood handbook [75], because the current C_M value chooses the fifth percentile limit as the calculation basis (C_M = R_w0.05/R_d0.05), complying Madsen’s [24,71] biased estimation. The tabulated green and dry clear-wood’s mechanical properties in ASTM D2555:2005 [11] and wood handbook [75] are the average values (μ_w and μ_d). This study proposes to change the calculation basis of C_M values from the fifth percentile values to the average of all within species’ possible combinations of wet to dry wood’s mechanical property ratio (${\mu }_{\frac{{\sigma }_w}{{\sigma }_d}}$). The calculation basis promoted by this study shall result in a smaller C_M than the fifth percentile basis calculation (R_w0.05/R_d0.05) but slightly higher than the ratio of the average wet wood’s mechanical properties to the average dry ones (μ_w/μ_d) (Figure 6). The average of σ_w/σ_d is the unbiased statistical estimation for C_M; thus, it represents the better fit actual reduction to consider the moisture content effects than the ratio of near minimum values (R_w0.05/R_d0.05). This unbiased estimation resulted in similar C_M value for bending of small-clear-specimen (Figure 6, C_M = 0.76), full-sized timber (Figure 5, C_M = 0.76–0.77), and 4” timber or less in nominal thickness (Table 11, C_M = 0.74–0.80 ≅ 0.77), which prove its fair independence from the size’s effects.

In general, this study finds that the tabulated C_M values are higher than the empirical values; thus, building code revision is necessary. The lacked conservativeness is mainly attributed to the building code’s recent choices, e.g., (1) the wet service environment basis is the green timber rather than the fully water-saturated one, and (2) the ratio of near minimum (5% lower) distribution value is chosen as the C_M value rather than the average of the ratio of the wet timber’s mechanical property to the air-dry one. Designers need more conservative C_M values to design wooden members of safe and reliable constructions that serve in wet and aquatic environments. This study proposes to change the C_M calculation basis from R_w0.05/R_d0.05 to the average of σ_w/σ_d.

4. Conclusions

Wood in wet (water-saturated) stated conditions has significantly lower strength than in air-dry conditions; thus, the wet service factor (C_M) must adjust the reference design value when wooden construction serves in wet or aquatic environments. The C_M value, empirically measured in this study, ranges from 0.59 to 0.76.

The empirical C_M values to adjust the reference design value of modulus of elasticity (E), modulus of rupture (σ_b), shear strength parallel-to-grain (τ), tensile strength parallel-to-grain (σ_t), and maximum crushing strength (σ_c) (C_M = 0.59, 0.76, 0.65, 0.73, and 0.67, respectively) are significantly lower than SNI 7973-2013-designated values. The experimental C_M values to adjust compressive stress perpendicular-to-grain at the proportional limit (σ_c⊥pl) and that at the 0.04″ deformation (σ_c⊥0.04) reference design values (C_M = 0.66 and 0.66) are a bit lower than the designated values (C_M = 0.67), though the one-point t-test shows they are not significantly different.

In general, this study finds that the designated C_M values in the building code are higher than the laboratory test results, which indicates that the building code lacked conservativeness. Designers need more conservative C_M values to design wooden members of safe and reliable constructions that serve in wet and aquatic environments. This study proposes to change the C_M calculation basis from R_w0.05/R_d0.05 to the average of σ_w/σ_d to obtain more conservative and reliable C_M values.