Site Index Modeling of Larch Using a Mixed-Effects Model across Regional Site Types in Northern China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site and Data Description
2.2. Influencing Factors of Stand Dominant Height
2.3. Clustering of Site Types and Base Model Selection
2.4. Nonlinear Mixed-Effects Model
2.5. Predicition with Nonlinear Mixed-Effects Model
- (i)
- 20 percent of plots whose dominant heights are the highest per forest site type (highest);
- (ii)
- 20 percent of plots whose dominant heights are the lowest per forest site type (lowest);
- (iii)
- 20 percent of plots randomly selected per forest site type (random).
2.6. Model Evaluation
3. Results
3.1. Importance Ranking of the Site Factors
3.2. Base Model Selection and Simulation
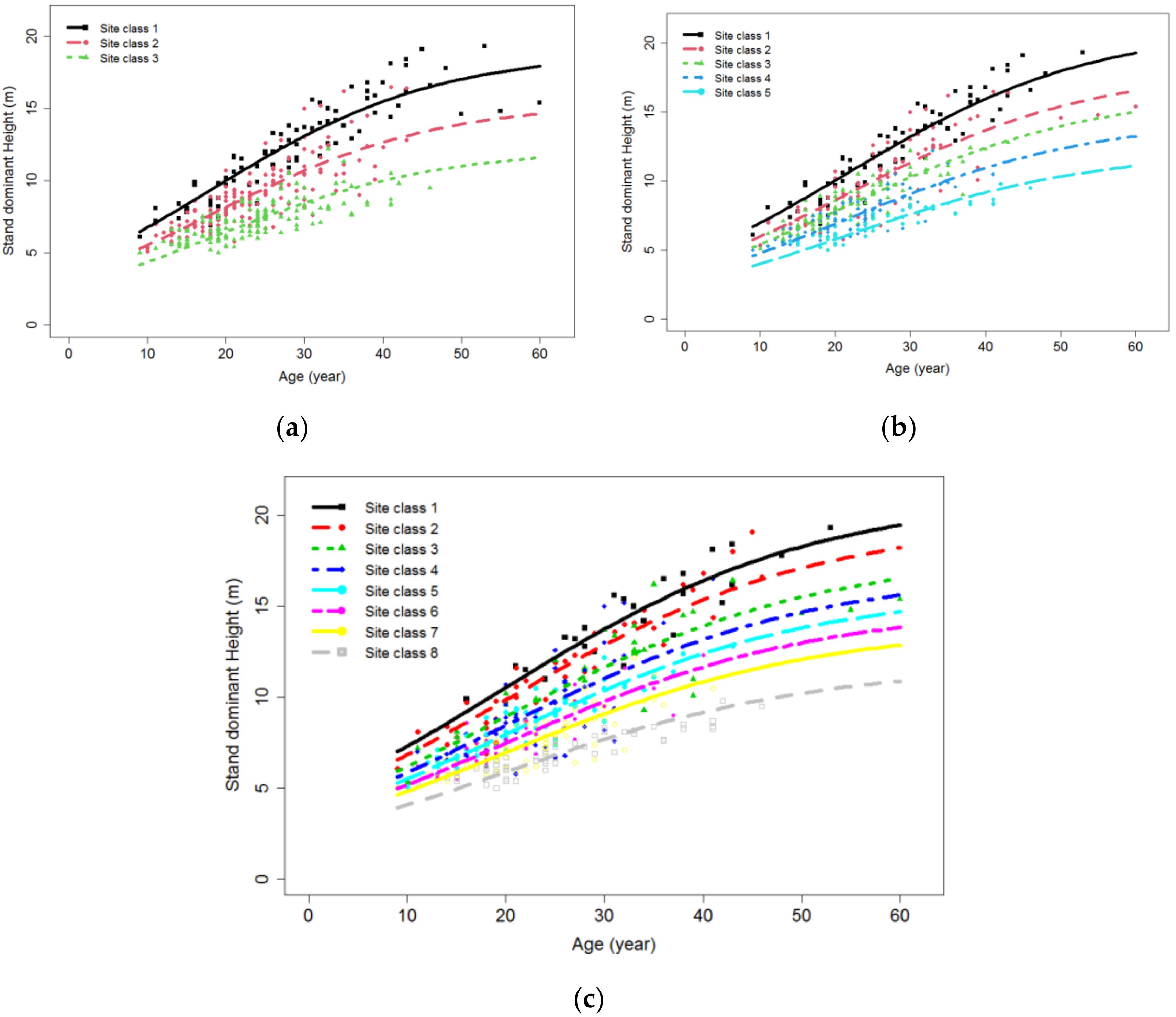
3.3. Site Index Models for Different Site Type Combinations
3.4. Clustering of the Site Types and Model Simulation
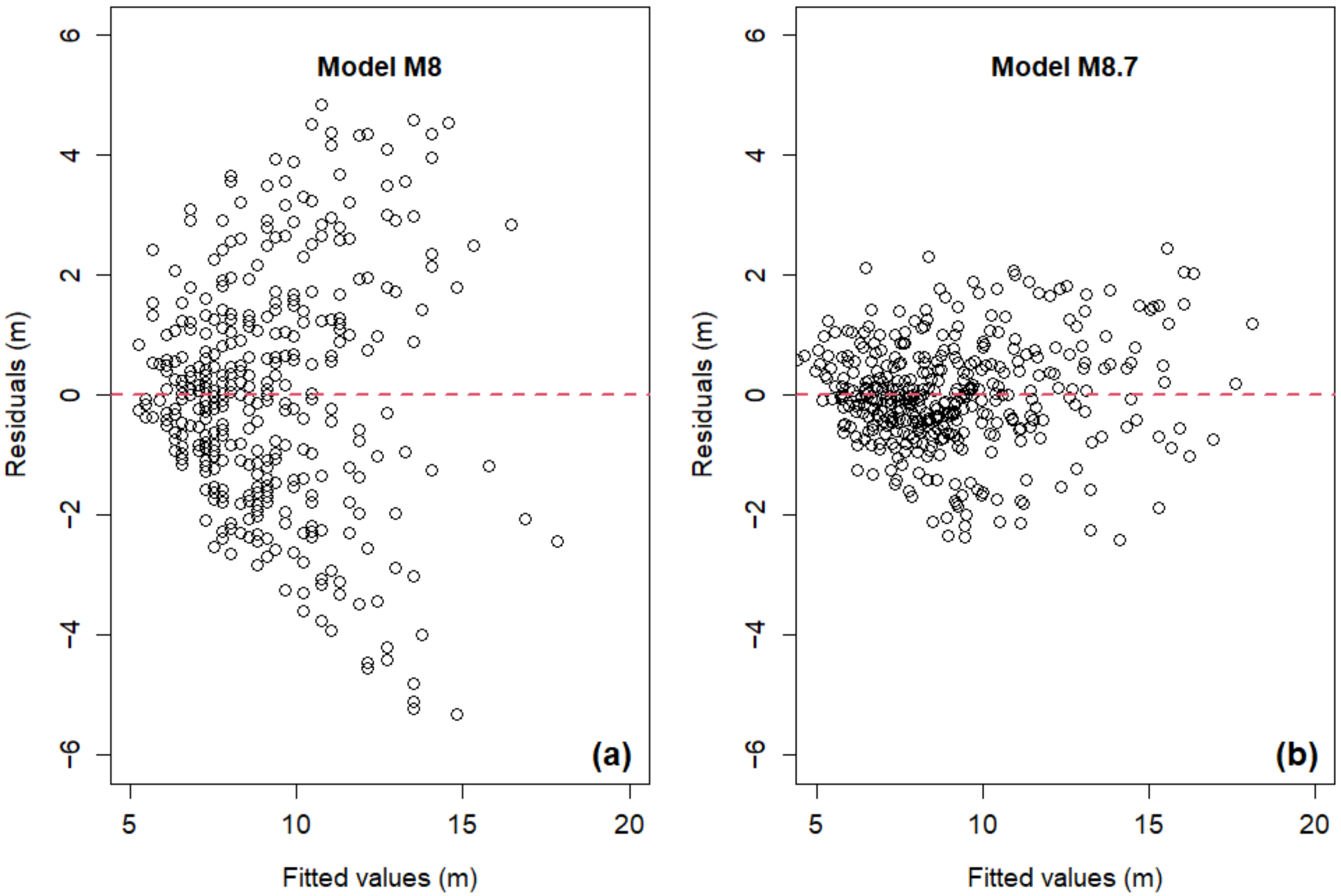
3.5. Evaluation of the Predictive Performance of Mixed Effects Models
4. Discussion
4.1. Dominant Factors of the Site Index
4.2. Site Index Model
4.3. Clustering of the Site Types
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Herrera-fernandez, B.; Campos, J.J.; Kleinn, C. Site productivity estimation using height-diameter relationships in Costa Rican secondary forests. For. Syst. 2004, 13, 295–304. [Google Scholar]
- Liu, X.; Duan, G.; Chhin, S.; Lei, X.; Zhang, X. Evaluation of potential versus realized site productivity of Larix principis-rupprechtii plantations across northern China. For. Ecol. Manag. 2021, 479, 118608. [Google Scholar] [CrossRef]
- Bravo-Oviedo, A.; Tome, M.; Bravo, F.; Montero, G.; Del Rio, M. Dominant height growth equations including site attributes in the generalized algebraic difference approach. Can. J. For. Res. 2008, 38, 2348–2358. [Google Scholar] [CrossRef]
- Westfall, J.A.; Hatfield, M.A.; Sowers, P.A.; O’Connell, B.M. Site index models for tree species in the northeastern United States. For. Sci. 2017, 63, 283–290. [Google Scholar]
- Corona, P. Relationship between environmental factors and site index in douglas-fir plantations in central Italy. For. Ecol. Manag. 1998, 110, 195–207. [Google Scholar] [CrossRef]
- Chen, H.Y.; Krestov, P.V.; Klinka, K. Trembling aspen site index in relation to environmental measures of site quality at two spatial scales. Can. J. For. Res. 2002, 32, 112–119. [Google Scholar] [CrossRef]
- Auten, J. Prediction of site index for yellow poplar from soil and topography. J. For. 1945, 43, 662–668. [Google Scholar]
- Antón-Fernández, C.; Mola-Yudego, B.; Dalsgaard, L.; Astrup, R. Climate-sensitive site index models for Norway. Can. J. For. Res. 2016, 46, 794–803. [Google Scholar] [CrossRef]
- Yue, C.; Kahle, H.P.; Wilpert, K.V.; Kohnle, U. A dynamic environment-sensitive site index model for the prediction of site productivity potential under climate change. Ecol. Model. 2016, 337, 48–62. [Google Scholar] [CrossRef]
- Swenson, J.J.; Waring, R.H.; Fan, W.; Coops, N. Predicting site index with a physiologically based growth model across Oregon, USA. Can. J. For. Res. 2005, 35, 1697–1707. [Google Scholar] [CrossRef] [Green Version]
- Aertsen, W.; Kint, V.; Muys, B.; Orshoven, J. Effects of scale and scaling in predictive modelling of forest site productivity. Environ. Model. Softw. 2012, 31, 19–27. [Google Scholar] [CrossRef] [Green Version]
- Aertsen, W.; Kint, V.; Orshoven, J.V.; Özkan, K.; Muys, B. Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests. Ecol. Model. 2010, 221, 1119–1130. [Google Scholar] [CrossRef]
- Pietrzykowski, M.; Socha, J.; Van Doorn, N.S. Scots pine (Pious sylvestris L.) site index in relation to physieo-chemical and biological properties in reclaimed mine soils. New For. 2015, 46, 247–266. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.; Ozdogan, M.; Zhu, X.; Ye, Z.; Hain, C.; Anderson, M. Comparative assessment of environmental variables and machine learning algorithms for maize yield prediction in the US Midwest. Environ. Res. Lett. 2020, 15, 064005. [Google Scholar] [CrossRef]
- John, K.; Isong, I.A.; Kebonye, N.M.; Ayito, E.O.; Agyeman, P.C.; Afu, S.M. Using Machine Learning Algorithms to Estimate Soil Organic Carbon Variability with Environmental Variables and Soil Nutrient Indicators in an Alluvial Soil. Land 2020, 9, 487. [Google Scholar] [CrossRef]
- Stage, A.R.; Salas, C. Interactions of Elevation, Aspect, and Slope in Models of Forest Species Composition and Productivity. For. Sci. 2007, 53, 486–492. [Google Scholar]
- Zhu, G.; Kang, L.; He, H.; Lv, Y.; Yin, Y.; Wu, Y. Study on polymorphic site index curve model based on height-age classification for Cuninghamia lanceolata plantation. J. Cent. South Univ. For. Sci. Technol. 2017, 7, 18–29. (In Chinese) [Google Scholar]
- Curt, T.; Bouchaud, M.; Agrech, G. Predicting site index of Douglas-fir plantations from ecological variables in the Massif Central area of France. For. Ecol. Manag. 2001, 149, 61–74. [Google Scholar] [CrossRef]
- Jerez-Rico, M.; Moret-Barillas, A.Y.; Carrero-Gamez, O.E.; Macchiavelli, R.E.; Quevedo-Rojas, A.M. Site index curves based on mixed models for teak (Tectona grandis LF) plantations in the Venezuelan plains. Agrociencia 2011, 45, 135–145. [Google Scholar]
- Calegario, N.; Daniels, R.F.; Maestri, R.; Neiva, R. Modeling Dominant Height Growth Based on Nonlinear Mixed-effects Model: A Clonal Eucalyptus Plantation Case Study. For. Ecol. Manag. 2005, 204, 11–21. [Google Scholar] [CrossRef]
- Zhu, G.; Hu, S.; Chhin, S.; Zhang, X.; He, P. Modelling site index of Chinese fir plantations using a random effects model across regional site types in Hunan province, China. For. Ecol. Manag. 2019, 446, 143–150. [Google Scholar] [CrossRef]
- Wang, D.; Hu, X.; Li, D. Creating site index for needle and broadleaved mixed forest using nonlinear mixed effects model. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2020, 44, 159–166. (In Chinese) [Google Scholar]
- Zhang, J.; Meng, D. Spatial pattern analysis of individuals in different age-classes of Larix principis-rupprechtii in Luya mountain reserve, Shanxi, China. Acta Ecol. Sin. 2004, 24, 35–40. (In Chinese) [Google Scholar]
- Liu, X.; Han, W.; Gao, R.; Jia, J.; Bai, J.; Xu, J.; Gao, W. Potential impacts of environmental types on geographical distribution of Larix principis-rupprechtii. Acta Ecol. Sin. 2021, 41, 1885–1893. (In Chinese) [Google Scholar]
- Di, X.; Meng, X.; Wang, M. Range-wide genetic diversity in natural populations of Larix principis-rupprechtii Mayr. J. For. Res. 2020, 32, 319–327. [Google Scholar] [CrossRef]
- Wang, M.; Borders, B.E.; Zhao, D. An empirical comparison of two subject-specific approaches to dominant heights modeling: The dummy variable method and the mixed model method. For. Ecol. Manag. 2008, 255, 2659–2669. [Google Scholar] [CrossRef]
- GB/T 26424-2010; Technical Regulations for Inventory for Forest Management Planning and Design. State Forestry Bureau: Beijing, China, 2010.
- Huang, X.; Ma, C.; Xu, X. Management Technical Procedures for Plantation Forest of Larix Principis-Rupprechtii Mayr; State Forestry Administration (LY/Y 1897–2010): Beijing, China, 2010. [Google Scholar]
- Sabatia, C.O.; Burkhart, H.E. Predicting site index of plantation loblolly pine from biophysical variables. For. Ecol. Manag. 2014, 326, 142–156. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C 1979, 28, 100–108. [Google Scholar]
- Park, B.; Kargupta, H.; Johnson, E.; Sanseverino, E.; Hershberger, D.; Silvestre, L. Distributed, collaborative data analysis from heterogeneous sites using a scalable evolutionary technique. Appl. Intell. 2002, 16, 19–42. [Google Scholar] [CrossRef]
- Fang, Z.; Bailey, R.L. Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments. For. Sci. 2001, 47, 287–300. [Google Scholar]
- Paulo, J.A.; Tomé, J.; Tomé, M. Nonlinear fixed and random generalized height–diameter models for Portuguese cork oak stands. Ann. For. Sci. 2011, 68, 295–309. [Google Scholar] [CrossRef] [Green Version]
- Lindstrom, M.J.; Bates, D.M. Nonlinear mixed effects models for repeated measures data. Biometrics 1990, 46, 673–687. [Google Scholar] [CrossRef] [PubMed]
- Meng, S.X.; Huang, S. Improved calibration of nonlinear mixed effects models demonstrated on a height growth function. For. Sci. 2009, 55, 238–247. [Google Scholar]
- Calama, R.; Montero, G. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain. Can. J. For. Res. 2004, 34, 150–163. [Google Scholar] [CrossRef] [Green Version]
- Subedi, N.; Sharma, M. Individual-tree diameter growth models for black spruce and jack pine plantations in northern Ontario. For. Ecol. Manag. 2011, 261, 2140–2148. [Google Scholar] [CrossRef]
- Tang, S.; Lang, K.; Li, H. Statistics and Computation of Biomathematical Models (ForStat Course); Science Press: Beijing, China, 2009. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 12 October 2021).
- Bontemps, J.D.; Bouriaud, O. Predictive approaches to forest site productivity: Recent trends, challenges and future perspectives. Forestry 2014, 87, 109–128. [Google Scholar] [CrossRef]
- Farrelly, N.; Ní Dhubháin, Á.; Nieuwenhuis, M. Site index of Sitka spruce (Picea sitchensis) in relation to different measures of site quality in Ireland. Can. J. For. Res. 2011, 41, 265–278. [Google Scholar] [CrossRef]
- Pacheco, C. Evaluating site quality of even-aged maritime pine stands in northern Portugal using direct and indirect methods. For. Ecol. Manag. 1991, 41, 193–204. [Google Scholar]
- Holmgren, P. Topographic and geochemical influence on the forest site quality, with respect to Pinus sylvestris and Picea abies in Sweden. Scand. J. For. Res. 1994, 9, 75–82. [Google Scholar] [CrossRef]
- Lv, Z.; Li, W.; Huang, X.; Zhang, Z. Predicting Suitable Distribution Area of Three Dominant Tree Species under Climate Change Scenarios in Hebei Province. Sci. Silvae Sin. 2019, 55, 13–21. (In Chinese) [Google Scholar]
- Seynave, I.; Gégout, J.C.; Hervé, J.C.; DhTe, J.F.; Drapier, J.; Bruno, É. Picea abies site index prediction by environmental factors and understory vegetation, a two-scale approach based on survey databases. Can. J. For. Res. 2005, 35, 1669–1678. [Google Scholar] [CrossRef]
- Socha, J. Effect of topography and geology on the site index of Picea abies in the West Carpathian, Poland. Scand. J. For. Res. 2008, 23, 203–213. [Google Scholar] [CrossRef]
- Roise, J.P.; Betters, D.R. An aspect transformation with regard to elevation and site productivity models. For. Sci. 1981, 27, 483–486. [Google Scholar]
- Fang, J.; Shen, Z.; Cui, H.T. Ecological characteristics of mountains and research issues of mountain ecology. Biodivers. Sci. 2004, 12, 10–19. [Google Scholar]
- Fekedulegna, D.; Hicks, R.R., Jr.; Colberta, J.J. Influence of topographic aspect, precipitation and drought on radial growth of four major tree species in an Appalachian watershed. For. Ecol. Manag. 2003, 177, 409–425. [Google Scholar] [CrossRef]
- Zhang, B.; Tian, J.; Yao, Y.H. Digital Integration and Patterns of Mountain Altitudinal Belts; Environment Science Press: Beijing, China, 2009; pp. 218–224. [Google Scholar]
- Stage, A.R. An expression for the effect of aspect, slope, and habitat type on tree growth. For. Sci. 1976, 22, 457–460. [Google Scholar]
- Li, C.; Li, C.W. The significance of aspect in mountain geography. Acta Geogr. Sin. 1985, 40, 20–28. [Google Scholar]
- Verbyla, D.L.; Fisher, R.F. Effect of aspect on ponderosa height and diameter growth. For. Ecol. Manag. 1989, 27, 93–98. [Google Scholar] [CrossRef]
- Ercanli, I.; Gunlu, A.; Altun, L.; Baskent, E.Z. Relationship between site indexes of oriental spruce [Picea orientalis (L.) Link] and ecological variables in Maçka, Turkey. Scand. J. For. Res. 2008, 23, 319–329. [Google Scholar] [CrossRef]
- Ashton, P.M.S.; Harris, P.G.; Thadani, R. Soil seed bank dynamics in relation to topographic position of a mixed-deciduous forest in southern New England, USA. For. Ecol. Manag. 1998, 111, 15–22. [Google Scholar] [CrossRef]
- Tian, X.; Gao, K.; Zhang, L.J.; Yu, Y.Q.; Han, G.D. Effect of slope position on spatial distribution of soil water and vegetation in sandy land. Bull. Soil Water Conserv. 2015, 35, 12–16. [Google Scholar]
- Wen, Y.; Hu, J.; Yang, X.; Liu, W.; Zhong, L.; Zhu, C.; Ma, J.H. Study of slop position effect on the tree structure characteristic of mixed pobulus dacidiana and Betula platyphylla plantation. J. Agric. Univ. Hebei 2017, 40, 32–38. [Google Scholar]
- Wang, X.; Sun, H.; Yu, X.; Gu, C.C. Influence of aspect and position of slope on the growth of Mid-age fraxinus mandshurica plantation. J. Shanxi Agric. Univ. (Nat. Sci. Ed.) 2011, 31, 30–34. [Google Scholar]
- Paulo, J.A.; Palma, J.N.; Gomes, A.A.; Faias, S.P.; Tome, J.; Tome, M. Predicting site index from climate and soil variables for cork oak (Quercus suber L.) stands in Portugal. New For. 2015, 46, 293–307. [Google Scholar] [CrossRef] [Green Version]
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. Forestry 2008, 81, 13–31. [Google Scholar] [CrossRef] [Green Version]
- Fang, Z.; Bailey, R.L.; Shiver, B.D. A multivariate simultaneous prediction system for stand growth and yield with fixed and random effects. For. Sci. 2001, 47, 550–562. [Google Scholar]
- Brandl, S.; Mette, T.; Falk, W.; Vallet, P.; Rotzer, T.; Pretzsch, H. Static site indices from different national forest inventories: Harmonization and prediction from site conditions. Ann. For. Sci. 2018, 75, 56. [Google Scholar] [CrossRef] [Green Version]
- Guisan, A.; Edwards, T.C. Generalized linear and generalized additive models in studies of species distributions: Setting the scene. Ecol. Model. 2002, 157, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Huang, S. Comparison of different methods for fitting nonlinear mixed forest models and for making predictions. Can. J. For. Res. 2011, 41, 1671–1686. [Google Scholar] [CrossRef]
- Wang, Y.; LeMay, V.M.; Baker, T.G. Modelling and prediction of dominant height and site index of Eucalyptus globulus plantations using a nonlinear mixed-effects model approach. Can. J. For. Res. 2007, 37, 1390–1403. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Hao, K.; Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. For. Ecol. Manag. 2017, 389, 364–373. [Google Scholar] [CrossRef]

| Province | Number of Plot | Index | DBH (cm) | H (m) | Age (Years) | Stand Basal Area (m2/ha) | Stand Density (n/ha) | Elevation (m) | Slope (˚) | Soil Depth (cm) |
|---|---|---|---|---|---|---|---|---|---|---|
| Total | 394 | Mean | 11.2 | 9.1 | 24.7 | 10.5 | 1009.7 | 1467.5 | 15.4 | 52.2 |
| STD | 3.9 | 2.9 | 8.5 | 8.0 | 598.0 | 395.2 | 8.6 | 13.4 | ||
| Min | 5.5 | 5.0 | 9.0 | 0.3 | 90.0 | 690.0 | 0.0 | 20.0 | ||
| Max | 24.2 | 19.3 | 60.0 | 38.5 | 2970.0 | 2383.0 | 39.0 | 100.0 | ||
| Beijing | 30 | Mean | 12.9 | 10.7 | 29.2 | 11.1 | 703.0 | 1075.0 | 18.0 | 40.4 |
| STD | 3.7 | 3.8 | 9.9 | 11.4 | 453.7 | 334.8 | 7.5 | 12.7 | ||
| Min | 7.5 | 6.0 | 13.0 | 0.9 | 150.0 | 740.0 | 8.0 | 20.0 | ||
| Max | 21.5 | 19.3 | 53.0 | 37.6 | 1710.0 | 1890.0 | 30.0 | 61.0 | ||
| Hebei | 225 | Mean | 11.2 | 8.9 | 24.3 | 10.3 | 1005.0 | 1350.0 | 13.9 | 50.4 |
| STD | 4.1 | 2.9 | 8.1 | 7.6 | 580.1 | 312.6 | 8.9 | 15.7 | ||
| Min | 5.5 | 5.0 | 9.0 | 0.3 | 90.0 | 690.0 | 0.0 | 20.0 | ||
| Max | 24.2 | 18.4 | 46.0 | 32.2 | 2970.0 | 2120.0 | 35.0 | 100.0 | ||
| Inner Mongolia | 44 | Mean | 11.5 | 9.0 | 24.0 | 9.2 | 811.4 | 1398.0 | 10.8 | 58.0 |
| STD | 4.4 | 3.3 | 7.8 | 7.0 | 572.0 | 326.5 | 5.7 | 8.3 | ||
| Min | 5.6 | 5.0 | 10.0 | 0.3 | 120.0 | 970.0 | 3.0 | 30.0 | ||
| Max | 23.7 | 18.0 | 43.0 | 25.5 | 1980.0 | 1890.0 | 25.0 | 65.0 | ||
| Shanxi | 95 | Mean | 10.7 | 8.9 | 24.6 | 11.5 | 1209.5 | 1901.9 | 20.4 | 57.3 |
| STD | 2.8 | 2.3 | 8.9 | 8.0 | 625.4 | 248.0 | 6.8 | 19.3 | ||
| Min | 5.9 | 5.4 | 10.0 | 1.6 | 315.0 | 1480.0 | 2.0 | 20.0 | ||
| Max | 19.4 | 15.4 | 60.0 | 38.5 | 2940.0 | 2383.0 | 39.0 | 100.0 |
| Site Factors | Class | |||||
|---|---|---|---|---|---|---|
| EL | 9 classes by 200 m | |||||
| SL | <5° | 5°–14° | 15°–24° | 25°–34° | ≥35° | |
| AS | sunny slope | semi-sunny slope | shady slope | semi-shady slope | ||
| SP | ridge | upper slope | middle slope | lower slope | valley | flat |
| ST | red earth | yellow earth | yellow-brown earth | |||
| SD | <40 cm | 40–79 cm | ≥80 cm | |||
| Model | Equation Form | Expression |
|---|---|---|
| M1 | Hyperbolic model | |
| M2 | Logarithm model | |
| M3 | Schumacher model | |
| M4 | Mitscherlich model | |
| M5 | Parabola model | |
| M6 | Hybrid model | |
| M7 | Roляcp model | |
| M8 | Logistic model | |
| M9 | Gompertz model |
| Model | a | SE | b | SE | c | SE | MAE | RMSE | R² | TRE |
|---|---|---|---|---|---|---|---|---|---|---|
| M1 | 14.5604 * | 0.3315 | 120.6185 * | 6.8689 | 0.0000 | 2.1950 | 0.4403 | 5.5940 | ||
| M2 | −10.6986 * | 0.9405 | 6.2788 * | 0.2969 | 0.0000 | 2.0052 | 0.5329 | 4.6258 | ||
| M3 | 19.2622 * | 0.6963 | 17.4203 * | 0.8932 | 0.0336 | 2.0398 | 0.5166 | 4.7943 | ||
| M4 | 23.7941 * | 2.575 | 0.0199 * | 0.00289 | 0.0358 | 1.9474 | 0.5594 | 4.3514 | ||
| M5 | 2.9270 * | 0.7223 | 0.2357 * | 0.0535 | 0.0005 | 0.0009 | 0.0000 | 1.9149 | 0.5740 | 4.2012 |
| M6 | 2.5575 * | 0.3204 | 0.1498 | 0.1405 | 1.2003 * | 0.3868 | 0.0002 | 1.9144 | 0.5743 | 4.1987 |
| M7 | 1.5986 * | 0.5343 | 0.4704 * | 0.1432 | −0.0092 | 0.0050 | 0.0011 | 1.9191 | 0.5721 | 4.2205 |
| M8 | 22.2896 * | 3.5595 | 5.1001 * | 0.6161 | 0.0503 * | 0.0074 | 0.0021 | 1.9076 | 0.5773 | 4.1678 |
| M9 | 31.3098 * | 10.3487 | 2.2316 * | 0.2275 | 0.0237 * | 0.0071 | 0.0015 | 1.9109 | 0.5758 | 4.1828 |
| Model | Random Effect | RP | Levels | a | b | c | AIC | BIC | Log-Likelihood | R² |
|---|---|---|---|---|---|---|---|---|---|---|
| M8 | None | 22.2896 | 5.1001 | 0.0503 | 1635.0423 | 1650.9477 | −813.5212 | 0.5773 | ||
| M8.1 | EL | a | 9 | 19.6303 | 4.3670 | 0.0521 | 1585.2894 | 1605.1712 | −787.6447 | 0.6542 |
| M8.2 | AS | a | 9 | 21.6037 | 4.8867 | 0.0514 | 1628.4907 | 1648.3725 | −809.2454 | 0.6005 |
| M8.3 | SL | a | 6 | 20.1798 | 4.3664 | 0.0516 | 1617.8581 | 1637.7399 | −803.9291 | 0.6132 |
| M8.4 | EL × AS | a | 56 | 15.8473 | 3.8550 | 0.0676 | 1554.6373 | 1574.5191 | −772.3187 | 0.7517 |
| M8.5 | EL × SL | a | 33 | 15.9739 | 3.8222 | 0.0652 | 1538.0907 | 1557.9725 | −764.0454 | 0.7356 |
| M8.6 | SL × AS | a | 31 | 17.4115 | 4.2344 | 0.0609 | 1607.7826 | 1627.6644 | −798.8913 | 0.6520 |
| M8.7 | EL × AS × SL | a | 94 | 14.1784 | 3.6668 | 0.0760 | 1438.9924 | 1458.8742 | −714.4962 | 0.8678 |
| Groups | Site Type Group | Sample Size (# of Plots) | Number of Site Types |
|---|---|---|---|
| 3 | STG1 | 79 | 17 |
| STG2 | 181 | 42 | |
| STG3 | 134 | 35 | |
| 5 | STG1 | 65 | 13 |
| STG2 | 85 | 17 | |
| STG3 | 108 | 28 | |
| STG4 | 86 | 21 | |
| STG5 | 50 | 15 | |
| 8 | STG1 | 33 | 6 |
| STG2 | 46 | 11 | |
| STG3 | 74 | 14 | |
| STG4 | 76 | 20 | |
| STG5 | 42 | 11 | |
| STG6 | 65 | 15 | |
| STG7 | 30 | 10 | |
| STG8 | 28 | 7 |
| Random Effect | a | b | c | AIC | BIC | Log-Likelihood | R² |
|---|---|---|---|---|---|---|---|
| M8.7-with 3 groups | 15.5084 | 3.5906 | 0.0698 | 1290.0387 | 1309.9212 | −640.0194 | 0.8333 |
| M8.7-with 5 groups | 16.4753 | 3.7311 | 0.0610 | 1228.1468 | 1248.0288 | −609.0737 | 0.8616 |
| M8.7-with 8 groups | 15.3467 | 3.4925 | 0.0649 | 1223.2336 | 1243.1153 | −606.6168 | 0.8683 |
| Prediction | Sub-Sampling Methods | M8.7-with 3 Groups | M8.7-with 5 Groups | M8.7-with 8 Groups | |||
|---|---|---|---|---|---|---|---|
| RMSE | R² | RMSE | R² | RMSE | R² | ||
| M response | none | 2.6148 | 0.2057 | 2.3180 | 0.3758 | 2.1774 | 0.4492 |
| S response | Highest | 1.4755 | 0.7471 | 1.2830 | 0.8088 | 1.3417 | 0.7909 |
| Lowest | 1.6341 | 0.6898 | 1.5681 | 0.7143 | 1.3969 | 0.7733 | |
| Random | 1.2597 | 0.8157 | 1.1498 | 0.8464 | 1.1444 | 0.8479 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, G.; Lei, X.; Zhang, X.; Liu, X. Site Index Modeling of Larch Using a Mixed-Effects Model across Regional Site Types in Northern China. Forests 2022, 13, 815. https://doi.org/10.3390/f13050815
Duan G, Lei X, Zhang X, Liu X. Site Index Modeling of Larch Using a Mixed-Effects Model across Regional Site Types in Northern China. Forests. 2022; 13(5):815. https://doi.org/10.3390/f13050815
Chicago/Turabian StyleDuan, Guangshuang, Xiangdong Lei, Xiongqing Zhang, and Xianzhao Liu. 2022. "Site Index Modeling of Larch Using a Mixed-Effects Model across Regional Site Types in Northern China" Forests 13, no. 5: 815. https://doi.org/10.3390/f13050815
APA StyleDuan, G., Lei, X., Zhang, X., & Liu, X. (2022). Site Index Modeling of Larch Using a Mixed-Effects Model across Regional Site Types in Northern China. Forests, 13(5), 815. https://doi.org/10.3390/f13050815







