Tracheidogram’s Classification as a New Potential Proxy in High-Resolution Dendroclimatic Reconstructions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Climate Data
2.3. Sample Collection, Measurement and Tree-Ring Data Processing
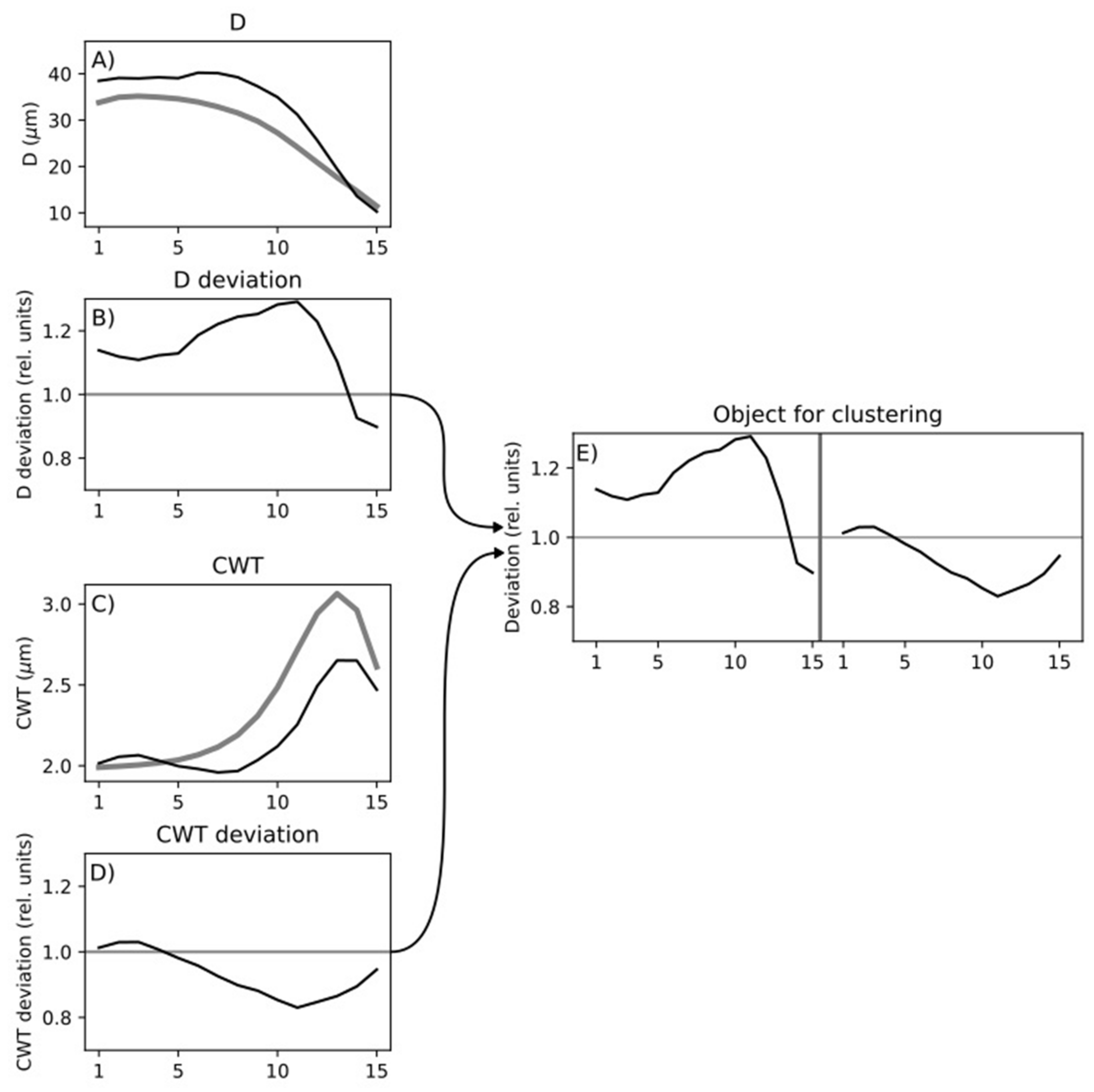
2.4. Cell Data Processing
2.5. Statistical Analysis of Tracheidograms
3. Results
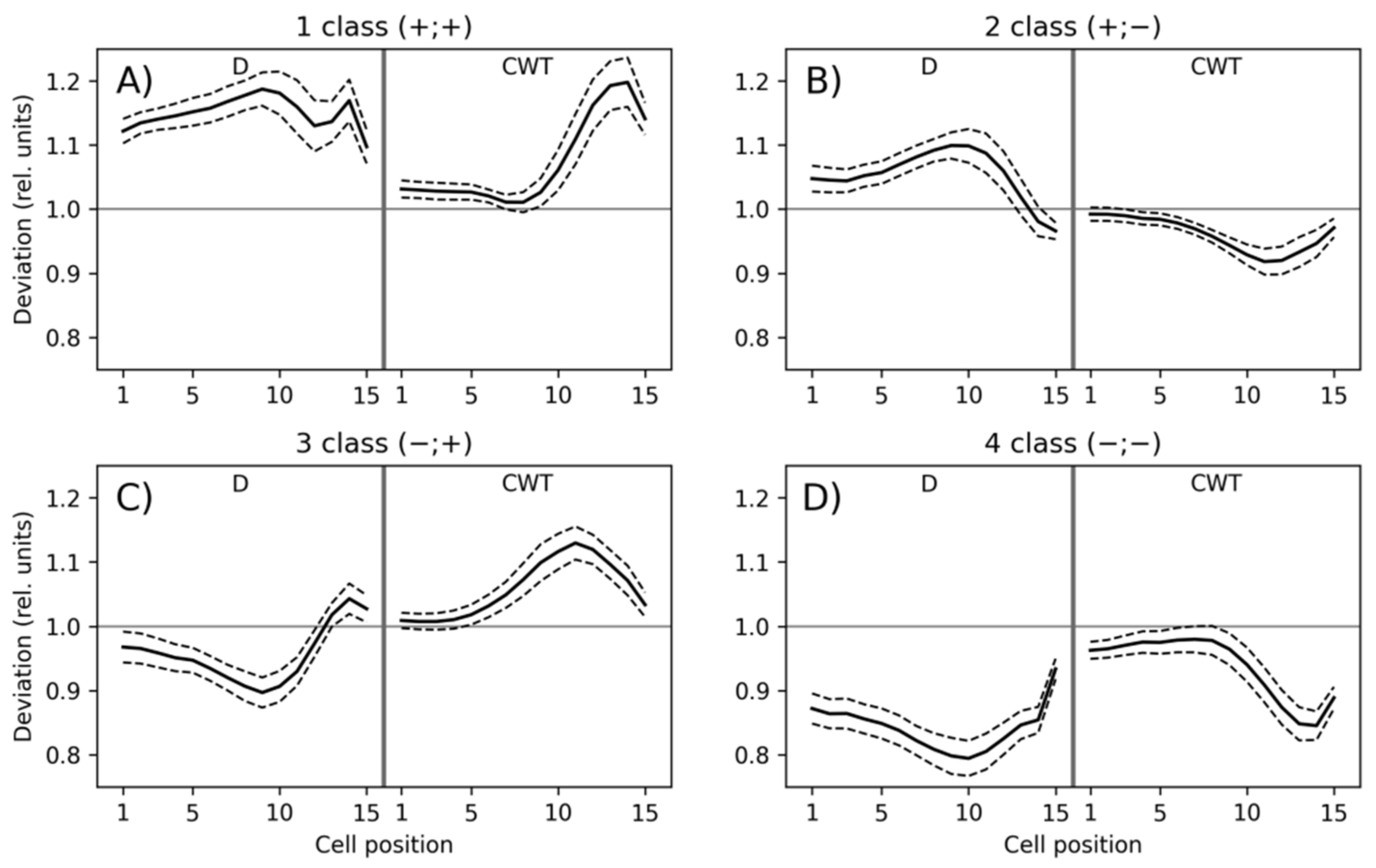
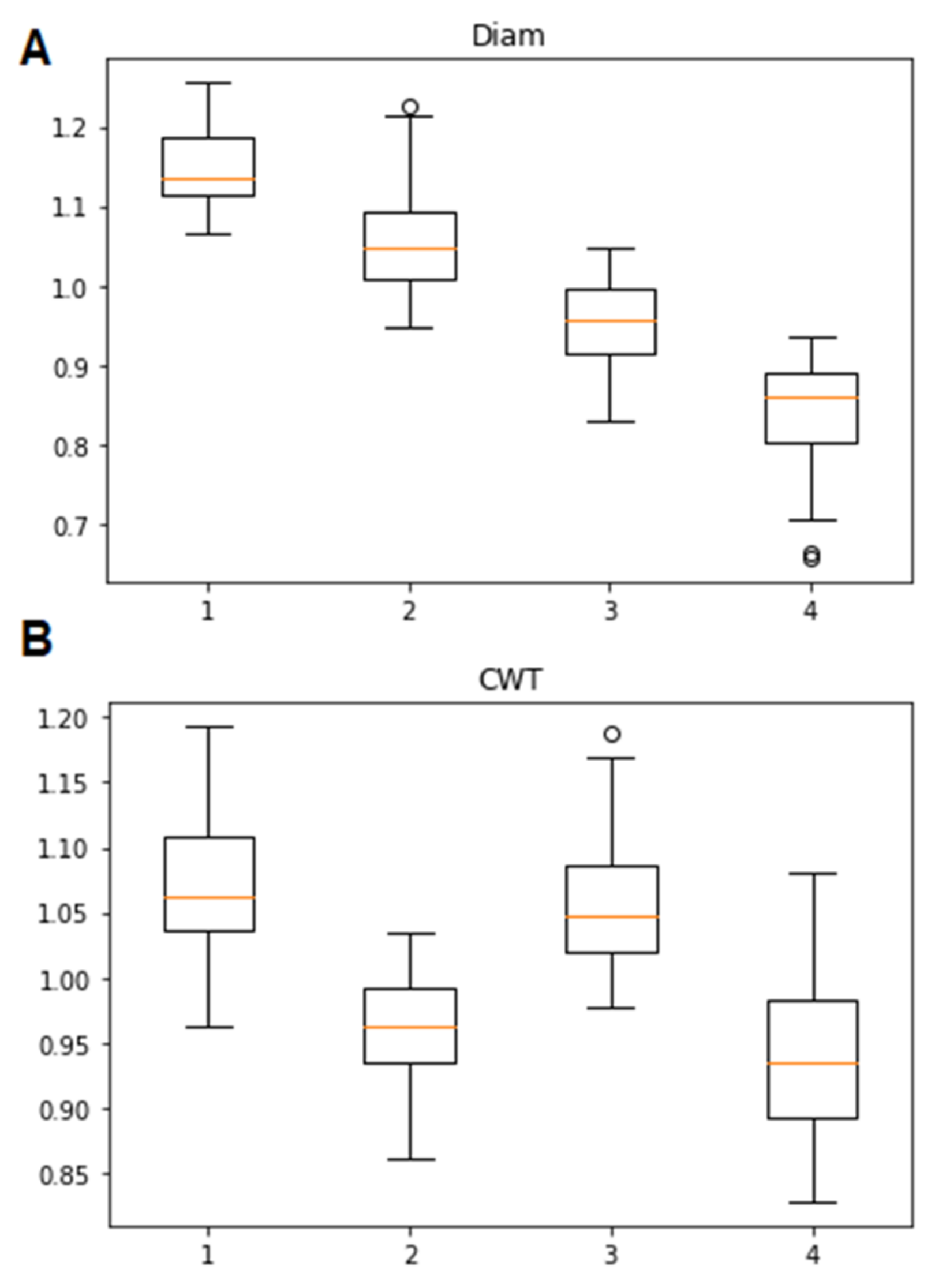
3.1. Classification of Tracheidograms
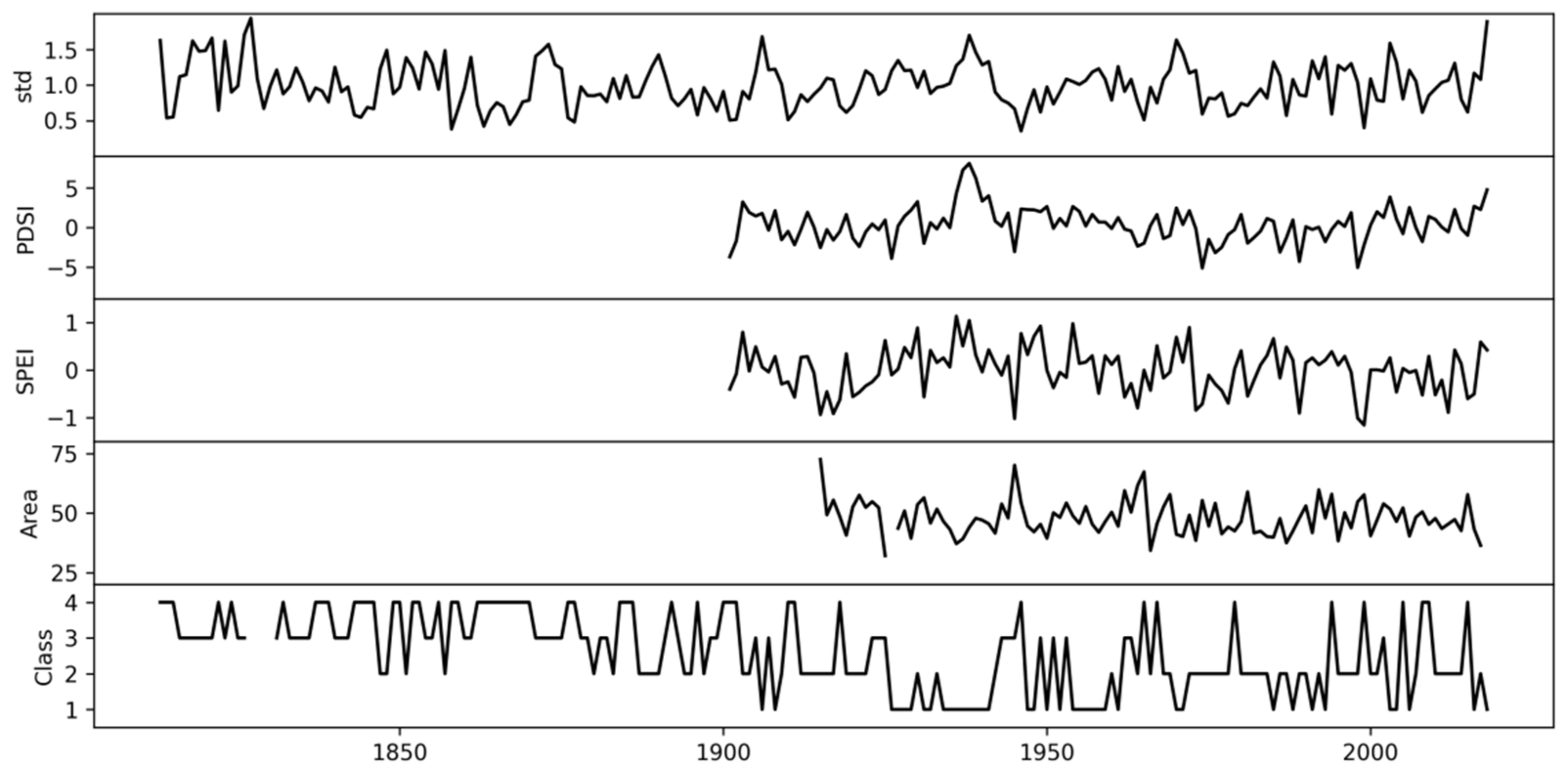
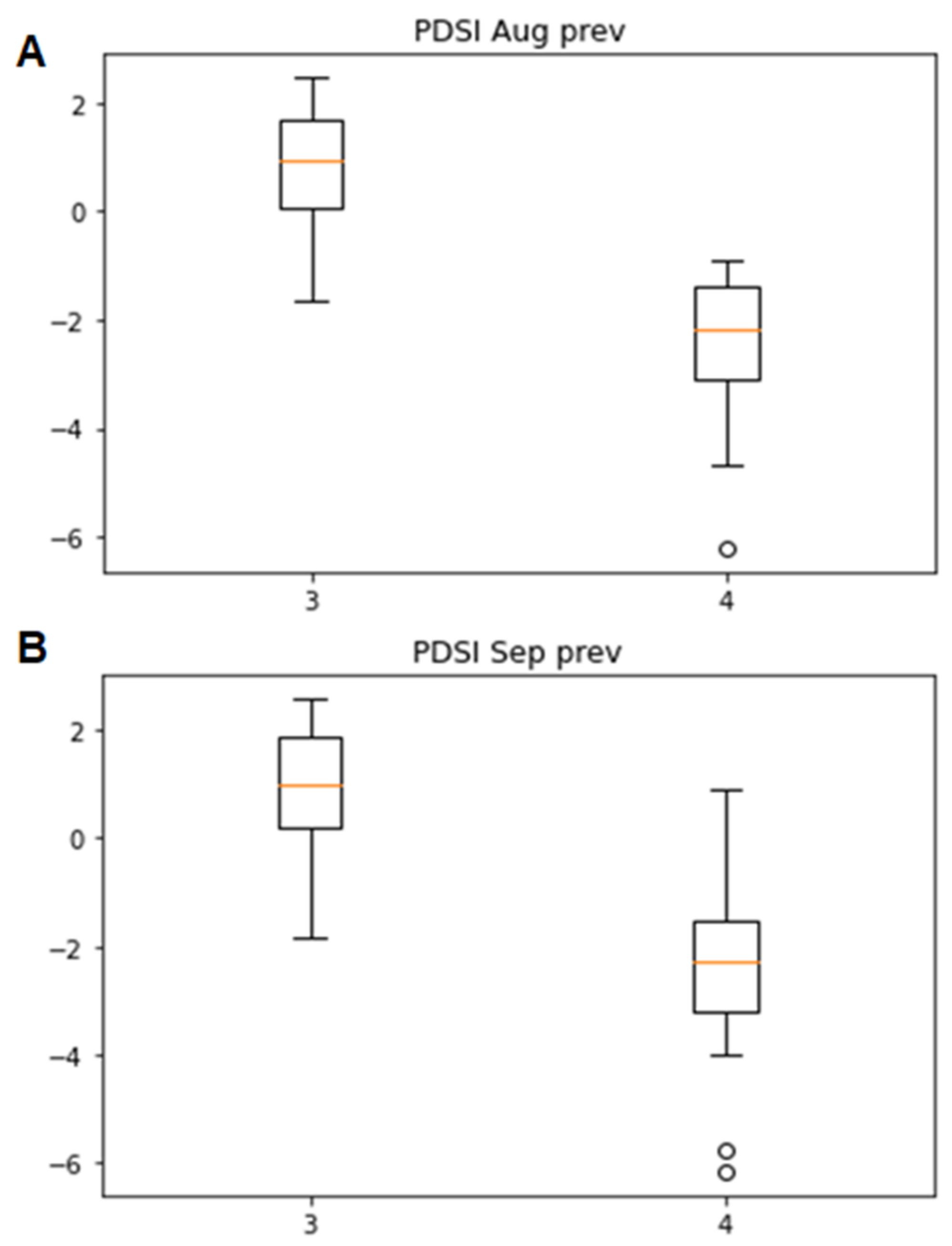
3.2. Associations of the Tracheidogram Clusters with Climate Peculiarities
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holmes, C.D. Air pollution and forest water use. Nature 2014, E1–E2. [Google Scholar] [CrossRef] [PubMed]
- Mayor, J.R.; Sanders, N.J.; Classen, A.T.; Bardgett, R.D.; Clément, J.C.; Fajardo, A.; Lavorel, S.; Sundqvist, M.K.; Bahn, M.; Chisholm, C.; et al. Elevation alters ecosystem properties across temperate treelines globally. Nature 2017, 542, 91–95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, T.; Niinemets, Ü.; Sheffield, J.; Lichstein, J.W. Shifts in tree functional composition amplify the response of forest biomass to climate. Nature 2018, 556, 99–102. [Google Scholar] [CrossRef] [PubMed]
- Choat, B.; Jansen, S.; Brodribb, T.J.; Cochard, H.; Delzon, S.; Bhaskar, R.; Bucci, S.J.; Feild, T.S.; Gleason, S.M.; Hacke, U.G.; et al. Global convergence in the vulnerability of forests to drought. Nature 2012, 491, 752–755. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, Y.H.; Zhao, H.; Piao, S.; Peaucelle, M.; Peng, S.; Zhou, G.; Ciais, P.; Huang, M.; Menzel, A.; Peñuelas, J.; et al. Declining global warming effects on the phenology of spring leaf unfolding. Nature 2015, 526, 104–107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, J.; Yang, B.; He, M.; Shishov, V. Intra-annual stem radial increment patterns of Chinese pine, Helan Mountains, Northern Central China. Trees-Struct. Funct. 2019, 33, 751–763. [Google Scholar] [CrossRef]
- He, M.; Yang, B.; Shishov, V.; Rossi, S.; Bräuning, A.; Ljungqvist, F.C.; Grießinger, J. Projections for the changes in growing season length of tree-ring formation on the Tibetan Plateau based on CMIP5 model simulations. Int. J. Biometeorol. 2018, 62, 631–641. [Google Scholar] [CrossRef] [Green Version]
- Kirdyanov, A.V.; Krusic, P.J.; Shishov, V.V.; Vaganov, E.A.; Fertikov, A.I.; Myglan, V.S.; Barinov, V.V.; Browse, J.; Esper, J.; Ilyin, V.A.; et al. Ecological and conceptual consequences of Arctic pollution. Ecol. Lett. 2020, 23, 1827–1837. [Google Scholar] [CrossRef]
- Reich, P.B.; Sendall, K.M.; Stefanski, A.; Wei, X.; Rich, R.L.; Montgomery, R.A. Boreal and temperate trees show strong acclimation of respiration to warming. Nature 2016, 531, 633–636. [Google Scholar] [CrossRef]
- Yang, B.; He, M.; Shishov, V.; Tychkov, I.; Vaganov, E.; Rossi, S.; Ljungqvist, F.C.; Bräuning, A.; Grießinger, J. New perspective on spring vegetation phenology and global climate change based on Tibetan Plateau tree-ring data. Proc. Natl. Acad. Sci. USA 2017, 114, 6966–6971. [Google Scholar] [CrossRef] [Green Version]
- Fonti, P.; Jansen, S. Xylem plasticity in response to climate. New Phytol. 2012, 195, 734–736. [Google Scholar] [CrossRef]
- Li, X.; Liang, E.; Gričar, J.; Rossi, S.; Čufar, K.; Ellison, A.M. Critical minimum temperature limits xylogenesis and maintains treelines on the southeastern Tibetan Plateau. Sci. Bull. 2017, 62, 804–812. [Google Scholar] [CrossRef] [Green Version]
- Rossi, S.; Anfodillo, T.; Cufar, K.; Cuny, H.E.; Deslauriers, A.; Fonti, P.; Frank, D.; Gricar, J.; Gruber, A.; King, G.M.; et al. A meta-analysis of cambium phenology and growth: Linear and non-linear patterns in conifers of the northern hemisphere. Ann. Bot. 2013, 112, 1911–1920. [Google Scholar] [CrossRef]
- Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth Dynamics of Conifer Tree Rings: Images of Past and Future Environments; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Schweingruber, F.H. Trees and Wood in Dendrochronology; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1993. [Google Scholar]
- Huang, J.G.; Deslauriers, A.; Rossi, S. Xylem formation can be modeled statistically as a function of primary growth and cambium activity. New Phytol. 2014, 203, 831–841. [Google Scholar] [CrossRef]
- Rossi, S.; Morin, H.; Deslauriers, A. Causes and correlations in cambium phenology: Towards an integrated framework of xylogenesis. J. Exp. Bot. 2012, 63, 2117–2126. [Google Scholar] [CrossRef] [Green Version]
- Ziaco, E. A phenology-based approach to the analysis of conifers intra-annual xylem anatomy in water-limited environments. Dendrochronologia 2020, 59, 125662. [Google Scholar] [CrossRef]
- Cuny, H.E.; Rathgeber, C.B.K.; Frank, D.; Fonti, P.; Fournier, M. Kinetics of tracheid development explain conifer tree-ring structure. New Phytol. 2014, 203, 1231–1241. [Google Scholar] [CrossRef]
- Cuny, H.E.; Rathgeber, C.B.K. Xylogenesis: Coniferous trees of temperate forests are listening to the climate tale during the growing season but only remember the last words! Plant Physiol. 2016, 171, 306–317. [Google Scholar] [CrossRef] [Green Version]
- Shishov, V.V.; Tychkov, I.I.; Anchukaitis, K.J.; Zelenov, G.K.; Vaganov, E.A. A band model of cambium development: Opportunities and prospects. Forests 2021, 12, 1361. [Google Scholar] [CrossRef]
- Ziaco, E.; Biondi, F.; Rossi, S.; Deslauriers, A. Intra-annual wood anatomical features of high-elevation conifers in the Great Basin, USA. Dendrochronologia 2014, 32, 303–312. [Google Scholar] [CrossRef]
- Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Kluwer Acad. Publ.: Dordrecht, The Netherlands, 1990; ISBN 0792305868. [Google Scholar]
- Ziaco, E.; Biondi, F.; Rossi, S.; Deslauriers, A. Environmental drivers of cambial phenology in Great Basin bristlecone pine. Tree Physiol. 2016, 36, 818–831. [Google Scholar] [CrossRef] [Green Version]
- Belokopytova, L.V.; Babushkina, E.A.; Zhirnova, D.F.; Panyushkina, I.P.; Vaganov, E.A. Pine and larch tracheids capture seasonal variations of climatic signal at moisture-limited sites. Trees-Struct. Funct. 2019, 33, 227–242. [Google Scholar] [CrossRef] [Green Version]
- Popkova, M.I.; Vaganov, E.A.; Shishov, V.V.; Babushkina, E.A.; Rossi, S.; Fonti, M.V.; Fonti, P. Modeled tracheidograms disclose drought influence on Pinus sylvestris tree-rings structure from Siberian forest-steppe. Front. Plant Sci. 2018, 9, 1144. [Google Scholar] [CrossRef] [PubMed]
- Popkova, M.I.; Shishov, V.V.; Vaganov, E.A.; Fonti, M.V.; Kirdyanov, A.V.; Babushkina, E.A.; Huang, J.G.; Rossi, S. Contribution of xylem anatomy to tree-ring width of two larch species in permafrost and non-permafrost zones of Siberia. Forests 2020, 11, 1343. [Google Scholar] [CrossRef]
- Tumajer, J.; Shishov, V.V.; Ilyin, V.A.; Camarero, J.J. Intra-annual growth dynamics of Mediterranean pines and junipers determines their climatic adaptability. Agric. For. Meteorol. 2021, 311, 108685. [Google Scholar] [CrossRef]
- Tumajer, J.; Kašpar, J.; Kuželová, H.; Shishov, V.V.; Tychkov, I.I.; Popkova, M.I.; Vaganov, E.A.; Treml, V. Forward modeling reveals multidecadal trends in cambial kinetics and phenology at treeline. Front. Plant Sci. 2021, 12, 32. [Google Scholar] [CrossRef] [PubMed]
- Ziaco, E.; Liang, E. New perspectives on sub-seasonal xylem anatomical responses to climatic variability. Trees-Struct. Funct. 2019, 33, 973–975. [Google Scholar] [CrossRef] [Green Version]
- Babushkina, E.A.; Dergunov, D.R.; Belokopytova, L.V.; Zhirnova, D.F.; Upadhyay, K.K.; Tripathi, S.K.; Zharkov, M.S.; Vaganov, E.A. Non-linear response to cell number revealed and eliminated from long-term tracheid measurements of Scots pine in Southern Siberia. Front. Plant Sci. 2021, 12, 719796. [Google Scholar] [CrossRef]
- He, M.; Yang, B.; Shishov, V.; Rossi, S.; Bräuning, A.; Ljungqvist, F.C.; Grießinger, J. Relationships between wood formation and cambium phenology on the Tibetan plateau during 1960–2014. Forests 2018, 9, 86. [Google Scholar] [CrossRef] [Green Version]
- Arzac, A.; Popkova, M.; Anarbekova, A.; Olano, J.M.; Gutiérrez, E.; Nikolaev, A.; Shishov, V. Increasing radial and latewood growth rates of Larix cajanderi Mayr. and Pinus sylvestris L. in the continuous permafrost zone in Central Yakutia (Russia). Ann. For. Sci. 2019, 76, 96. [Google Scholar] [CrossRef] [Green Version]
- Belokopytova, L.V.; Babushkina, E.A.; Zhirnova, D.F.; Panyushkina, I.P.; Vaganov, E.A. Climatic response of conifer radial growth in forest-steppes of South Siberia: Comparison of three approaches. Contemp. Probl. Ecol. 2018, 11, 366–376. [Google Scholar] [CrossRef] [Green Version]
- Martin-Benito, D.; Anchukaitis, K.J.; Evans, M.N.; del Río, M.; Beeckman, H.; Cañellas, I. Effects of drought on xylem anatomy and water-use efficiency of two co-occurring pine species. Forests 2017, 8, 332. [Google Scholar] [CrossRef] [Green Version]
- Olano, J.; Eugenio, M.; García-Cervigón, A.I.; Folch, M.; Rozas, V. Quantitative tracheid anatomy reveals a complex environmental control of wood structure in continental Mediterranean climate. Int. J. Plant Sci. 2012, 173, 137–149. [Google Scholar] [CrossRef] [Green Version]
- Panyushkina, I.P.; Hughes, M.K.; Vaganov, E.A.; Munro, M.A.R. Summer temperature in northeastern Siberia since 1642 reconstructed from tracheid dimensions and cell numbers of Larix cajanderi. Can. J. For. Res. 2003, 33, 1905–1914. [Google Scholar] [CrossRef]
- Babushkina, E.A.; Vaganov, E.A.; Belokopytova, L.V.; Shishov, V.V.; Grachev, A.M. Competitive strength effect in the climate response of Scots pine radial growth in South-Central Siberia forest-steppe. Tree-Ring Res. 2015, 71, 106–117. [Google Scholar] [CrossRef]
- Alisov, B.P. Climate of the USSR; Moscow State University (MGU): Moscow, Russia, 1956. [Google Scholar]
- Shah, S.K.; Touchan, R.; Babushkina, E.; Shishov, V.V.; Meko, D.M.; Abramenko, O.V.; Belokopytova, L.V.; Hordo, M.; Jevšenak, J.; Kędziora, W.; et al. August to July precipitation from tree rings in the forest-steppe zone of Central Siberia (Russia). Tree-Ring Res. 2015, 71, 37–44. [Google Scholar] [CrossRef]
- Albon, C. Machine Learning with Python Cookbook; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018. [Google Scholar]
- Dai, A.; Trenberth, K.E.; Qian, T. A global dataset of Palmer Drought Severity Index for 1870-2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
- Grus, J. Data Science from Scratch: First Principles with Python; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2015. [Google Scholar]
- Cook, E.R.; Krusic, P.J. Program ARSTAN: A Tree-Ring Standardization Program Based on Detrending and Autoregressive Time Series Modeling, with Interactive Graphics; Lamont-Doherty Earth Observatory, Columbia University: Palisades, NY, USA, 2005. [Google Scholar]
- Mencuccini, M.; Grace, J.; Fioravanti, M. Biomechanical and hydraulic determinants of tree structure in Scots pine: Anatomical characteristics. Tree Physiol. 1997, 17, 105–113. [Google Scholar] [CrossRef]
- Dyachuk, P.; Arzac, A.; Peresunko, P.; Videnin, S.; Ilyin, V.; Assaulianov, R.; Babushkina, E.A.; Zhirnova, D.; Belokopytova, L.; Vaganov, E.A.; et al. AutoCellRow (ACR)—A new tool for the automatic quantification of cell radial files in conifer images. Dendrochronologia 2020, 60, 125687. [Google Scholar] [CrossRef]
- Larson, P.R. The Vascular Cambium: Development and Structure; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Seo, J.W.; Smiljanić, M.; Wilmking, M. Optimizing cell-anatomical chronologies of Scots pine by stepwise increasing the number of radial tracheid rows included-Case study based on three Scandinavian sites. Dendrochronologia 2014, 32, 205–209. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley Pub. Co.: Reading, MA, USA, 1977. [Google Scholar]
- Rathgeber, C.B.K.; Cuny, H.E.; Fonti, P. Biological basis of tree-ring formation: A crash course. Front. Plant Sci. 2016, 7, 734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhirnova, D.F.; Babushkina, E.A.; Belokopytova, L.V.; Vaganov, E.A. To which side are the scales swinging? Growth stability of Siberian larch under permanent moisture deficit with periodic droughts. For. Ecol. Manag. 2020, 459, 117841. [Google Scholar] [CrossRef]
- Fonti, P.; Babushkina, E.A. Tracheid anatomical responses to climate in a forest-steppe in Southern Siberia. Dendrochronologia 2016, 39, 32–41. [Google Scholar] [CrossRef]
- Shishov, V.V.; Kirdyanov, A.V. The reconstruction of growth season temperature characteristics with tree-ring cell measurements based on the methods of classification theory. Environ. Monit. Ecosyst. Model. Chall. 2003, 19, 200–216. (In Russian) [Google Scholar]
- Castagneri, D.; Vacchiano, G.; Hacket-Pain, A.; DeRose, R.J.; Klein, T.; Bottero, A. Meta-analysis reveals different competition effects on tree growth resistance and resilience to drought. Ecosystems 2022, 25, 30–43. [Google Scholar] [CrossRef]
- Kirdyanov, A.V.; Vaganov, E.A.; Hughes, M.K. Separating the climatic signal from tree-ring width and maximum latewood density records. Trees-Struct. Funct. 2007, 21, 37–44. [Google Scholar] [CrossRef]
- Vaganov, E.A.; Babushkina, E.A.; Belokopytova, L.V.; Zhirnova, D.F. Small fluctuations in cell wall thickness in pine and spruce xylem: Signal from cambium? PLoS ONE 2020, 15, e0233106. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: Synthesis Report; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- IPCC. Climate Change 2014: Synthesis Report; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]


| D | Spearman | p-Value | CWT | Spearman | p-Value |
|---|---|---|---|---|---|
| D1 | 0.9972 | 2.0 × 10−227 | CWT1 | 0.9906 | 6.9 × 10−175 |
| D2 | 0.9983 | 4.1 × 10−248 | CWT2 | 0.9918 | 1.7 × 10−180 |
| D3 | 0.9987 | 7.0 × 10−262 | CWT3 | 0.9917 | 5.3 × 10−180 |
| D4 | 0.9990 | 3.6 × 10−273 | CWT4 | 0.9901 | 2.1 × 10−172 |
| D5 | 0.9991 | 1.4 × 10−275 | CWT5 | 0.9883 | 2.5 × 10−165 |
| D6 | 0.9990 | 8.0 × 10−272 | CWT6 | 0.9893 | 4.1 × 10−169 |
| D7 | 0.9986 | 2.3 × 10−257 | CWT7 | 0.9878 | 1.5 × 10−163 |
| D8 | 0.9985 | 2.4 × 10−253 | CWT8 | 0.9894 | 1.3 × 10−169 |
| D9 | 0.9968 | 3.8 × 10−221 | CWT9 | 0.9889 | 9.6 × 10−168 |
| D10 | 0.9981 | 8.9 × 10−245 | CWT10 | 0.9876 | 1.2 × 10−162 |
| D11 | 0.9970 | 5.8 × 10−224 | CWT11 | 0.9914 | 2.0 × 10−178 |
| D12 | 0.9966 | 2.2 × 10−218 | CWT12 | 0.9923 | 1.9 × 10−183 |
| D13 | 0.9986 | 5.3 × 10−258 | CWT13 | 0.9944 | 5.1 × 10−197 |
| D14 | 0.9978 | 1.7 × 10−237 | CWT14 | 0.9959 | 5.8 × 10−211 |
| D15 | 0.9920 | 1.6 × 10−181 | CWT15 | 0.9970 | 1.4 × 10−224 |
| D | Statistic | p-Value | CWT | Statistic | p-Value |
|---|---|---|---|---|---|
| D1 | 116.8515 | 3.67 × 10−25 | CWT1 | 46.0809 | 5.45 × 10−10 |
| D2 | 127.1252 | 2.25 × 10−27 | CWT2 | 40.9941 | 6.55 × 10−9 |
| D3 | 133.8806 | 7.88 × 10−29 | CWT3 | 34.6134 | 1.47 × 10−7 |
| D4 | 143.0068 | 8.49 × 10−31 | CWT4 | 34.1818 | 1.81 × 10−7 |
| D5 | 145.6427 | 2.29 × 10−31 | CWT5 | 39.0002 | 1.73 × 10−8 |
| D6 | 152.4864 | 7.66 × 10−33 | CWT6 | 43.6884 | 1.75 × 10−9 |
| D7 | 158.7064 | 3.48 × 10−34 | CWT7 | 49.4108 | 1.06 × 10−10 |
| D8 | 158.8744 | 3.20 × 10−34 | CWT8 | 57.1523 | 2.38 × 10−12 |
| D9 | 155.0766 | 2.11 × 10−33 | CWT9 | 74.8697 | 3.86 × 10−16 |
| D10 | 147.9417 | 7.32 × 10−32 | CWT10 | 93.3626 | 4.15 × 10−20 |
| D11 | 129.2131 | 7.99 × 10−28 | CWT11 | 114.2045 | 1.36 × 10−24 |
| D12 | 113.8614 | 1.61 × 10−24 | CWT12 | 135.5797 | 3.39 × 10−29 |
| D13 | 113.3792 | 2.05 × 10−24 | CWT13 | 141.0537 | 2.24 × 10−30 |
| D14 | 121.4426 | 3.77 × 10−26 | CWT14 | 138.2426 | 9.04 × 10−30 |
| D15 | 85.0263 | 2.56 × 10−18 | CWT15 | 128.3065 | 1.25 × 10−27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zharkov, M.S.; Huang, J.-G.; Yang, B.; Babushkina, E.A.; Belokopytova, L.V.; Vaganov, E.A.; Zhirnova, D.F.; Ilyin, V.A.; Popkova, M.I.; Shishov, V.V. Tracheidogram’s Classification as a New Potential Proxy in High-Resolution Dendroclimatic Reconstructions. Forests 2022, 13, 970. https://doi.org/10.3390/f13070970
Zharkov MS, Huang J-G, Yang B, Babushkina EA, Belokopytova LV, Vaganov EA, Zhirnova DF, Ilyin VA, Popkova MI, Shishov VV. Tracheidogram’s Classification as a New Potential Proxy in High-Resolution Dendroclimatic Reconstructions. Forests. 2022; 13(7):970. https://doi.org/10.3390/f13070970
Chicago/Turabian StyleZharkov, Mikhail S., Jian-Guo Huang, Bao Yang, Elena A. Babushkina, Liliana V. Belokopytova, Eugene A. Vaganov, Dina F. Zhirnova, Victor A. Ilyin, Margarita I. Popkova, and Vladimir V. Shishov. 2022. "Tracheidogram’s Classification as a New Potential Proxy in High-Resolution Dendroclimatic Reconstructions" Forests 13, no. 7: 970. https://doi.org/10.3390/f13070970
APA StyleZharkov, M. S., Huang, J. -G., Yang, B., Babushkina, E. A., Belokopytova, L. V., Vaganov, E. A., Zhirnova, D. F., Ilyin, V. A., Popkova, M. I., & Shishov, V. V. (2022). Tracheidogram’s Classification as a New Potential Proxy in High-Resolution Dendroclimatic Reconstructions. Forests, 13(7), 970. https://doi.org/10.3390/f13070970









