Nondestructive Techniques for Determination of Wood Mechanical Properties of Urban Trees in Madrid
Abstract
:1. Introduction
2. Materials and Methods
2.1. Longitudinal Measurements
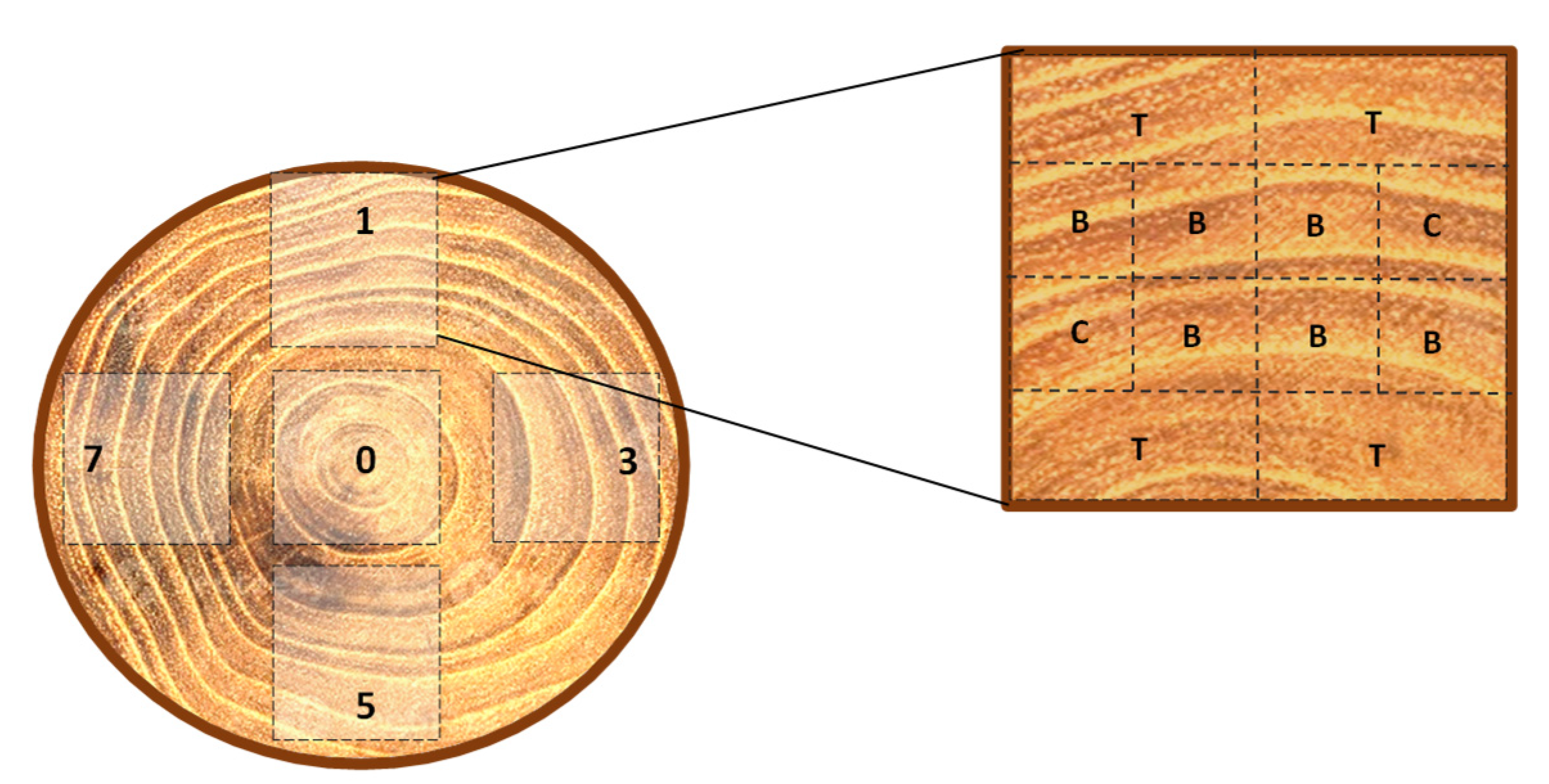
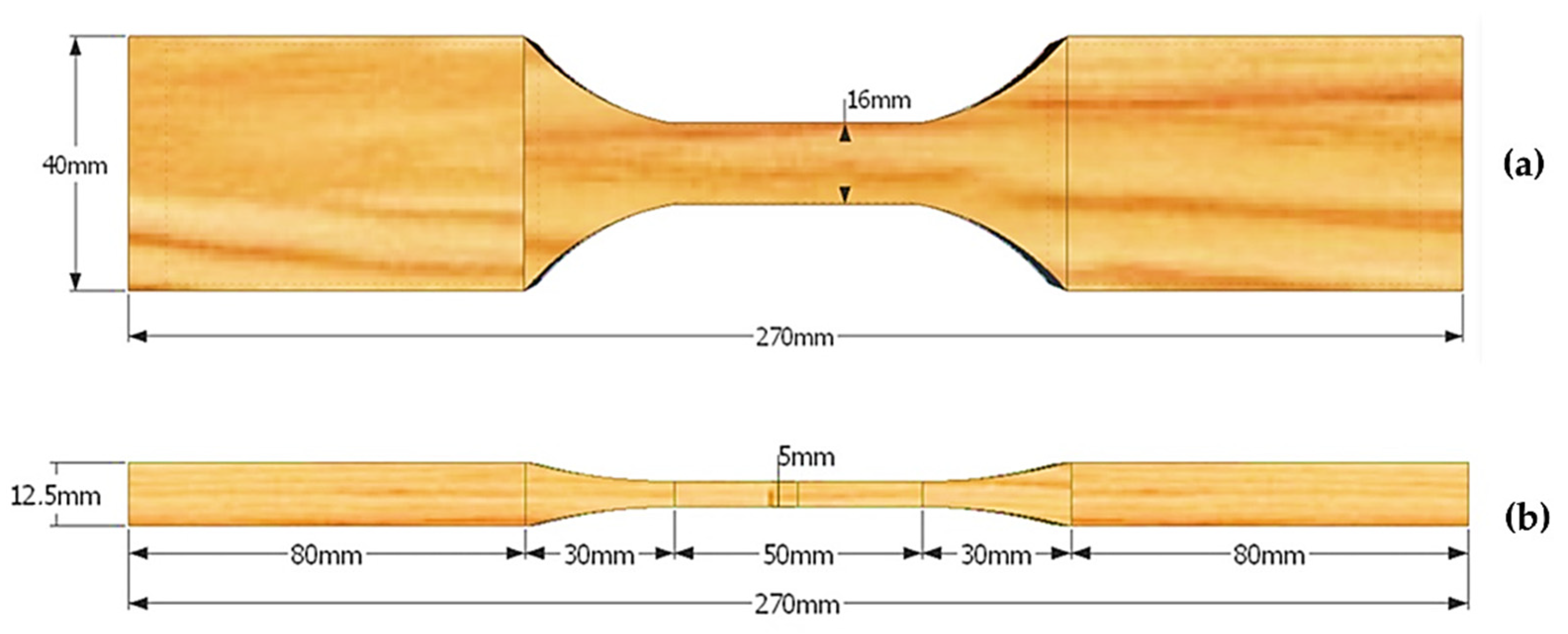
2.2. Preparation of Specimens
2.3. Nondestructive and Mechanical Tests on Specimens
2.4. Relationship between Dynamic MOE in Logs and Indirect Velocities in Standing Trees
2.5. Data Analysis
3. Results and Discussion
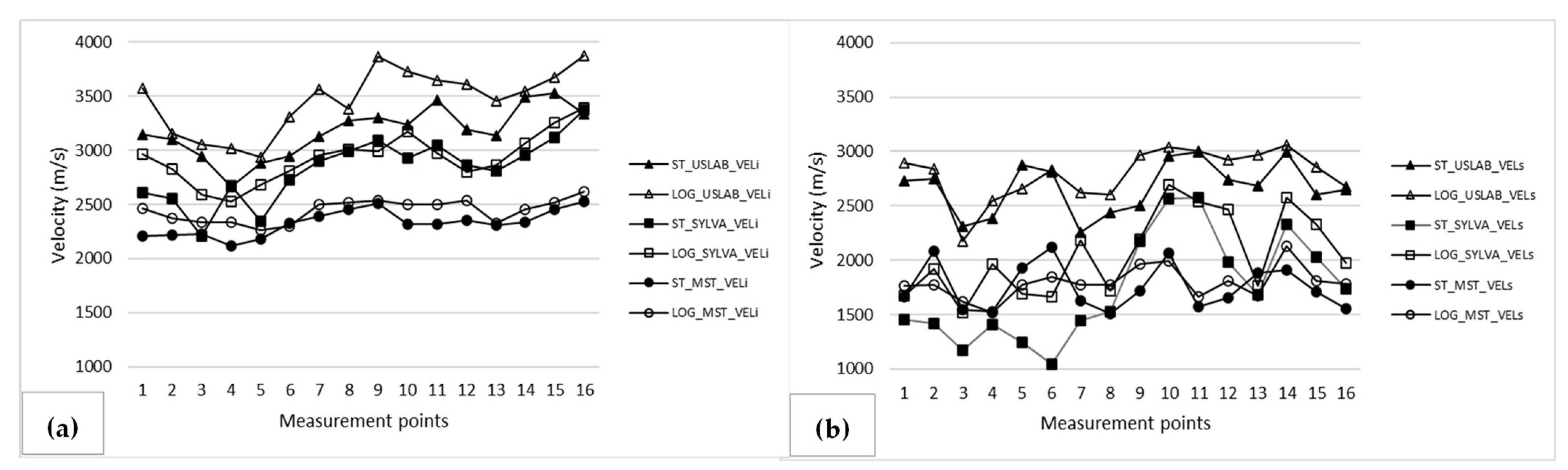
3.1. Standing Tree and Log Measurements
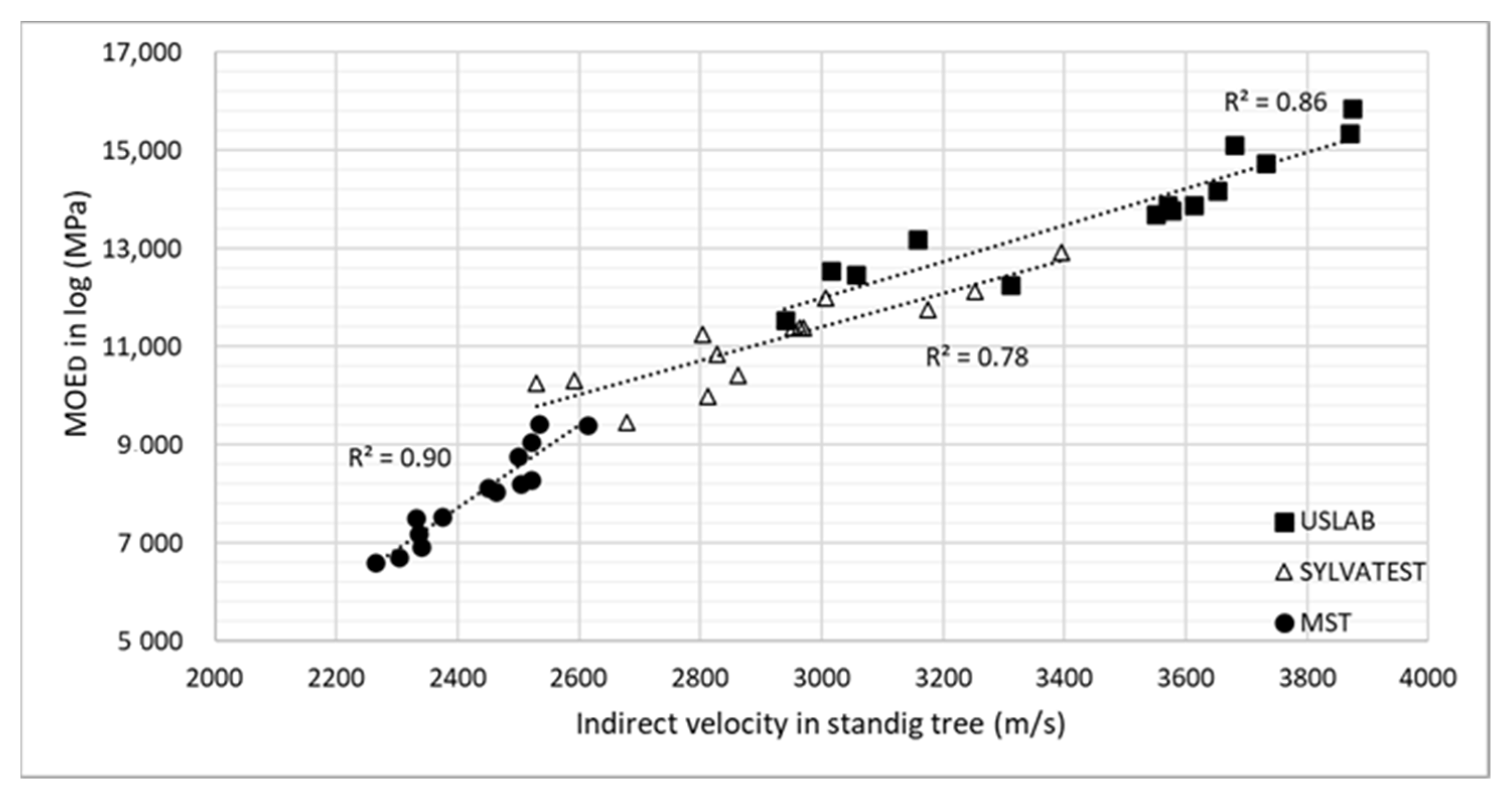
3.2. Relationship between Dynamic MOE in Logs and Indirect Velocities in Standing Trees
3.3. Nondestructive Tests and Destructive Tests on Specimens
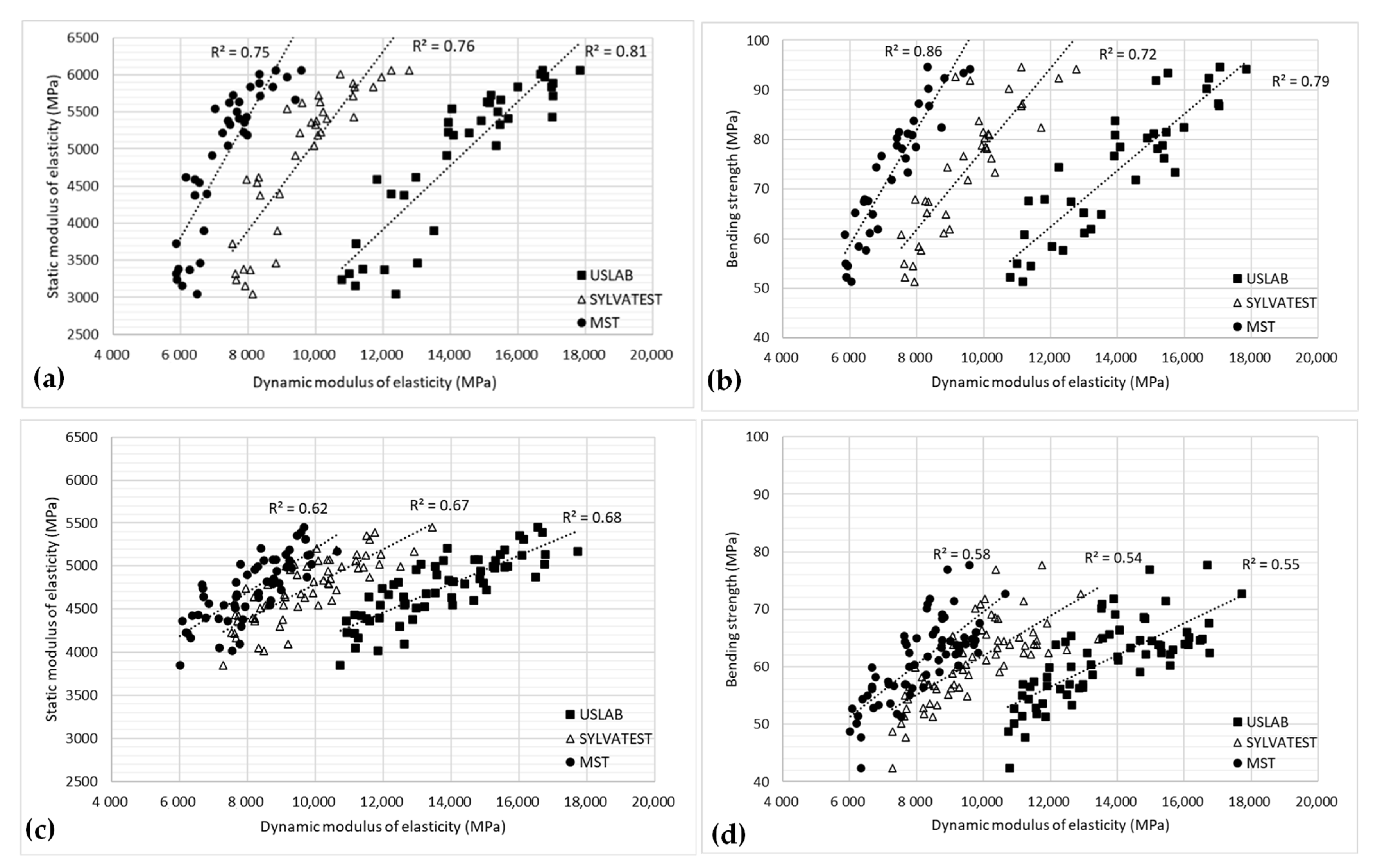
3.4. Relationship between Dynamic and Static Modulus of Elasticity in Specimens
3.5. Relationship of Mechanical Properties in Specimens and Indirect in Standing Trees
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Calaza, P.; Iglesias, M. El Riesgo Del Arbolado Urbano. Contexto, Concepto Y Evaluación; Mundi-Prensa: Madrid, Spain, 2016; p. 526. [Google Scholar]
- Allison, R.B.; Wang, X. Nondestructive Testing in the Urban Forest. In Nondestructive Evaluation of Wood, 2nd ed.; Ross, R.J., Ed.; General Technical Report, FPL-GTR-238; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2015; pp. 77–86. [Google Scholar]
- Tomao, A.; Secondi, A.; Corona, P.; Giuliarelli, D.; Quantrini, V.; Agrimi, M. Can composite indices explain multidimensionality of tree risk assessment? A case study in an historical monumental complex. Urban For. Urban Green. 2015, 14, 456–465. [Google Scholar] [CrossRef]
- Bucur, V. Ultrasonic techniques for nondestructive testing of standing trees. Ultrasonics 2005, 43, 237–239. [Google Scholar] [CrossRef] [PubMed]
- Mattheck, C.; Breloer, H. The Body Language of Trees: A Handbook for Failure Analysis; HMSO Publications Centre: London, UK, 1998. [Google Scholar]
- Weiler, M.; Missio, A.L.; Gatto, D.A.; Güths, W.G. Nondestructive evaluation of wood decayed by xylophagous organisms. Mater. Res. 2013, 16, 1203–1213. [Google Scholar] [CrossRef]
- Wang, X. Acoustic measurements on trees and logs: A review and analysis. Wood Sci. Technol. 2013, 47, 965–975. [Google Scholar] [CrossRef]
- Proto, A.; Macrì, G.; Bernardini, V.; Russo, D.; Zimbalatti, G. Acoustic evaluation of wood quality with a non-destructive method in standing trees: A first survey in Italy. iForest-Biogeosci. For. 2017, 10, 700–706. [Google Scholar] [CrossRef]
- Allison, R.B.; Wang, X.; Senalik, C.A. Methods for Nondestructive Testing of Urban Trees. Forests 2020, 11, 1341. [Google Scholar] [CrossRef]
- Wang, X.; Divos, F.; Pilon, C.; Brashaw, B.K.; Ross, R.J.; Pellerin, R.F. Assessment of Decay in Standing Timber Using Stress Wave Timing Non-Destructive Evaluation Tools: A Guide for Use and Interpretation; General Technical Report (GTR), FPL-GTR-147; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2004. [Google Scholar]
- Wang, X.; Ross, R.J.; Carter, P. Acoustic Evaluation of Wood Quality in Standing Trees: Part 1. Acoustic Wave Behavior in Standing Trees. Wood Fiber Sci. 2007, 39, 28–38. [Google Scholar]
- Moore, J.; Lyon, A.J.; Ridley-Ellis, D.; Gardiner, B.A. Properties of UK-grown Sitka spruce: Extent and sources of variation. In Proceedings of the 10th World Conference on Timber Engineering, Miyazaki, Japan, 2–5 June 2008. [Google Scholar]
- Yin, Y.; Nagao, H.; Liu, X.; Nakai, T. Mechanical properties assessment of Cunninghamia lanceolata plantation wood with three acoustic-based nondestructive methods. J. Wood Sci. 2010, 56, 33–40. [Google Scholar] [CrossRef]
- Gonçalves, R.; Bertoldo, C.; Massak, M.V.; Batista, F.; Secco, C.B. Velocity of ultrasonic waves in live trees and freshly-felled logs. Wood Fiber Sci. 2011, 43, 232–235. [Google Scholar]
- Gonçalves, R.; Bertoldo, C.B.; Massak, M.V. Acoustic and bending properties in Pinus elliottii beams obtained from trees of different ages. J. Wood Sci. 2013, 59, 127–132. [Google Scholar] [CrossRef]
- Bertoldo, C.; Gonçalves, R. Influence of measurement position, tree diameter, and bulk wood density on models that predict wave propagation velocity in logs according to the velocity in trees. For. Prod. J. 2015, 65, 166–172. [Google Scholar] [CrossRef]
- UNE-EN 56528; Physical-Mechanical Properties of Wood. Preparation of Specimens for Testing. AENOR: Madrid, Spain, 1978; p. 3.
- UNE-EN 408:2011+A1:2012; Timber Structures. Sawn and Glued Laminated Timber for Structural Use. Determination of some Physical-Mechanical Properties. AENOR: Madrid, Spain, 2011; p. 10.
- UNE-EN 56537; Physical-Mechanical Properties of Wood. Determination of Strength Against Static Flexion. AENOR: Madrid, Spain, 1979; p. 2.
- UNE-EN 56535; Physical-Mechanical Properties of Wood. Determination of Axial Compression Strength. AENOR: Madrid, Spain, 1977; p. 2.
- UNE-EN 28012 h8; Woods Used in Aircraft. Axial Traction Test. AENOR: Madrid, Spain, 1955; p. 2.
- UNE-EN 384:2016+A1; Madera estructural. Determinación de los Valores Característicos de Las Propiedades Mecánicas Y La Densidad. AENOR: Madrid, Spain, 2020; p. 23.
- Bucur, V. Acoustics of Wood, 2nd ed.; Springer: Berlin, Germany, 2006; p. 393. [Google Scholar]
- Íñiguez, G. Clasificación Mediante Técnicas no Destructivas Y Evaluación de las Propiedades Mecánicas de la Madera Aserrada de Coníferas de Gran Escuadría Para Uso Estructural. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2007. [Google Scholar]
- Balmori, R.J.A.; Acuña, R.L.; Basterra, O.L.A. Estudio de la influencia de la dirección de la fibra en la velocidad de propagación de ultrasonidos (FAKOPP) en madera estructural de “Pinus Sylvestris L. ” y “Pinus Radiata D. Don.”. In Proceedings of the Congreso Euro-Americano REHABEND, Burgos, Spain, 24–27 May 2016. [Google Scholar]
- Bertoldo, C. Propriedades de Resistência E de Rigidez da Madeira Obtidas a Partir da Avaliação Acústica na Árvore [Predicting of Strength and Stiffness of Wood Using Acoustic Measurement in Trees]. Ph.D. Thesis, Universidade Estadual de Campinas, São Paulo, Brazil, 2014. [Google Scholar]
- De Oliveira, F.G.R.; Candian, M.; Lucchette, F.F.; Salgon, J.L.; Sales, A. Moisture content effect on ultrasonic velocity in Goupia glabra. Mater. Res. 2005, 8, 11–14. [Google Scholar] [CrossRef]
- Gonçalves, R.; da Leme, C.O.A. Influence of moisture content on longitudinal, radial, and tangential ultrasonic velocity for two Brazilian wood species. Wood Fiber Sci. 2008, 40, 580–586. [Google Scholar]
- Moreno-Chan, J.; Walker, J.C.; Raymond, C.A. Effects of moisture content and temperature on acoustic velocity and dynamic MOE of radiata pine sapwood boards. Wood Sci. Technol. 2011, 45, 609–626. [Google Scholar] [CrossRef]
- Wang, X. Stress Wave E-Rating of Structural Timber—Size and Moisture Content Effects. In Proceedings of the 18th International Nondestructive Testing and Evaluation of Wood Symposium; General Technical Report FPL-GTR-226; Madison, WI, USA, 24–27 September 2013; Department of Agriculture, Forest Service, Forest Products Laboratory: Washington, DC, USA, 2013; pp. 38–46. [Google Scholar]
- Argüelles, R.; Arriaga, F.; Esteban, M.; Iñiguez, G.; Argüelles, R. Estructuras de Madera Bases de Cálculo, 1st ed.; AITIM: Madrid, Spain, 2013; pp. 30–40. [Google Scholar]
- Montero, M.J.; Mata, J.D.; Esteban, M.; Hermoso, E. Influence of moisture content on the wave velocity to estimate the mechanical properties of large cross-section pieces for structural use of Scots pine from Spain. Maderas Cienc. Tecnol. 2015, 17, 407–420. [Google Scholar] [CrossRef]
- Vignote Peña, S. Principales Maderas de Frondosas de España. Características, Tecnología Y Aplicaciones; Monograph (Technical Report); Universidad Politécnica de Madrid: Madrid, Spain, 2014. [Google Scholar]
- Vignote Peña, S.; Jiménez, F.J. Tecnología de La Madera; Mundi-Prensa: Madrid, Spain, 1996; p. 602. [Google Scholar]
- Esteban, H.M. Determinación de la Capacidad Resistente de la Madera Estructural de Gran Escuadría y Su Aplicación en Estructuras Existentes de Madera de Conífera. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2003. [Google Scholar]
- Arriaga, F.; Íñiguez, G.; Esteban, M.; Fernandez-Golfin, J. Structural Tali timber (Erythrophleum ivorense A. Chev., Erythrophleum suaveolens Brenan.): Assessment of strength and stiffness properties using visual and ultrasonic methods. Eur. J. Wood Wood Prod. 2006, 64, 357–362. [Google Scholar] [CrossRef]
- Hermoso, E.; Fernández-Golfín, J.I.; Díez, M.R.; Mier, R. Aplicación de los ultrasonidos a la evaluación de las propiedades mecánicas de la madera en rollo de pequeño diámetro. Inf. Constr. 2007, 59, 87–95. [Google Scholar] [CrossRef]
- Carballo, J.; Hermoso, E.; Fernández-Golfín, J.I. Comparación de la evaluación y clasificación mecánica del Pinus pinaster Ait. con dos equipos de ultrasonidos. In Proceedings of the 5° Congreso Forestal Español, Ávila, Spain, 21–25 September 2009. [Google Scholar]
- Vega, A.; Dieste, A.; Guaita, M.; Majada, J.; Baño, V. Modelling of the mechanical properties of Castanea sativa Mill. structural timber by a combination of non-destructive variables and visual grading parameters. Eur. J. Wood. Prod. 2012, 70, 839–844. [Google Scholar] [CrossRef]
- Vázquez, C.; Gonçalves, R.; Bertoldo, C.; Baño, V.; Vega, A.; Crespo, J.; Guaita, M. Determination of the mechanical properties of Castanea sativa Mill. using ultrasonic wave propagation and comparison with static compression and bending methods. Wood Sci. Technol. 2015, 49, 607–622. [Google Scholar] [CrossRef]
- Llana, D.F.; Short, I.; Harte, A.M. Use of non-destructive test methods on Irish hardwood standing trees and small-diameter round timber for prediction of mechanical properties. Ann. For. Sci. 2020, 77, 1–13. [Google Scholar] [CrossRef]
- Ross, R.J. Nondestructive Evaluation of Wood, 2nd ed.; General Technical Report FPL-GTR-238; USDA Forest Service: Washington, DC, USA, 2015; p. 169. [Google Scholar]
- Lam, F.; Varoğlu, E. Effect of length on the tensile strength of lumber. For. Prod. J. 1990, 40, 37–42. [Google Scholar]
- Wang, X.P.; Ross, R.J.; Brashaw, B.K.; Punches, J.; Erickson, J.R.; Forsman, J.W.; Pellerin, R.F. Diameter effect on stress-wave evaluation of modulus of elasticity of logs. Wood Fiber Sci. 2004, 36, 368–377. [Google Scholar]
- Divos, F.; Denes, L.; Iñiguez, G. Effect of cross-sectional change of a board specimen on stress wave velocity determination. Holzforschung 2005, 59, 230–231. [Google Scholar] [CrossRef]
- Rello, L.A.; Barra, R.D.; Sanz, M.C.; Fernández, A.L.; Sánchez, T.L.; Blázquez, L.M.; Otero, A.B.; Ganga, E.R.; Ramón, G.C. La transmisión de ultrasonidos aplicada a la madera estructural. In Proceedings of the Congreso Iberoamericano de Productos Forestales-Iberomadera, Buenos Aires, Argentina, 3–5 July 2007. [Google Scholar]
- Wang, X. Effects of size and moisture on stress wave E-rating of structural lumber. In Proceedings of the 10th World Conference on Timber Engineering, Miyazaki, Japan, 2–5 June 2008. [Google Scholar]
- Trinca, A.J.; Gonçalves, R. Efeito das dimensões da seção transversal e da frequência do transdutor na velocidade de propagação de ondas de ultra-som na madeira. Rev. Árvore 2009, 33, 177–184. [Google Scholar] [CrossRef] [Green Version]



| Measurements in Standing Trees | Measurements in Logs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tree | Log | Indirect | Semidirect | Direct | Indirect | Semidirect | |||||
| Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | ||
| Robinia pseudoacacia L. | LA | 3348 | 19.4 | 3041 | 14.3 | 4370 | 6.4 | 3286 | 23.1 | 2979 | 15.4 |
| LB | 3532 | 19.1 | 3351 | 11.8 | 4548 | 8.5 | 3474 | 23.7 | 3127 | 15.6 | |
| Platanus × hybrida Brot. | LA | 3011 | 6.3 | 2571 | 9.5 | 3658 | 3.8 | 3251 | 7.5 | 2644 | 8.6 |
| LB | 3335 | 4.3 | 2768 | 6.9 | 3857 | 3.5 | 3678 | 3.9 | 2938 | 4.2 | |
| Ulmus pumila L. 1 | LA | 774 | 27.1 | 564 | 34.0 | 3298 | 10.7 | 917 | 3.6 | 695 | 5.3 |
| LB | 584 | 44.7 | 481 | 28.9 | 3119 | 7.1 | 919 | 5.3 | 695 | 5.3 | |
| Ulmus pumila L. 2 | LA | 1247 | 51.5 | 6556 | 19.2 | 2255 | 30.9 | 846 | 7.0 | 677 | 6.4 |
| LB | 2409 | 6.6 | 1565 | 28.9 | 3123 | 13.0 | 2457 | 3.4 | 1581 | 17.3 | |
| Ulmus pumila L. 3 | LA | 2770 | 14.3 | 2254 | 12.2 | 3509 | 4.3 | 3015 | 13.5 | 2410 | 9.5 |
| LB | 2698 | 11.7 | 2318 | 11.6 | 3623 | 3.4 | 3058 | 9.1 | 2365 | 14.3 | |
| Populus alba L. | LA | n.d. | n.d. | n.d. | n.d. | 4184 | 9.5 | 3063 | 28.5 | 1147 | 9.2 |
| LB | n.d. | n.d. | n.d. | n.d. | 3974 | 8.0 | 2767 | 31.0 | 878 | 37.2 | |
| Measurements in Standing Trees | Measurements in Logs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tree | Log | Indirect | Semidirect | Direct | Indirect | Semidirect | |||||
| Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | ||
| Robinia pseudoacacia L. | LA | 3016 | 15.5 | 2906 | 8.9 | 3809 | 6.0 | 3037 | 14.5 | 2847 | 10.6 |
| LB | 3183 | 15.2 | 3015 | 9.9 | 3941 | 8.5 | 3109 | 17.6 | 2893 | 10.4 | |
| Platanus × hybrida Brot. | LA | 2625 | 9.8 | 1338 | 12.4 | 3313 | 4.1 | 2795 | 6.3 | 1791 | 11.8 |
| LB | 3025 | 5.8 | 2136 | 15.9 | 3459 | 3.6 | 3065 | 6.5 | 2318 | 13.8 | |
| Ulmus pumila L. 1 | LA | 1474 | 41.8 | 976 | 30.1 | 2971 | 7.6 | 1735 | 25.7 | 1270 | 9.8 |
| LB | 1268 | 8.8 | 950 | 16.2 | 2867 | 5.8 | 1554 | 34.7 | 1244 | 7.2 | |
| Ulmus pumila L. 2 | LA | 1656 | 23.7 | 1000 | 21.2 | 2306 | 13.3 | 1796 | 10.8 | 1209 | 6.9 |
| LB | 1612 | 31.5 | 1019 | 32.9 | 2841 | 8.6 | 2105 | 11.9 | 1473 | 8.2 | |
| Ulmus pumila L. 3 | LA | 2650 | 5.8 | 1815 | 6.5 | 3090 | 4.6 | 2777 | 8.5 | 1980 | 8.1 |
| LB | 2290 | 18.6 | 1664 | 17.0 | 3200 | 3.5 | 2585 | 12.0 | 1929 | 8.4 | |
| Populus alba L. | LA | n.d. | n.d. | n.d. | n.d. | 3559 | 8.5 | 2310 | 40.2 | 859 | 19.0 |
| LB | n.d. | n.d. | n.d. | n.d. | 3447 | 7.5 | 1599 | 46.8 | 878 | 9.3 | |
| Measurements in Standing Trees | Measurements in Logs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tree | Log | Indirect | Semidirect | Direct | Indirect | Semidirect | |||||
| Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | Average (m/s) | C.V. (%) | ||
| Robinia pseudoacacia L. | LA | 2673 | 8.8 | 2511 | 3.6 | 3201 | 6.8 | 2626 | 9.3 | 2469 | 5.0 |
| LB | 2735 | 14.0 | 2557 | 5.7 | 3293 | 8.9 | 2706 | 12.8 | 2569 | 4.4 | |
| Platanus × hybrida Brot. | LA | 2267 | 5.1 | 1751 | 14.4 | 2757 | 3.9 | 2387 | 3.9 | 1730 | 6.1 |
| LB | 2391 | 3.8 | 1759 | 10.1 | 2974 | 3.9 | 2499 | 3.2 | 1852 | 8.6 | |
| Ulmus pumila L. 1 | LA | 2114 | 4.9 | 1390 | 6.7 | 2544 | 6.6 | 2237 | 5.9 | 1508 | 2.4 |
| LB | 2010 | 4.1 | 1380 | 5.0 | 2442 | 4.7 | 2185 | 4.9 | 1469 | 2.7 | |
| Ulmus pumila L. 2 | LA | 1704 | 5.9 | 1287 | 5.1 | 2146 | 9.6 | 1751 | 7.8 | 1281 | 7.5 |
| LB | 1911 | 6.7 | 1576 | 6.6 | 2554 | 8.2 | 1964 | 2.8 | 1551 | 4.8 | |
| Ulmus pumila L. 3 | LA | 2416 | 6.6 | 1894 | 7.4 | 2843 | 4.0 | 2539 | 5.5 | 1982 | 5.1 |
| LB | 2492 | 8.3 | 2068 | 2.6 | 2946 | 3.9 | 2556 | 8.1 | 2088 | 3.3 | |
| Populus alba L. | LA | n.d. | n.d. | n.d. | n.d. | 3179 | 7.3 | 1810 | 16.8 | 1103 | 11.0 |
| LB | n.d. | n.d. | n.d. | n.d. | 3177 | 7.3 | 832 | 8.3 | 1060 | 29.8 | |
| Species | Specimens | n | Nondestructive Tests | Mechanical Tests | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Density * (Kg/m3) | USLab | Sylvatest Duo | MST | fm (MPa) | MOE (MPa) | n | fc,0 (MPa) | n | ft,0 (MPa) | ||||||
| VA (m/s) | VA (m/s) | VA (m/s) | |||||||||||||
| Robinia pseudoacacia L. | Conditioned | 21 | 755 | 4479 | 16,023 | 3794 | 11,455 | 3302 | 8596 | 89.5 | 7198 | 51 | 49.4 | 15 | 63.9 |
| Saturated | 43 | 1054 | 3899 | 16,440 | 3125 | 10,480 | 2795 | 8310 | 72.0 | 5712 | 93 | 35.4 | 27 | 61.8 | |
| Platanus × hybrida Brot. | Conditioned | 37 | 617 | 4786 | 14,304 | 3933 | 9650 | 3445 | 7405 | 74.9 | 4867 | 54 | 35.3 | 23 | 73.1 |
| Saturated | 71 | 1114 | 3475 | 13,555 | 2964 | 9827 | 2761 | 8543 | 61.4 | 4671 | 102 | 23.9 | 53 | 54.3 | |
| Ulmus pumila L. 1 | Conditioned | 41 | 582 | 4604 | 12,772 | 3744 | 8429 | 3308 | 6551 | 57.6 | 3882 | 56 | 29.5 | 24 | 57.5 |
| Saturated | 77 | 1067 | 3221 | 10,896 | 2675 | 7501 | 2482 | 6440 | 45.2 | 3460 | 90 | 15.4 | 62 | 37.6 | |
| Ulmus pumila L. 2 | Conditioned | 43 | 516 | 4457 | 10,477 | 3729 | 7310 | 3348 | 5857 | 47.1 | 4067 | 43 | 25.5 | 21 | 42.8 |
| Saturated | 77 | 1087 | 2927 | 9314 | 2473 | 6627 | 2311 | 5768 | 32.1 | 2899 | 85 | 12.1 | 47 | 27.1 | |
| Ulmus pumila L. 3 | Conditioned | 33 | 604 | 4663 | 12,889 | 3998 | 9480 | 3558 | 7475 | 63.8 | 4849 | 45 | 29.6 | 18 | 68.7 |
| Saturated | 71 | 1115 | 3424 | 12,736 | 2852 | 8825 | 2611 | 7396 | 49.5 | 3906 | 82 | 16.7 | 37 | 46.8 | |
| Populus alba L. | Conditioned | 56 | 457 | 5932 | 16,468 | 4773 | 10,662 | 4044 | 7637 | 60.2 | 5252 | 39 | 36.3 | 18 | 60.3 |
| Saturated | 145 | 1017 | 3955 | 14,873 | 3296 | 10,331 | 2880 | 7880 | 46.5 | 4748 | 117 | 20.8 | 17 | 45.0 | |
| Species | Normal Density (Kg/m3) | fm (MPa) | MOE (MPa) | fc,0 (MPa) | ft,0 (MPa) | Sourse |
|---|---|---|---|---|---|---|
| Robinia pseudoacacia L. | 770 | 133.4 | 11,082 | 74.5 | *** | [33] |
| Platanus x hybrida Brot. | 577 | 79.4 | *** | 33.0 | *** | [33] |
| Ulmus pumila L. | 639 * | 112.3 * | 10,591 * | 39.5 * | *** | [33] |
| Populus alba L. | 530 | 71.6 | 5639 ** | 36.6 | 61.3 | [33,34] |
| Tree | Specimens | Determination Coefficients (R2) | |||||
|---|---|---|---|---|---|---|---|
| USLab | Sylvatest Duo | MST | USLab | Sylvatest Duo | MST | ||
| Robinia pseudoacacia L. | Conditioned | 0.97 | 0.98 | 0.97 | 0.93 | 0.94 | 0.95 |
| Saturated | 0.94 | 0.95 | 0.93 | 0.90 | 0.91 | 0.90 | |
| Platanus × hybrida Brot | Conditioned | 0.74 | 0.76 | 0.80 | 0.85 | 0.72 | 0.79 |
| Saturated | 0.62 | 0.66 | 0.68 | 0.57 | 0.53 | 0.55 | |
| Ulmus pumila L. 1 | Conditioned | 0.74 | 0.77 | 0.77 | 0.68 | 0.69 | 0.67 |
| Saturated | 0.76 | 0.77 | 0.71 | 0.73 | 0.74 | 0.70 | |
| Ulmus pumila L. 2 | Conditioned | 0.94 | 0.95 | 0.95 | 0.77 | 0.78 | 0.82 |
| Saturated | 0.75 | 0.77 | 0.79 | 0.70 | 0.75 | 0.77 | |
| Ulmus pumila L. 3 | Conditioned | 0.76 | 0.75 | 0.73 | 0.72 | 0.72 | 0.71 |
| Saturated | 0.61 | 0.64 | 0.51 | 0.53 | 0.54 | 0.48 | |
| Populus alba L. | Conditioned | 0.74 | 0.75 | 0.77 | 0.58 | 0.63 | 0.65 |
| Saturated | 0.60 | 0.63 | 0.56 | 0.47 | 0.51 | 0.38 | |
| Tree | Equipment | Model | R2 (%) | p-Value |
|---|---|---|---|---|
| Robinia pseudoacacia L. | USLab | 86.7 | 0.002 | |
| 92.6 | 0.000 | |||
| 82.2 | 0.012 | |||
| Sylvatest | 74.8 | 0.011 | ||
| 80.2 | 0.006 | |||
| 74.9 | 0.025 | |||
| MST | 62.2 | 0.035 | ||
| 74.5 | 0.012 | |||
| 85.5 | 0.008 | |||
| Platanus × hybrida Brot. | USLab | 82.5 | 0.004 | |
| 58.6 | 0.044 | |||
| 61.0 | 0.060 | |||
| Sylvatest | 93.2 | 0.000 | ||
| 74.0 | 0.012 | |||
| 56.1 | 0.080 | |||
| MST | 83.7 | 0.003 | ||
| 90.9 | 0.000 | |||
| 38.2 | 0.190 | |||
| Ulmus pumila L. 1 | USLab | 45.2 | 0.090 | |
| 29.5 | 0.207 | |||
| 70.0 | 0.018 | |||
| Sylvatest | 87.9 | 0.005 | ||
| 61.5 | 0.060 | |||
| 56.1 | 0.080 | |||
| MST | 70.9 | 0.035 | ||
| 94.6 | 0.001 | |||
| 52.6 | 0.102 | |||
| Ulmus pumila L. 2 | USLab | 70.2 | 0.009 | |
| 56.3 | 0.031 | |||
| 85.1 | 0.001 | |||
| Sylvatest | 40.7 | 0.172 | ||
| 59.8 | 0.071 | |||
| 32.6 | 0.231 | |||
| MST | 69.0 | 0.040 | ||
| 59.1 | 0.073 | |||
| 71.2 | 0.034 | |||
| Ulmus pumila L. 3 | USLab | 0.126 | ||
| 65.3 | 0.027 | |||
| 50.7 | 0.112 | |||
| Sylvatest | 24.2 | 0.260 | ||
| 52.7 | 0.102 | |||
| 67.7 | 0.087 | |||
| MST | 59.2 | 0.043 | ||
| 61.5 | 0.065 | |||
| 21.6 | 0.350 | |||
| Populus alba L. | USLab | 68.3 | 0.021 | |
| 77.9 | 0.008 | |||
| 73.7 | 0.013 | |||
| Sylvatest | 71.1 | 0.034 | ||
| 68.7 | 0.041 | |||
| 24.3 | 0.150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Virgen-Cobos, G.H.; Olvera-Licona, G.; Hermoso, E.; Esteban, M. Nondestructive Techniques for Determination of Wood Mechanical Properties of Urban Trees in Madrid. Forests 2022, 13, 1381. https://doi.org/10.3390/f13091381
Virgen-Cobos GH, Olvera-Licona G, Hermoso E, Esteban M. Nondestructive Techniques for Determination of Wood Mechanical Properties of Urban Trees in Madrid. Forests. 2022; 13(9):1381. https://doi.org/10.3390/f13091381
Chicago/Turabian StyleVirgen-Cobos, Gabriel H., Guadalupe Olvera-Licona, Eva Hermoso, and Miguel Esteban. 2022. "Nondestructive Techniques for Determination of Wood Mechanical Properties of Urban Trees in Madrid" Forests 13, no. 9: 1381. https://doi.org/10.3390/f13091381
APA StyleVirgen-Cobos, G. H., Olvera-Licona, G., Hermoso, E., & Esteban, M. (2022). Nondestructive Techniques for Determination of Wood Mechanical Properties of Urban Trees in Madrid. Forests, 13(9), 1381. https://doi.org/10.3390/f13091381






