Numerical Modeling Based on Finite Element Analysis of 3D-Printed Wood-Polylactic Acid Composites: A Comparison with Experimental Data
Abstract
:1. Introduction
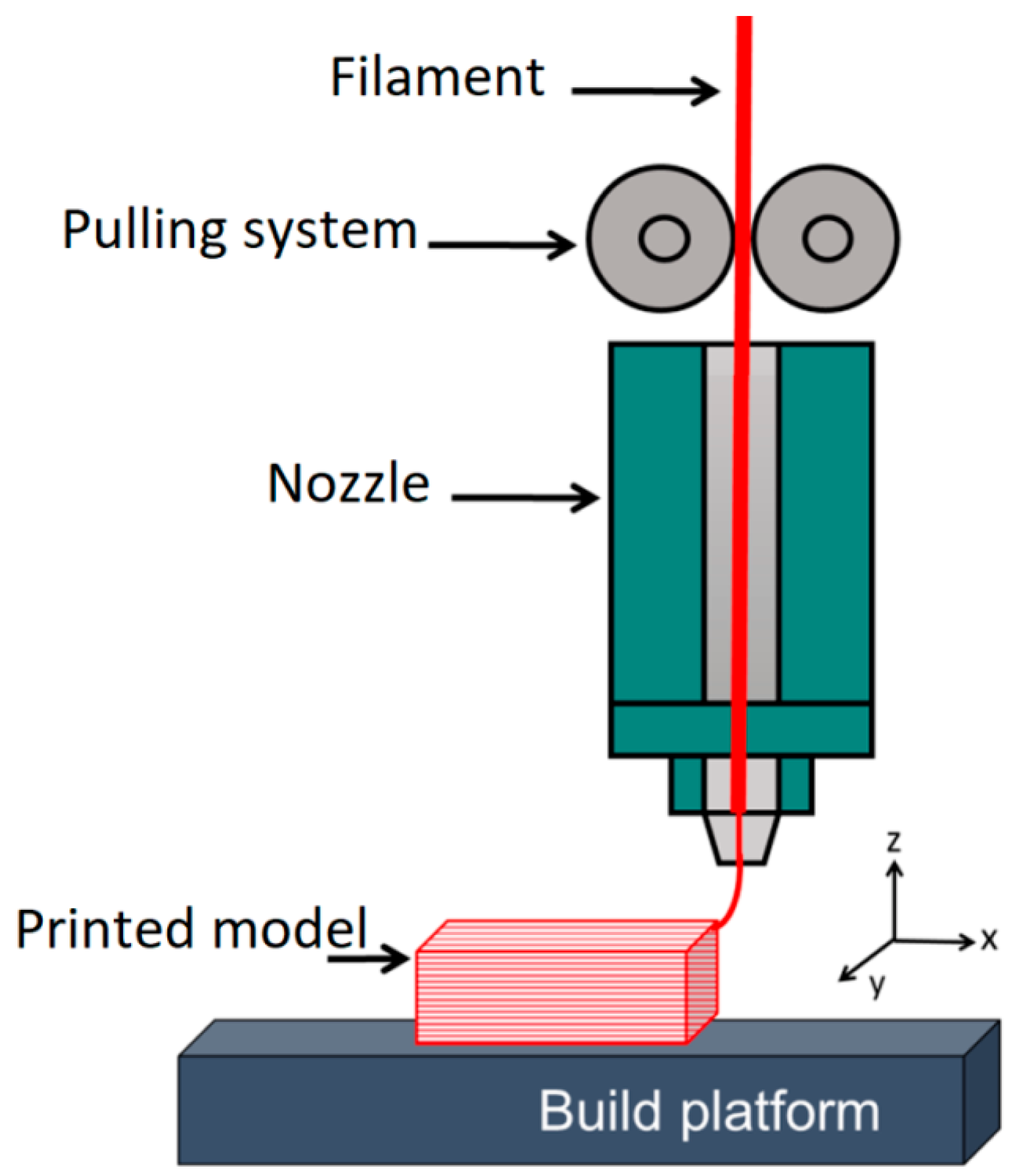
2. Materials and Methods
3. Numerical Homogenization-Based Finite Element Analysis
3.1. Basic Procedure
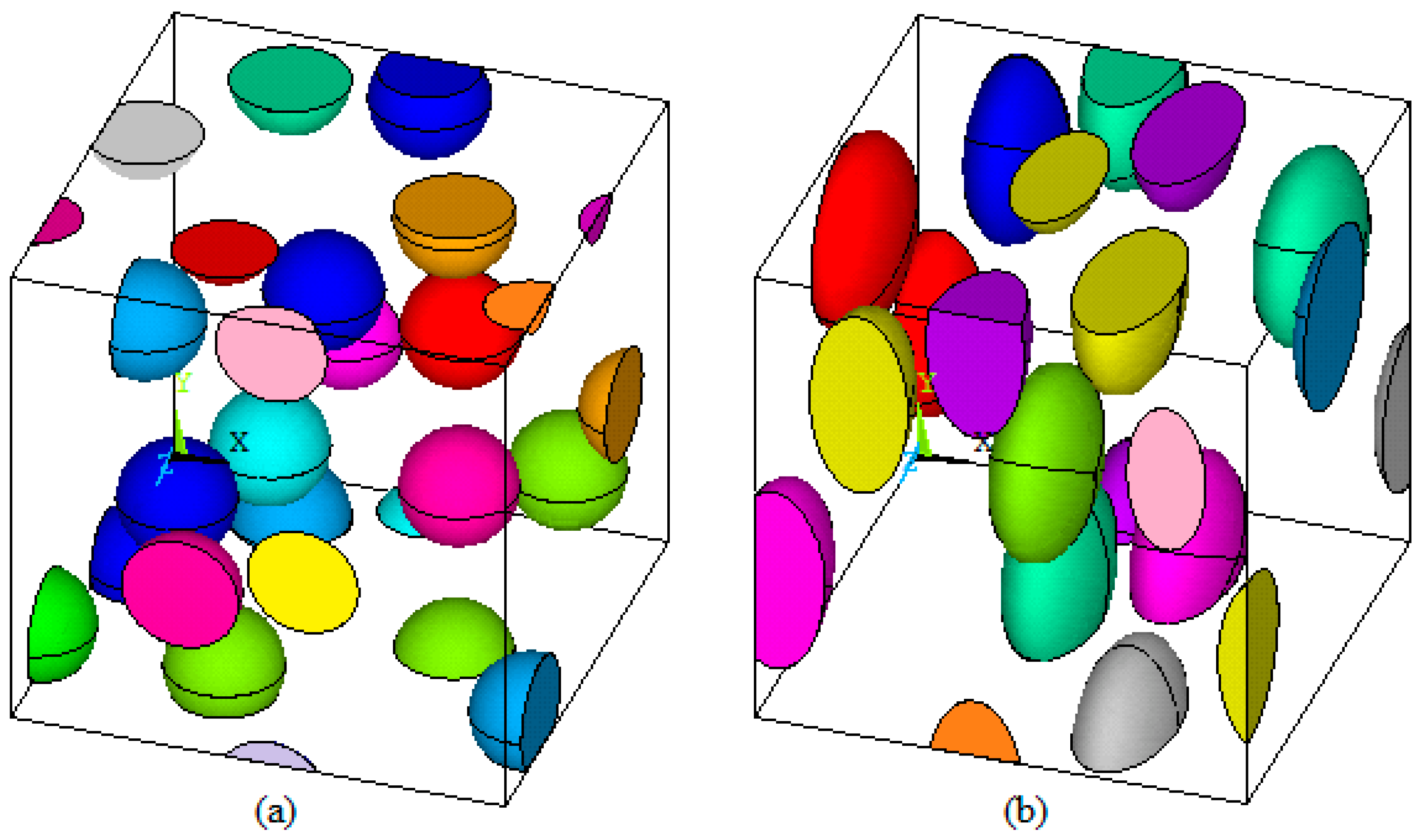
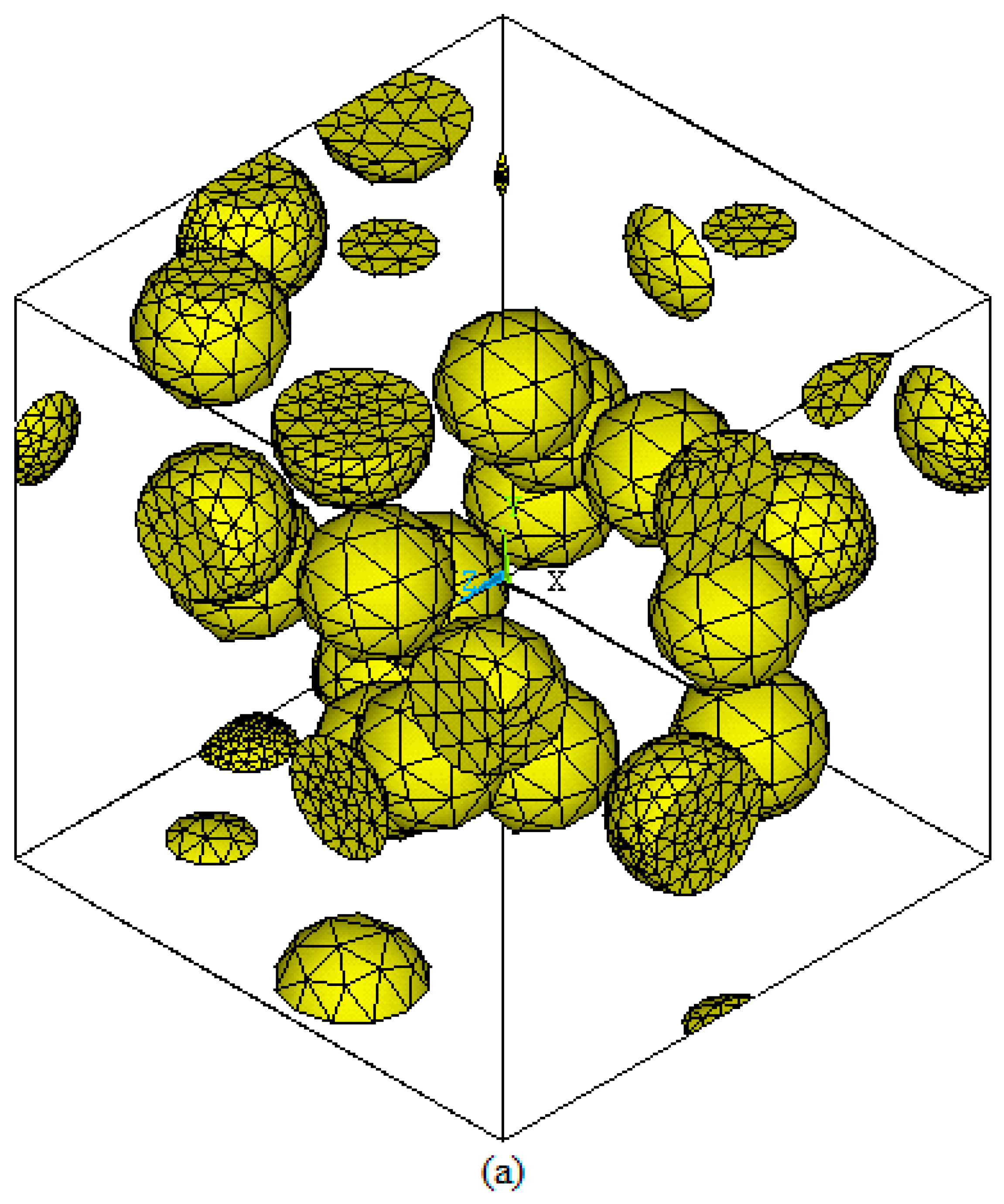
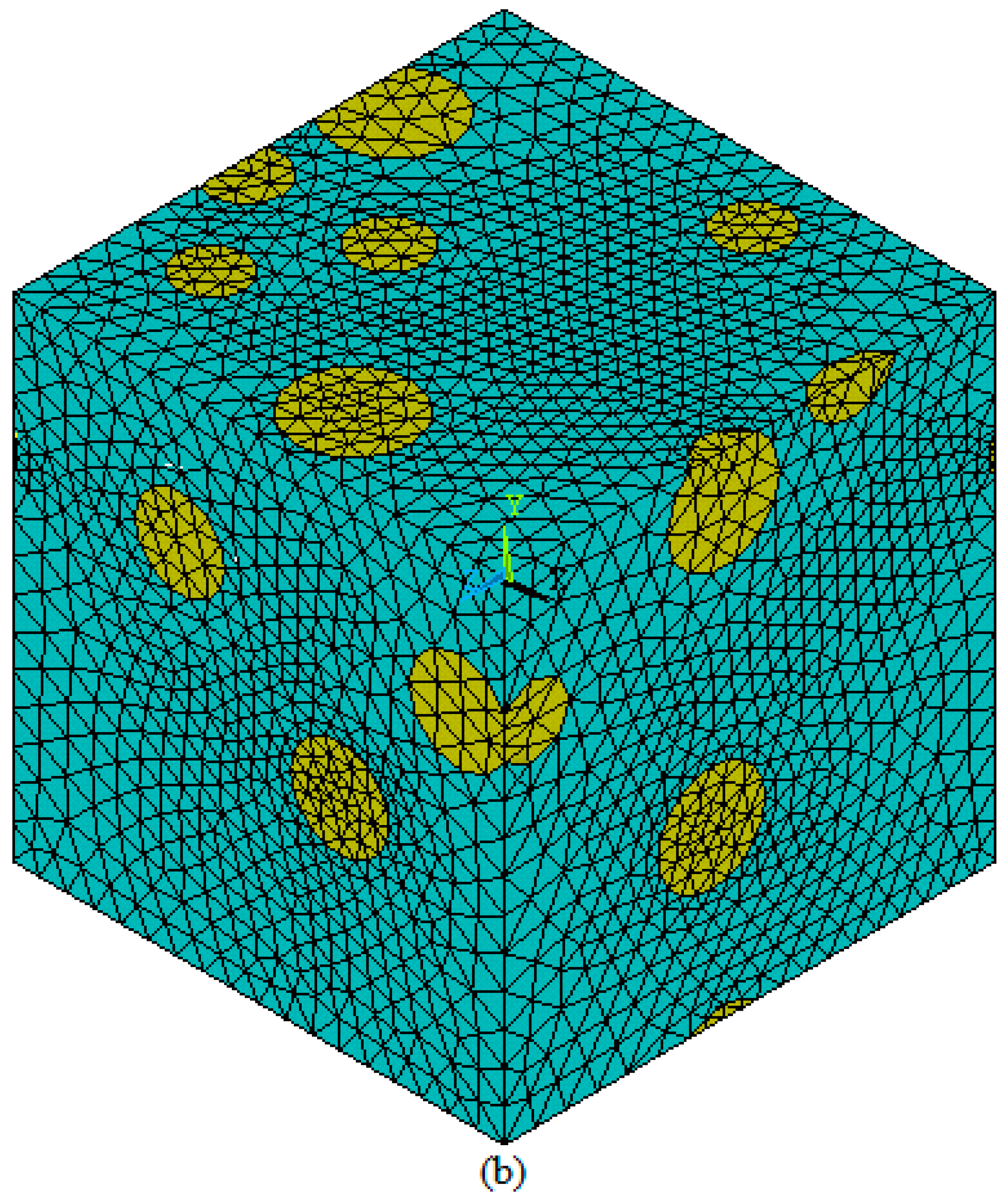
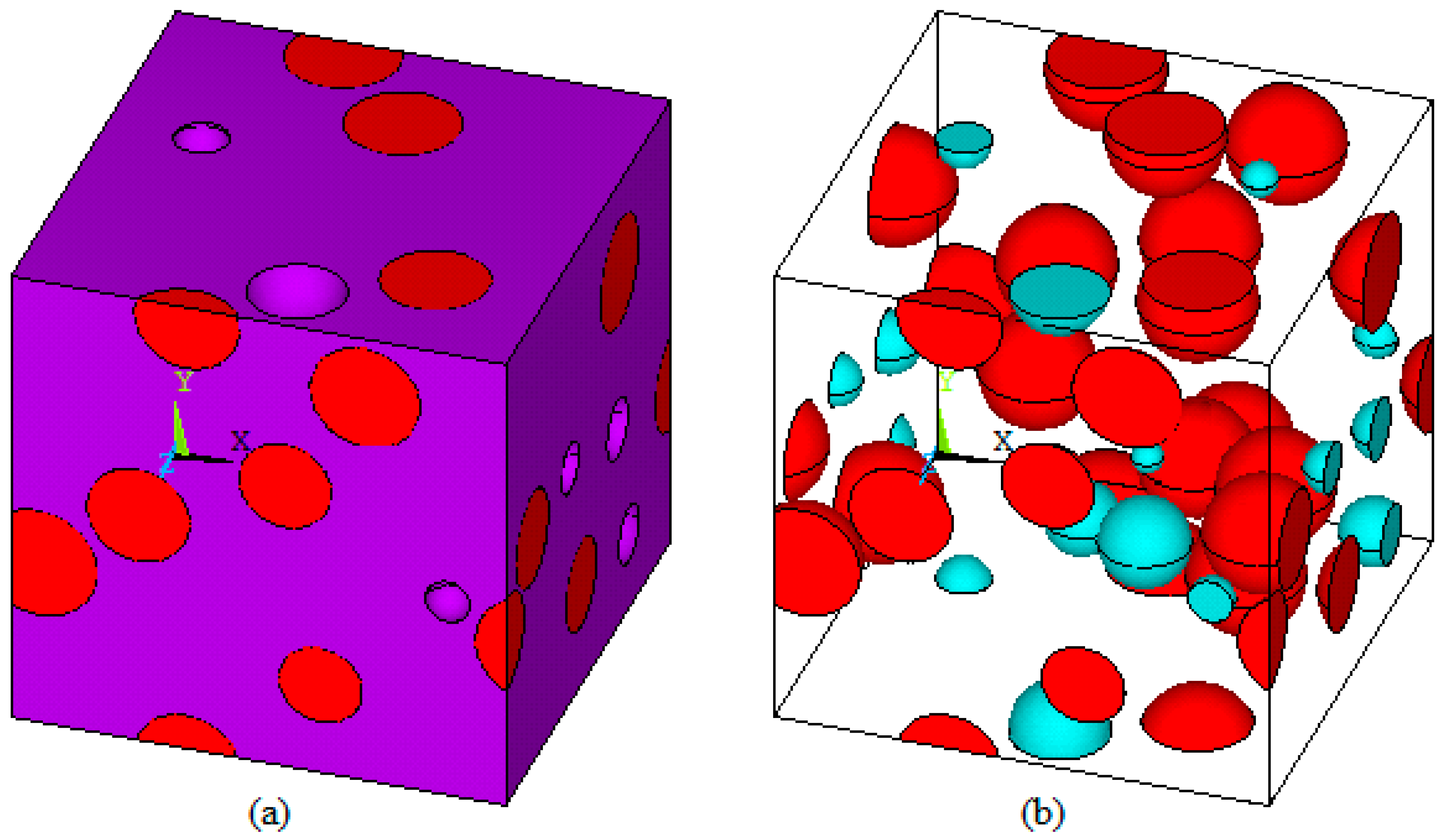
3.1.1. Representative Volume Element
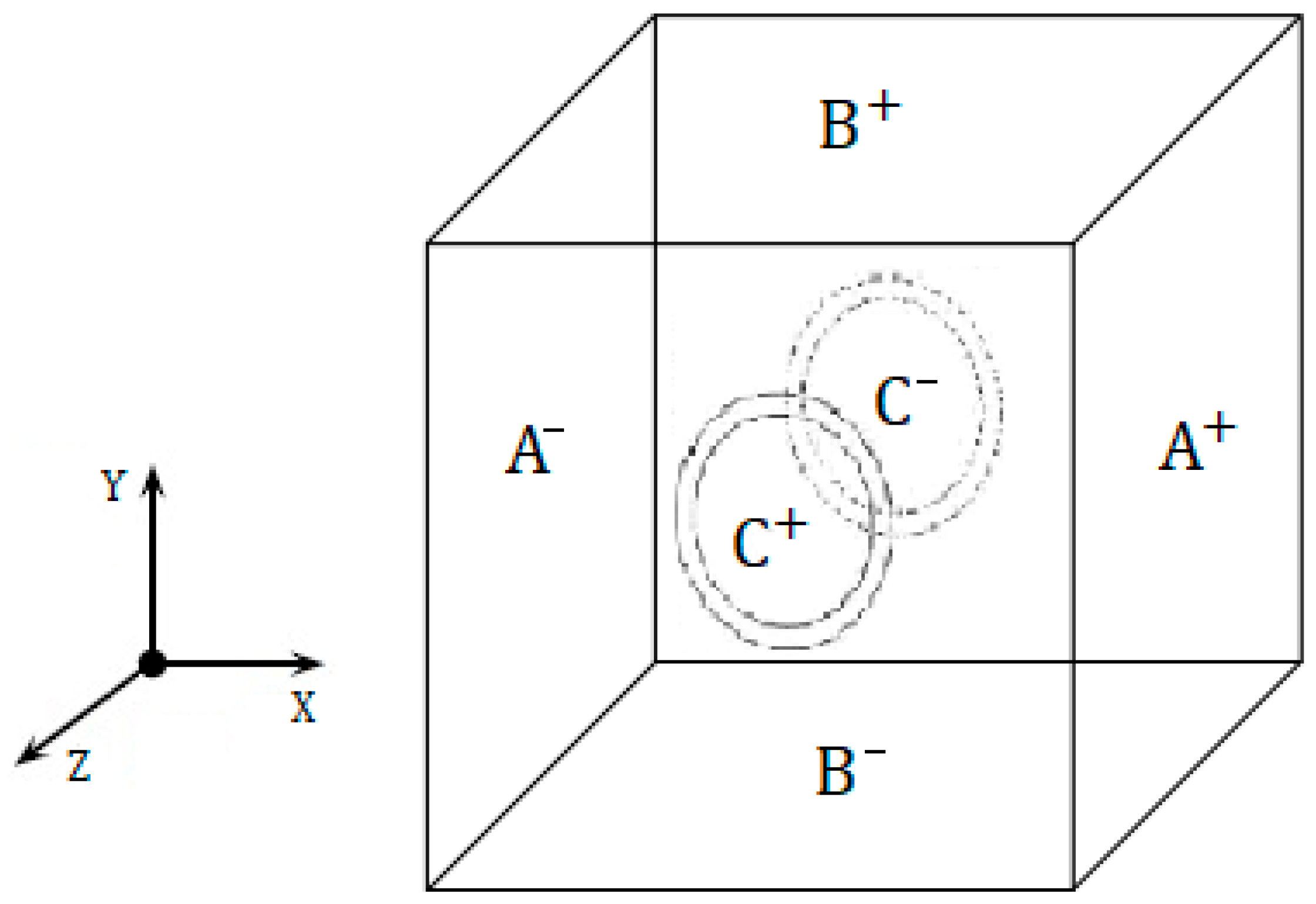
3.1.2. Boundary Conditions
3.1.3. Finite Element Simulation
4. Results and Discussion
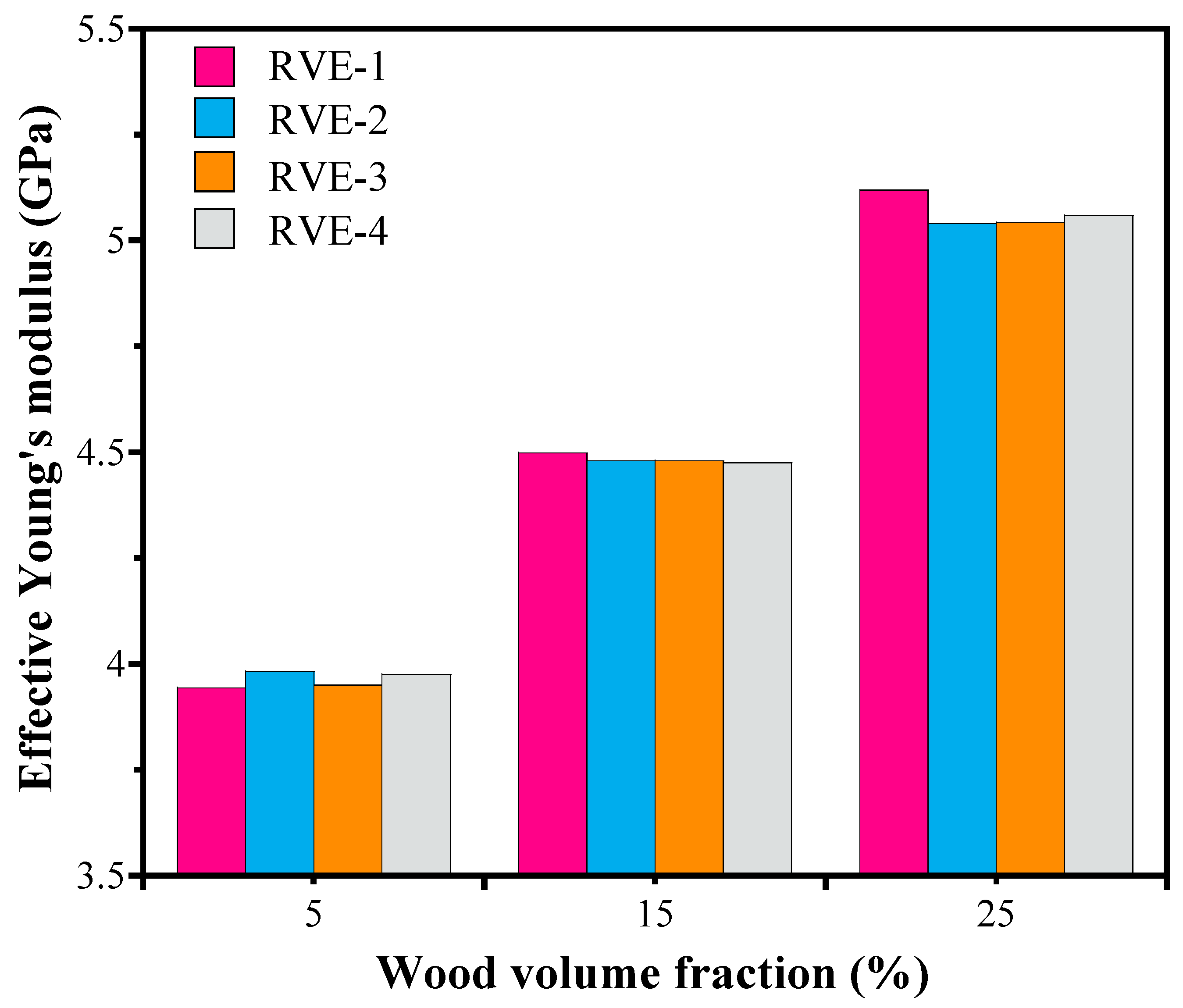
4.1. Effect of RVE Size
4.2. Effect of Random Particle Distribution
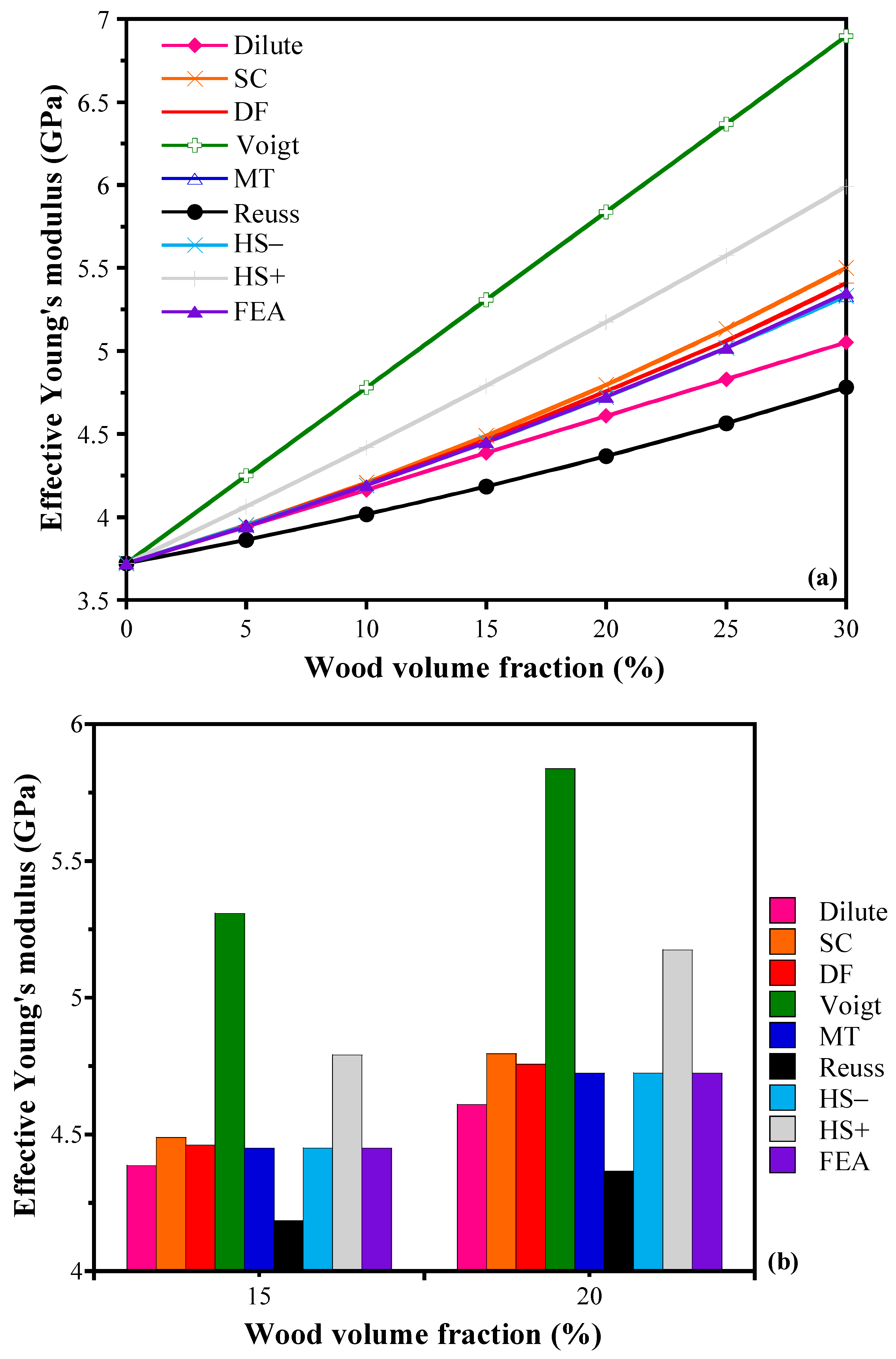
4.3. Effect of Wood Volume Fraction
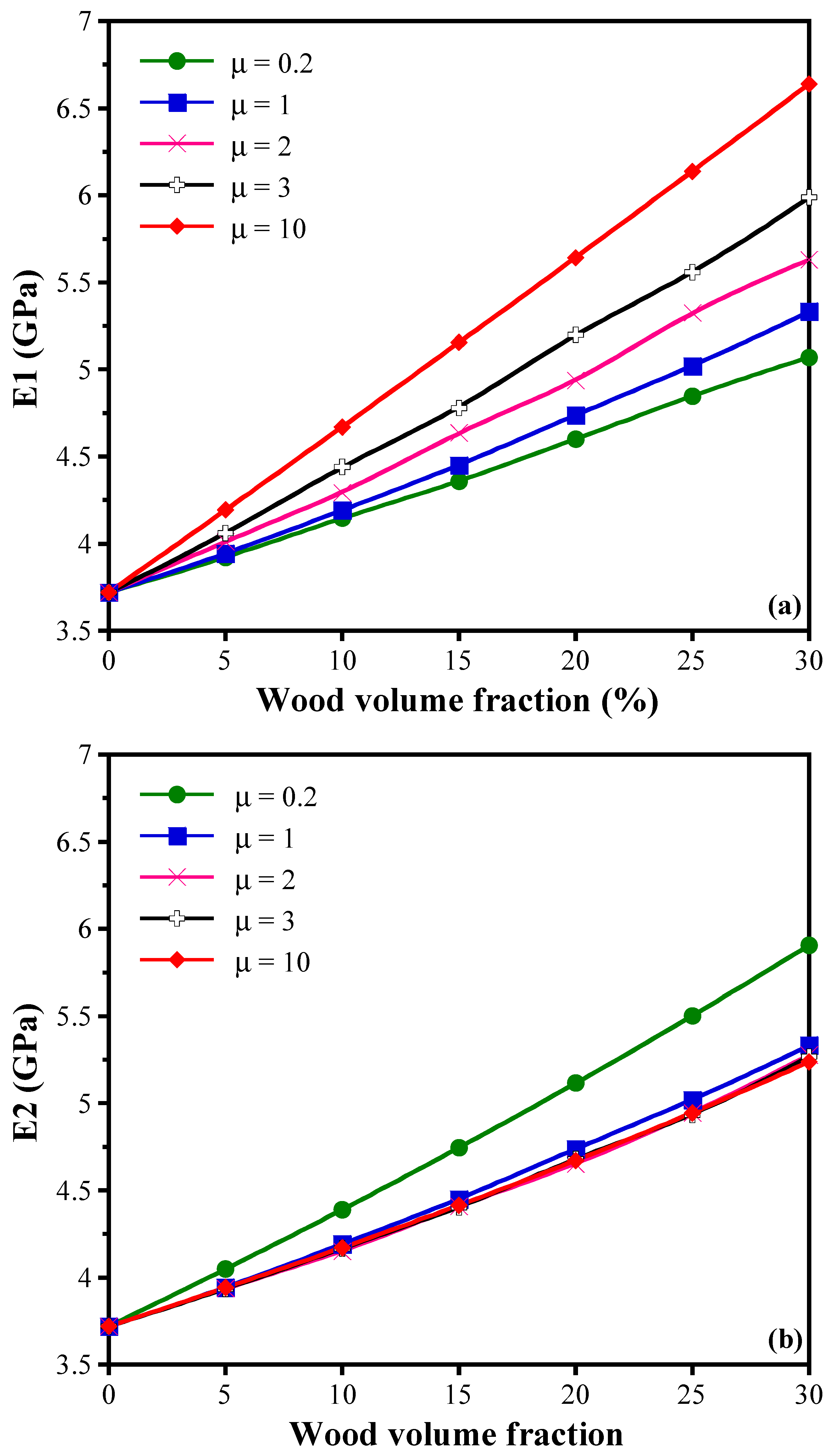
4.4. Effect of Wood Shape
- Case of elongated particles ():
- Case of spherical particles ():
- Case of needle-shaped particles ():
4.5. Effect of Porosity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lau, A.K.-T.; Cheung, K.H.Y. 1-Natural fiber-reinforced polymer-based composites. In Natural Fiber-Reinforced Biodegradable and Bioresorbable Polymer Composites; Woodhead Publishing: Sawston, UK, 2017; pp. 1–18. [Google Scholar] [CrossRef]
- Muthu, S.S. 1-Introduction to sustainability and the textile supply chain and its environmental impact. In Assessing the Environmental Impact of Textiles and the Clothing Supply Chain, 2nd ed.; Woodhead Publishing: Sawston, UK, 2020; pp. 1–32. [Google Scholar] [CrossRef]
- Sahayaraj, A.F.; Muthukrishnan, M.; Ramesh, M. Experimental investigation on physical, mechanical, and thermal properties of jute and hemp fibers reinforced hybrid polylactic acid composites. Polym. Compos. 2022, 43, 2854–2863. [Google Scholar] [CrossRef]
- Kern, J. Additive Manufacturing. In The Digital Transformation of Logistics; Wiley-Blackwell: New York, NY, USA, 2021; pp. 41–60. [Google Scholar] [CrossRef]
- Abouelmajd, M.; Bahlaoui, A.; Arroub, I.; Zemzami, M.; Hmina, N.; Lagache, M.; Belhouideg, S. Experimental analysis and optimization of mechanical properties of FDM-processed polylactic acid using Taguchi design of experiment. Int. J. Simul. Multidiscip. Des. Optim. 2021, 12, 30. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, M.; Zhou, Z.W.; Gou, J.H.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Velu, R.; Raspall, F.; Singamneni, S. Chapter 8-3D printing technologies and composite materials for structural applications. In Green Composites for Automotive Applications; Woodhead Publishing: Sawston, UK, 2019; pp. 171–196. [Google Scholar] [CrossRef]
- Calì, M.; Pascoletti, G.; Gaeta, M.; Milazzo, G.; Ambu, R. A New Generation of Bio-Composite Thermoplastic Filaments for a More Sustainable Design of Parts Manufactured by FDM. Appl. Sci. 2020, 10, 5852. [Google Scholar] [CrossRef]
- Pringle, A.M.; Rudnicki, M.; Pearce, J.M. Wood Furniture Waste-Based Recycled 3-D Printing Filament. For. Prod. J. 2017, 68, 86–95. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Roozbahani, H.; Alizadeh, M.; Handroos, H. 3D Printing of Plant-Derived Compounds and a Proposed Nozzle Design for the More Effective 3D FDM Printing. IEEE Access 2021, 9, 57107–57119. [Google Scholar] [CrossRef]
- Gardner, D.; Anderson, J.; Tekinalp, H.; Ozcan, S.; Sauerbier, P. Lignocellulosic-filled polymer feedstocks for large scale additive manufacturing of low cost composites. In Proceedings of the Internaional Forest Products Congress, Trabzon, Turkey, 26–29 September 2018; pp. 26–29. [Google Scholar]
- Estakhrianhaghighi, E.; Mirabolghasemi, A.; Zhang, Y.; Lessard, L.; Akbarzadeh, A. 3D-Printed Wood-Fiber Reinforced Architected Cellular Composites. Adv. Eng. Mater. 2020, 22, 2000565. [Google Scholar] [CrossRef]
- Tarrés, Q.; Melbø, J.; Delgado-Aguilar, M.; Espinach, F.; Mutjé, P.; Chinga-Carrasco, G. Bio-polyethylene reinforced with thermomechanical pulp fibers: Mechanical and micromechanical characterization and its application in 3D-printing by fused deposition modelling. Compos. Part B Eng. 2018, 153, 70–77. [Google Scholar] [CrossRef]
- Kariz, M.; Sernek, M.; Obućina, M.; Kuzman, M.K. Effect of wood content in FDM filament on properties of 3D printed parts. Mater. Today Commun. 2018, 14, 135–140. [Google Scholar] [CrossRef]
- Badouard, C.; Traon, F.; Denoual, C.; Mayer-Laigle, C.; Paës, G.; Bourmaud, A. Exploring mechanical properties of fully compostable flax reinforced composite filaments for 3D printing applications. Ind. Crop. Prod. 2019, 135, 246–250. [Google Scholar] [CrossRef]
- Coppola, B.; Garofalo, E.; Di Maio, L.; Scarfato, P.; Incarnato, L. Investigation on the use of PLA/hemp composites for the fused deposition modelling (FDM) 3D printing. AIP Conf. Proc. 2018, 1981, 020086. [Google Scholar] [CrossRef]
- Wang, C.; Smith, L.M.; Zhang, W.; Li, M.; Wang, G.; Shi, S.Q.; Cheng, H.; Zhang, S. Reinforcement of Polylactic Acid for Fused Deposition Modeling Process with Nano Particles Treated Bamboo Powder. Polymers 2019, 11, 1146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Depuydt, D.; Balthazar, M.; Hendrickx, K.; Six, W.; Ferraris, E.; Desplentere, F.; Ivens, J.; Van Vuure, A.W. Production and characterization of bamboo and flax fiber reinforced polylactic acid filaments for fused deposition modeling (FDM). Polym. Compos. 2018, 40, 1951–1963. [Google Scholar] [CrossRef]
- Le Duigou, A.; Barbé, A.; Guillou, E.; Castro, M. 3D printing of continuous flax fibre reinforced biocomposites for structural applications. Mater. Des. 2019, 180, 107884. [Google Scholar] [CrossRef]
- Naik, M.; Thakur, D.; Chandel, S.; Salunkhe, S. Experimental investigations on thermal, flame retardant, and impact properties of additively manufactured continuous FRPC. Polym. Compos. 2022, 43, 2941–2951. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, R.; Singh, M.; Preet, P. On compressive and morphological features of 3D printed almond skin powder reinforced PLA matrix. Mater. Res. Express 2019, 7, 025311. [Google Scholar] [CrossRef]
- Travieso-Rodriguez, J.A.; Zandi, M.D.; Jerez-Mesa, R.; Lluma-Fuentes, J. Fatigue behavior of PLA-wood composite manufactured by fused filament fabrication. J. Mater. Res. Technol. 2020, 9, 8507–8516. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, R.; Singh, T.P.; Batish, A. On flexural and pull out properties of 3D printed PLA based hybrid composite matrix. Mater. Res. Express 2020, 7, 015330. [Google Scholar] [CrossRef]
- Van Der Klift, F.; Koga, Y.; Todoroki, A.; Ueda, M.; Hirano, Y.; Matsuzaki, R. 3D Printing of Continuous Carbon Fibre Reinforced Thermo-Plastic (CFRTP) Tensile Test Specimens. Open J. Compos. Mater. 2016, 06, 18–27. [Google Scholar] [CrossRef] [Green Version]
- Naranjo-Lozada, J.; Ahuett-Garza, H.; Orta-Castañón, P.; Verbeeten, W.M.; Sáiz-González, D. Tensile properties and failure behavior of chopped and continuous carbon fiber composites produced by additive manufacturing. Addit. Manuf. 2019, 26, 227–241. [Google Scholar] [CrossRef]
- Chabaud, G.; Castro, M.; Denoual, C.; Le Duigou, A. Hygromechanical properties of 3D printed continuous carbon and glass fibre reinforced polyamide composite for outdoor structural applications. Addit. Manuf. 2019, 26, 94–105. [Google Scholar] [CrossRef]
- Polyzos, E.; Katalagarianakis, A.; Van Hemelrijck, D.; Pyl, L. A multi-scale analytical methodology for the prediction of mechanical properties of 3D-printed materials with continuous fibres. Addit. Manuf. 2020, 36, 101394. [Google Scholar] [CrossRef]
- Ezzaraa, I.; Ayrilmis, N.; Kuzman, M.K.; Belhouideg, S.; Bengourram, J. Micromechanical models for predicting the mechanical properties of 3D-printed wood/PLA composite materials: A comparison with experimental data. Mech. Adv. Mater. Struct. 2021, 1–13. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Gosling, P.; Pearce, C.; Ullah, Z.; Kaczmarczyk, L. Perturbation-based stochastic multi-scale computational homogenization method for woven textile composites. Int. J. Solids Struct. 2016, 80, 368–380. [Google Scholar] [CrossRef] [Green Version]
- Polyzos, E.; Van Hemelrijck, D.; Pyl, L. Numerical modelling of the elastic properties of 3D-printed specimens of thermoplastic matrix reinforced with continuous fibres. Compos. Part B Eng. 2021, 211, 108671. [Google Scholar] [CrossRef]
- Dutra, T.A.; Ferreira, R.T.L.; Resende, H.B.; Guimarães, A. Mechanical characterization and asymptotic homogenization of 3D-printed continuous carbon fiber-reinforced thermoplastic. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–15. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, D.; Sheng, Y. Performance-driven 3D printing of continuous curved carbon fibre reinforced polymer composites: A preliminary numerical study. Compos. Part B Eng. 2018, 151, 256–264. [Google Scholar] [CrossRef]
- Somireddy, M.; Czekanski, A. Mechanical Characterization of Additively Manufactured Parts by FE Modeling of Mesostructure. J. Manuf. Mater. Process. 2017, 1, 18. [Google Scholar] [CrossRef] [Green Version]
- Tian, C.; Li, X.; Chen, Z.; Guo, G.; Wang, L.; Rong, Y. Study on formability, mechanical property and finite element modeling of 3D-printed composite for metal-bonded diamond grinding wheel application. J. Manuf. Process. 2020, 54, 38–47. [Google Scholar] [CrossRef]
- Wang, Z.; Smith, D.E. Rheology Effects on Predicted Fiber Orientation and Elastic Properties in Large Scale Polymer Composite Additive Manufacturing. J. Compos. Sci. 2018, 2, 10. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Tian, X.; Zheng, Z.; Zhang, J.; Zhe, L.; Li, D.; Malakhov, A.V.; Polilov, A.N. A constitutive model for 3D printed continuous fiber reinforced composite structures with variable fiber content. Compos. Part B Eng. 2020, 189, 107893. [Google Scholar] [CrossRef]
- Cuan-Urquizo, A.B.E. Micromechanics of additively manufactured structures: Computational and laboratory experiments. In Proceedings of the XXIV Congreso Internacional Anual de la SOMIM, Campeche, Mexico, 21 September 2018; pp. 28–34. [Google Scholar]
- Park, S.-I.; Rosen, D.W. Quantifying effects of material extrusion additive manufacturing process on mechanical properties of lattice structures using as-fabricated voxel modeling. Addit. Manuf. 2016, 12, 265–273. [Google Scholar] [CrossRef] [Green Version]
- WOOD DATABASE, EUROPEAN BEECH. Available online: https://www.wood-database.com/european-beech/ (accessed on 29 December 2022).
- Shanmugam, V.; Das, O.; Babu, K.; Marimuthu, U.; Veerasimman, A.; Johnson, D.J.; Neisiany, R.E.; Hedenqvist, M.S.; Ramakrishna, S.; Berto, F. Fatigue behavior of FDM-3D printed polymers, polymeric composites and architected cellular materials. Int. J. Fatigue 2021, 143, 106007. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Pierard, O.; González, C.; Segurado, J.; Llorca, J.; Doghri, I. Micromechanics of elasto-plastic materials reinforced with ellipsoidal inclusions. Int. J. Solids Struct. 2007, 44, 6945–6962. [Google Scholar] [CrossRef] [Green Version]
- de Souza Neto, E.A.; Feijóo, R.A. Variational foundations of multi-scale constitutive models of solid: Small and large strain kinematical formulation. LNCC Res. Dev. Rep. 2006, 16, 1–53. [Google Scholar]
- Nguyen, V.-D.; Béchet, E.; Geuzaine, C.; Noels, L. Imposing periodic boundary condition on arbitrary meshes by polynomial interpolation. Comput. Mater. Sci. 2012, 55, 390–406. [Google Scholar] [CrossRef]




| Property | Young’s Modulus (GPa) | Poisson Ratio |
|---|---|---|
| Wood | 14.31 | 0.4 |
| PLA | 3.72 | 0.35 |
| Wood Volume Fraction | Pore Volume Fraction for Full Range (0.43 mm–0.09 mm) | Pore Volume Fraction for Small Range (0.2 mm–0.09 mm) | Experimental Values | ||||
|---|---|---|---|---|---|---|---|
| 2% | 5% | 7% | 2% | 5% | 7% | ||
| 0% | 3.5642 | 3.3724 | 3.1822 | 3.5818 | 3.397 | 3.2867 | 3.27 |
| 10% | 4.0084 | 3.7825 | 3.6383 | 4.0754 | 3.83 | 3.6934 | 3.63 |
| 20% | 4.5054 | 4.2765 | 4.0632 | 4.5206 | 4.3004 | 4.1524 | 3.94 |
| 30% | 4.9888 | 4.6385 | 4.3587 | 5.0023 | 4.6336 | 4.3701 | 3.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezzaraa, I.; Ayrilmis, N.; Abouelmajd, M.; Kuzman, M.K.; Bahlaoui, A.; Arroub, I.; Bengourram, J.; Lagache, M.; Belhouideg, S. Numerical Modeling Based on Finite Element Analysis of 3D-Printed Wood-Polylactic Acid Composites: A Comparison with Experimental Data. Forests 2023, 14, 95. https://doi.org/10.3390/f14010095
Ezzaraa I, Ayrilmis N, Abouelmajd M, Kuzman MK, Bahlaoui A, Arroub I, Bengourram J, Lagache M, Belhouideg S. Numerical Modeling Based on Finite Element Analysis of 3D-Printed Wood-Polylactic Acid Composites: A Comparison with Experimental Data. Forests. 2023; 14(1):95. https://doi.org/10.3390/f14010095
Chicago/Turabian StyleEzzaraa, Ismail, Nadir Ayrilmis, Mohamed Abouelmajd, Manja Kitek Kuzman, Ahmed Bahlaoui, Ismail Arroub, Jamaa Bengourram, Manuel Lagache, and Soufiane Belhouideg. 2023. "Numerical Modeling Based on Finite Element Analysis of 3D-Printed Wood-Polylactic Acid Composites: A Comparison with Experimental Data" Forests 14, no. 1: 95. https://doi.org/10.3390/f14010095
APA StyleEzzaraa, I., Ayrilmis, N., Abouelmajd, M., Kuzman, M. K., Bahlaoui, A., Arroub, I., Bengourram, J., Lagache, M., & Belhouideg, S. (2023). Numerical Modeling Based on Finite Element Analysis of 3D-Printed Wood-Polylactic Acid Composites: A Comparison with Experimental Data. Forests, 14(1), 95. https://doi.org/10.3390/f14010095







