Optimizing Wildlife Habitat Management in Socio-Ecological Systems: An Evolutionary Game Theory Approach

Abstract

This paper focuses on the issue of balancing interests between stakeholders and ecosystems in the process of wildlife habitat conservation. By employing evolutionary game theory, an analysis framework for the socio-ecological system of wildlife habitats is constructed, comprising four main entities: central government, farmers, local government, and ecosystems. This framework explores the influencing factors of habitat protection strategies adopted by various stakeholders and the conditions required for the socio-ecological system to evolve towards an ideal state. In this paper, we analyze how the central government can design cost–benefit-based policy mechanisms, control the evolution of the socio-ecological system by altering conditions, and achieve a balance of interests among all parties involved in the habitat protection process. In this study, we find that the central government should establish disturbance monitoring indicators for human activities and ecological restoration, based on different compensation standards. Moreover, the hierarchical management of wildlife habitat according to different management levels can enhance the probability of the socio-ecological system evolving towards an ideal state, while achieving the sum of social costs. Additionally, shifting the compensation strategies for farmers and local governments from cost compensation to benefit compensation will reduce the harmful costs that the ecosystem imposes on the social system, thereby facilitating the realization of an ideal wildlife habitat protection and management model. Therefore, the central government should intensify compensation efforts and design reasonable compensation standards, transitioning the compensation function from cost recovery to income generation. Simultaneously, guidance should be provided to farmers for the rational utilization of forest resources to increase their income. The alignment of agricultural activities with habitat protection goals should be encouraged, and local governments should establish mechanisms for realizing the value of ecological products, making relatively implicit long-term social welfare explicit.

1. Introduction

The ideal model for wildlife habitat protection and management entails a harmonious interaction between wildlife and the natural environment, while maintaining distinct boundaries between wildlife territories and human activity zones [1,2]. However, in comparison to habitats formed through natural succession, wildlife distribution areas in China have experienced various human disturbances since 1949, including deforestation, agricultural development, afforestation, and infrastructure construction. These activities have led to habitat fragmentation, reduced habitat quality, and diminished carrying capacity, resulting in the endangerment of certain species [3,4,5,6]. To counteract the decline in habitat quality, China initiated ecological restoration projects such as the “Grain for Green Program”, “Natural Forest Conservation Project”, and the establishment of nature reserves after 1992. These endeavors aimed to expand habitat ranges and enhance habitat quality. Over time, as a result of these efforts, endangered species populations such as the giant panda and Asian elephant experienced population recovery. However, certain unsustainable human interventions and policy measures within ecological restoration efforts have led to habitat unsuitability and fragmentation, consequently reducing ecosystem carrying capacity [1,7]. Wildlife exceeding the carrying capacity of their habitats gradually disperses into human-inhabited areas, increasing the risk of conflicts with humans [8,9].

In the realm of wildlife habitat protection and management, scholars have primarily focused on four areas: wildlife and habitat monitoring, factors influencing habitat carrying capacity, mechanisms of human policy interventions to enhance carrying capacity, and conflict management between humans and wildlife. Research in the first category centers on wildlife and habitat monitoring to understand the interaction between wildlife population sizes, densities, distributions, trends, and geographical patterns in relation to the surrounding environment. This aids in evaluating habitat quality and changes [10,11,12,13,14,15,16]. The second category quantitatively assesses the maximum wildlife population a habitat can sustain. It explores habitat evaluation, habitat selection, wildlife diet, behavior studies, and migratory dynamics to identify factors influencing habitat carrying capacity [17,18,19,20]. The third category focuses on human interventions and habitat environmental capacity through ecological restoration. It evaluates the effectiveness of ecological restoration projects, corridor construction, and habitat restoration plans to enhance habitat environmental capacity [21,22,23,24]. The fourth category explores optimized conflict management models between humans and wildlife, investigating the mechanisms and efficacy of conflict occurrence and mitigation measures [25,26,27,28,29].

The abovementioned studies focused on wild animals and habitats as research subjects using observational indicators such as habitat carrying capacity, population numbers, and habitat quality. These indicators are used to assess the effectiveness of habitat conservation policies by analyzing changes in these indicators over time. However, improving habitat quality and expanding habitat areas inevitably involve the interests of stakeholders in the vicinity of these habitats, and, specifically, the impact of forest management policies on the interests of these stakeholders. Therefore, the design and evaluation of wildlife habitat conservation and management systems must take into account the stakeholders in human society who interact with the ecosystem to pursue their own interests, forming a balance in the process. Existing research indicates that the surrounding environment of habitats is a complex system composed of interactions between the population, resources, and social and economic systems, with a certain structure and functionality. The four most important interest groups in this complex system are the central government, local government, farmers, and the ecosystem itself. The optimal mechanism for the protection and management of wildlife habitat should involve the central government controlling the behavior of local governments and farmers through cost–benefit-based policies, indirectly improving ecosystem stability, and thereby enhancing habitat quality while achieving a balance of interests among all parties.

To depict the equilibrium of interests arising from the mutual interactions between stakeholders, we draw insights from the socio-ecological framework, which captures the complex relationships between natural and social systems [29,30,31]. Additionally, the application of evolutionary game theory helps us to model the dynamic evolution of strategies toward equilibrium. We consider the giant panda as a flagship species, which has garnered the attention of researchers worldwide. Over the years, the forestry policies, conservation policies, and socio-economic conditions in the region of the giant panda in China have been characterized by their ability to reflect the interactive effects between the human-activity-disturbed social system and the ecosystem in which the habitat is located. Using this framework, this study aims to explore the factors influencing the strategies adopted by stakeholders and the conditions for the socio-ecological system to evolve towards an ideal state. It also analyzes how the central government can design cost–benefit-based policy mechanisms to control the evolution of the socio-ecological system, achieving a balance of interests among stakeholders in the habitat protection process. In the subsequent sections of this paper, we will construct a socio-ecological system and evolutionary game model to delve into the equilibrium dynamics between stakeholders and their interaction with the ecosystem. We will explore the factors influencing the strategies of each stakeholder, identify conditions for the evolution of the system to an optimal mode, and analyze how the central government’s policy interventions can shape the evolution of the system. Additionally, we will provide discussions and prospects for future research.

2. Materials and Methods

2.1. Model Assumption

In order to characterize the complex relationship of mutual interactions and feedback in the socio-ecological system, we use an evolutionary game model. In this article, we combine relevant policies such as the “Wildlife Protection Law of the People’s Republic of China” and the “China Giant Panda Conservation and Recovery Plan”, which include provisions for compensation, rewards, and penalties, as well as practical policies for habitat conservation. Drawing from the relevant literature, we make the following assumptions. Hypotheses 1–4 are primarily used to elucidate the influence of the social system on the ecological system, while Hypothesis 5 is primarily used to clarify the impact of the ecological system on the social system.

Hypothesis 1.

These assumptions primarily elucidate the four components of the socio-ecological system of the wildlife habitat and the strategic choice space within each of these four components.

At the landscape scale, the landscape is partitioned into protection patches managed by local governments, cultivated land managed by farmers, and collective forest patches, with the ecological system represented by forest patches. The suitability of the wildlife habitat at this scale hinges upon the spatial configuration, pattern, and dynamic alterations of these three patches. The central government’s selection of “profit-based compensation mechanisms” and “cost-based compensation mechanisms” is governed by probabilities $\left(x,1-x\right)$. Local governments opt between strategies of “controlling negative human activities” and “not controlling negative human activities” with probabilities $\left(y,1-y\right)$, while farmers choose strategies of “integrating production practices with habitat goals” and “conflicting production practices with habitat goals” with probabilities $\left(z,1-z\right)$. The ecological system, guided by its stability, determines the probabilities of “favorable succession behavior enhancing habitat suitability” and “unfavorable succession behavior detrimental to habitat suitability”$(w,1-w)$. Here, $0\le x,y,z,w\le 1$.

Hypothesis 2.

These assumptions mainly elaborate on the components within the social subsystem, particularly the farmers and local government entities, and their costs and benefits in the process of habitat conservation.

They also describe the mechanisms through which these components interact with the ecological subsystem. When farmers adopt “production practices integrated with habitat goals”, the associated benefits and costs are represented as $R_3$ and $C_3$, respectively. An ecological restoration index $\alpha \left(0<\alpha <1\right)$ characterizes the extent to which the conversion of cultivated land patches to habitat patches is achieved through farming practices. For instance, an increase in the proportion of cultivated land converted to ecological forest patches enhances habitat quality. In contrast, when farmers select “production practices conflicting with habitat goals,” the benefits and costs shift to $R_3^{\prime }$ and $C_3^{\prime }$, respectively. In cases where local governments opt for “controlling negative human activities”, the benefits and costs are denoted as $R_2$ and $C_1$, respectively. The human activity interference control index $\gamma$ $\left(0<\gamma <1\right)$ indicates the capacity of transforming interference patches (regions managed by local governments for economic development) into habitat patches. For instance, the establishment of a protective land system by the local government controls human activity interference, thereby mitigating the rate of patch changes.

Hypothesis 3.

This assumption outlines how the central government within the social subsystem influences the local government entities and farmers within the social subsystem through two different compensation strategies.

The central government implements profit-based and cost-based compensation mechanisms based on habitat quality monitoring results. The profit-based compensation mechanism entails compensating local governments for protection efforts and habitat quality restoration, in alignment with the benefits they accrue. A local government incentive coefficient $\sigma$ is designed to determine compensation, with profit-based compensation represented as $\sigma R_2$. For instance, it might involve transferring resource usage rights to local governments or delegating wildlife approval authority to provincial authorities. No incentives are provided if habitat quality remains unrecovered. A farmer incentive coefficient $\epsilon$ is established to motivate farmers whose production practices align with habitat goals and facilitate habitat recovery. In such cases, compensation is granted proportionally to their production revenue, represented as $\epsilon R_3$. For example, this might involve providing interest-free loans to support farmers in ecological industries. No compensation is offered if habitat quality remains unrecovered. The cost-based compensation mechanism involves compensating local governments for protection costs incurred during habitat quality restoration. A compensation coefficient ${\sigma }^{\prime }$ is designed for local governments, and the compensation amount is ${\sigma }^{\prime }{C}_1$ if habitat quality has been restored. Similarly, a compensation coefficient ${\epsilon }^{\prime }$ is designed for farmers who adhere to habitat goals and contribute to habitat quality restoration. Their compensation is ${\epsilon }^{\prime }{C}_3$ if habitat quality has been restored. In either compensation mechanism, when local governments and farmers fail to adopt proactive protection measures, penalties $P_1$ and $P_2$ are enforced individually $(P_1>P_2)$.

Hypothesis 4.

This assumption primarily explains the reasons behind the stability of the ecological system using insights drawn from economic theories regarding cost and benefit mechanisms.

It further elucidates the mechanisms through which the social subsystem impacts the ecological subsystem. Drawing on ecological restoration principles, the ecological system possesses resistance to invasion [32]. The pre- and post-implementation landscape changes due to ecological restoration and human activity control measures inducing net value variations in the ecological system. Conforming to the “Norm for Assessing Forest Ecosystem Services” (LY/T 1721-2008) [33], ecosystem benefits prior to protection measures are defined as $R_4$, encompassing water retention, soil conservation, and biodiversity preservation. Ecological costs entail disturbances detrimental to ecosystem stability, encompassing pest infestations, natural disasters, deforestation, environmental pollution, economic development, and greenhouse gas emissions, denoted as $C_5$. Ecosystem stability generates a surplus of $R_4-C_5>0$, favoring habitat quality restoration through favorable succession behavior. Additionally, under the profit-based compensation mechanism, the ecological restoration index $\alpha$ can enhance the stability of the ecosystem by increasing the density and connectivity of habitat patches, represented as αR_4. The human activity disturbance index $\gamma$ reflects the degree of fragmentation of habitat patches and reduces the ecosystem’s cost, expressed as $\gamma C_5$. In the case of the cost-based compensation mechanism, the ecological restoration index is denoted as ${\alpha }^{\prime }$, and it can enhance the stability of the ecosystem by increasing the density and connectivity of habitat patches, represented as ${\alpha }^{\prime }{R}_4$. The human activity disturbance index $\gamma$ reflects the degree of habitat patch fragmentation and reduces the ecosystem’s cost, expressed as ${\gamma }^{\prime }{C}_5$. Furthermore, when the ecosystem is favorable for habitat quality restoration, instances of wildlife-induced damage increase. Conversely, when the ecosystem is less favorable for restoration, incidents of wildlife-induced damage are relatively few.

Hypothesis 5.

This assumption primarily elucidates the mechanisms through which the ecological subsystem impacts the social subsystem.

Building upon the aforementioned set of assumptions, the impact of the ecosystem on the social system is outlined as follows. In scenarios where ecosystem succession behaviors favor the augmentation of habitat suitability, there ensues a restorative growth in the population of endangered wildlife species. This growth is tempered by the elevated carrying capacity of the habitat, leading to a reduction in the risk of wildlife spillover into human activity areas. Consequently, the resultant costs associated with harmful incidents caused by wildlife encroachment into human domains are denoted as $C_4$. The ecosystem concurrently generates a quantifiable service value designated as $S$, while various departments of the central government receive ecological benefits delineated as $R_1.$Contrarily, when ecosystem succession behaviors prove unfavorable to the enhancement of habitat suitability, a decline is observed in the population of endangered wildlife species. This decline is accentuated by the diminished carrying capacity of the habitat, consequently amplifying the detrimental costs resulting from the diffusion of wildlife into human activity areas. In this context, the harmful costs are represented as $C_4^{\prime }$, where $C_4<C_4^{\prime }$. The ecosystem produces a modified service value designated as $S^{\prime }$, while diverse departments of the central government acquire ecological benefits indicated as $R_1^{\prime }$. In alignment with the division of responsibilities between the central government and local administrations, the onus of wildlife prevention and control is borne by the local government. The local government predominantly employs a triad of strategies—compensation for harm, monitoring and early warning mechanisms, and population regulation—to proactively manage and mitigate wildlife-related incidents. The aggregated expenditure encompassing these prevention and control endeavors is quantified as $C_2$. This framework encompasses the formulation of a compensatory standard, referred to as $\beta$, which is designed to offer recompense to affected stakeholders or beneficiaries.

2.2. Model Construction

2.2.1. Model Parameters

In this article, we summarize and provide detailed explanations for the 34 parameters or variables mentioned in the above assumptions, as given in

Table 1. The parameters comprising the components of the wildlife habitat socio-ecosystem.

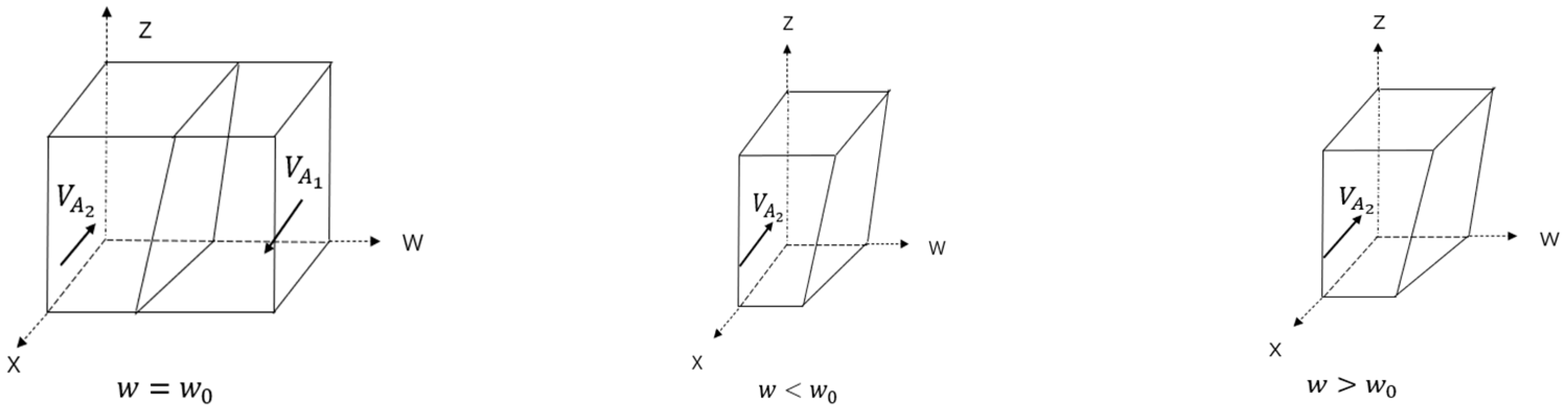
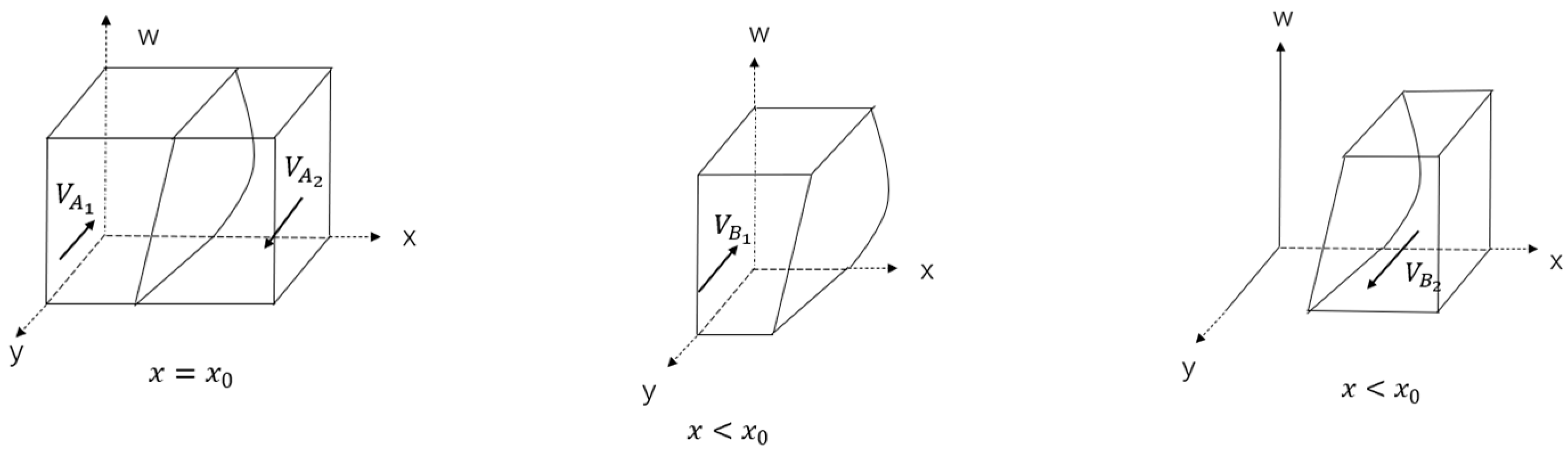
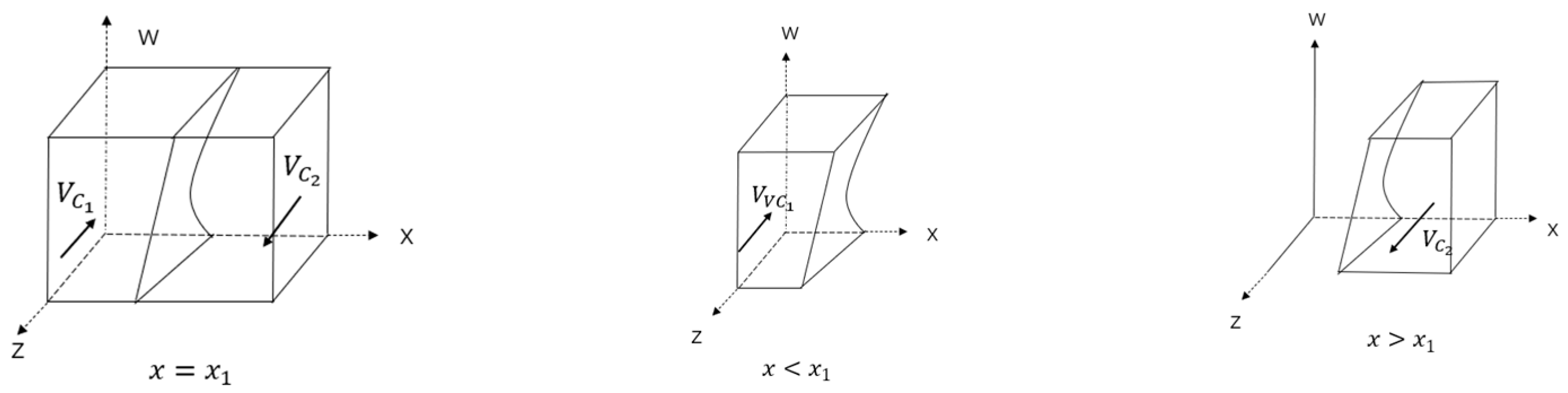
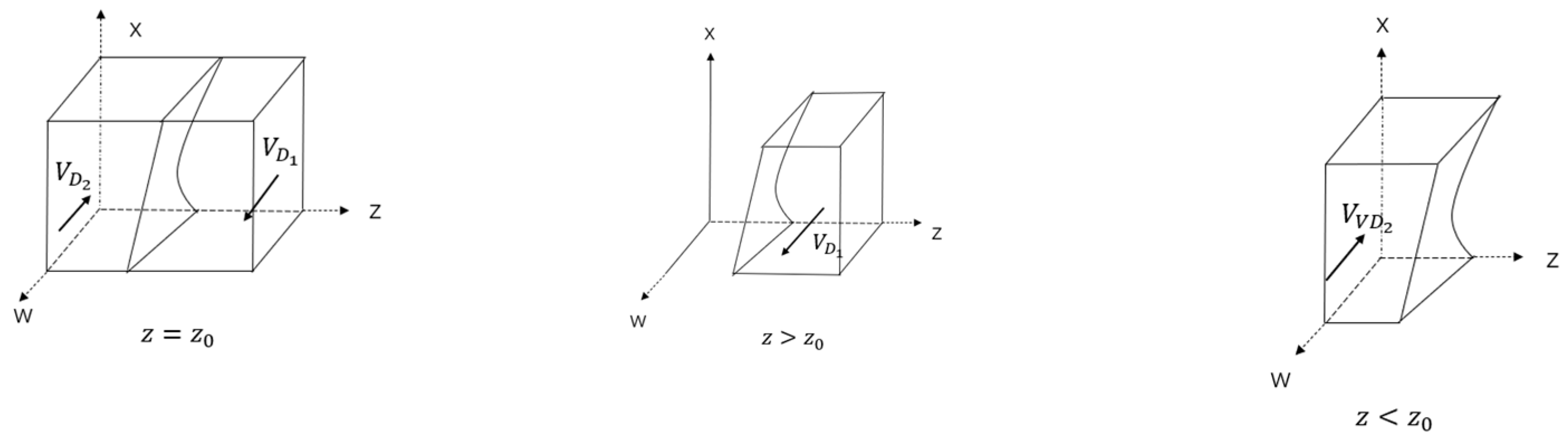
Parameter	Explanation
Central Government Costs and Benefits
$R_1$	Ecological Benefits: The gains obtained by the central government when habitat suitability increases due to effective conservation efforts.
$R_1^{\prime }$	Ecological Benefits: The gains obtained by the central government when habitat suitability decreases, resulting in negative ecological changes and potential environmental consequences.
$\sigma R_2$	Protection Compensation: The compensation provided by the central government to local governments in return for the protection benefits they generate through habitat conservation measures.
$\epsilon R_3$	Protection Compensation: The compensation provided by the central government to farmers in return for the protection benefits they contribute to through aligning their production behaviors with habitat conservation goals.
${\sigma }^{\prime }{C}_1$	Protection Compensation: The compensation provided by the central government to local governments to offset the protection costs they incur during habitat conservation activities.
${\epsilon }^{\prime }{C}_3$	Protection Compensation: The compensation provided by the central government to farmers to offset the protection costs they incur while aligning their production behaviors with habitat conservation goals.
$P_1$	Punitive Costs: The costs incurred by the central government when it enforces the strict delineation of protected areas within important habitat zones, resulting in the prohibition of economic activities.
$P_2$	Punitive Costs: The costs incurred by the central government when it enforces the strict delineation of protected areas within important habitat zones, leading to the prohibition of agricultural and forestry cultivation activities.
Local Government Costs and Benefits
$R_2$	Protection Benefits: The benefits accrued by the local government from engaging in ecological industries aimed at conserving the habitat.
$R_2^{\prime }$	Economic Benefits of Non-Protection: The ecological benefits gained by the local government due to a decrease in habitat quality, resulting in potential economic benefits associated with not protecting the habitat.
$C_1$	Opportunity and Direct Costs of Habitat Protection: The economic costs and direct investments incurred by the local government when implementing habitat restoration and expanding protective measures, including the economic development opportunities foregone.
$C_1^{\prime }$	Opportunity Cost of Non-Protection: The potential benefits forgone by the local government due to not protecting the habitat.
$C_2$	Compensation Costs for Wildlife Damage: The costs borne by the local government for compensating damages caused by wildlife incidents, as part of their preventive and control measures.
$\beta C_4$	Costs of Wildlife Damage Prevention and Control: The compensation provided by the local government to affected farmers in cases where ecological succession benefits habitat restoration and leads to improved habitat quality.
$\beta C_4^{\prime }$	Costs of Wildlife Damage Prevention and Control: The compensation provided by the local government to affected farmers in cases where ecological succession hinders habitat restoration and leads to decreased habitat quality.
Farmers’ Costs and Benefits
$R_3$	Habitat Conservation Benefit: The gains obtained by farmers through engaging in production activities that align with habitat conservation objectives, leading to improved habitat quality.
$R_3^{\prime }$	Non-Habitat Conservation Benefit: The gains achieved by farmers when their production practices conflict with habitat conservation goals, resulting in revenue generation.
$C_3$	Opportunity Cost of Habitat Conservation: The costs incurred by farmers when choosing production practices that align with habitat conservation goals, leading to potential economic losses.
$C_3^{\prime }$	Cost of Non-Habitat Conservation: The costs borne by farmers due to engaging in production practices that contradict habitat conservation objectives, resulting in economic expenses.
$C_4$	Cost of Wildlife Damage: The expenses incurred by farmers as a consequence of wildlife causing property damage, in situations where ecological succession behaviors contribute to habitat quality recovery.
$C_4^{\prime }$	Cost of Wildlife Damage: The expenses incurred by farmers as a consequence of wildlife causing property damage, in situations where ecological succession behaviors hinder habitat quality recovery.
Ecological System Costs and Benefits
$R_4$	Ecological Benefit: The gains in ecological system value resulting from habitat quality improvement, contributing to increased stability and enhanced ecosystem services.
$C_5$	Ecological Cost: The benefits derived from the functions of the ecological system, such as water conservation, soil preservation, and biodiversity protection, prior to the implementation of protective measures.
$S$	Ecological System Stability Cost: The disruptions to ecological system stability caused by factors such as plant diseases, pests, natural disasters, deforestation, environmental pollution, and economic activities.
$S^{\prime }$	Ecological System Service Value: The value of services generated by the ecological system when it contributes to habitat quality restoration.
Regulation Coefficient
$\gamma$	Human Activity Disturbance Index: Under the profit compensation mechanism, the interference of human activities such as economic development with the habitat, indirectly reflecting the local government’s control over human activity interference.
$\alpha$	Ecological Restoration Index: Under the profit compensation mechanism, the degree to which the production behavior chosen by farmers aligns with habitat protection goals, reflecting the density and connectivity of habitat patches.
${\gamma }^{\prime }$	Human Activity Disturbance Index: Under the cost compensation mechanism, the interference of human activities such as economic development with the habitat, indirectly reflecting the local government’s control over human activity interference.
${\alpha }^{\prime }$	Ecological Restoration Index: Under the profit compensation mechanism, the degree to which the production behavior chosen by farmers aligns with habitat protection goals, reflecting the density and connectivity of habitat patches.
$\beta$	Compensation Standard for Farmers’ Damage: The compensation ratio provided by local governments to farmers.
$\sigma$	Profit Compensation Coefficient: The compensation ratio provided by the central government to the local government for the protection benefits obtained.
${\sigma }^{\prime }$	Cost Compensation Coefficient: The compensation ratio provided by the central government to the local government for the protection costs incurred.
$\epsilon$	Profit Compensation Coefficient: The compensation ratio provided by the central government to farmers for the protection benefits obtained.
${\epsilon }^{\prime }$	Cost Compensation Coefficient: The compensation ratio provided by the central government to farmers for the protection costs incurred.

.

2.2.2. Model Construction Process

According to the model assumptions, the mechanism of social–ecological system interactions can be characterized by delineating the equilibrium of interests that arises through the mutual influence of the four stakeholders, including the ecological system, to achieve their respective goals. This process can be decomposed into three parts: the impact of the social subsystem on the ecological subsystem, the impact of the ecological subsystem on the social subsystem, and the mutual interactions between the social subsystem and the ecological subsystem. In each part, the four stakeholders are interconnected through their respective costs and benefits, forming chains of interests.

As shown in Figure 1, the impact of the social system on the ecological system constitutes two chains of interests. The first chain, Chain A (represented by the gray box in Figure 1), represents the influence of the ecological restoration index, constructed by the central government to control farmers’ production behaviors, on the benefits of ecological system stability. It attempts to change the costs or benefits of farmer stakeholders by selecting different compensation strategies, affecting their production behaviors. In this chain, the central government’s interests are reflected in the difference between the ecological benefits generated by changes in habitat quality and the compensation costs paid. The interests of the farmers are reflected in the total benefits obtained by summing the benefits generated by production behaviors that align or conflict with habitat conservation goals, minus the costs incurred by different production behaviors. The second chain, Chain B (represented by the red box in Figure 1), represents the impact of the human activity disturbance index, constructed by the central government to control the local government’s economic development behaviors in the vicinity of habitats, on the costs of ecological system stability. It aims to influence the efforts of various levels of local government in controlling human activity disturbance through different compensation strategies. In this chain, the central government’s benefits are reflected in the difference between the ecological benefits generated by changes in habitat quality and the compensation costs paid. The interests of local governments are reflected in the total benefits obtained by summing the benefits generated by choosing different degrees of human activity disturbance control strategies and subtracting the economic development benefits forfeited for habitat protection.

The ecological system’s interests are represented by the difference between the impact value of the ecological restoration index on stability benefits in the first chain and the impact value of the human activity disturbance index on stability costs in the second chain. When this value is positive, the ecological system gains surplus stability, and its successional behavior benefits habitat quality restoration. When it is negative, the ecological system incurs a deficit in stability, and its successional behavior is detrimental to habitat quality restoration.

The impact of the ecological system on the social system is primarily manifested in changes in ecological system stability, which subsequently lead to changes in the carrying capacity and range of the wildlife habitat. Among these, benefit chain C (represented by the yellow box in Figure 1), resulting from changes in wildlife habitat carrying capacity is characterized by the influence of different frequencies of wildlife damage behavior on farmer stakeholders’ costs. In this process, local government compensates farmers for their costs through a wildlife damage compensation system. Benefit chain D (represented by the white box in Figure 1), arising from changes in the range of wildlife habitat, is characterized by the possibility of an increase in the local government’s conservation costs due to the expansion in habitat range.

The interactive effects between the social system and the ecological system are reflected in the dynamic changes in the ecological restoration index and the human activity disturbance index. The ecological restoration index is measured through production behaviors based on farmer cost–benefit considerations, and it depends on the compensation strategies of the central government in benefit chain A and the compensation strategies chosen by farmers. The human activity disturbance index is measured through control measures related to human activities based on local government cost–benefit considerations. This index depends on three factors: firstly, the compensation strategies of the central government in benefit chain B and the conservation strategies of local government; secondly, the costs incurred by local government due to changes in habitat range, as shown in benefit chain D; and thirdly, the costs borne by local government for wildlife damage, as indicated in benefit chain C.

The above social–ecological system interaction process can be represented by a payoff matrix, as shown in

Table 2. Payoff matrix for four-way game within wildlife habitat social–ecological system.

Strategy Selection			Various Departments of the Central Government
		Farmers	$\mathbf{Profit}\mathbf{Compensation}\mathbf{Mechanism}$ x		$\mathbf{Cos}\mathbf{t}\mathbf{Compensation}\mathbf{Mechanism}$ 1 − x
			$\mathbf{Ecological}\mathbf{Succession}\mathbf{Favors}\mathbf{Habitat}\mathbf{Quality}\mathbf{Restoration}$ w	$\mathbf{Ecological}\mathbf{Succession}\mathbf{Hinders}\mathbf{Habitat}\mathbf{Quality}\mathbf{Restoration}.$ 1 −w	$\mathbf{Ecological}\mathbf{Succession}\mathbf{Favors}\mathbf{Habitat}\mathbf{Quality}\mathbf{Restoration}$ w	$\mathbf{Ecological}\mathbf{Succession}\mathbf{Hinders}\mathbf{Habitat}\mathbf{Quality}\mathbf{Restoration}.$ 1 −w
Local governments at various levels	Control of human activities interference $\mathit{y}$	$\mathrm{Production}\mathrm{behavior}\mathrm{aligned}\mathrm{with}\mathrm{habitat}\mathrm{conservation}\mathrm{objectives}$ z	$a_1=R_1+S-\sigma R_2-\epsilon R_3$	${b_1=R}_1^{\prime }+S^{\prime }$	$c_1=R_1+S-{\sigma }^{\prime }{C}_1-{\epsilon }^{\prime }{C}_3$	${d_1=R}_1^{\prime }+S^{\prime }$
			$a_2={S+(1+\sigma )R}_2-C_1-\beta C_4$	$b_2{=S}^{\prime }+R_2-C_1-\beta C_4^{\prime }$	$c_2=S+({\sigma }^{\prime }-1)C_1-\beta C_4$	$d_2{=S}^{\prime }+R_2-C_1-\beta C_4^{\prime }$
			$a_3=S+\left(1+\epsilon \right)R_3-C_3+(\beta -1)C_4$	$b_3=S^{\prime }+R_3-C_3+(\beta -1)C_4^{\prime }$	$c_3=S+R_3+({\epsilon }^{\prime }-1)C_3+(\beta -1)C_4$	$d_3{=S}^{\prime }+R_3-C_3-\beta C_4^{\prime }$
			$a_4=(1+\alpha )R_4{-(1+\gamma )C}_5$	$b_4=-[(1+\alpha )R_4{-(1+\gamma )C}_5]$	$c_4=(1+{\alpha }^{\prime })R_4{-(1+{\gamma }^{\prime })C}_5$	$d_4=-[(1+{\alpha }^{\prime })R_4{-(1+{\gamma }^{\prime })C}_5]$
		$\mathrm{Production}\mathrm{behavior}\mathrm{conflicting}\mathrm{with}\mathrm{habitat}\mathrm{conservation}\mathrm{objectives}$ 1 − z	${e_1=S+R}_1-{\sigma R}_2+P_2$	${{f_1=S}^{\prime }+R}_1^{\prime }+P_2$	$g_1=R_1+S-{\sigma }^{\prime }{C}_1+P_2$	${h_1=S^{\prime }+R}_1^{\prime }+P_2$
			$e_2={S+(1+\sigma )R}_2-C_1-\beta C_4$	$f_2{=S}^{\prime }+R_2-C_1-\beta C_4^{\prime }$	$g_2=S+R_2+({\sigma }^{\prime }-1)C_1-\beta C_4$	${h_2=S}^{\prime }+R_2-C_1-\beta C_4^{\prime }$
			$e_3={S+R}_3^{\prime }{-C}_3^{\prime }-P_2+\left(\beta -1\right)C_4$	$f_3{{=S}^{\prime }+R}_3^{\prime }-C_3^{\prime }-P_2+\left(\beta -1\right)C_4^{\prime }$	$g_3={S+R}_3^{\prime }{-C}_3^{\prime }-P_2+\left(\beta -1\right)C_4$	$h_3{{=S}^{\prime }+R}_3^{\prime }-C_3^{\prime }-P_2+\left(\beta -1\right)C_4^{\prime }$
			$e_4=R_4{-(1+\gamma )C}_5$	$f_4=-\left[R_4{-(1+\gamma )C}_5\right]$	$g_4=R_4{-(1+{\gamma }^{\prime })C}_5$	$h_4=-\left[R_4{-(1+{\gamma }^{\prime })C}_5\right]$
	$\mathrm{Uncontrolled}\mathrm{human}\mathrm{activities}\mathrm{interference}$ 1 − y	$\mathrm{Production}\mathrm{behavior}\mathrm{aligned}\mathrm{with}\mathrm{habitat}\mathrm{conservation}\mathrm{objectives}$ z	${i_1=S+R}_1-\epsilon R_3+P_1$	${j_1=S^{\prime }+R}_1^{\prime }+P_1$	$h_1=R_1+S-{\epsilon }^{\prime }{C}_3+P_1$	${l_1=S^{\prime }+R}_1^{\prime }+P_1$
			$i_2=S+R_2^{\prime }-C_1^{\prime }-\beta C_4-P_1$	$j_2=S^{\prime }+R_2^{\prime }-C_1^{\prime }-\beta C_4^{\prime }-P_1$	$h_2=S+R_2^{\prime }-C_1^{\prime }-\beta C_4-P_1$	$l_2=S^{\prime }+R_2^{\prime }-C_1^{\prime }-\beta C_4^{\prime }-P_1$
			$i_3=S+\left(1+\epsilon \right)R_3-C_3+(\beta -1)C_4$	$j_3{=S}^{\prime }+R_3-C_3+(\beta -1)C_4^{\prime }$	$h_3=S+R_3+\left(1-{\epsilon }^{\prime }\right)C_3+(\beta -1)C_4$	$l_3{=S}^{\prime }+R_3-C_3+(\beta -1)C_4^{\prime }$
			$i_4=(1+\alpha )R_4{-C}_5$	$j_4=-[(1+\alpha )R_4{-C}_5]$	$h_4=(1+{\alpha }^{\prime })R_4{-C}_5$	$d_4=-[(1+{\alpha }^{\prime })R_4{-C}_5]$
		$\mathrm{Production}\mathrm{behavior}\mathrm{conflicting}\mathrm{with}\mathrm{habitat}\mathrm{conservation}\mathrm{objectives}$ 1 − z	$m_1=R_1+S+P_1{+P}_2$	${n_1=S^{\prime }+R}_1^{\prime }+P_1{+P}_2$	$o_1=R_1+S+P_1{+P}_2$	${p_1=S^{\prime }+R}_1^{\prime }+P_1{+P}_2$
			$m_2={S+R}_2^{\prime }-C_1^{\prime }-P_1-\beta C_4$	$n_2={S^{\prime }+R}_2^{\prime }-C_1^{\prime }-P_1-\beta C_4^{\prime }$	$o_2={S+R}_2^{\prime }-C_1^{\prime }-P_1-\beta C_4$	$p_2={S^{\prime }+R}_2^{\prime }-C_1^{\prime }-P_1-\beta C_4^{\prime }$
			$m_3={S+R}_3^{\prime }{-C}_3^{\prime }-P_2+\left(\beta -1\right)C_4$	$n_3={S^{\prime }+R}_3^{\prime }{-C}_3^{\prime }-P_2+\left(\beta -1\right)C_4^{\prime }$	$o_3={S+R}_3^{\prime }{-C}_3^{\prime }-P_2+\left(\beta -1\right)C_4$	$p_3={S^{\prime }+R}_3^{\prime }{-C}_3^{\prime }-P_2+\left(\beta -1\right)C_4^{\prime }$
			$m_4=R_4{-C}_5$	$n_4=-(R_4{-C}_5)$	$o_4=R_4{-C}_5$	$p_4=-(R_4{-C}_5)$

, based on the principles of evolutionary game theory. This leads to the formation of 16 patterns of social–ecological system evolution, where each pattern consists of a payoff matrix for the four stakeholders, representing the gains obtained minus the costs incurred by each of them. Consequently, the problem of achieving stable equilibriums resulting from social–ecological system interactions can be transformed into four-player evolutionary games based on their respective strategies. This allows us to utilize the replicator dynamics equations from evolutionary game theory to study the factors influencing each stakeholder’s choice of habitat protection strategy within each system. Simultaneously, by solving the eigenvalues of the 16 evolutionary patterns, we can determine the conditions for achieving evolutionarily stable strategies (ESS). This helps us assess the idealized patterns of social–ecological system evolution under conditions where all parties achieve a balance of interests.

3. Analysis of Wildlife Habitat Social–Ecological System Stability

3.1. Stability Analysis of Strategies in the Wildlife Habitat Social–Ecological System Components

3.1.1. Stability Analysis of Central Government Strategies

The anticipated benefits of the “profit-based compensation mechanism” strategy chosen by the central government are denoted as $E_{11}$, while the expected benefits of the “cost-based compensation mechanism” strategy are represented as $E_{12}$. The average expected benefit is designated as $E_1$.

$$E_{11}=P_2-P_1-y\left(P_2-P_1+{\sigma }^{\prime }{C}_1+\sigma R_2\right)-z{\epsilon R}_3-zw\left(P_1-P_2\right)+yw(P_1-P_2)$$

$$E_{12}=y\left(P_2-P_1-2\sigma R_2\right)-z{\epsilon }^{\prime }{C}_3-yz(P_2-P_1+{2\epsilon R}_3+{2\epsilon }^{\prime }{C}_1)$$

$$E_1=x{E}_{11}+(1-x)E_{12}$$

$$\begin{array}{l}F\left(x\right)=\frac{\mathrm{d}x}{\mathrm{d}t}=x{(E}_{11}-E_1)\hfill \\ =x(1-x)[P_2-P_1-z\left({\epsilon R}_3-{\epsilon }^{\prime }{C}_3\right)+zw\left(P_1-P_2\right)\hfill \\ -y\left({\sigma }^{\prime }{C}_1-\sigma R_2\right)+yw\left(P_1-P_2\right)+yz(P_2-P_1+{2\epsilon R}_3\hfill \\ +{2\epsilon }^{\prime }{C}_1)]\hfill \end{array}$$

$$\begin{array}{c}A\left(w\right)=P_2-P_1-z\left({\epsilon R}_3-{\epsilon }^{\prime }{C}_3\right)+zw\left(P_1-P_2\right)-y\left({\sigma }^{\prime }{C}_1-\sigma R_2\right)\hfill \\ +yw\left(P_1-P_2\right)+yz\left(P_2-P_1+{2\epsilon R}_3+{2\epsilon }^{\prime }{C}_1\right)\hfill \end{array}$$

$$F^{\prime }\left(x\right)=\left(1-2\mathrm{x}\right)A\left(w\right)$$

Proposition 1 indicates that when $w>w_0$, the central government adopts a stable strategy of implementing a profit-based compensation mechanism. When the probability that ecological succession behavior favors habitat quality restoration is greater than $w_0$, the stable strategy of the central government shifts from a cost-based compensation mechanism to a profit-based compensation mechanism. The threshold value is

$$w_0=\frac{P_2-P_1-z\left({\epsilon R}_3-{\epsilon }^{\prime }{C}_3\right)-y\left({\sigma }^{\prime }{C}_1-\sigma R_2\right)+yz(P_2-P_1+{2\epsilon R}_3+{2\epsilon }^{\prime }{C}_1)}{\left(P_1-P_2\right)(y+z)}$$

According to the stability theorem of differential equations, the probability of the central government choosing a profit-based compensation strategy must be in a stable state, which satisfies the condition: $F\left(x\right)=0$ and $F^{\prime }\left(x\right)<0$. Since $\partial A\left(w\right)/\partial w<0$, it follows that $A\left(w\right)$ is an increasing function with respect to $w$. Therefore, when $w=w_0$, $A\left(w\right)=0$, at which point $F^{\prime }\left(x\right)=0$. In this case, the central government cannot determine a stable strategy. When $w>w_0$, $A\left(w\right)>0$, and at this point, $F{\left.\left(x\right)\right|}_{x=1}=0$ and $F^{\prime }{\left.\left(x\right)\right|}_{x=1}<0$. As a result, $x=1$ becomes the evolutionarily stable strategy (ESS) for the central government. Conversely, $x=0$ is the ESS. Proposition 1 indicates that the central government chooses to compensate farmers and local governments for their benefits only when the habitat quality has recovered to a certain state. Prior to reaching the threshold, the central government only chooses to compensate for costs.

The phase diagram of the central government’s strategy evolution is depicted in Figure 2. The diagram illustrates that the central government’s stable probability of adopting a cost-based compensation strategy is represented by the volume $V_{A_1}$, while the stable probability of adopting a profit-based compensation strategy is represented by the volume $V_{A_2}$. The calculations yield:

$$\begin{array}{c}{V}_{A_1}={\iint }_0^1\frac{P_2-P_1-z\left({\epsilon R}_3-{\epsilon }^{\prime }{C}_3\right)-y\left({\sigma }^{\prime }{C}_1-\sigma R_2\right)+yz(P_2-P_1+{2\epsilon R}_3+{2\epsilon }^{\prime }{C}_1)}{\left(P_2-P_1\right)(y+z)}dydz\hfill \\ \frac{\left[{8\epsilon }^{\prime }\left(1-\log \left(2\right))+3{\sigma }^{\prime }\right)\right]C_1-3\sigma R_2+8\log \left(2\right){\epsilon R}_3-4{\sigma }^{\prime }{C}_3}{6\left(P_2-P_1\right)}-\frac{2+4\log \left(2\right)}{3}\hfill \end{array}$$

$$V_{A_2}=1-V_{A_1}$$

Inference 1: The probability of the central government adopting a profit-based compensation strategy is positively correlated with the cost of habitat protection by local governments and the benefits of habitat protection by farmers. It is negatively correlated with the benefits of habitat protection by local governments and the cost of habitat protection by farmers.

Proof. 

According to the expression for the probability $V_{A_1}$ of the central government adopting a compensatory incentive strategy, we have $\partial V_{A_1}/\partial C_1)>0,\partial V_{A_1}/\partial R_3>0$, $\partial V_{A_1}/\partial R_2<0$, $\partial V_{A_1}/\partial C_3<0$. □

Inference 1 suggests that with the expansion in habitat scope, local governments would incur additional protection costs during the process of increasing their protection efforts. In such cases, the central government should implement policy compensations to ensure that local governments can benefit from habitat protection, thereby offsetting the incurred costs. At the level of individual farmers within the habitat, their profitable production behavior during ecological restoration should be further rewarded based on their gains, encouraging their production activities and enhancing habitat quality. At the local government level, if local governments continually benefit from habitat protection, the central government should evaluate how their profit-seeking behavior impacts the habitat. For instance, the excessive development of tourism might lead to significant artificial disturbances. In such cases, the central government should consider reducing policy support to avoid negative consequences. On the other hand, if farmers face increasing costs in aligning their production activities with habitat protection goals during the ecological restoration process, it could indicate poor market demand for their agricultural or forest products. In such scenarios, subsidizing their costs may be necessary to encourage them to continue cultivation.

3.1.2. Stability Analysis of Local Government Strategies

The local government’s expected benefits for choosing the “human activity interference control” strategy are denoted as $E_{21}$, while the expected benefits for selecting the “no control of negative human activity interference” strategy are represented as $E_{22}$. The average expected benefit is designated as $E_2$.

$$E_{21}={R_2}^{\prime }-P_1+x{C_1}^{\prime }+w\left(C_2+P_1\right)+zw({C_1}^{\prime }+P_1)$$

$$E_{22}=C_2{{+C}_1}^{\prime }+zw\left({C_1}^{\prime }+P_1\right)+w(C_1-\sigma R_2{-C}_2+{R_2}^{\prime })$$

$$\begin{array}{c}F\left(y\right)=\frac{dy}{dt}=y{(E}_{21}-E_2)=y(1-y)(E_{21}-E_{22})\hfill \\ =y(1-y)[{R_2}^{\prime }{-C}_2{{-C}_1}^{\prime }-P_1{{+C}_1}^{\prime }x+w\left({2C}_2+P_1-C_1+\sigma R_2-{R_2}^{\prime }\right)]\hfill \end{array}$$

$$B\left(x\right)={R_2}^{\prime }{-C}_2{{-C}_1}^{\prime }-P_1{{+C}_1}^{\prime }x+w\left({2C}_2+P_1-C_1+\sigma R_2-{R_2}^{\prime }\right)$$

$$F^{\prime }\left(y\right)=(1-2y)B\left(x\right)$$

According to the stability theorem of differential equations, the probability of the local government choosing the “control of human activity interference” strategy must be in a stable state, which satisfies the conditions $F\left(y\right)=0$ and $F^{\prime }\left(y\right)<0$. Since $B(x)$ is an increasing function, when $x=C_2{{+C}_1}^{\prime }+P_1-{R_2}^{\prime }-w\left({2C}_2{{+C}_1}^{\prime }+P_1-C_1+\sigma R_2\right)]/{C_1}^{\prime }=x_0$, $B\left(x\right)=0$, $dF\left(y\right)/dy=0$, and F(y) = 0. In this case, the local government cannot determine a stable strategy. When $x>x_0$, $B\left(x\right)>0$, $\mathrm{F}{\left.\left(y\right)\right|}_{y=1}=0$, and $F^{\prime }{\left.\left(y\right)\right|}_{y=1}<0$. Thus, $y=1$ becomes the evolutionarily stable strategy (ESS). Conversely, when $x<x_0$, $y=0$ is the ESS.

Proposition 2 asserts that the central government’s compensation to local governments is determined based on the scope of benefits from public goods. After the restoration of suitable conditions in the wild animal habitat, which possesses characteristics such as a broad beneficiary range and consumption externalities, such services should ideally be efficiently provided by higher-level governments such as the central government. However, the process of habitat protection unavoidably requires restricting the economic activities of local governments. Moreover, the scope of benefits following habitat quality restoration simultaneously has both local and central characteristics. Therefore, the division of rights and finances between “central” and “local” governments plays a crucial role in incentivizing local governments to protect the habitat. In the process of habitat protection, the central government should not solely rely on punitive financial instruments but should also utilize reward-based fiscal tools. It should reward local governments based on their gains during habitat protection, thus motivating them to control human activity interference.

The phase diagram of local government strategy evolution is depicted in Figure 3. As shown in the diagram, the volume of ${\mathrm{B}}_1$, denoted as $V_{{\mathrm{B}}_1}$, represents the probability of the local government choosing to protect the habitat. The volume of ${\mathrm{B}}_2$, denoted as $V_{{\mathrm{B}}_2}$, corresponds to the probability of the local government stably selecting not to protect the habitat. The calculations yield:

$$\begin{array}{c}{V}_{B_1}={\int }_0^1\frac{C_2{{+C}_1}^{\prime }+P_1-{R_2}^{\prime }-w\left({2C}_2{{+C}_1}^{\prime }+P_1-C_1+\sigma R_2\right)}{{C_1}^{\prime }}dw\\ =\frac{2{R_2}^{\prime }+\sigma R_2-{C_1}^{\prime }-P_1-C_1}{{{2C}_1}^{\prime }}\end{array}$$

$$V_{B_2}=1-V_{B_1}$$

Inference 2: The probability of the local government adopting the “control of human activity interference” strategy is positively correlated with the compensation standards set by the central government for their protection costs, the benefits gained from habitat protection, and the compensation coefficient for profit-based compensation. It is negatively correlated with punitive measures from the central government, the cost of preventing wildlife damage, and the cost of habitat protection.

Proof. 

By calculating the partial derivatives of each element, we find $\partial V_{B_1}/\partial \sigma >0$, $\partial V_{B_1}/\partial C_1<0,$ $\partial V_{B_1}/\partial R_2^{\prime }>0$, $\partial V_{B_1}/\partial P_1<0$, and $\partial V_{B_1}/\partial \beta <0$. □

Inference 2 indicates that the local government’s environmental benefits from protecting habitats primarily manifest through the management rights. In the process of habitat protection, the direct contribution of species recovery to the local government’s immediate benefits is limited. For instance, regulations such as the Wildlife Protection Law stipulate that local governments lack the authority to approve flagship species such as giant pandas and Asian elephants. Consequently, local governments cannot directly enjoy the benefits of successful habitat conservation for these species. However, protecting the habitats of these species often necessitates restricting or even prohibiting certain economic development activities as a trade-off. Without adequate compensation and with relatively mild punitive measures such as verbal warnings, local governments may tend to favor economic development over expanding habitat protection. Moreover, as habitat suitability improves and expands, there will be a likely increase in wildlife-related incidents. The responsibility for preventing and controlling wildlife-related incidents falls within the jurisdiction of local governments. The costs associated with monitoring, early warning systems, compensation, insurance, and population control for prevention and control all influence the local government’s strategy for habitat protection.

3.1.3. Stability Analysis of Farmers’ Strategies

Farmers’ expected benefits for choosing the “Integration of Production and Habitat Conservation Goals” and “Conflict between Production and Habitat Conservation Goals” strategies are denoted as $E_{31}$ and $E_{32}$, respectively. The average expected benefit is represented as $E_3$.

$$E_{31}={\beta C}_4+{R_3}^{\prime }+x\left(R_3^{\prime }+C_4+\epsilon C_3\right)+w\left(C_3^{\prime }-\epsilon C_3\right)$$

$$E_{32}={C_4}^{\prime }+{C_3}^{\prime }+P_2+x\left(R_3^{\prime }+\epsilon C_3\right)+w\left({{C_4}^{\prime }+{C_3}^{\prime }+P_2-R}_3^{\prime }\right)$$

$$E_3=z{E}_{31}+(1-z)E_{32}$$

$$\begin{array}{c}F\left(z\right)=\frac{dz}{dt}=z{(E}_{31}-E_3)=z(1-z)(E_{31}-E_{32})\hfill \\ =z(1-z)[{\beta C}_4+{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2+x{C}_4-w(C_3-\epsilon R_3+R_3^{\prime }\hfill \\ -{C_4}^{\prime }-{C_3}^{\prime }-P_2)]\hfill \end{array}$$

$$C\left(x\right)={\beta C}_4+{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2+x{C}_4-w(C_3-\epsilon R_3+R_3^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2)$$

$$F^{\prime }\left(z\right)=(1-2z)C\left(x\right)$$

According to the stability theorem of differential equations, the probability of farmers choosing the habitat protection strategy must be in a stable state, satisfying the following conditions: $F\left(z\right)=0$ and $F^{\prime }\left(z\right)<0$. Since $C\left(x\right)$ is an increasing function, when $x={\beta C}_4+{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2-w(C_3-\epsilon R_3+R_3^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2)/C_4=x_1$,$C\left(x,y\right)=0$, $F^{\prime }\left(z\right)=0$, C(x,y) = 0 and F’(z) = 0. In this case, farmers cannot determine a stable strategy. When $x>x_1$, $C\left(x,y\right)<0$, $F{\left.\left(z\right)\right|}_{z=1}=0$, and $F^{\prime }{\left.\left(z\right)\right|}_{z=1}<0$. Thus, $z=1$ becomes the evolutionarily stable strategy (ESS). Conversely, when $x<x_1$, $z=0$ is the ESS.

Proposition 3 indicates that when the central government’s compensation to farmers exceeds the threshold $x_1$, farmers will opt for the habitat protection strategy. The improvement in wildlife habitat quality crucially depends on whether the vegetation characteristics in the habitat space align with the survival requirements of the wildlife. Within the ecological space managed by farmers, their profitability is maximized by engaging in agricultural and forestry activities that might be detrimental to habitat quality restoration. Consequently, their likelihood of protecting the habitat decreases. If the central government can compensate farmers sufficiently to offset the opportunity costs of engaging in habitat-friendly activities, dual benefits can be achieved. On one hand, this can incentivize farmers to choose production behaviors that align with habitat quality, thereby enhancing the habitat. On the other hand, this can also expand the scope of wildlife habitat by fostering such protective practices.

The phase diagram of farmers’ strategy evolution is depicted in Figure 4. As shown in the diagram, the volume of ${\mathrm{C}}_1$, denoted as $V_{{\mathrm{C}}_1}$, represents the probability of the local government choosing to protect the habitat. The volume of ${\mathrm{C}}_2$, denoted as $V_{{\mathrm{C}}_2}$, corresponds to the probability of the local government stably selecting not to protect the habitat. The calculations yield

$$\begin{array}{c}{V}_{C_1}={\int }_0^1\frac{{\beta C}_4+{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2-w(C_3-\epsilon R_3+R_3^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2)}{C_4}dw\\ =\frac{2\beta C_4+{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2-C_3+\epsilon R_3}{R_3^{\prime }}\end{array}$$

$$V_{C_2}=1-V_{C_1}$$

Inference 5 states that the probability of farmers choosing the habitat protection strategy is positively correlated with the compensation ratio for wildlife damage received by farmers and the compensation ratio for their gains. It is negatively correlated with the costs incurred due to conflicting production behavior, the punitive measures for habitat destruction, and the costs of not protecting the habitat.

Proof. 

By calculating the partial derivatives of each element, we find $\partial V_{C_1}/\partial \epsilon R_3>0$, $\partial V_{C_1}/\partial \beta C_4>0$, $\partial V_{C_1}/\partial C_3<0$. □

Inference 5 suggests that whether farmers engage in habitat protection is primarily influenced by their own livelihood concerns. Following the reform of forest tenure rights, the profit potential of managing commercial forests has increased. For farmers participating in ecological restoration, choosing ecologically aligned forests that match habitat conservation objectives could significantly impact their economic interests. Therefore, establishing a standardized and rational utilization system, wherein the central government employs different compensation standards as regulatory tools to align farmers’ production activities with habitat conservation goals, can ensure the sustainable utilization of forests without compromising habitat quality. Governments and forestry departments should also construct and refine mechanisms that outline different types of operational activities. Additionally, they can provide enhanced technical guidance and support to farmers, thereby increasing the likelihood of habitat protection. Furthermore, the expansion in habitat range and improvement in suitability would inevitably lead to wildlife-related incidents. Local governments should engage in preventive measures and design compensation systems to alleviate farmers’ fears and aversions towards wildlife. In conclusion, addressing these considerations can contribute to raising the probability of farmers engaging in habitat protection, thereby achieving a balanced coexistence between ecological preservation and economic interests.

3.1.4. Ecological Subsystem Strategy Stability Analysis

The expected benefits for choosing the strategy “Ecological Succession Behavior Favors Habitat Suitability Enhancement” are denoted as $E_{41}$, while the expected benefits for choosing the strategy “Ecological Succession Behavior Adversely Affects Habitat Suitability Enhancement” are denoted as $E_{42}$. The average expected benefit is represented as $E_4$.

$$\begin{array}{c}{E}_{41}=C_5-R_4+z\left({\alpha }^{\prime }{R}_4+\gamma C_5-{\gamma }^{\prime }{C}_5\right)+y\left(C_5-{\gamma }^{\prime }{C}_5\right)+xz\left({\alpha }^{\prime }{R}_4-\alpha R_4+\gamma C_5\right)\\ +xy(\gamma C_5-{\gamma }^{\prime }{C}_5+{\alpha }^{\prime }{R}_4+\gamma C_5)\end{array}$$

$$E_{42}=z\left(\gamma C_5+R_4-{\gamma }^{\prime }{C}_5\right)+xz\gamma C_5+xy({\alpha }^{\prime }{R}_4+\gamma C_5)$$

$$E_4=w{E}_{41}+(1-w)E_{42}$$

$$\begin{array}{c}F\left(w\right)=\frac{dw}{dt}=w{(E}_{41}-E_4)\hfill \\ =w(1-w)[R_4-C_5-z{R}_4\left({1-\alpha }^{\prime }\right)-y{C}_5\left({\gamma }^{\prime }-1\right)-xz{R}_4\left({\alpha }^{\prime }-\alpha \right)\hfill \\ -xy{C}_5\left(\gamma -{\gamma }^{\prime }\right)]\hfill \end{array}$$

$$D\left(x,y,z\right)=R_4-C_5-z{R}_4\left({1-\alpha }^{\prime }\right)-y{C}_5\left({\gamma }^{\prime }-1\right)-xz{R}_4\left({\alpha }^{\prime }-\alpha \right)-xy{C}_5\left(\gamma -{\gamma }^{\prime }\right)$$

$$F^{\prime }\left(w\right)=(1-2w)D\left(x,y,z\right)$$

According to the stability theorem of differential equations, the probability of the ecological subsystem choosing the “Habitat Protection Strategy” must be in a stable state, satisfying the conditions $F\left(w\right)=0$ and $F^{\prime }\left(w\right)>0$. Since $D\left(x,y,z\right)$ is an increasing function with respect to $y$, when $y=[R_4-C_5-z{R}_4\left({1-\alpha }^{\prime }\right)-xz{R}_4\left({\alpha }^{\prime }-\alpha \right)]/[C_5\left({\gamma }^{\prime }-1\right)+x{C}_5\left(\gamma -{\gamma }^{\prime }\right)]=y_0$, $D\left(x,y,z\right)=0$ and $F^{\prime }\left(w\right)=0$. In this case, the ecological subsystem cannot determine a stable strategy. When $y>y_0$, $D\left(x,y,z\right)<0$, $F{\left.\left(w\right)\right|}_{w=1}=0$, $F^{\prime }{\left.\left(w\right)\right|}_{w=1}<0$. Thus, $w=1$ becomes the evolutionarily stable strategy (ESS). Similarly, when $z<z_0$, $w=0$ is the ESS. Similarly, when $z>z_2$, $w=1$ is the ESS.

Proposition 4 signifies that the core of wildlife habitat conservation is the protection of forest resources, with farmers serving as the primary agents of afforestation and forest management. Farmers predominantly engage in habitat restoration through agroforestry planting activities. If they adopt agroforestry practices that align with habitat conservation goals, such as planting ecological forests and emphasizing a combination of trees, shrubs, and grasses, this will enhance the stability of the ecosystem and indirectly protect habitats. Based on this reasoning, in ecological construction initiatives such as returning farmland to forests and ecological restoration projects, farmers who receive certain subsidies are encouraged to plant trees on steep slopes or join forest ranger teams, aligning their afforestation efforts with habitat goals. The higher the degree of integration between afforestation efforts and habitat objectives, the more favorable the ecological succession behavior of the ecosystem will be for habitat quality restoration. Local governments primarily focus on establishing protected area systems to limit or prohibit economic activities that impact habitats. Reducing interference from human activity is crucial for restoring ecological stability. Additionally, local government control over human activity disturbance contributes to enhancing the stability of the ecosystem.

Based on Proposition 4, the ecological subsystem’s strategy evolution phase diagram is illustrated in Figure 5. As shown in the diagram, the volume of ${\mathrm{D}}_1$, denoted as $V_{{\mathrm{D}}_1}$, represents the probability of the ecological subsystem choosing not to protect the habitat. The volume of ${\mathrm{D}}_2$, denoted as $V_{{\mathrm{D}}_2}$, corresponds to the probability of the ecological subsystem stably selecting to protect the habitat. The calculations yield:

$$\begin{array}{c}{V}_{D_1}={\iint }_0^1\frac{R_4-C_5-z{R}_4\left({1-\alpha }^{\prime }\right)-xz{R}_4\left({\alpha }^{\prime }-\alpha \right)}{C_5\left({\gamma }^{\prime }-1\right)+x{C}_5\left(\gamma -{\gamma }^{\prime }\right)}dxdy\\ =\frac{3{\alpha R}_4-{4C}_5(1+\gamma )}{C_5\left({\gamma }^{\prime }-1\right)}\end{array}$$

$$V_{D_2=}1-V_{D_1}$$

Inference 2: The probability of the ecological subsystem protecting the habitat is positively correlated with the ecological restoration index and negatively correlated with the human activity control index.

Proof. 

Based on the expression for the probability of the ecological subsystem adopting the “not protecting the habitat” strategy, $V_{D_1}$, we can calculate the partial derivatives as follows: $\partial V_{D_1}/\partial C_5\gamma <0$, $\partial V_{D_1}/\partial \alpha >0$. □

Inference 2 indicates that there are two effective measures to indirectly restore habitat quality by enhancing the stability of the ecological subsystem. The first measure involves controlling human activities that interfere with habitats. This is primarily achieved through the establishment of protected area systems by local governments. However, as observed earlier, when the compensation from the central government to local governments surpasses a certain threshold, local governments tend to control human activity interference to protect habitats. Therefore, by designing compensation standards that incentivize local governments to manage human activity interference and quantitatively identifying the relationship between compensation standards and the specific forms of human activity interference, the central government can indirectly influence local government actions in habitat protection. The second measure involves ecological restoration projects aimed at rehabilitating the ecosystem. These projects are carried out by numerous farmers residing around the habitats. When the central government’s compensation to farmers surpasses a specific threshold, farmers are more likely to engage in agroforestry practices that align with habitat protection. Consequently, by designing compensation standards for farmers and establishing a quantitative relationship between compensation standards and various aspects of ecological restoration, such as tree species planting, afforestation area, and the setup of public service positions, the central government can link compensation standards to the establishment of an ecological restoration index and its correlation with habitat quality. In summary, by implementing these measures and designing compensation strategies, the central government can exert influence over habitat protection and indirectly contribute to the restoration of habitat quality through the enhancement of ecological system stability.

3.2. Wildlife Habitat Socio-Ecological System Evolutionary Stability Analysis

In order to uncover the conditions and processes leading to the formation of the stable evolutionary patterns within the wildlife habitat socio-ecological system, this section constructs and solves a replicator dynamic system involving four players: farmers, local government, society/public, and central government. By setting $F\left(x\right)=0$, $F\left(y\right)=0$, $F\left(z\right)=0$, and $F\left(w\right)$ = 0, multiple feasible solutions are obtained. Considering that stable solutions in multi-population evolutionary games are strict Nash equilibria, Lyapunov’s first theorem is employed to analyze the stability of 16 sets of pure strategy equilibrium solutions. These solutions are presented in

Table 3. Stability analysis of equilibrium points in the wildlife habitat socio-ecological system.

Equilibrium Points	$\mathbf{Eigenvalues}{\mathit{\lambda }}_1\mathbf{, }{\mathit{\lambda }}_2\mathbf{, }{\mathit{\lambda }}_3\mathbf{, }{\mathit{\lambda }}_4$	Positive–Negative Determination	Stability Determination and Conditions	Social–Ecological System Evolution Patterns
$E_1($1,1,1,1$)$	$-\left({\sigma }^{\prime }{C}_1+{\epsilon }^{\prime }{C}_3+\sigma R_2+\epsilon R_3\right),C_1-C_2-\sigma R_2$$,{{C_3-C}_4-\epsilon R}_3-{\beta C}_4$$,\gamma C_5{-\alpha R}_4$	$-\times \times \times$	Condition 1	Optimal Evolutionary Patterns
$E_2($1,1,1,0$)$	$-\left(P_2-P_1{-\epsilon R_3+{\epsilon }^{\prime }{C}_3-\sigma }^{\prime }{C}_1+\sigma R_2\right),{{-(R}_2}^{\prime }-C_2-P_1),{\beta C}_4+{R_3}^{\prime }+{C_4}^{\prime }+{C_3}^{\prime }+P_2+C_4,{\alpha R}_4-$ $\gamma C_5$	$\times \times +\times$		Suboptimal Evolutionary Patterns
$E_3($1,1,0,0$)$	$-(P_2-P_1{-\sigma }^{\prime }{C}_1+\sigma R_2)$, ${{-(R}_2}^{\prime }-C_2-P_1),{\beta C}_4+{R_3}^{\prime }+{C_4}^{\prime }+{C_3}^{\prime }+P_2+C_4,R_4-\gamma C_5$	$\times \times +\times$		Suboptimal Evolutionary Patterns
$E_4($1,1,0,1$)$	${\sigma }^{\prime }{C}_1-\sigma R_2,C_1-C_2-\sigma R_2,{{{-(C}_3-C}_4-\epsilon R}_3-{\beta C}_4)$$,\gamma C_5-R_4$	$\times \times \times \times$	Condition 2	Less Optimal Evolutionary Patterns
$E_5($1,0,1,1$)$	$\epsilon R_3{-\epsilon }^{\prime }{C}_3$, $-(C_1-C_2-\sigma R_2)$, ${{C_3-C}_4-\epsilon R}_3-{\beta C}_4$$,C_5{-\alpha R}_4$	$\times \times \times \times$	Condition 3	Less Optimal Evolutionary Patterns
$E_6($0,1,1,1$)$	${\sigma }^{\prime }{C}_1+{\epsilon }^{\prime }{C}_3+\sigma R_2+\epsilon R_3,C_2+C_1$, $C_4+C_3$$,{\gamma }^{\prime }{C}_5-{\alpha }^{\prime }{R}_4$	$\times \times \times \times$		Less Optimal Evolutionary Patterns
$E_7($1,0,1,0$)$	$$\begin{gathered} P_2+P_1+\epsilon R_3+{\epsilon }^{\prime }{C}_3,{{-(R}_2}^{\prime }-C_2 \\ -P_1),-({\beta C}_4+{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2 \\ -C_4),{\alpha R}_4{-C}_5 \end{gathered}$$	$+\times \times \times$		Suboptimal Evolutionary Patterns
$E_8($0,1,1,0$)$	$$\begin{gathered} -{2P}_2-{2P}_1+2\epsilon R_3+2{\epsilon }^{\prime }{C}_3{-\sigma }^{\prime }{C}_1 \\ +\sigma R_2,{R_2}^{\prime }+C_2{{+C}_1}^{\prime }+P_1,-({\beta C}_4 \\ +{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2),{\alpha }^{\prime }{R}_4-{\gamma }^{\prime }{C}_5 \end{gathered}$$	$\times \times +\times$		Suboptimal Evolutionary Patterns
$E_9($0,1,0,1$)$	$-({\sigma }^{\prime }{C}_1-\sigma R_2)$$,C_2+C_1-R_2-{\sigma }^{\prime }{C}_1$, ${R_3}^{\prime }+{\beta C}_4-C_3^{\prime }-P_1$$,{\beta C}_4-C_3+\epsilon R_3$$,{\gamma }^{\prime }{C}_5-R_4$	$\times \times \times \times$	Condition 4	Less Optimal Evolutionary Patterns
$E_{10}($1,0,0,1$)$	$P_1-P_2,{-(C}_1-C_2-\sigma R_2),{{{{\beta C}_4+C}_3+C}_4+\epsilon R}_3$$,C_5-R_4$	$\times \times +\times$		Suboptimal Evolutionary Patterns
$E_{11}($1,0,0,0$)$	$P_1-P_2$$,{R_2}^{\prime }-C_2-P_1$, ${\beta C}_4+{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2$, $R_4-C_5$	$+\times \times \times$		Less Optimal Evolutionary Patterns
$E_{12}($0,1,0,0$)$	$P_2-P_1-{\sigma }^{\prime }{C}_1+\sigma R_2,{R_2}^{\prime }+C_2+P_1$, ${{C_3-C}_4-\epsilon R}_3-{\beta C}_4$, $R_4-{\gamma }^{\prime }{C}_5$	$\times +\times \times$		Suboptimal Evolutionary Patterns
$E_{13}($0,0,1,1$)$	$-\left(\epsilon R_3{-\epsilon }^{\prime }{C}_3\right),{R_2}^{\prime }{{-C}_1}^{\prime }{{-C}_2}^{\prime }-P_1$, ${{C_3+C}_4-R}_3-{\epsilon }^{\prime }{C}_3-{\beta C}_4$$,C_5-{\alpha }^{\prime }{R}_4$	$\times \times \times \times$	Condition 5	Less Optimal Evolutionary Patterns
$E_{14}($0,0,1,0$)$	$P_2-P_1-\epsilon R_3{+\epsilon }^{\prime }{C}_3,{R_2}^{\prime }-C_2-P_1$, ${\beta C}_4+{R_3}^{\prime }+{C_4}^{\prime }+{C_3}^{\prime }+P_2,{\alpha }^{\prime }{R}_4-C_5$	$\times \times +\times$		Suboptimal Evolutionary Patterns
$E_{15}($0,0,0,1$)$	$P_2-P_1,2C_2-{C_1}^{\prime }-C_1+\sigma R_2$$,{\beta C}_4+C_3+\epsilon R_3$$,C_5-R_4$	$-\times +\times$		Less Optimal Evolutionary Patterns
$E_{16}($0,0,0,0$)$	$P_2-P_1,{R_2}^{\prime }-C_2{{-C}_1}^{\prime }-P_1$$,{\beta C}_4+{R_3}^{\prime }-{C_4}^{\prime }-{C_3}^{\prime }-P_2$$,R_4-C_5$	$-\times \times \times$	Condition 6	Suboptimal Evolutionary Patterns

Note: “$\times$” represents uncertainty in positive or negative direction. Condition 1: $C_1-C_2<\sigma R_2$, ${{C_3-C}_4<\epsilon R}_3+{\beta C}_4$, $\gamma C_5{<\alpha R}_4$; Condition 2: ${\sigma }^{\prime }{C}_1<\sigma R_2,C_1-C_2<\sigma R_2,{{C_3-C}_4>\epsilon R}_3+{\beta C}_4$, $\gamma C_5<R_4$; Condition 3: $\epsilon R_3{<\epsilon }^{\prime }{C}_3$, $C_1-C_2>\sigma R_2$, ${{C_3-C}_4<\epsilon R}_3+{\beta C}_4$, $C_5{<\alpha R}_4$; Condition 4: ${\sigma }^{\prime }{C}_1>\sigma R_2$, $C_2+C_1<R_2+{\sigma }^{\prime }{C}_1$, ${R_3}^{\prime }+{\beta C}_4<C_3^{\prime }+P_1$, ${\beta C}_4+\epsilon R_3<C_3$, ${\gamma }^{\prime }{C}_5<R_4$; Condition 5: ${\epsilon }^{\prime }{C}_3<\epsilon R_3,{R_2}^{\prime }{{<C}_1}^{\prime }{{+C}_2}^{\prime }+P_2,$ ${{C_3+C}_4<R}_3+{\epsilon }^{\prime }{C}_3+{\beta C}_4$, $C_5<{\alpha }^{\prime }{R}_4$; Condition: ${R_2}^{\prime }<C_2{{+C}_1}^{\prime }+P_1$, ${\beta C}_4+{R_3}^{\prime }<{C_4}^{\prime }+{C_3}^{\prime }+P_2$, $R_4<C_5$.

, and the Jacobian matrix is as given below:

$$J=\begin{array}{cccc}\frac{\partial F(x)}{\partial x}& \frac{\partial F(x)}{\partial y}& \frac{\partial F(x)}{\partial z}& \frac{\partial F(x)}{\partial w}\\ \frac{\partial F(y)}{\partial x}& \frac{\partial F(y)}{\partial y}& \frac{\partial F(y)}{\partial z}& \frac{\partial F(y)}{\partial z}\\ \frac{\partial F(z)}{\partial x}& \frac{\partial F(z)}{\partial y}& \frac{\partial F(z)}{\partial z}& \frac{\partial F(z)}{\partial w}\\ \frac{\partial F(w)}{\partial x}& \frac{\partial F(w)}{\partial y}& \frac{\partial F(w)}{\partial z}& \frac{\partial F(w)}{\partial w}\end{array}$$

Categorizing the 16 evolutionary patterns within the wildlife habitat socio-ecological system based on whether the ecological subsystem’s succession behavior is conducive to improving habitat suitability yields three distinct classes: “Suboptimal Evolutionary Patterns,” “Less Optimal Evolutionary Patterns,” and “Optimal Evolutionary Patterns.”

• Suboptimal Evolutionary Patterns: In this category, regardless of the strategies chosen by the other three main entities (farmers, local government, and society/public), the ecological subsystem’s succession behavior does not contribute to enhancing habitat suitability.
• Less Optimal Evolutionary Patterns: These patterns involve the ecological subsystem’s succession behavior benefiting the improvement in habitat suitability. However, at least one of the main entities (either farmers or local government) chooses not to protect the habitat.
• Optimal Evolutionary Patterns: Here, the ecological subsystem’s succession behavior is advantageous for increasing habitat suitability. Both farmers and local government select the strategy of protecting the habitat.

Following computational analysis, out of the 16 socio-ecological system evolutionary patterns, four sets of solutions may converge to form asymptotically stable strategy combinations. Among these, there is one set belonging to the suboptimal category, two sets belonging to the less optimal category, and one set representing the optimal category.

3.2.1. Stability Analysis of Transition from Less Ideal Mode to Ideal Mode in Evolution

Based on the conditions for the evolutionarily stable modes $E_{16}$ (Less Ideal Mode), $E_9$ (Less Ideal Mode), $E_{13}$ (Less Ideal Mode), $E_4$ (Less Ideal Mode), and $E_5$ (Less Ideal Mode), it can be understood that the transition from $E_{16}$ to the $E_9$, $E_{13}$, $E_4$, and $E_5$ modes relies on the central government’s implementation of a compensation strategy to achieve a surplus of benefits for the ecological system, local government, and farmers in the process of habitat protection. The stability condition of the $E_{16}$ mode indicates that in the early stages of significant habitat degradation, attempting to mitigate habitat fragmentation by increasing penalty costs and reducing human activity interference (${R_2}^{\prime }<C_2{{+C}_1}^{\prime }+P_1$) may not be sufficient to reverse the trend of habitat fragmentation ($R_4-C_5$). This could be attributed to the relatively high economic development opportunity cost for the local government (${C_1}^{\prime }$) and livelihood cost for farmers (${C_3}^{\prime }$) during the phase of habitat destruction. To transition from the “neither protect” mode to the “at least one party protects” mode for achieving higher habitat suitability, as seen in the evolution from $E_{16}$ to $E_9$, $E_{13}$, $E_4$, and $E_5$, the central government must implement a compensatory strategy to offset the costs for both the local government and farmers. These conditions include either $C_1{+C}_2<R_2+{\sigma }^{\prime }{C}_1$ or $C_1-C_2<\sigma R_2$ for the local government’s costs, and either ${{C_3+C}_4<R}_3+{\epsilon }^{\prime }{C}_3+{\beta C}_4$ or ${{C_3-C}_4<\epsilon R}_3+{\beta C}_4$ for the farmers’ losses. Under the $E_{13}$ and $E_5$ modes, the central government achieves this transition by compensating farmers and enhancing the ecological restoration index $\alpha$ and ${\alpha }^{\prime }$, resulting in increased benefits for the ecosystem, either $C_5<{\alpha R}_4$ or $C_5{<{\alpha }^{\prime }R}_4$. In the $E_9$ and $E_4$ modes, the central government facilitates the transition through compensating the local government. By reducing the human activity disturbance indices $\gamma$ and ${\gamma }^{\prime }$, the central government increases the ecosystem benefits, either ${\gamma C}_5<R_4$ or ${\gamma }^{\prime }{C}_5-R_4$.

Comparing the effects of cost-based compensation ($E_9$, $E_{13}$) and benefit-based compensation mechanisms ($E_4$, $E_5$), it is evident that the benefit-based compensation mechanism reduces the costs associated with the feedback of the ecosystem to the social system. By analyzing the eigenvalues of the four entities under both compensation mechanisms, if the compensation mechanisms can drive the local government and farmers to value the ecological products, then the harmful costs incurred when the ecosystem feeds back to the social system will decrease (comparing the local government eigenvalue $C_1{+C}_2<{\sigma }^{\prime }{C}_1$ to $C_1-C_2<\sigma R_2$, and the farmer eigenvalue ${{C_3+C}_4<R}_3+{\epsilon }^{\prime }{C}_3+{\beta C}_4$ to ${{C_3-C}_4-{\epsilon }^{\prime }R}_3-{\beta C}_4$. Possible reasons are as follows. In comparison to solely compensating for costs, both the local government and farmers stand to benefit from habitat conservation. They become more willing to reduce human activity interference and increase ecological restoration efforts, thereby enhancing the habitat’s carrying capacity and suitability while reducing the risk of wildlife spillover from the original habitat. However, compensating only for the protection costs of farmers and local governments might lead to an increase in habitat area, but the lower suitability of the habitat could still put endangered species at risk of extinction. Species with low habitat quality requirements but strong reproductive abilities, such as wild boars, might expand their range outside the original habitat as a result of habitat expansion, leading to increased harmful costs for farmers and heightened prevention and control costs for local governments. Furthermore, under a cost-based compensation mechanism, both farmers and local governments actively protecting the habitat to enhance habitat suitability, as seen in the $E_6$ mode, may fail to evolve into a stable state. This could be due to the fact that, despite the central government increasing cost-based compensation standards ${\epsilon }^{\prime }$, ${\sigma }^{\prime }$, the compensation for costs discourages the local government from actively controlling human activity interference. In turn, farmers, receiving compensation for their costs, might engage in production activities that contradict habitat protection goals to maximize their profits. The dynamic expansion in the habitat leads to excessively high harmful costs and prevention and control costs$C_2+C_1$ and $C_3+C_4$ for these two entities, making it challenging for the cost-based compensation mechanism mode to achieve evolutionary stability.

3.2.2. Stability Analysis of Evolution from Less Ideal Mode to Ideal Mode

Both types of compensation mechanisms can drive the ecological succession behavior to enhance habitat suitability. However, the benefit-based compensation mechanism further motivates farmers and local governments to protect the habitat by reducing harmful costs. According to the stability conditions of $E_1$, an ideal socio-ecological system evolution mode involves the central government increasing the benefit-based compensation coefficients ($\epsilon \mathrm{a}\mathrm{n}\mathrm{d}\sigma$) to provide economic or policy incentives. This encourages farmers and local governments to gain benefits from habitat protection ($C_1-C_2<\sigma R_2$, ${{C_3-C}_4<\epsilon R}_3+{\beta C}_4$). Local governments become more willing to control human activity interference, and farmers are more inclined to engage in production aligned with habitat protection goals. This results in increased habitat carrying capacity, reduced risks of wildlife spillover harm, and lower harm prevention and control costs, which in turn motivates farmers and local governments to protect the habitat while minimizing total social costs.

Furthermore, transitioning from the less ideal modes ($E_9$, $E_{13}$, $E_4$, and $E_5$) to the $E_1$ mode cannot solely rely on administrative orders using $P_1$ and $P_2$ to penalize local governments and farmers. Instead, it requires policy incentive approaches to motivate local governments to realize the value of ecological products. Simultaneously, considering the livelihood of farmers and increasing their income should be taken into account during habitat transformation projects.

4. Results

This study explores the influencing factors behind the habitat protection strategies adopted by various stakeholders. It has been observed that when the central government employs administrative directives with relatively weak punitive measures, a prisoner’s dilemma scenario emerges. In this scenario, all three parties, apart from the central government, tend to choose not to protect the habitat. This leads to a decline in habitat quality. Only when the central government implements a compensation mechanism to reduce the opportunity costs of habitat protection for farmers and local governments can it ensure that at least one of these stakeholders chooses a habitat protection strategy. This helps enhance ecosystem stability and restore habitat quality. Furthermore, when designing policies, the central government should consider implementing fiscal and credit-based policies to increase the benefits for both farmers and local governments, rather than just compensating for their costs. The rationale behind this is as follows. Compensating farmers for the benefits they generate through production behaviors aligned with habitat protection goals would increase the ecological restoration index. Similarly, if local governments can obtain positive benefits through tourism or other supporting policies during habitat protection, it would reduce the human activity disturbance index. With a higher ecological restoration index and a lower human activity disturbance index, the ecosystem is better equipped to promote successional behaviors that favor habitat quality restoration due to increased stability.

The key to achieving an idealized social–ecological system evolution pattern for wildlife habitat is for the central government to shift its compensation strategy for farmers and local governments from cost-based compensation to profit-based compensation. In an idealized social–ecological system evolution pattern, all parties choose strategies that favor habitat protection, and they are reluctant to change their strategies because they maximize their own interests. To meet the conditions for achieving this pattern, the central government should design a combination of ecological compensation tools that transform the function of compensation from cost reimbursement to profit acquisition under different compensation strategies. This would incentivize local governments and farmers at different habitat management levels to engage in habitat protection activities. Farmers would receive continuous compensation for adopting production behaviors aligned with habitat protection goals, while local governments would benefit from reducing human activity disturbances. As a result, the ecosystem’s successional behavior would improve habitat carrying capacity. With increased habitat carrying capacity, the risk of wildlife leaving the original habitat decreases, and both farmers’ damage costs and local governments’ damage prevention and control costs would decrease. Considering these results, the central government can steer the social–ecological system toward the ideal pattern through profit-based compensation.

5. Conclusions

This paper focuses on the issue of habitat protection strategies in the context of dynamic changes in wildlife habitat quality and range, as well as the interactions among stakeholders. Taking the perspective of the four stakeholders involved in habitat management, we construct a social–ecological system evolution model to investigate the reasons for the formation of an idealized wildlife habitat management pattern and the control conditions for achieving it.

This paper focuses on the issue of wildlife habitat protection, with a particular emphasis on controlling the negative impacts of human activities on habitats. In China, wildlife conservation policies primarily involve ecological restoration projects such as the Grain-to-Green Program, Natural Forest Protection Project, and the establishment of nature reserves. These initiatives aim to expand habitat ranges and improve habitat quality. However, China’s endangered species are predominantly found in regions with abundant natural resources but relatively underdeveloped economies. Additionally, these wildlife habitats are often inhabited by a large number of farmers who rely on agriculture and forestry for their livelihoods. Moreover, the land space and forest resources within wildlife habitats are essential elements for economic development. Consequently, there is an inherent tension between wildlife habitat protection and the surrounding society and development. Scholars have discussed how to promote habitat protection by various stakeholders, with a primary focus on compensating farmers for their efforts in habitat protection. According to economic theory, compensation can incentivize farmers to adopt production behaviors that align with habitat protection goals [34,35,36,37]. The conclusions of this study further refine these viewpoints. They suggest that policymakers should use fiscal and credit-based policies to increase farmers’ income, encouraging them to choose production behaviors that align with habitat protection goals. This can ultimately enhance ecosystem stability and improve habitat quality. Currently, some regions in China are grappling with issues related to wildlife damage, particularly from species such as wild boars. Research indicates that frequent recoveries in the population of wild boars can pose risks to farmers in the vicinity. However, the survival status of co-endangered species such as giant pandas and Siberian tigers remains a concern. This is attributed to the fact that while China’s ecological environment has improved through ecological restoration projects, habitat quality remains relatively low, leading to reduced carrying capacity. To address this, scholars recommend the implementation of wildlife habitat transformation processes to protect endangered species and reduce the risk of wildlife spillover [38,39,40].

Wildlife habitat restoration projects involve the interests of local governments, farmers, the central government, and the ecosystem. The successful implementation of these projects necessitates the establishment of a state of stable equilibrium where the interests of all parties are realized. The conclusions of this paper suggest that in the policy design process, the central government can shift the function of compensation from cost reimbursement to profit acquisition under different compensation strategies. This would reduce the overall costs of wildlife damage to society, even if not all stakeholders consistently adopt habitat protection strategies that are favorable to the habitat. The findings of this study align with the conclusions drawn from the impact of forest policies in the Forêt des Pins Reserve on nearby farmers in Haiti [41]. Both studies find that farmers tend to hold more positive attitudes toward forest protection when they believe that their agricultural activities will benefit from conservation programs.

This paper employs a framework based on evolutionary game theory to analyze the issue of interest equilibrium among the four stakeholders, including the ecosystem, in the habitat protection process. Although evolutionary game theory can consider changes in different stakeholders’ interests over time through the replicator dynamic equations, it is worth noting that the rewards for each stakeholder have a lag. For example, the rewards that the central or local governments may have to pay to farmers may only be observed in the ecosystem’s impact after a certain period. Therefore, future research should consider the optimal time frame for analysis. Furthermore, when the central government implements incentive measures for farmers and local governments, there are “policy evaluation costs” involved. These costs may include assessing whether farmers or local governments are complying with policy requirements and whether habitat quality has improved before making further strategic decisions. Therefore, future research should also incorporate these policy evaluation costs into the construction of the model. Overall, addressing these temporal and evaluation cost issues in future research will enhance the accuracy and realism of the social–ecological system evolution framework.