Next Article in Journal
Modulating the Acoustic Vibration Performance of Wood by Introducing a Periodic Annular Groove Structure
Next Article in Special Issue
Synergistic Effects of Heating Platens’ Temperature and Compression Ratio on the Periodic Hot-Press Drying of Chinese Fir Lumber
Previous Article in Journal
Spatiotemporal Variation in Vegetation and Its Driving Mechanisms in the Southwest Alpine Canyon Area of China
Previous Article in Special Issue
Combining Artificial Neural Network and Response Surface Methodology to Optimize the Drilling Operating Parameters of MDF Panels
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 14
Issue 12
10.3390/f14122359
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Characterization and Yield of Eucalyptus regnans F. Muell Logs for Lumber Production

by
Carlos Rozas
1,*,
Barbara Zapata
2,
Fernando Muñoz
3,
Virna Ortiz-Araya
4 and
Oswaldo Erazo
1
1
Department of Wood Engineering, Faculty of Engineering, University of Bío-Bío, Concepción 4030000, Chile
2
Forestal Arauco S.A., Arauco 4617200, Chile
3
Forest Engineering, Faculty of Forestry Sciences, University of Concepción, Concepción 4030000, Chile
4
Department of Business Management, University of Bío-Bío, Chillán 3800708, Chile
*
Author to whom correspondence should be addressed.
Forests 2023, 14(12), 2359; https://doi.org/10.3390/f14122359
Submission received: 31 October 2023 / Revised: 16 November 2023 / Accepted: 28 November 2023 / Published: 30 November 2023
(This article belongs to the Special Issue Wood Quality and Wood Processing)
Browse Figures
Versions Notes

Abstract

:
The yield of Eucalyptus regnans logs for lumber production was evaluated. Crack width and length at each log end were measured. Two log-cutting plans were used to obtain sawn lumber. The first plan (PA) considered logs with diameters varying from 28 to 40 cm, and in the second plan (PB), the log diameters ranged from 42 to 56 cm (PB). Lumber yield was determined using two log volume methods: the Japanese Agricultural Standards (JAS) and Smalian’s equation. The deformations of E. regnans lumber were measured. The Australian and Chilean standards were used to classify sawn lumber. The results showed that logs had radial cracks at both log ends. Cracks were classified into two groups, considering the crack length. Regarding the lumber deformations, most boards exhibited level B bows and crooks in both cutting plans. Levels A and B twists were prevalent in PA, whereas in PB, level A significantly outnumbered level B. The lumber yield of E. regnans in PB was higher than in PA. The lumber yield determined by Smalian’s equation was higher than that determined by the JAS method. This research provides insight into the characterization of E. regnans for lumber production, highlighting its relevance in the forestry industry.

1. Introduction

Eucalyptus regnans belongs to the genus Eucalyptus (Family Myrtaceae). This species is native to the southeast of New South Wales, Victoria, and Tasmania in Australia. E. regnans trees can grow rapidly to heights ranging from 50 to 60 m due to their high hydraulic efficiency, standing as the tallest among most other hardwood species [1]. The wood basic density of E. regnans ranges from 390 to 580 kg/m3 [2]. The E. regnans wood has moderate strength and high hardness. It also has a distinctive pattern with a medium to coarse texture and light brown color. The sapwood color of E. regnans is indistinct from the heartwood [3]. In Australia, E. regnans lumber is generally classified into three grades: select, standard, and utility. Select grade refers to lumber that is free of any defects and is mainly used in appearance-based products, including doors, stairs, floors, cabinets, moldings, and furniture. Standard-grade lumber may have some characteristics that disqualify it, such as knots and gum veins, among others. It can be used in products that require a decent appearance and in construction, mainly in wall structures, solid-section beams, and double T-beams. Utility- or general-use-grade lumber is used in applications such as pallets and fences, among others. E. regnans wood has the potential to be used in the manufacturing of valuable structural lumber products [4,5].
According to the technical report on forest resources published by the Forest Institute (INFOR) in 2022, forest plantations in Chile were 2,309,563 hectares [6]. Pinus radiata is the most commonly planted Pinus species in Chile, representing 54.8% of the total plantation area, and to a lesser extent, Eucalyptus globulus and Eucalyptus nitens are the most cultivated hardwood species, accounting for 21.9% and 12.4% of the total plantation area, respectively. On the other hand, the planted area of Eucalyptus regnans was not indicated in the technical report, but it was included in the item ‘other species’, which accounts for 1.8% of the total plantations [6]. However, a study carried out by Lisboa and colleagues reported a planted area of 1200 ha of Eucalyptus regnans [7].
Some studies have been conducted on the ecology and silvicultural practices of Eucalyptus regnans, mainly in Australia and New Zealand. These studies have assessed the tree size and total sawlog volume [8], as well as the relationship of biomass to tree size and age [9], age and growth pattern [10], genetic parameters [11], effects of pruning treatments [12], and wood production based on silvicultural systems [13]. E. regnans was introduced to Chile to evaluate its adaptability and potential in the forestry industry due to its fast growth and straight trunk [14]. This species has exhibited remarkable growth rates, surpassing even Pinus radiata, which is the primary species used in the production of sawn lumber in Chile [15]. The consumption of E. regnans lumber and other exotic species in Chile was approximately 1.5% of 16.7 million cubic meters of wood produced in 2021 [16].
Like most Eucalyptus species, E. regnans exhibits growth stresses in its structure. The growth stresses in the standing tree originate from vascular tissues, as it produces new cells each year to form a growth ring. As the tree ages, the cells inside the trunk contract longitudinally and expand laterally. However, this process is restricted by the older cells, leading to the development of stresses. The accumulation of stresses produced annually in the standing tree causes the inner part of the trunk to be under compressive stresses, which increase toward the pith, while the outer part of the trunk is subjected to tensile stresses, increasing toward the bark. This gradient of mechanical stress in standing trees constitutes a pre-stressed and self-balancing field [17].
Once the tree is felled, stresses begin to be released, causing tissues under tension to contract longitudinally and under compression to expand laterally, resulting in log end cracks. Likewise, during the sawing process, the distribution and transformation of longitudinal stresses into transverse stresses lead to the presence of cracks. The formation of cracks along the stem results from stress relaxation in both tension and opposite wood sides, exhibiting remarkably different behavior [18]. On the other hand, after sawing, the release of stresses results in various types of wood warping [19], including bow, crook, twist, kink, and cup. Furthermore, wood warping is strongly influenced by changes in moisture content that occur from the felled tree to the sawing process [20]. Most species of the genus Eucalyptus are widely known for the development of abundant cracks, collapses, and the presence of various defects, as described above [21].
Lumber yield can be obtained through the ratio between the volume of sawn wood and the log volume. This yield is highly important to be considered, as it indicates the efficiency and sustainability of the wood industries [22,23]. Determining lumber yield requires volume equations, including some such as Smalian, Huber, JAS, or laser measurement systems [24]. On the other hand, lumber yield and log grading are affected by some factors such as diameter, shape, length, taper, volume, sawing type, and sawing practices [25,26,27]. Defects such as knots also considerably affect the wood strength and, consequently, the wood quality [28]. In addition to the above factors, the presence of growth stresses induces defects such as cracks and warping in E. regnans wood, resulting in low yields in lumber production and a poor quality of lumber [29]. The detection of these defects is very important to grade lumber. Some methods have been developed for the detection of defects, such as machine vision techniques, which have proven to be effective in detecting cracks and knots [30]. Measuring lumber yield in sawmills has been a topic of great interest for many researchers worldwide, especially in areas where important wood species for the forest industry are concentrated. In this way, a substantial improvement in lumber yield has been reported, taking into account the technologies and techniques used in sawmills [31]. Research has also been conducted on lumber recovery for different species, such as Quercus rubra, Liriodendron tulipifera [25], Eucalyptus saligna [32], Cupressus lusitanica [23], Pinus kesiya, and Pinus patula [33]. As for E. regnans, Wardlaw and colleagues presented a study conducted in a sawmill, in which they compared the recovery of green lumber and the grades of defects in Eucalyptus globulus and E. regnans from adjacent thinned and unthinned stands [34]. However, there is limited information on the lumber yield of E. regnans, specially cultivated in plantations. Moreover, E. regnans presents greater challenges in the sawing process than other hardwood species due to the development of internal stresses, which produce defects in the wood. Thus, to maximize its potential and create a major participation in the forestry industry of Chile, a comprehensive study is required, covering material selection, characterization, and lumber yield. Therefore, the objective of this research was to assess the lumber yield of Eucalyptus regnans logs.

2. Materials and Methods

2.1. Material Description: Site and Stand Details

The 21-year-old Eucalyptus regnans trees were obtained from the El Lingue stand, located at 37°20′57″ south latitude and 73°30′04″ west longitude, owned by the company Forestal Regnans Ltda., Province of Arauco, Biobío Region. This place has an average annual precipitation of 1330 mm, along with a dry period of 3 to 4 months. It also has an average annual temperature of 13 °C, with maximums of 23 °C in January and minimums of 6 °C in July [35]. The silvicultural practices included 3 prunings at 5, 7, and 8 years and 3 thinnings at 6, 8, and 10 years. The logs were cut into sections of 6.30 m and 3.15 m in length.

2.2. Sample Size, Measurement of Cracks, and Estimation of Log Volumes

To determine the log sample size, we considered the average sawmill weekly processing capacity, ranging from 630 to 1050 logs, i.e., from 90 to 150 logs. The sample size was random and representative of all logs. According to NCh44Of2007 [36], the sample size should be 80 logs. However, in this research, a larger sample size of 130 logs was chosen, considering 20 logs processed per day, except on day 7, when only 10 logs were processed. The radial cracks were counted and measured at the ends of each log, and the width and length of the crack were measured.
In Chile, the most widely applied methods to determine log volume are the Japanese Agricultural Standards (JAS), Empresa Forestal Arauco (EFA), and Smalian’s formula [37]. In this study, the JAS [38] and Smalian methods were considered. Each method was calculated using Equations (1) and (2), respectively.
V = D 2 × L × 10 − 4
where V = log volume in cubic meters;
D is the shortest diameter in centimeters;
L = log length in meters.
V = a + A 2 L
where V = log volume (barkless logs) in cubic meters;
L = log length in meters;
A = area of the largest end diameter in square meters;
a = area of the smallest end diameter in square meters.

2.3. Sawing Process and Lumber Grading

The sawing of logs was carried out at sawmill Forestal Regnans Ltd., de Arauco, Chile. Two log-cutting plans were used, which were coded as PA for log diameters ranging from 28 to 40 cm and PB for diameters greater than 42 to 56 cm. The cutting pattern of plan PA consisted of two main cuts, where the log is partially peeled on both sides of the circumference. Then, a cut is made in the middle of the peeled log, obtaining two half-cants that are sent to the re-saw to obtain the boards. The cutting pattern of Plan PB consisted of a main cut, where the log is partially peeled on one side of the circumference. Then, a cut in the middle of the log is made, obtaining five half-cants, which are processed on the band saw re-saw with a 19-gauge blade. This allowed for a small cut and improved lumber yield.
After sawing, lumber was classified and grouped according to the parameters set by the sawmill Forest Regnans for green and square lumber. Lumber grading was based on Australian standards, which include three grades: select, standard, and utility or general use. Select grade is defect-free lumber and is used in appearance-based products, including floors, stairs, doors, cabinets, moldings, and furniture. This category includes AP7, which refers to green lumber of a 3 m or 7-foot piece with a knot in the last 3 feet, signifying its utilization for 4 feet. In the second grade, lumber exhibits defects such as knots, resin pockets, or variable color. It is sometimes used in products that require an acceptable appearance, but it is generally used in construction applications, wall structures, solid-section beams, and double T-beams. The utility grade refers to wood used as pallets and fences. Posts and poles must be chemically treated for outdoor use.

2.4. Evaluation of Wood Warping

Wood warping was determined according to the NCh.993:2018 standard. Defects such as bow, crook, and twist were evaluated in each piece [39].

2.5. Sawing Yield in Eucalyptus regnans Logs

The sawing yield was determined using the following equation [40]:
L u m b e r   y e i l d   ( % ) = V o l u m e   o f l u m b e r   i n   m 3   V o l u m e   o f   l o g   i n   m 3 × 100
The log volume was determined using Equations (1) and (2). The dimensions of each board were used to calculate the volume of lumber. Furthermore, the quality of the wood was assessed according to the criteria established by the customer, with separation based on cutting type (plain sawn, quarter sawn, and rift sawn).

2.6. Statistical Analysis

The statistical software program SPSS version 27 (IBM Corp., Armonk, NY, USA) was utilized for a linear regression between log diameters and lumber yield.

3. Results and Discussion

3.1. Distribution of Log Diameters

The processed log diameters exhibited different values ranging from 30 cm to 56 cm (Table 1). The largest proportion of logs, accounting for 24.6% of the total logs, was observed in the 40 cm diameter category, comprising 32 pieces. Following this, the diametrical classes of 38 and 36 cm added up to 40 logs, representing 18.5% and 12.3% of the total pieces, respectively. There were two logs, each with diameters of 42 cm and 44 cm, and only one log with a 30 cm diameter.

3.2. Assessment of Log Quality

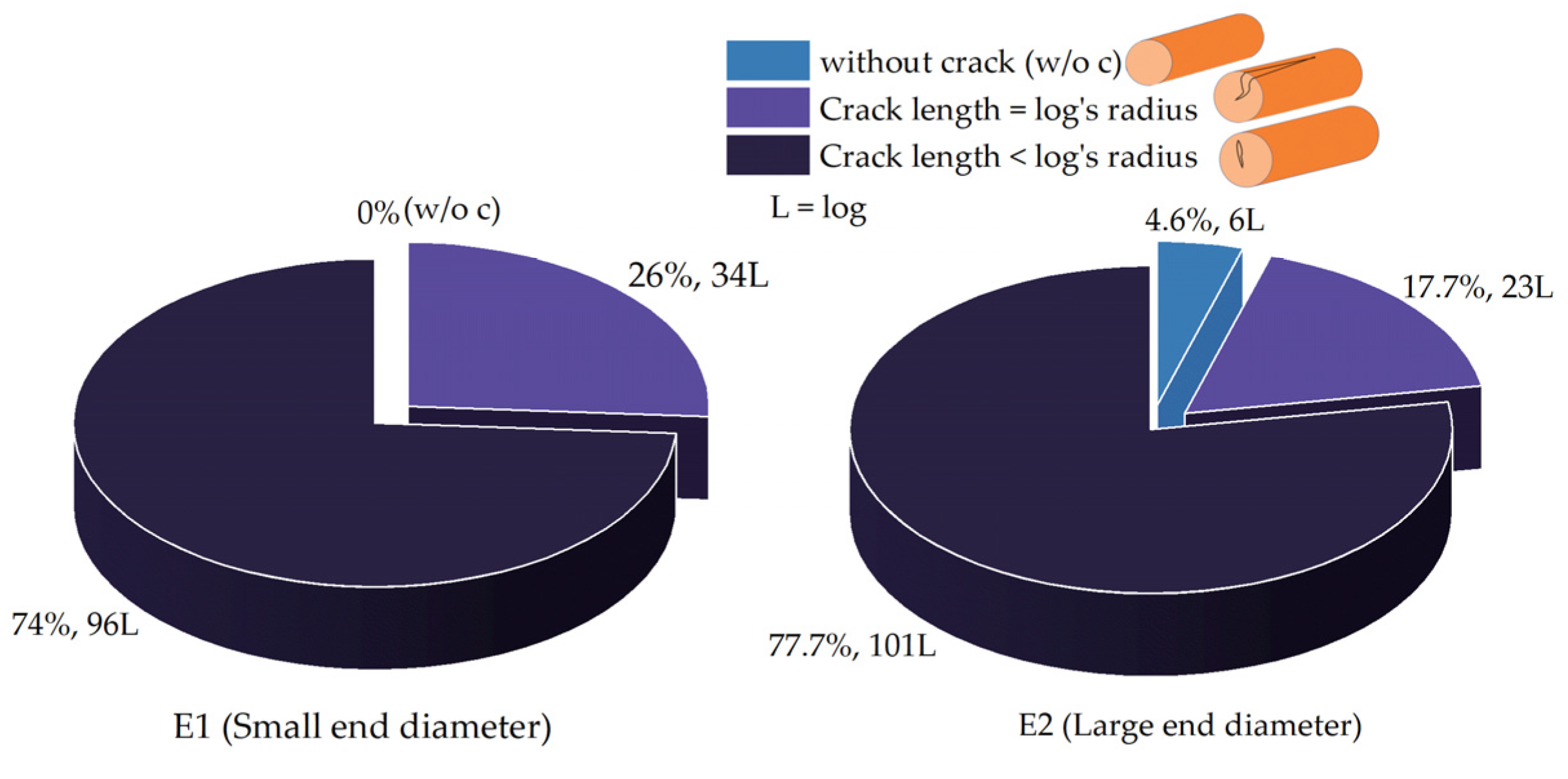
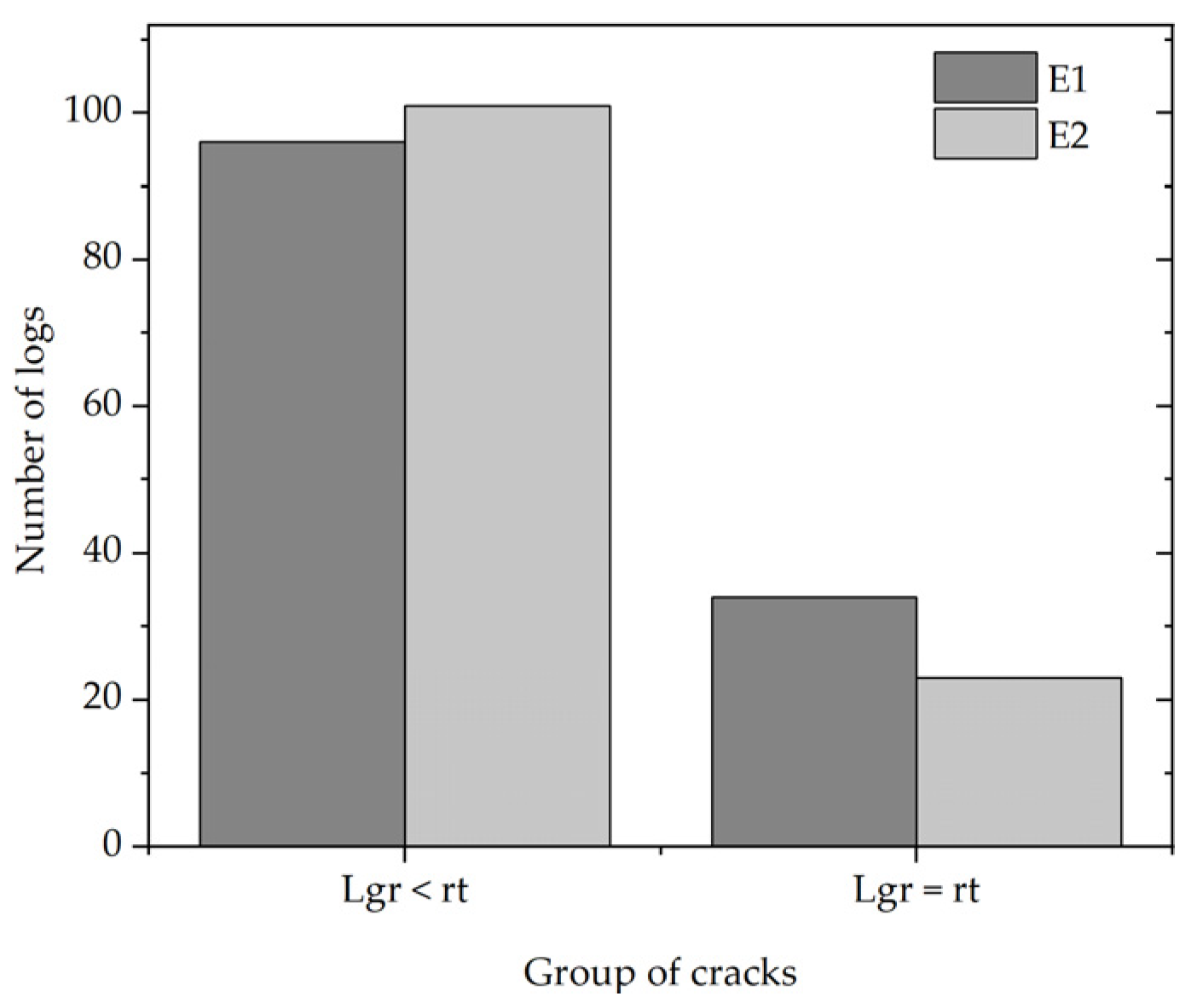
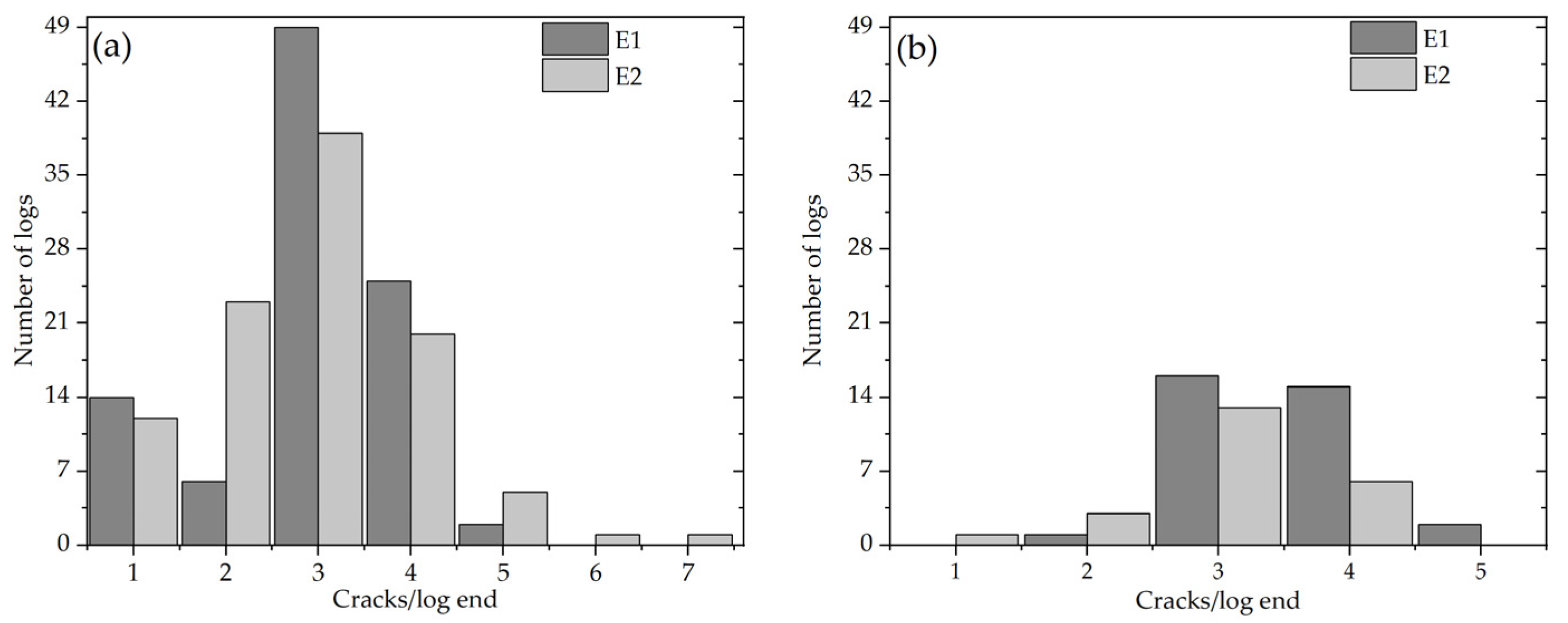
3.2.1. Radial Cracks in Log Ends

Cracks were measured at both ends of each log. The small-end diameter and large-end diameter were coded as E1 and E2, respectively. Figure 1 shows that all logs displayed radial cracks, at least on one log end. In regard to E1, 100% of the logs had radial cracks, whereas at E2, only 95.4% (Figure 1). Cracks were classified into two groups: The first group included cracks that extend from the pith to the edge, where the crack length is equal to the log’s radius (Lgr = rt). In the second group, the crack length is smaller than the log’s radius (Lgr < rt). In general, 57 logs exhibited cracks from the first group, with 34 and 23 logs for E1 and E2, respectively. On the other hand, at E1, 96 y 101 logs had cracks from the second group for E1 and E2, respectively. Additionally, only six pieces did not have cracks in E2.
Figure 2 illustrates the number of logs with radial cracks based on their length. It is evident that at both E1 and E2, the number of logs that had radial cracks (Lgr < rt) was 2.8 and 4.4 times higher, respectively, compared to the first group (Lgr = rt). However, despite being a smaller group in terms of log quantity, logs with these types of cracks had a more significant impact on the sawing process due to the widening and length of cracks along the longitudinal direction. Consequently, this affected both the lumber yield and quality. Additionally, due to this defect, the pieces had to be trimmed, resulting in a reduction in the piece length.
Figure 3 shows the number of radial cracks per log. Figure 3a displays the number of cracks with lengths smaller than the log’s radius. The maximum quantity of cracks found in logs was seven and five, in E2 and E1, respectively. However, most logs had three cracks in both log ends, which were a little bigger in E1, with 49 logs versus 39 in E2. Similarly, 12 and 14 logs had one radial crack in small-end diameter 1 and large-end diameter 2, respectively.
Figure 3b presents the number of cracks with lengths equal to the log’s radius. It is observed that, under this condition, the cracks are less numerous compared to those shown in Figure 3a. In fact, the highest number of cracks found was five in small-end diameter, but only in two logs. On the other hand, the highest number of radial cracks was three, which were concentrated in 16. It also found 15 logs with four cracks in E1.

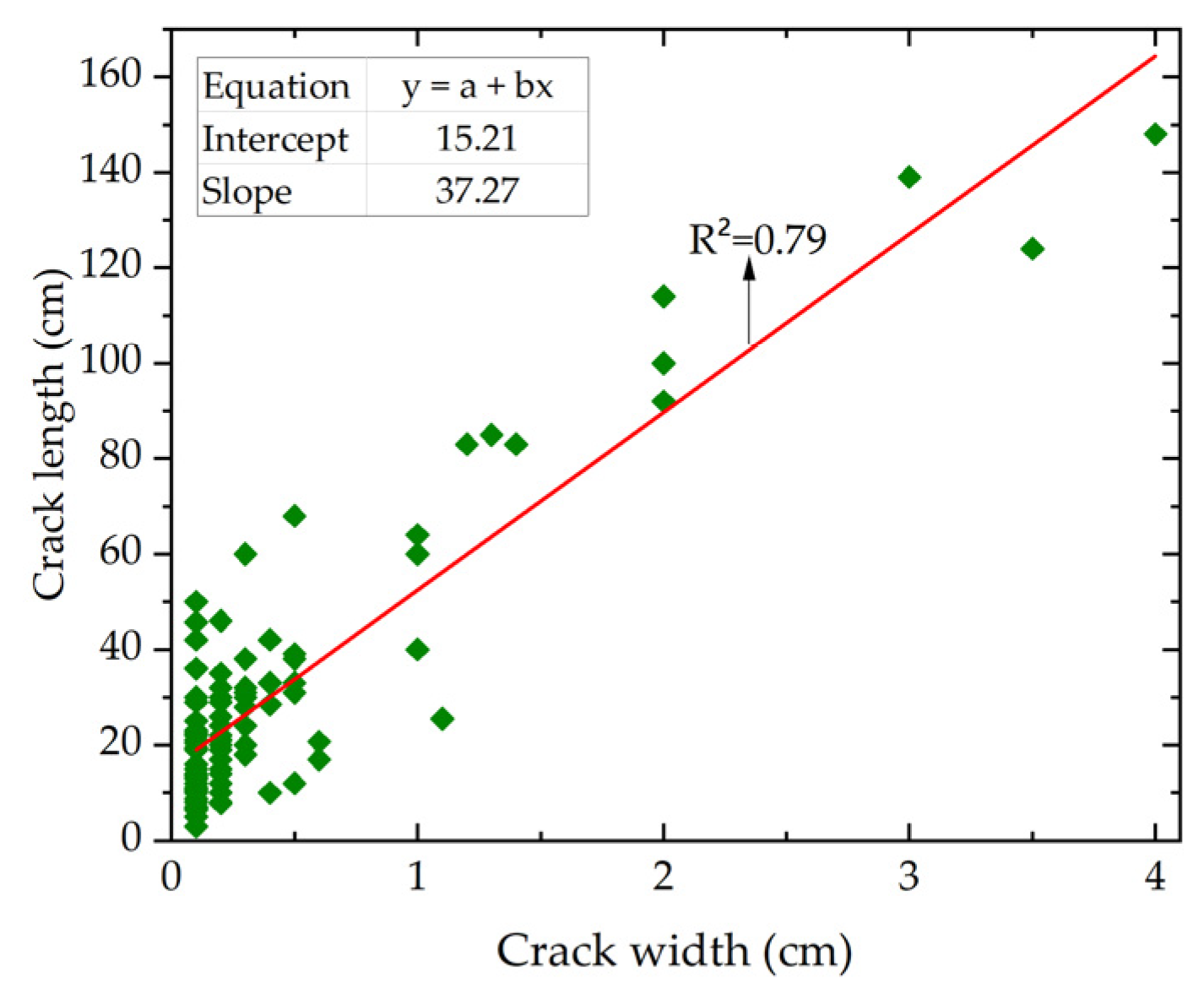
3.2.2. Relationship between the Width and Length of Longitudinal Cracks

The relationship between the width and length of the longitudinal cracks was determined using a regression model (Figure 4). This relationship showed a high determination coefficient of 0.79%. This indicates that the variability of the crack length can be explained by the crack width variability. It is worth noting that there may be factors not considered in this model that might contribute to explaining better this correlation. Furthermore, the correlation between the crack width and length may be attributed to the physical and mechanical behavior of the wood and its exposure to different conditions. Internal stresses generated by the wood’s structure lead to the formation of cracks. As crack width increases, the tension at the crack edges tends to increase, resulting in greater propagation. This is because the crack edges are under a higher concentration of stress and are more susceptible to separation. Additionally, the wood moisture content plays a significant role in crack propagation, as wider cracks allow for greater moisture penetration into the wood, further weakening the structure and contributing to crack propagation. Similarly, the intrinsic characteristics of the wood contribute to crack propagation. It is important to note that the evaluated pieces had crack widths ranging from 1 to 4 cm, while the longitudinal cracks exhibited a wide range, with a maximum length of 148 cm.

3.3. Sorting of Sawn Lumber

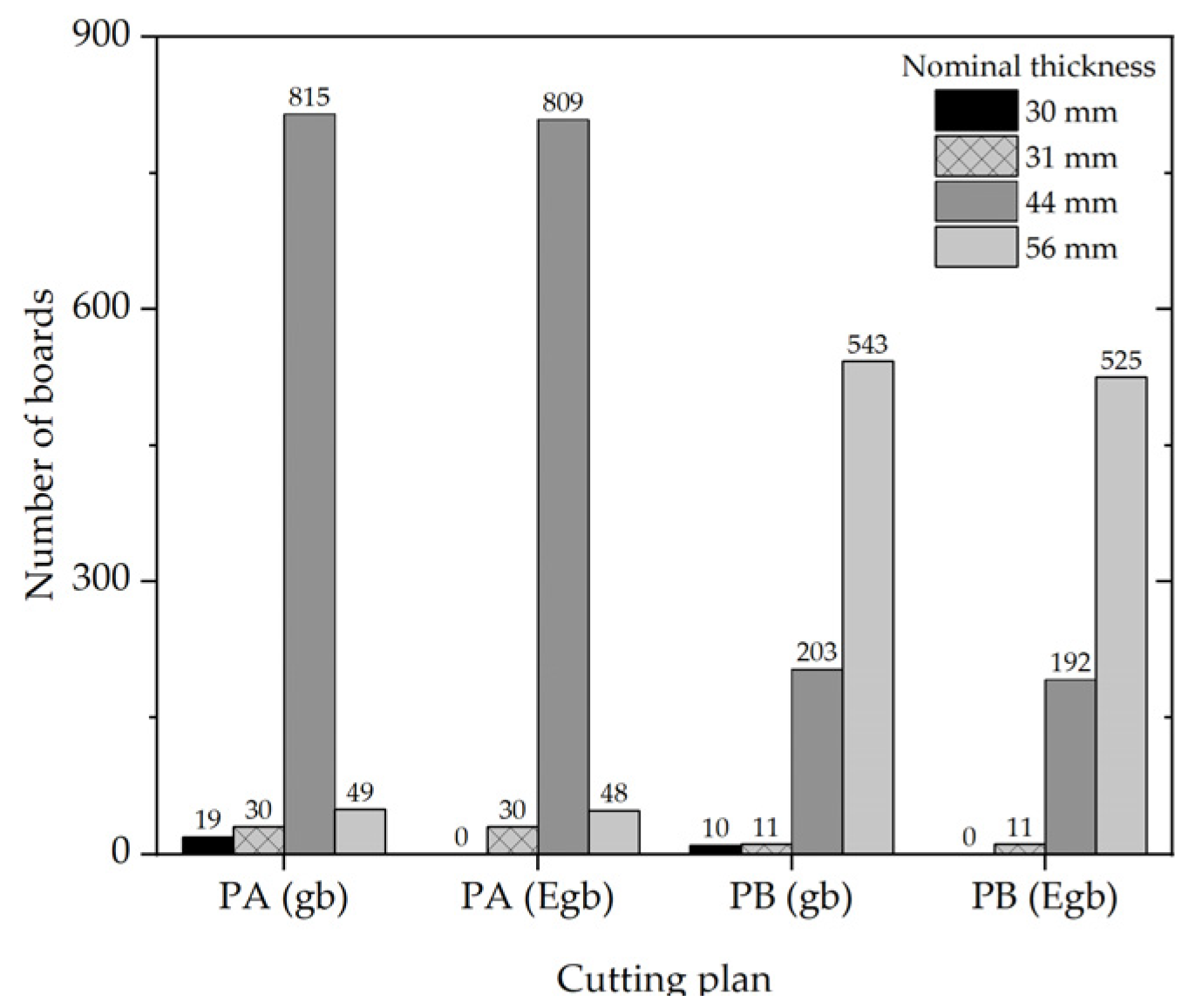
3.3.1. Lumber by Thickness and Cutting Plan

Figure 5 displays the number of boards based on the thickness of the green board and cutting plan (PA-PB). The results indicated that for PA, there were 815 boards with a thickness of 44 mm. For PB, the number of boards was 543 boards, but with a thickness of 56 mm. On the other hand, losses of boards were observed in PB, with 11 and 18 boards with thicknesses of 44 and 56 mm, respectively. These losses represented 4.5% and 3.3% of the total of 203 and 543 boards, respectively. Furthermore, in both cutting plans, all boards with a thickness of 30 mm were classified as rejects (29 boards) because they did not meet the nominal value.

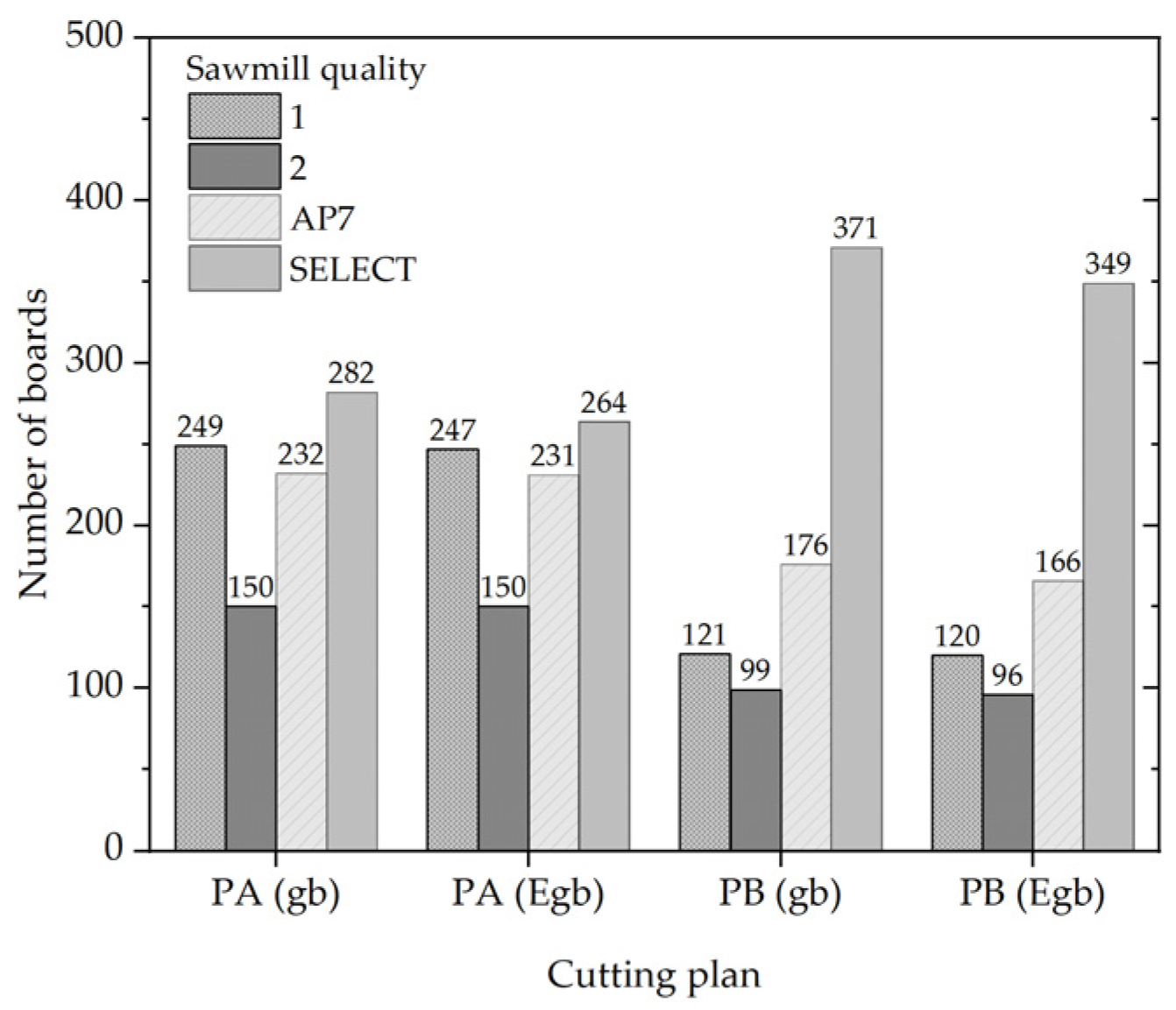
3.3.2. Lumber Grading According to Australian Standards

It was found in PA that 282 boards reached the highest value grade, “Select grade”, followed by 249 and 232 grade 1 and AP7-grade boards, respectively. In PB, a higher number of select-grade boards was found compared to PA (Figure 6). Specifically, 371 pieces were counted, followed by 176 and 121 AP7 and grade 1 boards, respectively. When analyzing the board losses for both cutting plans, in PA, there was a loss of 18 select-grade boards. However, for the other grades, loss boards were minimal. In PB, there were 22 select-grade boards and 10 AP7-grade boards. Grades 1 and 2 boards had losses of one and three pieces, respectively.

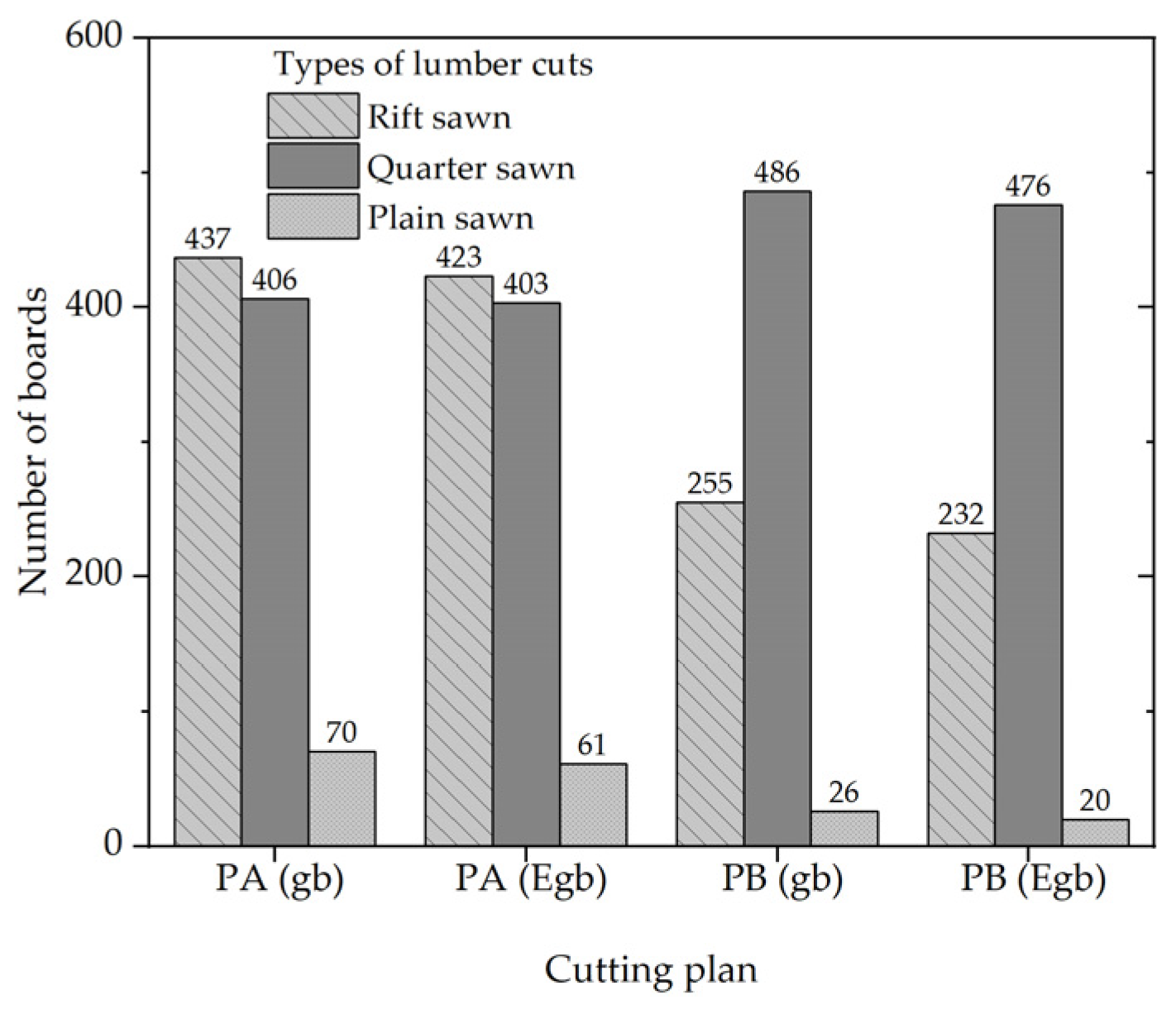
3.3.3. Lumber Grading Based on Customer-Defined Criteria Based on the Types of Wood Cuts: Plain Sawn, Quarter Sawn, and Rift Sawn

Figure 7 shows the distribution of boards classified by the types of cuts (plain sawn, quarter plain, and rift sawn) for both PA and PB. In PA, it was found that most boards were rift sawn, totaling 437, followed by 406 quarter-sawn boards. Regarding boards that were perfectly plain sawn, they numbered 70. In terms of losses, there were 14 rift-sawn boards and 3 quarter-sawn boards. Contrary to PA, in PB, a higher proportion of quarter-sawn board was found, followed by rift sawn. In general, out of the total boards analyzed, 486 were quarter sawn, while 255 were rift sawn. In the latter, there was a loss of 23 boards compared to 10 in quarter sawn.

3.4. Measurements of Wood Warping

3.4.1. Evaluation of Wood Warping in the Different Cutting Plans

Table 2 presents a summary of the number of boards exhibiting warping in the different cutting plans and losses resulting from dimensioning. Boards were assessed to determine the warp: bow, crook, and twist. Warp was determined for both PA (28–40 cm log diameters) and PB (42–56 cm log diameters). Furthermore, a comparison was conducted between boards classified as green boards (with high moisture content) and expected green boards. This comparison allowed for the visualization of board losses caused by declassification based on the thickness and width of the boards, meaning those boards deviated from the anticipated dimensions of green lumber. This approach facilitated the determination of warps in the boards for each cutting plan. The Chilean standard NCh993: 2018 sets admissible levels or values (A, B, C, and D) for each defect [39].
Concerning bow, level B was the predominant for most of the boards in both cutting plans. However, a loss total of 25 (3.3%) and 38 (5.3%) boards was found in PA and PB, respectively, totaling 63 boards. Also, a number of boards graded level A was found, but it was significantly lower compared to level B boards. Minimal or no losses were observed in levels A, C, and D. The total loss due to bow amounted to 3.9%, that is, 65 boards out of the 1680 studied. Losses were attributed to problems during the sawing process, followed by the quality of boards.
On the other hand, the highest proportion of boards exhibited level B crook, with a higher incidence in PB, specifically, 73.4% and 73.8% of the total green boards and 728 expected green boards, respectively. In PA, the number of boards was higher compared to the number of boards in PB. Following in proportion are the boards that had level C crook. In this case, PA had the highest number of boards. Regarding board losses with crook, for level B, it was 3.1% (13 boards) in PA and 4.6% (26 boards) in PB. As for level C, losses were low, with eight boards found in PB.
When considering twists in boards, the highest concentration of boards with level A was observed in PB. To a lesser extent, a significant number of boards with level A twist were also present in PA. Similarly, a notable number of boards with level B twist were found, but the highest concentration occurred in PA, while in PB, it was much lower. The board losses for level A in PA and PB were 4.2% (19 boards) and 4.9% (33 boards), respectively. On the other hand, there were no board losses for levels C and D.
Warping in green lumber can affect the lumber yield. However, twisting and bowing defects have a lesser impact compared to crook. For example, twist recovery can be increased with the overload and steaming time during the drying process [41,42]. Also, after planning, twist and bow defects can decrease [43]. Crooking cannot be rectified during the drying process as it occurs with twists and bows. One solution to this problem is the resawing of the pieces to eliminate this defect, which would result in a decrease in the lumber yield of E. regnans.

3.4.2. Wood Warping According to the Thickness of Board

Warping was also assessed based on the nominal green thickness (30; 31.5; 44; 56 mm) for both PA and PB (Table 3). Furthermore, boards classified as green boards and expected green boards were compared, enabling the visualization of board losses due to declassification based on thickness and width (boards that did not meet the expected ranges). As a result, the actual number of boards, categorized by thickness and graded according to NCh993:2018, was determined [39].
As for bowing, the results indicated that the 30 mm thick boards did not meet the nominal dimensions. However, there was a total loss of 29 boards, which were graded in level B. Similarly, level B experienced losses of 16 and 18 for the 44 mm and 56 mm thick boards, respectively. Furthermore, there was only one board loss in level A (56 mm thick) and in level D (44 mm thick), while there were no board losses in level C. On the other hand, regarding the total loss of boards with crooks, there were a total of 29 boards with a thickness of 30.0 mm. In level B, there were no board losses observed with a thickness of 31.5 mm. However, for boards with thicknesses of 30, 44, and 56 mm, the board losses were 11, 13, and 15, respectively. Similarly, levels C and D experienced board losses with the same thicknesses, but board losses were considerably lower than reported in level B. It is important to note that the boards classified under these levels were very low. On the other hand, according to Rozas and colleagues [21], crook warping is a defect that cannot be recovered completely during the drying process, leading to high lumber loss after the sawing process. Likewise, the dimensions of the pieces are a factor to be considered after the sawing and drying processes. Warp defects can be influenced by the cross-section size of lumber pieces [44]. For twist warping, a total loss of 29 boards with a thickness of 30 mm was found. The most significant loss of boards was concentrated in level A, with nearly identical quantities of board losses with thicknesses of 30, 44, and 56 mm. The total loss of boards in this level was 52, while in level B, it was 12 boards.

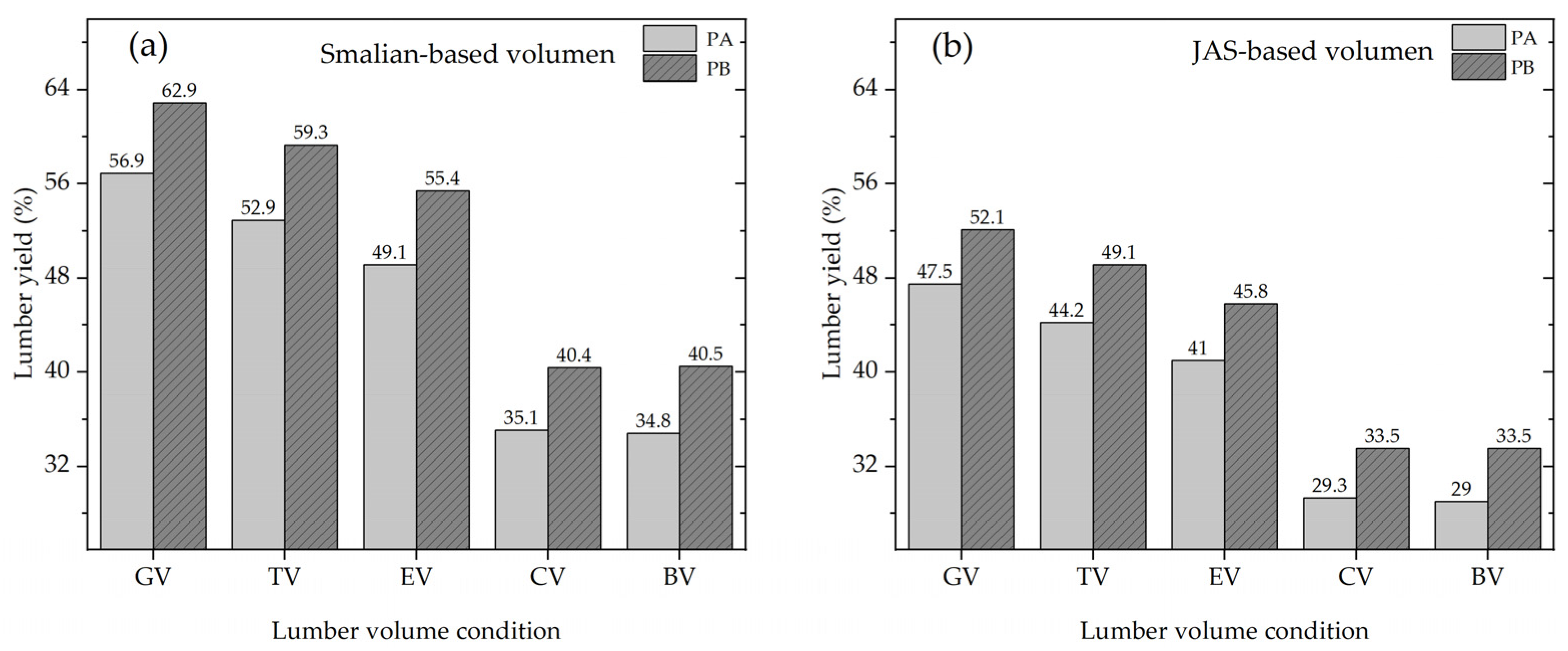
3.5. Lumber Yield

The crack length at both log ends was measured for all pieces. Taking into account crack lengths, trimming was carried out to determine the lumber loss. The Australian standard for product quality allows for cracks of up to 12 mm in length. The final dimension of lumber was used to determine the lumber yield. Figure 8 shows that the yield of PB exceeded that of PA. This was observed in both the JAS and Smalian equations for all conditions (Figure 8). These results might be expected, as large-diameter logs yield more lumber than small-diameter logs. However, it can also happen that thicker logs may have smaller volumes due to internal defects like cracks, decay, and insect attacks [45]. Nevertheless, it is worth noting that the main problem during the sawmilling process of E. regnans is the presence of growth stresses, which generate log end cracks. Cracks and warping limit maximizing lumber yield from logs. The increase in the logs’ diameter range does not guarantee greater yield, and when large-diameter logs need to be sawn, the sawing process must be carefully selected. The sawing of Eucalyptus is not recommended to be performed in a massive way as it is performed with Pinus radiata. The process is carried out log by log, determining the best sawing method to increase the yield. It has also been proven that there is a relationship between the increase in diameter and the reduction in growth stresses and, consequently, the presence of cracks at the ends of the logs.
The log volume calculated using the JAS method for the different conditions was greater than Smalian’s equation. However, when considering both volume equations, green lumber (GV) yield determined according to the Smalian equation, which turned out to be the highest of all conditions, was 56.9% and 62.9% for PA and PB, respectively (Figure 8a). In contrast, the JAS volume showed yields of 47.5% and 52.1% for PA and PB, respectively (Figure 8b). This variation in JAS scaling occurred due to the utilization of rounded-down values for the small-end diameter in the formula. Moreover, JAS also considered the smaller of the two rounded-down small-end diameter values for the calculation of JAS volume [46]. In contrast to JAS, Smalian’s method considered cross-sectional areas measured at both log ends [47]; therefore, the log volume turned out to be smaller than the JAS volume. On the other hand, Smalian’s method may lead to bias [48]. The log volume methods used are a relevant aspect to be highlighted since they directly provide information on the lumber yield, which can be higher or lower depending on the volume equation used, as presented in this research. Likewise, the type of log-sawing pattern has a remarkable influence on lumber yield [49]. The yields found in this research are higher than those reported by da Silva and colleagues in logs from 21 native species from Brazil, which presented an average yield of 45% [26]. A yield of 43.95% for 10 commercial species from Brazil has also been reported. In this study, the researchers used Smalian’s equation [50]. However, it is clear that one of the reasons for the lowest values is the sawing process used. In contrast, our yield results were lower than those reported for sugi logs [51]. Again, lumber yield depends on many factors, as discussed above.
Furthermore, the yield of trimmed (without cracks) lumber (TV) using Smalian’s equation for PA and PB was 52.9% and 59.3%, respectively. This percentage was significantly higher than that calculated with JAS (44.2% for PA and 49.1% for PB). As for the yield of expected green lumber (EV), it was lower than the two above yields, but it can still be considered a high lumber yield, around 50% for PA and PB, calculated using Smalian. In contrast, according to JAS, the lumber yield was 41% for PA and 45.8% for PB. The yield of commercial lumber (CV) and billing lumber (BV) were lower than the other lumber yields and were similar for both the Smalian and JAS methods.

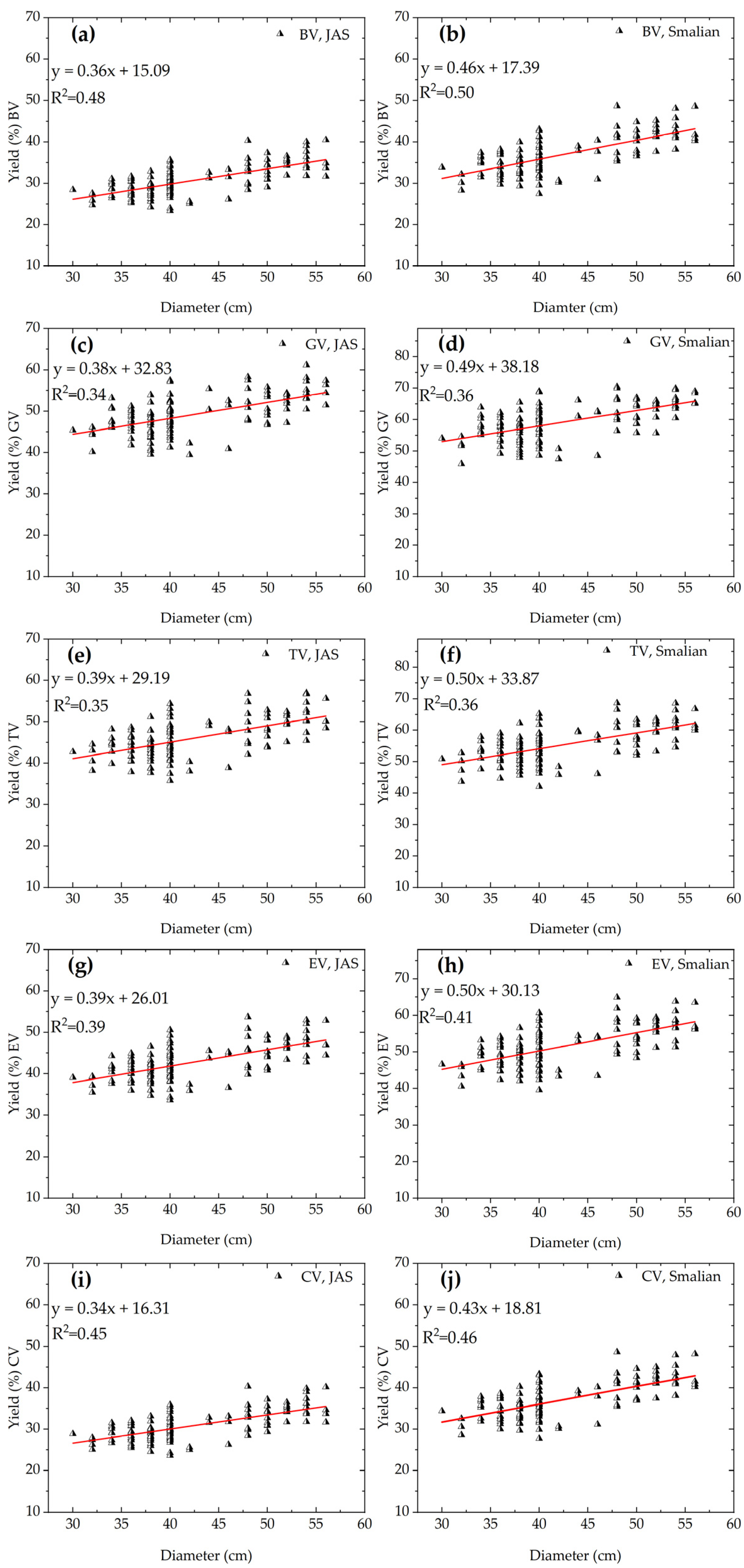
3.6. Relationship between Log Size and Lumber Yield

The linear relationship between log diameters and lumber yield for different stages of the process is depicted in Figure 9. The analysis of regression showed that the lumber yield increased gradually as the diameter increased. It is evident that, in all cases, there was a high variation in the data, leading to coefficients of determination ranging between 0.34 and 0.50. It is noteworthy that the Smalian volume-based lumber yield showed higher correlation coefficients compared to those determined by the JAS method. The strongest relationship was observed between log diameter and billing yield, with an R-squared value of 0.5. This trend indicated that a larger log diameter is associated with a higher yield.

4. Conclusions

All the logs showed radial cracks on at least one end. Most of the cracks did not extend beyond the log’s radius. However, despite being less numerous, cracks equal to the log’s radius had a higher impact on the sawing process due to crack widening and the length of longitudinal cracks. The longitudinal crack length affected the lumber yield. The Smalian volume-based lumber yield method was greater than the JAS method. It was determined that there was a linear relationship between log size and lumber yield. Large log diameters exhibited a lower proportion of boards with crook, which is crucial in the forestry industry because this defect cannot be rectified during the drying process. This study provided a comprehensive perspective on the characterization and sustainable utilization of Eucalyptus regnans in lumber production, highlighting its importance in the forestry industry.

Author Contributions

Conceptualization, C.R. and F.M.; methodology, C.R. and F.M.; validation, C.R., F.M., B.Z., and V.O.-A.; formal analysis, B.Z., V.O.-A., O.E., and C.R.; investigation, B.Z., F.M., and C.R.; resources, C.R.; data curation, B.Z., O.E., and F.M.; writing—original draft preparation, O.E. and B.Z.; writing—review and editing, C.R., O.E., F.M., V.O.-A., and B.Z.; visualization, O.E., C.R., F.M., and V.O.-A.; supervision, C.R.; project administration, C.R. All authors have read and agreed to the published version of the manuscript.

Funding

We would like to thank the project 92-INES “Integrated management tool for the decision-making process to improve competitiveness in remanufacturing companies”, with the INES R&D code 22-17, for financial support.

Data Availability Statement

The data presented in this article are available upon reasonable request from the corresponding authors.

Acknowledgments

The authors would like to thank Magdalena Lisboa for providing the material for this study and the staff of Forestal Regnas Ltda. for their collaboration.

Conflicts of Interest

No conflicts of interest. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The Forestal Regnas Ltda company had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results. Author Barbara Zapata was employed by the company Forestal Arauco S.A. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The company Forestal Arauco S.A. in affiliation had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Petit, G.; Pfautsch, S.; Anfodillo, T.; Adams, M.A. The Challenge of Tree Height in Eucalyptus Regnans: When Xylem Tapering Overcomes Hydraulic Resistance. New Phytol. 2010, 187, 1146–1153. [Google Scholar] [CrossRef]
  2. Ilic, J. Woods of Eucalyptus—Part 1. Distinguishing Three Species from the Ash Group. IAWA J. 1997, 18, 27–36. [Google Scholar] [CrossRef]
  3. Xu, K.; Tu, D.; Peng, P.; Guo, Q.; Yun, H. The Air-Kiln Drying Technology Research on Australian Eucalyptus Regnans Board. Adv. Mater. Res. 2012, 393–395, 507–514. [Google Scholar] [CrossRef]
  4. Belleville, B.; Ashley, P.; Ozarska, B. Wood Planing Properties of Australian Plantation-Grown Eucalypts. Maderas Cienc. Tecnol. 2016, 18, 425–434. [Google Scholar] [CrossRef]
  5. Yang, J.L.; Waugh, G. Potential of Plantation-Grown Eucalypts for Structural Sawn Products. II. Eucalyptus nitens (Dean and Maiden) Maiden and E. regnans F. MuelL. Aust. For. 1996, 59, 99–107. [Google Scholar] [CrossRef]
  6. INFOR. Los Recursos Forestales En Chile 2022. Informe Técnico N°258; INFOR: Santiago, Chile, 2022. [Google Scholar]
  7. Lisboa, M.; Acuña, E.; Cancino, J.; Muñoz, F.; Rodriguez, R.; Volker, P. Primeros Resultados de Un Ensayo de Severidad de Podas En Eucalyptus Regnans. Efectos En El Crecimiento y Respuesta Fisiológica. Cienc. Investig. For. INFOR 2014, 20, 39–50. [Google Scholar] [CrossRef]
  8. La Sala, A.V. Long-Term Response of Eucalyptus Regnans F.Muell. to Commercial Thinning in a Regrowth Eucalypt Forest in Tasmania. Aust. For. 2007, 70, 167–172. [Google Scholar] [CrossRef]
  9. Sillett, S.C.; Van Pelt, R.; Kramer, R.D.; Carroll, A.L.; Koch, G.W. Biomass and Growth Potential of Eucalyptus Regnans up to 100m Tall. For. Ecol. Manag. 2015, 348, 78–91. [Google Scholar] [CrossRef]
  10. Wood, S.W.; Hua, Q.; Allen, K.J.; Bowman, D.M.J.S. Age and Growth of a Fire Prone Tasmanian Temperate Old-Growth Forest Stand Dominated by Eucalyptus Regnans, the World’s Tallest Angiosperm. For. Ecol. Manag. 2010, 260, 438–447. [Google Scholar] [CrossRef]
  11. Suontama, M.; Low, C.B.; Stovold, G.T.; Miller, M.A.; Fleet, K.R.; Li, Y.; Dungey, H.S. Genetic Parameters and Genetic Gains across Three Breeding Cycles for Growth and Form Traits of Eucalyptus Regnans in New Zealand. Tree Genet. Genomes 2015, 11, 133. [Google Scholar] [CrossRef]
  12. Hawthorne, S.N.D.; Lane, P.N.J.; Bren, L.J.; Sims, N.C. The Long Term Effects of Thinning Treatments on Vegetation Structure and Water Yield. For. Ecol. Manag. 2013, 310, 983–993. [Google Scholar] [CrossRef]
  13. Van Der Meer, P.J.; Dignan, P. Regeneration after 8 Years in Artificial Canopy Gaps in Mountain Ash (Eucalyptus Regnans F. Muell.) Forest in South-Eastern Australia. For. Ecol. Manag. 2007, 244, 102–111. [Google Scholar] [CrossRef]
  14. INFOR. Eucalyptus Regnans. Antecedentes Silviculturales y Tecnología Para Sus Uso En Chile. Informe Técnico N°181; INFOR: Santiago, Chile, 2011. [Google Scholar]
  15. Lisboa, M.; Acuña, E.; Cancino, J.; Chao, F.; Muñoz, F.; Rodríguez, R.; Volker, P. Physiological Response to Pruning Severity in Eucalyptus Regnans Plantations. New For. 2014, 45, 753–764. [Google Scholar] [CrossRef]
  16. INFOR. Anuario Forestal-Chilean Statistical Yearbook of Forestry 2022; INFOR: Santiago, Chile, 2022. [Google Scholar]
  17. Yang, J.L.; Baillères, H.; Okuyama, T.; Muneri, A.; Downes, G. Measurement Methods for Longitudinal Surface Strain in Trees: A Review. Aust. For. 2005, 68, 34–43. [Google Scholar] [CrossRef]
  18. Chauhan, S.S.; Walker, J.C.F. Wood Quality in Artificially Inclined 1-Year-Old Trees of Eucalyptus Regnans—Differences in Tension Wood and Opposite Wood Properties. Can. J. For. Res. 2011, 41, 930–937. [Google Scholar] [CrossRef]
  19. Touza, M. Tensiones de Crecimiento En Eucalyptus Globulus de Galicia (España). Influencia de La Silvicultura y Estrategias de Aserrado. Maderas Cienc. Tecnol. 2001, 3, 68–89. [Google Scholar] [CrossRef]
  20. Rozas, C.; Burgos, R.; Opazo, A.; Moreno, P.; Erazo, O.; Lasserre, J.P. Distribution of Growth Stresses in Eucalyptus Nitens Maiden Logs Immersed in Water. Forests 2023, 14, 1517. [Google Scholar] [CrossRef]
  21. Rozas, C.; Sánchez, R.; Pinedo, P. Secado de Eucalyptus Nitens y Globulus y Su Aprovechamiento En Blocks, Pisos y Muebles. Maderas. Cienc. y Tecnol. 2005, 7, 109–120. [Google Scholar] [CrossRef]
  22. Silva, E.F.F.; de Mendonça Brasil, A.C.; Blanco, C.J.C. Wood Production and Its Correlation with Socioeconomic and Environmental Indicators in the Amazon Region. Sustainability 2023, 15, 11932. [Google Scholar] [CrossRef]
  23. Rawat, Y.S.; Eba, M.; Nebiyu, M. Lumber Recovery Rate of Cupressus Lusitanica in Arsi Forest Enterprise, Ethiopia. Sustainability 2023, 15, 1046. [Google Scholar] [CrossRef]
  24. Thomas, R.E.; Bennett, N. An Analysis of the Differences among Log Scaling Methods and Actual Log Volume. For. Prod. J. 2017, 67, 250–257. [Google Scholar] [CrossRef]
  25. Lin, W.; Wang, J.; Wu, J.; Devallance, D. Log Sawing Practices and Lumber Recovery of Small Hardwood Sawmills in West Virginia. For. Prod. J. 2011, 61, 216–224. [Google Scholar] [CrossRef]
  26. da Silva Luz, E.; Soares, Á.A.V.; Goulart, S.L.; Carvalho, A.G.; Monteiro, T.C.; de Paula Protásio, T. Challenges of the Lumber Production in the Amazon Region: Relation between Sustainability of Sawmills, Process Yield and Logs Quality. Environ. Dev. Sustain. 2021, 23, 4924–4948. [Google Scholar] [CrossRef]
  27. Balasso, M.; Hunt, M.; Jacobs, A.; O’Reilly-Wapstra, J. Quality Traits of Plantation Eucalyptus Nitens Logs Impacting Volume and Value Recovery of Structural Sawn Boards. Eur. J. Wood Wood Prod. 2022, 80, 657–668. [Google Scholar] [CrossRef]
  28. Hittawe, M.M.; Sidibé, D.; Mériaudeau, F. A Machine Vision Based Approach for Timber Knots Detection. In Proceedings of the Twelfth International Conference on Quality Control by Artificial Vision 2015, Le Creusot, France, 3–5 June 2015; Volume 9534, p. 95340L. [Google Scholar]
  29. Bergman, R.D.; Simpson, W.T.; Turk, C. Evaluating Warp of 2 by 4s Sawn from Panels Produced through Green Gluing Dimension Lumber from Small Ponderosa Pine Logs. For. Prod. J. 2010, 60, 57–63. [Google Scholar] [CrossRef]
  30. Hittawe, M.M.; Sidibé, D.; Beya, O.; Meriaudeau, F. Machine Vision for Timber Grading Singularities Detection and Applications. J. Electron. Imaging 2017, 26, 063015. [Google Scholar] [CrossRef]
  31. Keegan, C.E.; Morgan, T.A.; Blatner, K.A.; Daniels, J.M. Trends in Lumber Processing in the Western United States. Part II: Overrun and Lumber Recovery Factors. For. Prod. J. 2010, 60, 140–143. [Google Scholar] [CrossRef]
  32. Hambisa, M.; Rawat, Y.S.; Nebiyu, M.; Eba, M.; Tekleyohannes, A.T. Assessment of the Rate of Lumber Recovery of Eucalyptus Saligna at Gefere Sawmill in Gimbi Area, Ethiopia. J. Indian Acad. Wood Sci. 2023, 20, 62–72. [Google Scholar] [CrossRef]
  33. Missanjo, E.; Magodi, F. Impact of Taper and Sawing Methods on Lumber Volume Recovery for Pinus kesiya and Pinus patula Logs in Circular Sawmills. J. For. Prod. Ind. 2015, 4, 12–16. [Google Scholar]
  34. Wardlaw, T.J.; Plumpton, B.S.; Walsh, A.M.; Hickey, J.E. Comparison of Sawn Timber Recovery and Defect Levels in Eucalyptus Regnans and E. Globulus from Thinned and Unthinned Stands at Balts Road, Tasman Peninsula. Tasforests 2004, 15, 99–109. [Google Scholar]
  35. Lisboa, M. Efecto de La Poda de Ramas Vivas En La Fisiología, Estructura de Copa, Crecimiento y Densidad de La Madera de Plantaciones de Eucalyptus Regnans Destinadas a La Producción de Madera de Alto Valor. Ph.D. Thesis, Universidad de Concepción, Concepción, Chile, 2014. [Google Scholar]
  36. NCh44.Of2007; Procedimientos de Muestreo Para Inspección Por Atributos—Planes de Muestreo Indexados Por Nivel de Calidad Aceptable (AQL) Para La Inspección Lote Por Lote. Instituto Nacional de Normalización: Santiago, Chile, 2007.
  37. Vidaurre, S.; Melo, S.; Pavon, R. Manual 16: Principios de Organizacion y Operación Del Aserradero; INFOR: Santiago, Chile, 1989. [Google Scholar]
  38. Ministry of Agriculture, Forestry and Fisheries. Japanase Agricultural Standards for Logs; Ministry of Agriculture, Forestry and Fisheries: Tokyo, Japan, 2007. [Google Scholar]
  39. NCh993:2018; Madera—Procedimiento y Criterios de Evaluación Para Clasificación. Instituto Nacional de Normalización: Santiago, Chile, 2018.
  40. Rozas, C. Resultados Tecnológicos Proyecto Fondef D9811018: Diversificación y Aprovechamiento de Las Plantaciones de Eucalyptus Globulus y Eucalyptus Nitens Para Su Utilización En La Industria Del Mueble; Univerisad del Bío-Bío: Concepción, Chile, 2002. [Google Scholar]
  41. Salinas-Lira, C.; Acuña-Alegría, L.; Sepúlveda-Villarroel, V.; Ananías, R.A.; Salvo-Sepúlveda, L.; Torres-Mella, J.; Cancino-Mundaca, F.; Vasco, D.A. Warp Recovery in Radiata Pine Lumber Using Steam Treatment. BioResources 2018, 13, 8421–8431. [Google Scholar] [CrossRef]
  42. Zhuoting, J.; Hiroyuki, Y.; Miyuki, M.-U.; Yoshida, M.D.M.; Kento, T.; Hirokazu, K. Effect of High Temperature Drying with Load on Reduction of Residual Stress and Correction of Warp of Japanese Cedar Lumber. Dry. Technol. 2023, 41, 3–16. [Google Scholar] [CrossRef]
  43. Axelsson, A. Effect of Planing on Warp in Scots Pine (Pinus sylvestris). Wood Mater. Sci. Eng. 2012, 7, 154–161. [Google Scholar] [CrossRef]
  44. Montón, J.; Arriaga, F.; Íñiguez-González, G.; Segués, E. Warp Requirements and Yield Efficiency in the Visual Grading of Sawn Radiata Pine Timber. BioResources 2015, 10, 1115–1126. [Google Scholar] [CrossRef]
  45. Melo, R.R.; Dacroce, J.M.F.; Junior, F.R.; dos Santos Lisboa, G.; de Jesus França, L.C. Lumber Yield of Four Native Forest Species of the Amazon Region. Floresta e Ambient. 2019, 26, e20160311. [Google Scholar] [CrossRef]
  46. Ellis, J.C. A Log Volume Formula for Exporters. N. Z. J. For. 2011, 56, 20–26. [Google Scholar]
  47. de León, G.C.; Uranga-Valencia, L.P. Theoretical Evaluation of Huber and Smalian Methods Applied to Tree Stem Classical Geometries. Bosque 2013, 34, 311–317. [Google Scholar] [CrossRef]
  48. Li, C.; Barclay, H.; Hans, H.; Sidders, D. Estimation of Log Volumes: A Comparative Study; Information Report FI-X-11; Natural Resources Canada, Canadian Forest Service, Canadian Wood Fibre Centre: Edmonton, AB, Canada, 2015; 20p. [Google Scholar]
  49. Vilkovský, P.; Klement, I.; Vilkovská, T. The Impact of the Log-Sawing Patterns on the Quantitative and Qualitative Yield of Beech Timber (Fagus sylvatica L.). Appl. Sci. 2023, 13, 8262. [Google Scholar] [CrossRef]
  50. De Lima, R.B.; Ferreira, R.L.C.; Da Silva, J.A.A.; Guedes, M.C.; Da Silva, D.A.S.; De Oliveira, C.P.; Rabelo, F.G.; Silva, L.F.D.C. Effect of Species and Log Diameter on the Volumetric Yield of Lumber in Northern Brazilian Amazonia: Preliminary Results. J. Sustain. For. 2020, 39, 283–299. [Google Scholar] [CrossRef]
  51. Matsumura, Y.; Murata, K.; Ikami, Y.; Matsumura, J. Influence of Sawing Patterns on Lumber Quality and Yield in Large Sugi (Cryptomeria japonica) Logs. For. Prod. J. 2012, 62, 25–31. [Google Scholar] [CrossRef]
Forests 14 02359 g001
Figure 1. Measurements of radial cracks. Small-end diameter (E1) and large-end diameter (E2) of the log. L = log.
Figure 1. Measurements of radial cracks. Small-end diameter (E1) and large-end diameter (E2) of the log. L = log.
Forests 14 02359 g001
Forests 14 02359 g002
Figure 2. Number of logs with radial cracks at both ends. Radial cracks measured in E1 and E2. Lgr < rt: crack length is smaller than the log’s radius. Lgr = rt: length of the crack is equal to the log’s radius.
Figure 2. Number of logs with radial cracks at both ends. Radial cracks measured in E1 and E2. Lgr < rt: crack length is smaller than the log’s radius. Lgr = rt: length of the crack is equal to the log’s radius.
Forests 14 02359 g002
Forests 14 02359 g003
Figure 3. Number of logs with radial cracks at both ends. (a): Length of crack smaller than the log’s radius; (b) length of crack equal to the log’s radius. E1: small-end diameter; E2: large-end diameter.
Figure 3. Number of logs with radial cracks at both ends. (a): Length of crack smaller than the log’s radius; (b) length of crack equal to the log’s radius. E1: small-end diameter; E2: large-end diameter.
Forests 14 02359 g003
Forests 14 02359 g004
Figure 4. Relationship between the width and length of cracks. The green points represent each log.
Figure 4. Relationship between the width and length of cracks. The green points represent each log.
Forests 14 02359 g004
Forests 14 02359 g005
Figure 5. Total and losses of boards by cutting plan and thickness. PA: log-cutting plan 28–40 cm log diameters); PB: log-cutting plan (42–56 cm log diameters); gb: green board (ungraded board dimensions); Egb: expected green board (planned and classified board dimensions).
Figure 5. Total and losses of boards by cutting plan and thickness. PA: log-cutting plan 28–40 cm log diameters); PB: log-cutting plan (42–56 cm log diameters); gb: green board (ungraded board dimensions); Egb: expected green board (planned and classified board dimensions).
Forests 14 02359 g005
Forests 14 02359 g006
Figure 6. Number of boards graded by sawmill-based quality and cutting plan. PA: log-cutting plan (28–40 cm log diameters); PB: log-cutting plan (42–56 cm log diameters); gb: green board (ungraded board dimensions); Egb: expected green board (planned and classified board dimensions).
Figure 6. Number of boards graded by sawmill-based quality and cutting plan. PA: log-cutting plan (28–40 cm log diameters); PB: log-cutting plan (42–56 cm log diameters); gb: green board (ungraded board dimensions); Egb: expected green board (planned and classified board dimensions).
Forests 14 02359 g006
Forests 14 02359 g007
Figure 7. Number of boards by cutting plan and types of wood cuts. PA: log-cutting plan (28–40 cm log diameters); PB: log-cutting plan (42–56 cm log diameters); gb: green board (ungraded board dimensions); Egb: expected green board (planned and classified board dimensions).
Figure 7. Number of boards by cutting plan and types of wood cuts. PA: log-cutting plan (28–40 cm log diameters); PB: log-cutting plan (42–56 cm log diameters); gb: green board (ungraded board dimensions); Egb: expected green board (planned and classified board dimensions).
Forests 14 02359 g007
Forests 14 02359 g008
Figure 8. Lumber yield for cutting plans using (a) Smalian equation and (b) JAS standard. GV = green lumber volume; TV = trimmed (without cracks) green lumber volume; EV = expected green lumber volume; CV = commercial lumber volume; BV = billing lumber volume.
Figure 8. Lumber yield for cutting plans using (a) Smalian equation and (b) JAS standard. GV = green lumber volume; TV = trimmed (without cracks) green lumber volume; EV = expected green lumber volume; CV = commercial lumber volume; BV = billing lumber volume.
Forests 14 02359 g008
Forests 14 02359 g009
Figure 9. Relationship between log size and lumber yield, according to JAS (a,c,e,g,i) and Smalian (b,d,f,h,j). GV = green lumber volume; TV = trimmed (without cracks) green lumber volume; EV = expected green lumber volume; CV = commercial lumber volume; BV = billing lumber volume.
Figure 9. Relationship between log size and lumber yield, according to JAS (a,c,e,g,i) and Smalian (b,d,f,h,j). GV = green lumber volume; TV = trimmed (without cracks) green lumber volume; EV = expected green lumber volume; CV = commercial lumber volume; BV = billing lumber volume.
Forests 14 02359 g009
Table 1. E. regnans log diameters.
Table 1. E. regnans log diameters.
Diameter
(cm)		Number
of Logs		%Diameter
(cm)		Number
of Logs		%
3010.84421.5
3243.14632.3
3486.24886.2
361612.35096.9
382418.55286.2
403224.65496.9
4221.55643.1
Total 100
Table 2. Number of boards by warp type and losses due to dimensioning (*).
Table 2. Number of boards by warp type and losses due to dimensioning (*).
Cutting PlanWood Warping Level According to NCh993:2018 [39]
ABCDTotal
BOWPA (green board)91767514913
PA (expected green board)91742513887
PB (green board)32716190767
PB (expected green board)31678190728
PA losses 0250126
PB losses1380039
Total losses1630165
CROOKPA (green board)26425324138913
PA (expected green board)26412319130887
PB (green board)1356315437767
PB (expected green board)1253714633728
PA losses 0135826
PB losses1268439
Total Losses139131265
TWISTPA (green board)454424287913
PA (expected green board)435418277887
PB (green board)6779000767
PB (expected green board)6448400728
PA losses 1961026
PB losses3360039
Total Losses52121065
(*) PA: log-cutting plan (28–40 cm log diameters); PB: log-cutting plan (42–56 cm log diameters).
Table 3. Total losses by thickness according to wood warping.
Table 3. Total losses by thickness according to wood warping.
Nominal Green Thickness (mm)Wood Warping Grades According to NCh993:2018 [39]
ABCDTotal
BOW30 *0290029
31.500000
440160117
561180019
Total loss1630165
CROOK30 *01171129
31.500000
440133117
561153019
Total Loss139131265
TWIST30 *19100029
31.500000
441601017
561720019
Total loss52121065
* Thickness that applies within the nominal ranges.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Rozas, C.; Zapata, B.; Muñoz, F.; Ortiz-Araya, V.; Erazo, O. Characterization and Yield of Eucalyptus regnans F. Muell Logs for Lumber Production. Forests 2023, 14, 2359. https://doi.org/10.3390/f14122359

AMA Style

Rozas C, Zapata B, Muñoz F, Ortiz-Araya V, Erazo O. Characterization and Yield of Eucalyptus regnans F. Muell Logs for Lumber Production. Forests. 2023; 14(12):2359. https://doi.org/10.3390/f14122359

Chicago/Turabian Style

Rozas, Carlos, Barbara Zapata, Fernando Muñoz, Virna Ortiz-Araya, and Oswaldo Erazo. 2023. "Characterization and Yield of Eucalyptus regnans F. Muell Logs for Lumber Production" Forests 14, no. 12: 2359. https://doi.org/10.3390/f14122359

APA Style

Rozas, C., Zapata, B., Muñoz, F., Ortiz-Araya, V., & Erazo, O. (2023). Characterization and Yield of Eucalyptus regnans F. Muell Logs for Lumber Production. Forests, 14(12), 2359. https://doi.org/10.3390/f14122359

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop