Combining Artificial Neural Network and Response Surface Methodology to Optimize the Drilling Operating Parameters of MDF Panels
Abstract
:1. Introduction
2. Materials and Methods
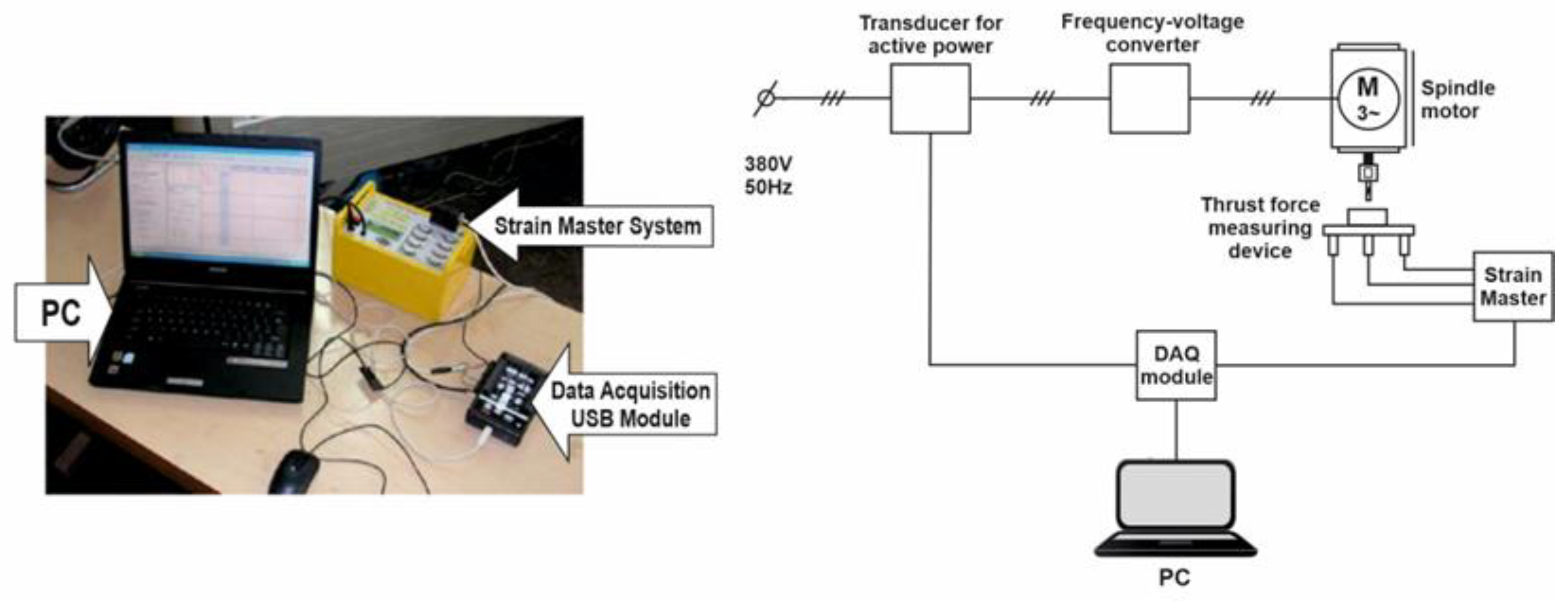
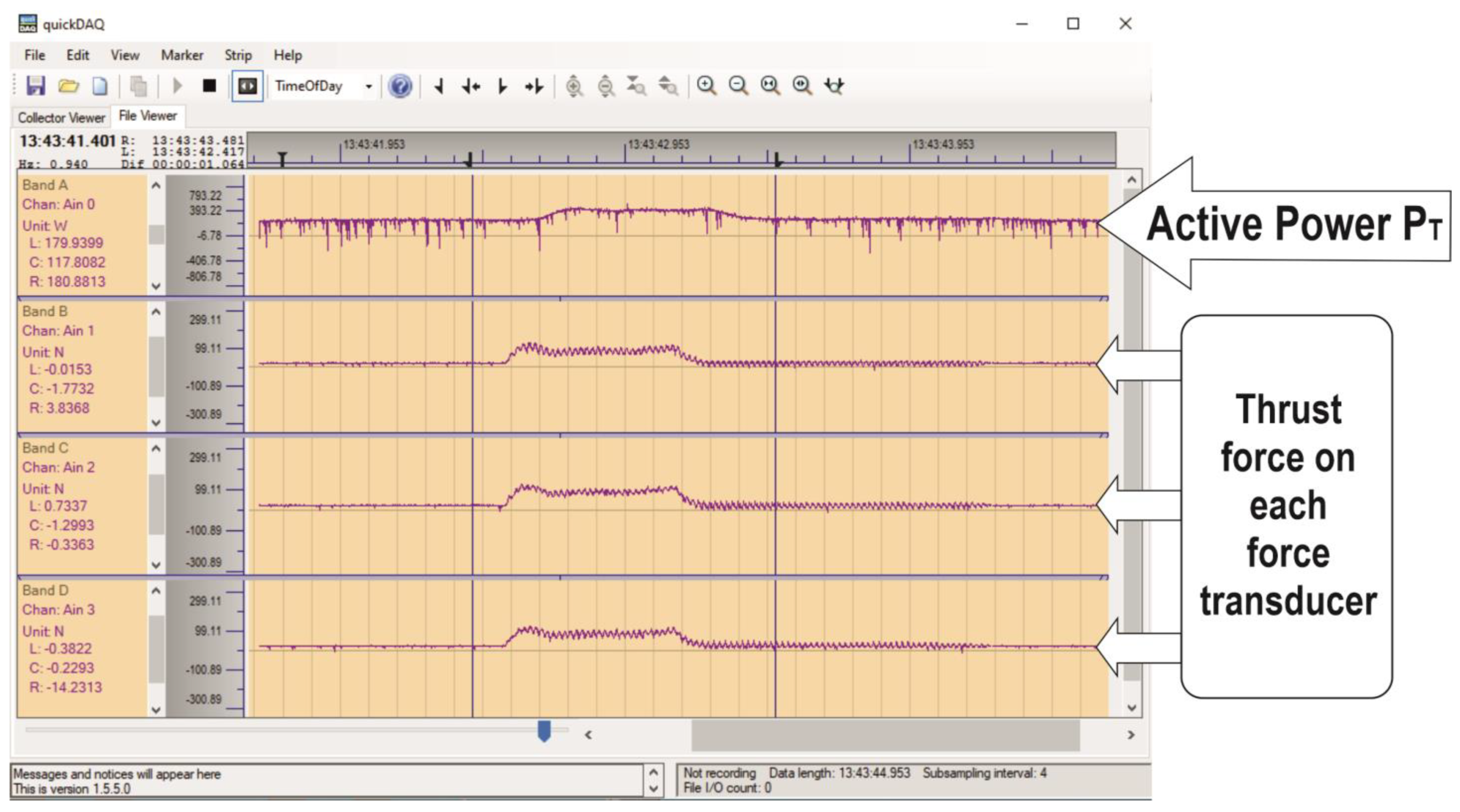
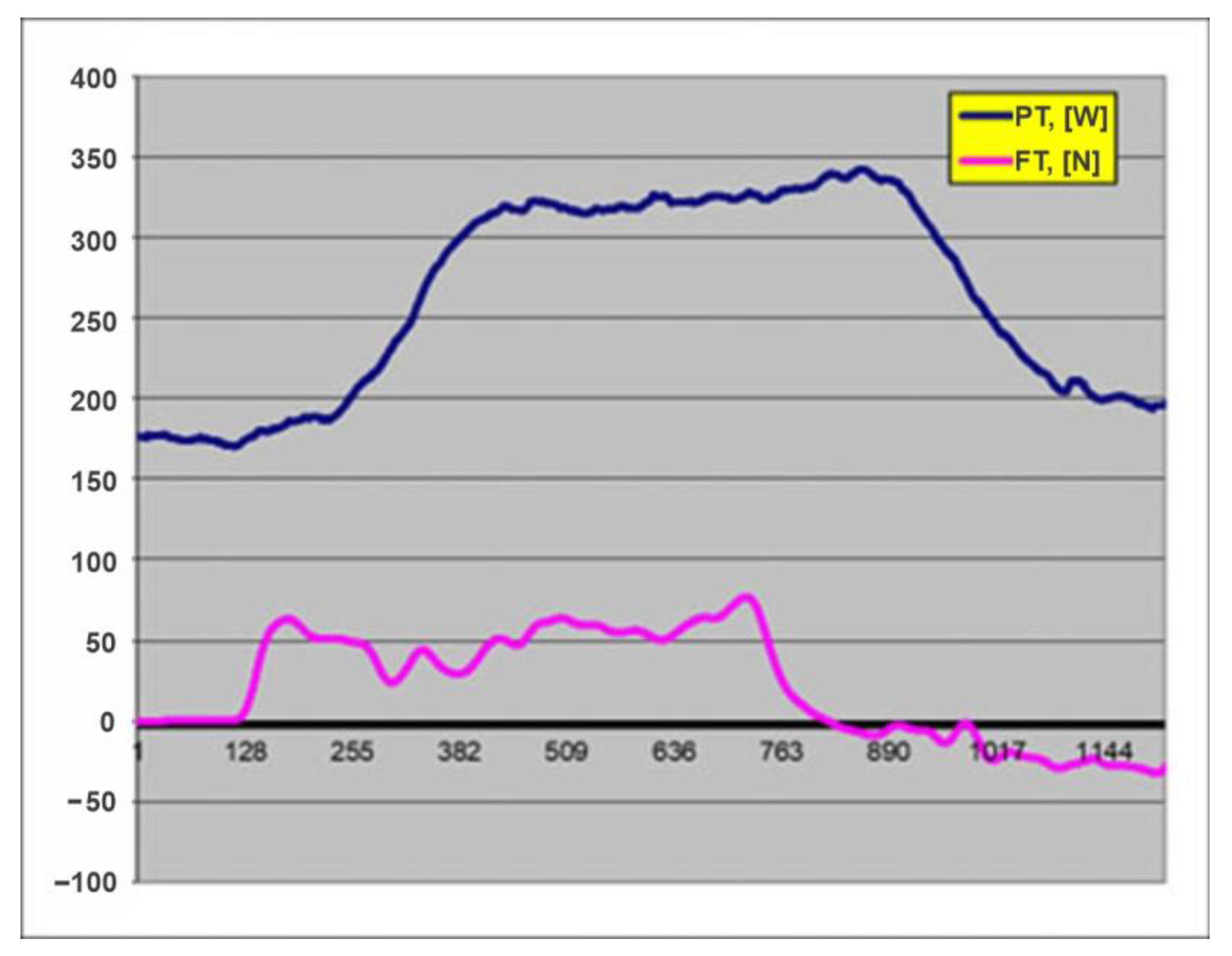
2.1. The Experiments
2.2. Data Modeling
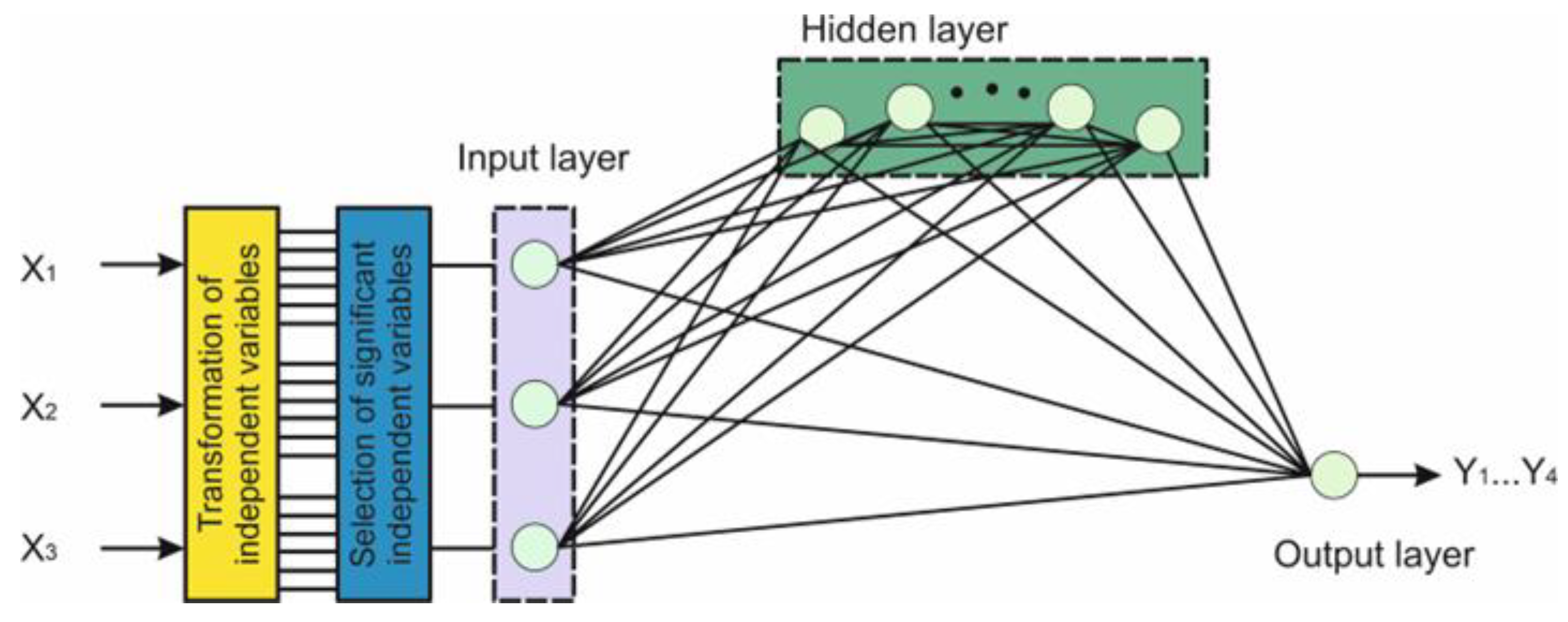
2.2.1. ANN Model Development
2.2.2. Response Surface Modeling
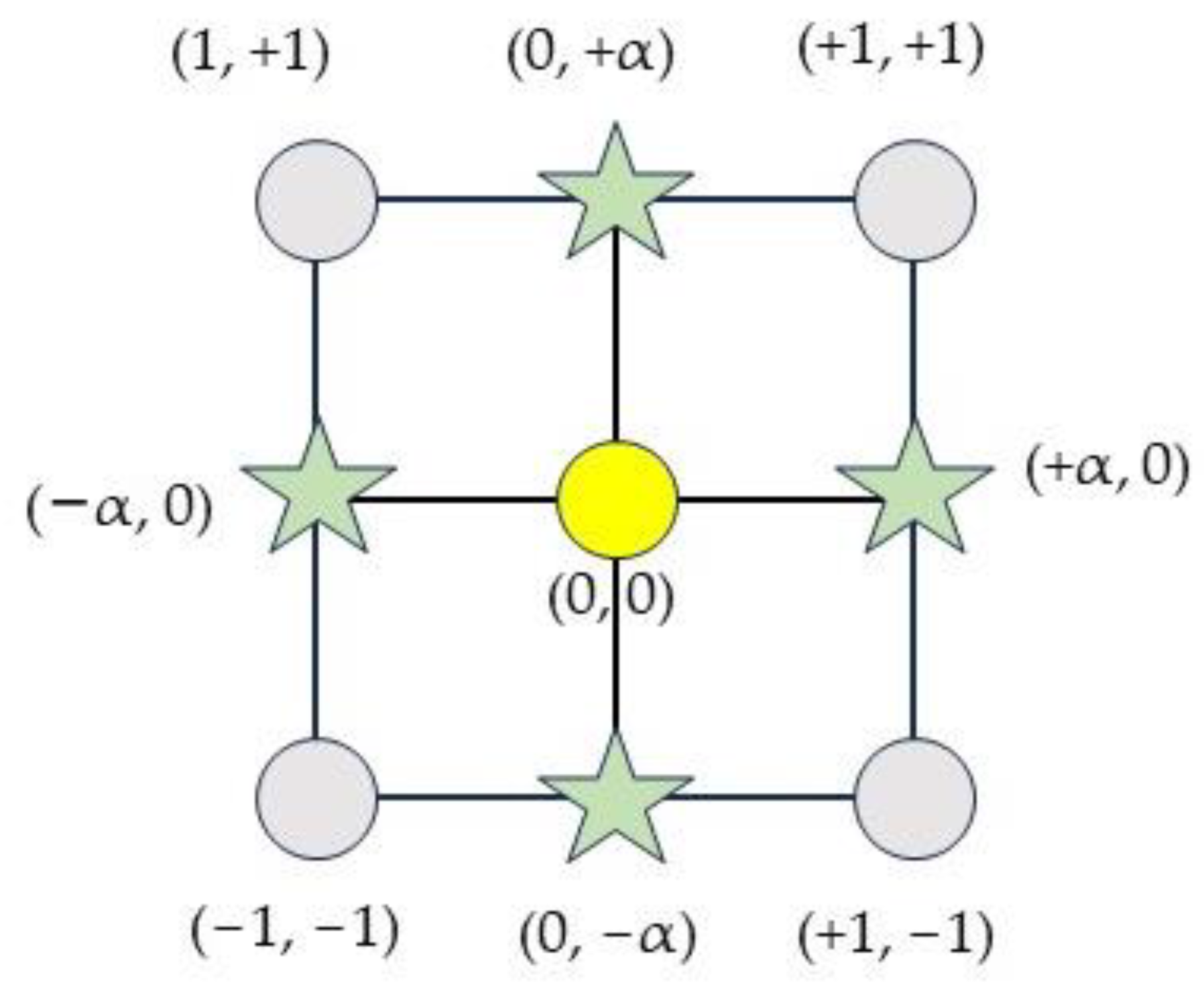
- two-level factorial points (Figure 7), which analyze all combinations of the low (−1) and high (+1) levels of analyzed factors, namely eight combinations (four combinations for flat drill and four combinations for helical drill), namely, combinations #1, #6, #8, #13, #16, #23, #24, and #25 (Table 3);
- axial points (Figure 7 and Table 3), which are needed to estimate the non-linear effect of analyzed factors. In this work, the α was equal to 1, therefore a face centered design was applied. Eight combinations (four combination for each type of drill) were analyzed in this study, namely (combinations #3, #4, #10, #14, #17, #18, #19, and #22);
3. Results and Discussion
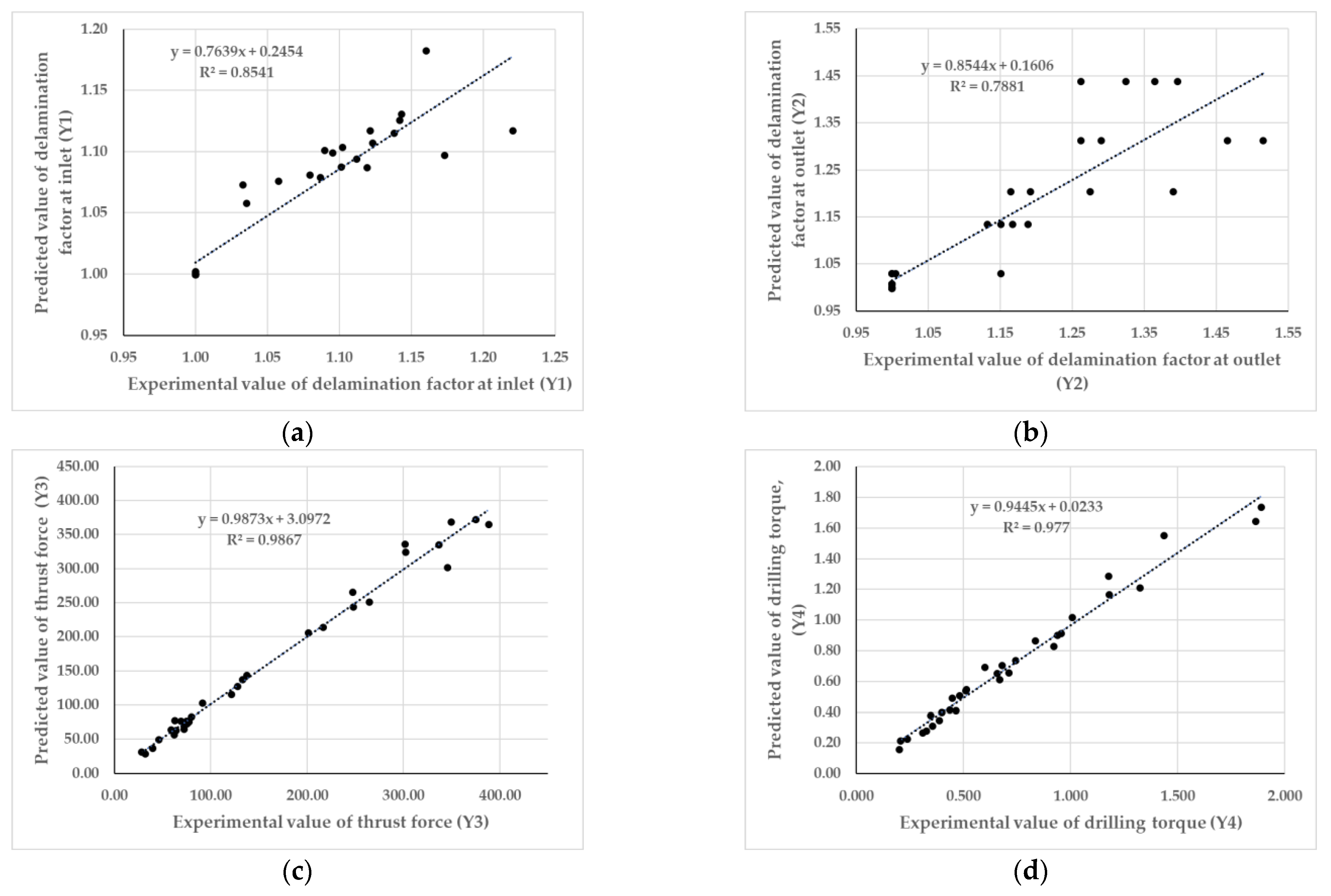
3.1. ANN Modeling
3.2. Response Surface Methodology
3.2.1. Delamination Factor at the Inlet
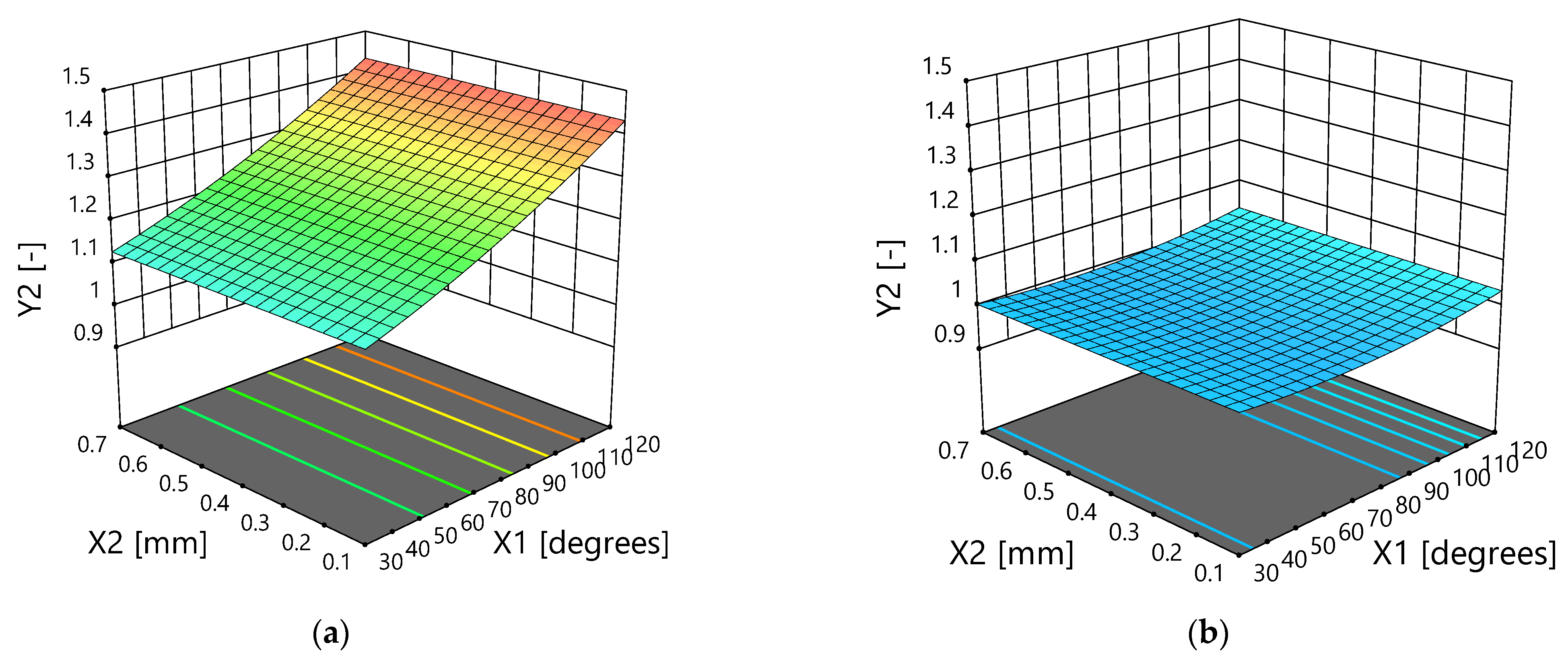
3.2.2. Delamination Factor at the Outlet
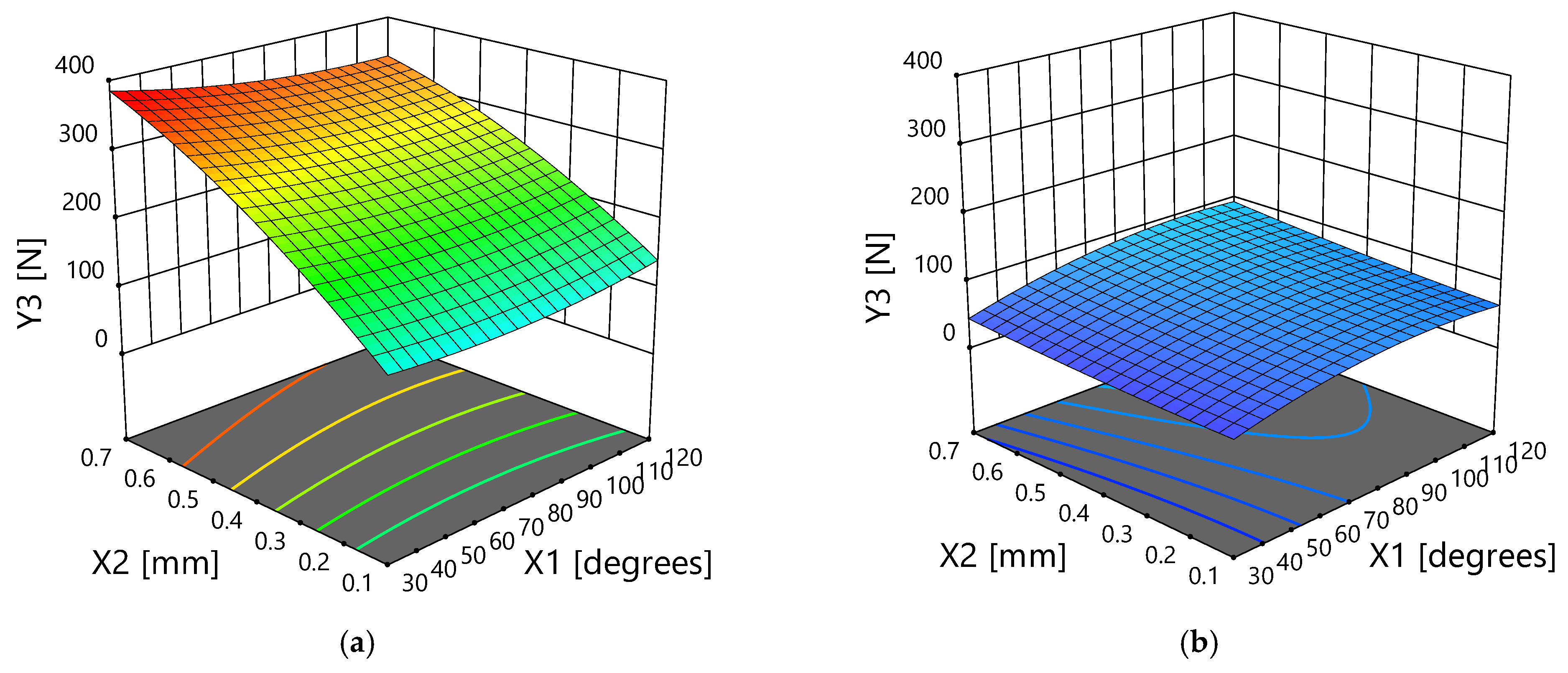
3.2.3. Thrust Force
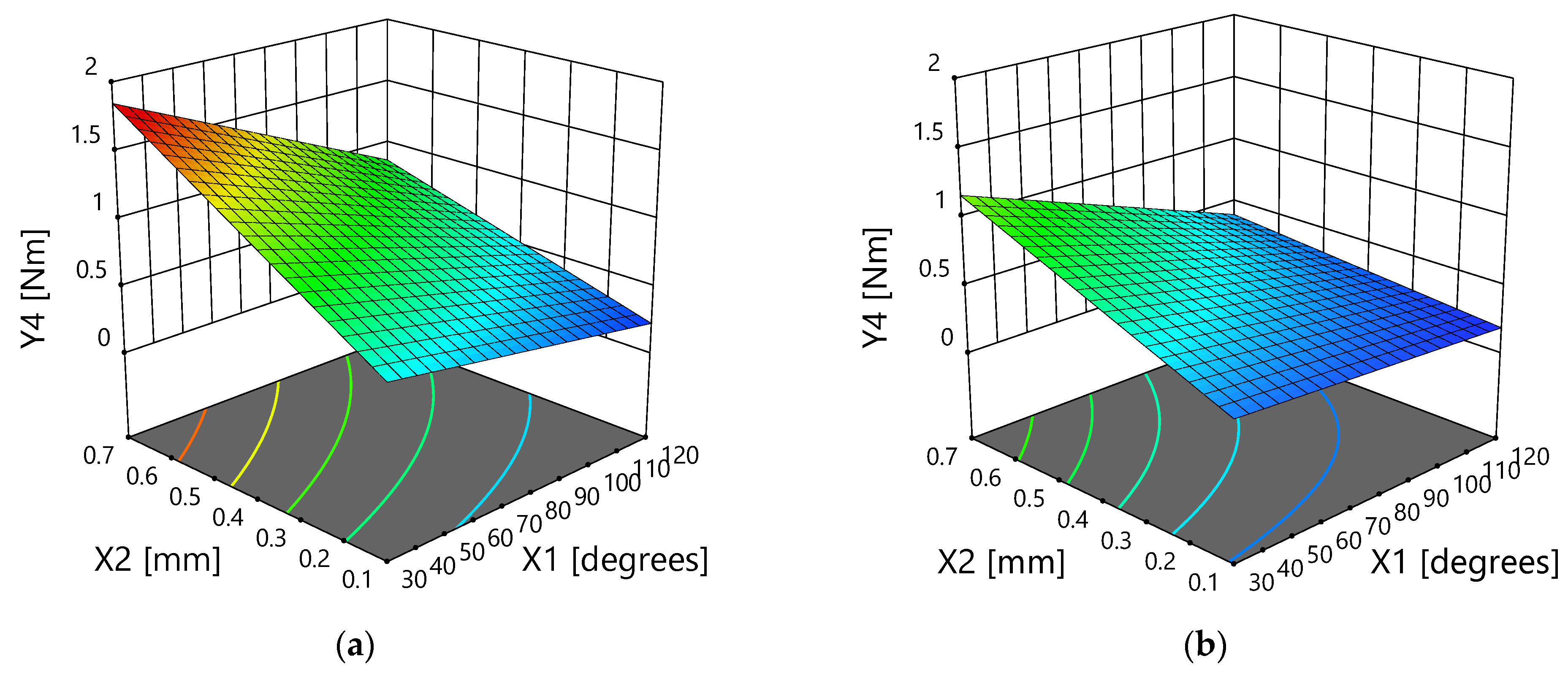
3.2.4. Drilling Torque
- The helical drill, together with a low tooth bite assure a high quality and low energy consumption both for MDF panels and prelaminated wood particleboards.
- Regarding the flat drill, the optimum value of drill tip angle (X1) is 30° or 60° for MDF boards, compared to prelaminated wood particleboards wherein the value was 30°, 60°, or 90°. Therefore, it could be concluded that for flat drills, a drill tip equal to 30° or 60° assures a high drilling quality and a lower energy consumption both in the case of MDF and prelaminated wood particleboards.
- The relative errors between predicted and experimental values are lower than those that were obtained in the case of our previous work regarding the drilling of prelaminated wood particleboards. In this study, the error was between 0.09 and 3.9% in the case of the delamination factor; 1.7 and 13.5% in the case of the thrust force; and 0.2 and 0.5% for the drilling torque. Therefore, it could be concluded that the developed regression equations for MDF boards performs better than those designed for prelaminated wood particleboards.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kamperidou, V. Drilling of Wood and Wood-Based Panels. In Proceedings of the Tenth Scientific and Technical Conference “Innovations in Forest Industry and Engineering Design” INNO 2020, Sofia, Bulgaria, 1–3 October 2020; Available online: https://www.researchgate.net/publication/344695192_DRILLING_OF_WOOD_AND_WOOD-BASED_PANELS (accessed on 11 November 2023).
- Szwajka, K.; Trzepiecinski, T. On the machinability of medium density fiberboard by drilling. Bioresources 2019, 13, 8263–8278. [Google Scholar] [CrossRef]
- Sydor, M.; Rogoziński, T.; Stuper-Szablewska, K.; Starczewski, K. The accuracy of holes drilled in the side surface of plywood. BioRes 2020, 15, 117–129. [Google Scholar] [CrossRef]
- Kurek, J.; Krupa, A.; Antoniuk, I.; Akhmet, A.; Abdiomar, U.; Bukowski, M.; Szymanowski, K. Improved Drill State Recognition during Milling Process Using Artificial Intelligence. Sensors 2023, 23, 448. [Google Scholar] [CrossRef] [PubMed]
- Ispas, M.; Răcășan, S. Study regarding the influence of the tool geometry and feed rate on the drilling quality of MDF panels. Pro Ligno 2017, 13, 174–180. [Google Scholar]
- Davim, P.J.; Clemente, V.C.; Silva, S. Drilling investigation of MDF (medium density fibreboard). J. Mater. Process. Technol. 2007, 203, 537–541. [Google Scholar] [CrossRef]
- Palanikumar, K.; Prakash, S.; Manoharan, N. Experimental Investigation and Analysis on Delamination in Drilling of Wood Composite Medium Density Fiber Boards. Mater. Manuf. Process. 2009, 24, 1341–1348. [Google Scholar] [CrossRef]
- Prakash, S.; Palanikumar, K.; Manoharan, N. Optimization of delamination factor in drilling medium-density fiberboards (MDF) using desirability-based approach. Int. J. Adv. Manuf. Technol. 2009, 45, 370–381. [Google Scholar] [CrossRef]
- Valarmathi, T.N.; Palanikumar, K.; Sekar, S. Parametric analysis on delamination in drilling of wood composite panels. Indian J. Sci. Technol. 2013, 6, 1–10. [Google Scholar] [CrossRef]
- Gaitonde, V.N.; Karnik, S.R.; Davim, J.P. Taguchi multiple-performance characteristics optimization in drilling of medium density fibreboard (MDF) to minimize delamination using utility concept. J. Mater. Process. Technol. 2008, 196, 73–78. [Google Scholar] [CrossRef]
- Ayyildiz, E.A.; Ayyildiz, M.; Kara, F. Optimization of Surface Roughness in Drilling Medium-Density Fiberboard with a Parallel Robot. Adv. Mater. Sci. Eng. 2021, 2021, 6658968. [Google Scholar] [CrossRef]
- Prakash, S.; LillyMercy, J.; Manoj, K.S.; Vineeth, K.S.M. Optimization of drilling characteristics using Grey Relational Analysis (GRA) in Medium Density Fiber Board (MDF). Mater. Today Proc. 2015, 2, 1541–1551. [Google Scholar]
- Prakash, S.; Palanikumar, K. Modeling for prediction of surface roughness in drilling MDF panels using response surface methodology. J. Compos. Mater. 2010, 45, 1639–1646. [Google Scholar] [CrossRef]
- Bedelean, B.; Ispas, M.; Răcășan, S.; Baba, M.N. Optimization of Wood Particleboard Drilling Operating Parameters by Means of the Artificial Neural Network Modeling Technique and Response Surface Methodology. Forests 2022, 13, 1045. [Google Scholar] [CrossRef]
- Szwajka, K.; Zielinska-Szwajka, J.; Gorski, J. Neural networks based in process tool wear prediction system in milling wood operations. In Proceedings of the Fifth International Symposium on Instrumentation Science and Technology, Shenyang, China, 12 January 2009. [Google Scholar] [CrossRef]
- Zbieć, M. Application of neural network in simple tool wear monitoring and identification system in MDF milling. Drv. Ind. 2011, 62, 43–54. [Google Scholar] [CrossRef]
- Tiryaki, S.; Özşahin, Ş.; Aydin, A. Employing artificial neural networks for minimizing surface roughness and power consumption in abrasive machining of wood. Eur. J. Wood Prod. 2017, 75, 347–358. [Google Scholar] [CrossRef]
- Tiryaki, S.; Malkoçoğlu, A.; Özşahin, Ş. Artificial neural network modeling to predict optimum power consumption in wood machining. Drewno 2016, 59, 109–125. [Google Scholar] [CrossRef]
- Özşahin, S.; Singer, H. Prediction of noise emission in the machining of wood materials by means of an artificial neural network. N. Z. J. For. Sci. 2022, 52, 1–10. [Google Scholar] [CrossRef]
- Nasir, V.; Cool, J. Characterization, optimization, and acoustic emission monitoring of airborne dust emission during wood sawing. Int. J. Adv. Manuf. Technol. 2020, 109, 2365–2375. [Google Scholar] [CrossRef]
- Rabiei, F.; Yaghoubi, S. A comprehensive investigation on the influences of optimal CNC wood machining variables on surface quality and process time using GMDH neural network and bees optimization algorithm. Mater. Today Commun. 2023, 36, 106482. [Google Scholar] [CrossRef]
- Demir, A.; Osman, E.C.; Aydin, I. Determination of CNC processing parameters for the best wood surface quality via artificial neural network. Wood Mater. Sci. Eng. 2022, 17, 685–692. [Google Scholar] [CrossRef]
- Cakmak, A.; Malkocoglu, A.; Ozsahin, S. Optimization of wood machining parameters using artificial neural network in CNC router. Mater. Sci. Technol. 2023, 39, 1728–1744. [Google Scholar] [CrossRef]
- Gürgen, A.; Çakmak, A.; Yildiz, S.; Malkoçoğlu, A. Optimization of CNC operating parameters to minimize surface roughness of Pinus sylvestris using integrated artificial neural network and genetic algorithm. Maderas. Cienc. Tecnol. 2022, 24, 1–12. [Google Scholar] [CrossRef]
- Sofuoglu, S.D. Using artificial neural networks to model the surface roughness of massive wooden edge-glued panels made of Scotch pine (Pinus sylvestris L.) in a machining process with computer numerical control. BioRes 2015, 10, 6797–6808. [Google Scholar] [CrossRef]
- Nasir, V.; Cool, J.; Sassani, F. Acoustic emission monitoring of sawing process: Artificial intelligence approach for optimal sensory feature selection. Int. J. Adv. Manuf. Technol. 2019, 102, 4179–4197. [Google Scholar] [CrossRef]
- Nasir, V.; Cool, J. Intelligent wood machining monitoring using vibration signals combined with self-organizing maps for automatic feature selection. Int. J. Adv. Manuf. Technol. 2020, 108, 1811–1825. [Google Scholar] [CrossRef]
- Nasir, V.; Dibaji, S.; Alaswad, K.; Cool, J. Tool wear monitoring by ensemble learning and sensor fusion using power, sound, vibration, and AE signals. Manuf. Lett. 2021, 30, 32–38. [Google Scholar] [CrossRef]
- Nasir, V.; Kooshkbaghi, M.; Cool, J.; Sassani, F. Cutting tool temperature monitoring in circular sawing: Measurement and multi-sensor feature fusion-based prediction. Int. J. Adv. Manuf. Technol. 2021, 112, 2413–2424. [Google Scholar] [CrossRef]
- Stanojevic, D.; Mandic, M.; Danon, G.; Svrzic, S. Prediction of the surface roughness of wood for machining. J. For. Res. 2017, 28, 1281–1283. [Google Scholar] [CrossRef]
- Ahmed, M.; Kamal, K.; Ratlamwala, T.A.H.; Hussain, G.; Alqahtani, M.; Alkahtani, M.; Alatefi, M.; Alzabidi, A. Tool Health Monitoring of a Milling Process Using Acoustic Emissions and a ResNet Deep Learning Model. Sensors 2023, 23, 3084. [Google Scholar] [CrossRef]
- Jegorowa, A.; Górski, J.; Kurek, J.; Kruk, M. Initial study on the use of support vector machine (SVM) in tool condition monitoring in chipboard drilling. Eur. J. Wood Prod. 2019, 77, 957–959. [Google Scholar] [CrossRef]
- Nasir, V.; Cool, J. A review on wood machining: Characterization, optimization, and monitoring of the sawing process. Wood Mater. Sci. Eng. 2020, 15, 1–16. [Google Scholar] [CrossRef]
- Nasir, V.; Sassani, F. A review on deep learning in machining and tool monitoring: Methods, opportunities, and challenges. Int. J. Adv. Manuf. Technol. 2021, 115, 2683–2709. [Google Scholar] [CrossRef]
- Budău, G.; Ispas, M. Woodworking Machine-Tools; Lux Libris Publishing House: Brasov, Romania, 2014. (In Romanian) [Google Scholar]
- Watanabe, K.; Korai, H.; Matsushita, Y.; Hayashi, T. Predicting internal bond strength of particleboard under outdoor exposure based on climate data: Comparison of multiple linear regression and artificial neural network. J. Wood Sci. 2015, 61, 151–158. [Google Scholar] [CrossRef]
- Fahlman, S.E.; Lebiere, C. The Cascade-Correlation Learning Architecture; Technical Report CMU-CS-90-100; School of Computer Science, Carnegie Mellon University: Pittsburgh, PA, USA, 1990. [Google Scholar]
- Avramidis, S.; Iliadis, L. Predicting wood thermal conductivity using artificial neural networks. Wood Fiber Sci. 2005, 37, 682–690. [Google Scholar]
- Monticeli, F.M.; Neves, R.M.; Ornaghi, H.L.; Almeida, J.H.S. Prediction of Bending Properties for 3D-Printed Carbon Fibre/Epoxy Composites with Several Processing Parameters Using ANN and Statistical Methods. Polymers 2022, 14, 3668. [Google Scholar] [CrossRef]
- Dubdub, I. Artificial Neural Network Study on the Pyrolysis of Polypropylene with a Sensitivity Analysis. Polymers 2023, 15, 494. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2016; pp. 6–262. [Google Scholar]
- NIST/SEMATECH. e-Handbook of Statistical Methods. Available online: http://www.itl.nist.gov/div898/handbook/ (accessed on 18 October 2023).
- Podziewski, P.; Szymanowski, K.; Górski, J.; Czarniak, P. Relative machinability of wood-based boards in the case of drilling Experimental study. BioResources 2018, 13, 1761–1772. [Google Scholar] [CrossRef]
- Valarmathi, T.N.; Palanikumar, K.; Sekar, S. Modeling of thrust force in drilling of plain medium density fiberboard (MDF) composite panels using RSM. Procedia Eng. 2012, 38, 1828–1835. [Google Scholar] [CrossRef]
- Kumar, K.; Davim, J.P. Biodegradable Composites: Materials, Manufacturing and Engineering; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; pp. 167–182. [Google Scholar] [CrossRef]




| Independent Variable | Analyzed Values | |||
|---|---|---|---|---|
| Drill point angle (X1), ° | 30 | 60 | 90 | 120 |
| Tooth bite (X2), mm | 0.1 | 0.3 | 0.5 | 0.7 |
| Drill type (X3) | Flat | Helical | ||
| Numeric Factor | Level | ||||
|---|---|---|---|---|---|
| −α * | −1 | 0 | +1 | +α * | |
| Drill tip angle (X1), ° | 30 | 30 | 75 | 120 | 120 |
| Tooth bite (X2), mm | 0.1 | 0.1 | 0.4 | 0.7 | 0.7 |
| Categoric Factor | Level 1 | Level 2 | |||
| Drill type (X3) | Flat (−1) | Helical (+1) | |||
| Combination # | Independent Variables (Factors) | Dependent Variables (Responses) | |||||
|---|---|---|---|---|---|---|---|
| Drill Tip Angle (X1), ° | Tooth Bite (X2), mm | Drill Type (X3) | Y1 | Y2 | Y3 | Y4 | |
| 1 | 30 (−1) | 0.1 (−1) | Flat (−1) | 1.07 | 1.13 | 115.34 | 0.55 |
| 2 | 75 (0) | 0.4 (0) | Flat (−1) | 1.10 | 1.25 | 252.07 | 0.89 |
| 3 | 120 (+α) | 0.4 (0) | Flat (−1) | 1.11 | 1.44 | 272.69 | 0.60 |
| 4 | 120 (+α) | 0.4 (0) | Helical (1) | 1.00 | 1.03 | 68.53 | 0.33 |
| 5 | 75 (0) | 0.4 (0) | Helical (1) | 1.00 | 1.00 | 76.85 | 0.53 |
| 6 | 120 (1) | 0.7 (1) | Helical (1) | 1.18 | 1.03 | 102.67 | 0.41 |
| 7 | 75 (0) | 0.4 (0) | Helical (1) | 1.00 | 1.00 | 76.85 | 0.53 |
| 8 | 120 (1) | 0.1 (−1) | Helical (1) | 1.00 | 1.03 | 64.23 | 0.16 |
| 9 | 75 (0) | 0.4 (0) | Helical (1) | 1.00 | 1.00 | 76.85 | 0.53 |
| 10 | 75 (0) | 0.7 (+α) | Flat (−1) | 1.12 | 1.25 | 366.90 | 1.52 |
| 11 | 75 (0) | 0.4 (0) | Flat (−1) | 1.10 | 1.25 | 252.07 | 0.89 |
| 12 | 75 (0) | 0.4 (0) | Helical (1) | 1.00 | 1.00 | 76.85 | 0.53 |
| 13 | 30 (−1) | 0.7 (1) | Helical (1) | 1.10 | 1.00 | 49.87 | 1.17 |
| 14 | 75 (0) | 0.1 (−α) | Helical (1) | 1.00 | 1.00 | 72.19 | 0.24 |
| 15 | 75 (0) | 0.4 (0) | Flat (−1) | 1.10 | 1.25 | 252.07 | 0.89 |
| 16 | 30 (−1) | 0.7 (1) | Flat (−1) | 1.06 | 1.13 | 372.29 | 1.74 |
| 17 | 75 (0) | 0.1 (−α) | Flat (−1) | 1.08 | 1.25 | 138.16 | 0.36 |
| 18 | 30 (−α) | 0.4 (0) | Flat (−1) | 1.09 | 1.13 | 305.67 | 1.28 |
| 19 | 75 (0) | 0.7 (+α) | Helical (1) | 1.00 | 1.00 | 75.38 | 0.73 |
| 20 | 75 (0) | 0.4 (0) | Flat (−1) | 1.10 | 1.25 | 252.07 | 0.89 |
| 21 | 75 (0) | 0.4 (0) | Flat (−1) | 1.10 | 1.25 | 252.07 | 0.89 |
| 22 | 30 (−α) | 0.4 (0) | Helical (1) | 1.00 | 1.00 | 33.46 | 0.77 |
| 23 | 120 (1) | 0.1 (−1) | Flat (−1) | 1.08 | 1.44 | 137.27 | 0.23 |
| 24 | 120 (1) | 0.7 (1) | Flat (−1) | 1.13 | 1.44 | 334.78 | 0.74 |
| 25 | 30 (−1) | 0.1 (−1) | Helical (1) | 1.00 | 1.00 | 28.89 | 0.35 |
| 26 | 75 (0) | 0.4 (0) | Helical (1) | 1.00 | 1.00 | 76.85 | 0.53 |
| Independent Variables | Goal Settings | Minimum Value | Maximum Value | Level of Factor Importance |
|---|---|---|---|---|
| Drill tip angle (X1) | In range | 30 | 120 | 3 |
| Tooth bite (X2) | 0.1 | 0.7 | 3 | |
| Drill type (X3) | Flat | Helical | 3 | |
| Dependent Variables | ||||
| Delamination factor at the inlet (Y1) | Minimize | 1 | 1.18 | 3 |
| Delamination factor at the outlet (Y2) | 1 | 1.43 | 3 | |
| Thrust force (Y3) | 28.88 | 372.28 | 3 | |
| Drilling torque (Y4) | 0.15 | 1.73 | 3 |
| Model Output | Number of Neurons in the Layers of ANN Models | Coefficient of Correlation (R) | Coefficient of Determination (R2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Input | Hidden | Outlet | Training | Testing | Validation | Training | Testing | Validation | |
| Delamination factor at the inlet | 3 | 6 | 1 | 0.86 | 0.89 | 0.92 | 0.73 | 0.79 | 0.85 |
| Delamination factor at the outlet | 3 | 9 | 1 | 0.85 | 0.88 | 0.88 | 0.72 | 0.77 | 0.78 |
| Thrust force | 3 | 10 | 1 | 0.99 | 0.98 | 0.99 | 0.98 | 0.96 | 0.98 |
| Drilling torque | 3 | 11 | 1 | 0.98 | 0.98 | 0.98 | 0.96 | 0.96 | 0.97 |
| Model Output | Number of Neurons in the Layers of ANN Models | Coefficient of Correlation (R) | Coefficient of Determination (R2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Input | Hidden | Outlet | Training | Testing | Validation | Training | Testing | Validation | |
| Delamination factor at the inlet | 3 | 13 | 1 | 0.76 | 0.72 | 0.67 | 0.57 | 0.51 | 0.44 |
| Delamination factor at the outlet | 3 | 6 | 1 | 0.88 | 0.88 | 0.90 | 0.77 | 0.77 | 0.82 |
| Thrust force | 3 | 4 | 1 | 0.94 | 0.95 | 0.96 | 0.88 | 0.90 | 0.92 |
| Drilling torque | 3 | 9 | 1 | 0.97 | 0.97 | 0.98 | 0.94 | 0.94 | 0.97 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Observation |
|---|---|---|---|---|---|---|
| Model | 0.067 | 11 | 0.006114 | 7.68 | 0.0003 | Significant |
| Drill tip angle (X1) | 0.0268 | 1 | 0.002683 | 3.37 | 0.087 | Not significant |
| Tooth bite (X2) | 0.011 | 1 | 0.011 | 13.68 | 0.0024 | Significant |
| Drill type (X3) | 0.038 | 1 | 0.038 | 47.87 | <0.0001 | Significant |
| X1X2 | 0.00259 | 1 | 0.00259 | 3.25 | 0.0928 | Not significant |
| X1X3 | 0.0000312 | 1 | 0.0000312 | 0.039 | 0.8457 | Not significant |
| X2X3 | 0.003789 | 1 | 0.003789 | 4.76 | 0.0467 | Significant |
| X12 | 0.0009446 | 1 | 0.0009446 | 1.19 | 0.2943 | Not significant |
| X22 | 0.00079 | 1 | 0.0007909 | 0.99 | 0.3357 | Not significant |
| X1X2X3 | 0.00002274 | 1 | 0.00002274 | 0.029 | 0.8682 | Not significant |
| X12X3 | 0.002513 | 1 | 0.002513 | 3.16 | 0.0973 | Not significant |
| X22 X3 | 0.002725 | 1 | 0.002725 | 3.42 | 0.0854 | Not significant |
| R2 | 0.85 | |||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Observation |
|---|---|---|---|---|---|---|
| Model | 0.59 | 8 | 0.073 | 2409.57 | <0.0001 | Significant |
| Drill tip angle (X1) | 0.084 | 1 | 0.084 | 2757.18 | <0.0001 | Significant |
| Tooth bite (X2) | 0 | 1 | 0 | 0 | 1 | Not significant |
| Drill type (X3) | 0.44 | 1 | 0.44 | 14587.86 | <0.0001 | Significant |
| X1X2 | 0 | 1 | 0 | 0 | 1 | Not significant |
| X1X3 | 0.055 | 1 | 0.055 | 1826.64 | <0.0001 | Significant |
| X2X3 | 0 | 1 | 0 | 0 | 1 | Not significant |
| X12 | 0.0027 | 1 | 0.0027 | 89.64 | <0.0001 | Significant |
| X22 | 0 | 1 | 0 | 0 | 1 | Not significant |
| R2 | 0.99 | |||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Observation |
|---|---|---|---|---|---|---|
| Model | 311,000 | 11 | 28271 | 171.78 | <0.0001 | Significant |
| Drill tip angle (X1) | 464.278 | 1 | 464.28 | 2.82 | 0.1152 | Not significant |
| Tooth bite (X2) | 46,351.60 | 1 | 46,351.61 | 281.66 | <0.0001 | Significant |
| Drill type (X3) | 98,114.63 | 1 | 98,114.63 | 596.19 | <0.0001 | Significant |
| X1X2 | 220.32 | 1 | 220.32 | 1.34 | 0.2666 | Not significant |
| X1X3 | 2458.85 | 1 | 2458.85 | 14.94 | 0.0017 | Significant |
| X2X3 | 32,092.03 | 1 | 32,092.03 | 195.007 | <0.0001 | Significant |
| X12 | 53.67 | 1 | 53.67 | 0.326 | 0.5777 | Not significant |
| X22 | 557.86 | 1 | 557.86 | 3.39 | 0.086 | Not significant |
| X1X2X3 | 739.12 | 1 | 739.12 | 4.49 | 0.0524 | Not significant |
| X12X3 | 1454.28 | 1 | 1454.28 | 8.84 | 0.0101 | Significant |
| X22X3 | 1005.80 | 1 | 1005.80 | 6.11 | 0.0269 | Significant |
| R2 | 0.99 | |||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Observation |
|---|---|---|---|---|---|---|
| Model | 3.786 | 6 | 0.63 | 166.44 | <0.0001 | Significant |
| Drill tip angle (X1) | 0.957 | 1 | 0.957 | 252.48 | <0.0001 | Significant |
| Tooth bite (X2) | 1.625 | 1 | 1.625 | 428.79 | <0.0001 | Significant |
| Drill type (X3) | 0.835 | 1 | 0.835 | 220.36 | <0.0001 | Significant |
| X1X2 | 0.19 | 1 | 0.19 | 51.35 | <0.0001 | Significant |
| X1X3 | 0.032 | 1 | 0.032 | 8.46 | 0.0090 | Significant |
| X2X3 | 0.14 | 1 | 0.14 | 37.24 | <0.0001 | Significant |
| R2 | 0.98 | |||||
| Solution No. | X1 | X2 | X3 | Delamination Factor at the Inlet | Delamination Factor at the Outlet | Trust Force (N) | Drilling Torque (Nm) | D | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y1 | ER1 | Y2 | ER2 | Y3 | ER3 | Y4 | ER4 | |||||||||
| 1 | 64 | 0.1 | Helical | 0.980 | 1 a | 2.00 | 0.995 | 1 a | 0.50 | 63.14 | 62.09 a | −1.7 | 0.281 | 0.33 a | 0.33 | 0.95 |
| 2 | 89 | 0.1 | Helical | 0.979 | 1 b | 2.10 | 1.004 | 1 b | −0.40 | 71.14 | 62.7 b | −13.5 | 0.240 | 0.21 b | 0.21 | 0.95 |
| 3 | 30 | 0.1 | Flat | 1.07 | 1.03 | −3.88 | 1.129 | 1.13 | 0.09 | 127.86 | 121.23 | −5.5 | 0.583 | 0.51 | 0.51 | 0.680 |
| 4 | 58 | 0.1 | Flat | 1.08 | 1.06 a | −1.89 | 1.20 | 1.16 a | −3.45 | 120.80 | 127.62 a | 5.4 | 0.470 | 0.44 a | 0.44 | 0.643 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedelean, B.; Ispas, M.; Răcășan, S. Combining Artificial Neural Network and Response Surface Methodology to Optimize the Drilling Operating Parameters of MDF Panels. Forests 2023, 14, 2254. https://doi.org/10.3390/f14112254
Bedelean B, Ispas M, Răcășan S. Combining Artificial Neural Network and Response Surface Methodology to Optimize the Drilling Operating Parameters of MDF Panels. Forests. 2023; 14(11):2254. https://doi.org/10.3390/f14112254
Chicago/Turabian StyleBedelean, Bogdan, Mihai Ispas, and Sergiu Răcășan. 2023. "Combining Artificial Neural Network and Response Surface Methodology to Optimize the Drilling Operating Parameters of MDF Panels" Forests 14, no. 11: 2254. https://doi.org/10.3390/f14112254
APA StyleBedelean, B., Ispas, M., & Răcășan, S. (2023). Combining Artificial Neural Network and Response Surface Methodology to Optimize the Drilling Operating Parameters of MDF Panels. Forests, 14(11), 2254. https://doi.org/10.3390/f14112254







