An Updated Cyclic CBR Test with Realistic Stress Values under the Plunger for Resilient Modulus Calculation
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Standard Cyclic CBR Test
2.2. The Updated Cyclic CBR Test Proposed
2.3. Study Area, Soil Sampling, and Specimen Preparation
2.4. Geotechnical Analysis
2.5. Statistical Analysis
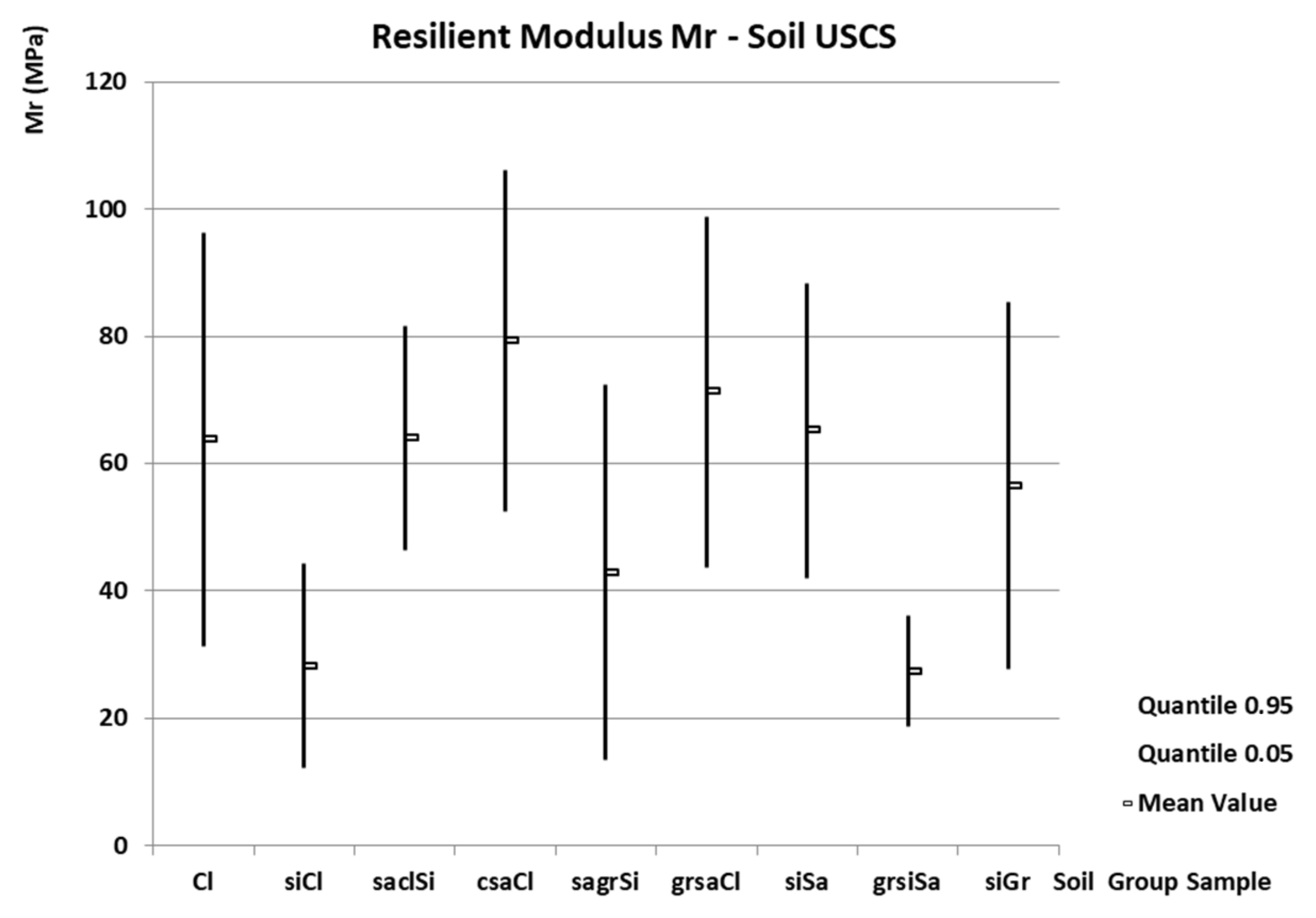
3. Results
The Updated Cyclic CBR Test Results
- -
- Soil type Cl
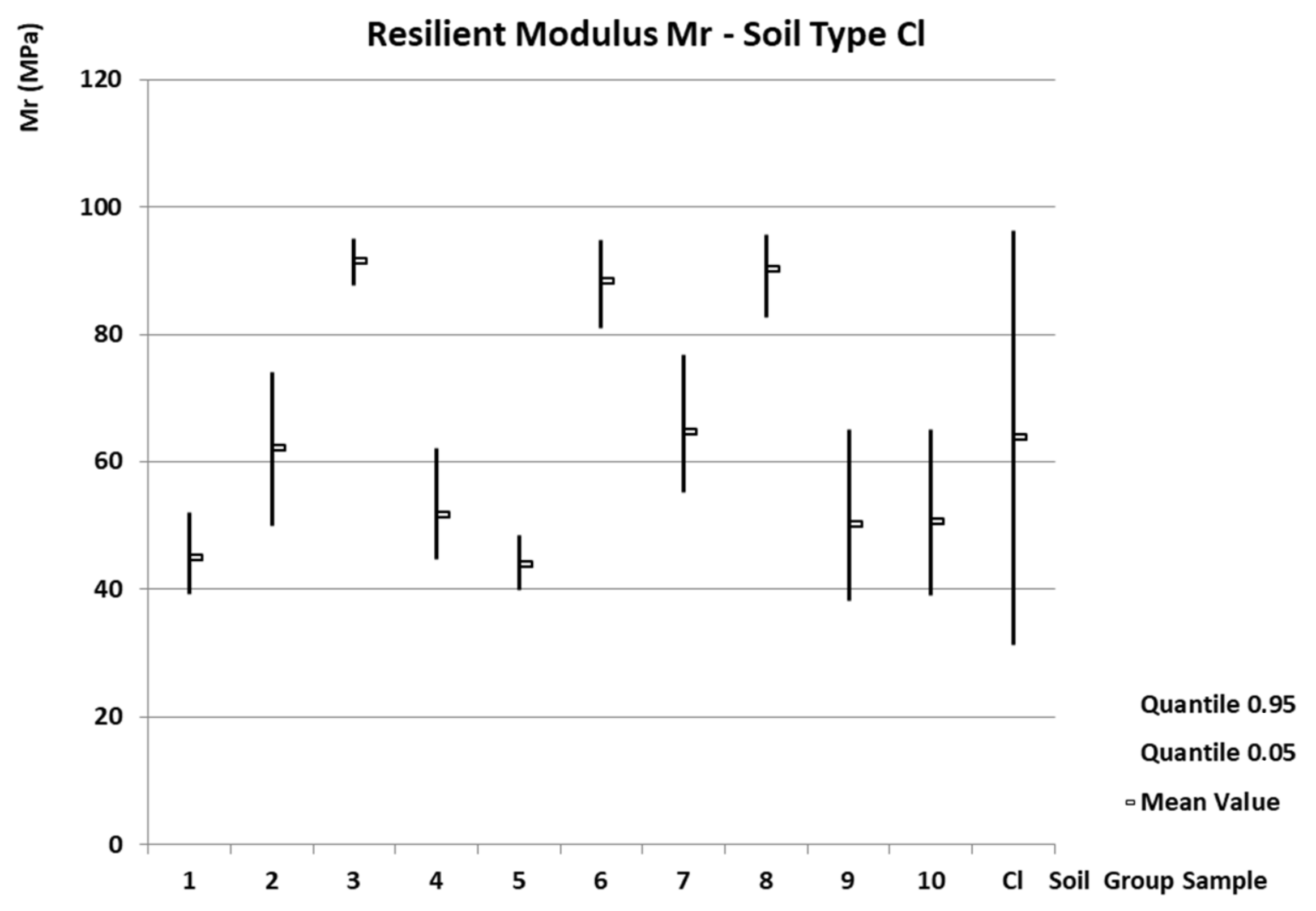
- -
- Soil type siCl
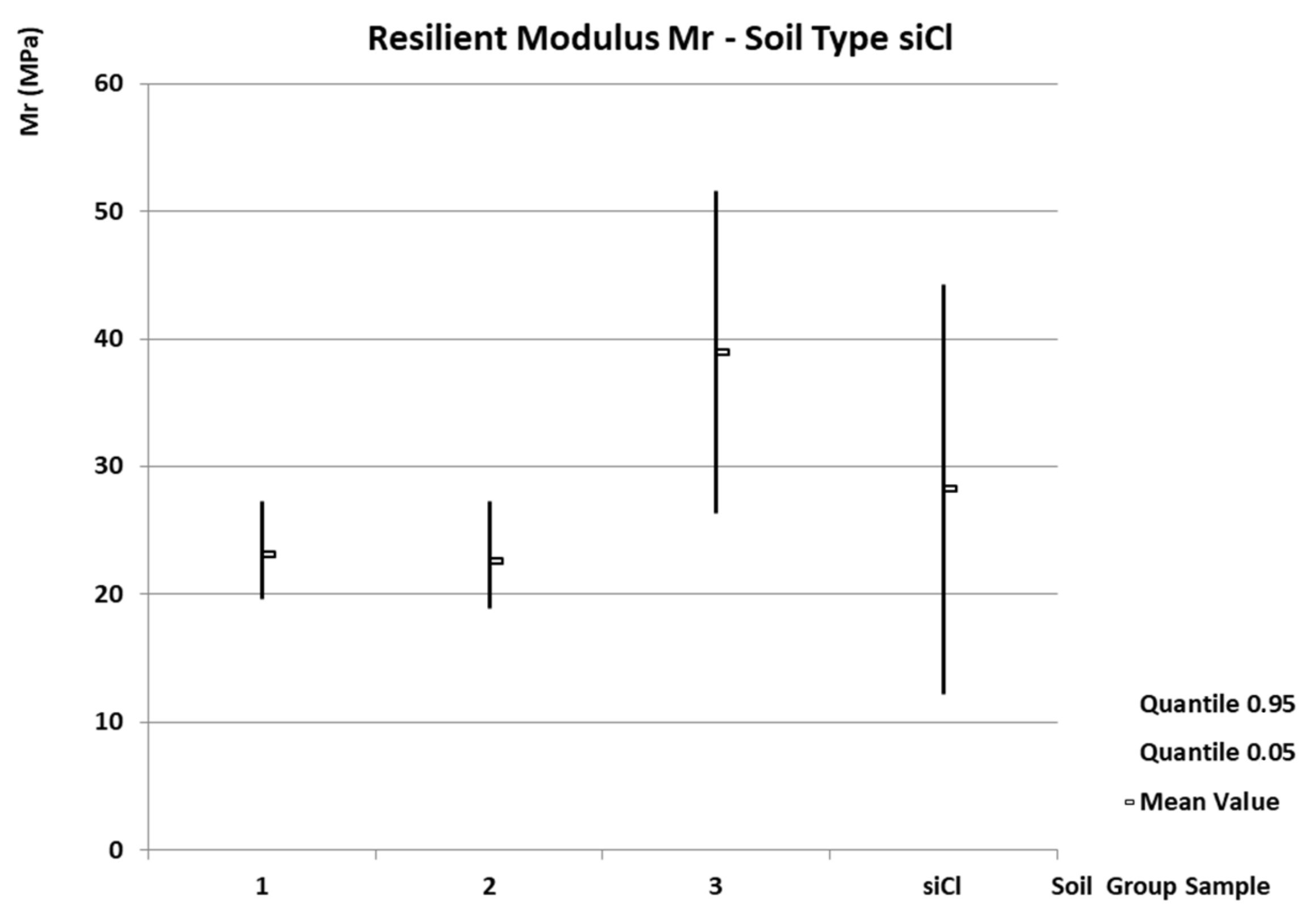
- -
- Soil type saclSi
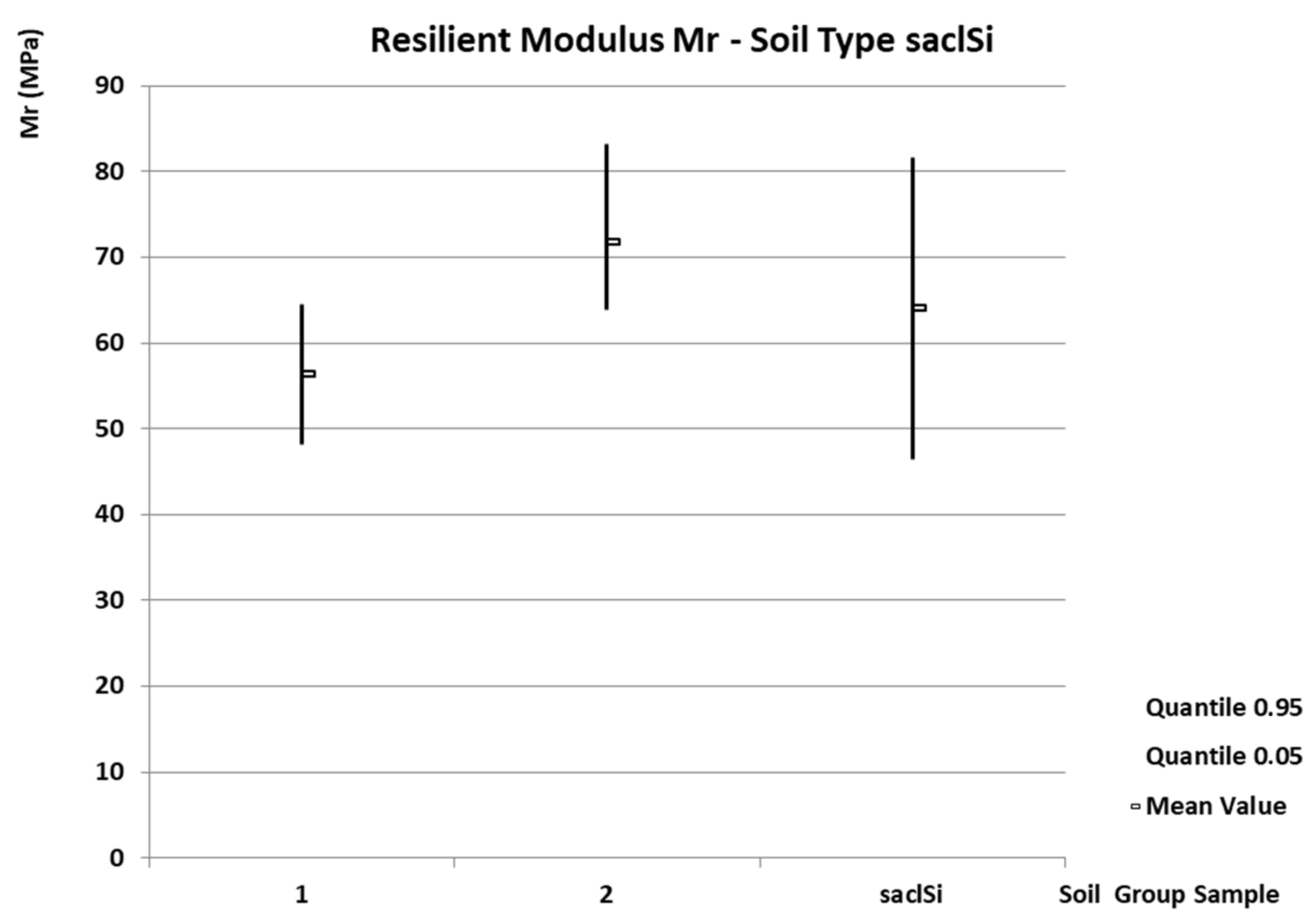
- -
- Soil type csaCl
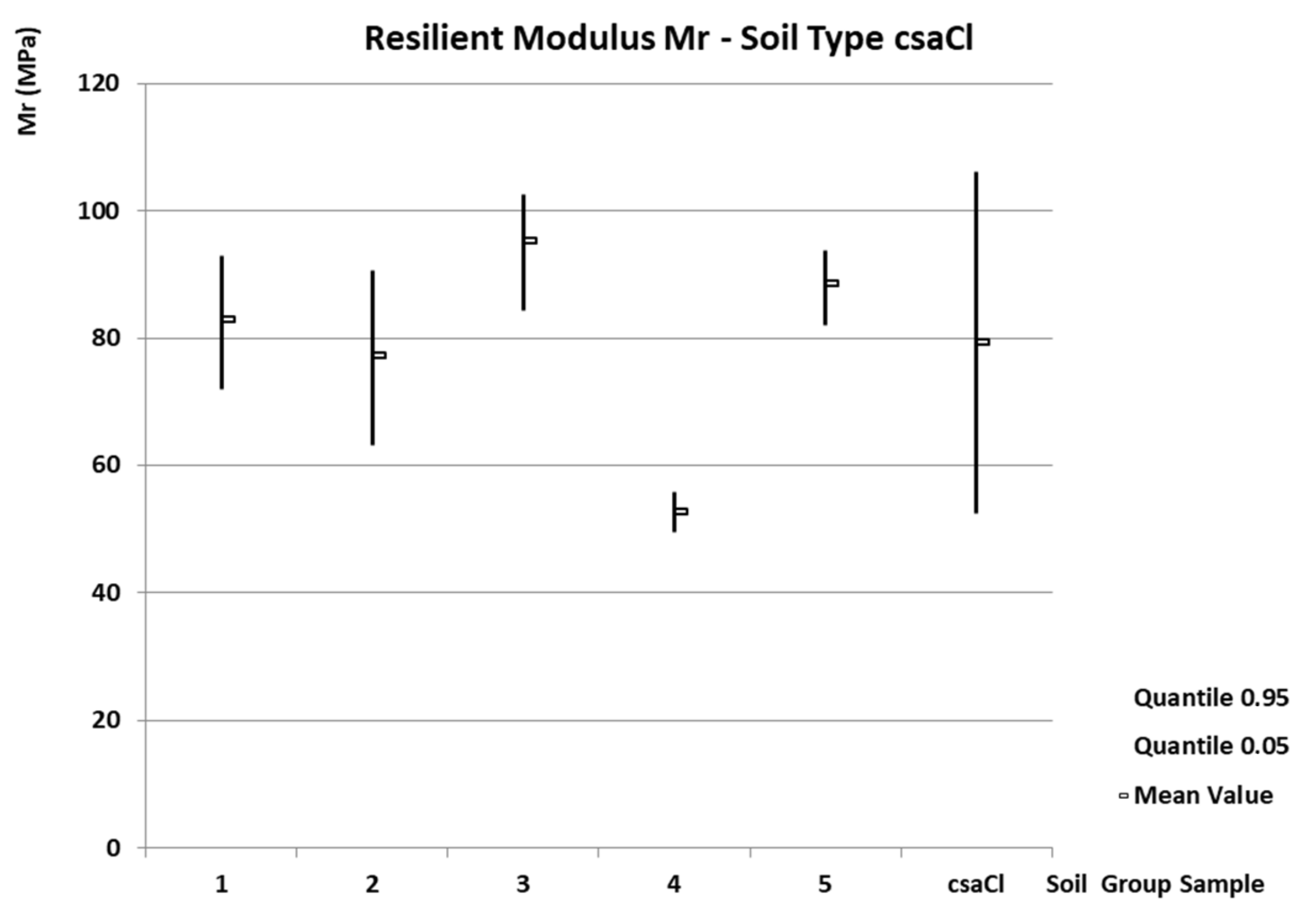
- -
- Soil type sagrSi
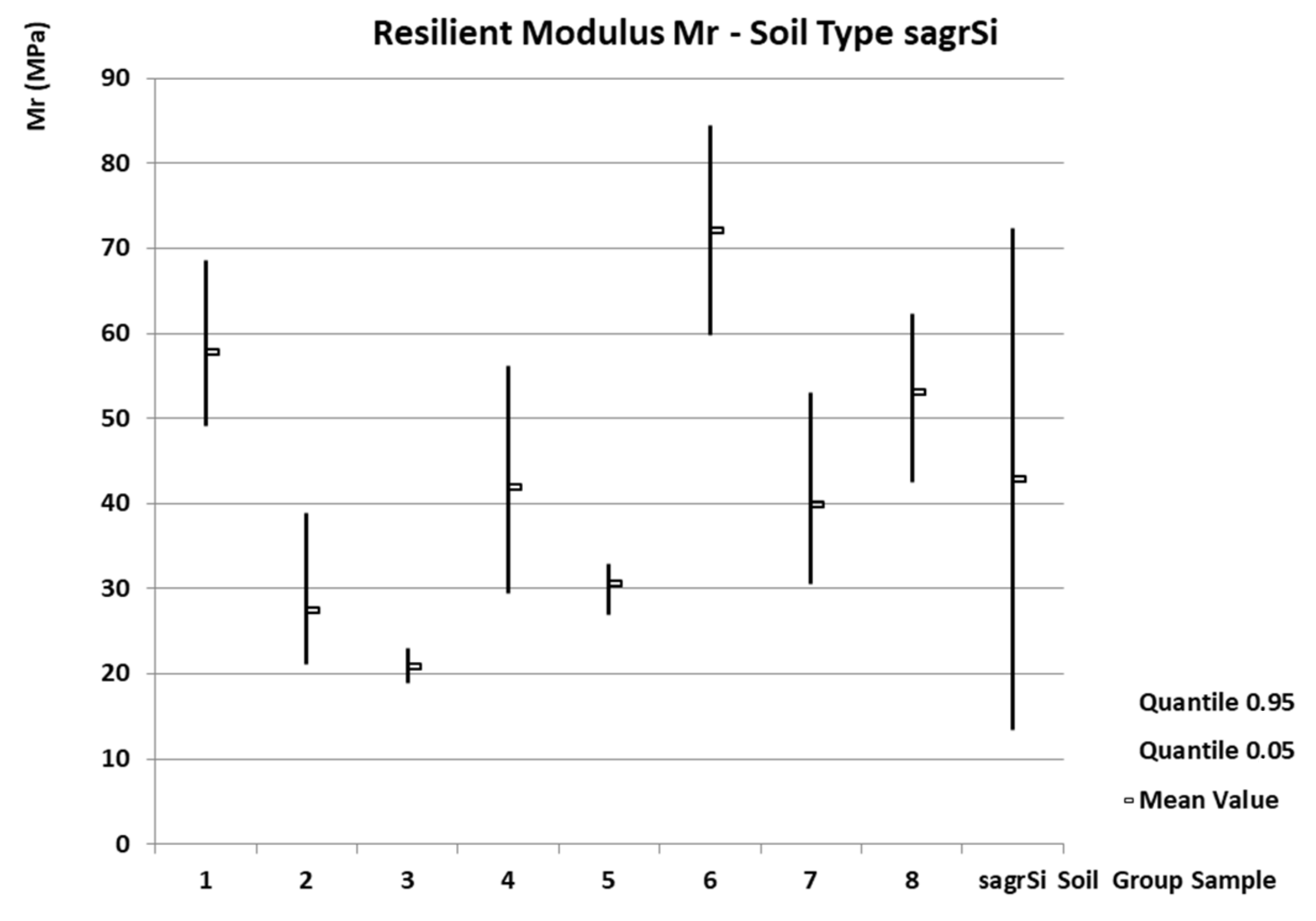
- -
- Soil type grsaCl
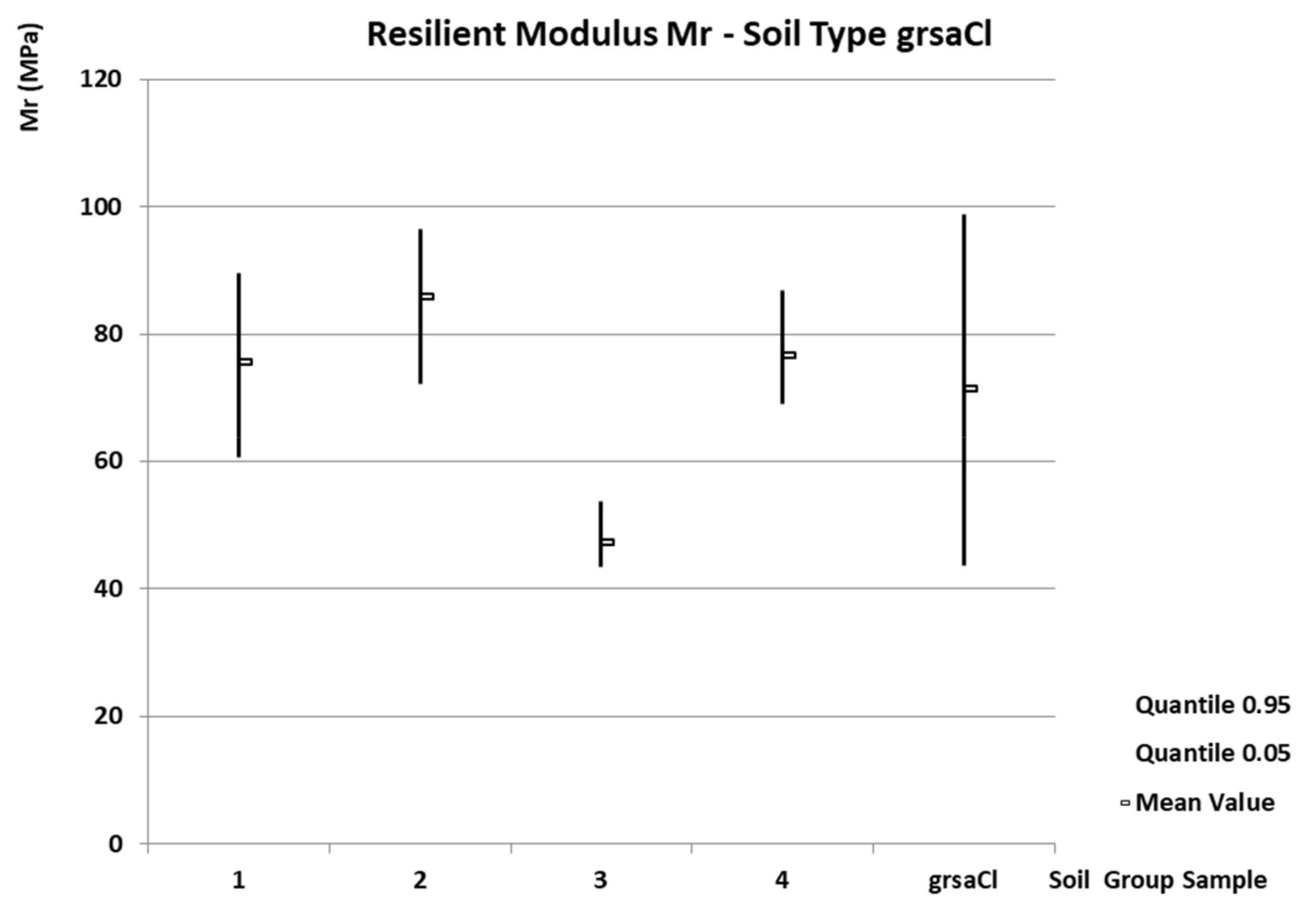
- -
- Soil type siSa
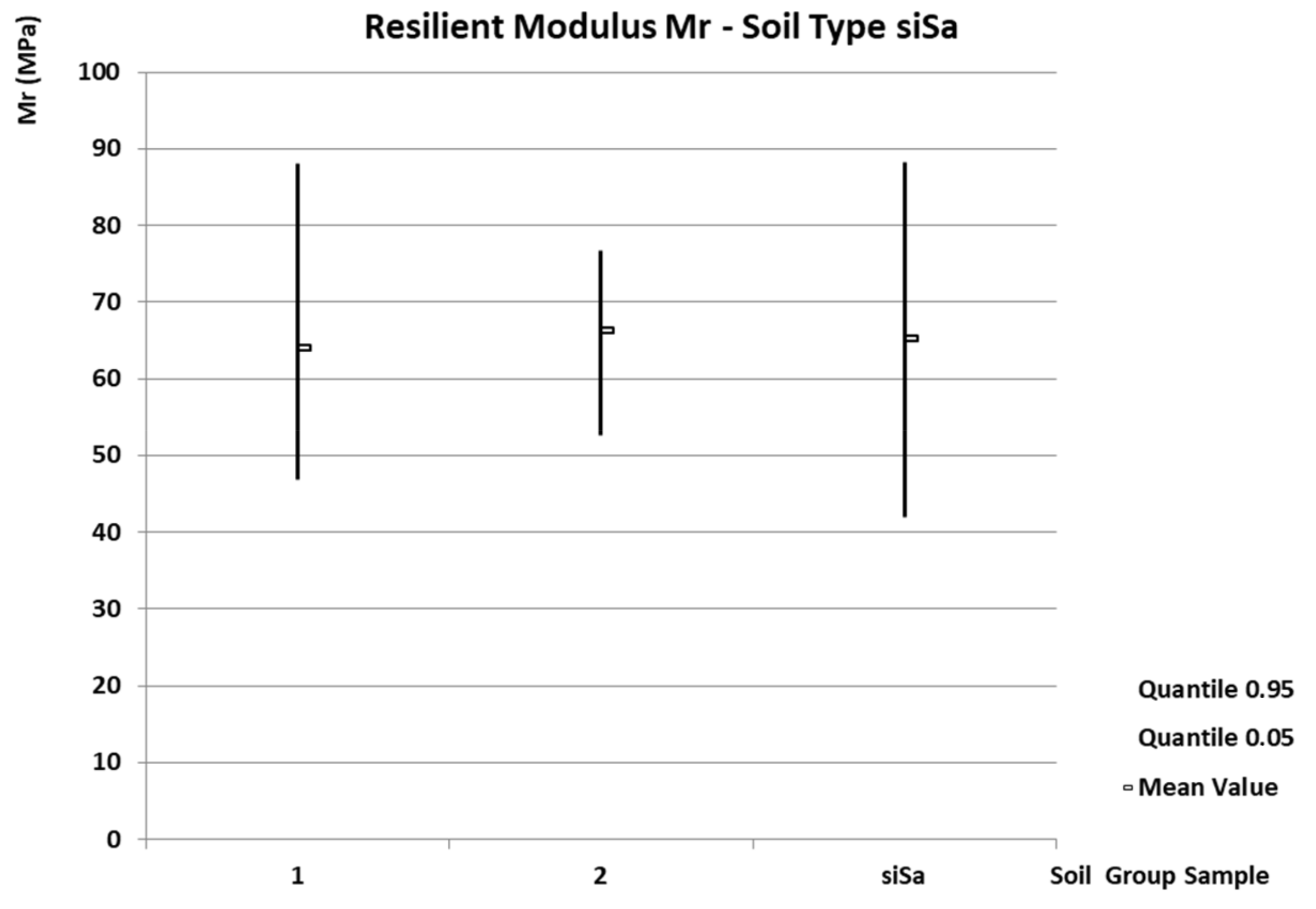
- -
- Soil type grsiSa
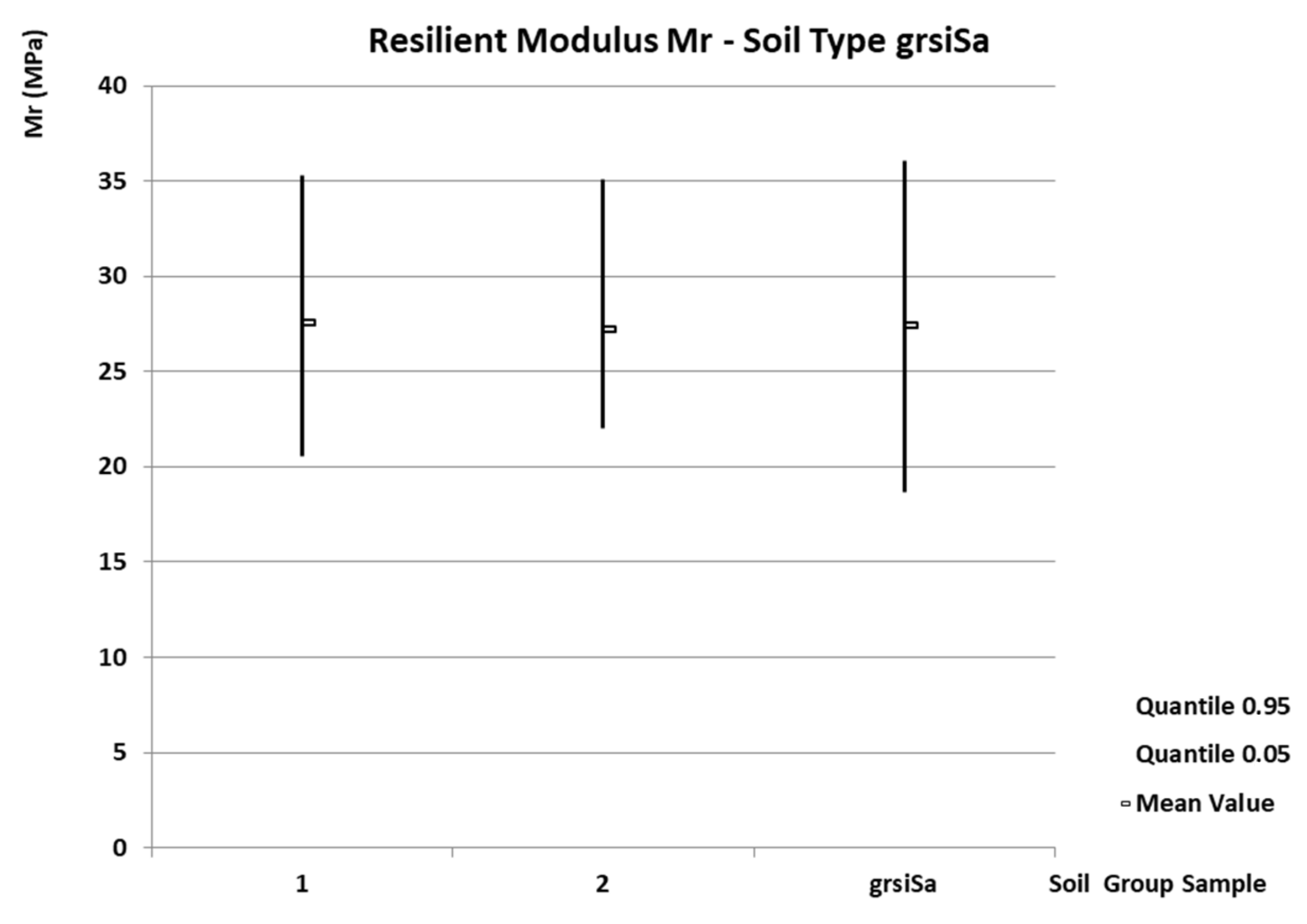
- -
- Soil type siGr
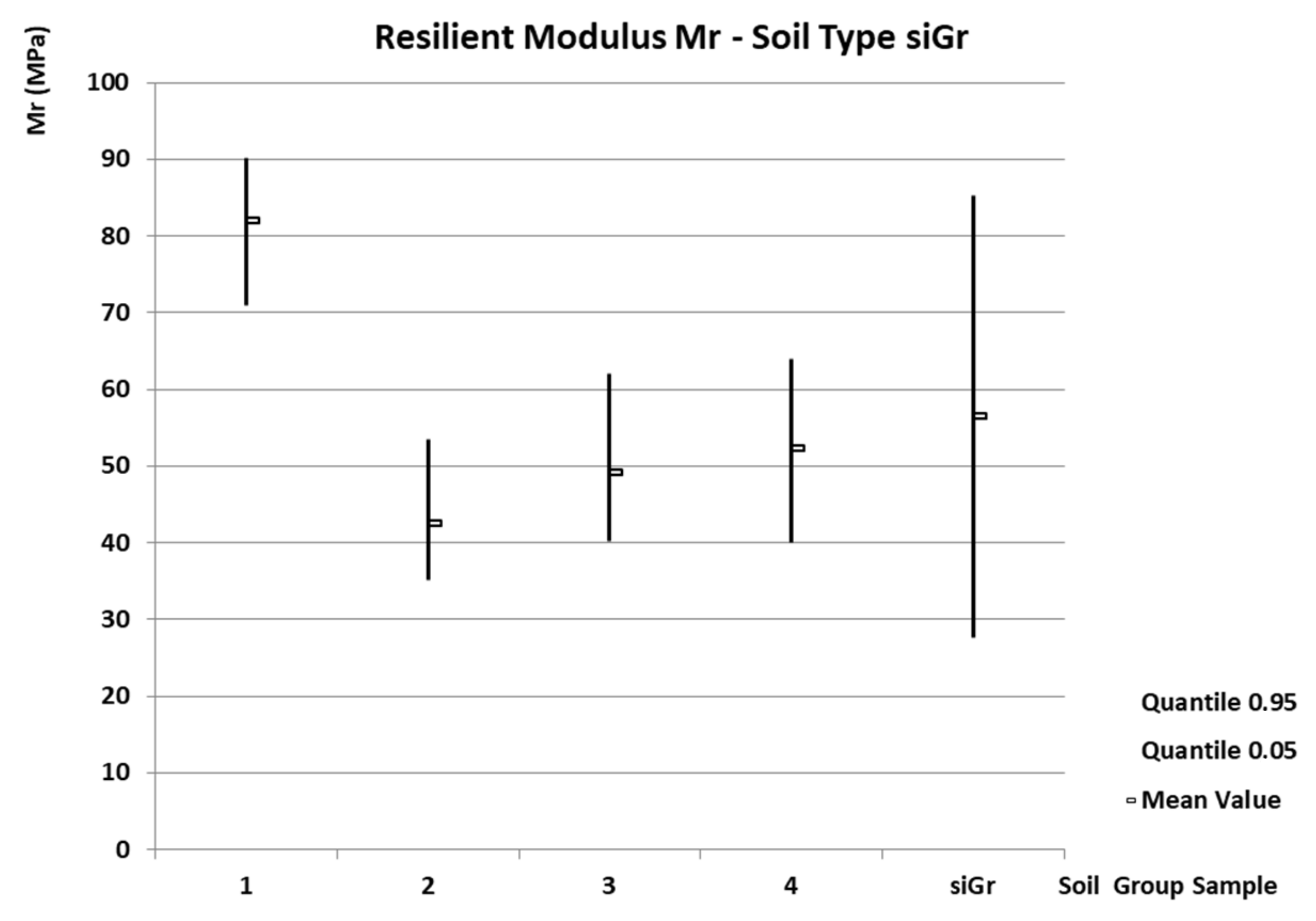
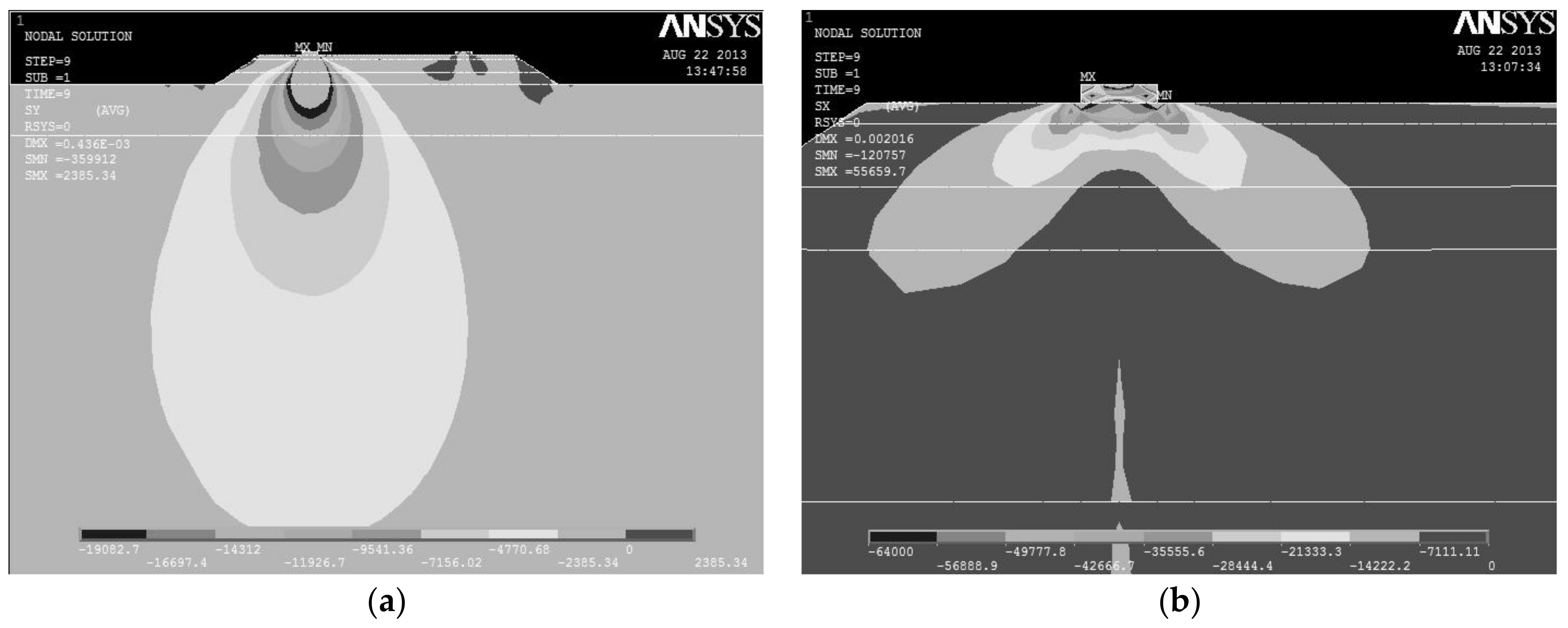
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Heinimann, H.R. Pavement Engineering for Forest Roads: Development and Opportunities. Croat. J. For. Eng. 2020, 42, 91–106. [Google Scholar] [CrossRef]
- AASHTO. Guidelines for Geometric Design of Very Low-Volume Local Roads; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2001. [Google Scholar]
- Anguas, P.G.; López, J.A.G.; Martínez, J.A.S. Mecánica de Materiales para Pavimentos; Publicación Técnica No. 197; Instituto Mexicano del Transporte: Sanfandila, Mexico, 2002. [Google Scholar]
- Florian, A.; Ševelová, L.; Žák, J. Influence of environmental humidity on mechanical properties of natural and recycled unbound materials. Acta Univ. Agric. Silvic. Mendel. Brun. 2015, 63, 405–409. [Google Scholar] [CrossRef]
- AASHTO. Mechanistic-Empirical Pavement Design Guide (MEPDG); American Association of State Highway and Transportation Officials: Washington, DC, USA, 2008. [Google Scholar]
- Díaz, M.M.; Peréz, I. Mechanistic-empirical pavement design guide: Features and distinctive elements. Rev. Construcción 2015, 14, 32–40. [Google Scholar] [CrossRef]
- Hauser, J.; Ševelová, L.; Matula, R.; Zedník, P. Optimization of low volume road pavement design and construction. J. For. Sci. 2018, 64, 74–85. [Google Scholar] [CrossRef]
- Nguyen, B.T.; Mohajerani, A. Resilient modulus of fine-grained soil and a simple testing and calculation method for determining an average resilient modulus value for pavement design. J. Transp. Geotech. 2016, 7, 59–70. [Google Scholar] [CrossRef]
- Yang, S.H.; Lin, H.D.; Kung, J.H.S.; Huang, W.H. Suction-Controlled Laboratory Test on Resilient Modulus of Unsaturated Compacted Subgrade Soils. J. Geotech. Geoenviron. Eng. 2008, 134, 1375–1384. [Google Scholar] [CrossRef]
- Brinch Hansen, J. A General Formula for Bearing Capacity; Bulletin No. 11; Geoteknisk Institut, Institute Akademict for de Tekniske Videuskaber: Copenhagen, Denmark, 1961. [Google Scholar]
- Hauser, J.; Kozumplíková, A.; Ševelová, L. CBR and IBI tests for practices the design of the earth body and based layers of the road construction. In Geotechnical Problems of Line Structures; Slovak University of Technology in Bratislava: Bratislava, Slovakia, 2011; pp. 101–108. [Google Scholar]
- CSN EN 13286-7; Unbound and Hydraulically Bound Mixtures—Part 7: Cyclic Load Triaxial Test for Unbound Mixtures. Institute for Technology Standardization. Metrology and State Testing: Prague, Czech Republic, 2004.
- CSN EN ISO 14688-2; Geotechnical Investigation and Testing-Identification and Classification of Soil—Part 2: Principles for a Classification. Institute for Technology Standardization. Metrology and State Testing: Prague, Czech Republic, 2005.
- CSN EN ISO 14689-1; Geotechnical Investigation and Testing-Identification and Classification of Rock—Part 1: Identification and Description. Institute for Technology Standardization. Metrology and State Testing: Prague, Czech Republic, 2004.
- Ševelová, L.; Florian, A.; Hrůza, P. Using Resilient Modulus to Determine the Subgrade Suitability for Forest Road Construction. Forests 2020, 11, 1208. [Google Scholar] [CrossRef]
- Molenaar, A.A.A. Repeated Load CBR Testing, a Simple but Effective Tool for the Characterization of Fine Soils and Unbound Materials; Delft University of Technology: Delft, The Netherlands, 2008. [Google Scholar]
- CSN EN ISO 13286-2; Unbound and Hydraulically Bound Mixtures—Part 2: Test Methods for the Determination of the Laboratory Reference Density and Water Content-Proctor Compaction. Institute for Technology Standardization. Metrology and State Testing: Prague, Czech Republic, 2015.
- CSN EN ISO 13286-47; Unbound and Hydraulically Bound Mixtures—Part 47: Test Method for the Determination of California Bearing Ratio, Immediate Bearing Index and Linear Swelling. Institute for Technology Standardization. Metrology and State Testing: Prague, Czech Republic, 2015.
- Sas, W.; Głuchowski, A.; Miturski, M. Studies on resilient modulus value from cyclic loading tests for cohesive soil. J. Ann. Wars. Univ. Life Sci.-SGGW Land Reclam. 2017, 49, 117–127. [Google Scholar] [CrossRef]
- Araya, A.A. Characterization of Unbound Granularmaterials for Pavements. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2011. [Google Scholar]
- Leunga, G.L.M.; Wong, A.W.G.; Wanga, Y.H. Prediction of resilient modulus of compacted saprolitic soils by CBR approach for road pavement subgrade: A re-examination. Int. J. Pavement Eng. 2013, 14, 403–417. [Google Scholar] [CrossRef]
- Sas, W.; Głuchowski, A.; Gabryś, K.; Soból, E.; Szymański, A. Resilient modulus testing with application of cyclic CBR test for road subgrade materials. In Proceedings of the XVI Danube—European Conference on Geotechnical Engineering, Skopje, North Macedonia, 7–9 June 2018. [Google Scholar]
- Bojacá Torres, D.C.; Campagnoli Martínez, S.X. CBR cíclico como método alternativo para la determinación del módulo resiliente en suelos blandos de subrasante. Cienc. E Ing. Neogranadina 2022, 2, 85–98. [Google Scholar] [CrossRef]
- Hao, S.; Pabst, T. Estimation of resilient behavior of crushed waste rocks using repeated load CBR tests. Transp. Geotech. 2021, 28, 100525. [Google Scholar] [CrossRef]
- Rincón-Morantes, J.; Alvarez, A.; Reyes-Ortiz, O. Estimación de la rigidez de materiales granulares marginales no ligados mediante ensayo CBR dinámico. Ing. Desarro. 2022, 40, 92–113. [Google Scholar] [CrossRef]
- Primusz, P.; Kisfaludi, B.; Péterfalvi, J. Evaluating the bearing capacity of hydraulic road binder treated soils by the cyclic CBR method. Eng. Sci. J. Field Transp. Eng. 2019, 71, 14–23. [Google Scholar] [CrossRef]
- Salmi, A.; Bousshinea, L.; Lahlou, K. A New Model of Equivalent Modulus Derived from Repeated Load CBR Test. Int. J. Eng. 2020, 7, 1321–1330. [Google Scholar] [CrossRef]
- Haghighia, H.; Arulrajaha, A.; Mohammadiniab, A.; Horpibulsuka, S. A new approach for determining resilient moduli of marginal pavement base materials using the staged repeated load CBR test method. Road Mater. Pavement Des. 2018, 8, 1848–1867. [Google Scholar] [CrossRef]
- Mehrpazhouh, A.; Tafreshi, S.N.M.; Mirzababaei, M. Impact of repeated loading on mechanical response of a reinforced sand. J. Rock Mech. Geotech. Eng. 2019, 11, 804–814. [Google Scholar] [CrossRef]
- Abid, A.N.; Salih, A.O.; Nawaf, E.A. The Influence of Fines Content on the Mechanical Properties of Aggregate Subbase Course Material for Highway Construction using Repeated Load CBR Test. Al-Nahrain J. Eng. Sci. 2017, 3, 615–624. [Google Scholar]
- Ševelová, L.; Florian, A.; Žák, J. Influence of Plunger Stress on Resilient Modulus of Forest Subgrade Soils Obtained from Cyclic CBR Test. Forests 2021, 12, 1456. [Google Scholar] [CrossRef]
- Robinson, R.G.; Krishnan, J.M. Use of repeated load CBR test to characterize pavement granular materials. In Functional Pavement Design, Proceedings of the 4th Chinese-European Workshop on Functional Pavement Design, CEW 2016, Delft, The Netherlands, 29 June–1 July 2016; CRC Press: Boca Raton, FL, USA, 2016; pp. 965–976. [Google Scholar]
- Rahman, M.M.; Gassman, S.L.; Islam, K.M. Effect of Moisture Content on Subgrade Soils Resilient Modulus for Predicting Pavement Rutting. Geosciences 2023, 13, 103. [Google Scholar] [CrossRef]
- Hauser, J.; Kozumplíková, A.; Ševelová, L. The Influence of the Soil Treatment on the CBR Test Values. In Proceedings of the International Conference on Ground Improvement and Ground Control: Transport Infrastructure Development and Natural Hazards Mitigation-ICGI 2012, Singapore, 30 October–2 November 2012; pp. 1623–1628. [Google Scholar]
- De Zarate, G.O.; Ševelová, L. The statistical analysis of the resilient modulus. In Public Recreation and Landscape Protection—With Man Hand in Hand; Mendel University in Brno: Prague, Czech Republic, 2015; pp. 258–264. [Google Scholar]
- TP 170; Design of Pavement Structures. Ministry of Transportation: Prague, Czech Republic, 2023.
- Kärhä, K.; Seuri, M.; Mac Donagh, P.M. Overview of Global Long-Distance Road Transportation of Industrial Roundwood. Croat. J. For. Eng. 2023, 45, 25. [Google Scholar] [CrossRef]
- Florian, A.; Ševelová, L.; Žák, J. Reliability analysis of temperature influence on stresses in rigid pavement made from recycled materials. Acta Univ. Agric. Silvic. Mendel. Brun. 2016, 64, 423–432. [Google Scholar] [CrossRef]
- Ševelová, L.; Florian, A. Comparison of Material Constitutive Models Used in FEA of Low Volume Roads. Int. J. Civ. Environ. Eng. 2013, 10, 421–425. [Google Scholar]
- Florian, A.; Ševelová, L. Computer Simulation of Low Volume Roads Made from Recycled Materials. Int. J. Civ. Environ. Eng. 2013, 10, 744–748. [Google Scholar]
- CSN EN ISO 17892-1; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 1: Determination of Water Content. Institute for Technology Standardization, Metrology and State Testing: Prague, Czech Republic, 2015.
- CSN EN ISO 17892-4; Geotechnical Investigation and Testing-Laboratory Testing of Soil—Part 4: Determination of Particle Size Distribution. Institute for Technology Standardization, Metrology and State Testing: Prague, Czech Republic, 2017.
- CSN EN ISO 17892-12; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 12: Determination of the Liquid and Plastic Limits. Institute for Technology Standardization, Metrology and State Testing: Prague, Czech Republic, 2018.
| Number N° | Soil Type USCS | Amount of Samples | Amount of Specimens | Mean Density kg·m−3 | Mean Humidity % |
|---|---|---|---|---|---|
| 1 | Cl | 10 | 60 | 1598.8 | 23.8 |
| 2 | siCl | 3 | 18 | 1655.9 | 20.7 |
| 3 | saclSi | 2 | 12 | 1748.3 | 18.6 |
| 4 | csaCl | 5 | 30 | 1813.7 | 15.7 |
| 5 | sagrSi | 8 | 48 | 1858.5 | 13.4 |
| 6 | grsaCl | 4 | 24 | 1635.5 | 21.5 |
| 7 | siSa | 2 | 12 | 1796.0 | 14.7 |
| 8 | grsiSa | 2 | 12 | 1827.3 | 13.6 |
| 9 | siGr | 4 | 24 | 1929.6 | 12.7 |
| Soil | Mean Value [MPa] | COV | Quantile 0.05 [MPa] | Quantile 0.95 [MPa] | Triaxial [MPa] | ||||
|---|---|---|---|---|---|---|---|---|---|
| CBR Test | Updated | Standard | Updated | Standard | Updated | Standard | Updated | Standard | Indicative |
| Cl | 63.8 | 123.4 | 0.31 | 0.83 | 31.3 | 39.0 | 96.2 | 371.7 | 20–134 |
| siCl | 28.2 | 140.8 | 0.34 | 1.08 | 12.2 | 18.7 | 44.2 | 299.4 | - |
| saclSi | 64.0 | 122.7 | 0.17 | 0.59 | 46.4 | 48.8 | 81.6 | 235.3 | 58–102 |
| csaCl | 79.3 | 106.9 | 0.21 | 0.46 | 52.4 | 51.8 | 106.2 | 205.7 | 11–84 |
| sagrSi | 42.9 | 101.8 | 0.42 | 0.78 | 13.4 | 24.1 | 72.4 | 271.3 | - |
| grsaCl | 71.2 | 107.9 | 0.24 | 0.82 | 43.7 | 44.0 | 98.8 | 310.7 | - |
| siSa | 65.2 | 153.4 | 0.22 | 0.67 | 42.0 | 29.9 | 88.3 | 357.6 | 32–111 |
| grsiSa | 27.4 | 116.9 | 0.19 | 0.24 | 18.7 | 67.4 | 36.1 | 159.3 | 57–148 |
| siGr | 56.5 | 32.2 | 0.31 | 0.60 | 27.6 | 10.7 | 85.3 | 64.0 | 88–141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Florian, A.; Ševelová, L.; Žáková, K.; Žák, J. An Updated Cyclic CBR Test with Realistic Stress Values under the Plunger for Resilient Modulus Calculation. Forests 2023, 14, 2425. https://doi.org/10.3390/f14122425
Florian A, Ševelová L, Žáková K, Žák J. An Updated Cyclic CBR Test with Realistic Stress Values under the Plunger for Resilient Modulus Calculation. Forests. 2023; 14(12):2425. https://doi.org/10.3390/f14122425
Chicago/Turabian StyleFlorian, Aleš, Lenka Ševelová, Kateřina Žáková, and Jaroslav Žák. 2023. "An Updated Cyclic CBR Test with Realistic Stress Values under the Plunger for Resilient Modulus Calculation" Forests 14, no. 12: 2425. https://doi.org/10.3390/f14122425
APA StyleFlorian, A., Ševelová, L., Žáková, K., & Žák, J. (2023). An Updated Cyclic CBR Test with Realistic Stress Values under the Plunger for Resilient Modulus Calculation. Forests, 14(12), 2425. https://doi.org/10.3390/f14122425