Effects of Biotic and Abiotic Factors on Biomass Conversion and Expansion Factors of Natural White Birch Forest (Betula platyphylla Suk.) in Northeast China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Forest Survey and Design Data
2.3. Climate Data
2.4. Methods
2.4.1. Basic and Generalized Model
2.4.2. Mixed-Effects Models
2.4.3. Model Assessment and Calibration Prediction
3. Results
3.1. Basic and Generalized Model
3.2. Mixed-Effects Models
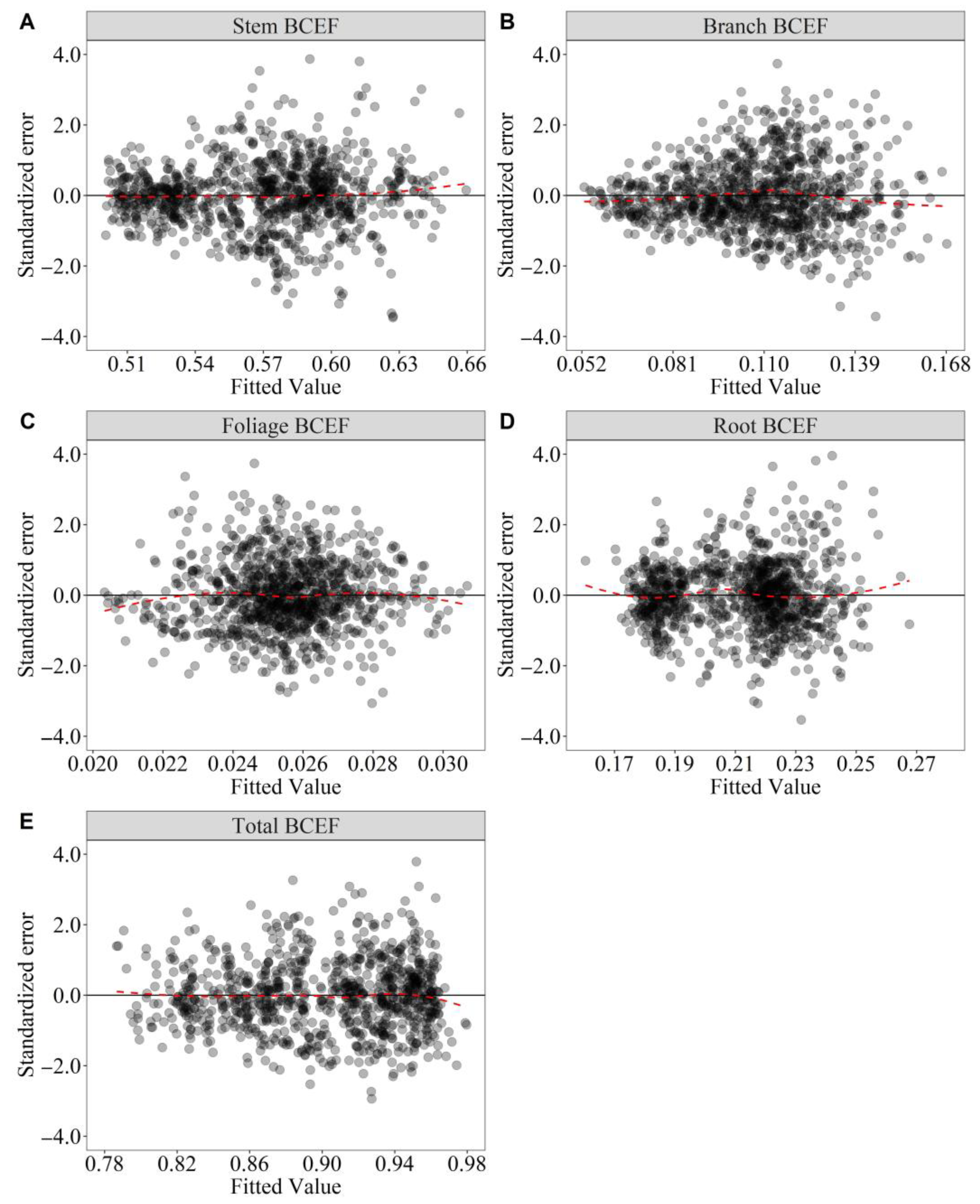
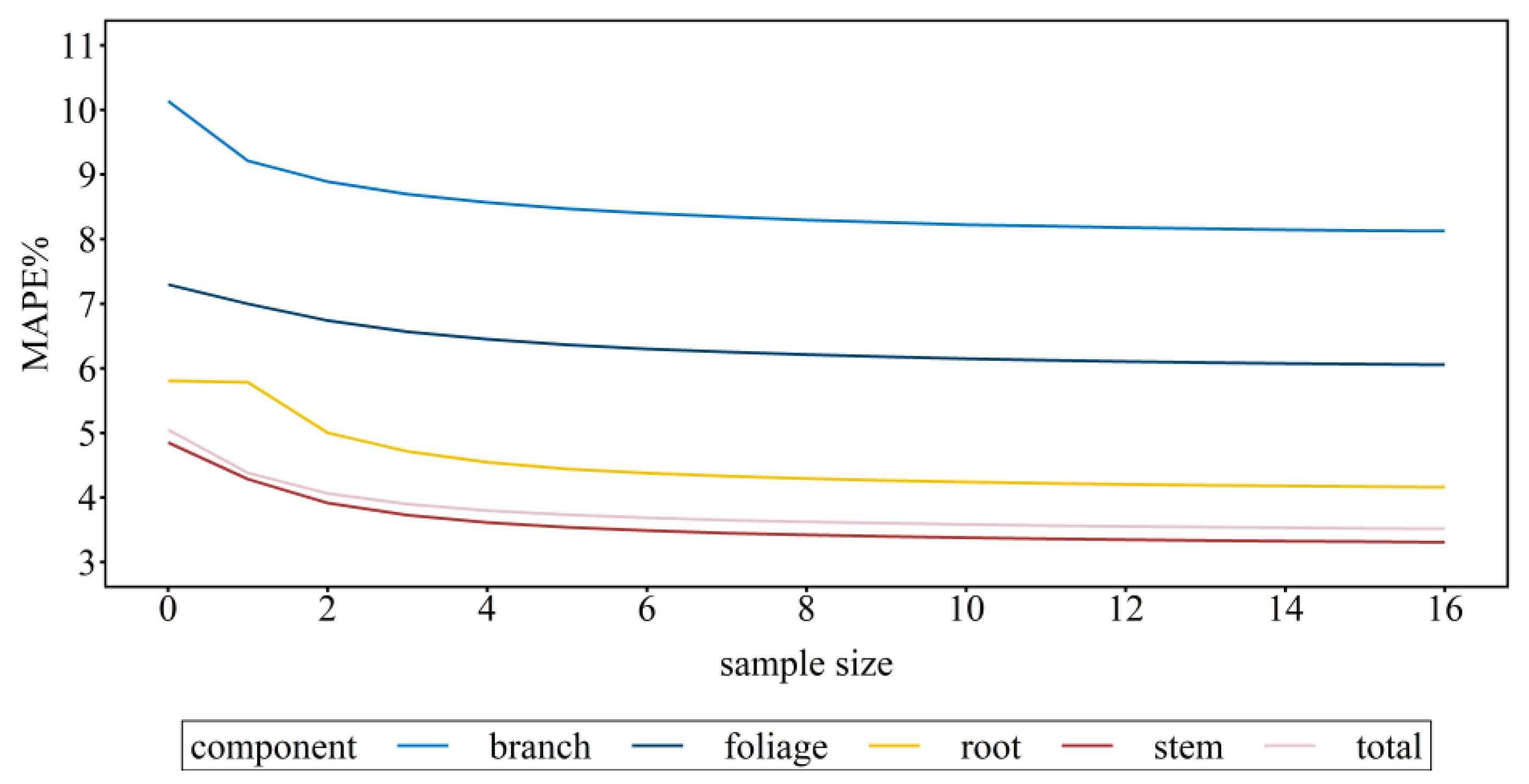
3.3. Model Assessment and Calibration Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cui, J.; Lam, S.K.; Xu, S.; Lai, D.Y.F. The response of soil-atmosphere greenhouse gas exchange to changing plant litter inputs in terrestrial forest ecosystems. Sci. Total Environ. 2022, 838, 155995. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Niu, S.; Tian, D.; Zhang, C.; Liu, W.; Yu, Z.; Yan, T.; Yang, W.; Zhao, X.; Wang, J. A global synthesis reveals increases in soil greenhouse gas emissions under forest thinning. Sci. Total Environ. 2022, 804, 150225. [Google Scholar] [CrossRef] [PubMed]
- Ma, A.; Miao, Z.; Xie, L.; Dong, L.-H.; Li, F. Crown width prediction for Larix olgensis plantations in Northeast China based on nonlinear mixed-effects model and quantile regression. Trees 2022, 36, 1761–7176. [Google Scholar] [CrossRef]
- Singh, V.; Tewari, A.; Kushwaha, S.P.S.; Dadhwal, V.K. Formulating allometric equations for estimating biomass and carbon stock in small diameter trees. For. Ecol. Manag. 2011, 261, 1945–1949. [Google Scholar] [CrossRef]
- Keith, H.; Lindenmayer, D.B.; Mackey, B.G.; Blair, D.; Carter, L.; McBurney, L.; Okada, S.; Konishi-Nagano, T. Accounting for Biomass Carbon Stock Change Due to Wildfire in Temperate Forest Landscapes in Australia. PLoS ONE 2014, 9, e107126. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Evaluation of Stand Biomass Estimation Methods for Major Forest Types in the Eastern Da Xing’an Mountains, Northeast China. Forests 2019, 10, 715. [Google Scholar] [CrossRef]
- IPCC. Good Practice Guidance for Land Use. Land-Use Change and Forestry; Penman Hayama, J., Ed.; IPCC National Greenhouse Gas Inventories Programme Technical Support Unit: Institute for Global Environmental Strategies: Kanagawa, Japan, 2003. [Google Scholar]
- Canadell, J.; Ciais, P.; Cox, P.; Heimann, M. Quantifying terrestrial carbon sinks—Preface. Clim. Chang. 2004, 67, 145–146. [Google Scholar]
- Canadell, J.G.; Raupach, M.R. Managing forests for climate change mitigation. Science 2008, 320, 1456–1457. [Google Scholar] [CrossRef] [PubMed]
- Jagodziński, A.M.; Zasada, M.; Bronisz, K.; Bronisz, A.; Bijak, S. Biomass conversion and expansion factors for a chronosequence of young naturally regenerated silver birch (Betula pendula Roth) stands growing on post-agricultural sites. For. Ecol. Manag. 2017, 384, 208–220. [Google Scholar] [CrossRef]
- Lehtonen, A.; Mäkipää, R.; Heikkinen, J.; Sievänen, R.; Liski, J. Biomass expansion factors (BEFs) for Scots pine, Norway spruce and birch according to stand age for boreal forests. For. Ecol. Manag. 2004, 188, 211–224. [Google Scholar] [CrossRef]
- Teobaldelli, M.; Somogyi, Z.; Migliavacca, M.; Usoltsev, V.A. Generalized functions of biomass expansion factors for conifers and broadleaved by stand age, growing stock and site index. For. Ecol. Manag. 2009, 257, 1004–1013. [Google Scholar] [CrossRef]
- Bruchwald, A.; Dmyterko, E.; Wojtan, R. Model wzrostu dla modrzewia europejskiego (Larix decidua Mill.) wykorzystujący cechy taksacyjne drzewostanu. Leśne Pr. Badaw. 2011, 72, 77–81. [Google Scholar]
- Aholoukpe, H.; Dubos, B.; Flori, A.; Deleporte, P.; Amadji, G.; Chotte, J.L.; Blavet, D. Estimating aboveground biomass of oil palm: Allometric equations for estimating frond biomass. For. Ecol. Manag. 2013, 292, 122–129. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Additive Biomass Equations Based on Different Dendrometric Variables for Two Dominant Species (Larix gmelini Rupr. and Betula platyphylla Suk.) in Natural Forests in the Eastern Daxing’an Mountains, Northeast China. Forests 2018, 9, 261. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Developing additive systems of biomass equations for nine hardwood species in Northeast China. Trees 2015, 29, 1149–1163. [Google Scholar] [CrossRef]
- Fayolle, A.; Doucet, J.L.; Gillet, J.F.; Bourland, N.; Lejeune, P. Tree allometry in Central Africa: Testing the validity of pantropical multi-species allometric equations for estimating biomass and carbon stocks. For. Ecol. Manag. 2013, 305, 29–37. [Google Scholar] [CrossRef]
- Kuyah, S.; Dietz, J.; Muthuri, C.; Jamnadass, R.; Mwangi, P.; Coe, R.; Neufeldt, H. Allometric equations for estimating biomass in agricultural landscapes: II. Belowground biomass. Agric. Ecosyst. Environ. 2012, 158, 225–234. [Google Scholar] [CrossRef]
- Ngomanda, A.; Engone Obiang, N.L.; Lebamba, J.; Moundounga Mavouroulou, Q.; Gomat, H.; Mankou, G.S.; Loumeto, J.; Midoko Iponga, D.; Kossi Ditsouga, F.; Zinga Koumba, R.; et al. Site-specific versus pantropical allometric equations: Which option to estimate the biomass of a moist central African forest? For. Ecol. Manag. 2014, 312, 1–9. [Google Scholar] [CrossRef]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar] [CrossRef]
- Zuo, S.; Ren, Y.; Wang, X.; Zhang, X.; Luo, Y. Biomass Estimation Factors and Their Determinants of Cunninghamia lanceolata Forests in China. Sci. Silvae Sin. 2014, 50, 1–12. [Google Scholar]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories Volume 4 Agriculture, Forestry and Other Land Use; IPCC: Geneva, Switzerland, 2006. [Google Scholar]
- Luo, Y.; Zhang, X.; Wang, X.; Ren, Y. Dissecting Variation in Biomass Conversion Factors across China’s Forests: Implications for Biomass and Carbon Accounting. PLoS ONE 2014, 9, e94777. [Google Scholar] [CrossRef]
- Löwe, H.; Seufert, G.; Raes, F. Comparison of methods used within Member States for estimating CO2 emissions and sinks according to UNFCCC and EU Monitoring Mechanism: Forest and other wooded land. Biotechnol. Agron. Société Et Environ. 2000, 4, 315–319. [Google Scholar]
- Petersson, H.; Melin, Y. Estimating the biomass and carbon pool of stump systems at a national scale. For. Ecol. Manag. 2010, 260, 466–471. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Zhang, Y.; Wan, C. Carbon sequestration potential of the stands under the Grain for Green Program in Yunnan Province, China. For. Ecol. Manag. 2009, 258, 199–206. [Google Scholar] [CrossRef]
- Lisboa, S.N.; Guedes, B.S.; Ribeiro, N.; Sitoe, A. Biomass allometric equation and expansion factor for a mountain moist evergreen forest in Mozambique. Carbon Balance Manag. 2018, 13, 23. [Google Scholar] [CrossRef] [PubMed]
- Krejza, J.; Svetlik, J.; Bednar, P. Allometric relationship and biomass expansion factors (BEFs) for above- and below-ground biomass prediction and stem volume estimation for ash (Fraxinus excelsior L.) and oak (Quercus robur L.). Trees 2017, 31, 1303–1316. [Google Scholar] [CrossRef]
- Jagodziński, A.M.; Dyderski, M.K.; Gęsikiewicz, K.; Horodecki, P.; Cysewska, A.; Wierczyńska, S.; Maciejczyk, K. How do tree stand parameters affect young Scots pine biomass?—Allometric equations and biomass conversion and expansion factors. For. Ecol. Manag. 2018, 409, 74–83. [Google Scholar] [CrossRef]
- Enes, T.; Fonseca, T. Biomass conversion and expansion factors are afected by thinning. For. Syst. 2014, 23, 438–447. [Google Scholar] [CrossRef]
- Brown, S.; Lugo, A.E. Biomass of tropical forests: A new estimate based on forest volumes. Science 1984, 223, 1290–1293. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Wang, X.; Zhang, X.; Zhu, J.; Zhang, Z.; Hou, Z. Biomass Estimation Factors of Larix principis-rupprechtii Plantations in Northern China. Sci. Silvae Sin. 2010, 46, 6–11. [Google Scholar]
- Zhang, X.; Wang, Z.; Chhin, S.; Wang, H.; Duan, A.G.; Zhang, J. Relative contributions of competition, stand structure, age, and climate factors to tree mortality of Chinese fir plantations: Long-term spacing trials in southern China. For. Ecol. Manag. 2020, 465, 118103. [Google Scholar] [CrossRef]
- Miao, Z.; Zhang, L.; Widagdo, F.R.A.; Dong, L.; Li, F. Modeling the number of the first- and second-order branches within the live tree crown of Korean larch plantations in Northeast China. Can. J. For. Res. 2021, 51, 704–719. [Google Scholar] [CrossRef]
- Li, C. Application of Mixed Effects Models in Forest Growth Model. Sci. Silvae Sin. 2009, 45, 131–138. [Google Scholar]
- Liu, X.; Hao, Y.S.; Widagdo, F.R.A.; Xie, L.F.; Dong, L.H.; Li, F.R. Predicting Height to Crown Base of Larix olgensis in Northeast China Using UAV-LiDAR Data and Nonlinear Mixed Effects Models. Remote Sens. 2021, 13, 1834. [Google Scholar] [CrossRef]
- Calegario, N.; Daniels, R.; Maestri, R.; Neiva, R. Modeling dominant height growth based on nonlinear mixed-effects model: A clonal Eucalyptus plantation case study. For. Ecol. Manag. 2005, 204, 11–21. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. For. Ecol. Manag. 2007, 249, 187–198. [Google Scholar] [CrossRef]
- Lindstrom, M.L.; Bates, D.M. Nonlinear mixed effects models for repeated measures data. Biometrics 1990, 46, 673–687. [Google Scholar] [CrossRef]
- Hall, D.B.; Clutter, M. Multivariate multilevel nonlinear mixed effects models for timber yield predictions. Biometrics 2004, 60, 16–24. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, H.; Sharma, R.P.; Pang, L.; Wang, G. A generalized nonlinear mixed-effects height to crown base model for Mongolian oak in northeast China. For. Ecol. Manag. 2017, 384, 34–43. [Google Scholar] [CrossRef]
- Calama, R.; Montero, G. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain. Can. J. For. Res. 2004, 34, 150–163. [Google Scholar] [CrossRef]
- Han, Y.Y.; Huang, W.; Sun, T.; Lu, B.; Mao, Z.J. Soil organic carbon stocks and fluxes in different age stands of secondary Betula platyphylla in Xiaoxing’an Mountain, China. Acta Ecol. Sin. 2015, 35, 1460–1469. [Google Scholar]
- Jiang, L.; Liu, Z. Structure Characteristics of Natural Birch Community and Species Diversity in Great Xing’an Mountains. For. Enginee Ring 2014, 30, 14–17. [Google Scholar]
- Hou, L.; Sun, T.; Mao, Z.; Lv, H.; Zhao, J.; Song, Y. Litter Decomposition and Nutrient Dynamic of Betula platyphylla Secondary Forest with Different Stand Ages in Xiaoxing’an Mountains. Bull. Bot. Res. 2012, 32, 492–496. [Google Scholar]
- Zhang, Y.; Mu, C.C.; Zheng, T.; Li, N.N. Ecosystem carbon storage of natural secondary birch forests in Xiaoxing’an Mountains of China. J. Beijing For. Univ. 2015, 37, 38–47. [Google Scholar]
- Wang, X.; Zhao, D.; Liu, G.; Yang, C.; Teskey, R.O. Additive tree biomass equations for Betula platyphylla Suk. plantations in Northeast China. Ann. For. Sci. 2018, 75, 60. [Google Scholar] [CrossRef]
- Dong, L.; Li, F.; Jia, W. Compatible Tree Biomass Models for Natural White Birch (Betula platyphylla) in Northeast China Forest Area. Sci. Silvae Sin. 2013, 49, 75–85. [Google Scholar]
- Wykoff, W. A Basal Area Increment Model for Individual Conifers in the Northern Rocky Mountains. For. Sci. 1990, 36, 1077–1104. [Google Scholar]
- Monserud, R.; Sterba, H. A basal area increment model for even-and uneven-aged forest stands in Austria. For. Ecol. Manag. 1996, 80, 57–80. [Google Scholar] [CrossRef]
- Liu, Q.; Meng, S.; Zhou, H. Tree Volume Tables of China; China Forestry Publishing House: Beijing, China, 2017. [Google Scholar]
- Zhu, W.; Xu, Y.; Wang, Z.; Du, A. Biomass Estimation Coefficient and Its Impacting Factors for Eucalyptus Plantation in China. Sci. Silvae Sin. 2020, 56, 1–11. [Google Scholar]
- He, X.; Lei, X.D.; Dong, L.H. How large is the difference in large-scale forest biomass estimations based on new climate-modified stand biomass models? Ecol. Indic. 2021, 126, 107569. [Google Scholar] [CrossRef]
- Wang, T.; Wang, G.; Innes, J.; Seely, B.; Chen, B. ClimateAP: An application for dynamic local downscaling of historical and future climate data in Asia Pacific. Front. Agric. Sci. Eng. 2017, 4, 448–458. [Google Scholar] [CrossRef]
- Butte, W.; Blum, J.K. Calculation of bioconcentration factors from kinetic data by non-linear iterative least-squares regression analysis using a programmable minicalculator. Chemosphere 1984, 13, 151–160. [Google Scholar] [CrossRef]
- Inoue, K. Iterative weighted least-squares estimates in a heteroscedastic linear regression model. J. Stat. Plan. Inference 2003, 110, 133–146. [Google Scholar] [CrossRef]
- Qiu, H.; Liu, S.; Zhang, Y.; Li, J. Variation in height-diameter allometry of ponderosa pine along competition, climate, and species diversity gradients in the western United States. For. Ecol. Manag. 2021, 497, 119477. [Google Scholar] [CrossRef]
- Vizcaino-Palomar, N.; Ibanez, I.; Benito-Garzon, M.; Gonzalez-Martinez, S.C.; Zavala, M.A.; Alia, R. Climate and population origin shape pine tree height-diameter allometry. New For. 2017, 48, 363–379. [Google Scholar] [CrossRef]
- Tian, D.; Jiang, L.; Shahzad, M.K.; He, P.; Wang, J.; Yan, Y. Climate-sensitive tree height-diameter models for mixed forests in Northeastern China. Agric. For. Meteorol. 2022, 326, 109182. [Google Scholar] [CrossRef]
- Dong, L.; Widagdo, F.R.A.; Xie, L.; Li, F. Biomass and Volume Modeling along with Carbon Concentration Variations of Short-Rotation Poplar Plantations. Forests 2020, 11, 780. [Google Scholar] [CrossRef]
- Harris, D.L.; Lofgren, D.L.; Stewart, T.S.; Schinckel, A.P. Adapting best linear unbiased prediction (BLUP) for timely genetic evaluation: I. Progeny traits in a single contemporary group for each sex. J. Anim. Sci. 1989, 67, 3209–3222. [Google Scholar] [CrossRef]
- Nothdurft, A.; Saborowski, J.; Breidenbach, J. Spatial prediction of forest stand variables. Eur. J. For. Res. 2009, 128, 241–251. [Google Scholar] [CrossRef]
- Viana, J.M.S.; Mundim, G.B.; Delima, R.O.; Silva, F.F.E.; De Resende, M.D.V. Best linear unbiased prediction for genetic evaluation in reciprocal recurrent selection with popcorn populations. J. Agric. Sci. 2014, 152, 428–438. [Google Scholar] [CrossRef]
- Wang, X.W.; Weng, Y.H.; Liu, G.F.; Krasowski, M.J.; Yang, C.P. Variation in carbon concentration, sequestration and partitioning among white birch (Betula platyphylla) provenances. For. Ecol. Manag. 2015, 358, 344–352. [Google Scholar] [CrossRef]
- Yao, P.; Chen, X.; Zhou, Y.; Zhao, W.; Lu, M.; Tu, J. Carbon sequestration potential of the major stands under the Grain for Green Program in Southwest China in the next 50 years. Acta Ecol. Sin. 2014, 34, e0150992. [Google Scholar]
- Fang, J.; Liu, G.; Zhu, B.; Wang, X.; Liu, S. Carbon budgets of three temperate forest ecosystems in Dongling Mt., Beijing, China. Sci. China Ser. D Earth Sci. 2007, 50, 92–101. [Google Scholar] [CrossRef]
- Syed Moazzam, N.; Alam, K. Assessing Biomass Expansion Factor of Birch Tree Betula utilis D. DON. Open J. For. 2014, 4, 181–190. [Google Scholar]
- Eggleston, S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. 2006 IPCC Guidelines for National Greenhouse Gas Inventories. V.4. Agriculture, Forestry and Other Land Use; IPCC: Geneva, Switzerland, 2006. [Google Scholar]
- Jagodziński, A.M.; Dyderski, M.; Gęsikiewicz, K.; Horodecki, P. Tree and stand level estimations of Abies alba Mill. aboveground biomass. Ann. For. Sci. 2019, 76, 56. [Google Scholar] [CrossRef]
- Wirth, C.; Schumacher, J.; Schulze, E.D. Generic biomass functions for Norway spruce in Central Europe—A meta-analysis approach toward prediction and uncertainty estimation. Tree Physiol. 2004, 24, 121–139. [Google Scholar] [CrossRef]
- Yu, M.; Liu, X.; Xue, L. Progress on effects of temperature and precipitation on forest biomass allocation patterns. Ecol. Sci. 2021, 40, 204–209. [Google Scholar]
- Guo, J.; Guo, Y.; Chai, Y.; Liu, X.; Yue, M. Shrubland biomass and root-shoot allocation along a climate gradient in China. Plant Ecol. Evol. 2021, 154, 5–14. [Google Scholar] [CrossRef]
- Zhou, L.; Li, B.G.; Zhou, G.S. ADVANCES IN CONTROLLING FACTORS OF SOIL ORGANIC CARBON. Adv. Earth Sci. 2005, 20, 99–105. [Google Scholar]
- Fang, Y.; Zou, X.; Lie, Z.; Xue, L. Variation in Organ Biomass with Changing Climate and Forest Characteristics across Chinese Forests. Forests 2018, 9, 521. [Google Scholar] [CrossRef]
- Poorte, A.; Nagel, O. The role of biomass allocation in the growth response of plants to different levels of light, CO2, nutrients and water: A quantitative review. IMF Occas. Pap. 2000, 27, 595–607. [Google Scholar]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogee, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A.; et al. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Lei, X.; Zeng, W.; Feng, L.; Zhou, C.; Wu, B. Quantifying the Effects of Stand and Climate Variables on Biomass of Larch Plantations Using Random Forests and National Forest Inventory Data in North and Northeast China. Sustainability 2022, 14, 5580. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, X.; Zhang, X.; Ren, Y.; Poorter, H. Variation in biomass expansion factors for China’s forests in relation to forest type, climate, and stand development. Ann. For. Sci. 2013, 70, 589–599. [Google Scholar] [CrossRef]
- Wang, G.; Guan, D.; Xiao, L.; Peart, M.R. Forest biomass-carbon variation affected by the climatic and topographic factors in Pearl River Delta, South China. J. Environ. Manag. 2019, 232, 781–788. [Google Scholar] [CrossRef]
- Konopka, B.; Pajtik, J.; Seben, V. Biomass functions and expansion factors for young trees of European ash and Sycamore maple in the Inner Western Carpathians. Austrian J. For. Sci. 2015, 132, 1–26. [Google Scholar]
- Zhang, W.; Li, H.; Li, J.; Lu, Z.; Liu, G. Individual and modular biomass dynamics of Kingdonia uninflora population in Qinling Mountain. J. Appl. Ecol. 2003, 14, 530–534. [Google Scholar]
- Guo, Z.; Lin, H.; Chen, S.; Yang, Q. Altitudinal Patterns of Leaf Traits and Leaf Allometry in Bamboo Pleioblastus amarus. Front. Plant Sci. 2018, 9, 1110. [Google Scholar] [CrossRef]
- Brown, S. Measuring carbon in forests: Current status and future challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
- Turner, D.P.; Koerper, G.J.; Harmon, M.E.; Lee, J.J. A Carbon Budget for Forests of the Conterminous United States. Ecol. Appl. 1995, 5, 421–436. [Google Scholar] [CrossRef]
- Schroeder, P.; Brown, S.; Mo, J.; Birdsey, R.; Cieszewski, C. Biomass estimation for temperate broadleaf forests of the United States using inventory data. For. Sci. 1997, 43, 424–434. [Google Scholar]
- Albaugh, T.J.; Bergh, J.; Lundmark, T.; Nilsson, U.; Stape, J.L.; Allen, H.L.; Linder, S. Do biological expansion factors adequately estimate stand-scale aboveground component biomass for Norway spruce? For. Ecol. Manag. 2009, 258, 2628–2637. [Google Scholar] [CrossRef]
- Petersson, H.; Holm, S.; Ståhl, G.; Alger, D.; Fridman, J.; Lehtonen, A.; Lundström, A.; Mäkipää, R. Individual tree biomass equations or biomass expansion factors for assessment of carbon stock changes in living biomass—A comparative study. For. Ecol. Manag. 2012, 270, 78–84. [Google Scholar] [CrossRef]
- Soares, P.; Tomé, M. Biomass expansion factors for Eucalyptus globulus stands in Portugal. For. Syst. 2012, 21, 141–152. [Google Scholar] [CrossRef]


| Attribute | Variable | Units | Descriptions |
|---|---|---|---|
| Stand attributes | Ha | m | The average tree height is the average height of 3 to 5 standard trees in the stand. |
| Dq | cm | The quadratic mean diameter: , | |
| Ddom | cm | The quadratic mean diameter of dominant species | |
| G | m2 hm−2 | The quadratic mean dominant diameter: | |
| NHa | tree·hm−2 | The number of trees per hectare | |
| M | m3 hm−2 | stand volume: M = Σvi; vi is individual tree volume: vi = aDBHb a and b are model coefficients based on [51] | |
| Wi | Mg hm−2 | Biomass: Wi = aDBHb; a and b are model coefficients based on Dong, et al. [16] | |
| BCEFi | Mg m3 | Biomass conversion and expansion factor: BCEFi = Wi/M | |
| Topographic conditions | ELV | m | Elevation |
| SL | The slope rate value: SL = tan(SLP) | ||
| SLP | Slope direction | ||
| SLC | The slope rate value multiplied by the slope cosine value. | ||
| SLS | The slope rate value multiplied by the slope sine value |
| Attribute | Variable | Mean | Min. | Max. | SD. |
|---|---|---|---|---|---|
| Stand attributes | Dg | 13.51 | 5.50 | 27.20 | 4.91 |
| G | 12.64 | 0.55 | 33.19 | 7.08 | |
| Ha | 12.52 | 5.00 | 22.70 | 3.44 | |
| M | 82.62 | 2.50 | 247.30 | 54.01 | |
| N | 1125.20 | 200.00 | 3467.00 | 617.46 | |
| Dq | 12.12 | 5.50 | 21.70 | 3.39 | |
| BCEFst | 0.5687 | 0.4549 | 0.7183 | 0.0449 | |
| BCEFbr | 0.1076 | 0.0524 | 0.1785 | 0.0248 | |
| BCEFfol | 0.0255 | 0.0180 | 0.0322 | 0.0026 | |
| BCEFro | 0.2117 | 0.1610 | 0.2907 | 0.0235 | |
| BCEFto | 0.9139 | 0.7473 | 1.1250 | 0.0719 | |
| Topographic conditions | ELV | 582 | 122 | 1150 | 200 |
| SL | 0.0888 | 0 | 0.488 | 0.0723 | |
| SLP | 5.0473 | 0 | 26.000 | 4.0071 | |
| SLC | 0.0106 | −0.364 | 0.404 | 0.0785 | |
| SLS | 0.0016 | −0.330 | 0.488 | 0.0827 |
| Variable | Units | Description |
|---|---|---|
| MAT | °C | Mean annual temperature |
| MWMT | °C | Mean warmest month temperature |
| MCMT | °C | Mean coldest month temperature |
| DD.0 | °C | Degree-days below 0 °C, chilling degree-days |
| DD.5 | °C | Degree-days above 5 °C, growing degree-days |
| DD.18 | °C | Degree-days below 18 °C, heating degree-days |
| DD.18.1 | °C | Degree-days above 18 °C, cooling degree-days |
| TD | °C | Temperature difference between MWMT and MCMT, or continentality (°C) |
| MAP | mm | Mean annual precipitation |
| AHM | — | Annual heat (MAT + 10)/(MAP/1000) |
| NFFD | The number of frost-free days | |
| PAS | mm | Precipitation as snow (mm) between August in previous year and July in current year |
| EMT | °C | Extreme minimum temperature over 30 years |
| EXT | °C | Extreme maximum temperature over 30 years |
| Eref | mm | Hargreaves reference evaporation |
| CMD | mm | Hargreaves climatic moisture deficit |
| Component | BCEFst | BCEFbr | BCEFfol | BCEFro | BCEFto | |
|---|---|---|---|---|---|---|
| Predictors | M (m3 hm−2) | Dq (cm) | Dq (cm) | M (m3 hm−2) | M (m3 hm−2) | |
| parameter | a | 0.668 | 0.021 | 0.018 | 0.284 | 1.019 |
| b | −0.040 | 0.662 | 0.134 | −0.073 | −0.027 | |
| statistical index | 0.206 | 0.692 | 0.155 | 0.365 | 0.104 | |
| −2LL | −3719.254 | −5935.322 | −9577.212 | −5307.534 | −2732.799 | |
| AIC | −3713.254 | −5929.322 | −9571.212 | −5301.534 | −2726.799 | |
| RMSE | 0.040 | 0.014 | 0.001 | 0.019 | 0.065 |
| Generalized Model | Model |
|---|---|
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (5) |
| Index | Model (1) | Model (2) | Model (3) | Model (4) | Model (5) | |
|---|---|---|---|---|---|---|
| parameter | a | 0.746 | 0.018 | 0.018 | 0.554 | 1.131 |
| a1 | −0.214 | 0.227 | −0.003 | −0.356 | −0.311 | |
| a2 | 0.151 | |||||
| b | −0.023 | 0.640 | 0.172 | −0.048 | −0.011 | |
| statistical index | 0.393 | 0.709 | 0.264 | 0.561 | 0.295 | |
| −2LL | −3997.374 | −5994.685 | −9721.432 | −5692.578 | −2982.493 | |
| AIC | −3989.374 | −5986.685 | −9713.432 | −5682.578 | −2974.493 | |
| RMSE | 0.035 | 0.013 | 0.002 | 0.016 | 0.057 | |
| Mixed-Effects Model | Model |
|---|---|
| (6) | |
| (7) | |
| (8) | |
| (9) | |
| (10) |
| Index | Model (6) | Model (7) | Model (8) | Model (9) | Model (10) | |
|---|---|---|---|---|---|---|
| fixed-effect | a | 0.656 | 0.013 | 0.016 | 0.317 | 1.020 |
| a1 | −0.083 | 0.161 | −0.001 | −0.081 | −0.156 | |
| a2 | 0.039 | |||||
| b | −0.016 | 0.760 | 0.193 | −0.043 | −0.004 | |
| random-effect | σu1 | 0.031 | 0.001 | 0.001 | 0.043 | 0.048 |
| σ | 0.026 | 0.011 | 0.002 | 0.012 | 0.041 | |
| statistical index | 0.676 | 0.791 | 0.445 | 0.749 | 0.648 | |
| −2LL | −4478.723 | −6201.959 | −10048.370 | −6070.187 | −3533.493 | |
| AIC | −4468.723 | −6191.959 | −.370 | −6058.187 | −3523.493 | |
| RMSE | 0.026 | 0.011 | 0.002 | 0.012 | 0.041 | |
| Component | Generalized Model | Mixed-Effect Model | ||||
|---|---|---|---|---|---|---|
| MAE/Mg m−3 | MAPE/% | FE | MAE/Mg m−3 | MAPE/% | FE | |
| stem | 0.028 | 4.851 | 0.361 | 0.019 | 3.275 | 0.671 |
| breach | 0.011 | 10.138 | 0.689 | 0.009 | 8.033 | 0.790 |
| foliage | 0.002 | 7.297 | 0. 233 | 0.002 | 6.011 | 0.436 |
| root | 0.012 | 5.808 | 0.522 | 0.009 | 4.167 | 0.742 |
| total | 0.046 | 5.050 | 0.254 | 0.032 | 3.487 | 0.643 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Miao, Z.; Hao, Y.; Dong, L.; Li, F. Effects of Biotic and Abiotic Factors on Biomass Conversion and Expansion Factors of Natural White Birch Forest (Betula platyphylla Suk.) in Northeast China. Forests 2023, 14, 362. https://doi.org/10.3390/f14020362
Wang Y, Miao Z, Hao Y, Dong L, Li F. Effects of Biotic and Abiotic Factors on Biomass Conversion and Expansion Factors of Natural White Birch Forest (Betula platyphylla Suk.) in Northeast China. Forests. 2023; 14(2):362. https://doi.org/10.3390/f14020362
Chicago/Turabian StyleWang, Yanrong, Zheng Miao, Yuanshuo Hao, Lihu Dong, and Fengri Li. 2023. "Effects of Biotic and Abiotic Factors on Biomass Conversion and Expansion Factors of Natural White Birch Forest (Betula platyphylla Suk.) in Northeast China" Forests 14, no. 2: 362. https://doi.org/10.3390/f14020362
APA StyleWang, Y., Miao, Z., Hao, Y., Dong, L., & Li, F. (2023). Effects of Biotic and Abiotic Factors on Biomass Conversion and Expansion Factors of Natural White Birch Forest (Betula platyphylla Suk.) in Northeast China. Forests, 14(2), 362. https://doi.org/10.3390/f14020362







