A Fast Instance Segmentation Technique for Log End Faces Based on Metric Learning
Abstract
:1. Introduction
- (1)
- Different from mainstream methods like Mask-RCNN, our approach uses a novel parallel architecture for object detection and segmentation, which improves the speed of extracting the end faces of logs.
- (2)
- By using the metric learning paradigm to distinguish the overlapping areas of adjacent logs, a higher quality of log end face instance segmentation is achieved in this paper.
- (3)
- In this paper, we use least squares to fit the mask contour, combine it with the true size of the scale to obtain the log ruler diameter, and finally achieve intelligent and fast log ruler diameter measurement.
2. Fast Instance Segmentation Method Based on Metric Learning
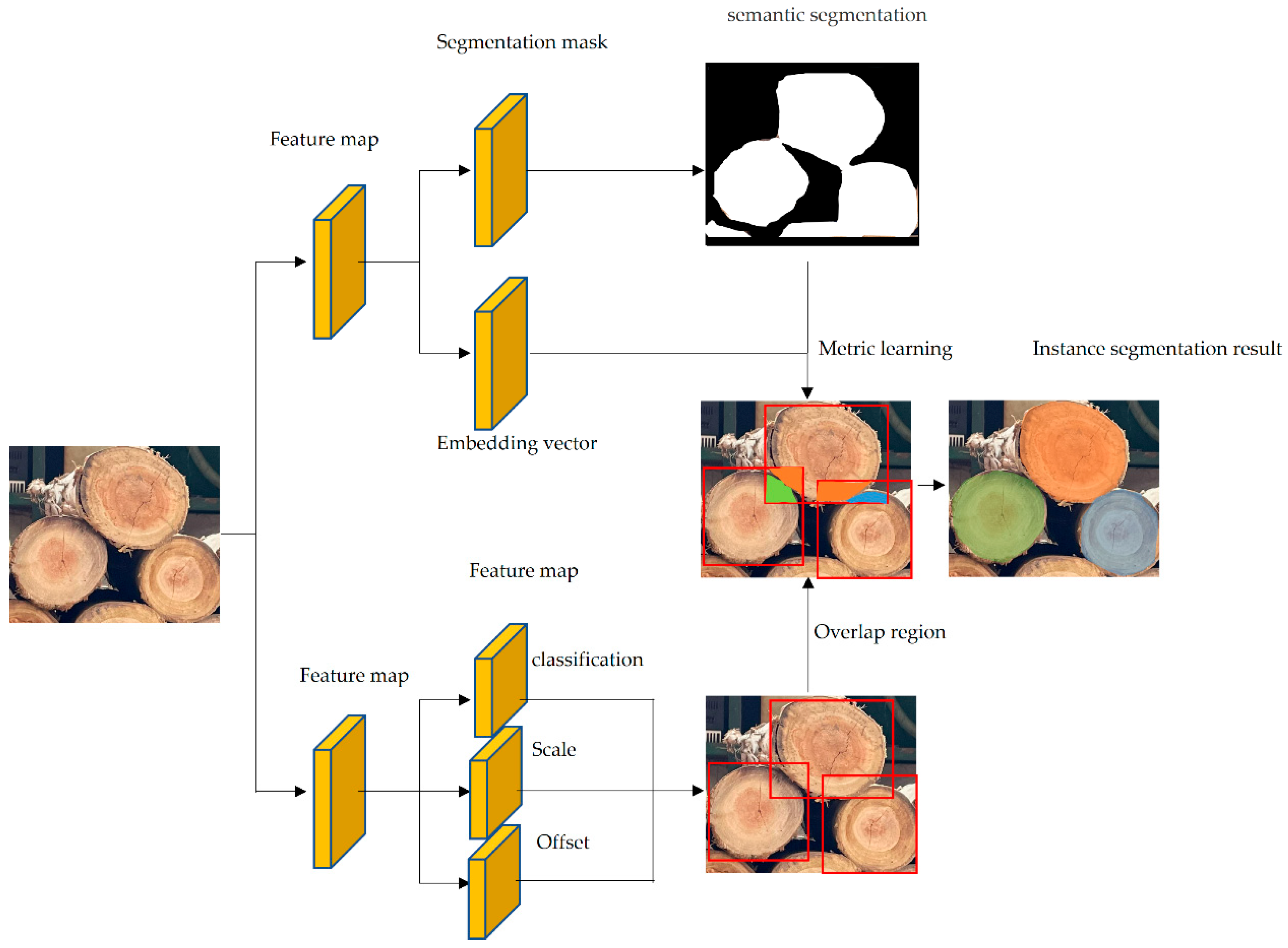
2.1. Network Structure of Instance Segmentation Model
2.2. Instance Segmentation Model Loss Function
2.3. Metric Learning Representation
2.4. Training Methods for Instance Segmentation Models
2.5. Application of Proposed Instance Segmentation Model for Log End Detection
3. Results and Analysis of the Instance Segmentation Model
Results of Log End-Face Mask Extraction Using Instance Segmentation Model
4. Model Detection Diameter Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- National Bureau of Statistics of China. China Statistical Yearbook (2020); China Statistics Press: Beijing, China, 2020. [Google Scholar]
- Jiang, W. Lumber Inspection and Its Importance in Lumber Shipping Inspection. Jiangxi Agric. 2019, 4, 92–93. [Google Scholar]
- Li, M. Research on Optimal Algorithm of Logistics System for Timber Transportation in Forest Area; Beijing Forestry University: Beijing, China, 2016. [Google Scholar]
- Hua, B.; Cao, P.; Huang, R.W. Research on log volume detection method based on computer vision. J. Henan Inst. Sci. Technol. Nat. Sci. Ed. 2022, 50, 64–69. [Google Scholar]
- Chen, G.H.; Zhang, Q.; Chen, M.Q.; Li, J.W.; Yin, H.Y. Log diameter-level fast detection algorithm based on binocular vision. J. Beijing Jiaotong Univ. 2018, 42, 9. [Google Scholar]
- Keck, C.; Schoedel, R. Reference Measurement of Roundwood by Fringe Projection. For. Prod. J. 2021, 71, 352–361. [Google Scholar] [CrossRef]
- Tang, H.; Wang, K.J.; Li, X.Y.; Jian, W.H.; Gu, J.C. Detection and statistics of log image end face based on color difference clustering. China J. Econom. 2020, 41, 7. [Google Scholar]
- Tang, H.; Wang, K.; Gu, J.C.; Li, X.; Jian, W. Application of SSD framework model in detection of logs end. J. Phys. Conf. Ser. 2020, 1486, 072051. [Google Scholar] [CrossRef]
- Cai, R.X.; Lin, P.J.; Lin, Y.H.; Yu, P.P. Bundled log end face detection algorithm based on improved YOLOv4-Tiny. Telev. Technol. 2021, 45, 9. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 2961–2969. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Zhou, X.; Wang, D.; Krähenbühl, P. Objects as points. arXiv 2019, arXiv:1904.07850. [Google Scholar]
- Li, X.; You, A.; Zhu, Z.; Zhao, H.; Yang, M.; Yang, K.; Tan, S.; Tong, Y. Semantic flow for fast and accurate scene parsing. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 775–793. [Google Scholar]
- Li, Y.; Qi, H.; Dai, J.; Ji, X.; Wei, Y. Fully convolutional instance-aware semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2359–2367. [Google Scholar]
- Zhang, R.; Tian, Z.; Shen, C.; You, M.; Yan, Y. Mask encoding for single shot instance segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 10226–10235. [Google Scholar]
- Papandreou, G.; Zhu, T.; Chen, L.C.; Gidaris, S.; Tompson, J.; Murphy, K. Personlab: Person pose estimation and instance segmentation with a bottom-up, part-based, geometric embedding model. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 269–286. [Google Scholar]
- Ying, H.; Huang, Z.; Liu, S.; Shao, T.; Zhou, K. Embedmask: Embedding coupling for one-stage instance segmentation. arXiv 2019, arXiv:1912.01954. [Google Scholar]
- Cheng, T.; Wang, X.; Chen, S.; Zhang, W.; Zhang, Q.; Huang, C.; Liu, W. Sparse Instance Activation for Real-Time Instance Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 4433–4442. [Google Scholar]
- Liu, Y.; Sun, P.; Wergeles, N.; Shang, Y. A survey and performance evaluation of deep learning methods for small object detection. Expert Syst. Appl. 2021, 172, 114602. [Google Scholar] [CrossRef]
- Lim, J.S.; Astrid, M.; Yoon, H.J.; Lee, S.I. Small object detection using context and attention. In Proceedings of the 2021 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Jeju Island, Republic of Korea, 13–16 April 2021; pp. 181–186. [Google Scholar]
- Bosquet, B.; Mucientes, M.; Brea, V.M. STDnet-ST: Spatio-temporal ConvNet for small object detection. Pattern Recognit. 2021, 116, 107929. [Google Scholar] [CrossRef]
- Leng, J.; Ren, Y.; Jiang, W.; Sun, X.; Wang, Y. Realize your surroundings: Exploiting context information for small object detection. Neurocomputing 2021, 433, 287–299. [Google Scholar] [CrossRef]
- Liu, M.; Wang, X.; Zhou, A.; Fu, X.; Ma, Y.; Piao, C. Uav-yolo: Small object detection on unmanned aerial vehicle perspective. Sensors 2020, 20, 2238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, H.; Wang, Y.; Dayoub, F.; Sunderhauf, N. Varifocalnet: An iou-aware dense object detector. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8514–8523. [Google Scholar]
- Qiu, H.; Ma, Y.; Li, Z.; Liu, S.; Sun, J. Borderdet: Border feature for dense object detection. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Part I 16. Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 549–564. [Google Scholar]
- Chen, Z.; Yang, C.; Li, Q.; Zhao, F.; Zha, Z.J.; Wu, F. Disentangle your dense object detector. In Proceedings of the 29th ACM International Conference on Multimedia, New York, NY, USA, 20–24 October 2021; pp. 4939–4948. [Google Scholar]
- Zhu, B.; Wang, J.; Jiang, Z.; Zong, F.; Liu, S.; Li, Z.; Sun, J. Autoassign: Differentiable label assignment for dense object detection. arXiv 2020, arXiv:2007.03496. [Google Scholar]
- Gao, Z.; Wang, L.; Wu, G. Mutual supervision for dense object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 3641–3650. [Google Scholar]
- Glowacz, A. Thermographic fault diagnosis of electrical faults of commutator and induction motors. Eng. Appl. Artif. Intell. 2023, 121, 105962. [Google Scholar] [CrossRef]




| 0.3 | 0.4 | 0.3 | 0.5 | 0.5 | 0.912 |
| 0.2 | 0.5 | 0.3 | 0.4 | 0.6 | 0.910 |
| 0.4 | 0.3 | 0.3 | 0.5 | 0.5 | 0899 |
| 0.5 | 0.3 | 0.2 | 0.6 | 0.4 | 0.897 |
| 0.2 | 0.3 | 0.5 | 0.3 | 0.7 | 0.896 |
| K | Training Time | |
|---|---|---|
| 1 | 32 min | 0.902 |
| 3 | 56 min | 0.905 |
| 3 | 1 h 20 min | 0.912 |
| 4 | 2 h 50 min | 0.913 |
| 5 | 5 h 12 min | 0.925 |
| Models | FPS | ||||
|---|---|---|---|---|---|
| Mask-RCNN | 0.842 | 0.878 | 0.838 | 0.810 | 8.6 |
| FCIS | 0.827 | 0.848 | 0.831 | 0.803 | 8.1 |
| MEinst | 0.835 | 0.852 | 0.835 | 0.820 | 4.2 |
| PersonLab | 0.818 | 0.844 | 0.821 | 0.791 | 24.7 |
| EmbedMask | 0.864 | 0.881 | 0.862 | 0.851 | 16.7 |
| SparseInst | 0.714 | 0.810 | 0.579 | 0.753 | 44.6 |
| Our | 0.912 | 0.912 | 0.911 | 0.913 | 50.2 |
| Model | Mean Relative Error/% | Standard Deviation/% | Frame Rate/FPS |
|---|---|---|---|
| Mask-RCNN | −5.13 | 5.81 | 8.6 |
| EmbedMask | −5.09 | 5.78 | 16.7 |
| Ours | −4.62 | 5.16 | 50.2 |
| Distance/m | Mean Absolute Error/mm | Mean Relative Error/% |
|---|---|---|
| 1 | −4.13 | −4.81 |
| 2 | −4.09 | −4.78 |
| 3 | −4.01 | −4.62 |
| 4 | −5.40 | −6.18 |
| 5 | −8.79 | −8.14 |
| Height/m | Mean Absolute Error/mm | Mean Relative Error/% |
|---|---|---|
| 1.6 | −4.01 | −4.62 |
| 1.8 | −3.98 | −4.60 |
| 2.0 | −4.04 | −4.63 |
| 2.2 | −4.06 | −4.64 |
| Angle | Mean Absolute Error/mm | Mean Relative Error/% |
|---|---|---|
| 30 degrees to the left | −12.51 | −13.98 |
| 20 degrees to the left | −9.49 | −10.83 |
| 10 degrees to the left | −5.21 | −6.35 |
| Is on | −4.01 | −4.62 |
| 10 degrees to the right | −5.23 | −6.36 |
| 20 degrees to the right | −9.53 | −10.85 |
| 30 degrees to the right | −12.79 | −14.02 |
| Nation | Method | True Volume/m3 | Measure Volume/m3 | Error/% |
|---|---|---|---|---|
| China | 4.87 | 4.66 | −4.25 | |
| Russia | none | 4.63 | 4.39 | −5.02 |
| The U.S. | 5.32 | 4.98 | −6.32 | |
| Japan | 4.28 | 4.03 | −5.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, J.; Wang, D. A Fast Instance Segmentation Technique for Log End Faces Based on Metric Learning. Forests 2023, 14, 795. https://doi.org/10.3390/f14040795
Li H, Liu J, Wang D. A Fast Instance Segmentation Technique for Log End Faces Based on Metric Learning. Forests. 2023; 14(4):795. https://doi.org/10.3390/f14040795
Chicago/Turabian StyleLi, Hui, Jinhao Liu, and Dian Wang. 2023. "A Fast Instance Segmentation Technique for Log End Faces Based on Metric Learning" Forests 14, no. 4: 795. https://doi.org/10.3390/f14040795
APA StyleLi, H., Liu, J., & Wang, D. (2023). A Fast Instance Segmentation Technique for Log End Faces Based on Metric Learning. Forests, 14(4), 795. https://doi.org/10.3390/f14040795






