Influence of the External Environment on the Moisture Spectrum of Norway Spruce (Picea abies (L.) KARST.)
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Data Collection
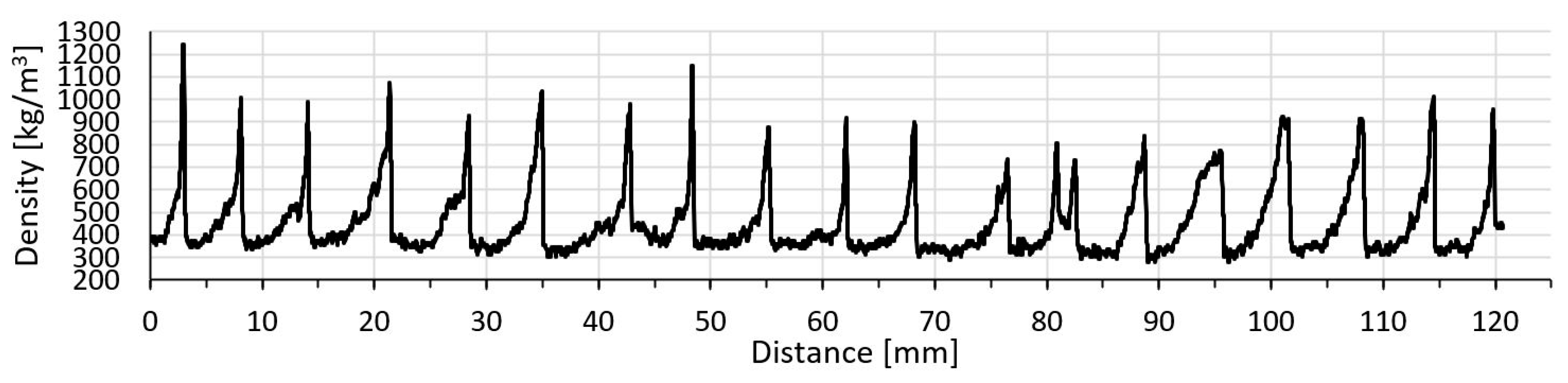
2.3. Initial Observation

2.4. Data Processing
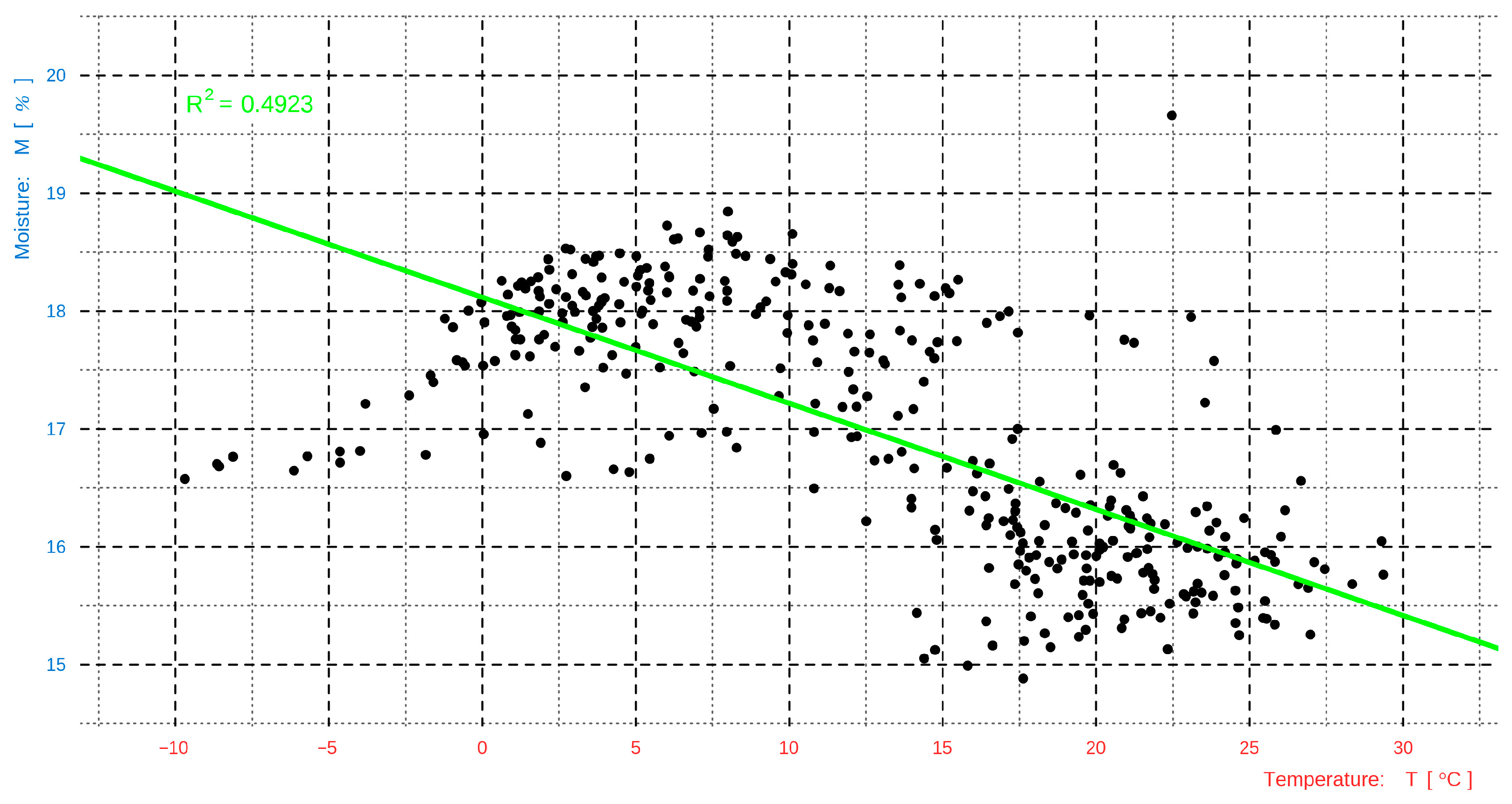
2.4.1. Reasons for the Insufficiency of the Linear Model
2.4.2. Year Choice
2.4.3. Predictor Choice
2.5. Model Preparation
Illustration of Modeling Procedure
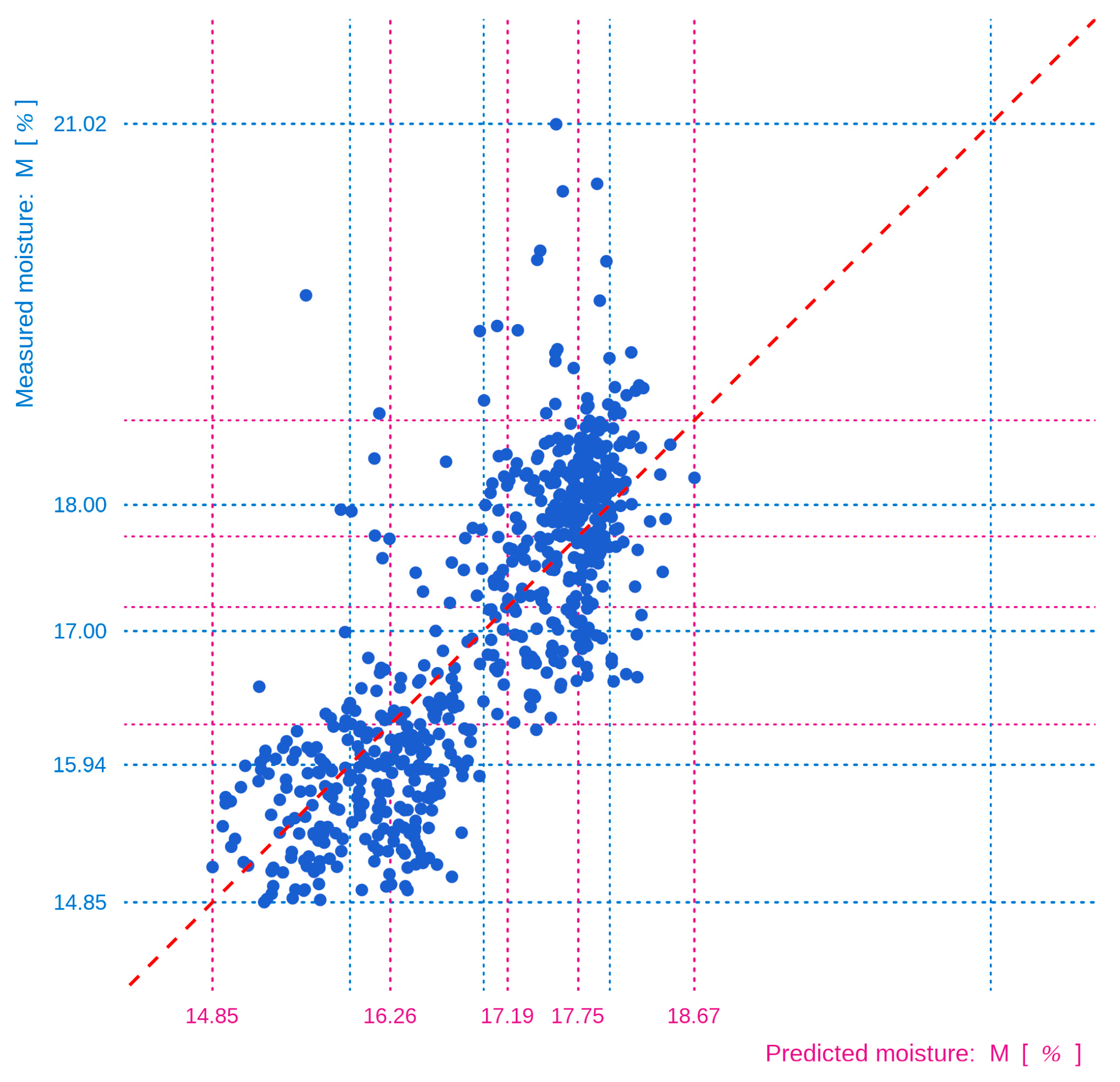
3. Results and Discussion
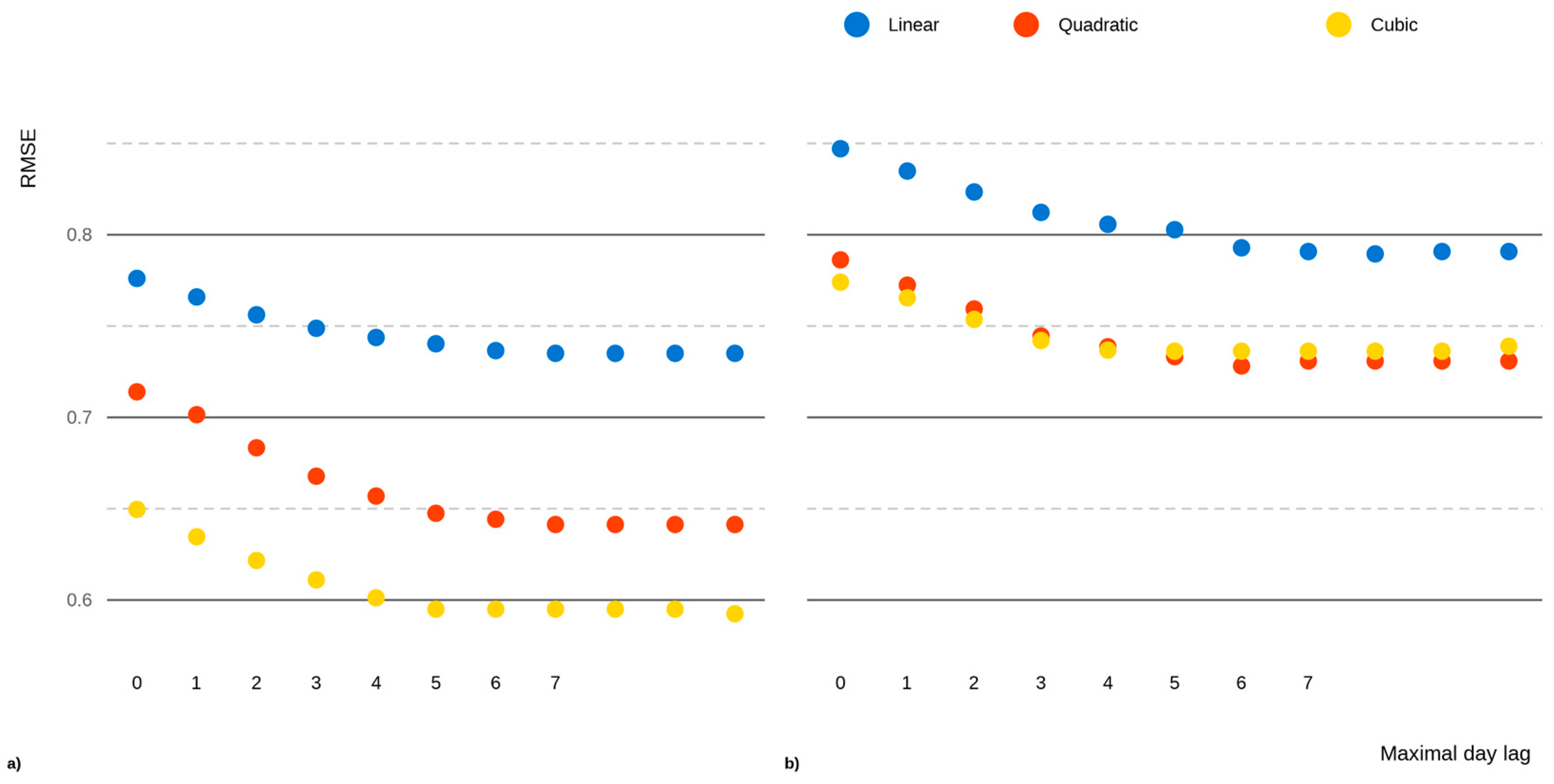
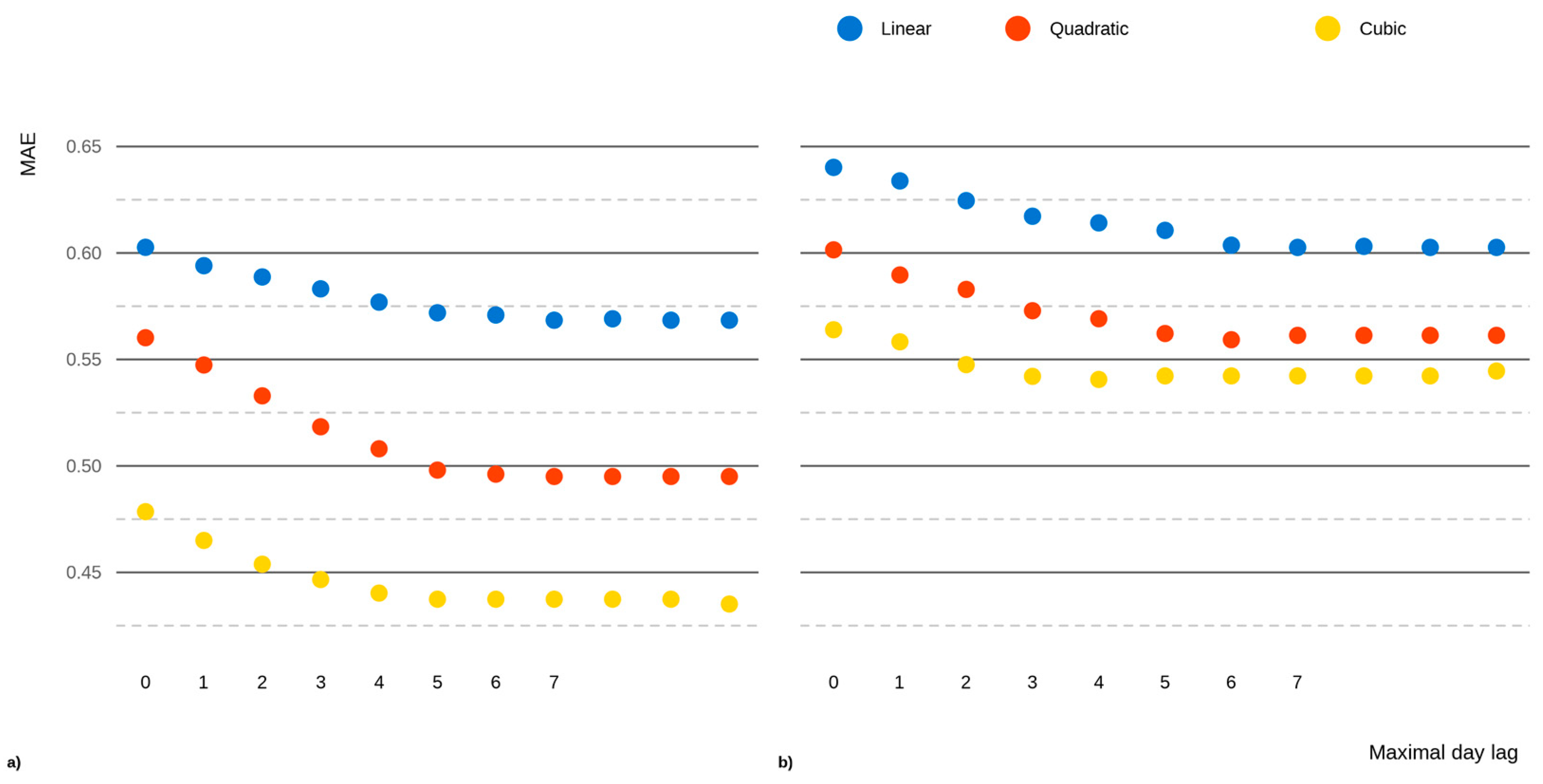
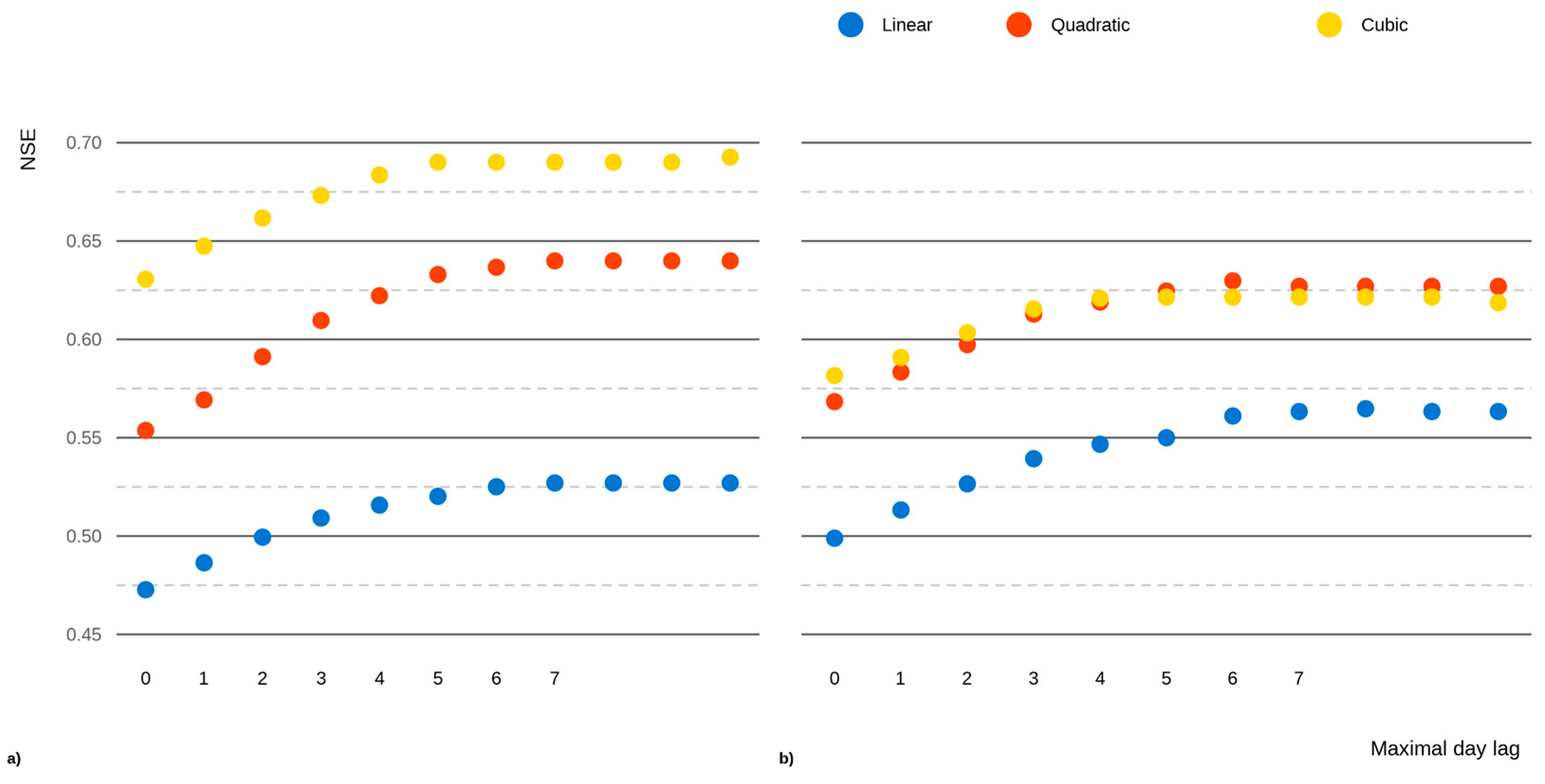
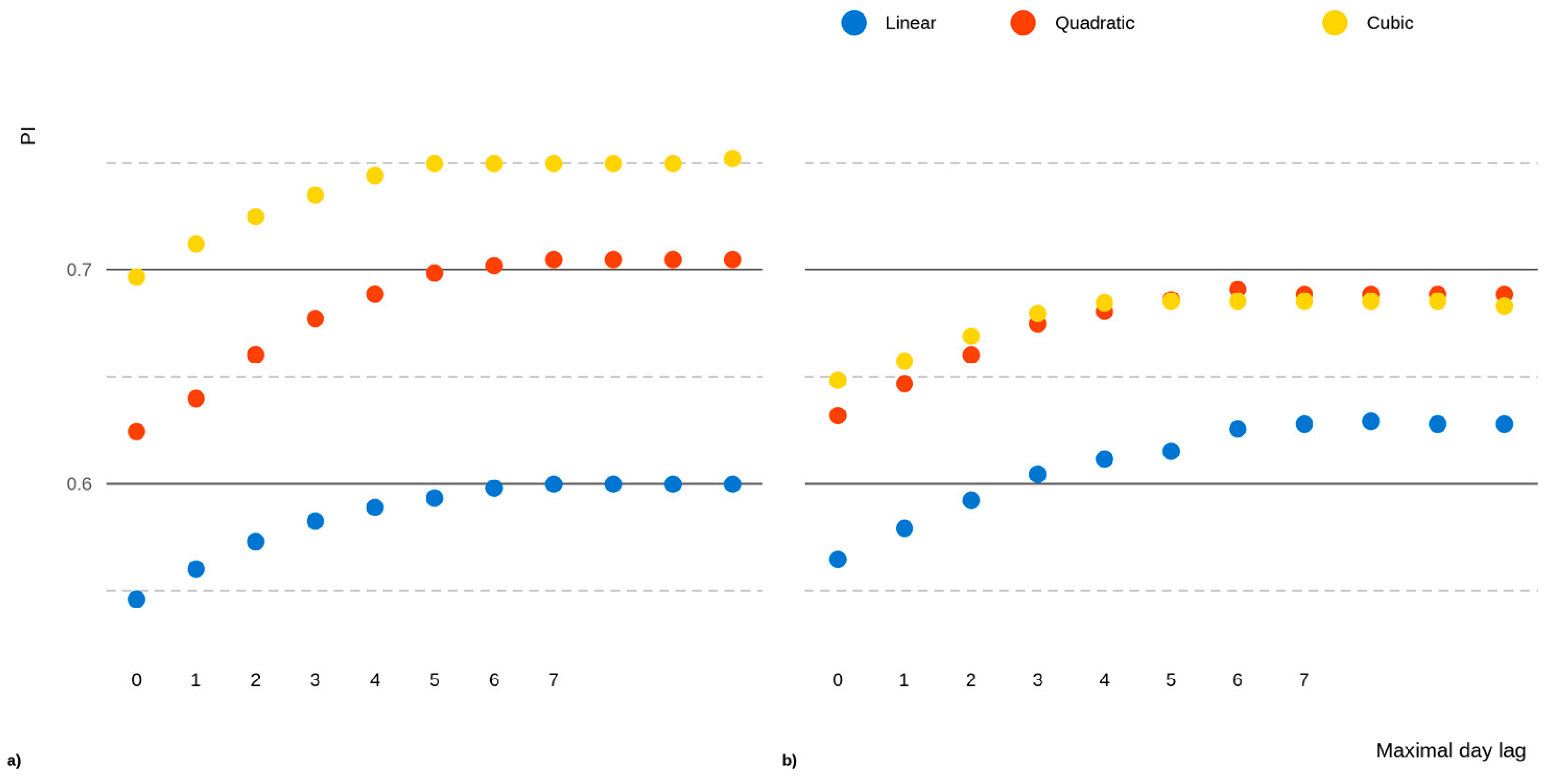
3.1. Model Comparison and Rating
3.2. Final Tuning
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buchanan, A.H.; Levine, S.B. Wood-Based Building Materials and Atmospheric Carbon Emissions. Environ. Sci. Policy 1999, 2, 427–437. [Google Scholar] [CrossRef]
- Karjalainen, T.; Kellomäki, S.; Pussinen, A. Role of Wood-Based Products in Absorbing Atmospheric Carbon. Silva Fennica. 1994. 28, 67–80. [CrossRef]
- Mantau, U. Wood Flow Analysis: Quantification of Resource Potentials, Cascades and Carbon Effects. Biomass Bioenergy 2015, 79, 28–38. [Google Scholar] [CrossRef]
- Belgacem, M.N.; Pizzi, A. (Eds.) Lignocellulosic Fibers and Wood Handbook: Renewable Materials for Today’s Environment; Scrivener Publishing: Beverly, MA, USA; Wiley: Beverly, MA, USA; Hoboken, NJ, USA, 2016; ISBN 978-1-118-77352-9. [Google Scholar]
- Dinwoodie, J.M. Timber; CRC Press: Boca Raton, FL, USA, 2000; ISBN 978-1-135-80810-5. [Google Scholar]
- Mitterpach, J.; Fojtík, R.; Machovčáková, E.; Kubíncová, L. Life Cycle Assessment of a Road Transverse Prestressed Wooden–Concrete Bridge. Forests 2022, 14, 16. [Google Scholar] [CrossRef]
- Record, S.J. The Mechanical Properties of Wood: Including a Discussion of the Factors Affecting the Mechanical Properties and Methods of Timber Testing; Publishers Printing Company: New York, NY, USA, 1914. [Google Scholar]
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; Krieger Pub Co.: Malabar, FL, USA, 1993; ISBN 978-0-89464-777-2. [Google Scholar]
- Vasiliev, V.V.; Morozov, E.V. Advanced Mechanics of Composite Materials and Structures, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 978-0-08-102209-2. [Google Scholar]
- Fojtík, R.; Dubovský, V.; Kozlová, K.; Kubíncová, L. Prestress Losses in Spruce Timber. Wood Res. 2020, 65, 645–652. [Google Scholar] [CrossRef]
- Wenzel, H. Health Monitoring of Bridges; Wiley: Chichester, UK, 2009; ISBN 978-0-470-03173-5. [Google Scholar]
- Wadi, H.; Amziane, S.; Taazount, M. The Lateral Load Resistance of Unclassified Cross-Laminated Timber Walls: Experimental Tests and Theoretical Approach. Eng. Struct. 2018, 166, 402–412. [Google Scholar] [CrossRef]
- Wang, J.; Cao, X.; Liu, H. A Review of the Long-Term Effects of Humidity on the Mechanical Properties of Wood and Wood-Based Products. Eur. J. Wood Prod. 2021, 79, 245–259. [Google Scholar] [CrossRef]
- Startsev, O.V.; Makhonkov, A.; Erofeev, V.; Gudojnikov, S. Impact of Moisture Content on Dynamic Mechanical Properties and Transition Temperatures of Wood. Wood Mater. Sci. Eng. 2017, 12, 55–62. [Google Scholar] [CrossRef]
- Vololonirina, O.; Coutand, M.; Perrin, B. Characterization of Hygrothermal Properties of Wood-Based Products—Impact of Moisture Content and Temperature. Constr. Build. Mater. 2014, 63, 223–233. [Google Scholar] [CrossRef]
- Buell, T.W.; Saadatmanesh, H. Strengthening Timber Bridge Beams Using Carbon Fiber. J. Struct. Eng. 2005, 131, 173–187. [Google Scholar] [CrossRef]
- Lukowsky, D.; Wade, D. Failure Analysis of Wood and Wood-Based Products; Mc Graw-Hill education: New York, NY, USA, 2015; ISBN 978-0-07-183937-2. [Google Scholar]
- Obućina, M.; Kitek Kuzman, M.; Sandberg, D. Use of Sustainable Wood Building Materials in Bosnia and Herzegovina, Slovenia and Sweden; University of Sarajevo, Mechanical Engineering Faculty, Department of Wood Technology: Sarajevo, Bosnia and Herzegovina, 2017. [Google Scholar]
- Fojtík, R.; Dědková, K. Analysis of Diagnostic Methods for Detecting the Presence of Gloeophyllum spp. Wood Res. 2018, 63, 479–486. [Google Scholar]
- Thybring, E.E.; Fredriksson, M. Wood Modification as a Tool to Understand Moisture in Wood. Forests 2021, 12, 372. [Google Scholar] [CrossRef]
- Fojtík, R.; Kubíncová, L.; Dubovský, V.; Kozlová, K. Moisture at Contacts of Timber-Concrete Element. Wood Res. 2020, 65, 917–924. [Google Scholar] [CrossRef]
- Sandberg, K.; Pousette, A.; Nilsson, L. Moisture Conditions in Coated Glulam Beams and Columns during Weathering. In Proceedings of the International Conference on Durability of Building Materials and Components, Porto, Portugal, 12–15 April 2011; pp. 1–8. [Google Scholar]
- Almeida, G.; Hernández, R.E. Changes in Physical Properties of Tropical and Temperate Hardwoods below and above the Fiber Saturation Point. Wood Sci. Technol. 2006, 40, 599–613. [Google Scholar] [CrossRef]
- Brischke, C.; Rapp, A.O.; Bayerbach, R. Measurement System for Long-Term Recording of Wood Moisture Content with Internal Conductively Glued Electrodes. Build. Environ. 2008, 43, 1566–1574. [Google Scholar] [CrossRef]
- Reiterer, A.; Sinn, G.; Stanzl-Tschegg, S.E. Fracture Characteristics of Different Wood Species under Mode I Loading Perpendicular to the Grain. Mater. Sci. Eng. A 2002, 332, 29–36. [Google Scholar] [CrossRef]
- Zhang, S.Y. Effect of Growth Rate on Wood Specific Gravity and Selected Mechanical Properties in Individual Species from Distinct Wood Categories. Wood Sci. Technol. 1995, 29, 451–465. [Google Scholar] [CrossRef]
- Fojtík, R.; Dubovský, V.; Kubíncová, L.; Stejskalová, K.; Machovčáková, E.; Lesňák, M. Probabilistic Expression of the Function of the Change in Prestressing Force of Timber Elements Depending on Climatic Conditions in Situ. Constr. Build. Mater. 2023, 377, 130955. [Google Scholar] [CrossRef]
- Fransson, E.; Eriksson, F.; Erhart, P. Efficient Construction of Linear Models in Materials Modeling and Applications to Force Constant Expansions. NPJ Comput. Mater. 2020, 6, 135. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Duc, L.; Sawada, Y. A Signal-Processing-Based Interpretation of the Nash–Sutcliffe Efficiency. Hydrol. Earth Syst. Sci. 2023, 27, 1827–1839. [Google Scholar] [CrossRef]
- Dubovsky, V.; Dlouhá, D.; Pospíšil, L. The Calibration of Evaporation Models against the Penman–Monteith Equation on Lake Most. Sustainability 2020, 13, 313. [Google Scholar] [CrossRef]
- Dlouhá, D.; Dubovsky, V.; Pospíšil, L. Optimal Calibration of Evaporation Models against Penman–Monteith Equation. Water 2021, 13, 1484. [Google Scholar] [CrossRef]
- Camargo, A.P.; Sentelgas, P.C. Avaliação Do Desempenho de Diferentes Métodos de Estimativa Da Evapotranspiração Potencial No Estado de São Paulo, Brasil. Rev. Bras. Meteorol. 1997, 5, 89–97. [Google Scholar]
- Sobenko, L.R.; Pimenta, B.D.; Camargo, A.P.D.; Robaina, A.D.; Peiter, M.X.; Frizzone, J.A. Indicators for Evaluation of Model Performance: Irrigation Hydraulics Applications. Acta Sci. Agron. 2022, 45, e56300. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Information Criteria and Statistical Modeling; Springer: New York, NY, USA, 2006; ISBN 978-0-387-71886-6. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- RStudio, PBC. RStudio Team RStudio: Integrated Development Environment for R; RStudio, PBC: Boston, MA, USA, 2020. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]

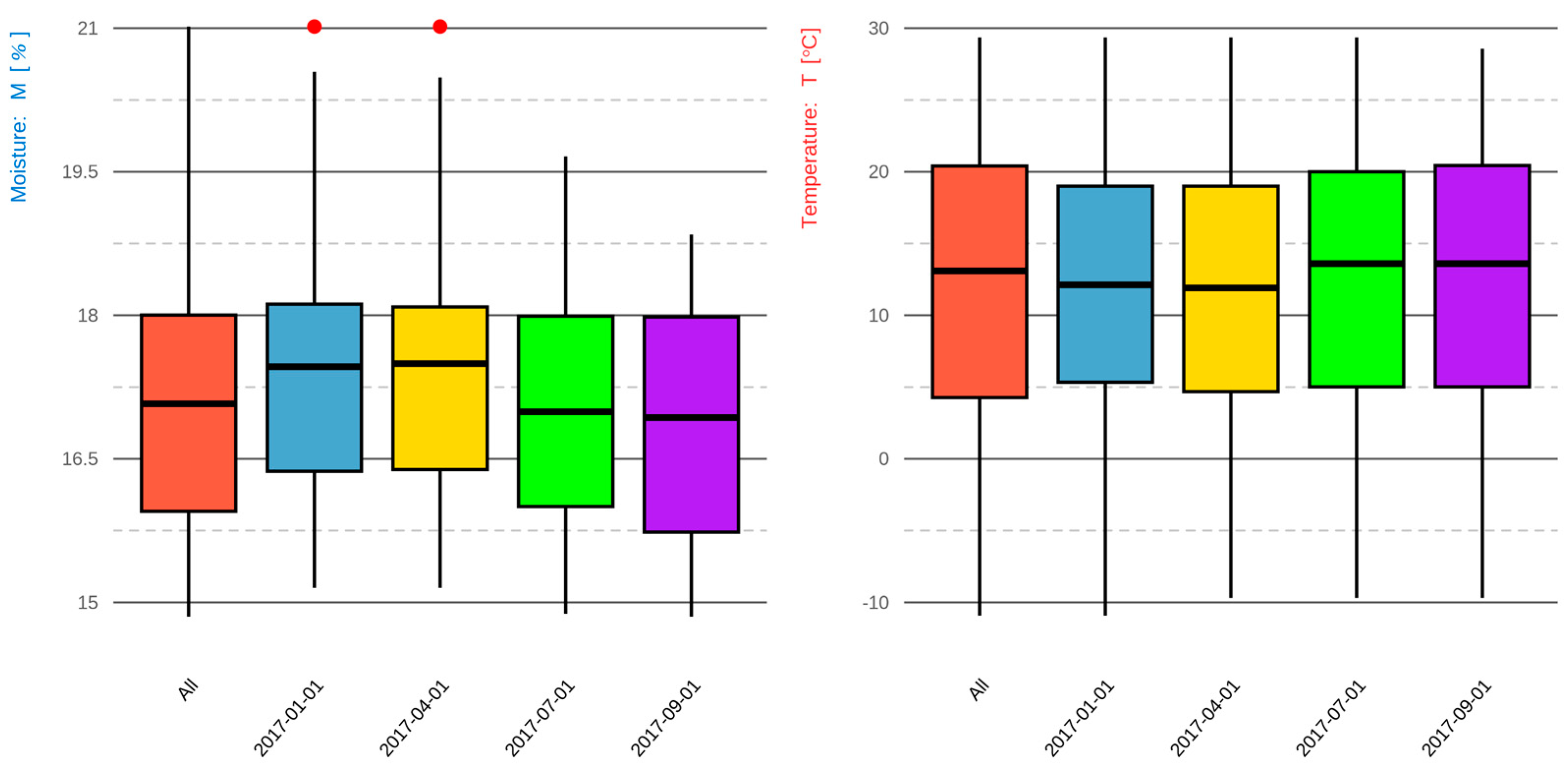


| All | 1 January 2017 | 1 April 2017 | 1 July 2017 | 1 September 2017 | |
|---|---|---|---|---|---|
| Min | 14.227 | 15.151 | 15.151 | 14.882 | 14.851 |
| 1st Q | 15.947 | 16.369 | 16.387 | 16.002 | 15.733 |
| Median | 17.069 | 17.462 | 17.494 | 16.992 | 16.931 |
| Mean | 17.008 | 17.326 | 17.287 | 17.003 | 16.864 |
| 3rd Q | 18.001 | 18.116 | 18.087 | 17.991 | 17.982 |
| Max | 21.017 | 21.017 | 21.017 | 19.66 | 18.845 |
| IQR | 2.054 | 1.747 | 1.699 | 1.989 | 2.249 |
| sd | 1.195 | 1.073 | 1.025 | 1.07 | 1.183 |
| All | 1 July 2017 | 1 April 2017 | 1 July 2017 | 1 September 2017 | |
|---|---|---|---|---|---|
| Min | −12.746 | −12.746 | −9.692 | −9.692 | −9.692 |
| 1st Q | 4.271 | 5.306 | 4.685 | 5.019 | 5.019 |
| Median | 13.068 | 12.121 | 11.91 | 13.599 | 13.599 |
| Mean | 12.302 | 11.781 | 11.745 | 12.561 | 12.773 |
| 3rd Q | 20.392 | 18.994 | 18.994 | 20.003 | 20.437 |
| Max | 29.357 | 29.357 | 29.357 | 29.357 | 28.577 |
| IQR | 16.121 | 13.688 | 14.309 | 14.984 | 15.419 |
| sd | 9.307 | 8.619 | 8.42 | 8.722 | 8.958 |
| RMSE | MAE | NSE | PI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lag | L | Q | C | L | Q | C | L | Q | C | L | Q | C |
| 0 | 0.847 | 0.786 | 0.774 | 0.640 | 0.601 | 0.564 | 0.499 | 0.568 | 0.582 | 0.565 | 0.632 | 0.648 |
| 1 | 0.835 | 0.772 | 0.765 | 0.634 | 0.59 | 0.558 | 0.513 | 0.583 | 0.591 | 0.579 | 0.647 | 0.657 |
| 2 | 0.823 | 0.759 | 0.754 | 0.625 | 0.583 | 0.548 | 0.527 | 0.597 | 0.603 | 0.592 | 0.660 | 0.669 |
| 3 | 0.812 | 0.745 | 0.742 | 0.617 | 0.573 | 0.542 | 0.539 | 0.613 | 0.615 | 0.604 | 0.675 | 0.680 |
| 4 | 0.806 | 0.739 | 0.737 | 0.614 | 0.569 | 0.541 | 0.547 | 0.619 | 0.621 | 0.612 | 0.681 | 0.685 |
| 5 | 0.803 | 0.733 | 0.736 | 0.611 | 0.562 | 0.542 | 0.550 | 0.625 | 0.621 | 0.615 | 0.686 | 0.685 |
| 6 | 0.793 | 0.728 | 0.736 | 0.604 | 0.559 | 0.542 | 0.561 | 0.630 | 0.621 | 0.626 | 0.691 | 0.685 |
| 7 | 0.791 | 0.731 | 0.736 | 0.603 | 0.561 | 0.542 | 0.563 | 0.627 | 0.621 | 0.628 | 0.689 | 0.685 |
| 8 | 0.790 | 0.731 | 0.736 | 0.603 | 0.561 | 0.542 | 0.565 | 0.627 | 0.621 | 0.629 | 0.689 | 0.685 |
| 9 | 0.791 | 0.731 | 0.736 | 0.603 | 0.561 | 0.542 | 0.563 | 0.627 | 0.621 | 0.628 | 0.689 | 0.685 |
| 10 | 0.791 | 0.731 | 0.739 | 0.603 | 0.561 | 0.545 | 0.563 | 0.627 | 0.619 | 0.628 | 0.689 | 0.683 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lexa, M.; Fojtík, R.; Dubovský, V.; Sedlecký, M.; Zeidler, A.; Sikora, A. Influence of the External Environment on the Moisture Spectrum of Norway Spruce (Picea abies (L.) KARST.). Forests 2023, 14, 1342. https://doi.org/10.3390/f14071342
Lexa M, Fojtík R, Dubovský V, Sedlecký M, Zeidler A, Sikora A. Influence of the External Environment on the Moisture Spectrum of Norway Spruce (Picea abies (L.) KARST.). Forests. 2023; 14(7):1342. https://doi.org/10.3390/f14071342
Chicago/Turabian StyleLexa, Martin, Roman Fojtík, Viktor Dubovský, Miroslav Sedlecký, Aleš Zeidler, and Adam Sikora. 2023. "Influence of the External Environment on the Moisture Spectrum of Norway Spruce (Picea abies (L.) KARST.)" Forests 14, no. 7: 1342. https://doi.org/10.3390/f14071342
APA StyleLexa, M., Fojtík, R., Dubovský, V., Sedlecký, M., Zeidler, A., & Sikora, A. (2023). Influence of the External Environment on the Moisture Spectrum of Norway Spruce (Picea abies (L.) KARST.). Forests, 14(7), 1342. https://doi.org/10.3390/f14071342





