Analysis of the Operating Parameters of Wood Transport Vehicles from the Point of View of Operational Reliability
Abstract
1. Introduction
2. Materials and Methods
- Device passport processing (for each examined vehicle, a device passport with operating data for the monitored period was created)
- Using mathematical statistics for the definition of mathematical characteristics
- Creation of a histogram and a curve of cumulative relative frequency of time between failures or fault-free indicator
- Defining the disturbance intensity λ (t)
- Defining the mean time to failure TS (h)
- Defining other indicators of operation depending on monitored kilometers, numbers of replaced parts, and economic indicators (costs)
3. Results and Discussion
3.1. Failure Instensity λ(t)
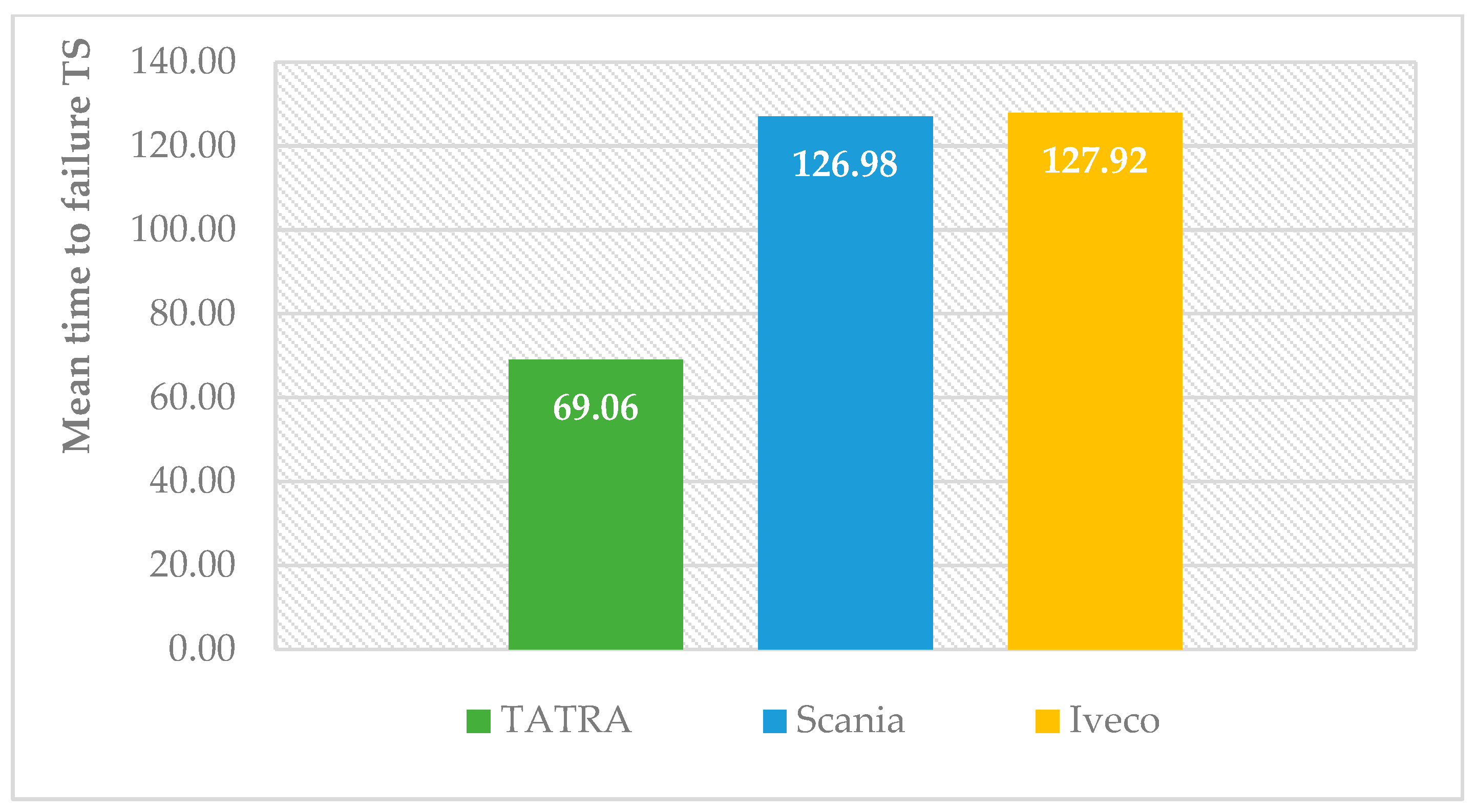
3.2. Mean Time to Failure TS (h)
- a is the size parameter of the Weibull distribution,
- b is the shape parameter of the Weibull distribution,
- is the gamma function (value determined in a table).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ormon, S.W.; Cassady, C.R.; Greenwood, A.G. Reliability Prediction Models to Support Conceptual Design. IEEE Trans. Reliab. 2002, 51, 151–157. [Google Scholar] [CrossRef]
- Manshin, Y.; Manshina, E. Problems of Parts Reliability in the Design of Mechanical System. Her. Bauman Mosc. State Tech. Univ. Ser. Mech. Eng. 2019, 5, 56–73. [Google Scholar] [CrossRef]
- Moubray, J. Reliability-Centetred Maintenance; Butterworth-Heinemann Oxford: Oxford, UK, 1997. [Google Scholar]
- Kováč, J. Environmental analysis of working aspects in the harvester technologies. In Kolokvium ku Grantovej Úlohe č. 1/3534/06; Technická univerzita vo Zvolene: Zvolen, Slovakia, 2006; pp. 28–36. ISBN 80-228-1692-2. [Google Scholar]
- Kováčová, K. Research of forest machines. In Problemy Inżynierii Rolniczej i Leśnej. Problems of Argo and Forestry Engineering, XIX Międzynarodowa Konferencja Naukowa Studentów, Warszawa, 26 Maja 2010r; Szkoła Glówna Gospodarstwa Wiejskiego w Warszawie: Warszawa, Poland, 2010; pp. 139–145. ISBN 978-83-928072-8-5. [Google Scholar]
- Činnosti v Lese Dostupné na Internete. Available online: http://www.forestportal.sk/les-pre-verejnost/o-lesoch-pre-verejnost/Stranky/cinnosti-v-lese.aspx (accessed on 3 March 2021).
- Mikleš, M.; Kučera, M.; Mikleš, J. Cestné Motorové Vozidlá; Technická univerzita vo Zvolene: Zvolen, Slovakia, 2007; 244p, ISBN 978-80-228-1716-5. [Google Scholar]
- Müller, M. Maintenance success control (key figures and controlling in maintenance). In Eksploatacja i Niezawodność—Maintenance and Reliability; No. 4/2007; Polish Maintenance Society: Warsaw, Poland, 2007; ISSN 1507-2711. [Google Scholar]
- Migdalski, J.; Bartoszewicz, J.; Bobrowski, D.; Ciechanowicz, K.; Dwilinski, L.; Jazwinski, J.; Kalinowska, H.; Kilinski, A. Probabilistic Methods in Reliability. In Reliability Handbook: Mathematical Basics; Migdalski, J., Ed.; Wema: Warsaw, Poland, 1982; p. 68. [Google Scholar]
- Zurek, J.; Ziółkowski, J.; Borucka, A. A method for Determination of Combat Vehicles Availability by Means of Statistic and Econometric Analysis. In Proceedings of the 27th European Safety and Reliability Conference, Portoroz, Slovenia, 18–22 June 2017; pp. 2925–2933. [Google Scholar]
- Karpínski, J.; Firkowicz, S. Preventive Maintenance Policies of Technical Objects; National Scientific Publishers: Warsaw, Poland, 1981; p. 85. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A. Statistical Methods for Reliability Data; Wiley-Interscience: Hoboken, NJ, USA, 1998; Volume 314. [Google Scholar]
- Neruda, J.; Simanov, V.; Klvač, R.; Skoupý, A.; Kadlec, J.; Zemánek, T.; Nevrkla, P. Technika a Technologie v Lesnictví—Díl První; Mendelova Univerzita v Brně, 364s: Brno, Czech Republic, 2013; ISBN 978-80-7375-839-4. [Google Scholar]
- Dal’skii, A.M. Tekhnologicheskoe Obespechenie Nadezhnosti Vysokotochnykh Detalei Mashin; Mashinostroenie: Moskva, Russia, 1975. [Google Scholar]
- Samoilenko, D.; Marchenko, A.; Cho, H.M. Improvement of Torque and Power Characteristics of V-Type Diesel Engine Applying New Design of Variable Geometry Turbocharger (VGT). J. Mech. Sci. Technol. 2017, 31, 5021–5027. [Google Scholar] [CrossRef]
- Mikleš, M.; Marko, J. Teória a Stavba Lesných Strojov I; ES TU vo Zvolene: Zvolen, Slovakia, 1992; 243p. [Google Scholar]
- Pačaiová, H. Riadenie Údržby (Vývoj, Stratégie, Postupy a Metódy v Rámci Integrovaných Systémov Manažérstva); TU v Košiciach, Katedra Bezpečnosti a Kvality Produkcie, Strojnícka Fakulta: Košice, Slovakia, 2006; 127p, ISBN 978-80-8073-751-1. [Google Scholar]
- Väätäinen, K.; Sikanen, L.; Asikainen, A. Feasibility of Excavator-Based Harvester in Thinnings of Peatland Forests. Int. J. For. Eng. 2004, 15, 103–111. [Google Scholar] [CrossRef]
- Shukhanov, S.N.; Skutelnik, V.V.; Malomyzhev, O.L. Technique of Carrying Out Heat Tests of Units of Transmission of the Autotractor Machinery of Agro-Industrial Complex. Int. Tech. Econ. J. 2019, 3, 77–83. [Google Scholar] [CrossRef]
- Pačaiova, H.; Izarikova, G. Base Principles and Practices for Implementation of Total Productive Maintenance in Automotive Industry. Qual. Innov. Prosper. 2019, 23, 45–59. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Jarvis, J.J.; Sherali, H.D. Linear Programming and Network Flows, 4th ed.; John Wiley & Sons Inc.: New York, NY, USA, 2010; p. 748. [Google Scholar]
- Kececioglu, D.B. Reliability Engineering Handbook; DEStech Publications: Lancaster, PA, USA, 2002; Volume 1, p. 62. [Google Scholar]
- Macha, E.; Niesłony, A. Reliability of Mechatronic Systems; Academic Handbook; Opole University of Technology Publishing House: Opole, Poland, 2010; pp. 27–45. [Google Scholar]
- Rausand, M.; Høyland, A. System Reliability Theory, Models, Statistical Methods and Applications, 2nd ed.; John Wiley & Sons Inc.: New Jersey, NJ, USA, 2004; p. 148. [Google Scholar]
- Szkutnik-Rogoz, J.; Ziółkowski, J. Determine Transportation Costs with Using Octave 3.4.3. In Research Approach in Logistics Processes and Transport Systems; Warsaw University of Technology Publishing House: Warsaw, Poland, 2016; pp. 531–542. [Google Scholar]
- Woropay, M.; Landowski, B.; Zurek, J. Operational Availability of the Executive Subsystem in the Transport System within Serial Changing Maintenance Stages. Mach. Exploit. Issues 2004, 39, 87–100. [Google Scholar]
- Birolini, A. Reliability Engineering Theory and Practice, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1999; p. 298. [Google Scholar]
- Rodger, J.A.; George, J.A. Triple bottom line accounting for optimizing natural gas sustainability: A statistical linear programming fuzzy ILOWA optimized sustainment model approach to reducing supply chain global cybersecurity vulnerability through information and communications technology. J. Clean. Prod. 2017, 142, 1931–1949. [Google Scholar] [CrossRef]
- Sankararaman, S.; Mahadevan, S. Separating the contributions of variability and parameter uncertainty in probability distributions. Reliab. Eng. Syst. Saf. 2013, 112, 187–199. [Google Scholar] [CrossRef]
- Stone, R.B.; Tumer, I.Y.; Wie, V.M. The Function-Failure Design Method. J. Mech. Des. 2005, 127, 397–407. [Google Scholar] [CrossRef]
- Nassar, M.A.; Alzaatreh, M.; Abo-kasem, O. Alpha power Weibull distribution: Properties and applications. Commun. Stat. Theory Methods 2017, 46, 10236–10252. [Google Scholar] [CrossRef]

| Operator | Production | Model | Evidenc Number of Cars | Monitored Period | The Number of km at the Beginning of the Monitored Period | Number of km at the End of the Monitored Period | Number of Hours of Operation during Observation (h) |
|---|---|---|---|---|---|---|---|
| ŠLP TU vo Zvolene | IVECO TRAKKER | 380T | ZV104BI | 1 July 2017–14 September 2020 | 78,352 | 259,876 | 3784 |
| 380T | ZV364BG | 1 July 2017–14 September 2020 | 69,741 | 271,262 | 4232 | ||
| 380T | ZV261AX | 1 July 2017–14 September 2020 | 74,953 | 269,322 | 4025 | ||
| SCANIA | G490 | ZV481DF | 1 July 2017–14 September 2020 | 72,478 | 274,635 | 4309 | |
| G490 | ZV259DG | 1 July 2017–14 September 2020 | 69,846 | 298,563 | 4852 | ||
| G490 | ZV631CH | 1 July 2017–14 September 2020 | 73,258 | 271,875 | 4136 | ||
| Lesy SR, š.p. | TATRA PHOENIX | T 158 EKO | BB686GA | 1 July 2017–14 September 2020 | 45,819 | 178,516 | 2564 |
| T158 EKO | BB68 | 1 July 2017–14 September 2020 | 48,741 | 169,852 | 2332 | ||
| T158 EKO | BB157HT | 1 July 2017–14 September 2020 | 43,358 | 154,658 | 2175 | ||
| Producer | Number Plate of the Vehicle | The Number of km Driven during the Monitored Period | Total Time of Operation during the Monitored Period | The Number of Replaced Parts during the Monitored Period | Total Costs of Operating the Equipment during the Monitored Period | Number of Repairs |
|---|---|---|---|---|---|---|
| [km] | [h] | [pcs] | [EUR] | |||
| TATRA | BB686GA | 132,697 | 2564 | 232 | 55,013.10 | 44 |
| BB684GA | 121,111 | 2332 | 191 | 44,099.90 | 41 | |
| BB157HT | 111,300 | 2175 | 167 | 35,020.50 | 33 | |
| SCANIA | ZV481DF | 202,157 | 4309 | 161 | 42,249.59 | 34 |
| ZV259DG | 228,717 | 4852 | 194 | 46,402.60 | 43 | |
| ZV631CH | 198,617 | 4136 | 231 | 54,692.91 | 44 | |
| IVECO | ZV104BI | 181,524 | 3784 | 161 | 33,846.61 | 29 |
| ZV364BG | 201,521 | 4232 | 190 | 38,596.93 | 36 | |
| ZV261AX | 194,369 | 4025 | 213 | 50,281.93 | 44 |
| Producer | The Average Number of Kilometers Driven during the Monitored Period | Average Time of Operation during the Monitored Period | Average Number of Replaced Parts during the Monitored Period | Average Costs of Operating the Equipment during the Monitored Period | Average Number of Repairs |
|---|---|---|---|---|---|
| [km] | [h] | [pcs] | [EUR] | ||
| TATRA | 121,702.67 | 2357.00 | 196.67 | 44,711.20 | 39.33 |
| SCANIA | 209,830.33 | 4432.11 | 195.33 | 47,781.70 | 40.33 |
| IVECO | 192,471.33 | 4013.67 | 188.00 | 40,908.50 | 36.33 |
| Producer | Number Plate of the Vehicle | The Number of Kilometers Traveled per 1 h of Operation | Maintenance Costs for 1 h of Operation | Number of Kilometers Driven for 1 Repair | Number of Driving Hours per Repair | Maintenance Costs per 1 km of Travel |
|---|---|---|---|---|---|---|
| [km] | [EUR] | [km] | [h] | [EUR] | ||
| TATRA | BB686GA | 51.75 | 21.46 | 3015.84 | 58.27 | 0.41 |
| BB684GA | 51.93 | 18.91 | 2953.93 | 56.88 | 0.36 | |
| BB157HT | 51.17 | 16.10 | 3372.73 | 65.91 | 0.31 | |
| SCANIA | ZV481DF | 46.92 | 9.80 | 5945.79 | 126.74 | 0.21 |
| ZV259DG | 47.14 | 9.56 | 5319.00 | 112.84 | 0.20 | |
| ZV631CH | 48.02 | 13.22 | 4514.02 | 94.00 | 0.28 | |
| IVECO | ZV104BI | 47.97 | 8.94 | 6259.45 | 130.48 | 0.19 |
| ZV364BG | 47.62 | 9.12 | 5597.81 | 117.56 | 0.19 | |
| ZV261AX | 48.29 | 12.49 | 4417.48 | 91.48 | 0.26 |
| Producer | Average Number of Kilometers Driven per 1 h of Operation | Average Repair and Maintenance Costs for 1 h of Operation | Average Number of Kilometers Driven for 1 Repair and Maintenance | Average Number of Driving Hours per Repair and Maintenance | Average Cost of Repairs and Maintenance per 1 km of Driving |
|---|---|---|---|---|---|
| [km] | [EUR] | [km] | [h] | [EUR] | |
| TATRA | 51.63 | 18.97 | 1031.38 | 19.97 | 0.37 |
| SCANIA | 47.34 | 10.78 | 1778.22 | 36.63 | 0.23 |
| IVECO | 47.95 | 10.19 | 1631.11 | 36.82 | 0.21 |
| Producer | a (Parameter of Size) | b (Parameter Shape) | c (Parameter Position) | n (Number of Measurements) |
|---|---|---|---|---|
| TATRA | 69.0616 | 2.3614 | 0 | 115 |
| SCANIA | 126.975 | 2.3908 | 0 | 118 |
| IVECO | 127.9213 | 2.2061 | 0 | 106 |
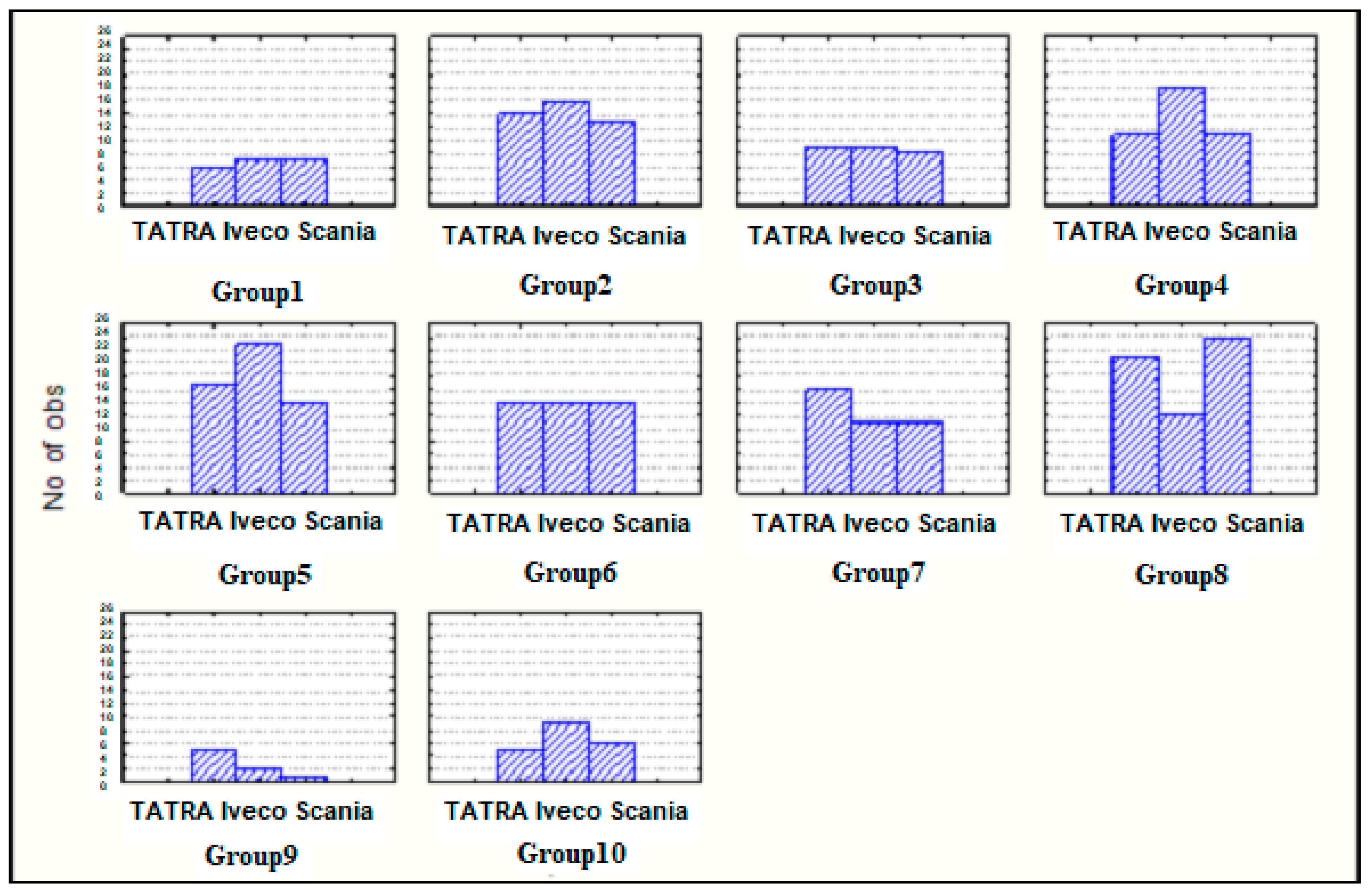
| Construction Group | Producer | Total | ||
|---|---|---|---|---|
| TATRA | SCANIA | IVECO | ||
| Cabin and sensors | 6.78 | 6.95 | 6.26 | 20 |
| Sensors | 14.58 | 14.95 | 13.47 | 43 |
| Engine | 8.82 | 9.04 | 8.14 | 26 |
| Engine and its cooling and lubrication | 13.56 | 13.91 | 12.53 | 40 |
| Gearboxes and gear mechanisms | 18.31 | 18.78 | 16.91 | 54 |
| Chassis | 14.24 | 14.60 | 13.16 | 42 |
| Hydraulic system of the machine | 12.89 | 13.21 | 11.90 | 38 |
| Hydraulic crane with a log grab | 19.33 | 19.82 | 17.85 | 57 |
| Trailer/semi-trailer | 2.71 | 2.78 | 2.51 | 8 |
| Crossbars | 6.78 | 6.95 | 6.26 | 20 |
| All construction groups altogether (10) | 118 | 121 | 109 | 348 |
| Construction Group | Producer | Total | ||
|---|---|---|---|---|
| TATRA | SCANIA | IVECO | ||
| Cabin and sensors | −0.78 | 0.05 | 0.74 | 0 |
| Sensors | −0.58 | 1.05 | −0.47 | 0 |
| Engine | 0.18 | −0.04 | −0.14 | 0 |
| Engine and its cooling and lubrication | −2.56 | 4.09 | −1.53 | 0 |
| Gearboxes and gear mechanisms | −1.31 | 4.22 | −2.91 | 0 |
| Chassis | −0.24 | −0.60 | 0.84 | 0 |
| Hydraulic system of the machine | 3.11 | −2.21 | −0.90 | 0 |
| Hydraulic crane with a log grab | 1.67 | −7.82 | 6.15 | 0 |
| Trailer/semi-trailer | 2.29 | −0.78 | −1.51 | 0 |
| Crossbars | −1.78 | 2.05 | −0.26 | 0 |
| All construction groups altogether (10) | 0 | 0 | 0 | 0 |
| Chi-Square | df | p | |
|---|---|---|---|
| Pearson Chi-square | 14.47 | df = 18 | 0.698 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kováč, J.; Gregor, I.; Melicherčík, J.; Kuvik, T. Analysis of the Operating Parameters of Wood Transport Vehicles from the Point of View of Operational Reliability. Forests 2023, 14, 1511. https://doi.org/10.3390/f14071511
Kováč J, Gregor I, Melicherčík J, Kuvik T. Analysis of the Operating Parameters of Wood Transport Vehicles from the Point of View of Operational Reliability. Forests. 2023; 14(7):1511. https://doi.org/10.3390/f14071511
Chicago/Turabian StyleKováč, Ján, Igor Gregor, Ján Melicherčík, and Tomáš Kuvik. 2023. "Analysis of the Operating Parameters of Wood Transport Vehicles from the Point of View of Operational Reliability" Forests 14, no. 7: 1511. https://doi.org/10.3390/f14071511
APA StyleKováč, J., Gregor, I., Melicherčík, J., & Kuvik, T. (2023). Analysis of the Operating Parameters of Wood Transport Vehicles from the Point of View of Operational Reliability. Forests, 14(7), 1511. https://doi.org/10.3390/f14071511






