Sampling Estimation and Optimization of Typical Forest Biomass Based on Sequential Gaussian Conditional Simulation
Abstract
:1. Introduction
2. Data and Methods
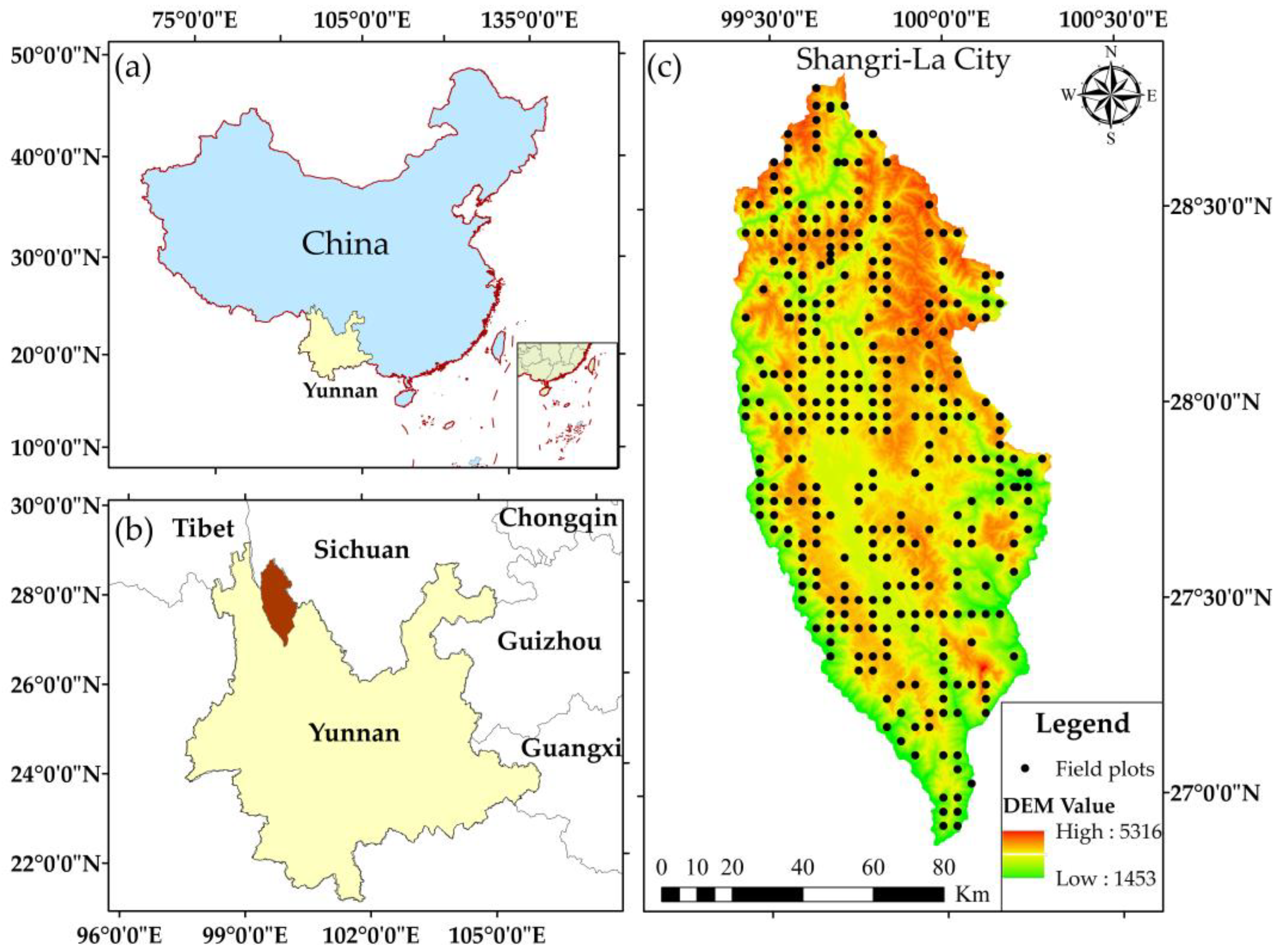
2.1. Study Area
2.2. Data and Processing
2.2.1. Data
- Field plots data
- Other data
2.2.2. Data Processing
2.3. Methods
2.3.1. Methods for Estimating Forest Biomass
- Variogram
- Sequential Gaussian Conditional Simulation (SGCS)
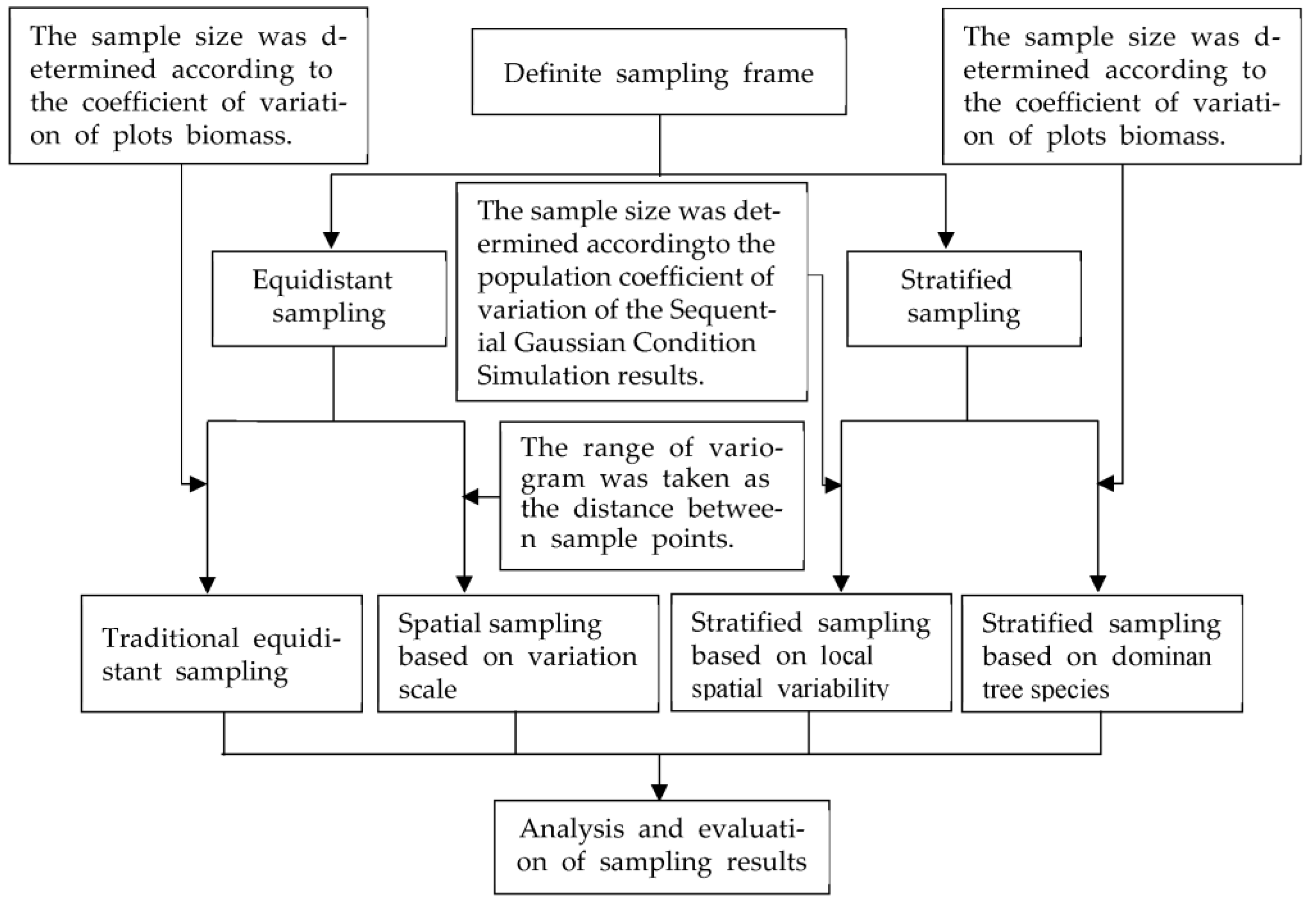
2.3.2. Traditional Sampling Methods
- Equidistant sampling (ES)
- Stratified sampling (SS)
2.3.3. Spatial Sampling Methods and Comparisons with Traditional Approaches
- Spatial sampling based on variation scale
- SS based on local spatial variability
2.3.4. Accuracy Evaluation
- Forest biomass simulation accuracy
- Sampling accuracy
3. Results
3.1. Sequential Gaussian Condition Simulation of Forest Biomass
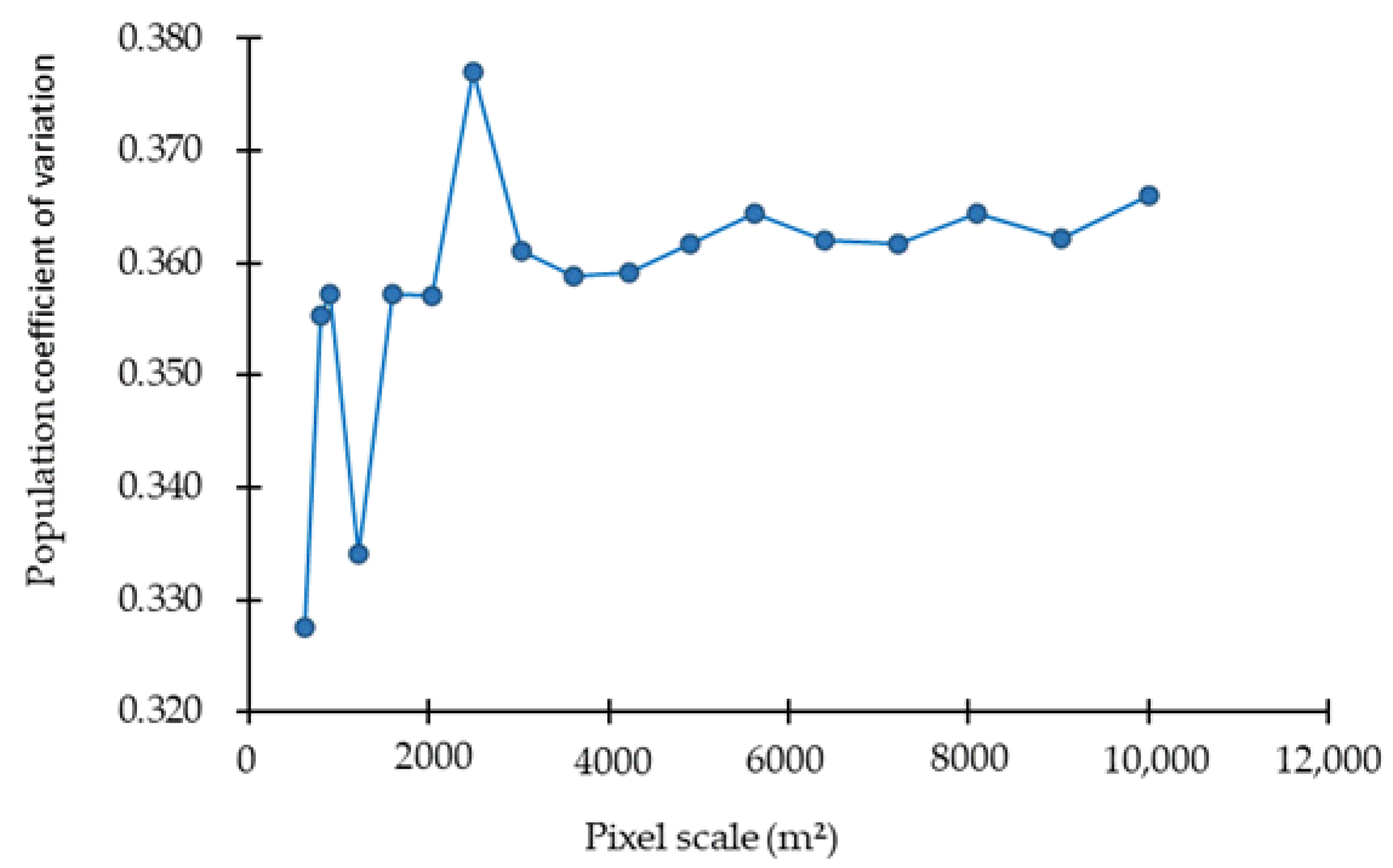
3.1.1. Variogram Analysis of Forest Biomass
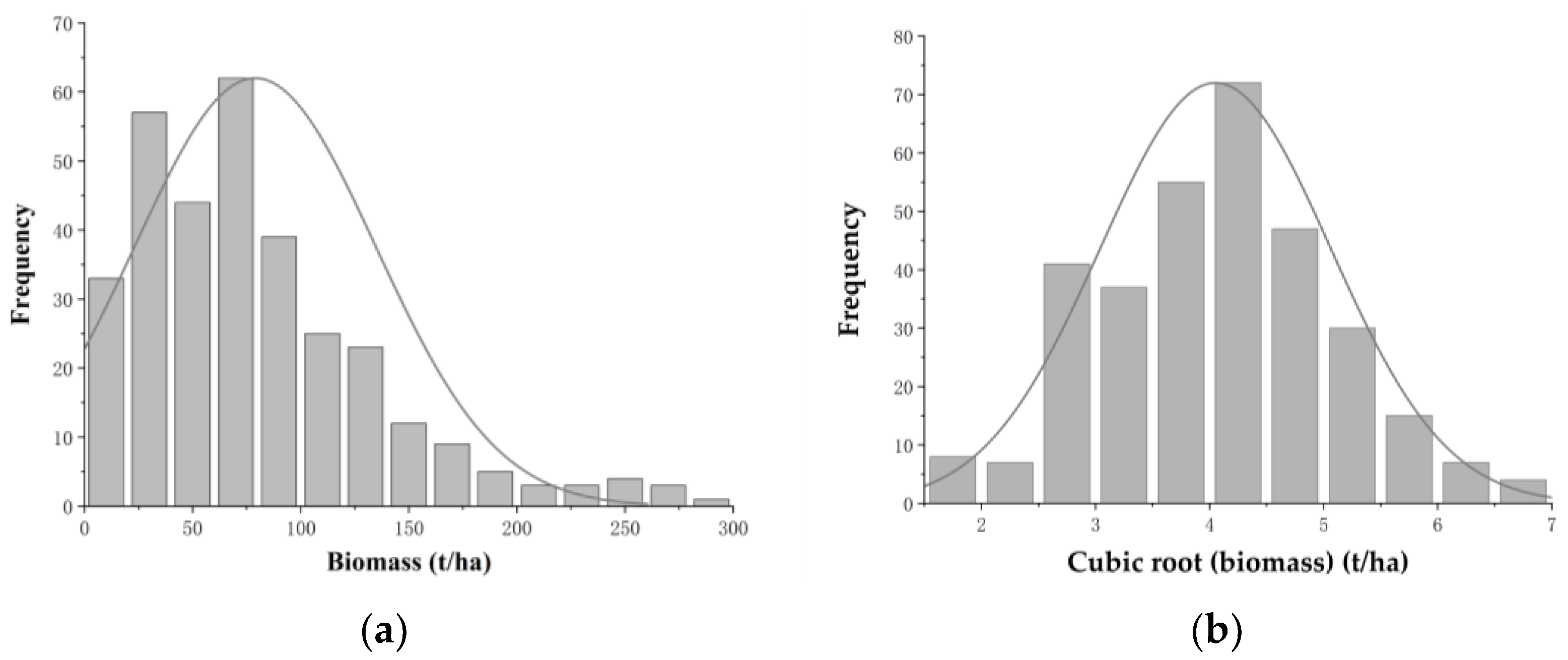
- Normal distribution test of data
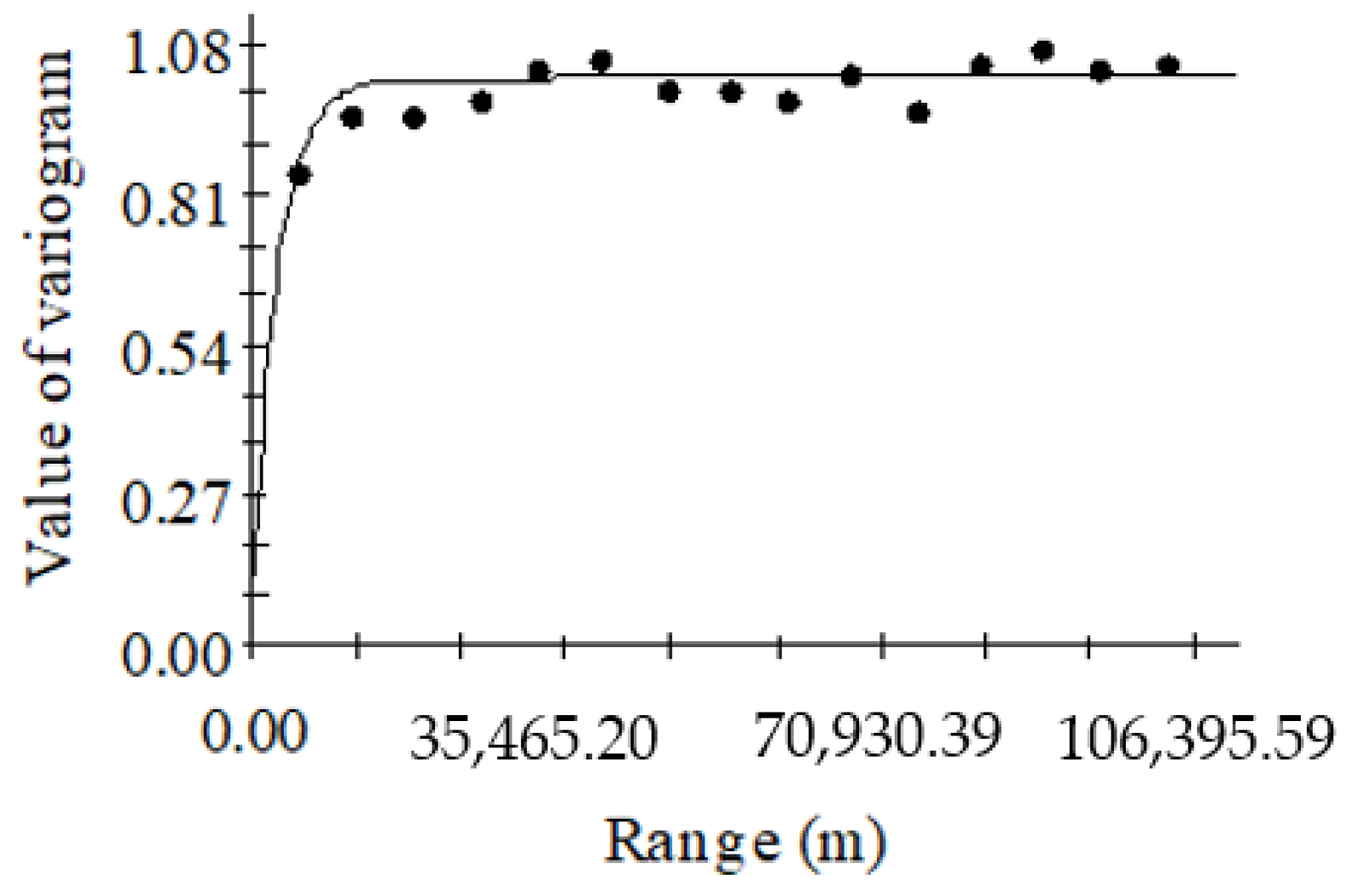
- Variogram analysis of forest biomass
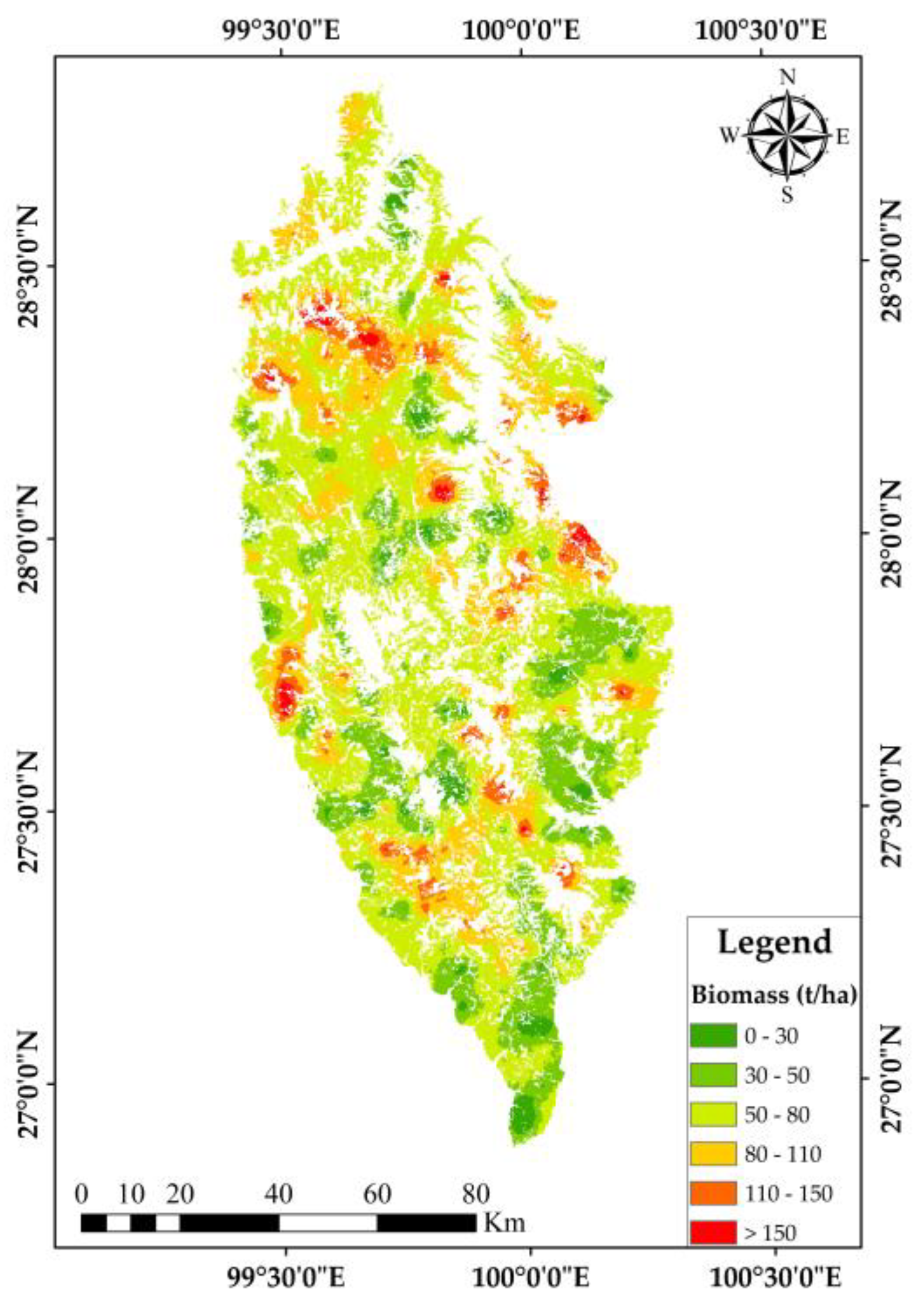
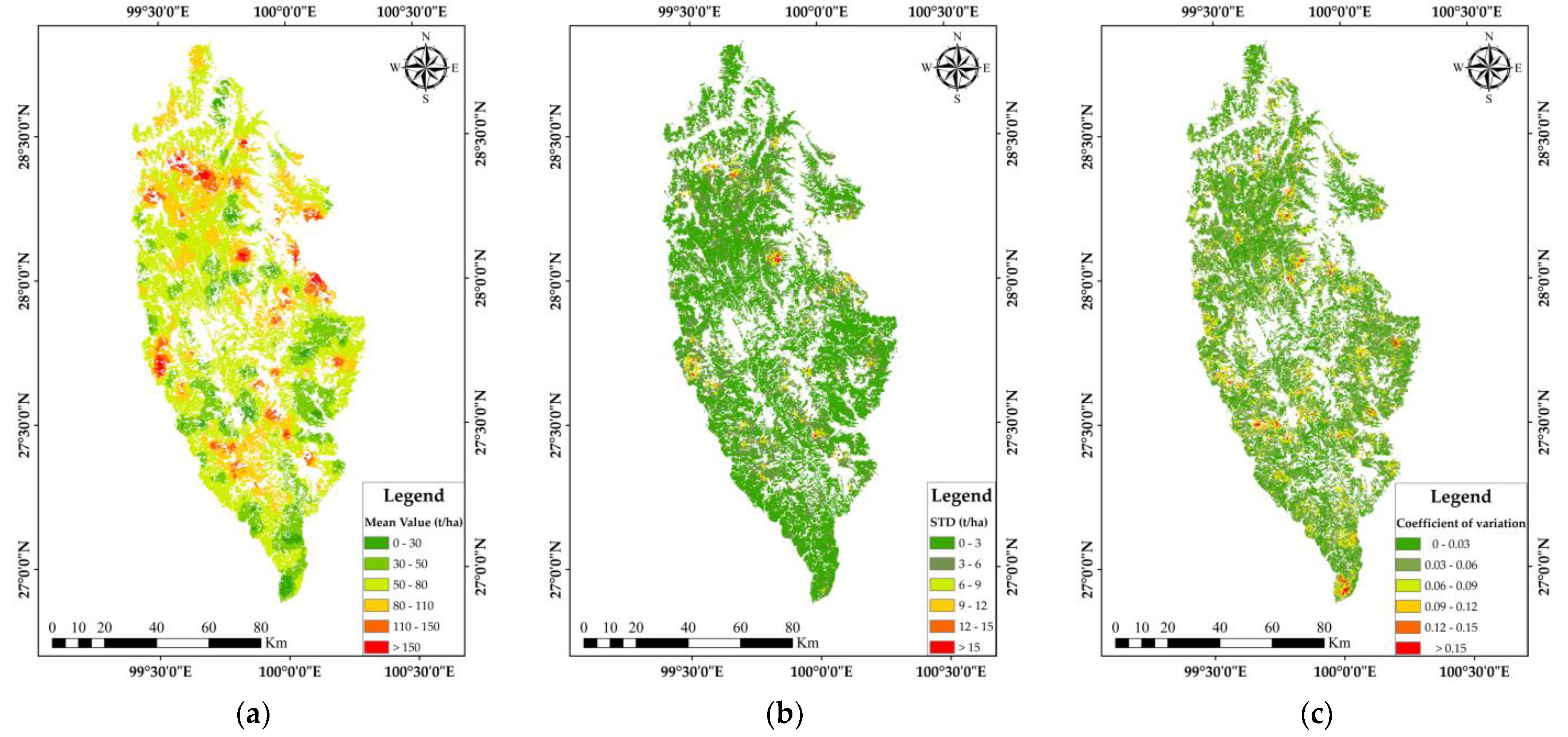
3.1.2. Sequential Gaussian Condition Simulation of Forest Biomass
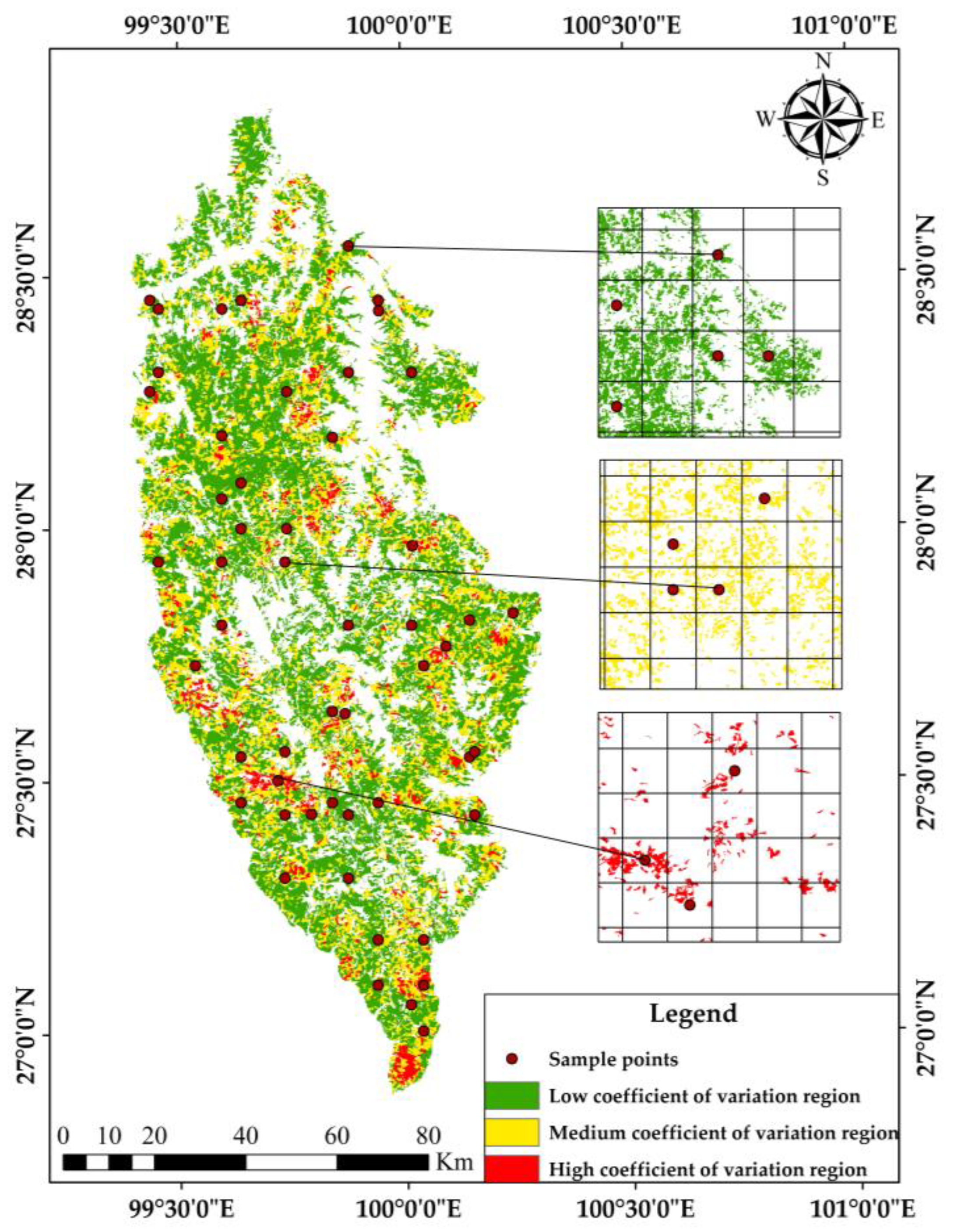
3.2. Analysis of Local Spatial Variability for Four Typical Forests Biomass
3.3. Sampling of Forest Biomass
3.3.1. Equidistant Sampling
3.3.2. Stratified Sampling
- SS based on local spatial variability
- SS based on dominant tree species
3.4. Accuracy Analysis of Sampling Results
3.4.1. Analysis of Variance for Stratified Variables
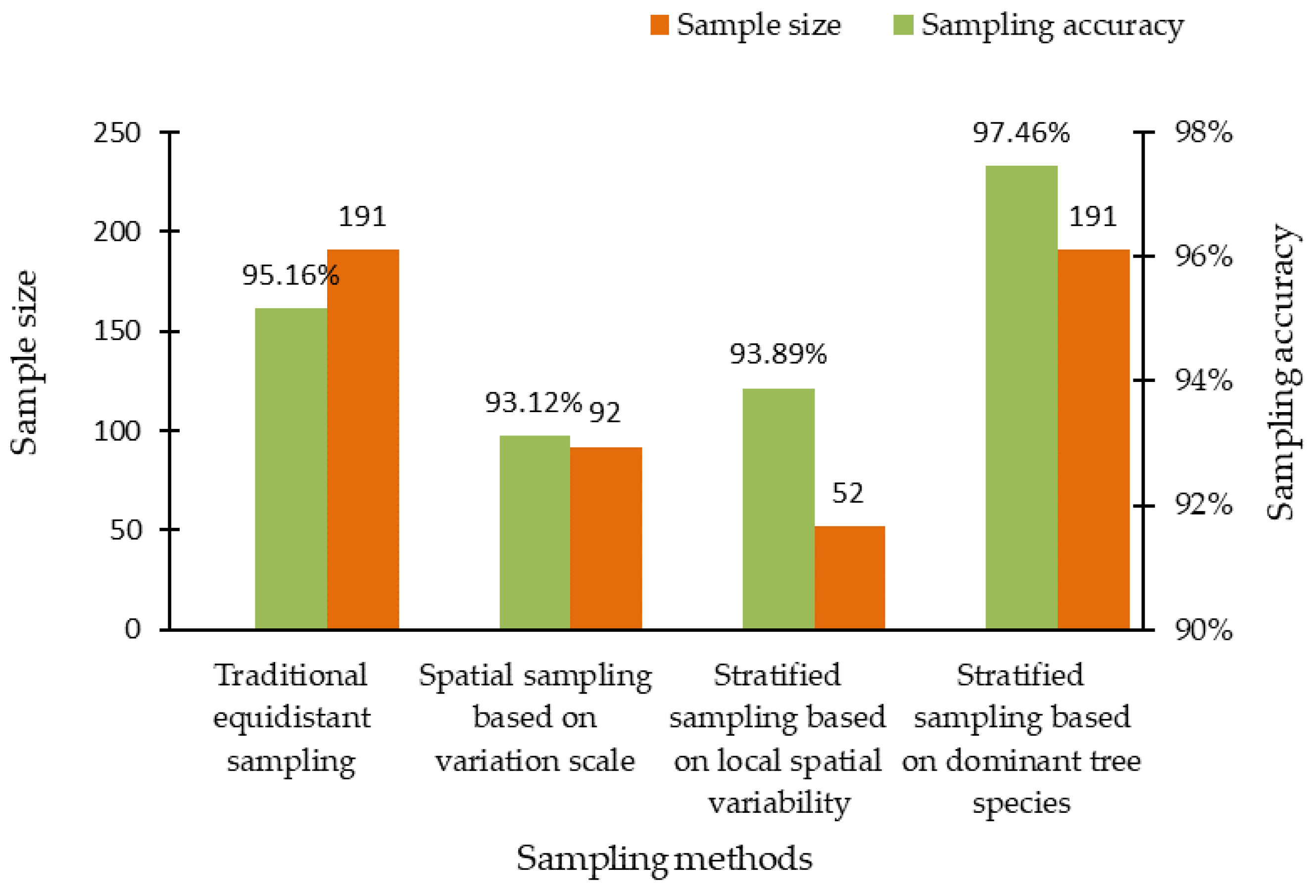
3.4.2. Sampling Accuracy Comparison
4. Discussion
4.1. Application of Geostatistics in Spatial Sampling
4.2. Spatial Autocorrelation Analysis of Survey Samples
4.3. Sensitivity Analysis of Sampling Intensity for Different Sampling Methods
4.4. Determination of Stratified Variables in Stratified Sampling
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herold, M.; Carter, S.; Avitabile, V.; Espejo, A.B.; Jonckheere, I.; Lucas, R.; McRoberts, R.E.; Næsset, E.; Nightingale, J.; Petersen, R.; et al. The Role and Need for Space-Based Forest Biomass-Related Measurements in Environmental Management and Policy. Surv. Geophys. 2019, 40, 757–778. [Google Scholar]
- Lisboa, S.N.; Guedes, B.S.; Ribeiro, N.; Sitoe, A. Biomass Allometric Equation and Expansion Factor for a Mountain Moist Evergreen Forest in Mozambique. Carbon Balance Manag. 2018, 13, 23. [Google Scholar] [CrossRef] [PubMed]
- Parresol, B.R. Assessing Tree and Stand Biomass: A Review with Examples and Critica1 Comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar]
- Li, D.; Wang, C.; Hu, Y.; Liu, S. General Review on Remote Sensing-Based Biomass Estimation. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 631–635. (In Chinese) [Google Scholar]
- Scott, C.T. Sampling Methods for Estimating Change in Forest Resources. Ecol. Appl. 1998, 8, 228–233. [Google Scholar] [CrossRef]
- Rafael, M.N.C.; Eduardo, G.F.; Jorge, G.G.; Carlos, J.C.R.; Rocío, H.C. Impact of Plot Size and Model Selection on Forest Biomass Estimation Using Airborne LiDAR: A Case Study of Pine Plantations in Southern Spain. J. For. Sci. 2017, 63, 88–97. [Google Scholar]
- Nelson, R.; Gobakken, T.; Næsset, E.; Gregoire, T.G.; Ståhl, G.; Holm, S.; Flewelling, J. Lidar Sampling: Using an Airborne Profiler to Estimate Forest Biomass in Hedmark County, Norway. Remote Sens. Environ. 2012, 123, 563–578. [Google Scholar] [CrossRef]
- ÖZÇELİK, R.; Eraslan, T. Two-stage Sampling to Estimate Individual Tree Biomass. Turk. J. Agric. For. 2012, 36, 389–398. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, W.; Sun, G.; Chi, H.; Zhang, Z.; Guo, Z. Slope-adaptive Waveform Metrics of Large Footprint LiDAR for Estimation of Forest Aboveground Biomass. Remote Sens. Environ. 2019, 224, 386–400. [Google Scholar]
- Keller, M.; Palace, M.; Hurtt, G. Biomass Estimation in the Tapajos National Forest, Brazil: Examination of Sampling and Allometric Uncertainties. For. Ecol. Manag. 2001, 154, 371–382. [Google Scholar]
- Song, X.M.; Li, J.L. Sampling Techniques, 2nd ed.; China Forestry Publishing House: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Talvitie, M.; Leino, O.; Holopainen, M. Inventory of Sparse Forest Populations Using Adaptive Cluster Sampling. Silva Fenn. 2005, 40, 101–108. [Google Scholar] [CrossRef]
- Fu, Y.; Lei, Y.; Zeng, W. Uncertainty Assessment in Regional-Scale Above Ground Biomass Estimation of Chinese Fir. Sci. Silvae Sin. 2014, 50, 79–86. (In Chinese) [Google Scholar]
- Yim, J.S.; Kleinn, C.; Kim, S.H.; Jeong, J.H.; Shin, M.Y. A Comparison of Systematic Sampling Designs for Forest Inventory. J. Korean For. Soc. 2009, 98, 133–141. [Google Scholar]
- Stehman, S.V.; Hansen, M.C.; Broich, M.; Potapov, P.V. Adapting a Global Stratified Random Sample for Regional Estimation of Forest Cover Change Derived from Satellite Imagery. Remote Sens. Environ. 2010, 115, 650–658. [Google Scholar] [CrossRef]
- Wang, R.; Yang, Q.; Ou, G.; Xu, H. Forest Biomass Investigation Design Using Stratified Sampling in Simao District. For. Resour. Manag. 2021, 1, 197–202. (In Chinese) [Google Scholar]
- Sullivan, M.J.P.; Lewis, S.L.; Hubau, W.; Qie, L.; Baker, T.R.; Banin, L.F.; Chave, J.; Cuni-Sanchez, A.; Feldpausch, T.R.; Lopez-Gonzalez, G.; et al. Field Methods for Sampling Tree Height for Tropical Forest Biomass Estimation. Methods Ecol. Evol. 2018, 9, 1179–1186. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.M.; Xu, S.C.; Yang, X.M. The Application of Random Sampling Survey Method in the Survey of Non-Productive Consumption of Forest Resources. For. Resour. Manag. 1995, 4, 35–37. (In Chinese) [Google Scholar] [CrossRef]
- Jin, L.W.; Zhao, R.H. A Simple Random Sampling Method for Determining the Optimal Quadrat Size of Dendrolimus Tabulaeformis Pupae. Liaoning For. Sci. Technol. 2001, 2, 42–44. (In Chinese) [Google Scholar]
- Pang, E.; Xu, L.; Zhang, M.; Xu, H. Application of Stratified Sampling of DN Value in Remote Sensing Estimation of Urban Forest Biomass. J. Southwest For. Univ. 2018, 38, 132–138. (In Chinese) [Google Scholar]
- Dillabaugh, K.A.; King, D.J. Riparian Marshland Composition and Biomass Mapping Using Ikonos Imagery. Can. J. Remote Sens. 2008, 34, 143–158. [Google Scholar] [CrossRef]
- Silvio, M.; Federica, L.; Antonio, R.; Gentile, F.F. Cost-effective Spatial Sampling Designs for Field Surveys of Species Distribution. Biodivers. Conserv. 2019, 28, 2891–2908. [Google Scholar]
- Zhang, X.W.; She, G.H.; Wen, X.R.; Lin, G.; Cao, L.; Luo, Y. The Application of Spatial Stratified Sampling in Remote Sensing Monitoring of Forest Cover. J. Nanjing For. Univ. 2012, 36, 81–84. (In Chinese) [Google Scholar]
- Xu, Y.; Li, M.; Hao, S. GIS-Based Sampling Method of Urban Forest Biomass. For. Resour. Manag. 2018, 5, 123–127. (In Chinese) [Google Scholar]
- Gilbert, B.; Lowell, K. Forest Attributes and Spatial Autocorrelation and Interpolation: Effects of Alternative Sampling Schemata in the Boreal Forest. Landsc. Urban Plan 1997, 37, 235–244. [Google Scholar] [CrossRef]
- Matheron, G. Principles of Geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Hock, B.K.; Payn, T.W.; Shirley, J.W. Using a Geographic Information System and Geostaticstics to Estimate Site Index of Pinus Radiata for Kaingaroa Forest. N. Z. J. For. Sci. 1993, 23, 264–277. [Google Scholar]
- Stark, K.E.; Arsenault, A.; Bradfield, G.E. Variation in Soil Seed Bank Species Composition of a Dry Coniferous Forest: Spatial Scale and Sampling Considerations. Plant Ecol. 2008, 197, 173–181. [Google Scholar] [CrossRef]
- Lark, R.M. Optimized Spatial Sampling of Soil for Estimation of The Variogram by Maximum Likelihood. Geoderma 2002, 105, 49–80. [Google Scholar] [CrossRef]
- Dessard, H.; Bar-Hen, A. Experimental Design for Spatial Sampling Applied to the Study of Tropical Forest Regeneration. Can. J. For. Res. 2005, 35, 1149–1155. [Google Scholar] [CrossRef]
- Samra, J.S.; Gill, H.S.; Bhatia, V.K. Spatial Stochastic Modeling of Growth and Forest Resource Evaluation. For. Sci. 1989, 35, 663–676. [Google Scholar]
- Wang, Z.Q. Geostatistics and Its Applications in Ecology; Science Press: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Ping, Y.; Hua, P.; Yan, L.; Lin, K. Spatial Variability of Soil Physical Properties Based on GIS and Geo-Statistical Methods in the Red Beds of the Nanxiong Basin, China. Pol. J. Environ. Stud. 2019, 28, 2961–2972. [Google Scholar]
- Sahu, B.; Ghosh, A.K.; Seema. Deterministic and Geostatistical Models for Predicting Soil Organic Carbon in A 60 Ha Farm on Inceptisol in Varanasi, India. Geoderma Reg. 2021, 26, e00413. [Google Scholar] [CrossRef]
- Shu, Y.J. Study of Optimization Algorithm about Spherical Model of Semi-Variogram in Geostatistics. Master’s Thesis, East China Institute of Technology, Nanchang, China, 2012. (In Chinese). [Google Scholar]
- Matheron, G. Les Variables Régionalisées et Leur Estimation; Masson: Paris, France, 1965. [Google Scholar]
- Matheron, G. The Theory of Regionalized Variables and Its Applications; Ecole de Mines: Paris, France, 1971. [Google Scholar]
- Facchinelli, A.; Sacchi, E.; Mallen, L. Multivariate Statistical and GIS-Based Approach to Identify Heavy Metal Sources in Soils. Environ. Pollut. 2001, 114, 313–324. [Google Scholar] [CrossRef]
- Zhang, S.; Shao, M.; Li, D. Prediction of Soil Moisture Scarcity Using Sequential Gaussian Simulation in an Arid Region of China. Geoderma 2017, 295, 119–128. [Google Scholar] [CrossRef]
- Qu, M.; Li, W.; Zhang, C. Spatial Distribution and Uncertainty Assessment of Potential Ecological Risks of Heavy Metals in Soil Using Sequential Gaussian Simulation. Hum. Ecol. Risk Assess. 2014, 20, 764–778. [Google Scholar] [CrossRef]
- Zhao, Y.; Shi, X.; Yu, D.; Wang, H.; Sun, W. Uncertainty Assessment of Spatial Patterns of Soil Organic Carbon Density Using Sequential Indicator Simulation, A Case Study of Hebei Province, China. Chemosphere 2005, 59, 1527–1535. [Google Scholar] [CrossRef]
- Juang, K.W.; Chen, Y.S.; Lee, D.Y. Using Sequential Indicator Simulation to Assess the Uncertainty of Delineating Heavy Metal Contaminated Soils. Environ. Pollut. 2004, 127, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.H.; Liu, W.C.; Zeng, G.M.; Li, F.; Huang, X.L.; Gu, Y.L.; Shi, L.X.; Shi, Y.H.; Wan, J. An Exploration of Spatial Human Health Risk Assessment of Soil Toxic Metals Under Different Land Uses Using Sequential Indicator Simulation. Ecotoxicol. Environ. Saf. 2016, 129, 199–209. [Google Scholar] [CrossRef] [PubMed]
- State Forestry Administration of China (SFAC). Tree Biomass Models and Related Parameters to Carbon Accounting for Pinus yunnanensis; State Forestry Administration: Beijing, China, 2014. (In Chinese) [Google Scholar]
- State Forestry Administration of China (SFAC). Tree Biomass Models and Related Parameters to Carbon Accounting for Picea asperata; State Forestry Administration: Beijing, China, 2016. (In Chinese) [Google Scholar]
- State Forestry Administration of China (SFAC). Tree Biomass Models and Related Parameters to Carbon Accounting for Abies fabri; State Forestry Administration: Beijing, China, 2016. (In Chinese) [Google Scholar]
- State Forestry Administration of China (SFAC). Tree Biomass Models and Related Parameters to Carbon Accounting for Quercus; State Forestry Administration: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Wang, J.X.; Tang, W.J. Estimation and Analysis of Above-ground Biomass and Carbon Storage of Forest Based on Forest Resource Planning and Design Survey Data: A Case Study of Shangri-La City. J. Green Sci. Technol. 2021, 23, 14–16. (In Chinese) [Google Scholar]
- Feng, Y.M.; Tang, S.Z.; Li, Z.Y. Simulation of spatial distribution pattern of forest types by using sequential indicator simulation. Acta Ecol. Sin. 2004, 24, 946–952. (In Chinese) [Google Scholar]
- Zhao, Y.F.; Sun, Z.Y.; Chen, J. Analysis and Comparison in Arithmetic for Kriging Interpolation and Sequential Gaussian Conditional Simulation. J. Geo-Inf. Sci. 2010, 12, 767–776. (In Chinese) [Google Scholar] [CrossRef]
- Wang, M.; Fan, C.; Gao, B.; Ren, Z.; Li, F. A Spatial Random Forest Interpolation Method with Semi-variogram. Chin. J. Eco-Agric. 2022, 30, 451–457. (In Chinese) [Google Scholar]
- Zhao, Y.; Hua, Q.; Chen, J. Comparison of Kriging Interpolation with Conditional Sequential Gaussian Simulation in Principles and Case Analysis of Their Application in Study on Soil Spatial Variation. Acta Pedol. Sin. 2011, 48, 856–862. (In Chinese) [Google Scholar]
- Lü, X.G.; Wang, D.F.; Jiang, H.F. Reservoir Geological Model and Stochastic Modeling Technique. Pet. Geol. Oilfieid Dev. Daqin 2000, 19, 10–16. (In Chinese) [Google Scholar]
- Kangas, A.; Maltamo, M. Forest Inventory-Methodology and Applications; Springer: New York, NY, USA, 2006. [Google Scholar]
- Yang, G.J.; Yin, J.; Meng, J.; Wang, W.Z. Applied Sampling Techniques, 2nd ed.; China Statistics Press: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Sun, H.H. Application Research of Spatial Stratified Sampling in Forest-Covered Monitoring. Master’s Thesis, Nanjing Forestry University, Nanjing, China, 2013. (In Chinese). [Google Scholar]
- Zhang, M.; Wang, G.; Ge, H.; Xu, L. Estimation of Forest Carbon Distribution for Xianju County Based on Spatial Simulation. Sci. Silvae Sin. 2014, 50, 13–22. (In Chinese) [Google Scholar]
- Shen, G.; Zhang, M. Multi-Scale Regional Forest Carbon Density Estimation Based on Sequential Gaussian Co-Simulation. J. Southwest For. Univ. 2015, 35, 55–62. (In Chinese) [Google Scholar] [CrossRef]
- Akhavan, R.; Amiri, G.H.; Zobeiri, M. Spatial Variability of Forest Growing Stock Using Geostatistics in the Caspian region of Iran. Casp. J. Environ. Sci. 2010, 8, 43–53. [Google Scholar]
- Xu, C.X.; Pu, L.J.; Zhu, M.; Xu, C.Y.; Zhang, M.; Xu, Y. Prediction of Soil Heavy Metals Content Based on Sequential Gaussian Simulation and Evaluation of Its Uncertainties: A Case Study of Soil Hg Content in Yixing. Acta Pedol. Sin. 2018, 55, 999–1006. [Google Scholar]
- Wang, G.; Gertner, G.; Anderson, A.B.; Howard, H. Repeated measurements on permanent plots using local variability sampling for monitoring soil cover. Catena 2008, 73, 75–88. [Google Scholar] [CrossRef]
- Anderson, A.B.; Wang, G.; Gertner, G. Local variability based sampling for mapping a soil erosion cover factor by co-simulation with Landsat TM images. Int. J. Remote Sens. 2006, 27, 2423–2447. [Google Scholar] [CrossRef]
- Xiao, X.; Gertner, G.; Wang, G.; Anderson, A.B. Optimal sampling scheme for estimation landscape mapping of vegetation cover. Landsc. Ecol. 2005, 20, 375–387. [Google Scholar] [CrossRef]
- McBratney, A.B.; Webster, R. The design of optimal sampling schemes for local estimation and mapping of regionalized variables—II: Program and examples. Comput. Geosci. 1981, 7, 335–365. [Google Scholar] [CrossRef]
- McBratney, A.B.; Webster, R.; Burgess, T.M. The design of optimal sampling schemes for local estimation and mapping of regionalized variables—I: Theory and method. Comput. Geosci. 1981, 7, 331–334. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Rogerson, P.A. Statistical Methods for Geographical; Sage Publications: London, UK, 2001. [Google Scholar]
- Zhang, X.W. Spatial Sampling Technology and Its Application in Remote Sensing Monitoring of Forest Cover Area. Master’s Thesis, Nanjing Forestry University, Nanjing, China, 2011. (In Chinese). [Google Scholar]
- Wong, D.W.S.; Lee, J. Statistics Analysis of Geographic Information with ArcView GIS and ArcGIS; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chen, K. Accuracy Assessment Methods Based on Spatial Sampling for Remote Sensing Classification. Master’s Thesis, Shanghai Ocean University, Shanghai, China, 2016. (In Chinese). [Google Scholar]
- Wu, H.; Xu, H.; Tian, X.L.; Zhang, W.F.; Lu, C. Multistage Sampling and Optimization for Forest Volume Inventory Based on Spatial Autocorrelation Analysis. Forests 2023, 14, 250. [Google Scholar] [CrossRef]
- Lewis, J. Stemflow estimation in a redwood forest using model-based stratified random sampling. Environmetrics 2003, 14, 559–571. [Google Scholar] [CrossRef]
- Zhang, C. Forest Carbon Estimation in Three Gorges Region. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2016. (In Chinese). [Google Scholar]
- Wang, G.; Gertner, G.; Anderson, A.B. Sampling and mapping a soil erosion cover factor by integrating stratification, model updating and Cokriging with images. Environ. Manag. 2007, 39, 84–97. [Google Scholar] [CrossRef]

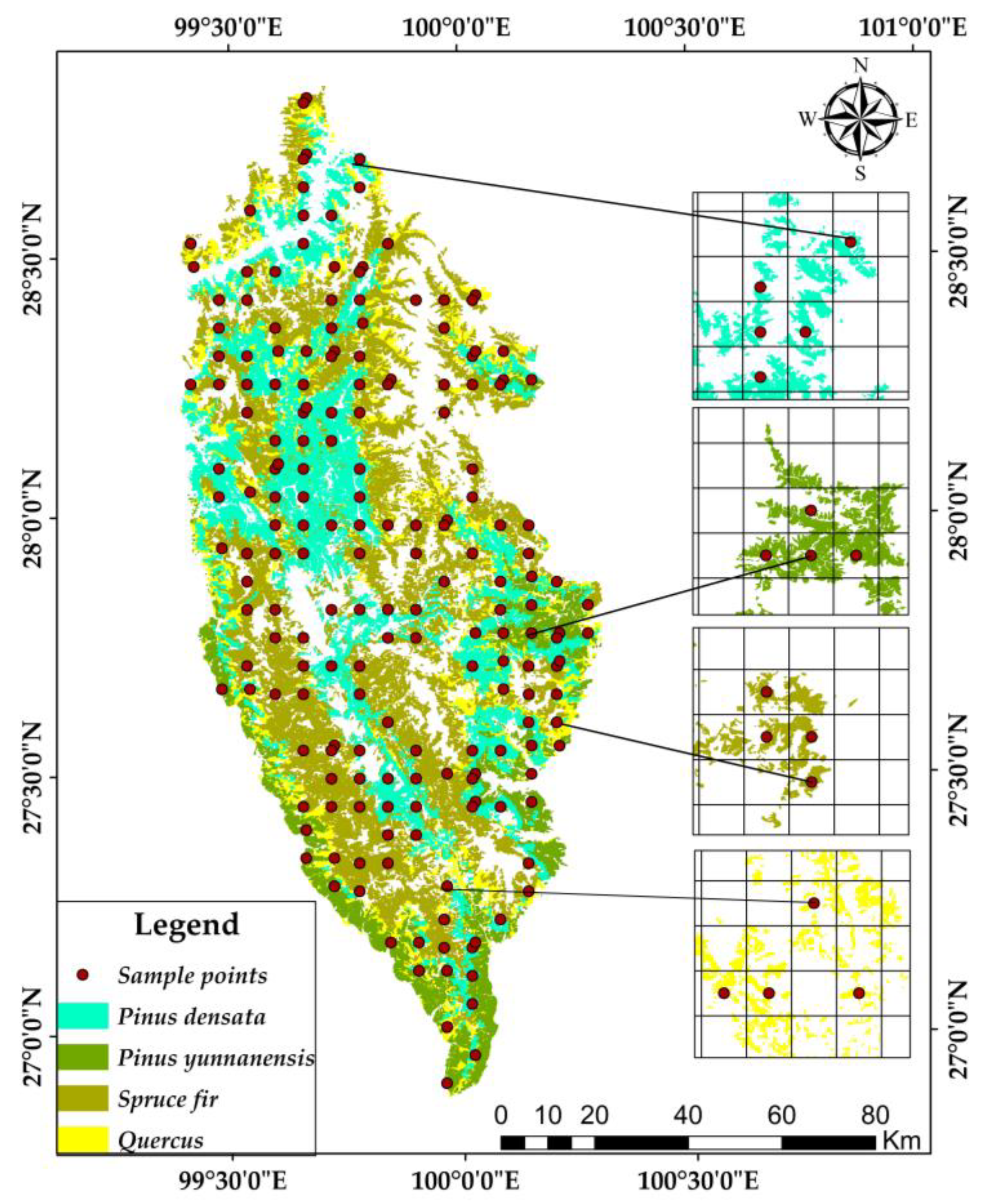
| Tree Species | The Average Diameter at Breast Height (cm) | Biomass Model |
|---|---|---|
| Pinus yunnanensis | D > 5 | |
| Pinus densata | D > 5 | |
| Picea asperata | D ≥ 5 | |
| D < 5 | ||
| Abies fabri | D ≥ 5 | |
| D < 5 | ||
| Quercus | D ≥ 5 | |
| D < 5 |
| Statistical Index | Number | Min (t/ha) | Max (t/ha) | Mean (t/ha) | STD (t/ha) | Coefficient of Variation |
|---|---|---|---|---|---|---|
| Value | 323 | 4.20 | 289.03 | 78.90 | 55.70 | 0.706 |
| Model | Model Parameters | Evaluation Index | ||||
|---|---|---|---|---|---|---|
| C0 | C0 + C | C0/(C0 + C)/% | Range/m | R2 | RSS | |
| Spherical | 0.047 | 1.017 | 4.62 | 7300 | 0.521 | 0.0210 |
| Exponential | 0.119 | 1.020 | 11.67 | 8700 | 0.571 | 0.0190 |
| Gaussian | 0.155 | 1.017 | 15.24 | 6235 | 0.522 | 0.0211 |
| Stratum | Area (ha) | Weight (%) | Number |
|---|---|---|---|
| Low coefficient of variation region | 423,000.48 | 42.64% | 22 |
| Medium coefficient of variation region | 230,680.32 | 43.37% | 23 |
| High coefficient of variation region | 37,921.49 | 13.99% | 7 |
| Stratum | Area (ha) | Proportion (%) | Number | L (m) |
|---|---|---|---|---|
| Pinus yunnanensis | 79,534.26 | 11.50 | 22 | 6013 |
| Pinus densata | 184,796.13 | 26.72 | 51 | 6018 |
| Spruce fir | 300,570.36 | 43.46 | 83 | 6017 |
| Quercus | 126,701.54 | 18.32 | 35 | 6016 |
| Stratified Variables | Group | Mean (t/ha) | STD (t/ha) |
|---|---|---|---|
| Spatial variability | Low coefficient of variation region | 75.06 | 23.44 |
| Medium coefficient of variation region | 61.83 | 21.78 | |
| High coefficient of variation region | 70.44 | 31.58 | |
| Dominant tree species | Pinus yunnanensis | 51.44 | 17.68 |
| Pinus densata | 64.78 | 19.78 | |
| Spruce fir | 76.12 | 23.26 | |
| Quercus | 70.81 | 20.60 |
| Sampling Methods | Population Mean (t/ha) | Population Mean Variance (t/ha) | E (%) | P (%) |
|---|---|---|---|---|
| Traditional equidistant sampling | 69.76 | 567.869 | 4.84 | 95.16 |
| Spatial sampling based on variation scale | 69.20 | 542.424 | 6.88 | 93.12 |
| Stratified sampling based on local spatial variability | 68.68 | 208.645 | 6.11 | 93.89 |
| Stratified sampling based on dominant tree species | 69.28 | 148.492 | 2.54 | 97.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Xu, L.; Yu, J.; Zhou, W.; Yang, Z.; Wang, S.; Guo, C.; Gao, Y.; Xiao, J.; Shu, Q. Sampling Estimation and Optimization of Typical Forest Biomass Based on Sequential Gaussian Conditional Simulation. Forests 2023, 14, 1792. https://doi.org/10.3390/f14091792
Luo S, Xu L, Yu J, Zhou W, Yang Z, Wang S, Guo C, Gao Y, Xiao J, Shu Q. Sampling Estimation and Optimization of Typical Forest Biomass Based on Sequential Gaussian Conditional Simulation. Forests. 2023; 14(9):1792. https://doi.org/10.3390/f14091792
Chicago/Turabian StyleLuo, Shaolong, Li Xu, Jinge Yu, Wenwu Zhou, Zhengdao Yang, Shuwei Wang, Chaosheng Guo, Yingqun Gao, Jinnan Xiao, and Qingtai Shu. 2023. "Sampling Estimation and Optimization of Typical Forest Biomass Based on Sequential Gaussian Conditional Simulation" Forests 14, no. 9: 1792. https://doi.org/10.3390/f14091792
APA StyleLuo, S., Xu, L., Yu, J., Zhou, W., Yang, Z., Wang, S., Guo, C., Gao, Y., Xiao, J., & Shu, Q. (2023). Sampling Estimation and Optimization of Typical Forest Biomass Based on Sequential Gaussian Conditional Simulation. Forests, 14(9), 1792. https://doi.org/10.3390/f14091792







